第三章离散傅里叶变换(DFT)

第三章离散傅里叶变换（DFT ）

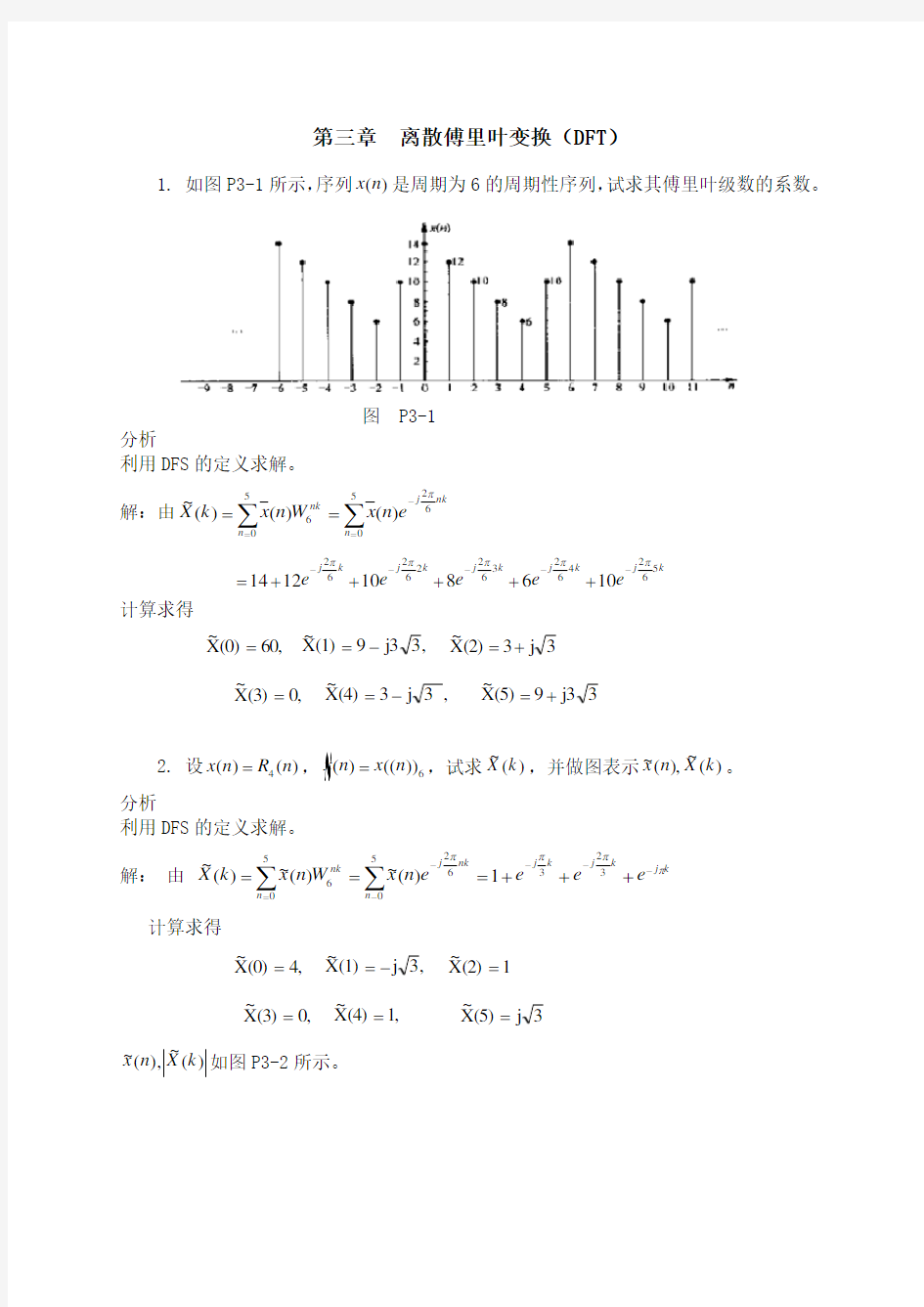
1. 如图P3-1所示，序列)(n x 是周期为6的周期性序列，试求其傅里叶级数的系数。

图 P3-1 分析

利用DFS 的定义求解。

解：由nk j n nk

n e n x W n x k X 6250650

)()()(~π

-==∑∑==

k j

246

236

226

21068101214πππππ-----+++++=

计算求得

,3j39(1)X ~ 60,(0)X ~-== 3j 3(2)X ~

+= , 3j 3(4)X ~ 0,(3)X ~-== 3j39(5)X ~

2. 设4()()x n R n =，6()(())x n x n =，试求)(~k X ，并做图表示)(~

),(~

k X n x 。分析

利用DFS 的定义求解。

解：由 k j k j k j nk j n nk n e e

e e n x W n x k X ππ

-----=+++===∑∑3

236250

650

1)(~)(~)(~

计算求得

,3j (1)X ~ 4,(0)X ~-== 1(2)X ~

,1(4)X ~ 0,(3)X ~== 3j (5)X ~

)(~),(~k X n x 如图P3-2所示。

图 P3-2

3. 已知)(n x 是N 点有限长序列，)]([)(n x DFT k X =。现将长度变成rN 点的有限长序列)(n y

???-≤≤-≤≤=1,01

0),()(rN n N N n n x n y

试求rN 点DFT[)(n y ]与)(k X 的关系。分析

利用DFT 定义求解，)(n y 是rN 点序列，因而结果相当于在频域序列进行插值。解：由)(k X = DFT[)(n x ]∑-=-=1

02)(N n nk N

j e

n x π

，10-≤≤N k

可得 nk

rN N n nk rN

N n W n x W

n y n y DFT k Y ∑∑-=-====10

)()()]([)(

)()(1

X e

n x N n l

n N j

==∑-=-π， 1,...,0,-==N l lr k

所以在一个周期内，)(k Y 的抽样点数是)(k X 的r 倍（)(k Y 的周期为Nr ），相当于在)(k X 的每两个值之间插入r-1个其他的数值（不一定为零），儿当k 为r 烦人整数l

倍时，)(k Y 与)(r

X 相等。

4. 已知)(n x 是N 点有限长序列，)]([)(n x DFT k X =，现将)(n x 的每两点之间补进

r-1个零值点，得到一个rN 点的有限长序列)(n y

???-===else N i ir n r n x n y ,01

,...,1,0,),()(

试求rN 点)]([n y DFT 与)(k X 的关系。分析

离散时域每两点间插入r-1个零值点，相当于频域以N 为周期延拓r 次，即)(k Y 周期为rN 。

解：由 )(k X = DFT[)(n x ]∑-==1

0)(N n nk

N W n x ， 10-≤≤N k

可得 k n N n nk rN

N n nk

N n W i x W

r ir x W

n y n y DFT k Y ∑∑∑-=-=-=====1

)()()()]([)(，10-≤≤rN k

而 )())(()(k R k X k Y rN N =

所以)(k Y 是将)(k X （周期为N ）延拓r 次形成的，即)(k Y 周期为rN 。

5. 频谱分析的模拟信号以8kHz 被抽样，计算了512个抽样的DFT ，试确定频谱抽样之间的频率间隔，并证明你的回答。分析

利用频域抽样间隔0F 和时域抽样频率s f ，以及抽样点数N 的关系0NF f s =。证明

由 π2s s f Ω=

， π

200Ω

=F 得

0ΩΩ=s s F f 其中s Ω是以角频率为变量的频谱周期，0Ω是频谱抽样之间的频谱间隔。

又

N F f s

s =ΩΩ=0

则 N

f F s

0 对于本题有 8=s f kHz ，512=N

所以 625.15512

8000

0==

F Hz 6. 设有一谱分析用的信号处理器，抽样点数必须为2的整数幂，假定没有采用任何特殊数据处理措施，要求频率分辨力≤10 Hz ，如果采用的抽样时间间隔为0.1ms ，试确定：(1)最小记录长度；(2)所允许处理的信号的最高频率；(3)在一个记录中的最少点数。分析

抽样间隔T 和抽样频率s f 满足T f s /1=,记录长度0T 和频域分辨力0F 的关系为

001F T =。抽样定理为h h s f f f (2>为信号最高频率分量),一个记录中最少抽样总数N

满足

002F f F f T T N h s >== 解：（1）因为00

T F =

，而010F Hz ≤，所以 01

T s ≥

即最小记录长度为0.1s 。

（2）因为311

10100.1

s f kHz T ==?=，而

2s h f f >

所以

h s f f kHz <

= 即允许处理的信号的最高频率为5 kHz 。

（3）300.1

1010000.1

T N T ≥=?=，又因N 必须为2的整数幂，所以一个记录中的最少点数

为1021024N ==。

7. 令)(k X 表示N 点序列)(n x 的N 点离散傅里叶变换，（1）证明如果)(n x 满足关系式)1()(n N x n x ---=，则0)0(=X 。（2）证明当N 为偶数时，如果)1()(n N x n x --=，则0)2(=N X 。分析

这两个是有限长序列，当)(n x 满足关系式)1()(n N x n x --=时称)(n x 为偶对称序列，偶对称中心为2/)1(-=N n ；当)1()(n N x n x ---=时称)(n x 为奇对称序列，奇对称中心为2/)1(-=N n 。在第七章中会讨论以它们作为单位抽样响应时滤波器特性的情况。证明

（1）因为 ∑-==1

0)()(N n nk

N W n x k X ，10-≤≤N k

当)1()(n N x n x ---=时

∑-=---=1

0])()1([)(N n nk

N W n R n N x k X ∑-=------=1

)

1()1(])())1(([N n N k N n N k N

N N W W n R n N x )

1(1

)(--=-∑-=N k N N n nk N W W n x

可以求得 )())(()()

1(k R W K X k X N N k N

N ---= 当0=k 时 )0()0()0(X X X -=--= 即 0)0(=X

(2) 依照（1），当)1()(n N x n x --=时，可得

∑-=--=1

0])())1(([)(N n nk

N N W n R n N x k X )())(()

1(k R W k X N N n N

N --= 当2

n =

（N 为偶数）时 )1(2

2)2

())2(()2(---=N N

j N N e

N R N X N X π

由N 为偶数，则有 1)1()1(2

2-==----N j N N

N j

e e

ππ 所以 )2

()2()2()2(N

X N N X N X N X -=--=--=

即 0)2

( N

傅里叶变换在信号与系统系统中的应用

河北联合大学本科毕业设计（论文）题目傅里叶变换在信号与系统中的应用院系理学院专业班级07数学一班学生姓名刘帅学生学号200710050113 指导教师佟玉霞 2011年5月24日

题目傅里叶变换在信号与系统中的应用专业数学与应用数学姓名刘帅学号200710050113 主要内容、基本要求、主要参考资料等主要内容傅里叶变换是一种重要的变换，且在与通信相关的信号与系统中有着广泛的应用。本文主要研究傅里叶变换的基本原理；其次，掌握其在滤波，调制、解调，抽样等方面中的应用。分析了信号在通信系统中的处理方法，通过傅里叶变换推导出信号调制解调的原理，由此引出对频分复用通信系统的组成原理的介绍。基本要求通过傅里叶变换实现一个高通滤波，低通滤波，带通滤波。用傅里叶变换推导出信号调制解调的原理。通过抽样实现连续信号离散化，简化计算。另外利用调制的原理推导出通信系统中的时分复用和频分复用。参考资料 [1]《信号与系统理论、方法和应用》徐守时著中国科技大学出版社 2006年3月修订二版 [2]《信号与系统》第二版上、下册郑君里、应启珩、杨为理著高等教育出版社 [3]《通信系统》第四版 Simon Haykin 著宋铁成、徐平平、徐智勇等译沈连丰审校电子工业出版社 [4]《信号与系统—连续与离散》第四版 Rodger E.Ziemer 等著肖志涛等译腾建辅审校电子工业出版社 [5]《现代通信原理》陶亚雄主编电子工业出版社 [6]《信号与系统》乐正友著清华大学出版社 [7]《信号与线性系统》阎鸿森、王新风、田惠生编西安交通大学出版社 [8]《信号与线性系统》张卫钢主编郑晶、徐琨、徐建民副主编西安电子科技大学出版社 [9] https://www.360docs.net/doc/1b1673626.html,/view/191871.htm//百度百科傅里叶变换 [10]《通信原理》第六版樊昌信曹丽娜编著国防工业出版社 [11]A．V．Oppenheim,A.S.Willsky with S.H.Nawab.Siganals and systems(Second edition).Prentice-Hall,1997.中译：刘树棠。信号与系统。西安交通工业大学出版社完成期限指导教师专业负责人

离散傅里叶变换应用举例

x=[1,1,1,1];w=[0:1:500]*2*pi/500; [H]=freqz(x,1,w); magH=abs(H);phaH=angle(H); subplot(2,1,1);plot(w/pi,magH);grid;xlabel('');ylabel('|X|'); title('DTFT的幅度') subplot(2,1,2);plot(w/pi,phaH/pi*180);grid; xlabel('以pi为单位的频率');label('度'); title('DTFT的相角')

N=4;w1=2*pi/N;k=0:N-1; X=fft(x,N); magX=abs(X);phaX=angle(X)*180/pi; subplot(2,1,1);plot(w*N/(2*pi),magH,'--');axis([-0.1,4.1,0,5]);hold on; stem(k,magX);ylabel('|X(k)|');title('DFT的幅度:N=4');text(4.3,-1,'k'); hold off; subplot(2,1,2);plot(w*N/(2*pi),phaH*180/pi,'--');axis([-0.1,4.1,-200,200]); hold on; stem(k,phaX);ylabel('度');title('DFT的相角:N=4');text(4.3,-200,'k')

n=(0:1:9);x=cos(0.48*pi*n)+cos(0.52*pi*n); w=[0:1:500]*2*pi/500; X=x*exp(-1i*n'*w); magx=abs(X); x1=fft(x);magx1=abs(x1(1:1:10)); k1=0:1:9;w1=2*pi/10*k1; subplot(3,1,1);stem(n,x);title('signalx(n),0<=n<=9'); axis([0,10,-2.5,2.5]);line([0,10],[0,0]); subplot(3,1,2);plot(w/pi,magx);title('DTFT幅度');xlabel('w');axis([0,1,0,10]); subplot(3,1,3);stem(w1/pi,magx1);title('DFT幅度'); xlabel('频率（单位：pi)');axis([0,1,0,10]) 实验总结：补零运算提供了一个较密的频谱和较好的图示形式，但因为在信号中只是附加了零，而没有增加任何新的信息，因此不能提供高分辨率的频谱。

傅里叶变换及应用

傅里叶变换在MATLZB里的应用摘要：在现代数学中，傅里叶变换是一种非常重要的变换，且在数字信号处理中有着广泛的应用。本文首先介绍了傅里叶变换的基本概念、性质及发展情况；其次，详细介绍了分离变数法及积分变换法在解数学物理方程中的应用。傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号，再利用傅立叶反变换将这些频域信号转换成时域信号。应用MATLAB实现信号的谱分析和对信号消噪。关键词：傅里叶变换；MA TLAB软件；信号消噪 Abstract: In modern mathematics,Fourier transform is a transform is very important ,And has been widely used in digital signal processing.This paper first introduces the basic concepts, properties and development situation of Fourier transform ;Secondly, introduces in detail the method of separation of variables and integral transform method in solving equations in Mathematical Physics.Fourier transformation makes the original time domain signal whose analysis is difficult easy, by transforming it into frequency domain signal that can be transformed into time domain signal by inverse transformation of Fourier. Using Mat lab realizes signal spectral analysis and signal denoising. Key word: Fourier transformation, software of mat lab ,signal denoising 1、傅里叶变换的提出及发展在自然科学和工程技术中为了把较复杂的运算转化为较简单的运算，人们常常采用所谓变换的方法来达到目的"例如在初等数学中，数量的乘积和商可以通过对数变换化为较简单的加法和减法运算。在工程数学里积分变换能够将分析运算（如微分，积分）转化为代数运算，正是积分变换这一特性，使得它在微分方程和其它方程的求解中成为重要方法之一。 1804年，法国科学家J-.B.-J.傅里叶由于当时工业上处理金属的需要，开始从事热流动的研究"他在题为<<热的解析理论>>一文中，发展了热流动方程，并且指出如何求解"在求解过程中，他提出了任意周期函数都可以用三角级数来表示的想法。他的这种

傅里叶变换的应用.

傅立叶变换在图像处理中有非常非常的作用。因为不仅傅立叶分析涉及图像处理的很多方面，傅立叶的改进算法，比如离散余弦变换，gabor与小波在图像处理中也有重要的分量。印象中，傅立叶变换在图像处理以下几个话题都有重要作用： 1.图像增强与图像去噪绝大部分噪音都是图像的高频分量，通过低通滤波器来滤除高频——噪声; 边缘也是图像的高频分量，可以通过添加高频分量来增强原始图像的边缘； 2.图像分割之边缘检测提取图像高频分量 3.图像特征提取：形状特征：傅里叶描述子纹理特征：直接通过傅里叶系数来计算纹理特征其他特征：将提取的特征值进行傅里叶变换来使特征具有平移、伸缩、旋转不变性 4.图像压缩可以直接通过傅里叶系数来压缩数据；常用的离散余弦变换是傅立叶变换的实变换；傅立叶变换傅里叶变换是将时域信号分解为不同频率的正弦信号或余弦函数叠加之和。连续情况下要求原始信号在一个周期内满足绝对可积条件。离散情况下，傅里叶变换一定存在。冈萨雷斯版<图像处理>里面的解释非常形象：一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器，每个成分的颜色由波长（或频率）来决定。傅里叶变换可以看作是数学上的棱镜，将函数基于频率分解为不同的成分。当我们考虑光时,讨论它的光谱或频率谱。同样,傅立叶变换使我们能通过频率成分来分析一个函数。傅立叶变换有很多优良的性质。比如线性，对称性（可以用在计算信号的傅里叶变换里面）; 时移性：函数在时域中的时移，对应于其在频率域中附加产生的相移，而幅度频谱则保持不变；频移性：函数在时域中乘以e^jwt，可以使整个频谱搬移w。这个也叫调制定理，通讯里面信号的频分复用需要用到这个特性（将不同的信号调制到不同的频段上同时传输）；卷积定理：时域卷积等于频域乘积；时域乘积等于频域卷积（附加一个系数）。（图像处理里面这个是个重点）信号在频率域的表现在频域中，频率越大说明原始信号变化速度越快；频率越小说明原始信号越平缓。当频率为0时，表示直流信号，没有变化。因此，频率的大小反应了信号的变化

傅里叶变换及其在图像处理中的应用

傅里叶变换及其在数字图像处理中的应用王家硕学号：1252015 一、 Fourier 变换 1. 一维连续傅里叶变换设 f (x)为x 的实变函数，如果f (x)满足下面的狄里赫莱条件：（1）具有有限个间隔点。（2）具有有限个极点。（3）绝对可积。则 f (x )的傅里叶变换（Fourier Transformation ，FT ）定义为: Fourier 正变换：dt e t f t f f F t j ? +∞ ∞ --==ωω)()]([)(； Fourier 逆变换：ωωπ ωd e f t F f t f t j ? ∞ +∞ ---= =)(21)]([)(1 ，式中：1-= j ，ω 为频域变量。 f (x )与F (w )构成傅里叶变换对，可以证明傅里叶变换对总是存在的。由于f (x )为实函数，则它的傅里叶变换F (w )通常是复函数，于是F (w )可写成 F (w ) = R (w ) + j I (w ) (1) 式中：R (w )和I (w )分别是F (w )的实部和虚部。公式1可表示为指数形式：式中： F (w ) 为f (x )的傅里叶幅度谱，f (w )为f (x )的相位谱。 2. 二维连续傅里叶变换如果二维函数f (x , y )是连续可积的，即∞

MATLAB离散傅里叶变换及应用资料

MATLAB 离散傅里叶变换及应用一、DFT 与IDFT 、DFS 、DTFT 的联系 1、序列的傅里叶变换(DFT)和逆变换(IDFT) 在实际中常常使用有限长序列。如果有限长序列信号为x(n)，则该序列的离散傅里叶变换对可以表示为 1N ,0,1,k , W x(n)DFT [x(n)]X(k)1 N 0n nk N -===∑-= (12-1) 1N ,0,1,n , W X(k)N 1IDFT[X(k)]x(n)1N 0 k nk N -===∑-=- (12-2) 已知x(n)＝［0，1，2，3，4，5，6，7］，求x(n)的DFT 和IDFT 。要求： (1)画出序列傅里叶变换对应的|X(k)|和arg ［X(k)］图形。 (2)画出原信号与傅里叶逆变换IDFT ［X(k)］图形进行比较。程序源代码： xn=[0,1,2,3,4,5,6,7]; N=length(xn); n=0:(N-1);k=0:(N-1); Xk=xn*exp(-j*2*pi/N).^(n'*k); x=(Xk*exp(j*2*pi/N).^(n'*k))/N; subplot(2,2,1),stem(n,xn); title('x(n)');

subplot(2,2,2),stem(n,abs(x)); title('IDFT|X(k)|'); subplot(2,2,3),stem(k,abs(Xk)); title('|X(k)|'); subplot(2,2,4),stem(k,angle(Xk)); title('arg|X(k)|'); 运行图如下： x(n) IDFT|X (k)| 2 4 6 8 |X (k)| 2 4 6 8 arg|X (k)| 从得到的结果可见，与周期序列不同的是，有限长序列本身是仅有N 点的离散序列，相当于周期序列的主值部分。因此，其频谱也对应序列的主值部分，是含N 点的离散序列。 2、序列DFT 与周期序列DFS 已知周期序列的主值x(n)＝［0，1，2，3，4，5，6，7］，

MATLAB的离散傅里叶变换的仿真

应用MATLAB对信号进行频谱分析及滤波设计目的要求学生会用MATLAB语言进行编程，绘出所求波形，并且运用FFT求对连续信号进行分析。一、设计要求 1、用Matlab产生正弦波，矩形波，并显示各自的时域波形图； 2、进行FFT变换，显示各自频谱图，其中采样率、频率、数据长度自选，要求注明； 3、绘制三种信号的均方根图谱； 4、用IFFT回复信号，并显示恢复的正弦信号时域波形图。二、系统原理用FFT对信号作频谱分析是学习数字信号处理的重要内容。经常需要进行频谱分析的信号是模拟信号和时域离散信号。频谱分辨率直接和FFT的变换区间N有关，因为FFT能够实现频率分辨率是2π/N。 x(n)是一个长度为M的有限长序列，则x(n)的N点离散傅立叶变换为： N?1?2?kn)(nx j?W W NN e?0?n N X(k)=DFT[x(n)]=,k=0,1,...,N-1N?11?kn?)(WXk N N0?n x(n) =IDFT[X(k)]= 逆变换：,k=0,1,...,N-1 但FFT是一种比DFT更加快速的一种算法，提高了DFT的运算速率,为数字信号处理技术应用于各种信号处理创造了条件，大大提高了数字信号处理技术的发展。本实验就是采用FFT，IFFT对信号进行谱分析。三、程序设计 fs=input('please input the fs:');%设定采样频率 N=input('please input the N:');%设定数据长度 t=0:0.001:1; f=100;%设定正弦信号频率 %生成正弦信号 x=sin(2*pi*f*t); figure(1); subplot(211); plot(t,x);%作正弦信号的时域波形 axis([0,0.1,-1,1]); title('正弦信号时域波形'); z=square(50*t); subplot(212) plot(t,z) axis([0,1,-2,2]); title('方波信号时域波形');grid;

离散傅里叶变换应用与计算

离散傅里叶变换应用与计算 1 离散傅里叶变换基本原理与计算 1822年，法国工程师傅里叶(Fourier)指出，任意一个函数X(t)均可分解为无穷多个不同频率正弦信号的和，这即是谐波分析的基本概念。在数字计算机时代，模拟信号所携带的信息均被处理为基于0和1的二值离散数据。模拟信号通过A／D变换为离散的数字信号。连续函数X(t)因此被抽样为离散的有限长序列X(nT s) (n=0，1，2，…，N-1,T s为采样周期)。离散傅里叶变换(DFT)将离散的时域信号X(nT s)与离散的频率点结合，使谱分析得以在数字计算机上实现。根据DFT理论，X(t)的N个抽样点的频谱为：其中：，n=0，1，2，…，N-1；k=0，1，2，…，N-1。通常，为应用DFT的快速算法(快速傅里叶变换，FFT)，N取值为2的整数次幂。式(1)的处理结果为复数，在绘制信号频谱时需进行相应的取模运算；另外，为使频谱图直观，通常还会采用半对数图。 2 离散傅里叶级数（DFS）的应用离散傅里叶变换是信号系统中频谱分析最常用的方法，基于离散傅里叶变换插值的方法测量信号频率，在采样率较低的情况下仍然有较好的精度，在提高采样率或增加采样点数的情况下，频率分辨精度能进一步提高，采用滤波和加窗的方法能更好地避免插值方向错误，该方法具有计算简单、速度快、精度高等特点[1]。在电力系统发展中，一般的感应式电能表准确度只能达到2.0级或1.0级，而且功能单一，已经不能适应现代电能管理的要求。在现阶段的电量测量仪表中，越来越多的采用交流采样技术。交流采样技术是将被测电流、电压直接送入数据采集装置，在装置中使用精密电流、电压互感器将其变成小电流(或低电压)，通过A／D转换和CPU计算得到电流、电压的有效值、有功功率、无功功率、有功电度和无功电度等参数。其中傅立叶变换法可以计算出各次谐波的参数值，总的电参数由各次谐波分量求出，具有很强的滤波功能[2]。近年来，多速率滤波器组广泛应用于子带编码、语音信号处理、图像压缩和通信系统等

离散傅里叶变换及其应用

实验三离散傅立叶变换及其应用一、实验目的： 1.进一步加深DFT 算法的原理和基本性质的理解； 2.学习用FFT 对信号进行谱分析的方法，并分析其误差及其原因； 3.学习利用DFT 计算程序计算IDFT 的方法。二、实验原理： 1．N 点序列的DFT 和IDFT 变换定义式如下： km N N k W k x m X ∑-==1 0][][， km N N m W m X N k x - -=∑=10][1][ 利用旋转因子km N W 具有周期性，可以得到快速算法（FFT ）。在MATLAB 中，可以用函数 X=fft(x) %计算N 点的DFT ，N 为序列x[k]的长度，即N=length （x ）； X=fft （x ，N ）%计算序列x[k]的N 点DFT ； x=ifft （X ） %计算N 点的IDFT ，N 为序列x[m]的长度； x=ifft （X ，N ）%计算序列x[m]的N 点IDFT ； 2． impz 函数是求解离散系统单位脉冲响应，并绘制其时域波形，其调用格式为： impz(b,a) 3.MATLAB 计算循环卷积函数的调用格式：y=circonv(x,h) 4．求有限长序列的DTFT ，并画出它的幅度谱，相位谱，实部和虚部。三、实验内容 1.假设现含有3种频率成分，Hz f 201=，Hz f 5.202=，Hz f 403=， )2sin()2sin()2sin()(321t f t f t f t x πππ++=，取采样频率Hz f s 100=对)(t x 进行等间隔采样得)(k x ，对)(k x 加长度为128的矩形窗进行截断得有限长序列)(1k x ，对)(1k x 做128点的DFT ，画出原信号此时的频谱图，然后对)(1k x 做512 的DFT ，画出原信号此时的频谱图，分析两副图的特点，总结实验中的主要结论。 2.若)(k x 加矩形窗的长度为512，并作512点的DFT ，画出原信号的此时的

实验三离散傅里叶变换

————————————————————————————————作者：————————————————————————————————日期：

实验三离散傅里叶变换一实验目的 1、理解和加深DFS 和DFT 的概念及其性质； 2、学习利用离散傅里叶变换分析信号的频谱。二实验设备 1、计算机 2、MA TLAB R2007a 仿真软件三实验原理离散傅里叶变换在时域和频域都离散有限的特点，使其成为信号分析与处理中的一个最根本的也是最常用的变换。然而，但序列的长度N 很大时，直接计算DFT 需要很大的计算量。快速傅里叶变换使DFT 的运算效率提高数个数量级，为数字信号处理技术应用与各种信号的实时处理创造了良好的条件。MA TLAB 提供了用于快速计算DFT 的fft 函数，其调用格式为：y=fft(x) 或 y=fft(x,N);fft 函数用来计算序列)(n x 的N 点DFT ，如果序列的长度小于N ，则函数在序列的尾部补零至N 点；而当序列的长度大于N 时，函数对序列进行截短。为了提高运行速度，通常将N 取为2的整数次幂。四实验内容 1、上机实验前，认真阅读实验原理，掌握DFS 和DFT 的基本概念； 2、掌握离散傅里叶变换分析信号频谱的MATLAB 实现方法。实例1：求周期序列)()(~ 5 ~ n R n x ，周期分别为N=20 和N=60时的)(~ k X 。将下列指令编辑到“exlfft.m ”文件中： clc; close all; clear all; L=5;N1=20;N2=60; xn1=[ones(1,L),zeros(1,N1-L)]; xn2=[ones(1,L),zeros(1,N2-L)]; n1=0:N1-1; n2=0:N2-1; Xk1=fft(xn1,N1); Xk2=fft(xn2,N2); magXk1=abs(Xk1); magXk2=abs(Xk2);

离散傅里叶变换

第三章离散傅里叶变换离散傅里叶变换不仅具有明确的物理意义，相对于DTFT他更便于用计算机处理。但是，直至上个世纪六十年代，由于数字计算机的处理速度较低以及离散傅里叶变换的计算量较大，离散傅里叶变换长期得不到真正的应用，快速离散傅里叶变换算法的提出，才得以显现出离散傅里叶变换的强大功能，并被广泛地应用于各种数字信号处理系统中。近年来，计算机的处理速率有了惊人的发展，同时在数字信号处理领域出现了许多新的方法，但在许多应用中始终无法替代离散傅里叶变换及其快速算法。 § 3-1 引言一.DFT是重要的变换 1.分析有限长序列的有用工具。 2.在信号处理的理论上有重要意义。 3.在运算方法上起核心作用，谱分析、卷积、相关都可以通DFT在计算机上实现。二.DFT是现代信号处理桥梁 DFT要解决两个问题：一是离散与量化，二是快速运算。信号处理 § 3-2 傅氏变换的几种可能形式一.连续时间、连续频率的傅氏变换-傅氏变换

对称性：时域连续，则频域非周期。反之亦然。二.连续时间、离散频率傅里叶变换-傅氏级数 t 时域信号频域信号连续的非周期的非周期的连续的 ? ∞ ∞ -Ω-= Ωdt e t x j X t j )()(:

*时域周期为Tp, 频域谱线间隔为2π/Tp 三.离散时间、连续频率的傅氏变换 --序列的傅氏变换时域信号频域信号连续的周期的非周期的离散的 p T 0= Ω

四.离散时间、离散频率的傅氏变换--DFT t 0 T 2T 1 2 N n NT 时域信号频域信号离散的非周期的周期的连续的 -T T 2T t ∑ ∞ -∞ =Ω-Ω= n T jn T j e nT x e X )()(:正