第9章 非线性问题的有限单元法

第9章非线性问题的有限单元法
9.1 非线性问题概述
前面章节讨论的都是线性问题,但在很多实际问题中,线弹性力学中的基本方程已不能满足,需要用非线性有限单元法。非线性问题的基本特征是变化的结构刚度,它可以分为三大类:材料非线性、几何非线性、状态非线性。
1. 材料非线性(塑性, 超弹性, 蠕变)
材料非线性指的是材料的物理定律是非线性的。它又可分为非线性弹性问题和非线性弹塑性问题两大类。例如在结构的形状有不连续变化(如缺口、裂纹等)的部位存在应力集中,当外载荷到达一定数值时该部位首先进入塑性,这时在该部位线弹性的应力应变关系不再适用,虽然结构的其他大部分区域仍保持弹性。
2. 几何非线性(大应变, 大挠度, 应力刚化)
几何非线性是有结构变形的大位移引起的。例如钓鱼杆,在轻微的垂向载荷作用下,会产生很大的变形。随着垂向载荷的增加,杆不断的弯曲,以至于动力臂明显减少,结构刚度增加。
3. 状态非线性(接触, 单元死活)
状态非线性是一种与状态相关的非线性行为。例如,只承受张力的电缆的松弛与张紧;轴承与轴承套的接触与脱开;冻土的冻结与融化。这些系统的刚度随着它们状态的变化而发生显著变化。
9.2 非线性有限元问题的求解方法
对于线性方程组,由于刚度方程是常数矩阵,可以直接求解,但对于非线性方程组,由于刚度方程是某个未知量的函数则不能直接求解。以下将简要介绍借助于重复求解线性方程组以得到非线性方程组解答的一些常用方法。
1.迭代法
迭代法与直接法不同,它不是求方程组的直接解,而是用某一近似值代人,逐步迭代,使近似值逐渐逼近,当达到允许的规定误差时,就取这些近似值为方程组的解。
与直接法相比,迭代法的计算程序较简单,但迭代法耗用的机时较直接法长。它不必存贮带宽以内的零元素,因此存贮量大大减少,且计算中舍入误差的积累也较小。以平面问题
为例,迭代法的存贮量一般只需直接法的14左右。在求解非线性方程组时,一般采用迭代
法。
2. 牛顿—拉斐逊方法
ANSYS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应。然而,非线性结构的行为不能直接用这样一系列的线性方程表示。需要一系列的带校正的线性近似来求解非线性问题。
一种近似的非线性救求解是将载荷分成一系列的载荷增量,即逐步递增载荷和平衡迭代。它可以在几个载荷步内或者在一个载荷步的几个子步内施加载荷增量。在每一个增量的
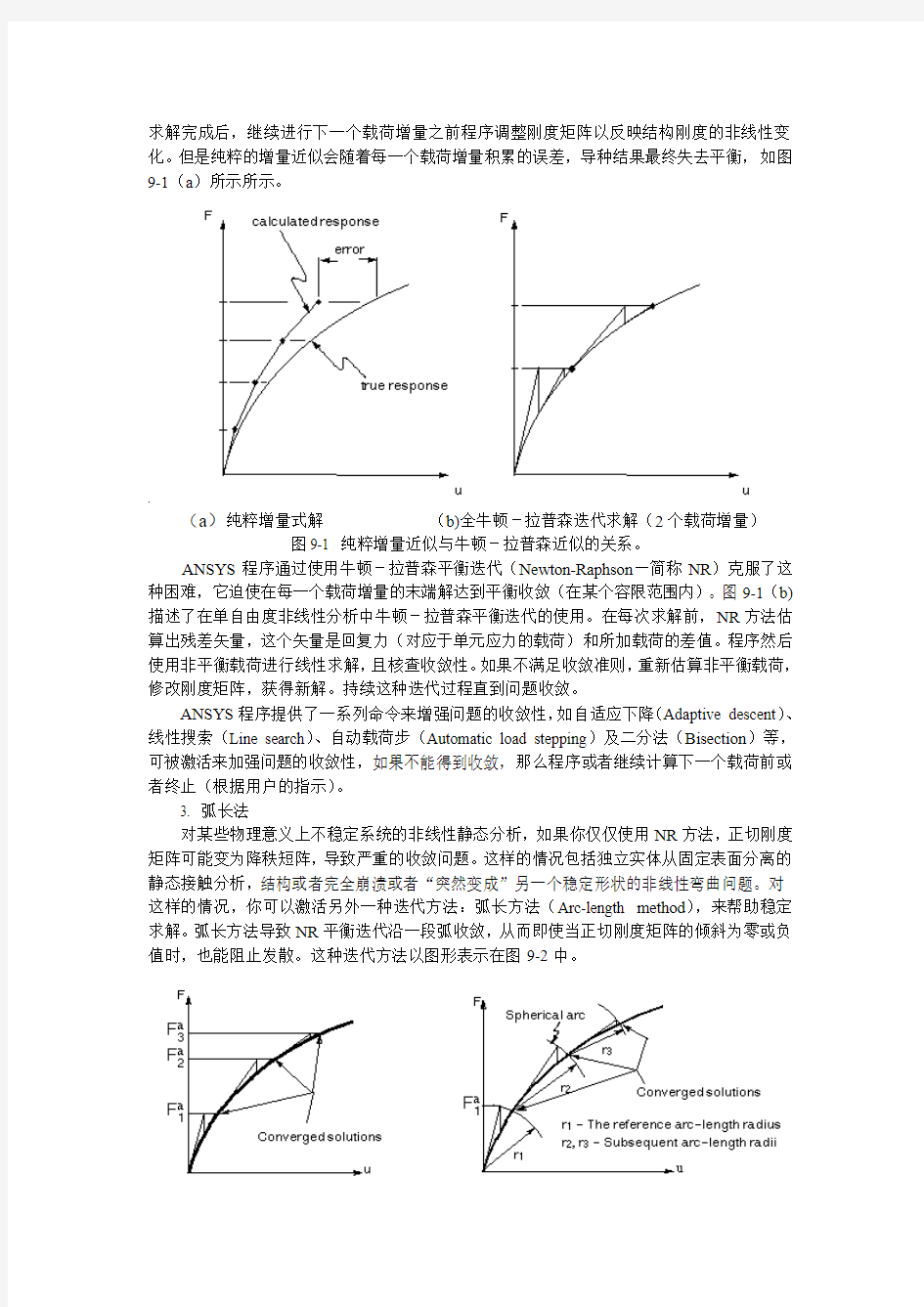
求解完成后,继续进行下一个载荷增量之前程序调整刚度矩阵以反映结构刚度的非线性变化。但是纯粹的增量近似会随着每一个载荷增量积累的误差,导种结果最终失去平衡,如图9-1(a)所示所示。
.
(a)纯粹增量式解(b)全牛顿-拉普森迭代求解(2个载荷增量)
图9-1 纯粹增量近似与牛顿-拉普森近似的关系。
ANSYS程序通过使用牛顿-拉普森平衡迭代(Newton-Raphson—简称NR)克服了这种困难,它迫使在每一个载荷增量的末端解达到平衡收敛(在某个容限范围内)。图9-1(b)描述了在单自由度非线性分析中牛顿-拉普森平衡迭代的使用。在每次求解前,NR方法估算出残差矢量,这个矢量是回复力(对应于单元应力的载荷)和所加载荷的差值。程序然后使用非平衡载荷进行线性求解,且核查收敛性。如果不满足收敛准则,重新估算非平衡载荷,修改刚度矩阵,获得新解。持续这种迭代过程直到问题收敛。
ANSYS程序提供了一系列命令来增强问题的收敛性,如自适应下降(Adaptive descent)、线性搜索(Line search)、自动载荷步(Automatic load stepping)及二分法(Bisection)等,可被激活来加强问题的收敛性,如果不能得到收敛,那么程序或者继续计算下一个载荷前或者终止(根据用户的指示)。
3. 弧长法
对某些物理意义上不稳定系统的非线性静态分析,如果你仅仅使用NR方法,正切刚度矩阵可能变为降秩短阵,导致严重的收敛问题。这样的情况包括独立实体从固定表面分离的静态接触分析,结构或者完全崩溃或者“突然变成”另一个稳定形状的非线性弯曲问题。对这样的情况,你可以激活另外一种迭代方法:弧长方法(Arc-length method),来帮助稳定求解。弧长方法导致NR平衡迭代沿一段弧收敛,从而即使当正切刚度矩阵的倾斜为零或负值时,也能阻止发散。这种迭代方法以图形表示在图9-2中。
图9-2 传统的NR方法与弧长法的比较
4. 非线性求解的组织级别
非线性求解被分成三个操作级别:载荷步(Load steps)、子步(Substeps or time steps)、平衡迭代(Equilibrium iterations)。
“顶层”级别由在一定“时间”范围内明确定义的载荷步组成,并假定载荷在载荷步内是线性地变化的。
在每一个载荷步内,为了逐步加载可以控制程序来执行多次求解(子步或时间步)。
在每一个子步内,程序将进行一系列的平衡迭代以获得收敛的解。
图9-3说明了一段用于非线性分析的典型的载荷历史。
图9-3 载荷步、子步、及“时间”
5. 收敛容限
当确定收敛准则时,ANSYS程序会列出一系列的选择:将收敛检查建立在力、力矩、位移、转动或这些项目的任意组合上。另外,每一个项目可以有不同的收敛容限值。对多自由度问题,同样也有收敛准则的选择问题。
以力为基础的收敛提供了收敛的绝对量度,而以位移为基础的收敛仅提供了表观收敛的相对量度。因此,如果需要总是使用以力为基础(或以力矩为基础的)收敛容限。如果需要可以增加以位移为基础的(或以转动为基础的)收敛检查,但是通常不单独使用它们。
图9-4说明了一种单独使用位移收敛检查导致出错情况。在第二次迭代后计算出的位移很小可能被认为是收敛的解,尽管问题仍旧远离真正的解。要防止这样的错误,应当使用力收敛检查。
图9-4 完全依赖位移收敛检查
6. 保守行为与非保守行为:过程依赖性
如果通过外载输入系统的总能量当载荷移去时复原,那么这个系统是保守的。如果能量被系统消耗(如由于塑性应变或滑动摩擦),则是非保守的。如图9-5所示的非守恒系统。
图9-5 非守恒(过程相关的)过程
一个保守系统的分析是与过程无关的:通常可以任何顺序和以任何数目的增量加载而不影响最终结果。相反地,一个非保守系统的分析是过程相关的;必须紧紧跟随系统的实际加载历史,以获得精确的结果。如果对于给定的载荷范围,可以有多于一个的解是有效的(如在突然转变分析中)这样的分析也可能是过程相关的。过程相关问题通常要求缓慢加载(也就是,使用许多子步)到最终的载荷值。
7. 子步
较多的子步能得到较好的精度,但它是以增加运行时间为代价的,ANSYS提供了两种
方法来控制子步数。
?子步数或时间步长,即用户可以指定实际的子步数,也可以通过指定时间步长来控制子步数。
?自动时间步长。ANSYS软件会根据结构的特性和系统的响应,自动检查时间步长。
8. 子步数
如果结构在它的整个加载历史过程中显示出高度的非线性特点,而且用户也对结构的行为非常了解,以至于可以保证能得到收敛的解,这样用户就可以自己来确定时间步长的大小,并且对所有的载荷步都可以使用同一时间步。
9. 自动时间步
如果结构的行为将从线性变化到非线性,或者用户想要在系统响应的非线性部分变化时间步长,这时可以激活自动时间步长,以便系统根据需要自动调节步长,可以获得精度和代价之间的良好平衡。但是,如果用户不能保证分析问题能否成功收敛,这时可以使用自动时间分步来激活ANSYS软件的二分法。
二分法提供了一种对收敛失败自动矫正的方法,无论何时只要平衡迭代收敛失败,二分法将把时间步长分成两半,然后从最后收敛的子步自动重启动,如果已二分的时间步长再次收敛失败,二分法将再次分割时间步长然后再重启动,如此循环下去,直到获得收敛或者到达用户指定的最小时间步长。
10. 载荷和位移方向
当结构经历大变形时应该考虑到载荷将发生了什么变化。在许多情况中,无论结构如何变形施加在系统中的载荷保持恒定的方向。而在另一些情况中,力将改变方向,随着单元方向的改变而变化。
ANSYS程序对这两种情况都可以建模,依赖于所施加的载荷类型。加速度和集中力将不管单元方向的改变而保持它们最初的方向,表面载荷作用在变形单元表面的法向,且可被用来模拟“跟随”力。图9-6说明了恒力和跟随力。
注意:在大变形分析中不修正节点坐标系方向。因此计算出的位移在最初的方向上输出。
图9-6 变形前后载荷方向
9.3 材料非线性问题的有限单元法
许多与材料有关的参数可以使结构刚度在分析期间改变。塑性、非线性弹性、超弹性材
料、混凝土材料的非线性应力—应变关系。可以使结构刚度在不同载荷水平下(以及在不同温度下)改变。蠕变、粘塑性和粘弹性可以引起与时间、温度和应力相关的非线性。膨胀可以引起作为温度、时间、中子流水平(或其他类似量)函数的应变。
ANSYS程序应可以考虑多种材料非线性特性:
1.率不相关塑性指材料中产生的不可恢复的即时应变。
2.率相关塑性也可称之为粘塑性,材料的塑性应变大小将是加载速度与时间的函数。
3.材料的蠕变行为也是率相关的。产生随时间变化的不可恢复的应变,但蠕变的时间
尺度要比率相关塑性大的多。
4.非线性弹性允许材料的非线性应力—应变关系,但应变是可以恢复的。
5.超弹性材料应力—应变关系由一个应变能密度势函数定义,用于模拟橡胶,泡菜类
材料,变形是可以恢复的。
6.粘弹性是一种率相关的材+料特性,这种材料应变中包含了弹性应变和粘性应变。
7.混凝土材料具有模拟断裂和压碎的能力。
8.膨胀是指材料在中子流作用下的体积扩大效应。
9.3.1 塑性分析
1. 塑性理论简介
许多常用的工程材料,在应力水平低于比例极限时,应力—应变关系为线性的。超过这一极限后,应力—应变关系变为非线性,但却不一定是非弹性的。以不可恢复的应变为特征的塑性,则在应力超过屈服点开始出现。由于屈服极限与比例极限相差很小,ANSYS程序在塑性分析中,假设这两点相同,如图9-7所示
塑性是一种非保守的(不可逆的),与路径无关的现象。换句话说,载荷施加的顺序,以及什么时候发生塑性响应,影响最终求解结果。如果用户预计在分析中会出现塑性响应,则应把载荷处理成一系列的小增量载荷步或时间步,以使模型尽可能符合载荷响应路径。最大塑性应变是在输出(Jobname.OUT)文件的子步信息中打印的。
在一个子步中,如果执行了大量的平衡迭代,或得到大于15%的塑性应变增量,则塑性将激活自动时间步选项[AUTOTS]{GUI:Main menu | Solution | Sol’n Control:Basic Tab或Main Menu | Solution | Unabridged Menu | Time/Frequenc | Time and Substps }。如果取了太大的时间步,则程序将二分时间步,并重新求解。
其他类型的非线性行为可以与塑性同时产生。实际上,大位移和大应变几何非线性经常
伴随有塑性响应,如果用户预计在结构中存在大变形,则必须在分析中用NLGEOM 命令激
活这些效应{GUI :Main Menu | Solution | Sol ’n Control :Basic Tab or Main Menu | Solution |
Unbridged Menu | Anslysis }。对于大应变分析,材料应力—应变特征必须按真实应力和对数
应变输入。
在这一节中,将依次介绍塑性理论的三个主要方面:
? 屈服准则
? 流动准则
? 强化准则
(1) 屈服准则
对单向受拉试件,可以通过简单的比较轴向应力与材料的屈服应力来决定是否有塑性变
形发生,然而,对于一般的应力状态,是否到达屈服点并不是明显的。
屈服准则是一个可以用与单轴测试的屈服应力相比较的应力状态的标量表示。因此,知
道了应力状态和屈服准则,程序就能确定是否有塑性应变产生。
屈服准则的值有时候也叫作等效应力,一个通用的屈服准则是Von Mises 屈服准则,当
等效应力超过材料的屈服应力时,将会发生塑性变形。
在多轴应力状态下,屈服准则可以用下式来表示:
{}()c y f σσσ==
式中,c σ为等效应力,y σ为屈服应力。
当等效应力超过材料的屈服应力时,将会发生塑性变形。
可以在主应力空间中画出Mises 屈服准则,如图9-8所示。
图9-8
在3-D 中,屈服面是一个以123σσσ==为轴的圆柱面,在2-D 中,屈服面是一个椭
圆,在屈服面内部的任何应力状态,都是弹性的,屈服面外部的任何应力状态都会引起屈服。
注意:静水压应力状态(123σσσ==)不会导致屈服:屈服与静水压应力无关,而只
与偏差应力有关,因此,1180σ=,230σσ==的应力状态比123180σσσ==的应力状
态接近屈服。Mises 屈服准则是一种除了土壤和脆性材料外典型使用的屈服准则,在土壤和
脆性材料中,屈服应力是与静水压应力(侧限压力)有关的,侧限压力越高,发生屈服所需
要的剪应力越大。
(2)流动准则
流动准则描述了发生屈服时,塑性应变的方向,也就是说,流动准则定义了单个塑性应
变分量(x πε,y π
ε等)随着屈服是怎样发展的。流动方程则是由以下方程给出:
{}Q d πελσ???=?????
式中,λ是塑性乘子(决定了塑性应变量);Q 为塑性势,是应力的函数(决定了塑性应变方向)。
一般来说,流动方程是塑性应变在垂直于屈服面的方向发展的屈服准则中推导出来的,即Q 等于屈服函数。这种流动准则叫作相关流动准则,如果不用其它的流动准则(从其它不同的函数推导出来)。则叫作不相关的流动准则。
(2) 强化准则
强化准则描述了初始屈服准则随着塑性应变的增加是怎样发展的。
一般来说,屈服面的变化是以前应变历史的函数,在ANSYS 程序中,使用了两种强化准则。
等向强化
等向强化是指屈服面以材料中所作塑性功的大小为基础在尺寸上扩张。对M ises 屈服准则来说,屈服面在所有方向均匀扩张。如图9-9所示。
图9-9 等向强化时的屈服面变化图
由于等向强化,在受压方向的屈服应力等于受拉过程中所达到的最高应力。
?随动强化
随动强化假定屈服面的大小保持不变而仅在屈服的方向上移动,当某个方向的屈服应力升高时,其相反方向的屈服应力应该降低。如图9-10所示。
图9-10 随动强化时的屈服面变化图
在随动强化中,由于拉伸方向屈服应力的增加导致压缩方向屈服应力的降低,所以在对应的两个屈服应力之间总存一个2y σ的差值,初始各向同性的材料在屈服后将不再是向同性的。
9.3.2 塑性选项
ANSYS 程序提供了多种塑性材料选项,在此主要介绍四种典型的材料选项可以通过激活一个数据表来选择这些选项。
? 经典双线性随动强化 BKIN
? 双线性等向强化 BISO
? 多线性随动强化 MKIN
? 多线性等向强化 MISO
(1) 经典的双线性随动强化(BKIN )
经典双线性随动强化使用一个双线性来表示应力应变曲线,所以有两个斜率,弹性斜率和塑性斜率,由于随动强化的Von Mises 屈服准则被使用,所以包含有鲍辛格效应,此选项适用于遵守Von Mises 屈服准则,初始为各向同性材料的小应变问题,这包括大多数的金属。需要输入的常数是屈服应力y σ和切向斜率t E ,可以定义高达六条不同温度下的曲线。 注意:
1) 使用MP 命令来定义弹性模量;
2) 弹性模量也可以是与温度相关的;
3) 切向斜率t E 不可以是负数,也不能大于弹性模量。
在使用经典的双线性随动强化时,可以分下面三步来定义材料特性。
1)定义弹性模量;
2)激活双线性随动强化选项;
3)使用数据表来定义非线性特性。
(2)双线性等向强化(BIS0)
双线性等效强化也是使用双线性来表示应力-应变曲线,在此选项中,等向强化的Von Mises 屈服准则被使用,这个选项一般用于初始各向同性材料的大应变问题。需要输入的常数与BKIN选项相同。
(3)多线性随动强化(MKIN)
使用多线性来表示应力-应变曲线,模拟随动强化效应,这个选项使用Von Mises 屈服准则,对使用双线性选项(BKIN)不能足够表示应力-应变曲线的小应变分析是有用的。
需要的输入包括最多五个应力-应变数据点(用数据表输入),可以定义五条不同温度下的曲线。
在使用多线性随动强化时,可以使用与BKIN相同的步骤来定义材料特性,所不同的是在数据表中输入的常数不同,下面是一个用命令流定义多线性随动强化的标准输入。
MPTEMP,,10,70
MPDATA,EX,3,,30ES,25ES
TB,MK2N,3
TBTEMP,,STRA2N
TBDA TA,,0.01,0.05,0.1
TBTEMP,10
TBDA TA,,30000,37000,38000
TBTEMP,70
TBDA TA,,225000,31000,33000
(4)多线性等向强化(MISO)
使用多线性来表示使用Von Mises屈服准则的等向强化的应力-应变曲线,它适用于比例加载的情况和大应变分析。
需要输入最多100个应力-应变曲线,最多可以定义20条不同温度下的曲线。
其材料特性的定义步骤如下:
1)定义弹性模量;
2)定义MISO数据表;
3)为输入的应力-应变数据指定温度值;
4)输入应力-应变数据;
5)画材料的应力-应变曲线。
与MKIN 数据表不同的是,MISO的数据表对不同的温度可以有不同的应变值,因此,每条温度曲线有它自己的输入表。
9.4 几何非线性问题的有限单元法
前面所讨论的问题中,都是基于小变形的假设,即假定物体所发生的位移远小于物体自身的几何尺度,应变远小于1。在此前提下,建立物体或微元体的平衡条件时可以不考虑物体的位置和形状的变化,因此分析中不必区分变形前和变形后的位置和形状。同时在加载和变形过程中的应变可用一阶无穷小的线性应变进行度量。
实际上,我们会遇到很多不符合小变形假设的问题,例如板、壳等薄壁结构在一定载荷作用下,尽管应变很小、甚至未超过弹性极限,但是位移较大,材料线元素有较大的转动。这时必须考虑变形对平衡的影响,即平衡条件应建立在变形后的位置和形状上,同时应变表达式也应包括位移的二次项。这样一来,平衡方程和几何方程都将是非线性的。这种由于大位移和大转动引起的非线性问题称为几何非线性问题。
几何非线性问题和材料非线性问题一样在结构分析中具有重要意义。例如在平板的大挠度理论中,由于考虑中面内薄膜力的影响,可能使得按小挠度理论分析得到的挠度有很大程度的缩减。再如在薄壳的过屈曲问题中,载荷到达一定的数值以后,挠度和线性理论的预测值比较,将快速的增加。
实际上还有另一类几何非线性问题,例如金属的成型、橡皮型材料受载荷作用,都可能出现很大的应变,这时除了采用非线性的平衡方程和几何关系外,还需要引入相应的应力应变关系,尽管对后一问题材料通常还处于弹性状态。当然很多大应变问题是和材料的非弹性性质联系在一起的。
随着位移增长,一个有限单元已移动的坐标可以以多种方式改变结构的刚度。一般来说这类问题总是是非线性的,需要进行迭代获得一个有效的解。
9.4.1 大应变效应
一个结构的总刚度依赖于它的组成部件(单元)的方向和单刚。当一个单元的节点经历位移后,那个单元对总体结构刚度的贡献可以以两种方式改变。首先,如果这个单元的形状改变,它的单元刚度将改变。(如图9-11(a)所示)。其次,如果这个单元的取向改变,它的局部刚度转化到全局部件的变换也将改变。(如图9-11(b)所示)。小的变形和小的应变分析假定位移小到足够使所得到的刚度改变无足轻重。这种刚度不变假定意味着使用基于最初几何形状的结构刚度的一次迭代足以计算出小变形分析中的位移。(什么时候使用“小”变形和应变依赖于特定分析中要求的精度等级。)
相反,大应变分析说明由单元的形状和取向改变导致的刚度改变。因为刚度受位移影响,且反之亦然,所以在大应变分析中需要迭代求解来得到正确的位移。通过发出NLGEOM,ON(GUI:Main Menu | Solution | Sol’n Controls | Basic-Analysis Option),来激活大应变效应。这效应改变单元的形状和取向,且还随单元转动表面载荷。(集中载荷和惯性载荷保持它们最初的方向。)在大多数实体单元(包括所有的大应变和超弹性单元),以及部分的壳单元中大应变特性是可用的。在ANSYS/Linear Plus程序中大应变效应是不可用的。
图9-11 大应变和大转动
大应变处理对一个单元经历的总旋度或应变没有理论限制。(某些ANSYS单元类型将
受到总应变的实际限制─参看下面。)然而,应限制应变增量以保持精度。 因此,总载荷应当被分成几个较小的步,这可以〔NSUBST ,DELTIM ,AUTOTS 〕,通过GUI 路径(Main Menu | Solution | Sol ’n Controls | Basic-Analysis Option | Time Control )。无论何时当系统是非保守系统,来自动实现如在模型中有塑性或摩擦,或者有多个大位移解存在,如具有突然转换现象,使用小的载荷增量具有双重重要性。
9.4.2 关于大应变的特殊建模讨论
1.应力─应变
在大应变求解中,所有应力─应变输入和结果将依据真实应力和真实(或对数)应变。一维时,真实应变将表示为0()ln l ε=。 对于响应的小应变区,真实应变和工程应变基本上是一致的。)要从小工程应变转换成对数应变,使用(1)In eng ln εε=+。要从工程应力转换成真实应力,使用(1)true eng eng σσε=+。(这种应力转化仅对不可压缩塑性应力─应变数据是有效的。)
为了得到可接受的结果,对真实应变超过50%的塑性分析,应使用大应变单元(VISCO106,107及108)。
2. 单元的形状
应该认识到在大应变分析的任何迭代中低劣的单元形状(也就是大的纵横比,过度的顶角以及具有负面积的已扭曲单元)将是有害的。因此,你必须和注意单元的原始形状一样注意单元已扭曲的形状。(除了探测出具有负面积的单元外,ANSYS 程序对于求解中遇到的低劣单元形状不发出任何警告,必须进行人工检查)如果已扭曲的网格是不能接受的,可以人工改变开始网格(在容限内)以产生合理的最终结果(如图9-12所示)。
图9-12 在大应变分析中避免低劣单元形状的发展具有小应变的大偏移
3.小应变大转动
某些单元支持大的转动,但不支持大的形状改变。一种称作大挠度的大应变特性的受限形式对这类单元是适用的。在一个大挠度分析中,单元的转动可以任意地大,但是应变假定是小的。大挠度效应(没有大的形状改变)在ANSYS/Linear Plus 程序中是可用的。(在ANSYS/Mechanical,以及ANSYS/Structural 产品中,对于支持大应变特性的单元,大挠度效应不能独立于大应变效应被激活。)在所有梁单元和大多数壳单元中,以及许多非线性单元
中这个特性是可用的。通过打开NLGEOM,ON (GUI:Main Menu | Solution | Analysis Options)来激活那些支持这一特性的单元中的大位移效应。
4. 应力刚化
结构的面外刚度可能严重地受那个结构中面内应力的状态的影响。面内应力和横向刚度之间的联系,通称为应力刚化,在薄的、高应力的结构中,如缆索或薄膜中,是最明显的。一个鼓面,当它绷紧时会产生垂向刚度,这是应力强化结构的一个普通的例子。尽管应力刚化理论假定单元的转动和应变是小的,在某些结构的系统中(如图9-13(a)所示),刚化应力仅可以通过进行大挠度分析得到。在其它的系统中(如图9-13(b)所示),刚化应力可采用小挠度或线性理论得到。
图9-13 应力硬化梁
要在第二类系统中使用应力硬化,必须在第一个载荷步中发出SSTIF,ON(GUI路径Main Menu | Solution | Analysis Options)。ANSYS程序通过生成和使用一个称作“应力刚化矩阵”的辅助刚度矩阵来考虑应力刚化效应。尽管应力刚度矩阵是使用线性理论得到的,但由于应力(应力刚度矩阵)在每次迭代之间是变化的这个事实因而它是非线性的。
大应变和大挠度处理包括进初始应力效应作为它们的理论的一个子集,对于许多实体和壳单元,当大变型效应被激活时〔NLGEOM,ON〕(GUI:Main Menu | Solution | Analysis Options)自动包括进初始硬化效应。
在大变形分析中〔NLGEOM,ON〕包含应力刚化效应〔SSTIF,ON〕将把应力刚度矩阵加到主刚度矩阵上以在具有大应变或大挠度性能的大多数单元中产生一个“近似的”协调切向刚度矩阵。例外情况包括BEAM4和SHELL63,以及不把“应力刚化”列为特殊特点的任何单元。对于BEAM4和SHELL63,你可以通过设置KEYOPT(2)=1和NLGEOM,ON在初始求解前激活应力刚化。当大变形效应为ON(开)时这个KEYOPT设置激活一个协调切向刚度矩阵选项。当协调切向刚度矩阵被激活时(即,当KEYOPT(2)=1且NLGEOM,ON时)SSTIF对BEAM4和SHELL63将不起作用。
4.在大变形分析中何时应当使用应力刚化
?对于大多数实体单元,应力刚化的效应是与问题相关的;在大变形分析中的应用可能提高也可能降低收敛性。在大多数情况下,首先应该尝试一个应力刚化效应OFF(关闭)的分析。如果你正在模拟一个受到弯曲或拉伸载荷的薄的结构,当用应力刚化OFF(关)时遇到收敛困难,则尝试打开应力刚化。
?应力刚化不建议用于包含“不连续单元”(由于状态改变,刚度上经历突然的不连续变化的非线性单元,如各种接触单元,SOLID65,等等)的结构。对于这样的问题,当应力刚化为ON(开)时,结构刚度上的不连续线性很容易导致求解“胀破”。
?对于桁、梁和壳单元,在大挠度分析中通常应使用应力刚化。实际上,在应用这些单元进行非线性屈曲和后屈曲分析时,只有当打开应力刚化时才得到精确的解。(对于
BEAM4和SHELL63,你通过设置单元KEYOPT(2)=1激活大挠度分析中〔NLGEOM,ON〕的应力刚化。)然而,当应用杆、梁或者壳单元来模拟刚性连杆,耦合端或者结构刚度的大变化时,不应使用应力刚化。
注意:无论何时使用应力刚化,务必定义一系列实际的单元实常数。使用不是“成比例”(也就是,人为的放大或缩小)的实常数将影响对单元内部应力的计算,且将相应地降低那个单元的应力刚化效应。结果将降低解的精度。
5. 旋转软化
旋转软化为动态质量效应调整(软化)旋转物体的刚度矩阵。在小位移分析中这种调整近似于由于大的环形运动而导致几何形状改变的效应。通常它和预应力[PSTRES](GUI:Main Menu | Solution | Analysis Options)一起使用,这种预应力由旋转物体中的离心力所产生。它不应和其它变形非线性、大挠度和大应变一起使用。旋转软化用OMEGA命令中的KPSIN来激活(GUI:Main Menu | Preprocessor | Loads | -Loads-Apply | Structural-Other | Angular Velotity )。
9.5 接触非线性问题的有限单元法
日常生活中常见的一些普通结构表现出一种与状态相关的非线性行为。例如,只承受张力的电缆的松弛与张紧;轴承与轴承套的接触与脱开;冻土的冻结与融化。这些系统的刚度随着它们状态的变化而发生显著变化。
接触是一种很普遍的非线性行为。它是状态变化非线性类型中一个特殊而重要的子集。接触问题是一种高度非线性行为,需要较大的计算资源,为了进行实为有效的计算,理解问题的特性和建立合理的模型是很重要的。
接触分析中有两个较大的难点:
1. 求解问题之前,接触区域及表面是否接触是未知的,它们随载荷、材料、边界条件和其它因素而定;
2. 大多的接触问题需要计算摩擦,有几种摩擦和模型供你挑选,它们都是非线性的,摩擦使问题的收敛性变得困难。
9.5.1 接触问题简介
接触问题分为两种基本类型:刚体─柔体的接触,柔体─柔体的接触。在刚体─柔体的接触问题中,接触面的一个或多个被当作刚体(与它接触的变形体相比,有大得多的刚度),一般情况下,一种软材料和一种硬材料接触时,问题可以被假定为刚体─柔体的接触,许多金属成形问题归为此类接触,另一类,柔体─柔体的接触,是一种更普遍的类型,在这种情况下,两个接触体都是变形体(有近似的刚度)。
ANSYS支持三种接触方式:点─点,点─面,面─面,每种接触方式使用的接触单元适用于某类问题。
为了给接触问题建模,首先必须认识到模型中的哪些部分可能会相互接触,如果相互作用的其中之一是一点,模型的对立组元是一个节点。如果相互作用的其中之一是一个面,模型的对应组元是单元,例如梁单元,壳单元或实体单元,有限元模型通过指定的接触单元来识别可能的接触匹对。
接触单元是覆盖在分析模型接触面之上的一层单元。
9.5.2 点—点接触分析
点─点接触单元主要用于模拟点─点的接触行为,为了使用点─点的接触单元,需要预先知道接触位置,这类接触问题只适用于接触面之间有较小相对滑动的情况(即使在几何非线性情况下)
如果两个面上的节点一一对应,相对滑动又可以忽略不计,两个面挠度(转动)保持小量,那么就可以用点─点的接触单元来求解面─面的接触问题,过盈装配问题是一个用点─点的接触单元来模拟面─面接触问题的典型例子。
9.5.3 点—面接触分析
点─面接触单元主要用于给点─面的接触行为建模,例如两根梁的相互接触。
如果通过一组节点来定义接触面,生成多个单元,那么可以通过把表面指定为一组节点,从而用点─面的接触单元来模拟面─面的接触问题,面即可以是刚性体也可以是柔性体,这类接触问题的一个典型例子是插头到插座里。
使用这类接触单元,不需要预先知道确切的接触位置,接触面之间也不需要保持一致的网格,并且允许有大的变形和大的相对滑动。
Contact48和Contact49都是点─面的接触单元,Contact26用来模拟柔性点─刚性面的接触,对有不连续的刚性面的问题,不推荐采用Contact26因为可能导致接触的丢失,在这种情况下,Contact48通过使用伪单元算法能提供较好的建模能力。
点—面接触单元应注意如下几点:
1. 生成的接触单元数应不超过所需要的2~3倍,使用“限制半径”(RADC)或“生成的单元数”(NUMC)选项来限制生成的接触单元数;
2. 进行接触分析时,在接触面上建议使用无中节点的单元;
3. 对梁或壳单元需要通过“目标面”(TLAB)选项来指定单元哪边是目标面;
4. 对于卷曲的(非平面)目标面,使用CONTA49的“基本形状”(shape)选项来指定单元的基本形状是三角形。
5. 每次在新的接触对之间生成接触单元时,都指定一个新的实常数号,即使接触单元的实常数值没有改变,生成对称或反对称接触单元。
对称接触方式:把两个面都定义成目标面或接触面。
9.5.4 面—面接触分析
面—面接触单元用来建立刚-柔或柔-柔面间接触模型,其中涉及到“目标面”和“接触面”。对刚-柔接触,目标面总是刚性面,接触面总是变形面;对柔-柔接触,目标面和接触面都与变形体有关。这两个面组成“接触对”。用TARGE169和CONTA171或CONTA172定义二维接触对。用TARGE170和CONTA173或CONTA174定义三维接触对。每个接触对用相同的实常量号。
对于接触面的选择可参照下面的几点:
如凸面预期与一个平面或凹面接触,则平面/凹面应当被指定为目标面。
如一个面有较密的网格,而相比之下,另一个面网格较粗,则较密网格的面应当是接触面,而较粗网格的面则为目标面。
如一个面比另一个面刚,则较柔的面应当指定为接触面,而较刚的面则为目标面。
如果高阶单元位于一个外表面,而低价单元位于另一个面,则前者应指定为接触面,后者则为目标面
如果一个面明显比另一个面大(如一个面包围其他面)则较大的面应当指定为目标面。
与点─面接触单元相比,面─面接触单元有好几项优点:
1. 支持低阶和高阶单元;
2. 支持有大滑动和摩擦的大变形,协调刚度阵计算,单元提法不对称刚度阵的选项;
3. 提供工程目的采用的更好的接触结果,例如法向压力和摩擦应力;
4. 没有刚体表面形状的限制,刚体表面的光滑性不是必须允许有自然的或网格离散引起的表面不连续;
5. 与点─面接触单元比,需要较多的接触单元,因而造成需要较小的磁盘空间和CPU 时间;
6. 允许多种建模控制。例如:绑定接触、渐变初始渗透、目标面自动移动到补始接触、平移接触面(老虎梁和单元的厚度)、支持死活单元。
使用这些单元,能模拟直线(面)和曲线(面),通常用简单的几何形状例如圆、抛物线、球、圆锥、圆柱采模拟曲面,更复杂的刚体形状能使用特殊的前处理技巧来建模。
执行一个典型的面─面接触分析的基本步骤列示如下:
1. 建立模型,并划分网格;
2. 识别接触对;
3. 标识接触面和目标面;
4. 定义目标面;
5. 定义接触面;
6. 设置单元KEYOPTS实常量;
7. 定义/控制目标面的运动;
8. 应用必须的边界条件;
9. 定义求解选项和载荷步;
10. 求解接触问题;
11. 查看结果。
有限单元法基本思想,原理,数值计算过程
有限单元法学习报告 在对力学问题分析求解过程中,方法可以概括为两种方法,一种为解析法,对具体问题具体分析,通过一定的推导用具体的表达式获得解答,由于实际工程中结构物的复杂性,此方法在处理工程问题是十分困难的;另一种是数值法,有限元法是其中一种方法,其数学逻辑严谨,物理概念清晰,又采用矩阵形式表达基本公式,便于计算机编程,因此在工程问题中获得广泛的应用。 有限元法基本原理是,将复杂的连续体划分为简单的单元体;将无限自由度问题化为有限自由度问题,因为单元体个数是有限的;将偏微分方程求解问题化为有限个代数方程组的求解问题。通常以位移为基本未知量,通过虚功原理和最小势能原理来求解。 基本思想是先化整为零,即离散化整体结构,把整体结构看作是由若干个通过结点相连的单元体组成的整体;再积零为整,通过结点的平衡来建立代数方程组,最后计算出结果。我将采用最简单的三结点三角形为基本单元体,解决弹性力学中的平面问题为例,解释有限单元法的基本原理、演示数值计算过程和一般性应用结论。 一、离散化 解决平面问题时,主要单元类型包括三角形单元(三结点、六结点)和四边形单元(四结点矩形、四结点四边形、八结点四边形)等。选用不同的单元会有不同的精度,划分的单元数越多,精度越高,但计算量也会越大。因此在边界曲折,应力集中处单元的尺寸要小些,但最大与最小单元的尺寸倍数不宜过大。在集中力作用点及分布力突变的点宜选为结点,不同厚度,不同材料不能划分在同一单元中。三角形单元以内角接近60°为最好。充分利用对称性与反对称性。 二、单元分析 将一个单元上的所有未知量用结点位移表示,并将分布在单元上的外力等效到结点上。 1、位移函数选取: 根据有限元法的基本思路,将连续体离散为有限的单元集合后,此时单元体满足连续性、均匀性、各向同性、完全线弹性假设。单元与单元之间通过结点连接并传递力,位移法(应用最广)以结点位移δi=(u i v i)T为基本未知量,以离散位移场代替连续位移场。单元体内的位移变化可以用位移函数(位移模式)来表示,因为有限元分析所得结果是近似结果,为了保证计算精度和收敛性,x位移函数应尽可能反应物体中的真实位移,即满足完备性和连续性的要求:
空间问题的四面体单元
第三章 轴对称、三维和高次单元 § 3-2空间问题的四面体单元 空间问题的有限单元法,和平面问题及轴对称问题的有限单元法的原理和分析过程完 全相同。由于空间问题应采用三维坐标系,因此单元的自由度、刚度矩阵的元素个数,方 程组内方程个数等要较平面问题和轴对称问题多,所以空间问题的规模一般比轴对称问题 和平面问题大得多。它要求计算机的内存大,且计算时间长,费用高。这些问题都给三维 有限单元法的具体运用带来许多困难。 和平面问题一样,空间有限单元法采用单元 也是多种多样的,其中最简单的是四节点四面体 单元。采用四面体单元和线性位移模式来处理空 间问题,可以看作平面问题中三角形单元的推广。 在采用四面体单元离散化后的空间结构物 中,一系列不相互重叠的四面体之间仅在节点处 以空间铰相互连接。四节点四面体单元仅在四个 顶点处取为节点,其编号为i,j,m,p 。每个单元的 计算简图如图3-7所示。 在位移法中,取节点位移为基本未知量,四 节点四面体单元共有十二个自由度 (位移分量), 其节点位移列阵为 U i V i W i (i,j,m) 相应的节点力列阵为 U i V i w i U j V j w j U m T W m U p V p W p 其子矩阵 图3-7空间四面体单元
F i F j F m F p
其子矩阵 F i U i V i w 一、单元法位移函数 结构中各点的位移是坐标 X 、 y 、z 的函数。 当单元足够小时, 单元内各点的位移可用 简单的线性多项式来近似描述, 即 u 1 2 X 3y 4Z v 5 6 X 7 y 8 Z (3-49) w 0 10X ny 12Z 曰 2,…, 12是 卜二个待定系数,它们可由单元的节点位移和坐标确定。假定节 点 i,j,m,p 的坐标分别为(x i y i Z i )、 、(x j y j z j ) 、(X m 将它们代入 (3-49)式的第一式可得各个节点在 X 方向的位移 U i 1 2X i 3Y i 4 Z u j 1 2X j 3Y j 4Z j U m 1 2 X m 3Y m 4 Z m U p 1 2 X p 3 Y p 4 Z p 解上述线性方程组,可得到 1 , 2 , 3 , 4 , 再代入 U 6V [(a i bX cy d i Z)U i (a j b j x (a m b m X C m y d m z)U m (a p b p X C (3-50) y d p Z )U p ] 1 X i Y i Z i 1 X j y j Z j 1 X m y m Z m 1 X P Y P Z P (3-52) (3-50)式,得 y m Z m )、(X p y p Z p ), 5y 3)5 (3-51) 式中1 , 其中V 为四面体ijmp 的体积,a,b i ,…,c p ,d P 为系数。
弹性力学及有限元基础复习权威版(最新)
《弹性力学及有限元基础》复习思考题 ★1.对弹性体所做的基本假设? 答:连续性假设;均匀性假设;各向同性假设;弹性假设;小变形假设; ★2.用D'Alember 原理由平衡方程推导运动微分方程? 答:微元体的平衡微分方程的表达式为: 31 112111 2332 122221 23 132333 31 23000f x x x f x x x f x x x σσσσσσσσσ????+++=?????????+++=? ????????+++=? ???? 根据D'Alember 原理,将运动物体看成是静止的,将惯性力22()u t ρ?-?当作体力加到微元体上,由上式 可以直接写出弹性动力学问题的运动微分方程: 23111211 12123232 12222221 2321323333321 23()()() u f x x x t u f x x x t u f x x x t σσσρσσσρσσσρ?????+++=????????????+++=? ???????????+++=?????? ☆3.什么是应力张量? 我们说一点的应力状态是什么涵义? 答:应力张量是一点应力状态的完整描述,它有面元方向和分解方向两个方向性,共有九个分量,由于存在对称性,其独立分量只有六个。应力张量是与坐标选择无关的不变量,但其分量与坐标有关,当已知某坐标系中的九个分量时,其他坐标系中的分量均可由应力转换公式确定。 一点的应力状态是一个具有双重方向性的物理量,其中第一个是面元的方向,用其法矢量ν表示,第二个是作用在该面元上的应力矢量方向,一般用其三个分量来表示。 4.在引出 Cauchy 应力公式时, 我们假设四面体处于平衡状态, 如不处在平衡状态则如何? 答:如果不处在平衡状态,Cauchy 应力公式仍然满足,关系式的成立与是否平衡无关。 5.在什么情况下剪应力互等定律不成立? 答:无论在变形体的内部或者表面上,若存在体力偶时,剪应力互等定律不成立。 6.任意斜截面上的正应变和剪应变的意义是什么? 答:应变张量的三个对角分量x ε、y ε、z ε称为正应变,分别等于坐标轴方向三个线元的单位伸长率,伸长为正,缩短为负。应变张量的三个非对角分量xy ε、yz ε、zx ε称为剪应变,分别等于变形前沿该分量下标所示两坐标方向的、相互正交的线元在变形后的夹角减小量之半。 7.刚性位移,刚性转动,刚体位移,刚体转动有何区别? 答:(1)刚性位移:物体内任意两点间无相对位移;(2)刚性转动:应变张量为0,转动张量不为0;(3)刚体位移:运动分为变形运动和刚体运动,每点都发生相同的位移就叫作刚体位移;(4)刚体转动:用刚性
有限元分析理论基础
有限元分析概念 有限元法:把求解区域看作由许多小的在节点处相互连接的单元(子域)所构成,其模型给出基本方程的分片(子域)近似解,由于单元(子域)可以被分割成各种形状和大小不同的尺寸,所以它能很好地适应复杂的几何形状、复杂的材料特性和复杂的边界条件 有限元模型:它是真实系统理想化的数学抽象。由一些简单形状的单元组成,单元之间通过节点连接,并承受一定载荷。 有限元分析:是利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟。并利用简单而又相互作用的元素,即单元,就可以用有限数量的未知量去逼近无限未知量的真实系统。 线弹性有限元是以理想弹性体为研究对象的,所考虑的变形建立在小变形假设的基础上。在这类问题中,材料的应力与应变呈线性关系,满足广义胡克定律;应力与应变也是线性关系,线弹性问题可归结为求解线性方程问题,所以只需要较少的计算时间。如果采用高效的代数方程组求解方法,也有助于降低有限元分析的时间。 线弹性有限元一般包括线弹性静力学分析与线弹性动力学分析两方面。 非线性问题与线弹性问题的区别: 1)非线性问题的方程是非线性的,一般需要迭代求解; 2)非线性问题不能采用叠加原理; 3)非线性问题不总有一致解,有时甚至没有解。 有限元求解非线性问题可分为以下三类:
1)材料非线性问题 材料的应力和应变是非线性的,但应力与应变却很微小,此时应变与位移呈线性关系,这类问题属于材料的非线性问题。由于从理论上还不能提供能普遍接受的本构关系,所以,一般材料的应力与应变之间的非线性关系要基于试验数据,有时非线性材料特性可用数学模型进行模拟,尽管这些模型总有他们的局限性。在工程实际中较为重要的材料非线性问题有:非线性弹性(包括分段线弹性)、弹塑性、粘塑性及蠕变等。 2)几何非线性问题 几何非线性问题是由于位移之间存在非线性关系引起的。 当物体的位移较大时,应变与位移的关系是非线性关系。研究这类问题一般都是假定材料的应力和应变呈线性关系。它包括大位移大应变及大位移小应变问题。如结构的弹性屈曲问题属于大位移小应变问题,橡胶部件形成过程为大应变问题。 3)非线性边界问题 在加工、密封、撞击等问题中,接触和摩擦的作用不可忽视,接触边界属于高度非线性边界。 平时遇到的一些接触问题,如齿轮传动、冲压成型、轧制成型、橡胶减振器、紧配合装配等,当一个结构与另一个结构或外部边界相接触时通常要考虑非线性边界条件。 实际的非线性可能同时出现上述两种或三种非线性问题。
有限单元法第十章
复习题 10.8如何利用一个单元模型对K 非奇异性和s K 奇异性进行估计?为什么说仅是 估计?两种情况下,一个单元的模型有何区别?为什么? 解:由于不可能事先规定单元数和自由度数,常采用如下公式: K 非奇异性b b s s e n d n d N +≥——○1 s K 奇异性s s n d j <或1s s j r n d =>——○2 e N 一个单元仅给予刚体运动约束后的自由度数。 j 在已形成部分网格的基础上再增加一个单元所增加的自由度数。 r 奇异性指标,r 越大表示s K 的奇异性越高。 ○1式不是K 非奇异性的必要条件,也不是充分条件;○2不是s K 奇异性的充分条件,因为具有不同网格和边界约束情况的实际系统的自由度数N 既可能小于, 也肯能大于○ 2式中的自由度数j 推算出的M j ?。 两种情况? 10.9什么是用于Mindlin 板单元的假设剪切应变方法?如何选择它的取样点和插值函数? 如同Timoshenko 梁情况,为避免剪切锁死,可以从分析造成锁死的根源出发,另行假设剪切应变场以代替原泛函中按应变和位移的几何关系得到的剪切应变场。
C型拉格朗日单元的方法构造,8,12 节点Serendipity单元可按Serendipity单元的方法构造。即分别按两个方向一维拉格朗日插值函数相乘的方法和变结点的方法构造。 练习题 10.5 同上题分析的四边固支的方板受均布载荷q 作用。板边长L,厚度t。由于对称取1/4进行分析,网格分别取2×2,4×4,6×6;L/t 分别取100,300,500;对4 节点,8 节点,9 节点的Mindlin 板单元是否发生剪切锁死情况进行检验并对结果进行分析。 解: 10.6 问题同题10.5,只是板的四边改为简支。 解:
《弹性力学及有限单元法》学习指南
第一章绪 论 学习指导 在学习本章时,要求学生理解和掌握下面的主要内容: 1、弹性力学的研究内容,及其研究对象和研究方法,认清他们与材料力学的区别; 2、弹性力学的几个主要物理量的定义、量纲、正负方向及符号规定等,及其与材料力学相比的不同之处; 3、弹性力学的几个基本假定,及其在建立弹性力学基本方程时的应用。 §1-1弹性力学的内容 弹性体力学,简称弹性力学,弹性理论(Theory of Elasticity或Elasticity),研究弹性体由于受外力、边界约束或温度改变等原因而发生的应力、形变和位移。这里指出了弹性力学的研究对象是弹性体;研究的目标是变形等效应,即应力、形变和位移;而引起变形等效应的原因主要是外力作用,边界约束作用(固定约束,弹性约束,边界上的强迫位移等)以及弹性体内温度改变的作用。 首先,我们来比较几门力学的研究对象。理论力学一般不考虑物体内部的形变,把物体当成刚性体来分析其静止或运动状态。材料力学主要研究杆件,如柱体、梁和轴,在拉压、剪切、弯曲和扭转等作用下的应力、形变和位移。结构力学研究杆系结构,如桁架、刚架或两者混合
的构架等。而弹性力学研究各种形状的弹性体,除杆件外,还研究平面体、空间体,板和壳等。因此,弹性力学的研究对象要广泛得多。 其次,从研究方法来看,弹性力学和材料力学既有相似之外,又有一定区别。弹性力学研究问题,在弹性体区域内必须严格考虑静力学、几何学和物理学三方面条件,在边界上严格考虑受力条件或约束条件,由此建立微分方程和边界条件进行求解,得出较精确的解答。而材料力学虽然也考虑这几方面的条件,但不是十分严格的。例如,材料力学常引用近似的计算假设(如平面截面假设)来简化问题,使问题的求解大为简化;並在许多方面进行了近似的处理,如在梁中忽略了бy的作用,且平衡条件和边界条件也不是严格地滿足的。一般地说,由于材料力学建立的是近似理论,因此得出的是近似的解答。但是,对于细长的杆件结构而言,材料力学解答的精度是足够的,附合工程上的要求(例如误差在5%以下)。对于非杆件结构,用材料力学方法得出的解答,往往具有较大的误差。这就是为什么材料力学只研究和适用于杆件问题的原因。 弹性力学是固体力学的一个分支,实际上它也是各门固体力学的基础。因为弹性力学在区域内和边界上所考虑的一些条件,也是其他固体力学必须考虑的基本条件。弹性力学的许多基本解答,也常供其他固体力学应用或参考。 弹性力学在土木、水利、机械、航空等工程学科中占有重要的地位。这是因为,许多工程结构是非杆件形状的,须要用弹性力学方法进行分
有限单元法
有限单元法 有限元方法的基础是变分原理和加权余量法,其基本求解思想是把计算域划分为有限个互不重叠的单元,在每个单元内,选择一些合适的节点作为求解函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解。采用不同的权函数和插值函数形式,便构成不同的有限元方法。有限元方法最早应用于结构力学,后来随着计算机的发展慢慢用于流体力学的数值模拟。在有限元方法中,把计算域离散剖分为有限个互不重叠且相互连接的单元,在每个单元内选择基函数,用单元基函数的线形组合来逼近单元中的真解,整个计算域上总体的基函数可以看为由每个单元基函数组成的,则整个计算域内的解可以看作是由所有单元上的近似解构成。在河道数值模拟中,常见的有限元计算方法是由变分法和加权余量法发展而来的里兹法和伽辽金法、最小二乘法等。根据所采用的权函数和插值函数的不同,有限元方法也分为多种计算格式。从权函数的选择来说,有配置法、矩量法、最小二乘法和伽辽金法,从计算单元网格的形状来划分,有三角形网格、四边形网格和多边形网格,从插值函数的精度来划分,又分为线性插值函数和高次插值函数等。不同的组合同样构成不同的有限元计算格式。对于权函数,伽辽金(Galerkin)法是将权函数取为逼近函数中的基函数;最小二乘法是令权函数等于余量本身,而内积的极小值则为对代求系数的平方误差最小;在配置法中,先在计算域内选取N个配置点。令近似解在选定的N个配置点上严格满足微分方程,即在配置点上令方程余量为0。插值函数一般由不同次幂的多项式组成,但也有采用三角函数或指数函数组成的乘积表示,但最常用的多项式插值函数。有限元插值函数分为两大类,一类只要求插值多项式本身在插值点取已知值,称为拉格朗日(Lagrange)多项式插值;另一种不仅要求插值多项式本身,还要求它的导数值在插值点取已知值,称为哈密特(Hermite)多项式插值。单元坐标有笛卡尔直角坐标系和无因次自然坐标,有对称和不对称等。常采用的无因次坐标是一种局部坐标系,它的定义取决于单元的几何形状,一维看作长度比,二维看作面积比,三维看作体积比。在二维有限元中,三角形单元应用的最早,近来四边形等参元的应用也越来越广。对于二维三角形和四边形电源单元,常采用的插值函数为有Lagrange插值直角坐标系中的线性插值函数及二阶或更高阶插值函数、面积坐标系中的线性插值函数、二阶或更高阶插值函数等。 对于有限元方法,其基本思路和解题步骤可归纳为 (1)建立积分方程,根据变分原理或方程余量与权函数正交化原理,建立与微分方程初边值问题等价的积分表达式,这是有限元法的出发点。 (2)区域单元剖分,根据求解区域的形状及实际问题的物理特点,将区域剖分为若干相互连接、不重叠的单元。区域单元划分是采用有限元方法的前期准备工作,这部分工作量比较大,除了给计算单元和节点进行编号和确定相互之间的关系之外,还要表示节点的位置坐标,同时还需要列出自然边界和本质边界的节点序号和相应的边界值。 (3)确定单元基函数,根据单元中节点数目及对近似解精度的要求,选择满足一定插值条件的插值函数作为单元基函数。有限元方法中的基函数是在单元中选取的,由于各单元具有规则的几何形状,在选取基函数时可遵循一定的法则。 (4)单元分析:将各个单元中的求解函数用单元基函数的线性组合表达式进行逼近;再将近似函数代入积分方程,并对单元区域进行积分,可获得含有待定系数(即单元中各节点的参数值)的代数方程组,称为单元有限元方程。 (5)总体合成:在得出单元有限元方程之后,将区域中所有单元有限元方程按一定法则进行累加,形成总体有限元方程。
有限单元法
《有限元法》复习题 一. 单选题 1.平面刚架单元坐标转换矩阵的阶数为( ) A .2?2 B .2?4 C .4?4 D .6?6 2.图示的四根杆组成的平面刚架结构,用杆单元进行有限元分析,单元和节点的划分如图示,则总体刚度矩阵的大小为( ) A.8?8阶矩阵 B.10?10阶矩阵 C.12?12阶矩阵 D.16?16阶矩阵 3.坐标转换矩阵可归类为( ) A.正交矩阵 B.奇异矩阵 C.正定矩阵 D.对称矩阵 4.图示弹簧系统的总体刚度矩阵为( ) A 111123 2224443400 0000k k k k k k k k k k k k k k -????-++-???? -+??-+?? B. 111122224443400 0000k k k k k k k k k k k k k -????-+-???? -+-??-+?? C. 111123 2322443 4 3400 00 k k k k k k k k k k k k k k k k -????-++--???? -+-??--+?? D. 111122322443 4 340 00 k k k k k k k k k k k k k k k -????-+--???? -+??--+?? 5.确定已知三角形单元的局部码为1(e),2(e),3(e),对应总码依次为3,6,4,则其单元的刚度矩阵中的元素k 24应放在总体刚度矩阵的( )。 A.1行2列 B.3行12列 C.6行12列 D.3行6列 6.对一根只受轴向载荷的杆单元,k 12为负号的物理意义可理解为( ) A.当节点2沿轴向产生位移时,在节点1引起的载荷与其方向相同 B.当节点2沿轴向产生位移时,在节点1引起的载荷与其方向相反 C.当节点2沿轴向产生位移时,在节点1引起的位移与其方向相同 D.当节点2沿轴向产生位移时,在节点1引起的位移与其方向相反 7.平面桁架中,节点3处铅直方向位移为已知,若用置大数法引入支承条件,则应将总体刚度矩阵中的( ) A.第3行和第3列上的所有元素换为大数A B.第6行第6列上的对角线元素乘以大数A C.第3行和第3列上的所有元素换为零 D.第6行和第6列上的所有元素换为零 8.在任何一个单元内( ) A.只有节点符合位移模式 B.只有边界点符合位移模式 C.只有边界点和节点符合位移模式 D.单元内任意点均符合位移模式 9.平面应力问题中(Z 轴与该平面垂直),所有非零应力分量均位于( ) A.XY 平面内 B.XZ 平面内 C.YZ 平面内 D.XYZ 空间内 12.刚架杆单元与平面三角形单元( ) A.单元刚度矩阵阶数不同 B.局部坐标系的维数不同 C.无任何不同 D.节点截荷和位移分量数不同 13.图示平面结构的总体刚度矩阵[K]和竖带矩阵[K *]的元素总数分别是( ) A.400和200 B.400和160 C.484和200 D.484和160 14.在有限元分析中,划分单元时,在应力变化大的区域应该( ) A.单元数量应多一些,单元尺寸小一些 B.单元数量应少一些,单元尺寸大一些 C.单元数量应多一些,单元尺寸大一些 D.单元尺寸和数量随便确定 15.在平面应力问题中,沿板厚方向( ) A.应变为零,但应力不为零 B.应力为零,但应变不为零 C.应变、应力都为零 D.应变、应力都不为零 16.若把平面应力问题的单元刚度矩阵改为平面应变问题的单元刚度矩阵只需将( ) A. E 换成E/(1-μ2),μ换成μ/(1-μ2) B. E 换成E/(1-μ2),μ换成μ/(1-μ) C. E 换成E/(1-μ),μ换成μ/(1-μ2) D. E 换成E/(1-μ),μ换成μ/(1-μ) 17.图示三角形单元非节点载荷的节点等效载荷为( ) A.F yi =-100KN F yj =-50KN F yk =0 B. F yi =-80KN F yj =-70KN F yk =0 C. F yi =-70KN F yj =-80KN F yk =0
弹性力学及有限元试题
弹性力学及有限元试题 (一) 问答题(20分) 1、什么是圣维南原理?举例说明怎样把它应用于工程问题 的简化中。 2、什么叫做一点的应力状态?如何表示一点的应力状态(要 求具体说明或表达)。 3、何谓逆解法和半逆解法?它们的理论依据是什么? 4、什么是平面应力问题?什么是平面应变问题?分别写出弹性力学平面应力问题和平面应变问题的物理方程。 5、要保证有限元方法解答的收敛性,位移模式必须满足那些条 件? (二) (10分) 1.利用坐标变换从直角坐标的平衡方程推导极坐标下平衡方程(无体力)。 2.利用坐标变换从直角坐标下几何方程推导极坐标下几何方程。 (三)已知,其他应力分量为零,求位移场。(10分) (四)设有矩形截面的悬臂粱,在 自由端受有集中荷载F;体力可以不
计。试根据材料力学公式,写出弯应力σx和切应力τxy的表达式,并取挤压应力σy=0,然后证明,这些表达式满足平衡微分方程和相容方程,再说明,这些表达式是否就表示正确的解答(10分)。 (五)设半平面体在直边界上受有集中力偶,单位宽度上力偶矩为M,试求应力分量(10分)。 提示:单位厚度上的力偶矩M的量纲是LMT-2,应力只能是M/ρ2的形式,所以可假设应力函数由:Φ=Φ(φ). (六) 铅直平面内的正方形薄板,边长为2a,四边固定,图5—18,只受重力的作用。设μ=0,试取位移分量的表达式为 用瑞利—里茨法求解(15分)。
(七)试按图示网格求解结点位移,取t =1m,μ= 0(15分)。 (八)用刚度集成法求下图所示结构的整体刚度矩阵K。(10分) 要求:单元刚度矩阵元素用e k形式表示;单元刚度矩阵用e K形式表 ij 示,其中e为单元号。
平面问题的有限元法-Read
3 弹性力学平面问题的有限元法 本章包括以下的内容: 3.1弹性力学平面问题的基本方程 3.2单元位移函数 3.3单元载荷移置 3.4单元刚度矩阵 3.5单元刚度矩阵的性质与物理意义 3.6整体分析 3.7约束条件的处理 3.8整体刚度矩阵的特点与存储方法 3.9方程组解法 3.1弹性力学平面问题的基本方程 弹性力学是研究弹性体在约束和外载荷作用下应力和变形分布规律的一门学科。在弹性力学中针对微小的单元体建立基本方程,把复杂形状弹性体的受力和变形分析问题归结为偏微分方程组的边值问题。弹性力学的基本方程包括平衡方程、几何方程、物理方程。 弹性力学的基本假定如下: 1)完全弹性,2)连续,3)均匀,4)各向同性,5)小变形。 3.1.1基本变量 弹性力学中的基本变量为体力、面力、应力、位移、应变,各自的定义如下。 体力 体力是分布在物体体积内的力,例如重力和惯性力。 面力 面力是分布在物体表面上的力,例如接触压力、流体压力。 应力 物体受到约束和外力作用,其内部将产生内力。物体内某一点的内力就是应力。 图3.1
如图3.1假想用通过物体内任意一点p 的一个截面mn 将物理分为Ⅰ、Ⅱ两部分。将部分Ⅱ撇开,根据力的平衡原则,部分Ⅱ将在截面mn 上作用一定的内力。在mn 截面上取包含p 点的微小面积A ?,作用于A ?面积上的内力为Q ?。 令A ?无限减小而趋于p 点时,Q ?的极限S 就是物体在p 点的应力。 S A Q A =??→?0lim 应力S 在其作用截面上的法向分量称为正应力,用σ表示;在作用截面上的切向分量称为剪应力,用τ表示。 显然,点p 在不同截面上的应力是不同的。为分析点p 的应力状态,即通过p 点的各个截面上的应力的大小和方向,在p 点取出的一个平行六面体,六面体的各楞边平行于坐标轴。 图3.2 将每个上的应力分解为一个正应力和两个剪应力,分别与三个坐标轴平行。用六面体表面的应力分量来表示p 点的应力状态。应力分量的下标约定如下: 第一个下标表示应力的作用面,第二个下标表示应力的作用方向。 xy τ,第一个下标x 表示剪应力作用在垂直于X 轴的面上,第二个下标y 表示剪应力指 向Y 轴方向。 正应力由于作用表面与作用方向垂直,用一个下标。x σ表示正应力作用于垂直于X 轴的面上,指向X 轴方向。 应力分量的方向定义如下: 如果某截面上的外法线是沿坐标轴的正方向,这个截面上的应力分量以沿坐标轴正方向为正; 如果某截面上的外法线是沿坐标轴的负方向,这个截面上的应力分量以沿坐标轴负方向为正。 剪应力互等:xz zx zy yz yx xy ττττττ===,, 物体内任意一点的应力状态可以用六个独立的应力分量x σ、y σ、z σ、xy τ、yz τ、zx τ
最新有限单元法部分课后题答案
1.1 有限单元法中“离散”的含义是什么?有限单元法是如何将具有无限自由度的连续介质问题转变成有限自由度问题的?位移有限元法的标准化程式是怎样的? (1)离散的含义即将结构离散化,即用假想的线或面将连续体分割成数目有限的单元,并在其上设定有限个节点;用这些单元组成的单元集合体代替原来的连续体,而场函数的节点值将成为问题的基本未知量。 (2)给每个单元选择合适的位移函数或称位移模式来近似地表示单元内位移分布规律,即通过插值以单元节点位移表示单元内任意点的位移。因节点位移个数是有限的,故无限自由度问题被转变成了有限自由度问题。 (3)有限元法的标准化程式:结构或区域离散,单元分析,整体分析,数值求解。 1.3 单元刚度矩阵和整体刚度矩阵各有哪些性质?各自的物理意义是什么?两者有何区别?单元刚度矩阵的性质:对称性、奇异性(单元刚度矩阵的行列式为零)。整体刚度矩阵的性质:对称性、奇异性、稀疏性。单元 Kij 物理意义 Kij 即单元节点位移向量中第 j 个自由度发生单位位移而其他位移分量为零时,在第 j 个自由度方向引起的节点力。整体刚度矩阵 K 中每一列元素的物理意义是:要迫使结构的某节点位移自由度发生单位位移,而其他节点位移都保持为零的变形状态,在所有个节点上需要施加的节点荷载。 2.2 什么叫应变能?什么叫外力势能?试叙述势能变分原理和最小势能原理,并回答下述问题:势能变分原理代表什么控制方程和边界条件?其中附加了哪些条件? (1)在外力作用下,物体内部将产生应力σ和应变ε,外力所做的功将以变形能的形式储存起来,这种能量称为应变能。 (2)外力势能就是外力功的负值。 (3)势能变分原理可叙述如下:在所有满足边界条件的协调位移中,那些满足静力平衡条件的位移使物体势能泛函取驻值,即势能的变分为零 δ∏p=δ Uε+δV=0 此即变分方程。对于线性弹性体,势能取最小值,即 δ2∏P=δ2Uε+δ2V≥0 此时的势能变分原理就是著名的最小势能原理。 势能变分原理代表平衡方程、本构方程和应力边界条件,其中附加了几何方程和位移边界条件。 2.3 什么是强形式?什么是弱形式?两者有何区别?建立弱形式的关键步骤是什么? 等效积分形式通过分部积分,称式 ∫ΩCT(v)D(u)dΩ+∫ΓET(v)F(u)dΓ 为微分方程的弱形式,相对而言,定解问题的微分方程称为强形式。 区别:弱形式得不到解析解。建立弱形式的关键步骤:对场函数要求较低阶的连续性。2.4 为了使计算结果能够收敛于精确解,位移函数需要满足哪些条件?为什么? 只要位移函数满足两个基本要求,即完备性和协调性,计算结果便收敛于精确解。 2.6 为什么采用变分法求解通常只能得到近似解?变分法的应用常遇到什么困难?Ritz 法收敛的条件是什么? (1)在 Ritz 法中,N 决定了试探函数的基本形态,待定参数使得场函数具有一定的任意性。如果真实场函数包含在试探函数之内,则变分法得到的解答是精确的;如果试探函数取自完全的函数序列,则当项数不断增加时,近似解将趋近于精确解。然而,通常情况下试探函数不会将真实场函数完全包含在内,实际计算时也不可能取无穷多项。因此,试探函数只能是真实场函数的近似。可见,变分法就是在某个假定的范围内找出最佳解答,近似性就源于此。 (2)采用变分法近似求解,要求在整个求解区域内预先给出满足边界条件的场函数。通常情况下这是不可能的,因而变分法的应用受到了限制。 (3)Ritz 法的收敛条件是要求试探函数具有完备性和连续性,也就是说,如果试探函数满足完备性和连续性的要求,当试探函数的项数趋近于无穷时,则 Ritz 法的近似解将趋近于数学微分方程的精确解。 3.1 构造单元形函数有哪些基本原则? 形函数是定义于单元内坐标的连续函数。单元位移函数通常采用多项式,其中的待定常数应该与单元节点自由度数相等。为满足完备性要求,位移函数中必须包括常函数和一次式,即完全一次多项式。多项式的选取应由低阶到高阶,尽量选择完全多项式以提高单元的精度。若由于项数限制而不能选取完全多项式时,也应使完全多项式具有坐标的对称性,并且一
03-02 空间问题的四面体单元
第三章 轴对称、三维和高次单元 §3-2 空间问题的四面体单元 空间问题的有限单元法,和平面问题及轴对称问题的有限单元法的原理和分析过程完全相同。由于空间问题应采用三维坐标系,因此单元的自由度、刚度矩阵的元素个数,方程组内方程个数等要较平面问题和轴对称问题多,所以空间问题的规模一般比轴对称问题和平面问题大得多。它要求计算机的内存大,且计算时间长,费用高。这些问题都给三维有限单元法的具体运用带来许多困难。 和平面问题一样,空间有限单元法采用单元也是多种多样的,其中最简单的是四节点四面体单元。采用四面体单元和线性位移模式来处理空 间问题,可以看作平面问题中三角形单元的推广。 在采用四面体单元离散化后的空间结构物中,一系列不相互重叠的四面体之间仅在节点处以空间铰相互连接。四节点四面体单元仅在四个顶点处取为节点,其编号为i,j,m,p 。每个单元的计算简图如图3-7所示。 在位移法中,取节点位移为基本未知量,四节点四面体单元共有十二个自由度(位移分量),其节点位移列阵为 {}[ ] T p p p m m m j j j i i i p m j i e w v u w v u w v u w v u =??????????????=δδδδδ 其子矩阵 {}[]i i i i w v u =δ (i,j,m) 相应的节点力列阵为 {}[ ] T p m j i e F F F F F - 图3-7 空间四面体单元
其子矩阵 {}[]T i i i i W V U F = 一、单元法位移函数 结构中各点的位移是坐标x 、y 、z 的函数。当单元足够小时,单元内各点的位移可用简单的线性多项式来近似描述,即 ?? ? ??+++=+++=+++=z y x w z y x v z y x u 121110087654321αααααααααααα (3-49) 式中1α,2α,…,12α是十二个待定系数,它们可由单元的节点位移和坐标确定。假定节点i,j,m,p 的坐标分别为(i x i y i z )、(j x j y j z )、(m x m y m z )、 (p x p y p z ),将它们代入(3-49)式的第一式可得各个节点在x 方向的位移 ?? ? ? ? ?? ??? ?? ? ?+++=+++=+++=+++=p p p p m m m m j j j j i i i i z y x u z y x u z y x u z y x u 4321432143214321αααααααααααααααα (3-50) 解上述线性方程组,可得到1α,2α,3α,4α,再代入(3-50)式,得 ] )()()()[(61p p p p p m m m m m j j j j j i i i i i u z d y c x b a u z d y c x b a u z d y c x b a u z d y c x b a V u +++-+++++++-+++= (3-51) 其中V 为四面体ijmp 的体积,a i ,b i ,…,c p ,d p 为系数。 p p p m m m j j j i i i z y x z y x z y x z y x V 1 111= (3-52)
有限单元法原理与应用(第三版)
122123 60 组建 周年60组建 周年 主要完成人:朱伯芳 受奖单位:水电中心/结构材料所 【创新性】 全面系统地阐述了有限单元法的基本原理及其在土木、水利工程问题中的应用,包括弹性力学平面问题和空间问题、薄板、薄壳、厚板、厚壳、弹性稳定、塑性力学、大位移、断裂、动力反应、徐变、岩土力学、极限分析、混凝土和钢筋混凝土、流体力学、渗流分析、热传导、工程反分析、仿真分析、网格自动生成、误差估计及自适应技术等。本书取材实用、由浅入深、先易后难,便于自学;对于实际工程中有用的计算方法力求讲述清楚并给出具体计算公式,便于应用;对有限元法的工程应用,注意工程的物理特性,要求采用的概化假定、计算参数和计算荷载等尽量接近实际,注重计算方法精度的适应性等,并重视有限元计算结果与实际观测资料相验证。【影响力】 我国最早的有限元专著之一,为在我国推广有限元法发挥了重要作用;本书共出版三版,第一版于1976年8月,第二版于1998年10月,第三版于2009 年6月;曾作为多所高校的有限元课程教材使 用;英文版已由清华大学出版社和美国Wiley 出版社联合出版;中国科学技术信息研究所编著的《中国高被引指数分析》(2011版)中,本书列为国内水利工程领域高被引图书第2名。 有限单元法原理与应用(第三版) 著作类成果 【Innovation】 This book expounds, in an all-round and systematic manner, the basic theory of the finite element method and its application to civil engineering and hydraulic engineering , including plane and space problems of elasticity, thin plate, thin shell, thick plate, thick shell, elastic stability, plasticity, large displacement, fracture, dynamic response, creep, rock and soil mechanics, limit analysis, concrete and reinforced concrete, fluid mechanics, seepage analysis, heat conduction, back analysis in engineering, simulated analysis, automatic generation of meshes, error estimation and adaptive technique. This book is learner-friendly because it contains practical content and expounds knowledge step by step and from easy to difficult; and is also easy to use because it strives to clarify the computing methods usable in actual engineering and gives corresponding formulas. Regarding the engineering application of the finite element method, it pays attention to the physical characteristics of projects, requires adopted conceptualized assumption, calculation parameter and calculation load be close enough to reality and accuracy of calculation methods be adaptive, and stresses the verification between the calculation result of the finite element method and actual observational data. 【Influence】 Amongst the earliest finite element books in China, this book plays an important role in generalizing the finite element method in China. It has registered three editions, with the first edition published in August, 1976, the second edition in October, 1998 and the third edition in June, 2009. It served as a finite element textbook of many colleges and universities; and its English version has been published jointly by Tsinghua University Press and the U.S.-based Wiley & Sons, Inc. This book ranks second amongst the highly-cited books of hydraulic engineering in China, according to the Analysis Report of Chinese Highly Cited Paper 2011 of the Institute of Scientific and Technical Information of China (ISTIC) Main Contributor : Zhu Bofang Award-winning Unit : Research Center for Sustainable Hydropower/Department of Structures and Materials THE FINITE ELEMENT METHOD THEORY AND APPLICATIONS(EDITION III)
弹性力学与有限元分析试题及参考答案
弹性力学与有限元分析试题及参考答案 四、分析计算题 1、试写出无体力情况下平面问题的应力分量存在的必要条件,并考虑下列平面问题的应力分量是否可能在弹性体中存在。 (1)By Ax x +=σ,Dy Cx y +=σ,Fy Ex xy +=τ; (2))(22y x A x +=σ,)(22y x B y +=σ,Cxy xy =τ; 其中,A ,B ,C ,D ,E ,F 为常数。 解:应力分量存在的必要条件是必须满足下列条件:(1)在区域内的平衡微分方程 ????? ??=??+??=??+??0 0x y y x xy y yx x τστσ;(2)在区域内的相容方程()02222=+??? ? ????+??y x y x σσ;(3)在边界上的应力边界条件()()()() ???? ?=+=+s f l m s f m l y s xy y x s yx x τστσ;(4)对于多连体的位移单值条件。 (1)此组应力分量满足相容方程。为了满足平衡微分方程,必须A =-F ,D =-E 。此外还应满足应力边界条件。 (2)为了满足相容方程,其系数必须满足A +B =0;为了满足平衡微分方程,其系数必须满足A =B =-C /2。上两式是矛盾的,因此,此组应力分量不可能存在。 2、已知应力分量312x C Qxy x +-=σ,22 23xy C y -=σ,y x C y C xy 2 332--=τ,体力不计,Q 为常数。试利用平衡微分方程求系数C 1,C 2,C 3。 解:将所给应力分量代入平衡微分方程 ???? ?? ?=??+??=??+??00x y y x xy y yx x τστσ 得 ?? ?=--=--+-0 230 33322322212xy C xy C x C y C x C Qy 即 ()()()?? ?=+=+--0 230 333222231xy C C y C Q x C C 由x ,y 的任意性,得
