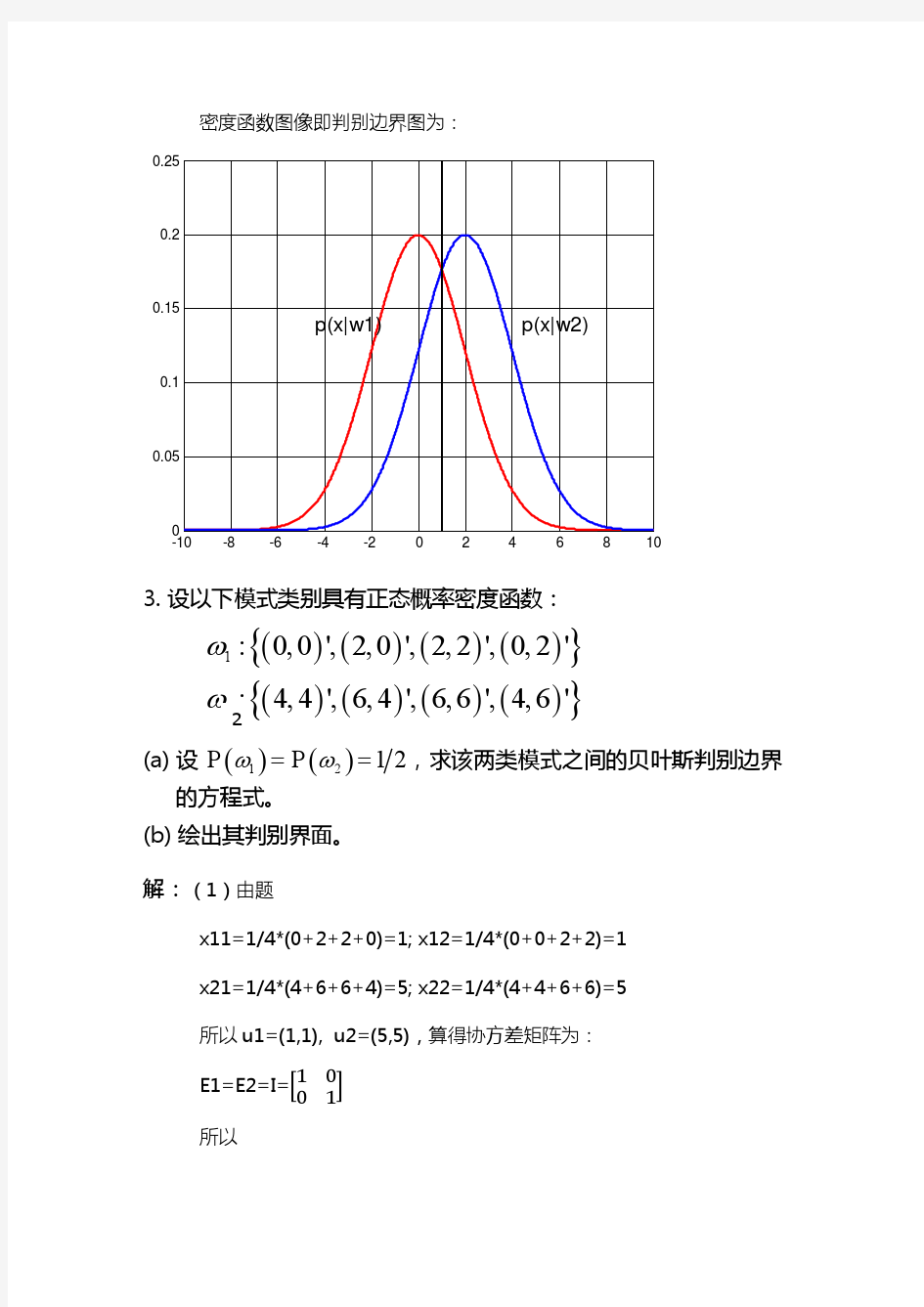
模式识别作业三

黄庆明模式识别与机器学习第三章作业

·在一个10类的模式识别问题中，有3类单独满足多类情况1，其余的类别满足多类情况2。问该模式识别问题所需判别函数的最少数目是多少？应该是252142 6 *74132 7=+=+ =++C 其中加一是分别3类和 7类 ·一个三类问题，其判别函数如下： d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-1 (1)设这些函数是在多类情况1条件下确定的，绘出其判别界面和每一个模式类别的区域。 (2)设为多类情况2，并使：d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。绘出其判别界面和多类情况2的区域。

(3)设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的，绘出其判别界面和每类的区域。 ·两类模式，每类包括5个3维不同的模式，且良好分布。如果它们是线性可分的，问权向量至少需要几个系数分量？假如要建立二次的多项式判别函数，又至少需要几个系数分量？（设模式的良好分布不因模式变化而改变。）如果线性可分，则4个建立二次的多项式判别函数，则102 5 C 个 ·(1)用感知器算法求下列模式分类的解向量w: ω1: {(0 0 0)T , (1 0 0)T , (1 0 1)T , (1 1 0)T } ω2: {(0 0 1)T , (0 1 1)T , (0 1 0)T , (1 1 1)T } 将属于ω2的训练样本乘以（-1），并写成增广向量的形式。 x ①=(0 0 0 1)T , x ②=(1 0 0 1)T , x ③=(1 0 1 1)T , x ④=(1 1 0 1)T x ⑤=(0 0 -1 -1)T , x ⑥=(0 -1 -1 -1)T , x ⑦=(0 -1 0 -1)T , x ⑧=(-1 -1 -1 -1)T 第一轮迭代：取C=1，w(1)=(0 0 0 0) T 因w T (1) x ① =(0 0 0 0)(0 0 0 1) T =0 ≯0，故w(2)=w(1)+ x ① =(0 0 0 1) 因w T (2) x ② =(0 0 0 1)(1 0 0 1) T =1>0，故w(3)=w(2)=(0 0 0 1)T 因w T (3)x ③=(0 0 0 1)(1 0 1 1)T =1>0，故w(4)=w(3) =(0 0 0 1)T 因w T (4)x ④=(0 0 0 1)(1 1 0 1)T =1>0，故w(5)=w(4)=(0 0 0 1)T 因w T (5)x ⑤=(0 0 0 1)(0 0 -1 -1)T =-1≯0，故w(6)=w(5)+ x ⑤=(0 0 -1 0)T 因w T (6)x ⑥=(0 0 -1 0)(0 -1 -1 -1)T =1>0，故w(7)=w(6)=(0 0 -1 0)T 因w T (7)x ⑦=(0 0 -1 0)(0 -1 0 -1)T =0≯0，故w(8)=w(7)+ x ⑦=(0 -1 -1 -1)T 因w T (8)x ⑧=(0 -1 -1 -1)(-1 -1 -1 -1)T =3>0，故w(9)=w(8) =(0 -1 -1 -1)T 因为只有对全部模式都能正确判别的权向量才是正确的解，因此需进行第二轮迭代。第二轮迭代：因w T (9)x ①=(0 -1 -1 -1)(0 0 0 1)T =-1≯0，故w(10)=w(9)+ x ① =(0 -1 -1 0)T

北邮模式识别课堂作业答案(参考)

第一次课堂作业 1.人在识别事物时是否可以避免错识 2.如果错识不可避免，那么你是否怀疑你所看到的、听到的、嗅到的到底是真是的，还是虚假的 3.如果不是，那么你依靠的是什么呢用学术语言该如何表示。 4.我们是以统计学为基础分析模式识别问题，采用的是错误概率评价分类器性能。如果不采用统计学，你是否能想到还有什么合理地分类器性能评价指标来替代错误率 1.知觉的特性为选择性、整体性、理解性、恒常性。错觉是错误的知觉，是在特定条件下产生的对客观事物歪曲的知觉。认知是一个过程，需要大脑的参与.人的认知并不神秘，也符合一定的规律，也会产生错误 2.不是 3.辨别事物的最基本方法是计算 . 从不同事物所具有的不同属性为出发点认识事物. 一种是对事物的属性进行度量，属于定量的表示方法(向量表示法 )。另一种则是对事务所包含的成分进行分析，称为定性的描述(结构性描述方法)。 4.风险第二次课堂作业作为学生，你需要判断今天的课是否点名。结合该问题(或者其它你熟悉的识别问题，如”天气预报”)，说明: 先验概率、后验概率和类条件概率按照最小错误率如何决策按照最小风险如何决策 ωi为老师点名的事件,x为判断老师点名的概率 1.先验概率: 指根据以往经验和分析得到的该老师点名的概率,即为先验概率 P(ωi ) 后验概率: 在收到某个消息之后，接收端所了解到的该消息发送的概率称为后验概率。在上过课之后,了解到的老师点名的概率为后验概率P(ωi|x) 类条件概率:在老师点名这个事件发生的条件下,学生判断老师点名的概率p(x| ωi ) 2. 如果P(ω1|X)>P(ω2|X)，则X归为ω1类别如果P(ω1|X)≤P(ω2|X)，则X归为ω2类别 3.1)计算出后验概率已知P(ωi)和P(X|ωi)，i=1,…，c，获得观测到的特征向量X 根据贝叶斯公式计算 j=1,…，x

模式识别大作业02125128(修改版)

模式识别大作业班级 021252 姓名谭红光学号 02125128 1.线性投影与Fisher 准则函数各类在d 维特征空间里的样本均值向量： ∑∈= i k X x k i i x n M 1 ，2,1=i (1) 通过变换w 映射到一维特征空间后，各类的平均值为： ∑∈= i k Y y k i i y n m 1，2,1=i (2) 映射后，各类样本“类内离散度”定义为： 22 ()k i i k i y Y S y m ∈= -∑，2,1=i (3) 显然，我们希望在映射之后，两类的平均值之间的距离越大越好，而各类的样本类内离散度越小越好。因此，定义Fisher 准则函数： 2 1222 12||()F m m J w s s -= + (4) 使F J 最大的解* w 就是最佳解向量，也就是Fisher 的线性判别式. 从 )(w J F 的表达式可知，它并非w 的显函数，必须进一步变换。已知： ∑∈= i k Y y k i i y n m 1，2,1=i , 依次代入上两式，有： i T X x k i T k X x T i i M w x n w x w n m i k i k === ∑∑∈∈)1 (1 ，2,1=i (5) 所以：2 21221221||)(||||||||M M w M w M w m m T T T -=-=- w S w w M M M M w b T T T =--=))((2121 (6)

其中：T b M M M M S ))((2121--= (7) b S 是原d 维特征空间里的样本类内离散度矩阵，表示两类均值向量之间的离散度大小，因此，b S 越大越容易区分。将(4.5-6) i T i M w m =和(4.5-2) ∑∈= i k X x k i i x n M 1代入(4.5-4)2i S 式中： ∑∈-= i k X x i T k T i M w x w S 22)( ∑∈?--? =i k X x T i k i k T w M x M x w ))(( w S w i T = (8) 其中：T i X x k i k i M x M x S i k ))((--= ∑=，2,1=i (9) 因此：w S w w S S w S S w T T =+=+)(212221 (10) 显然： 21S S S w += (11) w S 称为原d 维特征空间里，样本“类内离散度”矩阵。 w S 是样本“类内总离散度”矩阵。为了便于分类，显然 i S 越小越好，也就是 w S 越小越好。

贝叶斯决策理论-模式识别课程作业

研究生课程作业贝叶斯决策理论课程名称模式识别姓名xx 学号xxxxxxxxx 专业软件工程任课教师xxxx 提交时间2019.xxx 课程论文提交时间：2019 年3月19 日

需附上习题题目 1. 试简述先验概率，类条件概率密度函数和后验概率等概念间的关系：先验概率针对M 个事件出现的可能性而言，不考虑其他任何条件类条件概率密度函数是指在已知某类别的特征空间中，出现特征值X 的概率密度，指第类样品其属性X 是如何分布的。后验概率是指通过调查或其它方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正，而后得到的概率。贝叶斯公式可以计算出该样品分属各类别的概率，叫做后验概率；看X 属于那个类的可能性最大，就把X 归于可能性最大的那个类，后验概率作为识别对象归属的依据。贝叶斯公式为类别的状态是一个随机变量．而某种状态出现的概率是可以估计的。贝叶斯公式体现了先验概率、类条件概率密度函数、后验概率三者关系的式子。 2. 试写出利用先验概率和分布密度函数计算后验概率的公式 3. 写出最小错误率和最小风险决策规则相应的判别函数（两类问题）。最小错误率如果12(|)(|)P x P x ωω>，则x 属于1ω 如果12(|)(|)P x P x ωω<，则x 属于2ω 最小风险决策规则 If 12(|) (|) P x P x ωλω< then 1x ω∈ If 12(|) (|) P x P x ωλω> then 2x ω∈

4. 分别写出以下两种情况下，最小错误率贝叶斯决策规则：（1）两类情况，且12(|)(|)P X P X ωω= （2）两类情况，且12()()P P ωω= 最小错误率贝叶斯决策规则为： If 1...,(|)()max (|)i i j j c p x P P x ωωω==, then i x ω∈ 两类情况：若1122(|)()(|)()p X P p X P ωωωω>,则1X ω∈ 若1122(|)()(|)()p X P p X P ωωωω<,则2X ω∈ (1) 12(|)(|)P X P X ωω=, 若12()()P P ωω>，则1X ω∈ 若12()()P P ωω<，则2X ω∈ (2) 12()()P P ωω=,若12(|)(|)p X p X ωω>,则1X ω∈ 若12(|)(|)p X p X ωω<,则2X ω∈ 5. 对两类问题，证明最小风险贝叶斯决策规则可表示为，若 112222221111(|)()() (|)()() P x P P x P ωλλωωλλω->- 则1x ω∈，反之则2x ω∈ 计算条件风险 2 111111221(|)(|)(|)(|)j j j R x p x P x P x αλωλωλω===+∑ 2 222112221 (|)(|)(|)(|)j j j R x p x P x P x αλωλωλω===+∑ 如果 111122(|)(|)P x P x λωλω+<211222(|)(|)P x P x λωλω+ 2111112222()(|)()(|)P x P x λλωλλω->- 211111122222()()(|)()()(|)P p x P p x λλωωλλωω->-

中科院模式识别第三次(第五章)_作业_答案_更多

第5章：线性判别函数第一部分：计算与证明 1．有四个来自于两个类别的二维空间中的样本，其中第一类的两个样本为(1,4)T 和(2,3)T ，第二类的两个样本为(4,1)T 和(3,2)T 。这里，上标T 表示向量转置。假设初始的权向量a=(0,1)T ，且梯度更新步长ηk 固定为1。试利用批处理感知器算法求解线性判别函数g(y)=a T y 的权向量。解：首先对样本进行规范化处理。将第二类样本更改为(4,1)T 和(3,2)T .然后计算错分样本集： g(y 1)=(0,1)(1,4)T = 4 > 0 (正确) g(y 2)=(0,1)(2,3)T = 3 > 0 (正确) g(y 3)=(0,1)(-4,-1)T = -1 < 0 (错分) g(y 4)=(0,1)(-3,-2)T = -2 < 0 (错分) 所以错分样本集为Y={(-4,-1)T ,(-3,-2)T }. 接着，对错分样本集求和：(-4,-1)T +(-3,-2)T = (-7,-3)T 第一次修正权向量a ，以完成一次梯度下降更新：a=(0,1)T + (-7,-3)T =(-7,-2)T 再次计算错分样本集： g(y 1)=(-7,-2)(1,4)T = -15 <0 (错分) g(y 2)=(-7,-2)(2,3)T = -20 < 0 (错分) g(y 3)=(-7,-2)(-4,-1)T = 30 > 0 (正确) g(y 4)=(-7,-2)(-3,-2)T = 25 > 0 (正确) 所以错分样本集为Y={(1,4)T ,(2,3)T }. 接着，对错分样本集求和：(1,4)T +(2,3)T = (3,7)T 第二次修正权向量a ，以完成二次梯度下降更新：a=(-7,-2)T + (3,7)T =(-4,5)T 再次计算错分样本集： g(y 1) = (-4,5)(1,4)T = 16 > 0 (正确) g(y 2) =(-4,5)(2,3)T = 7 > 0 (正确) g(y 3) =(-4,5)(-4,-1)T = 11 > 0 (正确) g(y 4) =(-4,5)(-3,-2)T = 2 > 0 (正确) 此时，全部样本均被正确分类，算法结束，所得权向量a=(-4,5)T 。 2．在线性感知算法中，试证明引入正余量b 以后的解区(a T y i ≥b)位于原来的解区之中(a T y i >0)，且与原解区边界之间的距离为b/||y i ||。证明：设a*满足a T y i ≥b,则它一定也满足a T y i >0，所以引入余量后的解区位于原来的解区a T y i >0之中。注意，a T y i ≥b 的解区的边界为a T y i =b,而a T y i >0的解区边界为a T y i =0。a T y i =b 与a T y i =0两个边界之间的距离为b/||y i ||。（因为a T y i =0过坐标原点，相关于坐标原点到a T y i =b 的距离。） 3．试证明感知器准则函数正比于被错分样本到决策面的距离之和。证明：感知器准则函数为： ()() T Y J ∈=-∑y a a y 决策面方程为a T y=0。当y 为错分样本时，有a T y ≤0。此时，错分样本到决策面的

模式识别-作业4

第五章作业：作业一：设有如下三类模式样本集ω1，ω2和ω3，其先验概率相等，求S w 和S b ω1：{(1 0)T , (2 0) T , (1 1) T } ω2：{(-1 0)T , (0 1) T , (-1 1) T } ω3：{(-1 -1)T , (0 -1) T , (0 -2) T } 答案：由于三类样本集的先验概率相等，则概率均为1/3。多类情况的类内散布矩阵，可写成各类的类内散布矩阵的先验概率的加权和，即： ∑∑=== --= c i i i T i i c i i w C m x m x E P S 1 1 }|))(({)(ωω 其中C i 是第i 类的协方差矩阵。其中1m = ,2m = 则=++=321S w w w w S S S 1/3 + + = 类间散布矩阵常写成： T i i c i i b m m m m P S ))(()(001 --= ∑=ω 其中，m 0为多类模式（如共有c 类）分布的总体均值向量，即：

c i m P x E m i c i i i ,,2,1,,)(}{1 0K =?= =∑=ωω 0m = = 则 T i i c i i b m m m m P S ))(()(001 --= ∑=ω=++ = 作业二：设有如下两类样本集，其出现的概率相等： ω1：{(0 0 0)T , (1 0 0) T , (1 0 1) T , (1 1 0) T } ω2：{(0 0 1)T , (0 1 0) T , (0 1 1) T , (1 1 1) T } 用K-L 变换，分别把特征空间维数降到二维和一维，并画出样本在该空间中的位置。答案： =+=∑∑==i i N j j N j j x x m 1 21 1）4 1 4 1 （ 21 将所有这些样本的各分量都减去0.5，便可以将所有这些样本的均值移到原点，即(0,0,0)点。新得到的两类样本集为：

模式识别作业(全)

模式识别大作业一．K均值聚类（必做，40分） 1.K均值聚类的基本思想以及K均值聚类过程的流程图； 2.利用K均值聚类对Iris数据进行分类，已知类别总数为3。给出具体的C语言代码，并加注释。例如，对于每一个子函数，标注其主要作用，及其所用参数的意义，对程序中定义的一些主要变量，标注其意义； 3.给出函数调用关系图，并分析算法的时间复杂度； 4.给出程序运行结果，包括分类结果（只要给出相对应的数据的编号即可）以及循环迭代的次数； 5.分析K均值聚类的优缺点。二．贝叶斯分类（必做，40分） 1.什么是贝叶斯分类器，其分类的基本思想是什么； 2.两类情况下，贝叶斯分类器的判别函数是什么，如何计算得到其判别函数； 3.在Matlab下，利用mvnrnd()函数随机生成60个二维样本，分别属于两个类别（一类30个样本点），将这些样本描绘在二维坐标系下，注意特征值取值控制在（-5，5）范围以内； 4.用样本的第一个特征作为分类依据将这60个样本进行分类，统计正确分类的百分比，并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志（正确分类的样本点用“O”，错误分类的样本点用“X”）画出来； 5.用样本的第二个特征作为分类依据将这60个样本再进行分类，统计正确分类的百分比，并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来； 6.用样本的两个特征作为分类依据将这60个样本进行分类，统计正确分类的百分比，并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来； 7.分析上述实验的结果。 8.60个随即样本是如何产生的的；给出上述三种情况下的两类均值、方差、协方差矩阵以及判别函数；三．特征选择（选作，15分） 1.经过K均值聚类后，Iris数据被分作3类。从这三类中各选择10个样本点； 2.通过特征选择将选出的30个样本点从4维降低为3维，并将它们在三维的坐标系中

北邮模式识别课堂作业答案(参考)

第一次课堂作业 ? 1.人在识别事物时是否可以避免错识？ ? 2.如果错识不可避免，那么你是否怀疑你所看到的、听到的、嗅到的到底是真是的，还是虚假的？ ? 3.如果不是，那么你依靠的是什么呢？用学术语言该如何表示。 ? 4.我们是以统计学为基础分析模式识别问题，采用的是错误概率评价分类器性能。如果不采用统计学，你是否能想到还有什么合理地分类器性能评价指标来替代错误率？ 1.知觉的特性为选择性、整体性、理解性、恒常性。错觉是错误的知觉，是在特定条件下产生的对客观事物歪曲的知觉。认知是一个过程，需要大脑的参与.人的认知并不神秘，也符合一定的规律，也会产生错误 2.不是 3.辨别事物的最基本方法是计算.从不同事物所具有的不同属性为出发点认识事物.一种是对事物的属性进行度量，属于定量的表示方法(向量表示法)。另一种则是对事务所包含的成分进行分析，称为定性的描述(结构性描述方法)。 4.风险第二次课堂作业 ?作为学生，你需要判断今天的课是否点名。结合该问题(或者其它你熟悉的识别问题，如”天气预报”)，说明: ?先验概率、后验概率和类条件概率？ ?按照最小错误率如何决策？ ?按照最小风险如何决策？ ωi为老师点名的事件,x为判断老师点名的概率 1.先验概率:指根据以往经验和分析得到的该老师点名的概率,即为先验概率P(ωi ) 后验概率:在收到某个消息之后，接收端所了解到的该消息发送的概率称为后验概率。在上过课之后,了解到的老师点名的概率为后验概率P(ωi|x) 类条件概率:在老师点名这个事件发生的条件下,学生判断老师点名的概率p(x| ωi ) 2. 如果P(ω1|X)>P(ω2|X)，则X归为ω1类别如果P(ω1|X)≤P(ω2|X)，则X归为ω2类别 3.1)计算出后验概率已知P(ωi)和P(X|ωi)，i=1,…，c，获得观测到的特征向量X 根据贝叶斯公式计算 j=1,…，x 2)计算条件风险

模式识别大作业

作业1 用身高和/或体重数据进行性别分类（一）基本要求：用FAMALE.TXT和MALE.TXT的数据作为训练样本集，建立Bayes分类器，用测试样本数据对该分类器进行测试。调整特征、分类器等方面的一些因素，考察它们对分类器性能的影响，从而加深对所学内容的理解和感性认识。具体做法： 1．应用单个特征进行实验：以（a）身高或者（b）体重数据作为特征，在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到测试样本，考察测试错误情况。在分类器设计时可以考察采用不同先验概率（如0.5对0.5, 0.75对0.25, 0.9对0.1等）进行实验，考察对决策规则和错误率的影响。图1-先验概率0.5:0.5分布曲线图2-先验概率0.75:0.25分布曲线图3--先验概率0.9:0.1分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。程序：bayesflq1.m和bayeszcx.m

关（在正态分布下一定独立），在正态分布假设下估计概率密度，建立最小错误率Bayes 分类器，写出得到的决策规则，将该分类器应用到训练/测试样本，考察训练/测试错误情况。比较相关假设和不相关假设下结果的差异。在分类器设计时可以考察采用不同先验概率（如0.5 vs. 0.5, 0.75 vs. 0.25, 0.9 vs. 0.1等）进行实验，考察对决策和错误率的影响。训练样本female来测试图1先验概率0.5 vs. 0.5 图2先验概率0.75 vs. 0.25 图3先验概率0.9 vs. 0.1 图4不同先验概率对测试样本1进行试验得图

模式识别作业Homework#2

Homework #2 Note:In some problem (this is true for the entire quarter) you will need to make some assumptions since the problem statement may not fully specify the problem space. Make sure that you make reasonable assumptions and clearly state them. Work alone: You are expected to do your own work on all assignments; there are no group assignments in this course. You may (and are encouraged to) engage in general discussions with your classmates regarding the assignments, but specific details of a solution, including the solution itself, must always be your own work. Problem: In this problem we will investigate the importance of having the correct model for classification. Load file hw2.mat and open it in Matlab using command load hw2. Using command whos, you should see six array c1, c2, c3 and t1, t2, t3, each has size 500 by 2. Arrays c1, c2, c3 hold the training data, and arrays t1, t2, t3 hold the testing data. That is arrays c1, c2, c3 should be used to train your classifier, and arrays t1, t2, t3 should be used to test how the classifier performs on the data it hasn’t seen. Arrays c1 holds training data for the first class, c2 for the second class, c3 for the third class. Arrays t1, t2, t3 hold the test data, where the true class of data in t1, t2, t3 comes from the first, second, third classed respectively. Of course, array ci and ti were drawn from the same distribution for each i. Each training and testing example has 2 features. Thus all arrays are two dimensional, the number of rows is equal to the number of examples, and there are 2 columns, column 1 has the first feature, column 2 has the second feature. (a)Visualize the examples by using Matlab scatter command a plotting each class in different color. For example, for class 1 use scatter(c1(:,1),c1(:,2),’r’);. Other possible colors can be found by typing help plot. (b)From the scatter plot in (a), for which classes the multivariate normal distribution looks like a possible model, and for which classes it is grossly wrong? If you are not sure how to answer this part, do parts (c-d) first. (c)Suppose we make an erroneous assumption that all classed have multivariate normal Nμ. Compute the Maximum Likelihood estimates for the means and distributions()∑, covariance matrices (remember you have to do it separately for each class). Make sure you use only the training data; this is the data in arrays c1, c2, and c3. (d)You can visualize what the estimated distributions look like using Matlab contour(). Recall that the data should be denser along the smaller ellipse, because these are closer to the estimated mean. (e)Use the ML estimates from the step (c) to design the ML classifier (this is the Bayes classifier under zero-one loss function with equal priors). Thus we are assuming that priors are the same for each class. Now classify the test example (that is only those

模式识别课程作业proj03-01

模式识别理论与方法课程作业实验报告实验名称：Maximum-Likelihood Parameter Estimation 实验编号：Proj03-01 姓名：学号：规定提交日期：2012年3月27日实际提交日期：2012年3月27日摘要：参数估计问题是统计学中的经典问题，其中最常用的一种方法是最大似然估计法，最大似然估计是把待估计的参数看作是确定性的量，只是其取值未知。最佳估计就是使得产生已观测到的样本的概率为最大的那个值。本实验研究的训练样本服从多元正态分布，比较了单变量和多维变量的最大似然估计情况，对样本的均值、方差、协方差做了最大似然估计。实验结果对不同方式计算出的估计值做了比较分析，得出结论：对均值的最大似然估计就是对全体样本取平均；协方差的最大似然估计则是N 个)'?x )(?x (u u k k --矩阵的算术平均，对方差2 σ的最大似然估计是有偏估计。一、技术论述

（1）高斯情况：∑和u 均未知实际应用中，多元正态分布更典型的情况是：均值u 和协方差矩阵∑都未知。这样，参数向量θ就由这两个成分组成。先考虑单变量的情况，其中参数向量θ的组成成分是：221,σθθ==u 。这样，对于单个训练样本的对数似然函数为： 2 12 2 )(212ln 21)(ln θθπθ θ-- - =k k x x p （1）对上式关于变量θ对导： ???? ? ???????-+--=?=?2 2 2 12 12 2)(21 )(1 )(ln θθθθθθθθk k k x x x p l （2）运用式l θ?=0，我们得到对于全体样本的对数似然函数的极值条件 0)?(?1 n 112=-∑=k k x θθ （3） 0?) (?11 2 2 2 112 =-+ -∑ ∑==n k k n k x θθθ （4）其中1?θ，2?θ分别是对于1θ，2θ的最大似然估计。把1?θ，2?θ用u ?，2?σ代替，并进行简单的整理，我们得到下述的对于均值和方差的最大似然估计结果 ∑==n k k x n u 1 1 ? （5） 2 1 2 )?(1 ?∑=-= n k k u x n σ （6）当高斯函数为多元时，最大似然估计的过程也是非常类似的。对于多元高斯分布的均值u 和协方差矩阵∑的最大似然估计结果为： ∑=1 1 ?n k x n u （7） t k n k k u x u x )?()?(n 1 ?1 --=∑ ∑= （8）二、实验结果

模式识别第三章-感知器算法

模式识别第三章感知器算法一．用感知器算法求下列模式分类的解向量w ： })0,1,1(,)1,0,1(,)0,0,1(,)0,0,0{(:1T T T T ω })1,1,1(,)0,1,0(,)1,1,0(,)1,0,0{(:2T T T T ω 将属于2ω的训练样本乘以（-1），并写成增广向量的形式： T x )1,0,0,0(1 =，T x )1,0,0,1(2=，T x )1,1,0,1(3=，T x )1,0,1,1(4 = T x )1,1-,0,0(5-=，T x )1,1-,1-,0(6-=，T x )1,0,1-,0(7-=，T x )1,1-,1-,1-(8-= 第一轮迭代：取1=C ，T )0,0,0,0()1(=ω 因0)1,0,0,0)(0,0,0,0()1(1==T T x ω不大于0，故T x )1,0,0,0()1()2(1=+=ωω 因1)1,0,0,1)(1,0,0,0()2(2==T T x ω大于0，故T )1,0,0,0()2()3(==ωω 因1)1,1,0,1)(1,0,0,0()3(3==T T x ω大于0，故T )1,0,0,0()3()4(==ωω 因1)1,0,1,1)(1,0,0,0()4(4==T T x ω大于0，故T )1,0,0,0()4()5(==ωω 因1)1,1-,0,0)(1,0,0,0()5(5-=-=T T x ω不大于0，故T x )0,1-,0,0()5()6(5 =+=ωω 因1)1,1-,1-,0)(0,1-,0,0()6(6=-=T T x ω大于0，故T )0,1-,0,0()6()7(==ωω 因0)1,0,1-,0)(0,1-,0,0()7(7=-=T T x ω不大于0，故T x )1-,1-,1,0()7()8(7-=+=ωω 因3)1,1-,1-,1-)(1-,1-,1,0()8(8=--=T T x ω大于0，故T )1-,1-,1,0()8()9(-==ωω 第二轮迭代：因1)1,0,0,0)(1-,1-,1,0()9(1-=-=T T x ω不大于0，故T x )0,1-,1,0()9()10(1-=+=ωω 因0)1,0,0,1)(0,1-,1-,0()10(2==T T x ω不大于0，故T x )1,1,1,1()10()11(2--=+=ωω 因1)1,1,0,1)(1,1,1,1()11(3=--=T T x ω大于0，故T )1,1,1,1()11()12(--==ωω 因1)1,0,1,1)(1,1,1,1()12(4=--=T T x ω大于0，故T )1,1,1,1()12()13(--==ωω

北工大模式识别基础课程作业

姓名：学号： 2.1 设有10个二维模式样本，如图2.13所示。若21=θ，试用最大最小距离算法对他们进行聚类分析。 1 3 5 7 9 X 1

解：① 取T 11]0,0[==X Z 。 ②选离1Z 最远的样本作为第二聚类中心2Z 。 ()()201012221=-+-=D ，831=D ，5841=D ，4551=D 5261=D ，7471=D ，4581=D ，5891=D ，651,10=D ∵ 最大者为D 71，∴T 72]7,5[==X Z 742 121=-=Z Z θT ③计算各样本与{}21,Z Z 间距离，选出其中的最小距离。 7412=D ，5222=D ，3432=D ，…，132,10=D }13,20,17,0,2,5,4,8,2,0{),min(21=i i D D ④742 120)},max{min(9221=>==T D D D i i ,T 93]3,7[==∴X Z ⑤继续判断是否有新的聚类中心出现： ?????===58740131211D D D ，???????===40522232221D D D ，…???????===1 13653,102,101,10D D D }1,0,1,0,2,5,4,8,2,0{),,min(321=i i i D D D 742 18)},,max{min(31321= <==T D D D D i i i 寻找聚类中心的步骤结束。 ⑥按最近距离分到三个聚类中心对应的类别中： 3211,,:X X X ω；76542,,,:X X X X ω；10983,,:X X X ω 代码附录： clear all close all clc %坐标点，初始化选定比例系数 num = 10;eta = 0.5;

第三章作业(1)

题1：在一个10类的模式识别问题中，有3类单独满足多类情况1，其余的类别满足多类情况2。问该模式识别问题所需判别函数的最少数目是多少？答：将10类问题可看作4类满足多类情况1的问题，可将3类单独满足多类情况1的类找出来，剩下的7类全部划到4类中剩下的一个子类中。再在此子类中，运用多类情况2的判别法则进行分类，此时需要7*（7-1）/2=21个判别函数。故共需要4+21=25个判别函数。题2：一个三类问题，其判别函数如下： d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-1 1.设这些函数是在多类情况1条件下确定的，绘出其判别界面和每一个模式类别的区域。 2.设为多类情况2，并使：d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。绘出其判别界面和多类情况2的区域。 3.设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的，绘出其判别界面和每类的区域。答：三种情况分别如下图所示： 1． 2．

3．题3：两类模式，每类包括5个3维不同的模式，且良好分布。如果它们是线性可分的，问权向量至少需要几个系数分量？假如要建立二次的多项式判别函数，又至少需要几个系数分量？（设模式的良好分布不因模式变化而改变。）答：（1）若是线性可分的，则权向量至少需要14N n =+=个系数分量；（2）若要建立二次的多项式判别函数，则至少需要5! 102!3! N = =个系数分量。题4：用感知器算法求下列模式分类的解向量w : ω1: {(0 0 0)T, (1 0 0)T, (1 0 1)T, (1 1 0)T} ω2: {(0 0 1)T, (0 1 1)T, (0 1 0)T, (1 1 1)T} 解：将属于2w 的训练样本乘以(1)-，并写成增广向量的形式 x1=[0 0 0 1]',x2=[1 0 0 1]',x3=[1 0 1 1]',x4=[1 1 0 1]'; x5=[0 0 -1 -1]',x6=[0 -1 -1 -1]',x7=[0 -1 0 -1]',x8=[-1 -1 -1 -1]'; 迭代选取1C =，(1)(0,0,0,0)w '=，则迭代过程中权向量w 变化如下： (2)(0 0 0 1)w '=；(3)(0 0 -1 0)w '=；(4)(0 -1 -1 -1)w '=；(5)(0 -1 -1 0)w '=；(6)(1 -1 -1 1)w '=；(7)(1 -1 -2 0)w '=；(8)(1 -1 -2 1)w '=；(9)(2 -1 -1 2)w '=； (10)(2 -1 -2 1)w '=；(11)(2 -2 -2 0)w '=；(12)(2 -2 -2 1)w '=；收敛所以最终得到解向量(2 -2 -2 1)w '=，相应的判别函数为123()2221d x x x x =--+。题5：用多类感知器算法求下列模式的判别函数： ω1: (-1 -1)T ，ω2: (0 0)T ，ω3: (1 1)T

模式识别作业

模式识别作业班级：学号：姓名：

一、实验内容（1）了解与熟悉模式识别系统的基本组成和系统识别原理。（2）使用增添特征法对特征进行提取与选择。（3）编写MATLAB程序，对原始数据特征进行提取与选择，并选择适当的分类器对样本进行训练和分类，得出最后的分类结果以及识别正确率。二、实验原理模式识别系统的原理图如下：图1.模式识别系统原理图对原始样本数据进行一些预处理，使用增添特征法进行特征提取与选择。增添特征法也称为顺序前进法（SFS），每次从未选择的特征中选择一个，使得它与已选特征组合后判据值J最大，直到选择的特征数目达到d。特征选取后用SVM分类器对随机选取的训练样本和测试样本进行分类，最后得出不同特征维数下的最高SVM分类正确率，以及不同特征维数下的最大类别可分性判据。三、实验方法及程序 clear; clc; load('C:\Users\Administrator\Desktop\homework\ionosphere.mat'); m1=225;m2=126; p1=m1/(m1+m2);p2=m2/(m1+m2); chosen=[]; for j=1:34 [m,n]=size(chosen);n=n+1; J1=zeros(1,33); for i=1:34 Sw=zeros(n,n);Sb=zeros(n,n); S1=zeros(n,n);S2=zeros(n,n); p=any(chosen==i); if p==0 temp_pattern1=data(1:225,[chosen i]); temp_pattern2=data(226:351,[chosen i]);

模式识别习题及答案

模式识别作业三

黄庆明 模式识别与机器学习 第三章 作业

北邮模式识别课堂作业答案(参考)

模式识别大作业02125128(修改版)

贝叶斯决策理论-模式识别课程作业

中科院模式识别第三次(第五章)_作业_答案_更多

模式识别-作业4

模式识别作业(全)

北邮模式识别课堂作业答案(参考)

模式识别大作业

模式识别作业Homework#2

模式识别课程作业proj03-01

模式识别第三章-感知器算法

北工大模式识别基础课程作业

第三章作业(1)

模式识别作业

模式识别习题及答案

黄庆明模式识别与机器学习第三章作业