《材料力学》第章%B应力状态和强度理论%B习

第七章 应力状态和强度理论 习题解
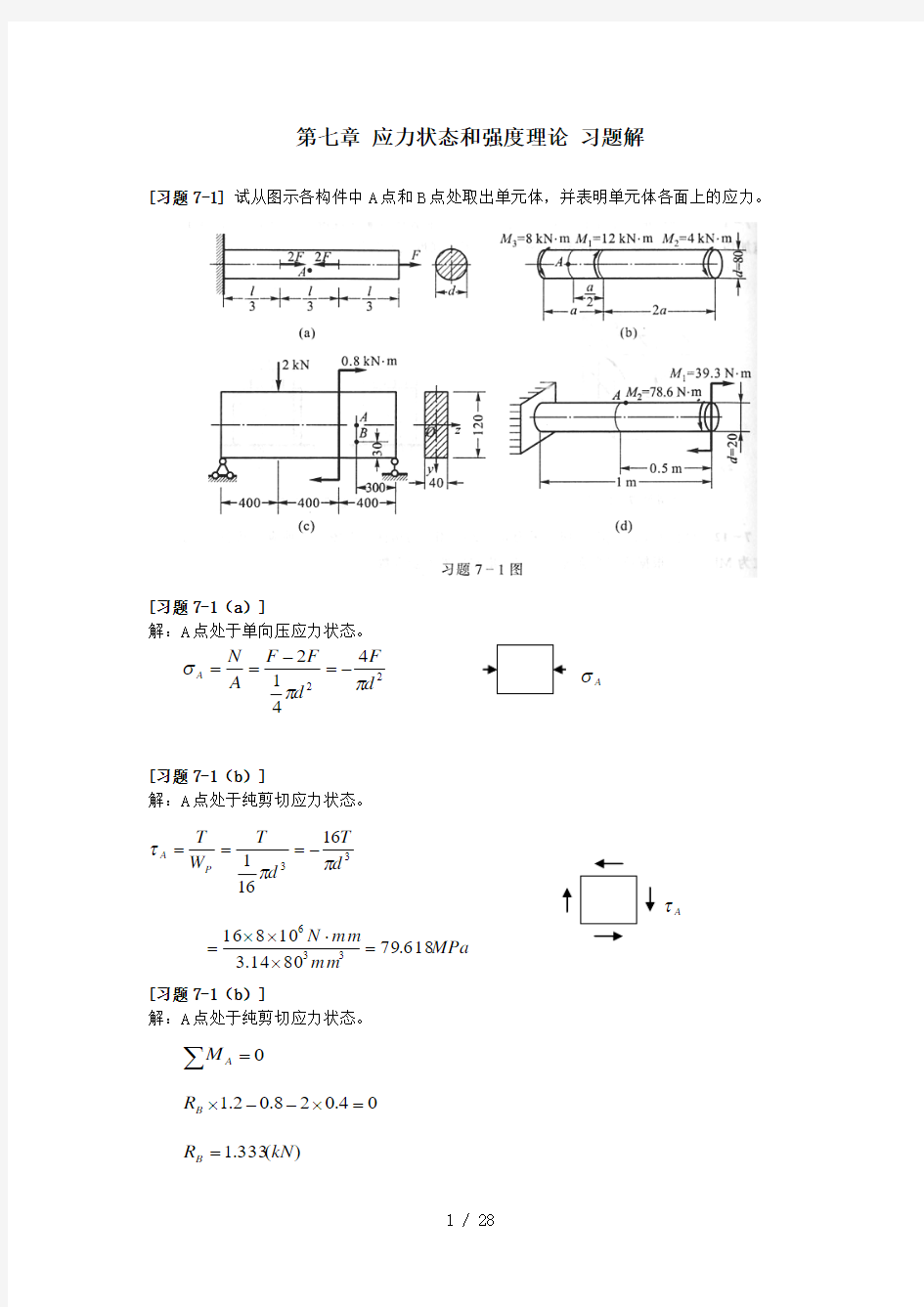
[习题7-1] 试从图示各构件中A 点和B 点处取出单元体,并表明单元体各面上的应力。
[习题7-1(a )]
解:A 点处于单向压应力状态。
2244
12d F d F F A N A ππσ-=-==
[习题7-1(b )]
解:A 点处于纯剪切应力状态。
331616
1d T d T W T P A ππτ-===
MPa mm mm N 618.798014.3108163
36=????=
[习题7-1(b )]
解:A 点处于纯剪切应力状态。
0=∑A
M
04.028.02.1=?--?B R )(333.1kN R B =
A σ
A τ
)(333.1kN R Q B A -=-=
MPa mm
N A Q A 417.01204013335.15.12-=??-=?
=τ
B 点处于平面应力状态
MPa
m m m m m m N I y M z
B B 083.21204012
130103.0333.1436=??????==σMPa m m m m m m
N b I QS z z
B 312.0401204012
145)3040(13334
33
*-=??????-==
τ
[习题7-1(d )]
解:A 点处于平面应力状态
MPa m m m m N W M z
A A 064.502014.332
1103.39333=????==σ
MPa m m m m N W T P
A 064.502014.316
1106.78333
=????==
τ [习题7-2] 有一拉伸试样,横截面为mm mm 540?的矩形。在与轴线成0
45=α角的面上切应力MPa 150=τ时,试样上将出现滑移线。试求试样所受的轴向拉力F 。 解:A
F
x =
σ;0=y σ;0=x τ 004590cos 90sin 2
x y
x τσστ+-=
A
F 20
45=
τ 出现滑移线,即进入屈服阶段,此时,
15020
45≤=
A
F
τ kN N mm mm N A F 6060000540/30030022==??==
[习题7-3] 一拉杆由两段沿n m -面胶合而成。由于实用的原因,图中的α角限于0
60
~0范围内。作为“假定计算”,对胶合缝作强度计算时,可以把其上的正应力和切应力分别与相应的许用应力比较。现设胶合缝的许用切应力][τ为许用拉应力][σ的4/3
,且这一拉杆
A τ
B τ
B
σA
τA σ
的强度由胶合缝强度控制。为了使杆能承受最大的荷载F ,试问α角的值应取多大? 解:A
F
x =
σ;0=y σ;0=x τ ατασσσσσα2sin 2cos 2
2
x y
x y
x --+
+=
][22cos 12cos 22σαασα≤+=+=
A F A F A F ][22cos 1σα
≤+A F
][cos 2σα≤A
F
α
σ2cos ][A F ≤
α
σ2max,cos ][A
F N =
ατασστα2cos 2sin 2
x y
x +-=
][43
][2sin 2στατα=≤=
A F ασ2sin ][5.1A F ≤
α
σ2sin ][5.1max,A
F T =
α(
)
0.9 10 20 30 36.8833 40 50 60
N F max,(A ][σ) 1.000 1.031 1.132 1.333 1.563 1.704 2.420 4.000 T F max,(A ][σ)
47.754 4.386 2.334 1.732 1.562
1.523 1.523 1.732
最大荷载随角度变化曲线
0.000
1.000
2.000
3.000
4.000
5.0000
10
20
304050
60
斜面倾角(度)
Fmax,N,Fmax,T
Fmax,N
Fmax,T
最大荷载随角度变化曲线
0.000
1.000
2.000
3.000
4.000
5.0000
10
20
304050
60
斜面倾角(度)
Fmax,N,Fmax,T
Fmax,N
Fmax,T
由以上曲线可知,两曲线交点以左,由正应力强度条件控制最大荷载;交点以右,由切应力强度条件控制最大荷载。由图中可以看出,当0
60=α时,杆能承受最大荷载,该荷载为:
A F ][732.1max σ=
[习题7-4] 若上题中拉杆胶合缝的许用应力][5.0][στ=,而M P a 7][=τ,MPa 14][=σ,则α值应取多大?若杆的横截面面积为2
1000
mm ,试确定其最大许可荷载。 解: 由上题计算得:α
σ2
max,cos ][A
F N =
ατασστα2cos 2sin 2
x y
x +-=
][5.0][2sin 2στατα=≤=
A F
α
σ2sin ][A F ≤
α
σ2sin ][max,A
F T =
α(0)
0.9
10
20
26.565051 30
40
50
60 N F max,(A ][σ)
1.000 1.031 1.132 1.250 1.333 1.704
2.420 4.000 T F max,(A ][σ)
31.836 2.924 1.556 1.250
1.155 1.015 1.015
1.155
由以上曲线可知,两曲线交点以左,由正应力强度条件控制最大荷载;交点以右,由切应力强度条件控制最大荷载。由图中可以看出,当0
565051.26=α时,杆能承受最大荷载,该荷载为:kN N mm mm N A F 5.17175001000/1425.1][25.122max ==??==σ
[习题7-5] 试根据相应的应力圆上的关系,写出图示单元体任一斜面n m -上正应力及切应力的计算公式。设截面n m -的法线与x 轴成α角如图所示(作图时可设||||x y σσ>)。
解:坐标面应力:X (x σ,0);Y (y σ,0)
设n m -斜面的应力为M (ασ,ατ)。X 、Y 点 作出如图所示的应力圆。
由图中的几何关系可知:
)(11N O O O NO --=-=ασ
)2cos 2
2|(|ασσσσσy
x y
x x --
-+
-=
)2cos 22
(ασσσσσy
x y
x x --
-+
--=
)2cos 2
22(
ασσσσσy
x y
x x --
-+--=
ασσσσ2cos 2
2
y
x y
x -+
+=
ασσατα2sin 2
2sin y
x OM -=
=
[习题7-6] 某建筑物地基中的一单元体如图所示,MPa y 2.0-=σ(压应力),
MP a
x 05.0-=σ(压应力)。试用应力圆求法线与x 轴成顺时针0
60夹角且垂直于纸面的斜面上的正应力及切应力,并利用习题7-5中得到的公式进行校核。
解:坐标面应力:X (-0.05,0);Y (-0.2,0)
060-=α。根据以上数据作出如图所示的应
力圆。图中比例尺为cm 1代表MPa 05.0。 按比例尺量得斜面的应力为:
MPa 1625.00
60-=-σ
MPa 065.00
60-=-τ
按习题7-5得到的公式计算如下:
ασσσσσα2cos 2
2
y
x y
x -+
+=
MPa 1625.0)120cos(2
2
.005.022.005.00600
-=-+-+--=
-σ
ασστα2sin 2
y
x -=
MPa 065.0)120sin(2
2
.005.00600
-=-+-=
-τ
作图法(应力圆法)与解析法(公式法)的结果一致。
[习题7-7] 试用应力圆的几何关系求图示悬臂梁距离自由端为m 72.0的截面上,在顶面以下mm 40的一点处的最大及最小主应力,并求最大主应力与x 轴之间的夹角。
解:(1)求计算点的正应力与切应力
MPa mm mm mm N bh My I My z 55.1016080401072.01012124
363=??????===σ
MPa m m m m m m N b
I QS z z 88.0801608012
160)4080(10104333*-=???????-==τ
(2)写出坐标面应力 X (10.55,-0.88)
Y (0,0.88)
(3) 作应力圆求最大与最小主应力,
并求最大主应力与x 轴的夹角 作应力圆如图所示。从图中按
比例尺量得:
MPa 66.101=σ
MPa 06.03-=σ
0075.4=α
[习题7-8] 各单元体面上的应力如图所示。试利用应力圆的几何关系求: (1)指定截面上的应力; (2)主应力的数值;
(3)在单元体上绘出主平面的位置及主应力的方向。
[习题7-8(a )]
解:坐标面应力:X (20,0);Y (-40,0)0
60=α。根据以上数据作出如图所示的应
力圆。图中比例尺为cm 1代表MPa 10。按比例尺量得斜面的应力为:
MPa 250
120-=σ, MPa 260
120=τ;MPa 201=σ,MPa 403-=σ;000=α。
[习题7-8(b )]
解:坐标面应力:X (0,30);Y (0,-30)0
30=α。根据以上数据作出如图所示的应力圆。图中比例尺为cm 1代表MPa 10。按比例尺量得斜面的应力为:
MPa 260
60-=σ ,MPa 150
60=τ;MPa 301=σ,MPa 303-=σ;0045-=α。
[习题7-8(c )]
解:坐标面应力:X (-50,0);Y (-50,0)0
30=α。根据以上数据作出如图所示的应力圆。图中比例尺为cm 1代表MPa 20。按比例尺量得斜面的应力为:
MPa 500
60-=σ ,00
60=τ;MPa 502-=σ,MPa 503-=σ。
单元体图
应力圆(O.Mohr 圆)
主单元体图
单元体图
应力圆(O.Mohr 圆)
主单元体图
1
σ3
σ
[习题7-8(d )]
解:坐标面应力:X (0,-50);Y (-20,50)0
0=α。根据以上数据作出如图所示的应力圆。图中比例尺为cm 1代表MPa 20。按比例尺量得斜面的应力为:
MPa 400
45=σ ,100
45=τ;MPa 411=σ,MPa 02=σ,MPa 613-=σ;'003539=α。
[习题7-9] 各单元体如图所示。试利用应力圆的几何关系求: (1)主应力的数值;
(2)在单元体上绘出主平面的位置及主应力的方向。 [习题7-9(a )]
解:坐标面应力:X (130,70);Y (0,-70)。根据以上数据作出如图所示的应
力圆。图中比例尺为cm 1代表MPa 20。按比例尺量得斜面的应力为:
MPa 5.1601=σ,MPa 02=σ,MPa 5.303-=σ;'005623-=α。
单元体图
应力圆(O.Mohr 圆)
主单元体图
单元体图
应力圆(O.Mohr 圆)
主单元体图
单元体图
应力圆(O.Mohr 圆)
主单元体图
2σ
3
σ
[习题7-9(b )]
解:坐标面应力:X (-140,-80);Y (0,80)。根据以上数据作出如图所示的应
力圆。图中比例尺为cm 1代表MPa 40。按比例尺量得斜面的应力为:
MPa 0.361=σ,MPa 02=σ,MPa 1763-=σ;006.65=α。
[习题7-9(c )]
解:坐标面应力:X (-20,-10);Y (-50,10)。根据以上数据作出如图所示的应
力圆。图中比例尺为cm 1代表MPa 10。按比例尺量得斜面的应力为:
MPa 01=σ,MPa 25.162-=σ,MPa 75.533-=σ;001.16=α。
[习题7-9(d )]
解:坐标面应力:X (80,30);Y (160,-30)。根据以上数据作出如图所示的应
力圆。图中比例尺为cm 1代表MPa 20。按比例尺量得斜面的应力为:
MPa 1701=σ,MPa 702=σ,MPa 03=σ;006.71-=α。
单元体图
应力圆(O.Mohr 圆)
主单元体图
单元体图
应力圆(O.Mohr 圆)
主单元体图
单元体图
应力圆(O.Mohr 圆)
主单元体图
[习题7-10] 已知平面应力状态下某点处的两个截面的的应力如图所示。试利用应力圆求该点处的主应力值和主平面方位,并求出两截面间的夹角α值。
平面应力状态下的两斜面应力
应力圆
解:两斜面上的坐标面应力为:
A (38,28),
B (114,-48)
由以上上两点作出的直线AB 是应力圆上的一条弦, 如图所示。作AB 的垂直平分线交水平坐标轴于C
点,则C 为应力圆的圆心。设圆心坐标为C (0,x ) 则根据垂直平线上任一点到线段段两端的距离相等 性质,可列以下方程:
2222)480()114()280()38(++-=-+-x x
解以上方程得:86=x 。即圆心坐标为C (86,0) 应力圆的半径:
570.55)280()3886(22=-+-=r
主应力为:
MPa r x 57.14157.55861=+=+=σ MPa r x 43.3057.55862=-=-=σ
03=σ
(2)主方向角
(上斜面A 与中间主应力平面之间的夹角)
(上斜面A 与最大主应力平面之间的夹角)
(3)两截面间夹角:
[习题7-11] 某点处的应力如图所示,设αατσ,及y σ值为已知,试考虑如何根据已知数据直接作出应力圆。
解:
0=∑X
0sin cos =+-ατασσααx (1)
0=∑Y
0cos sin =--ατασσααy (2)
(1)、(2)联立,可解得x σ和α。
至此,三个面的应力均为已知:X (x σ,0),Y (y σ,0)(x σ,y σ均为负值);
α(αατσ,)。由X ,Y 面的应力就可以作出应力圆。
[习题7-12] 一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示m m -上
c b a ,,三点处的主应力。
解:(1)求
a 点的主应力
)(7.3314666620011012
1
2201201211214333mm bh I z =??-??==∑
)(3336.301333110
7.331466663max mm y I W z z ===
MPa mm mm N W M z a 390.2123336.301333104.01603
6=???==σ
因a 点处于单向拉伸状态,故MPa 39.2121==ασσ,032==σσ。 (2)求b 点的主应力
MPa mm mm mm N I My z b 081.1937.33146666100104.01603
6=????==σ
在m m -的左邻截面上,kN
Q 160=
MPa mm
mm mm N d I QS z z b 821.60107.33146666105)10120(101604
3
3*=?????==τ 即坐标面应力为X (193.081,60.821),Y(0,-60.821).
2
214)(2
12x y x y
z τσσσσσ+-+
+=
MPa 64.210821.604081.1932
1
2081.19322=?++=
02=σ
2
234)(2
12
x y x y
z τσσσσσ+--
+=
MPa 56.17821.604081.1932
1
2081.19322-=?+-=
(3)求c 点的主应力
0=c σ
MPa mm
mm mm N d I QS z z c 956.84107.33146666)501001*********(101604
3
3*=???+????==τ 即坐标面应力为X (0,84.956),Y(0,-84.956).
2
214)(2
12x y x y
z τσσσσσ+-+
+=
MPa 956.84956.8442
1
2=?=
02=σ
2
234)(2
12
x y x y
z τσσσσσ+--
+=
MPa 956.84956.8442
1
2-=?-
= [习题7-13] 在一块钢板上先画上直径mm d 300=的圆,然后在板上加上应力,如图所示。试问所画的圆将变成何种图形?并计算其尺寸。已知钢板的弹性模量GPa E 206=,28.0=ν。
解:坐标面应力X (70,21),Y (14,-21)
所画的圆变成椭圆,其中
(长轴)
(短轴)
[习题7-14] 已知一受力构件表面上某点处的MPa x 80=σ,MPa y 160-=σ,0=z σ,单元体的三个面上都没有切应力。试求该点处的最大正应力和最大切应力。 解:最大正应力为MPa x 801==σσ。最小正应力是MPa y 1603-==σσ。
最大切应力是)(1202
)
160(802
3
1max MPa =--=
-=σστ
[习题7-15] 单元体各面上的应力如图所示。试用应力圆的几何关系求主应力及最大切应力。
[习题7-15(a )]
解:坐标面应力:X (70,-40),Y (30,-40),Z (50,0)
由XY 平面内应力值作a 、b 点,连接a 、b 交轴得圆心C (50,0)
应力圆半径:
单元体图
应力圆
[习题7-15(b )]
解:坐标面应力:X (60,40),Y (50,0),Z (0,-40)
由XZ 平面内应力作a 、b 点,连接a 、b 交轴于C 点,OC =30,故应力圆圆心C (30,0)
应力圆半径:
[习题7-15(c )]
解:坐标面应力:X (-80,0),Y (0,-50),Z (0,50)
由YZ 平面内应力值作a 、b 点,圆心为O ,半径为50,作应力圆得
单元体图
应力圆
单元体图
应力圆
[习题7-16] 已知一点处应力状态的应力圆如图所示。试用单元体示出该点处的应力状态,并在该单元体上绘出应力圆上A 点所代表的截面。
[习题7-16(a)]
解:该点处于三向应力状态:MPa 701=σ,MPa 502=σ,MPa 103=σ。A 点所代表的截面平行于1σ的方向。据此,可画出如图所示的单元体图和A 截的位置。
[习题7-16(b)]
解:该点处于三向应力状态:MPa 501=σ,MPa 102=σ,MPa 103-=σ。A 点所代表的截面平行于3σ的方向。据此,可画出如图所示的单元体图和A 截的位置。
应力圆
主单元体图与A 截面的位置
1σ
2σ
3σ
A
[习题7-17] 有一厚度为mm 6的钢板,在两个垂直方向受拉,拉应力分别为150MPa 及55MPa 。钢材的弹性常数为GPa E 210=,25.0=ν。试求钢板厚度的减小值。 解:4
3
1044.2)55150(1021025.0)(-?-=+?=
+-
=MPa MPa MPa
E
y x z σσν
ε 钢板厚度的减小值为:
)(10464.11044.26||34mm z --?=??==?εδδ
[习题7-18] 边长为mm 20的钢立方体置于钢模中,在顶面上均匀地受力kN F 14=作用。已知3.0=ν,假设钢模的变形以及立方体与钢模之间的摩擦力可略去不计。试求立方体各个面上的正应力。 解:
(1)
(2)
联解式(1),(2)得
应力圆
主单元体图与A 截面的位置
1σ
2σ
3σ
A
030
[习题7-19] 在矩形截面钢拉伸试样的轴向拉力kN F 20=时,测得试样中段B 点处与
其轴线成0
30方向的线应变为4301025.30-?=ε。已知材料的弹性模量GPa E 210=,
试求泊松比ν。
解:平面应力状态下的广义虎克定律)(1
y x x E
νσσε-=适用于任意两互相垂直的y x ,方向,故有:)(1
0006030
30--=
νσσεE 。钢杆处于单向拉应力状态: 拉杆横截面上的正应力 MPa 10010
2010203
=??=σ
斜截面上的应力 ()
MPa 7530cos 2
30=σ=σ
()()MPa 2560cos 2
60=-=-
σσ
由广义虎克定律 []
6030
301
-νσ-σ=
εE []25751021011025.33
4?ν-?=
?-
解得: 27.0=ν
[习题7-20] D =120mm ,d =80mm 的空心圆轴,两端承受一对扭转力偶矩,如图所示。在轴的中部表面A 点处,测得与其母线成方向的线应变为
。已知材料的
弹性常数
,
,试求扭转力偶矩
。
解:
方向如图
[习题7-21] 在受集中力偶e M 作用矩形截面简支梁中,测得中性层上 k 点处沿0
45方向的线应变为045ε。已知材料的弹性常数ν,E 和梁的横截面及长度尺寸l d a h b ,,,,。试求集中力偶矩e M 。
解:支座反力:
l M R e A =
(↑);l
M R e
B = (↓) K 截面的弯矩与剪力:
l aM a R M e A k =
=;l
M R Q e
A k == K 点的正应力与切应力:
0=σ;Al
M A Q e
k 235.1=?
=τ 故坐标面应力为:X (τ,0),Y (0,-τ)
Al
M e x y x y
z 234)(212
221==+-+
+=
ττσσσσσ
02=σ
Al
M e x y x y
z 234)(212
2
23-=-=+--
+=
ττσσσσσ ∞=--=
y
x x
σστα22tan 0
0045=α (最大正应力1σ的方向与x 正向的夹角),故
)(1
311450
νσσεε-=
=E
)1(23)]23(23[(10
45ννε+=--=
EAl
M Al M Al M E e e e
004545)
1(32)
1(32εννε+=
+=
Ebhl
EAl M e
[习题7-22] 一直径为mm 25的实心钢球承受静水压力,压强为MPa 14。设钢球的GPa E 210=,3.0=ν。试问其体积减小多少?
解:体积应变
=
[习题7-23] 已知图示单元体材料的弹性常数GPa E 200=,3.0=ν。试求该单元体的形状改变能密度。
解:坐标面应力:X (70,-40),Y (30,40),Z (50,0) 在XY 面内,求出最大与最小应力:
2
2max 4)(2
12
x y x y
z τσσσσσ+-+
+=
弹性力学教学大纲
课程编号:05z8514 弹性力学Theory of Elasticity 学分学时:3/48 先修课程: 高等数学;线性代数;理论力学;材料力学 一、课程教学目标 《弹性力学》是航空、航天结构强度和力学专业的重要专业基础课程,是固体力学的一个分支。主要研究弹性体受外力作用或温度改变等原因而产生的应力、位移和变形。弹性力学的任务是分析各种结构或其构件在弹性阶段的应力和位移,校核它们是否具有所需的强度、刚度和稳定性,并寻求或改进它们的计算方法。本课程的主要研究对象为非杆状结构,如板、壳以及其它实体结构。通过本课程的学习可为进一步学习力学类和相关工程类的后续课程打下坚实的力学基础。 二、教学内容及基本要求 1. 绪论(2学时) 弹性力学的发展史;研究内容;基本假设;矢量、张量基本知识。 2. 应力理论(4学时) 内力和应力;斜面应力公式;应力分量转换公式;主应力、应力不变量;最大剪应力;应力偏量;平衡微分方程。 3. 应变理论(4学时) 位移和变形;几何方程;转动张量;主应变和应变不变量;变形协调方程;位移场的单值条件;由应变求位移。 4. 本构关系(2学时) 热力学定律与应变能;本构关系;具有弹性对称面的弹性材料的本构关系;各向同性弹性材料的弹性常数;各向同性弹性材料的应变能密度 5. 弹性理论的建立与一般原理(4学时) 弹性力学基本方程和边界条件;位移解法和拉梅方程;应力解法与变形协调方程;叠加原理;解的唯一性原理;圣维南原理。 6.柱形杆问题(4学时) 圣维南问题;柱形扭转问题的基本解法;反逆法与半逆法,扭转问题解例;薄膜比拟;*柱形杆的一般弯曲。 7.平面问题(12学时) 平面问题及其分类;平面问题的基本解法;应力函数的性质;直角坐标解例(矩形梁的纯弯曲、简支梁受均布载荷和任意分布载荷);极坐标中的平面问题基本方程;轴对称问题(均匀圆筒或圆环、纯弯的曲梁、压力隧洞);非轴对称问题(小圆孔应力集中、楔体问题);关于解和解法的讨论。 8. 空间问题(2学时) 基本方程及求解方法;空间轴对称和球对称问题的基本方程;半空间体受重力及均布压力;半空间体在边界上受法向集中力;空心球受内压作用问题。 9.能量原理与变分法(6学时) 弹性体的变形比能与形变势能;变分法;位移变分方程;位移变分法;位移变分法应用于平面问题;应力变分方程与极小余能原理;应力变分法;应力变分法应用于平面问题;应力变分法应用于扭转问题。 10.复变函数解法或薄板弯曲(4学时)
应力状态及强度理论
图8-1 第 8章 应力状态及强度理论 例8-1 已知应力状态如图7-1所示,试计算截 面m-m 上的正应力m σ与切应力m τ 。 解:由图可知,x 与y 截面的应力分别为 MPa x 100-=σ MPa x 60-=τ MPa y 50=σ 而截面m-m 的方位角则为 α= -30o 将上述数据分别代入式(7-1)与(7-2), 于是得 ()()()()MPa m 5.11460sin 6060cos 250100250100-=?-?+?---++-=σ()()()MPa m 0.3560cos 6060sin 2 50100=?-?-?---=τ 例8-2 试用图解法解例8-1(图8-2a )。 (a) (b) 图8-2 解:首先,在τσ-平面内,按选定的比例尺,由坐标(-100,-60)与(50,60)分别确定A 和B 点图7-2b )。然后,以AB 为直径画圆,即得相应的应力圆。 为了确定截面m-m 上的应力,将半径CA 沿顺时针方向旋转α2=60o至CD 处,所得D 点即为截面m-m 的对应点。 按选定的比例尺,量得OE =115MPa (压应力),ED =35MPa ,由此得截面 m-m 的正应力与切应力分别为
MPa m 115-=σ MPa m 35=τ 例 8-3 从构件中切取一微体,各截面的应力如图8-3a 所示,试用解析法与图解法确定主应力的大小及方位。 (a) (b) 图8-3 解:1.解析法 x 和y 截面的应力分别为 MPa x 70-=σ,MPa x 50=τ,0=y σ 将其代入式 (7-3)与 (7-5),得 }{MPa MPa 2696502070207022max min -=+?? ? ??--±+-=σσ ?-=??? ??--=?? ? ??-- =5.6202650arctan arctan max y x o σστα 由此可见, MPa 261=σ,02=σ,MPa 963-=σ 而正应力1σ 的方位角 o α则为-62.5o(图8-3a )。 2.图解法 按选定的在τσ-平面内,按选定的比例尺,由坐标(-70,50)与(0,-50)分别确定D 和E 点(图8-3b )。然后,以DE 为直径画圆即得相应的应力圆。 应力圆与坐标轴σ相交于A 和B 点,按选定的比例尺,量得OA =26MPa ,
第二章弹性力学基础
第二章弹性力学基础 弹性力学又称弹性理论,它是固体力学的一个分支。弹性力学任务是确定结构或机械零件在外载荷作用或温度改变等原因而发生的应力、位移和应变。 弹性力学与材料力学总的任务是相同的,但弹性力学研究的问题比材料力学要更加深刻和精确,并研究材料力学所不能解决的一些问题。 材料力学-----研究杆状构件(长度>>高度和宽度)在拉压、剪切、弯曲、扭转作用下的应力和位移。 弹性力学-----研究板壳、挡土墙、堤坝、地基等实体结构。对杆状构件作较精确的分析,也需用弹性力学。 结构力学-----研究杆状构件所组成的结构。例如桁架、刚架。
第一节弹性力学假设 在弹性力学中,所研究的问题主要是理想弹性体的线性问题,所谓理想弹性体的线性问题,是指符合以下假定的物体。 1. 假设物体是线弹性的 假定物体服从虎克定律,即应变与引起该应变的应力成正比,反映这一比例关系的常数,就是弹性常数。即该比例关系不随应力、应变的大小和符号而变。 由材料力学已知: 脆性材料的物体:在应力?比例极限以前,可作为近似的完全弹性体; 韧性(塑性)材料的物体:在应力<屈服极限以前,可作为近似的完全弹性体。 这个假定,使得物体在任意瞬时的应变将完全取决于该瞬时物体所受到的外力或温度变化等因素,而与加载的历史和加载顺序无关。 2. 假设物体是连续性的 假设整个物体的体积都被该物体介质完全充满,不留下任何空隙。有了这一假定决定了应力、应变、位移是连续的,可用坐标的连续函数来表示他们的变化规律。 注:实际上,一切物体都是由微粒组成的,都不能符合该假定。但是由于物体粒子的尺寸以及相邻粒子间的距离,
都比物体自己本身的尺寸小得很多,因此连续性假设不会引起显着的误差。 3. 假设物体是均匀性、各向同性的 整个物体是由同一材料组成的。这样整个物体的所有各部分才具有相同的弹性,因而物体的弹性常数不随坐标而变化,可以取出该物体的任意一小部分来加以分析,然后把分析所得结果应用于整个物体。 各向同性是指物体内一点的弹性在所的各个方向上都是相同的,故物体的弹性常数不随方向而变化。 对于非晶体材料,是完全符合这一假定。而由木材,竹材等做成的构件,就不能作为各向同性体来研究;钢材构件基本上是各向同性的。 弹性常数? 凡是符合以上三个假定的物体,就称为理想弹性体。 4. 假设物体的位移和应变是微小的 假定物体在载荷或温度变化等外界因素的作用下所产生的位移远小于物体原来的尺寸,应变分量和转角都远小于1。 因此 ①在建立物体变形以后的平衡方程时,可用变形前的尺寸代替变形后的尺寸,而不至于引起显著的误差。
第7章-应力状态和强度理论03.
西南交it 大学应用力*与工程系材#^力学教研i 图示拉伸甄压缩的单向应力状态,材料的破 坏有两种形式: 塑性屈服;极限应力为0■力=<5;或bpO2 腌性斷裂;极限应力为O ■必= CJ\ 此时,4 O>2和偽可由实验测得.由此可建 互如下S 度余件: ^mai 其中n 为安全系数? 2)纯剪应力状态: 图示纯剪应力狀态,材料的破 坏有两 种形式: 塑性屈服:极限应力为 腌性斯裂:极限应力为5 = 5 %和昭可由实验测得.由此可建立如下 =(^■1 it §7.7强度理论及其相当应力 1、概述 1)单向应力状态: a. <亠[6 n 其中, ?度条件:
前述a 度条件对材料破坏的原因并不深究.例如 图示低碳钢拉(压)时的强度条件为: r V J - b, b|nw W — — — // n 然而,其屈服是由于 YnurJl 起的,对?示单向 应力状态,有: 「niu 依照切应力强度条件,有: 4)材料破坏的形式 常温、静栽时材料的破坏形式大致可分为: ?腌性斷裂型: 例如:铸铁:拉伸、扭转等; "钢:三向拉应力状态. -塑性屈月艮型: 例如:低碳钢:拉伸、扭转寻; 铸铁:三向压缩应力状态. 可见:材料破坏的形式不仅与材料有关,还与应力状态有关. , 5)强度理论 根据一些实验资料,针对上述两种破坏形式,分别针对它们发生破坏的原因提出假说,并认为不论材料处于何种应力状态,某种类型的破坏都是由同一因素引起,此即为强度理论. 常用的破坏判据有: 旎性断裂:5,磁可皿 ?性斷裂:V; 下面将讨论常用的-基于上述四种破坏判据的?虞理论. 一点应力状态概念及其表示方法 凡提到“应力”,必须指明作用在哪一点,哪个(方向)截面上。因为受力构件内同一截面上不同点的应力一般是不同的,通过同一点不同(方向)截面上应力也是不同的。例如,图8-1弯曲梁横截面上各点具有不同的正应力与剪应力; 图8-2通过轴向拉伸杆件同一点的不同(方向)截面上具有不同的应力。 2.一点处的应力状态是指通过一点不同截面上的应力情况,或指所有方位截面上应力的集合。应力分析就是研究这些不同方位截面上应力随截面方向的变化规律。如图8-3是通过轴向拉伸杆件内点不同(方向)截面上 的应力情况(集合) 3.一点处的应力状态可用围绕该点截取的微单元体(微正六面体)上三对互相垂直微面上的应力情况来表示。如图8-4(a,b)为轴向拉伸杆件内围绕点截取的两种微元体。 特点:根据材料的均匀连续假设,微元体(代表一个材料点)各微面上的应力均匀分布,相互平行的两个侧面上应力大小相等、方向相反;互相垂直的两个侧面上剪应力服从剪切互等关系。 §8-2平面应力状态的工程实例1.薄壁圆筒压力容器 为平均直径,为壁厚 由平衡条件 得轴向应力:(8-1a) 图8-5c(Ⅰ-Ⅰ,Ⅱ-Ⅱ为相距为的横截面,H-H为水平径向面) 由平衡条件或, 得环向应力:(8-1b) 2.球形贮气罐(图8-6) 由球对称知径向应力与纬向应力相同,设为 对半球写平衡条件: 得(8-2) 3.弯曲与扭转组合作用下的圆轴 4.受横向载荷作用的深梁 §8-3平面一般应力状态分析——解析法 空间一般应力状态 如图8-9a所示,共有9个应力分量:面上的,,;面上的,,;面上的,,。 1)应力分量的下标记法:第一个下标指作用面(以其外法线方向表示),第二个下标指作用方向。由剪应力互等定理,有: , , 。2)平面一般应力状态如图8-9b所示,即空间应力状态中,方向的应力分量全部为零();或只存在作用于x-y平面内的应力分量,,,,其中,分别为,的简写,而= 。 3)正负号规定:正应力以拉应力为正,压为负;剪应力以对微元体内任意一点取矩为顺时针者为正,反之为负。 2.平面一般应力状态斜截面上应力 如图8-10所示,斜截面平行于轴且与面成倾角,由力的平衡条件: 和 可求得斜截面上应力,: 40 MPa .word 可编辑 . 应力状态强度理论 1. 图示单元体,试求60100 MPa (1)指定斜截面上的应力; (2)主应力大小及主平面位置,并将主平面标在单元体上。 解: (1) x y x y cos 2x sin 276.6 MPa 22 x y sin 2x cos232.7 MPa 2 3 1 (2)max xy( x y) 2xy281.98MPa39.35 min22121.98 181.98MPa,2 ,3121.98MPa 12 xy1200 0arctan()arctan39.35 2x y240 200 6060 2. 某点应力状态如图示。试求该点的主应力。129.9129.9解:取合适坐标轴令x25 MPa,x 由 120xy sin 2xy cos20 得 y 2 所以m ax x y ( xy ) 2xy 2 m in 22 129.9 MPa 2525 (MPa) 125MPa 50752( 129.9)250 150100 MPa 200 1 100 MPa,20 ,3200MPa 3. 一点处两个互成45 平面上的应力如图所示,其中未知,求该点主应力。 解:y150 MPa,x120 MPa .word 可编辑 . 由得45x y sin 2xy cos 2x 15080 22 x10 MPa 所以max xy(x y) 22 22xy min y x 45 45 45 214.22 MPa 74.22 1214.22 MPa,20 , 45 374.22 MPa 4.图示封闭薄壁圆筒,内径 d 100 mm,壁厚 t 2 mm,承受内压 p 4 MPa,外力偶矩 M e 0.192 kN·m。求靠圆筒内壁任一点处的主应力。 0.19210 3 解: xπ(0.104 40.14)0.05 5.75MPa t 32 x y pd MPa 50 4t pd MPa 100 2t M e p M e max x y(x y ) 2 xy2 min22100.7 MPa 49.35 1100.7 MPa,249.35 MPa,3 4 MPa 5.受力体某点平面上的应力如图示,求其主应力大小。 解:取坐标轴使 x 100 MPa,x 20MPa40 MPa100 MPa xy x y 12020 MPa 22cos2x sin 2 第四章应力和应变关系知识点 应变能原理 应力应变关系的一般表达式完全各向异性弹性体 正交各向异性弹性体本构关系弹性常数 各向同性弹性体应变能格林公式 广义胡克定理 一个弹性对称面的弹性体本构关系各向同性弹性体的应力和应变关系应变表示的各向同性本构关系 一、内容介绍 前两章分别从静力学和运动学的角度推导了静力平衡方程,几何方程和变形协调方程。由于弹性体的静力平衡和几何变形是通过具体物体的材料性质相联系的,因此,必须建立了材料的应力和应变的内在联系。应力和应变是相辅相成的,有应力就有应变;反之,有应变则必有应力。对于每一种材料,在一定的温度下,应力和应变之间有着完全确定的关系。这是材料的固有特性,因此称为物理方程或者本构关系。 对于复杂应力状态,应力应变关系的实验测试是有困难的,因此本章首先通过能量法讨论本构关系的一般形式。分别讨论广义胡克定理;具有一个和两个弹性对称面的本构关系一般表达式;各向同性材料的本构关系等。 本章的任务就是建立弹性变形阶段的应力应变关系。 二、重点 1、应变能函数和格林公式; 2、广义胡克定律的一般表达式; 3、具 有一个和两个弹性对称面的本构关系;4、各向同性材料的本构关系; 5、材料的弹性常数。 §4.1 弹性体的应变能原理 学习思路: 弹性体在外力作用下产生变形,因此外力在变形过程中作功。同时,弹性体内部的能量也要相应的发生变化。借助于能量关系,可以使得弹性力学问题的求 解方法和思路简化,因此能量原理是一个有效的分析工具。 本节根据热力学概念推导弹性体的应变能函数表达式,并且建立应变能函数表达的材料本构方程。 根据能量关系,容易得到由于变形而存储于物体内的单位体积的弹性势能,即应变能函数。 探讨应变能的全微分,可以得到格林公式,格林公式是以能量形式表达的本构关系。 如果材料的应力应变关系是线性弹性的,则单位体积的应变能必为应变分量的齐二次函数。因此由齐次函数的欧拉定理,可以得到用应变或者应力表示的应变能函数。 学习要点:1、应变能;2、格林公式;3、应变能原理。 1、应变能 弹性体发生变形时,外力将要做功,内部的能量也要相应的发生变化。本节通过热力学的观点,分析弹性体的功能变化规律。 根据热力学的观点,外力在变形过程中所做的功,一部分将转化为内能,一部分将转化为动能;另外变形过程中,弹性体的温度将发生变化,它必须向外界吸收或释放热量。设弹性体变形时,外力所做的功为d W,则 d W=d W1+d W2 其中,d W1为表面力F s所做的功,d W2为体积力F b所做的功。变形过程中,由外界输入热量为d Q,弹性体的内能增量为d E,根据热力学第一定律, d W1+d W2=d E - d Q 因为 将上式代入功能关系公式,则 7.1已知应力状态如图所示(单位:MPa ),试求: ⑴指定斜截面上的应力; ⑵主应力; ⑶在单元体上绘出主平面位置及主应力方向; ⑷最大切应力。 解: 100x MPa σ= 200y MPa σ= 100x MPa τ= 0 30α=- (1)cos 2sin 2211.622 x y x y x ασσσσ σατα+-= + -=sin 2cos 293.32 x y x MPa ασστατα-=+= (2)max 261.82 x y MPa σσσ+= = min 38.22x y MPa σσσ+== MPa 8.2611=σ MPa 2.382=σ 03=σ (3)13 max 130.92 MPa σστ-== 7.2扭矩m kN T ?=5.2作用在直径mm D 60=的钢轴上,试求圆轴表面上任一点与母线成ο 30=α方向上的正应变。设E=200GPa, 0.3υ=。 解:表面上任一点处切应力为: max 59P T MPa W τ= = 表面上任一点处单元体应力状态如图 30sin 251MPa στα=-=- 120sin 251MPa στα=-= () 00430301201 3.310E εσυσ-= -=? 2 στ τ 7.3用电阻应变仪测得空心钢轴表面某点与母线成ο45方向上的正应 变4 100.2-?=ε,已知转速min /120r ,G=80GPa ,试求轴所传 递的功率。 解:表面任一点处应力为 max 9550P P P T n W W τ== max 9550 P W n P τ∴= 纯剪切应力状态下,0 45斜截面上三个主应力为:1στ= 20σ= 3στ=- 由广义胡克定律 ()11311E E υ εσυστ+= -= 又()21E G υ=+Q V 2G τε∴= 代入max 9550 P W n P τ= ,得109.4P KW = 7.4图示为一钢质圆杆,直径mm D 20=,已知A 点与水平线成ο 60 方向上的正应变4 60101.4-?=ο ε,E=200GPa ,0.3υ=, 试求荷载P 。 解:0P A σ= 204D P πσ=? 斜截面上 02 060cos 4 σσσα== 2001503cos 4 σσσα== 由广义胡克定律 () 0006015060134E E υεσυσσ-= -= 将060043E εσυ = -代入2 04 D P πσ=? 解得P=36.2KN ο 第五章应力状态分析与强度理论 1、内容提要 1.应力状态的概念 1.1一点的应力状态 通过受力构件的一点的各个截面上的应力情况的集合,称为该点的应力状态。 1.2一点的应力状态的表示方法——单元体 研究受力构件内一点处的应力状态,可以围绕该点取一个无限小的正六面体,即单元体。若单元体各个面上的应力已知或已计算出,则通过该点的其他任意方位截面上的应力就可用解析法或图解法确定。 1.3主平面、主应力 单元体上切应力为零的平面称为主平面,主平面上的正应力称为主应力。 过受力构件内任一点总有三对相互垂直的主平面。相应的主应力用、、来表示,它们按代数值的大小顺序排列,即。是最大主应力,是最小主应力,它们分别是过一点的所有截面上正应力中的最大值和最小值。 1.4应力状态的分类 (1)单向应力状态,只有一个主应力不为零,另两个主应力均为零;(2)二向或平面应力状态,两个主应力不为零,另一个为零; (3)三向或空间应力状态,三个主应力都不为零。 单向应力状态又称简单应力状态,二向、三向应力状态称为复杂应力状态。 2.平面应力状态分析的解析法 在平面应力状态的单元体中,有一对平面上的应力等于零,即为主平面,其上主应力为零。可将单元体用平面图形表示,如图5-1所示。 2.1任意斜截面上的应力 当已知、、时,应用截面法,可得 (5-1) 式中,正应力以拉应力为正,压应力为负;切应力以对单元体内任意点的矩为顺时针转向为正,反之为负;为斜截面外法线与x平面外法线即x 轴间的夹角,角从x轴量起,反时针转向为正,反之为负。 2.2主应力 (5-2) 式中,和分别表示单元体上垂直于零应力面的所有截面上正应力的最大值和最小值。它们是三个主应力中的两个,而另一个主应力为零。三个 知识点9:应力状态理论和强度理论 一、应力状态理论 (一)应力状态的概念 1.一般情况下,受力构件内各点的应力是不同的,且同一点的不同方位截面上应力也不相同。过构件内某一点不同方位上总的应力情况,称为该点的应力状态。 2.研究一点的应力状态,通常是围绕该点截取一个微小的正六面体(即单元体)来考虑。单元体各面上的应力假设是均匀分布的,并且每对互相平行截面上的应力,其大小和性质完全相同,三对平面上的应力代表通过该点互相垂直的三个截面上的应力。当单元体三个互相垂直截面上的应力已知时,可通过截面法确定该点任一截面上的应力。截取单元体时,应尽可能使其三个互相垂直截面的应力为已知。 3.单元体上切应力等于零的截面称为主平面,主平面上的正应力称为主应力。过受力构件内任一点,一定可以找到一个由三个相互垂直主平面组成的单元 体,称为主单元体。它的三个主应力通常用σ 1,σ 2 和σ 3 来表示,它们按代数值 大小顺序排列,即σ 1>σ 2 >σ 3 。 4.一点的应力状态常用该点的三个主应力来表示,根据三个主应力的情况可分为三类:只有一个主应力不等于零时,称为单向应力状态;有两个主应力不等于零时,称为二向应力状态(或平面应力状态);三个主应力都不等于零时,称为三向应力状态。其中二向和三向应力状态称为复杂应力状态,单向应力状态称为简单应力状态。 5.研究一点的应力状态是对构件进行强度计算的基础。 (二)平面应力状态的分析 1.分析一点的平面应力状态有解析法和图解法两种方法,应用两种方法时都必须已知过该点任意一对相互垂直截面上的应力值,从而求得任一斜截面上的应力。 2.应力圆和单元体相互对应,应力圆上的一个点对应于单元体的一个面,应力圆上点的走向和单元体上截面转向一致。应力圆一点的坐标为单元体相应截面上的应力值;单元体两截面夹角为α,应力圆上两对应点中心角为2α;应力圆与σ轴两个交点的坐标为单元体的两个主应力值;应力圆的半径为单元体的最大切应力值。 3.在平面应力状态中,过一点的所有截面中,必有一对主平面,也必有一对与主平面夹角为45?的最大(最小)切应力截面。 4.在平面应力状态中,任意两个相互垂直截面上的正应力之和等于常数。 图9-1(a )所示单元体为平面应力状态的一般情况。单元体上,与x 轴垂直的平面称为x 平面,其上有正应力σx 和切应力τxy ;与y 轴垂直的平面称为y 平面,其上有正应力σy 和切应力τyx ;与z 轴垂直的z 平面上应力等于零,该平面是主平面,其上主应力为零。平面应力状态也可用图9-1(b )所示单元体的平面图来表示。设正应力以拉应力为正,切应力以截面外法线顺时针转90?所得的方向为正,反之为负。 (a ) (b ) (c ) 图9-1 图9-1(c )所示斜截面的外法线与x 轴之间的夹角为α。规定α角从x 轴逆时针向转到截面外法线n 方向时为正。α斜截面上的正应力和切应力为: ??? ??? ? +-=--++=ατασστατασσσσσαα2cos 2sin 22sin 2cos 22xy y x xy y x y x 最大正应力和最小正应力 2 2 min max 22xy y x y x τσσσσσσ+??? ? ? ?-±+= 第二章应力状态分析 一、内容介绍 弹性力学的研究对象为三维弹性体,因此分析从微分单元体入手,本章的任务就是从静力学观点出发,讨论一点的应力状态,建立平衡微分方程和面力边界条件。 应力状态是本章讨论的首要问题。由于应力矢量与内力和作用截面方位均有关。因此,一点各个截面的应力是不同的。确定一点不同截面的应力变化规律称为应力状态分析。首先是确定应力状态的描述方法,这包括应力矢量定义,及其分解为主应力、切应力和应力分量;其次是任意截面的应力分量的确定—转轴公式;最后是一点的特殊应力确定,主应力和主平面、最大切应力和应力圆等。应力状态分析表明应力分量为二阶对称张量。本课程分析中使用张量符号描述物理量和基本方程,如果你没有学习过张量概念,请进入附录一,或者查阅参考资料。 本章的另一个任务是讨论弹性体内一点-微分单元体的平衡。弹性体内部单元体的平衡条件为平衡微分方程和切应力互等定理;边界单元体的平衡条件为面力边界条件。 二、重点 1、应力状态的定义:应力矢量;正应力与切应力;应力分量; 2、平衡微分方程与切应力互等定理; 3、面力边界条件; 4、应力分量的转轴公式; 5、应力状态特征方程和应力不变量; 知识点: 体力;面力;应力矢量;正应力与切应力;应力分量;应力矢量与应力 分量;平衡微分方程;面力边界条件;主平面与主应力;主应力性质; 截面正应力与切应力;三向应力圆;八面体单元;偏应力张量不变量; 切应力互等定理;应力分量转轴公式;平面问题的转轴公式;应力状态 特征方程;应力不变量;最大切应力;球应力张量和偏应力张量 §2.1 体力和面力 学习思路: 本节介绍弹性力学的基本概念——体力和面力,体力F b和面力F s的概念均不难理解。 应该注意的问题是,在弹性力学中,虽然体力和面力都是矢量,但是它们均为作用于一点的力,而且体力是指单位体积的力;面力为单位面积的作用力。 体力矢量用F b表示,其沿三个坐标轴的分量用F b i(i=1,2,3)或者F b x、F b y和F b z表示,称为体力分量。 面力矢量用F s表示,其分量用F s i(i=1,2,3)或者F s x、F s y和F s z表示。 体力和面力分量的方向均规定与坐标轴方向一致为正,反之为负。 学习要点: 1、体力; 2、面力。 1、体力 作用于物体的外力可以分为两种类型:体力和面力。 所谓体力就是分布在物体整个体积内部各个质点上的力,又称为质量力。例如物体的重力,惯性力,电磁力等等。 面力是分布在物体表面上的力,例如风力,静水压力,物体之间的接触力等。为了表明物体在xyz坐标系内任意一点P 所受体力的大小和方向,在P点的邻域取一微小体积元素△V,如图所示 设△V 的体力合力为△F,则P点的体力定义为 令微小体积元素△V趋近于0,则可以定义一点P的体力为 第6章 应力状态分析 一、选择题 1、对于图示各点应力状态,属于单向应力状态的是(A )。 20 (MPa ) 20 d (A )a 点;(B )b 点;(C )c 点;(D )d 点 。 2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。 (A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。 3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。 (A )AC AC /2,0 ττσ==; (B )AC AC /2,/2ττ σ==; (C )AC AC /2,/2 ττσ==;(D )AC AC /2,/2ττσ=-=。 4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。关于它们的正确性,现有四种答案,正确答案是( D )。 (b) (a) (A)点1、2的应力状态是正确的;(B)点2、3的应力状态是正确的; (C)点3、4的应力状态是正确的;(D)点1、5的应力状态是正确的。 5、对于图示三种应力状态(a)、(b)、(c)之间的关系,有下列四种答案,正确答案是( D )。 τ (a) (b) (c) (A)三种应力状态均相同;(B)三种应力状态均不同; (C)(b)和(c)相同;(D)(a )和(c)相同; 6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。 (A) (B) (D) (C) 解答: max τ发生在 1 σ成45的斜截面上 7、广义胡克定律适用围,有下列四种答案,正确答案是( C )。 (A)脆性材料;(B)塑性材料; (C)材料为各向同性,且处于线弹性围;(D)任何材料; 8、三个弹性常数之间的关系:/[2(1)] G E v =+适用于( C )。 (A)任何材料在任何变形阶级;(B)各向同性材料在任何变形阶级; (C)各向同性材料应力在比例极限围;(D)任何材料在弹性变形围。 8 应力状态与应变状态分析 1、应力状态的概念, 2、平面应力状态下的应力分析, 3、主平面是切应力为零的平面,主应力是作用于主平面上的正应力。 (1)过一点总存在三对相互垂直的主平面,对应三个主应力,主应力排列规定按代数值由大到小为: 321σσσ≥≥ 最大切应力为 13 2 max σστ-= (2)任斜截面上的应力 α τασσσσσα2sin 2cos 2 2 xy y x y x --+ += α τασστα2cos 2sin 2 xy y x +-= (3) 主应力的大小 2 2min max )2 ( 2 xy y x y x τσσσσσ+-±+= 主平面的方位 y x xy tg σστα--= 220 4、主应变 12 2122x y x y xy xy x y ()()tg εεεεεεγγ?εε? = +±-+? = - 5、广义胡克定律 )]([1 z y x x E σσμσε+-= )] ( [ 1 x z y y E σ σ μ σ ε+ - = )] ( [ 1 y x z z E σ σ μ σ ε+ - = G zx zx τ γ= G yz yz τ γ= ,G xy xy τ γ= 6、应力圆与单元体之间的对应关系可总结为“点面对应、转向相同、夹角两倍。” 8.1试画出下图8.1(a)所示简支梁A点处的原始单元体。 图8.1 [解](1)原始单元体要求其六个截面上的应力应已知或可利用公式直接计算,因此应选取如下三对平面:A点左右侧的横截面,此对截面上的应力可直接计算得到;与梁xy平面平行的一对平面,其中靠前的平面是自由表面,所以该对平面应力均为零。再取A点偏上和偏下的一对与xz平行的平面。截取出的单元体如图8.1(d)所示。 (2)分析单元体各面上的应力: A点偏右横截面的正应力和切应力如图8.1(b)、(c)所示,将A点的坐标x、y代入正应力和切应力公式得A点单元体左右侧面的应力为: z M y I σ= b I QS z z * = τ 由切应力互等定律知,单元体的上下面有切应力τ;前后边面为自由表面,应力为零。在单元体各面上画上应力,得到A点单元体如图8.1(d)。 8.2图8.2(a)所示的单元体,试求(1)图示斜截面上的应力;(2)主方向和主应力,画出主单元体;(3)主切应力作用平面的位置及该平面上的正应力,并画出该单元体。 解题范例 应力状态和强度理论 一、判断题 1.若单元体某一截面上的剪应力为零,则该截面称为主平面。() 2.主平面上的剪应力称为主应力。() 3.当单元体上只有一个主应力不为零时,称作二向应力状态。() 5.图2所示单元体最大剪应力为25Mpa。() 6.图3所示单元体为单向应力状态。() 图2图3图4 7. 向应力状态如图4所示,其最大主应力σ1=3σ()。 8. 任一单元体,在最大正应力作用面上,剪应力为零。() 9. 主应力是指剪力为零的截面上的正应力。() 10.力圆上任一点的横坐标值对应单元体某一截面上的正应力。() 二、选择题 1.图1所示应力圆对应的单元体为图()。 图5 三、选择题 1.若一点的应力状态为平面应力状态,那么该点的主应力不可能为:()。 A 、σ1> 0 σ2=σ3=0 B、σ1> 0 σ2 =0 σ3 < 0 C、σ1>σ2>0 σ3=0 D、σ1>σ2>σ3>0 2.已知单元体各面上的应力如图,则其主平面方位为()。 A、B、 C、D、 四、填空题 1.图示为一平面应力状态的单元体及其应力圆,试在应力圆上表示0-1,0-2,0-3平面的位置。 图6 2.试验表明,材料受力后的破坏主要有两种形式,一种是,是由于或所引起;另一种是,是由于所引起的。 3.一单元体如图所示,则单元体的主应力为__________ ,为 __________ ,为__________ ,最大主应力与x 轴的夹角为__________ 。 五、简单计算 1.单元体上的应力如图7所示,试求其它应力和最大剪应力。 2.图8所示单元体,试求图示斜截面上的正应力和剪应力。 图7图8 3.试求图示单元体o斜截面应力。已知:。 图9 2012年度弹性力学与有限元分析复习题及其答案 (绝密试题) 一、填空题 1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。 2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。 3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。 4、物体受外力以后,其内部将发生内力,它的集度称为应力。与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量,也就是正应力和切应力。应力及其分量的量纲是L -1MT -2。 5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。 6、平面问题分为平面应力问题和平面应变问题。 7、已知一点处的应力分量100=x σMPa ,50=y σMPa ,5010=xy τ MPa ,则主应力 =1σ150MPa ,=2σ0MPa ,=1α6135' 。 8、已知一点处的应力分量, 200=x σMPa ,0=y σMPa ,400-=xy τ MPa ,则主应力=1σ512 MPa ,=2σ-312 MPa ,=1α-37°57′。 9、已知一点处的应力分量,2000-=x σMPa ,1000=y σMPa ,400-=xy τ MPa ,则主应力 =1σ1052 MPa ,=2σ-2052 MPa ,=1α-82°32′。 10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。 11、表示应力分量与体力分量之间关系的方程为平衡微分方程。 12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。分为位移边界条件、应力边界条件和混合边界条件。 13、按应力求解平面问题时常采用逆解法和半逆解法。 14、有限单元法首先将连续体变换成为离散化结构,然后再用结构力学位移法进行求解。其具体步骤分为单元分析和整体分析两部分。 15、每个单元的位移一般总是包含着两部分:一部分是由本单元的形变引起的,另一部分是由于其他单元发生了形变而连带引起的。 16、每个单元的应变一般总是包含着两部分:一部分是与该单元中各点的位置坐标有关的,是各点不相同的,即所谓变量应变;另一部分是与位置坐标无关的,是各点相同的,即所谓常量应变。 17、为了能从有限单元法得出正确的解答,位移模式必须能反映单元的刚体位移和常量应变,还应当尽可能反映相邻单元的位移连续性。 18、为了使得单元内部的位移保持连续,必须把位移模式取为坐标的单值连续函数,为 第七章 应力状态和强度理论习题 一、单项选择题 1、第三强度理论和第四强度理论适合于何种材料? A 、塑性材料, B 、脆性材料 C 、金属材料, D 、非金属材料 2、第一强度理论和第二强度理论适合于何种材料? A 、塑性材料, B 、脆性材料, C 、金属材料, D 、非金属材料。 二、 填空题 1、 对于单元体,切应力等于零的平面叫做 ,该平面上的正应力叫做 。 2、第一、二强度理论适合于 材料;第三、四强度理论适合于 材料。 3、第三强度理论的相当应力为 。 4、单元体上只有一对主应力数值不等于零的应力状态称为 应力状态。 5、单元体上只有二对主应力数值不等于零的应力状态称为 应力状态。 6、单元体上三对主应力数值都不等于零的应力状态称为 应力状态。 三、填空题 1、求图示单元体的三个主应力和最大切应力 (图中应力单位:Mpa )。 答:单元体的三个主应力和最大切应力分别为: σ1= Mpa, σ2= Mpa, σ3= Mpa, τmax = Mpa 。 2、求图示单元体的三个主应力和最大切应力 (图中应力单位:Mpa )。 答:单元体的三个主应力和最大切应力分别为: σ1= Mpa, σ2= Mpa, 图 7.3.1 图 7.3.2 σ3= Mpa, τmax = Mpa 。 3、已知应力状态如图所示,应力单位为MPa 试求:(1)主应力大小;(2)最大切应力。 4、已知应力状态如图所示,应力单位为MPa 。 试求:(1)主应力大小;(2)最大切应力。 1、A 2、B 二、填空题 1、主平面 主应力 2、 脆性 塑性 3 、r313s s s =- 4、单向 5、二向 6、三向 二、填空题 1、 2、 3、解: (1)应力分量 50020x y x MPa MPa σστ===- max min 57.0507.022x y MPa MPa σσσσ+??===??-?? MPa MPa 0.70 0.57321-===∴σσσ (2)最大剪应力 MPa 0.3220 .70.572 3 1max =+= -= σστ 第10章 应力状态与强度理论 及其工程应用 10.1 概述 10.1.1 应力状态的基本概念 轴向拉伸或压缩杆: 横截面 1 P F A σ= 1A 横截面面积 斜截面 2 cos sin 22 x x θθσσθστθ? =??= ?? 即用不同方位的截面截取,任意点A 的应力是不同的。 受扭圆轴: 横截面 x P M I τρ= 斜截面 s i n2 α στα =-c o s2 α ττα = 即, A点的应力大小和方向随截面的方位不同而不同。 应力状态:构件受力后,通过一个点的所有截面上的应力情况的总体,称为该点的应力状态。 对于受力构件有必要研究其一点的应力状态。 研究应力状态的目的:找出一点处沿不同方向应力的变化规律,确定出最大应力,从而全面考虑构件破坏的原因,建立适当的强度条件。 10.1.2 应力状态分析的基本方法 研究一点的应力状态时,往往围绕所考察的点取一微小正六面体------ 单元体。 单元体:微小的立方体, dx dy dz 、、为无限小,其侧面上的应力可 看作是均匀分布的,立方体的两相对侧面的应力可看成是大小相等,方向相反。 在单元体各面上标上应力——应力单元体。 根据一点的应力状态中各应力在空间的不同位置,可以将 ?? ? 空间应力状态 应力状态平面应力状态 空间应力状态:所有面上均有应力作用的应力状态。 平面应力状态:所有应力作用线都处于同一平面内的应力状态(有一对面上总是没有应力)。 ?? ? 单向应力状态 平面应力状态纯剪切应力状态 单向应力状态:只受一个方向的正应力作用的应力状态。 纯剪切应力状态:只受剪应力作用的应力状态。 对于平面应力状态,由于单元体有一对面上没有应力作用,所以三维单元体可以用一平面微元表示。 第九章应力状态与强度理论 教学目标:了解一点的应力状态;掌握一点应力状态主应力及主平面的计算。 重点、难点:一点应力状态主应力及主平面的计算。 学时分配:4学时。 (一) 一点的应力状态 通过受力构件内一点的所有截面上的应力情况称为一点的应力状态。 (二) 一点的应力状态的表示法一一单元体 围绕所研究的点,截取一个边长为无穷小的正六面体, 用各面上的应力分量表示周围材料对 其作用。称为应力单元体。 特点: 1单元体的尺寸无限小,每个面上的应力为均匀分布。 2?单元体表示一点处的应力,故相互平行截面上的应力相同。 (三) 主平面、主应力、主单元体 主平面单元体中剪应力等于零的平面。 主应力 主平面上的正应力。 可以证明:受力构件内任一点,均存在三个互相垂直的主平面。三个主应力用 厂、(T 2 和(T 3表示,且按代数值排列即 (T l > (T 2> b 3。 主单元体 用三对互相垂直的主平面取出的单元体。 (四)应力状态的分类 根据主单元体上三个主应力中有几个是非零的数值,可将应力状态分为三类: 只有一个主应力不等于零。 有两个主应力不等于零。 三个主应力都不等于零。 1 .单向应力状态 2 .二向应力状态 3 .三向应力状态 单向应力状态又称为简单应力状态,二向和三向应力状态统称为复杂应力状态。单向及二向应力状态又称为平面应力状态。 (三)平面应力状态分析法 平面应力状态通常用单元体中主应力为零的那个主平面的正投影表示如图所示。 (四)任意斜截面成 a 的应力 (T x 、(T y 、(T xy ,则与I 轴成。角的斜截面上的应力分量为 ~ 2 _ T Ky sin2vt + r xv cos2a 式中 正应力T 以拉应力为正;剪应力 T 以对单元体产生顺时针力矩者为正, 时针转向为正。 (五)主平面 主应力 主平面的方位角 a 0 主应力 考虑到单元体零应力面上的主应力为零,因此若已知一平面应力状态 a 角以逆 第七章 应力状态和强度理论习题答案 一、单项选择题 1、A 2、B 二、填空题 1、主平面 主应力 2、 脆性 塑性 3、主平面 主应力 4 、eq313 s s s =- 5、主平面 主应力 6、单向 7、二向 8、三向 二、填空题 1、解: (1)应力分量 MPa MPa xy y x 200 50-===τσσ max min 57.0507.022x y MPa MPa σσσσ+??==±=??-?? MPa MPa 0.70 0.57321-===∴σσσ (2)最大剪应力 MPa 0.3220 .70.572 3 1max =+= -= σστ 2、解: (1)应力分量 MPa MPa MPa xy y x 253060-===τσσ max min 74.2603015.822x y MPa MPa σσσσ+??+=±= ±=???? 08 .152.74321===∴σσσMPa (2)最大剪应力 MPa 1.3720 2.742 3 1max =-= -=σστ 三、计算题 1、 解 简化力系 () ()() [] 200m m d 32 109.11025.1W T M m 25KN .12 1 5.22D F -2F M 9.5KN 522.52F F F F 3 2 62 6Z 2 Max 2Max r3P ≈≤?+?= +=?=?===++=++=解出总σπσd 2、解 由题 () ()() [] σπσ≤≈?+?= +=-=??=??=?=≤≤?-==??=??=?=∑MPa d W T M M T m m N L X X F Z r AB 12932 104.1105.1105.1150101L F M 0M 0M mm N 104.1140101L F M 3 2 52 52 2353AB Max 1A 53BC 所以符合强度 3、解: (1)外力分析,将作用在胶带轮上的胶带拉力F1、F2向轴线简化,结果如图 传动轴受竖向主动力: kN 1436521=++=++=F F G F , 此力使轴在竖向平面内弯曲。 附加力偶为: ()()m kN 8.16.03621?=?-=-=R F F M e , 此外力偶使轴发生变形。 故此轴属于弯扭组合变形。 (2)内力分析 分别画出轴的扭矩图和弯矩图如图。 危险截面上的弯矩m kN 2.4?=M ,扭矩m kN 8.1?=T (3)强度校核一点应力状态概念及其表示方法
材料力学B试题7应力状态_强度理论.docx
弹性力学 第四章 应力和应变关系
第7章应力状态和强度理论(答案)
应力状态分析与强度理论
知识点应力状态理论和强度理论
弹性力学 第二章 应力状态分析
材料力学习题第六章应力状态分析答案详解
工程力学-应力状态与应力状态分析报告
应力状态和强度理论习题及答案
11弹性力学试题及答案解析
第七章应力状态和强度理论习题
第10章应力状态与强度理论及其工程应用
第九章应力状态与强度理论.
第七章应力状态和强度理论习题答案
