相似三角形综合练习相似与圆(难)

N A
相似三角形与圆
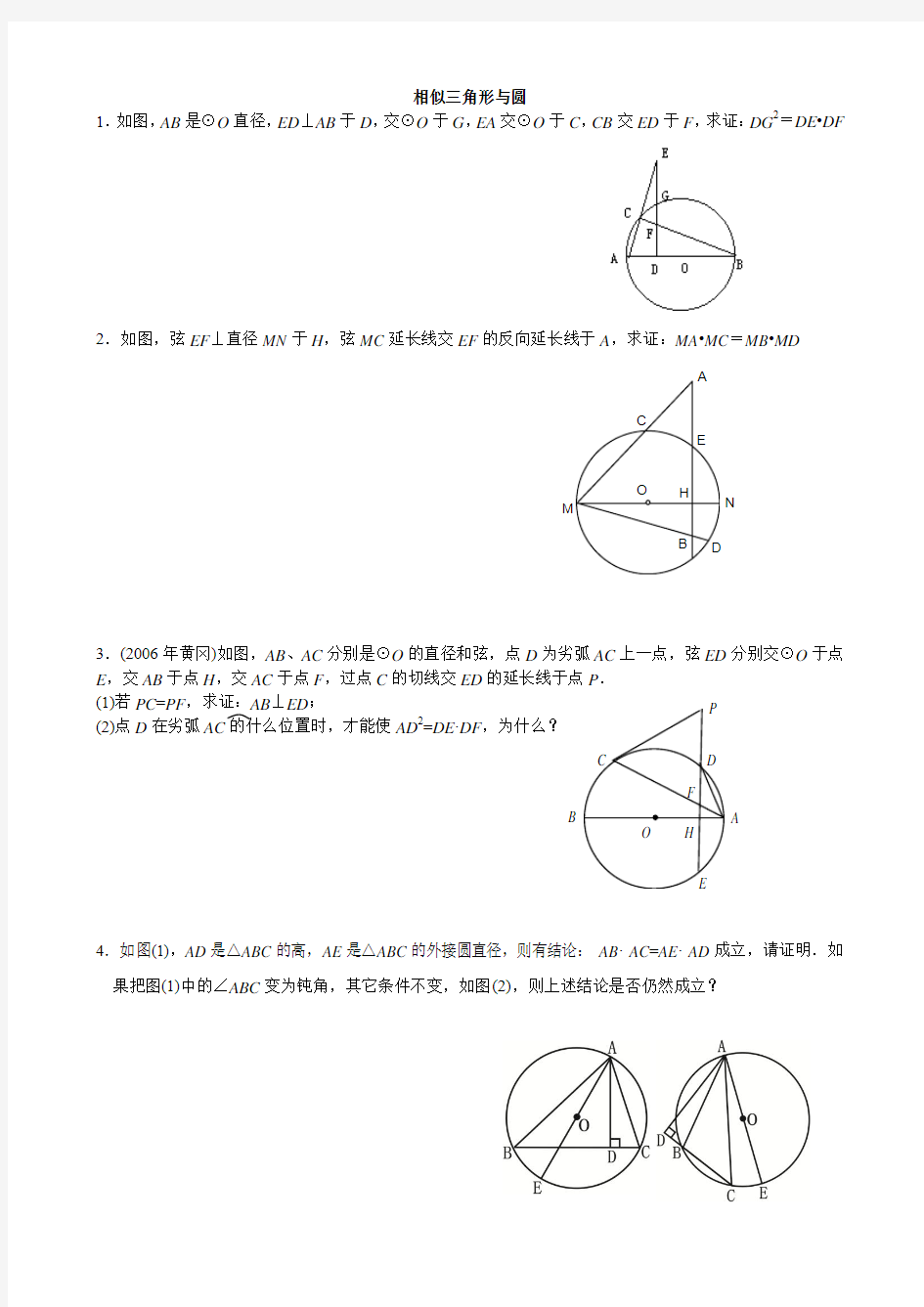
1.如图,AB是⊙O直径,ED⊥AB于D,交⊙O于G,EA交⊙O于C,CB交ED于F,求证:DG2=DE?DF 2.如图,弦EF⊥直径MN于H,弦MC延长线交EF的反向延长线于A,求证:MA?MC=MB?MD
3.(2006年黄冈)如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过点C的切线交ED的延长线于点P.
(1)若PC=PF,求证:AB⊥ED;
(2)点D在劣弧AC的什么位置时,才能使AD2=DE·DF,为什么?
4.如图(1),AD是△ABC的高,AE是△ABC的外接圆直径,则有结论:AB·AC=AE·AD成立,请证明.如果把图(1)中的∠ABC变为钝角,其它条件不变,如图(2),则上述结论是否仍然成立?
C
5.如图,AD 是△ABC 的角平分线,延长AD 交△ABC 的外接圆O 于点E ,过点C 、D 、E 三点的⊙O 1与AC 的延长线交于点F ,连结EF 、DF .
(1)求证:△AEF ∽△FED ;
(2)若AD =8,DE =4,求EF 的长.
6.如图,PC 与⊙O 交于B ,点A 在⊙O 上,且∠PCA =∠BAP .
(1)求证:P A 是⊙O 的切线.
(2)△ABP 和△CAP 相似吗?为什么?
(3)若PB :BC =2:3,且PC =20,求P A 的长.
7.已知:如图, AD 是⊙O 的弦,OB ⊥AD 于点E ,交⊙O 于点C ,OE =1,BE =8,AE :AB =1:3.
(1)求证:AB
是⊙
O 的切线;
(2)点F 是ACD 上的一点,当∠AOF =2∠B 时,求AF 的长.
8.如图,⊿ABC 内接于⊙O ,且BC 是⊙O 的直径,AD ⊥BC 于D ,F 是弧BC 中点,且AF 交BC 于E ,AB =6,AC =8,求CD ,DE ,及EF 的长.
9. 已知:如图,在Rt ABC △中,90ACB ∠=,4AC =
,BC =,以AC 为直径的O 交AB 于点D ,点E 是BC 的中点,连结OD ,OB 、DE 交于点F .
(1)求证:DE 是O 的切线;
(2)求EF :FD 的值.
10.如图,A 是以BC 为直径的O 上一点,AD BC ⊥于点D ,过点B 作O 的切线,与CA 的延长线相交于点E G ,是AD 的中点,连结CG 并延长与BE 相交于点F ,延长AF 与CB 的延长线相交于点P .
(1)求证:BF EF =;
(2)求证:PA 是O 的切线;
(3)若FG BF =,且O
的半径长为BD 和FG 的长度.
B C E
C
4.答:.连接BE ,证△ABE ∽△ADC 图(2)同理可证,结论仍成立;
5.答:.(1)连接EC ,可证∠DFE =∠DCE ,又
∠DCE =∠BAE =∠CAE ,从而△AEF ∽△FED ;(2)EF
=
6.答:.(1)作直径AC ',连接BC ',证∠P AC '=90即可;(2)△ABP ∽△CAP ,理由略;(3)P A
10.(1)证明:BC ∵是O 的直径,BE 是O 的切线,
EB BC ⊥∴.
又AD BC ⊥∵,AD BE ∴∥.
易证BFC DGC △∽△,FEC GAC △∽△.
BF CF EF CF DG CG AG CG
==∴,. BF EF DG AG
=∴. G ∵是AD 的中点,
DG AG =∴.
BF EF =∴.
(2)证明:连结AO AB ,.
BC ∵是O 的直径,90BAC ∠=∴°.
在Rt BAE △中,由(1),知F 是斜边BE 的中点,
AF FB EF ==∴.
FBA FAB ∠=∠∴.
又OA OB =∵,ABO BAO ∠=∠∴.
BE ∵是O 的切线,90EBO ∠=∴°.
90EBO FBA ABO FAB BAO FAO ∠=∠+∠=∠+∠=∠=∵°,
PA ∴是O 的切线.
(3)解:过点F 作FH AD ⊥于点H .
BD AD FH AD ⊥⊥∵,,
FH BC ∴∥.
由(1),知FBA BAF ∠=∠,BF AF =∴.
由已知,有BF FG =,AF FG =∴,即AFG △是等腰三角形.
FH AD ⊥∵,AH GH =∴.
DG AG =∵,
2DG HG =∴,即12
HG DG =. 90FH BD BF AD FBD ∠=∵∥,∥,°,
∴四边形BDHF 是矩形,BD FH =.
FH BC ∵∥,易证HFG DCG △∽△.
FH FG HG CD CG DG ==∴,即12BD FG HG CD CG DG ===. O ∵
的半径长为
BC =∴
12
BD BD CD BC BD ===-∴
.
C
解得BD =
BD FH ==∴
12FG HG CG DG ==∵,12
FG CG =∴. 3CF FG =∴.
在Rt FBC △中,3CF FG =∵,BF FG =, 由勾股定理,得222
CF BF BC =+.
222(3)FG FG =+∴.
解得3FG =(负值舍去).
3FG =∴.
[或取CG 的中点H ,连结DH ,则2CG HG =.易证AFC DHC △≌△, FG HG =∴,故2CG FG =,3CF FG =.
由GD FB ∥,易知CDG CBF △∽△,2233
CD CG FG CB CF FG ===∴.
23=
,解得BD = 又在Rt CFB △
中,由勾股定理,得222(3)FG FG =+,
3FG =∴(舍去负值).]
相似三角形与圆综合题
相似三角形与圆综合 第一部分:例题分析 例1、已知:如图,BC为半圆O的直径,AD⊥BC,垂足为D,过点B作弦BF交AD于点E,交半圆O于点F,弦A C与BF交于点H,且AE=BE.求证:(1)错误!=错误!;(2)AH·BC=2AB·BE. 例2、如图,PA为圆的切线,A为切点,PBC为割线,∠APC的平分线交AB于点D,交AC于点E,求证:(1)AD=A E;(2)AB·AE=AC·DB. 例3、AB是⊙O的直径,点C在⊙O上,∠BAC=60°,P是OB上一点,过P作AB的垂线与AC的延长线交于点Q,连结OC,过点C作CD⊥OC交PQ于点D. (1)求证:△CDQ是等腰三角形; (2)如果△CDQ≌△COB,求BP∶PO的值. 例4、△ABC内接于圆O,∠BAC的平分线交⊙O于D点,交⊙O的切线BE于F,连结BD,CD. 求证:(1)BD平分∠CBE;(2)AB·BF=AF·DC. 例3、⊙O内两弦AB,CD的延长线相交于圆外一点E,由E引AD的平行线与直线BC交于F,作切线FG,G为切点,求证:EF=FG. 第二部分:当堂练习 1.如图,AB是⊙O直径,ED⊥AB于D,交⊙O于G,EA交⊙O于C,CB交ED于F,求证:DG2=DE?DF 2.如图,弦EF⊥直径MN于H,弦MC延长线交EF的反向延长线于A,求证:MA?MC=MB?MD
D C B A O M N E H 3.如图,AB 、AC 分别是⊙O的直径和弦,点D为劣弧AC 上一点,弦E D分别交⊙O于点E ,交A B于点H,交AC 于点F ,过点C的切线交ED 的延长线于点P. (1)若PC =P F,求证:AB ⊥ED ; (2)点D 在劣弧AC 的什么位置时,才能使AD 2 =D E·DF ,为什么? 4.如图(1),AD 是△ABC 的高,AE 是△ABC 的外接圆直径,则有结论:AB · AC =AE · A D成立,请证明.如果把图(1)中的∠ABC 变为钝角,其它条件不变,如图(2),则上述结论是否仍然成立? 5.如图,AD 是△A BC的角平分线,延长AD 交△A BC 的外接圆O 于点E ,过点C 、D 、E 三点的⊙O 1与AC 的延长线交于点F ,连结E F、DF . (1)求证:△A EF ∽△F ED ; (2)若AD =8,DE =4,求EF 的长. 6.如图,PC 与⊙O 交于B ,点A 在⊙O 上,且∠PCA =∠B AP. (1)求证:P A 是⊙O 的切线. (2)△ABP 和△CAP 相似吗?为什么? (3)若PB :BC =2:3,且P C=20,求PA 的长. D C B A O E 7.已知:如图, AD 是⊙O 的弦,OB ⊥A D于点E,交⊙O 于点C ,OE =1,BE =8,A E:A B=1:3. (1)求证:AB 是⊙O 的切线; (2)点F 是A CD 上的一点,当∠AOF =2∠B时,求AF 的长. 8.如图,⊿AB C内接于⊙O ,且BC 是⊙O 的直径,AD ⊥B C于D ,F是弧BC 中点,且AF 交BC 于E ,A B=6,AC =8,求CD ,DE ,及EF 的长. 9. 已知:如图,在Rt ABC △中,90ACB ∠=,4AC =,43BC =,以AC 为直径的O 交AB 于点D ,点E 是BC 的中点,连结OD ,OB 、DE 交于点F. A C P E D H F O
完整版相似三角形与圆综合题
AB 于点D,交AC 于点E ,求证:(1)AD=AE ; C 在O O 上,/ BAC= 60°, P 是OB 上一点,过 P 作AB 的垂线与 AC 的延长线交于点 Q 连结OC 过点C 作CD L OC 交PQ 于点D. (1)求证:△ CDQi 等腰三角形; (2) 如果△ CDQ^A COB 求BP : PO 的值. 第一部分:例题分析 相似三角形与圆综合 △ ABC 内接于圆O, / BAC 勺平分线交O O 于D 点,交O O 的切线BE 于F ,连结 BD CD 求证:(1) BD 平分/ 例4、 例3、 O O 内两弦 E E AB CD 的延长线相交于圆外一点 E ,由E 引AD 的平行线与直线 BC 交于F ,作切线FG G 为切点, 求证: EF = FG 例3、AB 是O O 的直径,点 (2)AB ? AE=AC ? DB. BE. 例1、已知:如图,BC 为半圆O 的直径,ADI BC,垂足为D,过点B 作弦BF 交AD 于点E ,交半圆O 于点F ,弦AC
第二部分:当堂练习 1.如图,AB是O O直径,ED丄AB于D,交O O于G , EA交O O于C, CB交ED于F,求证:DG2= DE?DF
(1)若 PC=PF ,求证:AB 丄 ED ; ⑵点D 在劣弧AC 的什么位置时,才能使 AD 2 =DE DF ,为什么? 2 . 3. 如图,AB 、AC 分别是O O 的直径和弦,点 D 为劣弧AC 上一点, 弦ED 分别交O O 于点 E ,交AB 于点H ,交 AC 于点F ,过点C 的切线交ED 的延长线于点 P . 如图,弦EF 丄直径
相似三角形与圆的结合
E D C B A B E D C B A B B B 相似三角形与圆的结合 1、 如图,圆中的弦AB 、CD 相交于E 点, 已知CE=4,BE=5,DB=6;求:弦AC 的长 2、 如图,AB 是⊙O 的直径,CD ⊥AB 于E ,观察图形, 你能得到哪些结论,请将你所得的结论写下来,和同学交流, 看谁写的多写的对。 3、 已知:如图,ABCD 是圆内节四边形,AC 、BD 相交于点E , 求证:AD ?BE=BC ?AE 4、 已知:如图,△AOB 中,∠AOB=90°,OC ⊥AB 于C , OA=3cm ,OB=4cm ,以O 为圆心,以2.4cm 为半径作⊙O 。 求证:⊙O 与AB 相切 5、 已知:如图,AB 是⊙O 的直径,C 是⊙O 外一点, CB 交⊙O 于D ,AD 2=CD ?BD 求证:AC 是⊙O 的切线 6、 已知:如图,AB 是⊙O 的直径,CD 切⊙O 于B , AC 交⊙O 于E ,AD 交⊙O 于F , 求证:AE ?AC=AF ?AD 7、 已知:如图,AB 是⊙O 的直径,CA 与⊙O 相切于点A , CE ∥AB 交⊙O 于D 、E. 求证;BE 2 =CD ?AB 8、 如图,AD 是△ABC 的高,AE 是△ABC 的外接圆的直径; 求证:AB ?AC=AD ?AE
19、如图,4531===∠=∠∠=∠BC DE AB D B ,,, (1)ABC ?∽ADE ?吗?说明理由。 (2)求AD 的长。 20、如图4,已知AB 为⊙O 的直径,过点B 作⊙O 的切线BC ,连接OC ,弦AD ∥OC .求证:CD 是⊙O 的切线. 21、已知:如图,ΔABC 中,AD=DB,∠1=∠2. 求证:A E A C D E A B = 22、如图,在正方形ABCD 中,E 为AD 的中点,EF ⊥EC 交AB 于F ,连接FC (),AE AB >试证明: EF 平分∠AFC. 23、已知,如图20,AB 是⊙O 的直径,C 是⊙O 上一点,连接AC,过点C 作直线CD ⊥AB 于D(AD D C B A O M N E H A B C P E D H F O 相似三角形与圆 1.如图,AB 是⊙O直径,E D⊥AB 于D,交⊙O 于G ,EA 交⊙O 于C,CB 交ED 于F ,求证:DG 2=D E?DF 2.如图,弦EF ⊥直径MN 于H ,弦MC 延长线交EF 的反向延长线于A ,求证:M A?M C=MB ?MD 3.(2006年黄冈)如图,AB 、AC 分别是⊙O 的直径和弦,点D 为劣弧AC 上一点,弦ED 分别交⊙O 于点E ,交AB 于点H ,交AC 于点F,过点C 的切线交ED 的延长线于点P . (1)若PC =PF ,求证:AB ⊥ED ; (2)点D 在劣弧AC 的什么位置时,才能使AD 2=DE ·DF ,为什么? 4.如图(1),AD 是△ABC 的高,A E是△ABC 的外接圆直径,则有结论:AB · AC =A E· A D成立,请证明.如果把图(1)中的∠AB C变为钝角,其它条件不变,如图(2),则上述结论是否仍然成立? D C B A O E F 5.如图,AD 是△ABC 的角平分线,延长AD 交△ABC 的外接圆O于点E ,过点C、D 、E 三点的⊙O 1与A C的延长线交于点F,连结E F、DF . (1)求证:△AEF ∽△F ED ; (2)若AD =8,DE =4,求EF 的长. 6.如图,P C与⊙O 交于B ,点A 在⊙O上,且∠PCA =∠BAP . (1)求证:P A是⊙O的切线. (2)△ABP 和△CAP 相似吗?为什么? (3)若PB :BC =2:3,且PC =20,求P A的长. 7.已知:如图, AD 是⊙O 的弦,OB ⊥AD于点E,交⊙O于点C ,OE =1,BE =8,A E:AB =1:3. (1)求证:AB 是⊙O 的切线; (2)点F 是ACD 上的一点,当∠AOF =2∠B时,求AF 的长. 8.如图,⊿A BC 内接于⊙O ,且BC 是⊙O 的直径,AD ⊥BC于D ,F 是弧BC 中点,且A F交BC 于E,AB =6,AC =8,求CD ,DE ,及EF的长. 圆与相似三角形专题训练 例1.如图,PD切⊙O于D,PC = PD,B为⊙O上一点,PB交⊙O于A,连结AC、BC. 求证:AC·PB = PC·BC 证明: 训练1. 如图,⊙O是弦AB∥CD,延长DC到E,EB延长线交⊙O于F,连结DF. 求证:AD·ED = BE·DF 证明:连结CB 2. 如图,CD切⊙O于P,PE⊥AB于E,AC⊥CD,BD⊥CD. 求证:① PE:AC = PB:PA;② PE 2 = AC·BD 例2.如图,△ABC内接于⊙O,⊙O的直径BD交AC于E,AF⊥BD于F,延长AF 交BC于G. 求证:AB 2 = BG·BC 证明:连结AD 训练1. 如图,AB是⊙O的直径,弦CD垂直AB于M,P是CD延长线上一点,PE 切⊙O于E,BE交CD于F. 求证:PF 2 = PD·PC 证明:连结AE 2. 如图,△ABC中,AB = AC,O是BC上一点,以O为圆心,OB长为半径的圆与AC相切于点A,过点C作CD⊥BA,垂足为D. 求证:①∠DAC = 2∠B;② CA 2 = CD·CO 例3.如图,⊙O 1和⊙O 2 相交于点A和点B,且O 1 在⊙O 2 上;过点A的直线 CD分别与⊙O 1、⊙O 2 交于点C、D,过点B的直线EF分别与⊙O 1 、⊙O 2 交于 点E、F,⊙O 2的弦O 1 D 交AB于P. 求证:① CE∥DF;② O 1 A 2 = O 1 P·O 1 D 证明: 训练1. 如图,圆内接四边形ABCD的对角线AC平分∠BCD,BD交AC于点F,过点A作圆的切线AE交CB的延长线于E. 求证:①AE∥BD;②AD 2 = DF·AE 证明: 2. 已知:,过点D作直线交AC于E,交BC于F,交AB的延长线于G,经过B、G、F三点作⊙O,过E作⊙O的切线ET,T为切点. 求证:ET = ED 证明: 相似三角形综合试相似与圆(难) ————————————————————————————————作者:————————————————————————————————日期: 2 D C B A O M N E H A B C P E D H F O 相似三角形与圆 1.如图,AB 是⊙O 直径,ED ⊥AB 于D ,交⊙O 于G ,EA 交⊙O 于C ,CB 交ED 于F ,求证:DG 2=DE ?DF 2.如图,弦EF ⊥直径MN 于H ,弦MC 延长线交EF 的反向延长线于A ,求证:MA ?MC =MB ?MD 3.(2006年黄冈)如图,AB 、AC 分别是⊙O 的直径和弦,点D 为劣弧AC 上一点,弦ED 分别交⊙O 于点E ,交AB 于点H ,交AC 于点F ,过点C 的切线交ED 的延长线于点P . (1)若PC =PF ,求证:AB ⊥ED ; (2)点D 在劣弧AC 的什么位置时,才能使AD 2=DE ·DF ,为什么? 4.如图(1),AD 是△ABC 的高,AE 是△ABC 的外接圆直径,则有结论:AB · AC =AE · AD 成立,请证明.如果把图(1)中的∠ABC 变为钝角,其它条件不变,如图(2),则上述结论是否仍然成立? D C B A O E F 5.如图,AD是△ABC的角平分线,延长AD交△ABC的外接圆O于点E,过点C、D、E三点的⊙O1与AC的延长线交于点F,连结EF、DF. (1)求证:△AEF∽△FED; (2)若AD=8,DE=4,求EF的长. 6.如图,PC与⊙O交于B,点A在⊙O上,且∠PCA=∠BAP. (1)求证:P A是⊙O的切线. (2)△ABP和△CAP相似吗?为什么? (3)若PB:BC=2:3,且PC=20,求P A的长. 7.已知:如图,AD是⊙O的弦,OB⊥AD于点E,交⊙O于点C,OE=1,BE=8,AE:AB=1:3. (1)求证:AB是⊙O的切线; (2)点F是ACD上的一点,当∠AOF=2∠B时,求AF的长. 8.如图,⊿ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,AB=6,AC=8,求CD,DE,及EF的长. 圆与相似三角形专题训练 27、如图,已知⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,D 是AB 延长线上一点,AE ⊥DC 交DC 的延长线于点E ,且AC 平分∠EAB 。【2005成都】 ⑴求证:DE 是⊙O 的切线;⑵若AB =6,AE = 24 5 ,求BD 和BC 的长。 27、已知:如图,⊙O 与⊙A 相交于C 、D 两点,A 、O 分别是两圆的圆心,△ABC 内接于⊙O ,弦CD 交AB 于点G ,交⊙O 的直径AE 于点F ,连结BD 。【2006成都】 (1)求证:△ACG ∽△DBG ;(2)求证:2 AC AG AB =? ; (3)若⊙A 、⊙O 的直径分别为15,且CG :CD =1:4,求AB 和BD 的长。 E O D G C A E F B P 27.如图,A 是以BC 为直径的O e 上一点,AD BC ⊥于点D ,过点B 作O e 的切线,与CA 的延长线相交于点 E G ,是AD 的中点,连结CG 并延长与BE 相交于点 F ,延长AF 与CB 的延长线相交于点P .【2007成都】 (1)求证:BF EF =;(2)求证:PA 是O e 的切线; (3)若FG BF =,且O e 的半径长为32,求BD 和FG 的长度. 27. 如图,已知⊙O 的半径为2,以⊙O 的弦AB 为直径作⊙M ,点C 是⊙O 优弧? AB 上的一个动点(不与点A 、点B 重合).连结AC 、BC ,分别与⊙M 相交于点D 、点E ,连结DE.若AB=23.【2008成都】 (1)求∠C 的度数;(2)求DE 的长; (3)如果记tan ∠ABC=y ,AD DC =x (0 (一)知识复习巩固 圆的基本性质:圆周角性质,垂径定理逆定理,切线长定理 相似三角形四种判定,及性质 (二)例题精讲: 例1、已知:如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交⊙O的切线BF于点F,B为切点。求证:(1)BD平分∠CBF;(2)AB?BF=AF?CD. 考点: 相似三角形的判定与性质,角平分线的性质,圆周角定理,弦切角定理分析: (1)由于AF是∠BAC的角平分线,那么∠1=∠2,利用弦切角定理可得 ∠1=∠3,利用同弧所对的圆周角相等,可得∠2=∠4,那么,可证∠3=∠4,即 BD平分∠CBF; (2)由于∠3=∠1,∠F=∠F,那么可证△DBF∽△BAF,再利用相似三角形 的性质,可得相关比例线段AB:AF=BD:BF,又由于∠1=∠2,同圆里 相等的圆周角所对的弧相等,而同圆里相等的弧所对的弦相等,从而BD=CD, 等量代换,可得AB:AF=CD:BF,即AB?BF=AF?CD. 解答: 证明:(1)∵AD平分∠BAC, ∴∠1=∠2,(2分) ∵BF切⊙O于点B,∴∠3=∠2, ∴∠3=∠1,(4分) 又∵∠2=∠4, ∴∠3=∠4,即BD平分∠CBF;(6分) (2)在△DBF和△BAF中, ∵∠3=∠1,∠F=∠F, ∴△DBF∽△BAF,(8分) ∴BDAB=BFAF即AB?BF=AF?BD(10分) ∵∠1=∠2, ∴BD=CD,(11分) ∴AB?BF=AF?CD.(12分) 例2、已知:如图,△ABC内接于圆,AB=AC,D为延长线上一点,AD交圆于E. 求证:AB2=AD?AE. 考点:相似三角形的判定与性质,圆周角定理 分析: 如图,作辅助线;证明△ABE∽△ADB,列出比例式,即可解决问题.解答: 个性化辅导讲义 1在厶ABC 中,AB = AC, / A = 36° , / ABC 的平分线 BD 与AC 交于D,求证: 知识概括、方法总结与易错点分析 相似三 角形的概念与判定 (一) 定义:对应角相等,对应边成比例的两个三角形叫相似三角形。 相似三角形的对应边的比叫做相似比(也叫相似系数)。 (二) 判定: ① 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形 相似。 ② 两边对应成比例且夹角相等的两个三角形相似。 ③ 有两个角对应相等的两个三角形相似。 ④ 三条边对应成比例的两个三角形相似。 ⑤ 一条直角边和斜边对应成比例的两个直角三角形相似。 ⑥ 直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似。 相似三角形的性质 2.两个相似三角形对应中线之比是 3:7,周长之和为30cm,贝陀们的周长分别是 AB BC 3 ?如图,已知AD = DE AC 求证:△ ABM A ACE 4. 在 Rt △ ABC 中,/ ACB=90 , CD! AB 于 D,贝U BD : AD 等于( (A ) a : b (B ) a 2 : b 2 (C ) a : . b ( D )不能确定 5. 如图,在△ ABC 中,/ ACB= 90°, CD! AB 于 D, DEI AC 于 E , DE = 1 求BC 的值。 (1) BC = BD (2) 1. 相似比:相似三角形对应边的比值 2. 相似三角形各组对应角相等 3. 相似三角形各组对应边的比值相等 4. 相似三角形对应高线的比,对应中线的比和对应角平分线的比都等于相似比 5. 相似三角形周长的比等于相似比 6. 相似三角形面积的比等于相似比的平方 7. 直角三角形中,斜边上的高线是两条直角边在斜边上的射影的比例中项 针对性练习 1 .两个相似三角形的对应角平分线的长分别为10cm和20cm,若它们的周长的差是60cm,则较大的三角形的周长是--—--,若它们的面积之和为260cnf,则较小的三角形的面积为--—-- cm2 2. 如图,PLMh为矩形,AD丄BC于D, PL : LM=5: 9,且BC=36cm AD=12cm 求矩形PLMlN勺周长 A 3. 如图,在Rt△ ABD中,/ ADB=90 ,CD丄AB于C, AC=20cm,BC=9cm求AB及BD的长 B 圆中的基本图形和常见数学思想圆一直是初中阶段数学学习的一个难点,因为圆中知识点很多,综合性也很强。而且中考中圆常常和四边形,三角形,甚至代数中的二次函数结合起来考察学生的能力。 把圆中涵盖的知识点融入到几个基本图形中,并教会学生在复杂的图形中提炼出基本图形。另外一定要帮助学生进行解题方法的训练和总结。让他们熟悉圆中常用的数学方法。归纳了以下几个方面的内容,概述如下。 1 圆中基本图形主要有 这个图形中涵盖了: 1、垂径定理及其推论; 2、同弧所对的圆心角是圆周角的两倍; 3、半径、弦心距、弓形高、弦长四者的关系; 4、直径所对的圆周角是直角 这个图形中涵盖了: 1、圆的内接四边形的对角互补,外角等于内对角, 2、相似关系; 3、割线定理 这个图形中涵盖了: 1、弦切角等于所夹弧所对的圆周角, 2、相似关系; 3、切割线定理 这个图形中涵盖了: 1、三角形的外心是三角形三条垂直平分线的交点,并且到三角形三个顶点的距离相等2、同弧所对的圆心角是圆周角的两倍 这个图形中涵盖了: 1、从圆外引圆的两条切线,切线长相等。 2、三角形的内心是三角形三条角平分线的交点,并且到三角形三条边的距离相等3、三角形的面积和周长、内切圆半径三者的关系, 4、三角形两条内角角平分线组成的夹角与第三个内角的关系 这个图形中涵盖了: 1、同弧所对的圆周角相等, 2、相似关系, 3、相交弦定理 这个图形中涵盖了: 1、直径所对的圆周角是直角,90度的圆周角所对的弦是直径 2、相似关系,射影定理, 3、直角三角形的外心在斜边的中点 4、直角三角形的外接圆的半径等于斜边的一半 这个图形中涵盖了: 1、切线长定理 2、连心线垂直平分公共弦 3、圆的对称性 这个图形中涵盖了: 等边三角形的内切圆半径、外接圆半径、等边三角形的边长三者的比例关系。 这个图形中涵盖了: 正方形的内切圆半径、外接圆半径、正方形的边长三者的比例关系。 这个图形中涵盖了: 正六边形的内切圆半径、外接圆半径、正六边形的边长三者的比例关系。 D C B A O M N E H A B C P E D H F O 相似三角形与圆 1.如图,AB 是⊙O 直径,ED ⊥AB 于D ,交⊙O 于G ,EA 交⊙O 于C ,CB 交ED 于F ,求证:DG 2=DE ?DF 2.如图,弦EF ⊥直径MN 于H ,弦MC 延长线交EF 的反向延长线于A ,求证:MA ?MC =MB ?MD 3.(2006年黄冈)如图,AB 、AC 分别是⊙O 的直径和弦,点D 为劣弧AC 上一点,弦ED 分别交⊙O 于点E ,交AB 于点H ,交AC 于点F ,过点C 的切线交ED 的延长线于点P . (1)若PC =PF ,求证:AB ⊥ED ; (2)点D 在劣弧AC 的什么位置时,才能使AD 2=DE ·DF ,为什么? 4.如图(1),AD 是△ABC 的高,AE 是△ABC 的外接圆直径,则有结论:AB · AC =AE · AD 成立,请证明.如果把图(1)中的∠ABC 变为钝角,其它条件不变,如图(2),则上述结论是否仍然成立? D C B A O E F 5.如图,AD是△ABC的角平分线,延长AD交△ABC的外接圆O于点E,过点C、D、E三点的⊙O1与AC的延长线交于点F,连结EF、DF. (1)求证:△AEF∽△FED; (2)若AD=8,DE=4,求EF的长. 6.如图,PC与⊙O交于B,点A在⊙O上,且∠PCA=∠BAP. (1)求证:P A是⊙O的切线. (2)△ABP和△CAP相似吗?为什么? (3)若PB:BC=2:3,且PC=20,求P A的长. 7.已知:如图,AD是⊙O的弦,OB⊥AD于点E,交⊙O于点C,OE=1,BE=8,AE:AB=1:3. (1)求证:AB是⊙O的切线; (2)点F是ACD上的一点,当∠AOF=2∠B时,求AF的长. 8.如图,⊿ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,AB=6,AC=8,求CD,DE,及EF的长. N A 相似三角形与圆 1.如图,AB是⊙O直径,ED⊥AB于D,交⊙O于G,EA交⊙O于C,CB交ED于F,求证:DG2=DE?DF 2.如图,弦EF⊥直径MN于H,弦MC延长线交EF的反向延长线于A,求证:MA?MC=MB?MD 3.(2006年黄冈)如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过点C的切线交ED的延长线于点P. (1)若PC=PF,求证:AB⊥ED; (2)点D在劣弧AC的什么位置时,才能使AD2=DE·DF,为什么? 4.如图(1),AD是△ABC的高,AE是△ABC的外接圆直径,则有结论:AB·AC=AE·AD成立,请证明.如果把图(1)中的∠ABC变为钝角,其它条件不变,如图(2),则上述结论是否仍然成立? C 5.如图,AD 是△ABC 的角平分线,延长AD 交△ABC 的外接圆O 于点E ,过点C 、D 、E 三点的⊙O 1与AC 的延长线交于点F ,连结EF 、DF . (1)求证:△AEF ∽△FED ; (2)若AD =8,DE =4,求EF 的长. 6.如图,PC 与⊙O 交于B ,点A 在⊙O 上,且∠PCA =∠BAP . (1)求证:P A 是⊙O 的切线. (2)△ABP 和△CAP 相似吗?为什么? (3)若PB :BC =2:3,且PC =20,求P A 的长. 7.已知:如图, AD 是⊙O 的弦,OB ⊥AD 于点E ,交⊙O 于点C ,OE =1,BE =8,AE :AB =1:3. (1)求证:AB 是⊙ O 的切线; (2)点F 是ACD 上的一点,当∠AOF =2∠B 时,求AF 的长. 8.如图,⊿ABC 内接于⊙O ,且BC 是⊙O 的直径,AD ⊥BC 于D ,F 是弧BC 中点,且AF 交BC 于E ,AB =6,AC =8,求CD ,DE ,及EF 的长. 九年级圆中三角形相似复习专题 1、 黄金分割点:在线段AB 上,点C 把线段AB 分成两条线段AC 和BC (AC>BC ),如果 AC BC AB AC = ,即AC 2=AB×BC,那么称线段AB 被点C 黄金分割,点C叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比。其中AB AC 2 1 5-= ≈0.618AB 。 2、 黄金分割的几何作图:已知:线段AB.求作:点C 使C 是线段AB 的黄金分割点.作法: (1)过点B作BD⊥A B,使BD=0.5AB ; (2)连结AD,在DA 上截取DE=DB ; (3)在A B上截取AC =AE,则点C就是所求作的线段AB 的黄金分割点。 (4)矩形中,如果宽与长的比是黄金比,这个矩形叫做黄金矩形 3、相似三角形 1)定义:如果两个三角形中,三角对应相等,三边对应成比例,那么这两个三角形叫做相似三角形。 几种特殊三角形的相似关系:两个全等三角形一定相似。 两个等腰直角三角形一定相似。 两个等边三角形一定相似。 两个直角三角形和两个等腰三角形不一定相似。 补充:对于多边形而言,所有圆相似;所有正多边形相似(如正四边形、正五边形等等); 4、 性质:两个相似三角形中,对应角相等、对应边成比例。 5、 相似比:两个相似三角形的对应边的比,叫做这两个三角形的相似比。 如△ABC 与△DEF 相似,记作△A BC ∽△D EF 。相似比为k 。 6、判定:①定义法:对应角相等,对应边成比例的两个三角形相似。 ②三角形相似的预备定理:平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似。 三角形相似的判定定理: 判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似。(此定理用的最多) 判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似。 判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似;简述为:三边对应成比例,两三角形相似。 7、 直角三角形相似判定定理: (1) 斜边与一条直角边对应成比例的两直角三角形相似。 (2) 直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似,并且分成的两个直角三角 形也相似。 N M E D C B A E D C B A E D C B A l3 l2 l1 C/ B/ A/ C B A l3 l2 l1 B/ A/ B A 学生:科目:数学教师:谭前富 知识框架 相似三角形的性质是几何证明的重要工具,是证明线段和差问题、相等问题、比例问题、角相等问题的重要方法,尤其在圆中,相似三角形有着极其重要的作用. 1、相似三角形的性质 相似三角形的对应边成比例,对应角相等,对应边上的中线,角平分线,高线,周长之比等于相似比,面积之比等于相似比的平方. 2、相似三角形的判定方法 (1)三边对应成比例的两个三角形相似 (2)两边对应成比例,夹角相等的两个三角形相似 (3)两组角对应相等的两个三角形相似. 3、相似三角形中几个的基本图形 4、由相似三角形得到的几个常用定理 定理1 平行于三角形一边的直线截得的三角形与原三角形形似. 如图,若DE∥BC,则 AD AE DE AB AC BC ==, 或 AD BD AE CE =. 定理2 平行切割定理 如图,,D E分别是ABC D的边, AB AC上的点, 过点A的直线交, DE BC于, M N,若DE∥MN, 则 DM BN ME NC = 定理3 (平行线分线段成比例定理)两条直线被一组平行线截得的对应线段成比例. 如图,若 1 l∥ 2 l∥ 3 l,则 E D C B A AB BC AC A B B C A C == ⅱⅱⅱ, 定理4(角平分线性质定理) 如图,,AD AE 分别是 ABC D 的内角平分线与外角平分线, 则DB EB AB DC EC AC ==. 定理5 射影定理 直角三角形斜边上的高分原三角形成两个直角三角形,这两个三角形与原三角形相似. 定理6 相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。 即:在⊙O 中,∵弦AB 、CD 相交于点P , ∴PA PB PC PD ?=? 定理7 推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。 即:在⊙O 中,∵直径AB CD ⊥, ∴2 CE AE BE =? 定理8 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。 即:在⊙O 中,∵PA 是切线,PB 是割线 ∴ 2 PA PC PB =? 定理9 割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如上图)。 即:在⊙O 中,∵PB 、PE 是割线 ∴PC PB PD PE ?=? 【例题精讲】 二例题讲解 O E D C A D C B P A O P O D C B A 1 相似三角形 经典模型 “平行型”: A 字型和8字型 由DE ∥BC 可得:AC AE AB AD EA EC AD BD EC AE DB AD ===或或.此推论较原定理应用更加广泛,条件是平行. 例1:如图,111EE FF MM ∥∥,若 AE EF FM MB ===, 则1 11 1 1 1 :::_________AEE EE F F FF M M MM CB S S S S ?=四边形四边形四边形 M 1F 1E 1M E F A B C 总结:相似比和面积比,周长比的关系是 例2:如图,AD EF MN BC ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则_____EF =, _____MN = M N A B C D E F 2 例3.已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H 求证: PE PH PF PG = P H G F E D C B A 例4.已知:在ABC ?中,D 为AB 中点,E 为AC 上一点,且 2AE EC =,BE 、CD 相交于点F , 求 BF EF 的值 例5.已知:在ABC ?中,12AD AB = ,延长BC 到F ,使1 3 CF BC =,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE = A B C D F E 7.如图,在ABC ?中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F 求证:AE BF BE CF ?=? F E D C B A F E D C B A 中考数学—圆与相似的综合压轴题专题复习及答案一、相似 1.如图的中点 1,过等边三角形 M, N,连接 MN . ABC 边AB 上一点 D 作交边AC 于点E,分别取BC, DE (1)发现:在图 1 中,________; (2)应用:如图2,将绕点 A 旋转,请求出的值; (3)拓展:如图3,和是等腰三角形,且, M , N 分别是底边 BC, DE 的中点,若,请直接写出的值. 【答案】(1) (2)解:如图 2 中,连接AM、 AN, , , 都是等边三角形, , ,,,, , , , ∽, (3)解:如图 3 中,连接AM、 AN,延长 AD 交 CE于 H,交 AC 于 O, ,,,, ,, , , , , ,, , , ∽, , , , ,, ≌, , , , , , , , , , 【解析】【解答】解:(1)如图 1 中,作于H,连接AM, ,, , 时等边三角形, , , , , 平分线段DE, , 、 N、 M 共线, , 四边形 MNDH 时矩形, , , 故答案为:; 【分析】( 1)作DH ⊥ BC 于 H,连接AM.证四边形MNDH 时矩形,所以MN=DH,则MN : BD=DH:BD=sin60 ,°即可求解; (2)利用△ ABC ,△ ADE 都是等边三角形可得AM : AB=AN: AD,易得∠BAD = ∠MAN ,从而得△ BAD ∽ △ MAN,则 NM: BD=AM:AB=sin60 ,°从而求解; (3)连接 AM、 AN,延长 AD 交 CE 于 H,交 AC 于 O.先证明△BAD∽△ MAN可得 NM : BD=AM:AB=sin∠ ABC;再证明△ BAD ≌ △ CAE,则∠ ABD = ∠ ACE ,进而可得∠ABC = 45 ,可求出°答案 . 2.如图, Rt△ AOB 在平面直角坐标系中,已知:B(0,),点OA=3,∠BAD=30°,将△ AOB 沿 AB 翻折,点O 到点 C 的位置,连接A 在 x 轴的正半轴上,CB 并延长交 x 轴于点 圆与相似三角形、解直角三角形及二次函数的综合 类型一:圆与相似三角形的综合 1.如图,BC是⊙A的直径,△DBE的各个顶点均在⊙A上,BF⊥DE于点F.求证:BD·BE=BC·BF. 2.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O 的切线,交BC于点E. (1)求证:点E是边BC的中点; (2)求证:BC2=BD·BA; (3)当以点O,D,E,C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形. 解:(1)连结OD,∵DE为切线,∴∠EDC+∠ODC=90°.∵∠ACB=90°,∴∠ECD+∠OCD =90°.又∵OD=OC,∴∠ODC=∠OCD, ∴∠EDC=∠ECD,∴ED=EC.∵AC为直径,∴∠ADC=90°,∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,∴ED=EB,∴EB=EC,即点E为边BC的中点 (2)∵AC为直径,∴∠ADC=∠ACB=90°.又∵∠B=∠B,∴△ABC∽△CBD,∴ABBC=BCBD,∴BC2=BD?BA (3)当四边形ODEC为正方形时,∠OCD=45°.∵AC为直径,∴∠ADC=90°,∴∠CAD=90°-∠OCD=90°-45°=45°,∴Rt△ABC为等腰直角三角形 类型二:圆与解直角三角形的综合 3.如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点, DE⊥AB,垂足为点E,交AC的延长线于点F. (1)求证:直线EF是⊙O的切线; (2)已知CF=5,cosA=25,求BE的长. 解:(1)连结OD.∵CD=DB,CO=OA,∴OD是△ABC的中位线,∴OD∥AB,AB=2OD.∵DE⊥AB,∴DE⊥OD,即OD⊥EF,∴直线EF是⊙O的切线 (2)∵OD∥AB,∴∠COD=∠A,∴cos∠COD=cosA=25.在Rt△DOF中,∵∠ODF=90°,∴cos∠FOD=ODOF=25.设⊙O的半径为r,则rr+5=25,解得r=103,∴AB=2OD=AC=203.在Rt△AEF中,∵∠AEF=90°,∴cosA=AEAF=AE5+203=25,∴AE=143,∴BE=AB-AE =203-143=2 4.(2015·资阳)如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连结DE. (1)求证:DE是⊙O的切线; (2)连结AE,若∠C=45°,求sin∠CAE的值. 解:(1)连结OD,BD,∵OD=OB,∴∠ODB=∠OBD.∵AB是直径,∴∠ADB=90°,∴∠CDB =90°.∵E为BC的中点,∴DE=BE,∴∠EDB=∠EBD,∴∠ODB+∠EDB=∠OBD+∠EBD,即∠EDO=∠EBO.∵BC是以AB为直径的⊙O的切线,∴AB⊥BC,∴∠EBO=90°,∴∠ODE =90°,∴DE是⊙O的切线 (2)过点E作EF⊥CD于点F,设EF=x,∵∠C=45°,∴△CEF,△ABC都是等腰直角三角形,∴CF=EF=x,∴BE=CE=2x,∴AB=BC=22x.在Rt△ABE中,AE=AB2+BE2=10x,∴sin∠CAE=EFAE=1010 5.如图,△ABC内接于⊙O,直径BD交AC于点E,过点O作FG⊥AB,交AC于点F,交AB 于点H,交⊙O于点G. (1)求证:OF·DE=OE·2OH; (2)若⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,求阴影部分的面积.(结果保留根号)解:(1)∵BD是直径,∴∠DAB=90°.∵FG⊥AB,∴DA∥FO,∴△FOE∽△ADE,∴FOAD=OEDE,即OF?DE=OE?AD.∵O是BD的中点,DA∥OH,∴AD=2OH,∴OF?DE=OE?2OH (2)∵⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,∴OE=4,ED=8,OF=6,∴OH=6.在Rt △OBH中,OB=2OH,∴∠OBH=30°,∴∠BOH=60°,∴BH=BO?sin60°=12×32=63,∴S阴影=S扇形GOB-S△OHB=60×π×122360-12×6×63=24π-183 类型三:圆与二次函数的综合 6.如图,在平面直角坐标系中,已知A(-4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D. (1)求过A,B,C三点的抛物线的解析式; (2)求点D的坐标; (3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由. 25.如图,AB是⊙O的直径,C是⊙O上一点,D是 BC的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD. (1)求证:AF⊥EF; (2)若 1 tan 2 CAD ∠=,AB=5,求线段BE的长. 25.(1)证明:连结OD. ∵直线EF与⊙O相切于点D, ∴OD⊥EF. ∵OA = OD,∴∠1=∠3.………………………….. 1分∵点D为 BC的中点, ∴∠1=∠2,∴∠2=∠3, ∴OD∥AF,∴AF⊥EF.………………..………… 2分(2)解:连结BD. ∵ 1 tan 2 CAD ∠=, ∴ 1 tan1 2 ∠=,……………….………………..…… 3分 在Rt△ADB中,AB=5, ∴BD AD = 在Rt△AFD中,可得DF=2,AF=4, ∵OD∥AF,∴△EDO∽△EF A,….……………… 4分 ∴OD OE AF AE =, 又∵OD=2.5,设BE=x, ∴2.5 2.5 45 x x + = + , ∴ 5 3 x=,即BE= 5 3 .…………………….….……. 5分 3 2 1 O C B A D F E E F D A B C O 1 2 3 E A (1)圆题目的第二问通常需要作一条辅助线 (2)当涉及到求具体边的长度时,通常会利用到求半径长度 25.如图,在△ABC 中,AB=AC ,AD ⊥BC 于点D ,过点C 作⊙O 与边AB 相切于点E ,交BC 于点F ,CE 为⊙O 的直径. (1) 求证:OD ⊥CE ; (2) 若DF =1, DC =3,求AE 的长. 25. (本小题满分5分) (1)证明: ⊙O 与边AB 相切于点E ,且 CE 为⊙O 的直径. CE ⊥AB . AB=AC ,AD ⊥BC , . ………………………………1分 又 OE=OC , OD ∥EB . OD ⊥CE . (2) 分 (2)解:连接EF . CE 为⊙O 的直径,且点F 在⊙O 上, ∴∠EFC =90°. CE ⊥AB , ∠BEC =90°. =90°. . tan tan BEF ECF ∠=∠. ∴BF EF EF FC =. 又 DF =1, BD=DC =3, ∴ BF =2, FC =4. ∴EF =. ………………………………………………… 3分 ∵∠EFC =90°, ∴ BD DC ∴= ∴∴ ∴∴+BEF FEC FEC ECF ∠=∠+∠∠∴BEF ECF ∠=∠∴相似三角形综合练习相似与圆(难)
圆与相似三角形综合训练题
相似三角形综合试相似与圆(难)
(完整版)圆与相似三角形的综合常见题型
相似三角形与圆综合
相似三角形与圆的综合应用
圆与相似三角形复习知识点
最新相似三角形综合练习相似与圆(难)
相似三角形综合练习相似与圆(难)
九年级圆与相似三角形专题复习
圆与相似三角形综合问题演示教学
相似三角形_射影定理、圆
中考数学—圆与相似的综合压轴题专题复习及答案.doc
圆与相似三角形、三角函数专题
相似三角形在圆中的运用
