常见分布的期望和方差
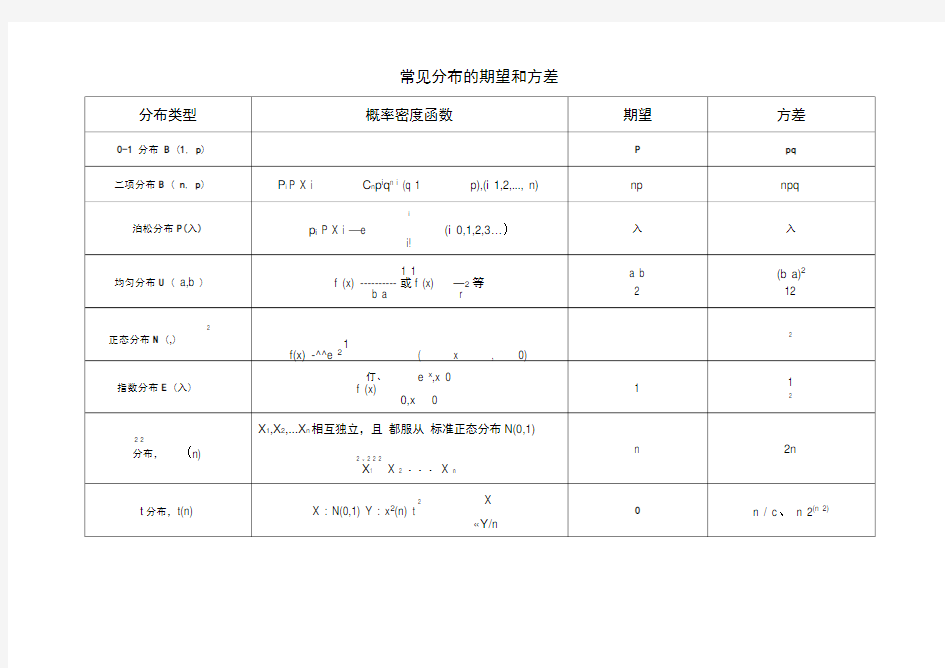

常见分布的期望和方差
6、随机变量的独立性:若
F(x,y) F X (x)F Y (y)则称随机变量 X , Y 相互独立。简称 X 与Y 独立。
概率与数理统计重点摘要
X
1正态分布的计算:
F(x) P(X x) ( )。
X 是服从某种分布的随机变量,求 Y f(X)的概率密度:f Y (y) f X (x)[h(y)] h'(y)。(参见P66?72)
x y ..
f (u, v)dudv 具有以下基本性质:
⑴、是变量x , y 的非降函数;
⑵、0 F(x, y) 1,对于任意固定的 x , y 有:F( , y) F(x, ) 0;
⑶、F(x, y)关于x 右连续,关于y 右连续;
⑷、对于任意的(为,yd (X 2, y 2),捲 X 2,y 1 y ,有下述不等式成立:
Fgy) F(X 1,y 2)F(X 2,yJ
5、二维随机变量的边缘分布:
f x (X ) f (x,y)dy 边缘概率密度:
f Y (y)
f (x, y)dx
F X (X )
X
F(x,) [ f (u, y)dy]du
边缘分布函数:
y
二维正态分布的边缘分布为一维正态分布。
F Y (¥)
y
F( ,y)
[
f (x, v)dx]dv
2、随机变量函数的概率密度:
3、分布函数F(x, y)
4、一个重要的分布函数:
arcta n -)(— 2
arCtany)
的概率密度为: 2
f(x,y)
F(x,y)
x y
6
2 2 2 (x 4)( y 9)
F(x, y)
7、两个独立随机变量之和的概率密度:
f z (Z ) f x (x)f Y (z x)dx f Y (y)f x (z y)dy 其中 Z = x + Y
8、两个独立正态随机变量的线性组合仍服从正态分布,即 Z aX bY : N (a 1 b 2,a 2 12 b 2 2。 9、期望的性质: (3)、E(X Y) E(X) E(Y) ;(4)、若 X ,Y 相互独立,则 E(XY) E(X)E(Y)。 2 2
10、方差:
D(X) E(X ) (E(X))。
不相关,则 D(X Y) D(X) D(Y),否则 D(X Y) D(X) D(Y) 2Cov(X,Y),
D(X Y) D(X) D(Y) 2Cov(X,Y) 11、协方差:Cov(X,Y) E[(X E(X))(Y E(Y))],若 X ,Y 独立,则Cov(X,Y) 0,此时称:X 与Y 不相关。
12、相关系数: XY Cov(X,Y) _Cov (X , Y)_
(X) (Y) D(X)jD(Y),
XY
1,当且仅当 X 与Y 存在线性关系时 XY
1,且
XY
1, 1, 当 b>0;
当
b<0。
13、k 阶原点矩:v k k
E (X )
, k 阶中心矩: k
E[(X k
E(X))]。
14、切比雪夫不等式:
P X E(X) E(X)
lim P
n 0
15、独立同分布序列的切比雪夫大数定律:
1 n
1 n
因
P
X i
1
2,所以
lim P X i
I i 1 I
n 0
I i 1
1
。贝努利大数定律:
畔或P
16、独立同分布序列的中心极限定理: (1)、当n 充分大时,独立同分布的随机变量之和
X i i 1
的分布近似于正态分布 N(n , n
2
)。
(2)、对于 X 1,X 2,...X n 的平均值 X
1
X
i
n i 1
有 E(X)
1 n
E(X i )亠
n i 1
n
,D(X) D(X i )
n "2 n
,即独立同分布的随机
变量的均值当n 充分大时,近似服从正态分布 N(
)。
m 是n 次独立重复试验中事件 A 发生的次数,p 是事件A 发生的概率,则对任意 x ,
(1) 、当n 充分大时,m 近似服从正态分布, N(np npq)。 (2) 、当n 充分大时,—近似服从正态分布,
N( p,卫。
n n
18、 参数的矩估计和似然估计: (参见P200) 19、 正态总体参数的区间估计:
(3)、由上可知:lim P a Z n
b
n
(b) (a) P a Z n b (b) (a)。
lim P
n
m np .npq
(x),其中 q 1 p 。
17、棣莫弗一拉普拉斯中心极限定理:设
20、关于正态总值均值及方差的假设检验,参见P243和P24&
20、关于正态总值均值及方差的假设检验,参见P243和P24&
