高考文科数列知识点总结

高考文科数列知识点

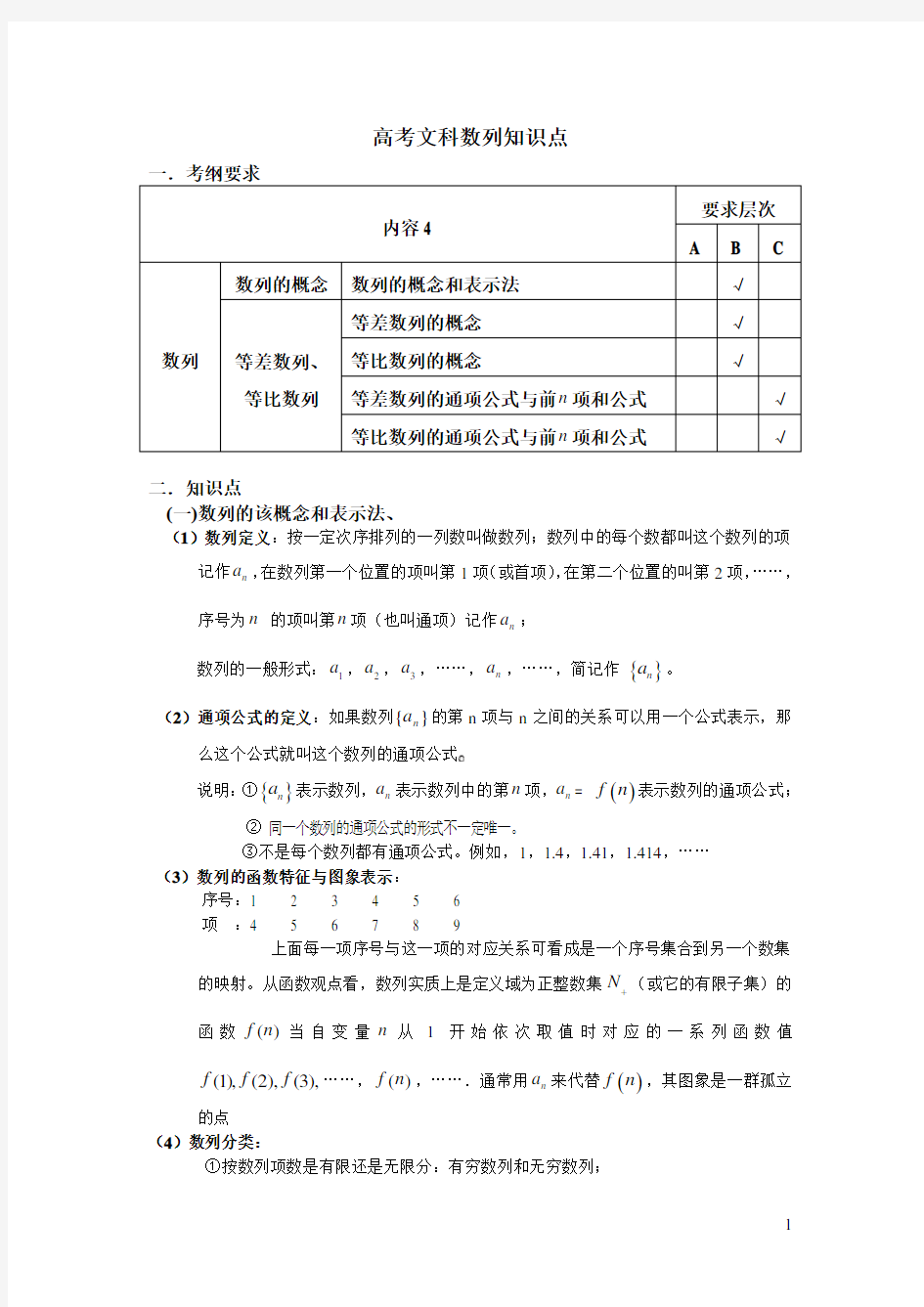
一．考纲要求

内容4

要求层次

A

B C 数列

数列的概念 数列的概念和表示法

√ 等差数列、 等比数列

等差数列的概念

√ 等比数列的概念 √ 等差数列的通项公式与前n 项和公式 √ 等比数列的通项公式与前n 项和公式

√

二．知识点

(一)数列的该概念和表示法、

（1）数列定义：按一定次序排列的一列数叫做数列；数列中的每个数都叫这个数列的项

记作n a ，在数列第一个位置的项叫第1项（或首项），在第二个位置的叫第2项，……，序号为n 的项叫第n 项（也叫通项）记作n a ；

数列的一般形式：1a ，2a ，3a ，……，n a ，……，简记作 {}n a 。

（2）通项公式的定义：如果数列}{n a 的第n 项与n 之间的关系可以用一个公式表示，那

么这个公式就叫这个数列的通项公式

说明：①{}n a 表示数列，n a 表示数列中的第n 项，n a = ()f n 表示数列的通项公式； ② 同一个数列的通项公式的形式不一定唯一。

③不是每个数列都有通项公式。例如，1，1.4，1.41，1.414，…… （3）数列的函数特征与图象表示：

序号：1 2 3 4 5 6 项 ：4 5 6 7 8 9

上面每一项序号与这一项的对应关系可看成是一个序号集合到另一个数集

的映射。从函数观点看，数列实质上是定义域为正整数集N +（或它的有限子集）的函数()f n 当自变量n 从1开始依次取值时对应的一系列函数值

(1),(2),(3),f f f ……，()f n ，……．通常用n a 来代替()f n ，其图象是一群孤立

的点

（4）数列分类：

①按数列项数是有限还是无限分：有穷数列和无穷数列；

②按数列项与项之间的大小关系分：单调数列（递增数列、递减数列）、常数列和摆动数列

（5）递推公式定义：如果已知数列{}n a 的第1项（或前几项），且任一项n a 与它的前一项

1n a -（或前几项）间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的

递推公式

（二）等差数列

1.等差数列的定义：d a a n n =--1（d 为常数）（2≥n ）；

2．等差数列通项公式：

*11(1)()n a a n d dn a d n N =+-=+-∈ ， 首项:1a ，公差:d ，末项:n a 推广： d m n a a m n )(-+=． 从而m

n a a d m

n --=；

3．等差中项

（1）如果a ，A ，b 成等差数列，那么A 叫做a 与b 的等差中项．即：

2

b

a A +=或

b a A +=2 （2）等差中项：数列{}n a 是等差数列)2(211-≥+=?+n a a a n n n 212+++=?n n n a a a

4．等差数列的前n 项和公式：

1()2n n n a a S +=

1(1)2n n na d -=+211

()22

d n a d n =+-2An Bn =+ （其中A 、B 是常数，所以当d ≠0时，S n 是关于n 的二次式且常数项为0）

特别地，当项数为奇数21n +时，1n a +是项数为2n+1的等差数列的中间项

()()()12121

121212

n n n n a a S n a +++++==

+（项数为奇数的等差数列的各项和等于项数

乘以中间项）

5．等差数列的判定方法

（1） 定义法：若d a a n n =--1或d a a n n =-+1(常数*

∈N n )? {}n a 是等差数列．

（2） 等差中项：数列{}n a 是等差数列)2(211-≥+=?+n a a a n n n 212+++=?n n n a a a ． （3） 数列{}n a 是等差数列?b kn a n +=（其中b k ,是常数）。 （4） 数列{}n a 是等差数列?2n S An Bn =+,（其中A 、B 是常数）。

6．等差数列的证明方法

定义法：若d a a n n =--1或d a a n n =-+1(常数*

∈N n )? {}n a 是等差数列．

7.等差数列的性质：

（1）当公差0d ≠时，等差数列的通项公式11(1)n a a n d dn a d =+-=+-是关于n 的一次函

数，且斜率为公差d ；前n 和211(1)()222

n n n d d

S na d n a n -=+

=+-是关于n 的二次函数且常数项为0.

（2）若公差0d >，则为递增等差数列，若公差0d <，则为递减等差数列，若公差0d =，

则为常数列。

（3）当m n p q +=+时,则有q p n m a a a a +=+，特别地，当2m n p +=时，则有

2m n p a a a +=.

（4）若{}n a 、{}n b 为等差数列，则{}{}12n n n a b a b λλλ++，都为等差数列

(5) 若{n a }是等差数列，则232,,n n n n n S S S S S -- ，…也成等差数列

（6）数列{}n a 为等差数列,每隔k(k ∈*

N )项取出一项(23,,,,m m k m k m k a a a a +++???)仍为等差数 列

（7）设数列{}n a 是等差数列，d 为公差，奇S 是奇数项的和，偶S 是偶数项项的和，n S 是

前n 项的和

1.当项数为偶数n 2时，

()

121135212n n n n a a S a a a a na --+=+++???+=

=奇

()

22246212

n n n n a a S a a a a na ++=+++???+==偶

()11=n n n n S S na na n a a nd ++-=-=-偶奇

11

n n n n S na a S na a ++==奇偶

2、当项数为奇数12+n 时，则

21(21)(1)1n S S S n a S n a S n S S a S na S n +?=+=+=+?+????=??

-==????

n+1n+1

奇偶奇奇n+1n+1奇偶偶偶 （其中a n+1是项数为2n+1的等差数列的中间项）．

（8）等差数列{}n a 的前n 项和m S n =，前m 项和n S m =，则前m+n 项和()m n S m n +=-+

(9)求n S 的最值

法一：因等差数列前n 项和是关于n 的二次函数，故可转化为求二次函数的最值，但要 注意数列的特殊性*

n N ∈。

法二：（1）“首正”的递减等差数列中，前n 项和的最大值是所有非负项之和

即当，，001<>d a 由??

?≤≥+0

1n n a a 可得n S 达到最大值时的n 值．

（2） “首负”的递增等差数列中，前n 项和的最小值是所有非正项之和。 即 当，，001>

1n n a a 可得n S 达到最小值时的n 值．

或求{}n a 中正负分界项

法三：直接利用二次函数的对称性：由于等差数列前n 项和的图像是过原点的二次函数，故n 取离二次函数对称轴最近的整数时，n S 取最大值（或最小值）。若S p = S q 则其对称轴

为2

p q

n +=

（三）等比数列

1. 等比数列的定义：()()*1

2,n

n a q q n n N a -=≠≥∈0且，q 称为公比 2. 通项公式：

()11110,0n n

n n a a a q q A B a q A B q

-==

=??≠?≠， 首项：1a ；公比：q 推广：n m n m a a q -=， 从而得n m

n m a q a -=

或n n m m

a q a -= 3. 等比中项

（1）如果,,a A b 成等比数列，那么A 叫做a 与b 的等差中项．即：

2

A ab =或A ab =± 注意：同号的两个数才有等比中项，并且它们的等比中项有两个（两个等比中项

互为相反数）

（2）数列{}n a 是等比数列?211n n n a a a -+=?

4. 等比数列的前n 项和n S 公式： (1) 当1q =时， 1n S na = (2) 当1q ≠时，()11111n n n a q a a q

S q

q

--=

=

--

5. 等比数列的判定方法

（1）用定义：对任意的n,都有1

1(0)n n n n n

a a qa q q a a ++==≠或为常数，?{}n a 为等比数列

（2） 等比中项：211n n n a a a +-=（11n n a a +-≠0）?{}n a 为等比数列 （3） 通项公式：()0n

n a A B

A B =??≠?{}n a 为等比数列

（4） 前n 项和公式：()

'',,','n

n

n n S A A B S A B A A B A B =-?=-或为常数?{}n a 为 等比数列

6. 等比数列的证明方法 依据定义：若

()()*1

2,n

n a q q n n N a -=≠≥∈0且或1n n a qa +=?{}n a 为等比数列

7. 等比数列的性质 (1) 当1q ≠时

①等比数列通项公式()1

110n n

n n a a a q q A B A B q

-==

=??≠是关于n 的带有系数的类指数函数，底数为公比q

②前n 项和()111111''1111n n n n n n a q a a q a a S q A A B A B A q

q q q

--=

=-=-?=-----，系数和

常数项是互为相反数的类指数函数，底数为公比q

(2) 对任何m,n ∈*N ,在等比数列{}n a 中,有n m n m a a q -=,特别的,当m=1时,便得到等比数列的通项公式.因此,此公式比等比数列的通项公式更具有一般性。 (3) 若m+n=s+t (m, n, s, t ∈*N ),则n m s t a a a a ?=?.特别的,当n+m=2k 时,得

2n m k a a a ?=

注：12132n n n a a a a a a --?=?=???

(4) 列{}n a ,{}n b 为等比数列,则数列{}n

k

a ,{}n k a ?,{}k n a ,{}n n k a

b ??{}n n a b (k 为非零

常数) 均为等比数列.

(5) 数列{}n a 为等比数列,每隔k(k ∈*N )项取出一项(23,,,,m m k m k m k a a a a +++???)仍为等比数列

(6) 如果{}n a 是各项均为正数的等比数列,则数列{log }a n a 是等差数列 (7) 若{}n a 为等比数列,则数列n S ，2n n S S -，32,n n S S -???，成等比数列

(8) 若{}n a 为等比数列,则数列12n a a a ??????, 122n n n a a a ++??????,

21223n n n a a a ++???????成等比数列

(9) ①当1q >时， ②当1q <0<时，

110{}0{}{n n a a a a ><，则为递增数列

，则为递减数列, 110{}0{}{n n a a a a ><，则为递减数列，则为递增数列

③当q=1时,该数列为常数列（此时数列也为等差数列）; ④当q<0时,该数列为摆动数列.

(10)在等比数列{}n a 中, 当项数为2n (n ∈*N )时,

1S S q

=奇偶,.

(11)若{}n a 是公比为q 的等比数列,则n n m n m S S q S +=+?