精选例题

一．改错题

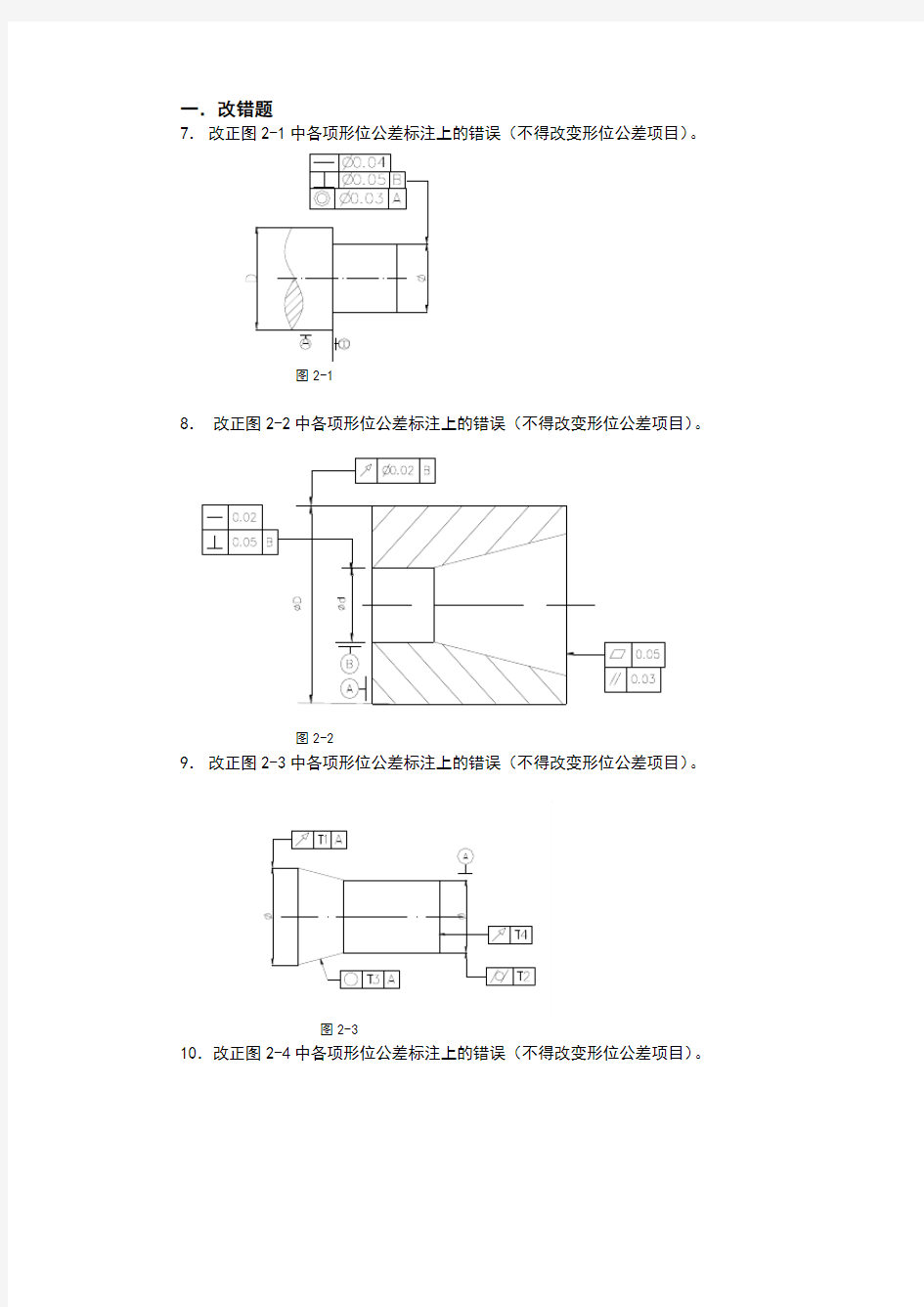
7．改正图2-1中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-1

8．改正图2-2中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-2

9．改正图2-3中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-3

10．改正图2-4中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-4

11．改正图2-5中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-5

12．改正图2-6中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-6

13．改正图2-7中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-7

14．改正图2-8中各项形位公差标注上的错误（不得改变形位公差项目）。

图2-8

二.标注题

15．将下列技术要求标注在图2-9上。

（1）φ100h6圆柱表面的圆度公差为0.005mm。

（2）φ100h6轴线对φ40P7孔轴线的同轴度公差为φ0.015mm。

（3）φ40P７孔的圆柱度公差为0.005mm。

（4）左端的凸台平面对φ40P7孔轴线的垂直度公差为0.01 mm。

（5）右凸台端面对左凸台端面的平行度公差为0.02 mm。

图2-9

16．将下列技术要求标注在图2-10。

（1）圆锥面的圆度公差为0.01 mm，圆锥素线直线度公差为0.02 mm。（2）圆锥轴线对φd1和φd2两圆柱面公共轴线的同轴度为0.05 mm。

（3）端面Ⅰ对φd1和φd2两圆柱面公共轴线的端面圆跳动公差为0.03 mm。（4）φd1和φd2圆柱面的圆柱度公差分别为0.008 mm和0.006 mm。

图2-10

17．将下列技术要求标注在图2-11上。

（1）左端面的平面度公差为0.01 mm，右端面对左端面的平行度公差为0.04 mm。

（2）φ70H7孔的轴线对左端面的垂直度公差为0.02mm。

（3）φ210h7轴线对φ70H7孔轴线的同轴度公差为φ0.03mm。

（4）4-φ20H8孔的轴线对左端面（第一基准）和φ70H7孔轴线的位置度公差为φ0.15mm。

图2-11

18．试将下列技术要求标注在图2-12上。

（1）2-φd轴线对其公共轴线的同轴度公差为φ0.02mm。

（2）φD轴线对2-φd公共轴线的垂直度公差为100 ：0.02 mm。

（3）槽两侧面对φD轴线的对称度公差为0．04 mm。

槽

图2-12

19．试将下列技术要求标注在图2-13上。

（1）圆锥面a的圆度公差为0．1 mm。

（2）圆锥面a对孔轴线b的斜向圆跳动公差为0．02mm。

（3）基准孔轴线b的直线度公差为0．005mm。

（4）孔表面c的圆柱度公差为0．0lmm。

（5）端面d对基准孔轴线b的端面全跳动公差为0．01mm。

（6）端面e对端面d的平行度公差为0．03mm。

图2-13

20．试将下列技术要求标注在图2－14上。

（1）φ30K7和φ50M7采用包容原则。

（2）底面F的平面度公差为0．02mm；φ30K7孔和φ50M7孔的内端面对它们的公共轴线的圆跳动公差为0．04 mm。

（3）φ30K7孔和φ50M7孔对它们的公共轴线的同轴度公差为0．03mm。

（4） 6-φ11H10对φ50M7孔的轴线和F面的位置度公差为0．05mm，基准要素的尺寸和被测要素的位置度公差应用最大实体要求。

图2-14

21．试将下列技术要求标注在图2-15上。

（l）φ5+0.05

mm的圆柱度误差不大于0．02mm，圆度误差不大于0．0015 mm。

-0.03

mm的轴线的端面圆跳动不大于（2）B面的平面度误差不大于0．001mm，B面对φ5+0.05

-0.03

0．04 mm，B面对C面的平行度误差不大于0．02mm。

mm轴线的端面圆跳动不大于0．04 mm。

（3）平面F对φ5+0.05

-0.03

mm内孔轴线的同轴度误差不大于0．2 mm。

（4）φ18d11外圆柱面的轴线对φ5+0.05

-0.03

（5）φ12b11外圆柱面轴线对φ5+0.05

mm孔轴线的同轴度误差不大于φ0．16 mm。

-0.03

mm孔轴线的同轴度误差不大于φ0．16 mm。

（6） 90°30″密封锥面G对φ5+0.05

-0.03

（7）锥面G 的圆度误差不大于0．002 mm 。

图2-15

22．试将下列技术要求标注在图2－16上。（1）大端圆柱面的尺寸要求为φ45 0 -0.02，并采用包容要求。

（2）小端圆柱面轴线对大端圆柱面轴线的同轴度公差为0．03mrn 。

（3）小端圆柱面的尺寸要求为φ25土0．007mrn ，素线直线度公差为0．01mrn ，并采用包容要求。

（4）大端圆柱面的表面粗糙度R a 值不允许大于0．8μrn ，其余表面R a 值不允许大于1．6μrn 。

图2-16

23．试将下列技术要求标注在图2-17上。（1）φd 圆柱面的尺寸为φ30 0 -0.025 mm ，采用包容要求，φD 圆柱面的尺寸为φ50 0 -0.039 mm ，采用独立原则。（2）φd 表面粗糙度的最大允许值为R a =1.25μm ，φD 表面粗糙度的最大允许值为R a =2μm 。

（3）键槽侧面对φD 轴线的对称度公差为0．02 mm 。（4）φD 圆柱面对φd 轴线的径向圆跳动量不超过0．03 mm ，轴肩端平面对φd 轴线的端面圆跳动不超过0．05 mm 。

图2-17

三.计算题：

43．若某零件的同轴度要求如图2-37所示，今测得实际轴线与基准轴线的最大距离为+0.04mm，最小距离为-0.01mm，求该零件的同轴度误差值，并判断是否合格。

37．如图2-31所示，被测要素采用的公差原则是＿＿，最大实体尺寸是＿＿mm，最小实体尺寸是＿＿mm，实效尺寸是＿＿mm。，垂直度公差给定值是＿＿mm，垂直度公差最大补偿值是＿＿mm。设孔的横截面形状正确，当孔实际尺寸处处都为φ60mm时，垂直度公差允许值是＿＿mm，当孔实际尺寸处处都为φ60．10mm时，垂直度公差允许值是＿＿mm。

28．按表2-5中的内容，说明图2-22中形位公差代号的含义。

表2-5

代号解释代号含义公差带形状

两处两处

计数原理与排列组合经典题型

计数原理与排列组合题型解题方法总结计数原理一、知识精讲 1、分类计数原理： 2、分步计数原理：特别注意:两个原理的共同点：把一个原始事件分解成若干个分事件来完成。不同点：如果完成一件事情共有n类办法，这n类办法彼此之间相互独立的，无论哪一类办法中的哪一种方法都能单独完成这件事情，求完成这件事情的方法种数，就用分类计数原理。分类时应不重不漏（即任一种方法必须属于某一类且只属于这一类）如果完成一件事情需要分成n个步骤，各个步骤都是不可缺少的，需要依次完成所有的步骤，才能完成这件事，而完成每一个步骤各有若干种不同的方法，求完成这件事情的方法种数就用分步计数原理。各步骤有先后，相互依存，缺一不可。 3、排列 (1)排列定义,排列数 (2)排列数公式: (3)全排列列: 4.组合 (1)组合的定义,排列与组合的区别; (2)组合数公式: (3)组合数的性质二、.典例解析题型1:计数原理例1.完成下列选择题与填空题 (1)有三个不同的信箱,今有四封不同的信欲投其中,则不同的投法有种。 A.81 B.64 C.24 D.4 (2)四名学生争夺三项冠军,获得冠军的可能的种数是( ) A.81 B.64 C.24 D.4 (3)有四位学生参加三项不同的竞赛, ①每位学生必须参加一项竞赛,则有不同的参赛方法有; ②每项竞赛只许有一位学生参加,则有不同的参赛方法有;

③每位学生最多参加一项竞赛,每项竞赛只许有一位学生参加,则不同的参赛方法有。例2（1）如图为一电路图，从A 到B 共有条不同的线路可通电。例3: 把一个圆分成3块扇形，现在用5种不同的颜色给3块扇形涂色，要求相邻扇形的颜色互不相同，问有多少钟不同的涂法？若分割成4块扇形呢？例4、某城在中心广场造一个花圃，花圃分为6个部分(如图).现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有 ________ 种.(以数字作答) 例5、四面体的顶点和各棱的中点共10个，在其中取4个不共面的点，问共有多少种不同的取法？例6、（1）电视台在”欢乐今宵”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封.现有主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果? （2）三边均为整数，且最大边长为11的三角形的个数是 D C B A

排列组合典型例题(带详细答案)

例1 用0到9这10 个数字．可组成多少个没有重复数字的四位偶数？例2三个女生和五个男生排成一排（1）如果女生必须全排在一起，可有多少种不同的排法？（2）如果女生必须全分开，可有多少种不同的排法？（3）如果两端都不能排女生，可有多少种不同的排法？（4）如果两端不能都排女生，可有多少种不同的排法？例3 排一张有5个歌唱节目和4个舞蹈节目的演出节目单。（1）任何两个舞蹈节目不相邻的排法有多少种？（2）歌唱节目与舞蹈节目间隔排列的方法有多少种？例4某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课，如果第一节不排体育，最后一节不排数学，那么共有多少种不同的排课程表的方法．例5现有3辆公交车、3位司机和3位售票员，每辆车上需配1位司机和1位售票员．问车辆、司机、售票员搭配方案一共有多少种？例6下是表是高考第一批录取的一份志愿表．如果有4所重点院校，每所院校有3个专业是你较为满意的选择．若表格填满且规定学校没有重复，同一学校的专业也没有重复的话，你将有多少种不同的填表方法？例77名同学排队照相． (1)若分成两排照，前排3人，后排4人，有多少种不同的排法？

(2)若排成两排照，前排3人，后排4人，但其中甲必须在前排，乙必须在后排，有多少种不同的排法？ (3)若排成一排照，甲、乙、丙三人必须相邻，有多少种不同的排法？ (4)若排成一排照，7人中有4名男生，3名女生，女生不能相邻，有多少种不面的排法？例8计算下列各题： (1) 215 A ； (2) 66 A ； (3) 1 1 11------?n n m n m n m n A A A ；例9 f e d c b a ,,,,,六人排一列纵队，限定a 要排在b 的前面（a 与b 可以相邻，也可以不相邻），求共有几种排法．例10 八个人分两排坐，每排四人，限定甲必须坐在前排，乙、丙必须坐在同一排，共有多少种安排办法？例11 计划在某画廊展出10幅不同的画，其中1幅水彩画、4幅油画、5幅国画，排成一行陈列，要求同一品种的画必须连在一起，并且不彩画不放在两端，那么不同陈列方式有例12 由数字5,4,3,2,1,0组成没有重复数字的六位数，其中个位数字小于十位数的个数共有（）．例13 用5,4,3,2,1，这五个数字，组成没有重复数字的三位数，其中偶数共有（）．例14 用543210、、、、、共六个数字，组成无重复数字的自然数，(1)可以组成多少个无重复数字的3位偶数？(2)可以组成多少个无重复数字且被3整除的三位数？

排列组合练习题及答案精选

排列组合习题精选一、纯排列与组合问题： 1. 从9人中选派2人参加某一活动，有多少种不同选法？ 2. 从9人中选派2人参加文艺活动，1人下乡演出，1人在本地演出，有多少种不同选派方法？ 3. 现从男、女8名学生干部中选出2名男同学和1名女同学分别参加全校“资源”、“生态” 和“环保”三个夏令营活动，已知共有 90种不同的方案，那么男、女同学的人数是（） A.男同学2人，女同学6人 B. 男同学3人，女同学5人 C.男同学5人，女同学3人 D. 男同学6人，女同学2人 4. 一条铁路原有m 个车站，为了适应客运需要新增加n 个车站（n>1），则客运车票增加了58 种（从甲站到乙站与乙站到甲站需要两种不同车票），那么原有的车站有（） A.12个 B.13 个 C.14 个 D.15 个答案：1、 2 2 72 3 、选 B. 设男生n 2 1 3 2 2 9 9 n 8 n3 。、mn m C 362、A 人，则有C C A 904 A A58 选 C. 二、相邻问题： 1. A 、B 、C 、D 、E 五个人并排站成一列，若A 、B 必相邻，则有多少种不同排法？ 2. 有8本不同的书，其中3本不同的科技书，2本不同的文艺书，3本不同的体育书，将这些书竖排在书架上，则科技书连在一起，文艺书也连在一起的不同排法种数为() A.720 B.1440 C.2880 D.3600 答案：1. 2 4 3 2 5 2 4 3 2 5 AA 48(2)选BAAA1440 三、不相邻问题： 1. 要排一个有4个歌唱节目和3个舞蹈节目的演出节目单，任何两个舞蹈节目都不相邻，有多少种不同排法？ 1

二元一次方程组应用题归类及精选例题

二元一次方程组精选应用题库二元一次方程组是最简单的方程组，其应用广泛，尤其是生活、生产实践中的许多问题，大多需要通过设元、列二元一次方程组来加以解决。列二元一次方程组解应用题的一般步骤可概括为“审、找、列、解、答”五步，即：（ 1）审：通过审题，把实际问题抽象成数学问题，分析已知数和未知数，并用字母表示其中的两个未知数；（ 2）找：找出能够表示题意两个相等关系；（ 3）列：根据这两个相等关系列出必需的代数式，从而列出方程组；（ 4）解：解这个方程组，求出两个未知数的值；（ 5）答：在对求出的方程的解做出是否合理判断的基础上，写出答案 . 现将中考中常见的几种题型归纳如下：一、市场营销问题例 1（2005 年河南省实验区）某商场购进甲、乙两种服装后，都加价 40%标价出售 . “春节”期间商场搞优惠促销，决定将甲、乙两种服装分别按标价的八折和九折出售 . 某顾客购买甲、乙两种服装共付款 182 元，两种服装标价之和为 210 元. 问这两种服装的进价和标价各是多少元？解：设甲种服装的标价为 x 元，则进价为 x 元；乙种服装的标价为 y 元，则进价为 y 元. 由题意，得 1.4 1.4 x y 210, 解得， x 70, 0.8x 0.9 y 182. y 140. 所以， x =50（元）， y =100（元） . 1.4 1.4 故甲种服装的进价和标价分别为 50 元、 70 元，乙种服装的进价和标价分别为 100 元、 140 元. 二、生产问题例 2（2005 年长沙市实验区）某工厂第一季度生产两种机器共 480 台. 改进生产技术后，计划第二季度生产两种机器共 5544 台，其中甲种机器产量要比第一季度增产 10%，乙种机器产量要比第一季度增产 20%. 该厂第一季度生产甲、乙两种机器各多少台？解：设该厂第一季度生产甲种机器 x 台，乙种机器 y 台. x y 480, 由题意，得 10%x 20% y 540 480. 解得， x 220, y 260.

排列组合知识点汇总及典型例题(全)

一．基本原理 1．加法原理：做一件事有n 类办法，则完成这件事的方法数等于各类方法数相加。 2．乘法原理：做一件事分n 步完成，则完成这件事的方法数等于各步方法数相乘。注：做一件事时，元素或位置允许重复使用，求方法数时常用基本原理求解。二．排列：从n 个不同元素中，任取m （m ≤n ）个元素，按照一定的顺序排成一 .m n m n A 有排列的个数记为个元素的一个排列，所个不同元素中取出列，叫做从 1.公式：1.()()()()! ! 121m n n m n n n n A m n -= +---=…… 2. 规定：0!1= (1)!(1)!,(1)!(1)!n n n n n n =?-+?=+ (2) ![(1)1]!(1)!!(1)!!n n n n n n n n n ?=+-?=+?-=+-； (3) 111111 (1)!(1)!(1)!(1)!!(1)! n n n n n n n n n +-+==-=- +++++ 三．组合：从n 个不同元素中任取m （m ≤n ）个元素并组成一组，叫做从n 个不同的m 元素中任取 m 个元素的组合数，记作 Cn 。 1. 公式： ()()()C A A n n n m m n m n m n m n m m m ==--+= -11……!!!! 10 =n C 规定：组合数性质：.2 n n n n n m n m n m n m n n m n C C C C C C C C 21011=+++=+=+--……，， ①；②；③；④ 111 12111212211r r r r r r r r r r r r r r r r r r n n r r r n n r r n n n C C C C C C C C C C C C C C C +++++-+++-++-+++++=+++ +=++ +=注：若1 2 m m 1212m =m m +m n n n C C ==则或四．处理排列组合应用题 1.①明确要完成的是一件什么事（审题） ②有序还是无序 ③分步还是分类。 2．解排列、组合题的基本策略（1）两种思路：①直接法； ②间接法：对有限制条件的问题，先从总体考虑，再把不符合条件的所有情况去掉。这是解决排列组合应用题时一种常用的解题方法。（2）分类处理：当问题总体不好解决时，常分成若干类，再由分类计数原理得出结论。注意：分类不重复不遗漏。即：每两类的交集为空集，所有各类的并集为全集。（3）分步处理：与分类处理类似，某些问题总体不好解决时，常常分成若干步，再由分步计数原理解决。在处理排列组合问题时，常常既要分类，又要分步。其原则是先分类，后分步。（43．排列应用题：（1）穷举法（列举法）：将所有满足题设条件的排列与组合逐一列举出来； (2)、特殊元素优先考虑、特殊位置优先考虑；（3）．相邻问题：捆邦法：对于某些元素要求相邻的排列问题，先将相邻接的元素“捆绑”起来，看作一“大”元素与其余元素排列，然后再对相邻元素内部进行排列。（4）、全不相邻问题，插空法：某些元素不能相邻或某些元素要在某特殊位置时可采用插空法.即先安排好没有限制条件的元素，然后再将不相邻接元素在已排好的元素之间及两端的空隙之间插入。（5）、顺序一定，除法处理。先排后除或先定后插解法一：对于某几个元素按一定的顺序排列问题，可先把这几个元素与其他元素一同进行全排列，然后用总的排列数除于这几个元素的全排列数。即先全排，再除以定序元素的全排列。解法二：在总位置中选出定序元素的位置不参加排列，先对其他元素进行排列，剩余的几个位置放定序的元素，若定序元素要求从左到右或从右到左排列，则只有1种排法；若不要求，则有2种排法；（6）“小团体”排列问题——采用先整体后局部策略对于某些排列问题中的某些元素要求组成“小团体”时，可先将“小团体”看作一个元素与其余元素排列，最后再进行“小团体”内部的排列。（7）分排问题用“直排法”把元素排成几排的问题，可归纳为一排考虑，再分段处理。（8）．数字问题（组成无重复数字的整数） ① 能被2整除的数的特征：末位数是偶数；不能被2整除的数的特征：末位数是奇数。②能被3整除的数的特征：各位数字之和是3的倍数； ③能被9整除的数的特征：各位数字之和是9的倍数④能被4整除的数的特征：末两位是4的倍数。 ⑤能被5整除的数的特征：末位数是0或5。 ⑥能被25整除的数的特征：末两位数是25，50，75。 ⑦能被6整除的数的特征：各位数字之和是3的倍数的偶数。 4．组合应用题：（1）.“至少”“至多”问题用间接排除法或分类法: （2）． “含”与“不含” 用间接排除法或分类法: 3．分组问题：均匀分组：分步取，得组合数相乘，再除以组数的阶乘。即除法处理。非均匀分组：分步取，得组合数相乘。即组合处理。混合分组：分步取，得组合数相乘，再除以均匀分组的组数的阶乘。 4．分配问题：定额分配：（指定到具体位置）即固定位置固定人数，分步取，得组合数相乘。

高中数学排列组合经典题型全面总结版

高中数学排列与组合（一）典型分类讲解一.特殊元素和特殊位置优先策略例1.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数. 解:由于末位和首位有特殊要求,应该优先安排, 先排末位共有1 3C 然后排首位共有1 4C 最后排其它位置共有 34A 由分步计数原理得1 1 3 434 288C C A = 练习题:7种不同的花种在排成一列的花盆里,若两种葵花不种在中间，也不种在两端的花盆里，问有多少不同的种法？二.相邻元素捆绑策略例2. 7人站成一排 ,其中甲乙相邻且丙丁相邻, 共有多少种不同的排法. 解：可先将甲乙两元素捆绑成整体并看成一个复合元素，同时丙丁也看成一个复合元素，再与其它元素进行排列，同时对相邻元素内部进行自排。由分步计数原理可得共有 522522480A A A =种不同的排法练习题:某人射击8枪，命中4枪，4枪命中恰好有3枪连在一起的情形的不同种数为 20 三.不相邻问题插空策略例3.一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种？解:分两步进行第一步排2个相声和3个独唱共有55A 种，第二步将4舞蹈插入第一步排好的6个元素中间包含首尾两个空位共有种 46 A 不同的方法,由分步计数原理,节目的不同顺序共有54 56A A 种练习题：某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目.如果将这两个新节目插入原节目单中，且两个新节目不相邻，那么不同插法的种数为 30 四.定序问题倍缩空位插入策略例4. 7人排队,其中甲乙丙3人顺序一定共有多少不同的排法解:(倍缩法)对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一起进行排列,然后用总排列数除以这几个元素之间的全排列数,则共有不同排法种数是： 73 73/A A (空位法)设想有7把椅子让除甲乙丙以外的四人就坐共有 47 A 种方法，其余的三个位置甲乙丙共有 1种坐法，则共有4 7A 种方法。思考:可以先让甲乙丙就坐吗? （插入法)先排甲乙丙三个人,共有1种排法,再把其余4四人依次插入共有方法练习题:10人身高各不相等,排成前后排，每排5人,要求从左至右身高逐渐增加，共有多少排法？ 5 10C 五.重排问题求幂策略例5.把6名实习生分配到7个车间实习,共有多少种不同的分法解:完成此事共分六步:把第一名实习生分配到车间有 7 种分法.把第二名实习生分配到车间也有7种分依此类推,由分步计数原理共有6 7种不同的排法练习题： 1．某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目.如果将这两个节目插入原节目单中，那么不同插法的种数为 42 4 4 3 允许重复的排列问题的特点是以元素为研究对象，元素不受位置的约束，可以逐一安排各个元素的位置，一般地n 不同的元素没有限制地安排在m 个位置上的排列数为n m 种

排列组合的21种例题

高考数学复习解排列组合应用题的21种策略排列组合问题是高考的必考题，它联系实际生动有趣，但题型多样，思路灵活，不易掌握，实践证明，掌握题型和解题方法，识别模式，熟练运用，是解决排列组合应用题的有效途径；下面就谈一谈排列组合应用题的解题策略. 1.相邻问题捆绑法:题目中规定相邻的几个元素捆绑成一个组，当作一个大元素参与排列. 例 1.,,,,A B C D E 五人并排站成一排，如果,A B 必须相邻且B 在A 的右边，那么不同的排法种数有 A 、60种 B 、48种 C 、36种 D 、24种 2.相离问题插空排:元素相离（即不相邻）问题，可先把无位置要求的几个元素全排列，再把规定的相离的几个元素插入上述几个元素的空位和两端. 例2.七人并排站成一行，如果甲乙两个必须不相邻，那么不同的排法种数是 A 、1440种 B 、3600种 C 、4820种 D 、4800种 3.定序问题缩倍法:在排列问题中限制某几个元素必须保持一定的顺序，可用缩小倍数的方法. 例 3.,,,,A B C D E 五人并排站成一排，如果B 必须站在A 的右边（,A B 可以不相邻）那么不同的排法种数是 A 、24种 B 、60种 C 、90种 D 、120种 4.标号排位问题分步法:把元素排到指定位置上，可先把某个元素按规定排入，第二步再排另一个元素，如此继续下去，依次即可完成. 例4.将数字1，2，3，4填入标号为1，2，3，4的四个方格里，每格填一个数，则每个方格的标号与所填数字均不相同的填法有 A 、6种 B 、9种 C 、11种 D 、23种 5.有序分配问题逐分法:有序分配问题指把元素分成若干组，可用逐步下量分组法. 例5.（1）有甲乙丙三项任务，甲需2人承担，乙丙各需一人承担，从10人中选出4人承担这三项任务，不同的选法种数是 A 、1260种 B 、2025种 C 、2520种 D 、5040种（2）12名同学分别到三个不同的路口进行流量的调查，若每个路口4人，则不同的分配方案有 A 、44412 8 4 C C C 种 B 、44412 8 4 3C C C 种 C 、44312 8 3 C C A 种 D 、4441284 3 3 C C C A 种 6.全员分配问题分组法: 例6.（1）4名优秀学生全部保送到3所学校去，每所学校至少去一名，则不同的保送方案有多少种？（2）5本不同的书，全部分给4个学生，每个学生至少一本，不同的分法种数为 A 、480种 B 、240种 C 、120种 D 、96种 7.名额分配问题隔板法: 例7.10个三好学生名额分到7个班级，每个班级至少一个名额，有多少种不同分配方案？ 8.限制条件的分配问题分类法: 例8.某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设，其中甲同学不到银川，乙不到西宁，共有多少种不同派遣方案？

7.1力精选练习题(带答案)

7.1精选练习 1．（2019春?新密市期中）如图所示，人在水平路面上骑车，以下关于物体受力的描述正确的是（） A．一个物体也能产生力的作用 B．相互接触的两个物体一定产生力的作用 C．路面受到人的压力 D．自行车受到路面的支持力 2．（2019?桂林）“梅西在发任意球时，能使足球由静止绕过人墙钻入球门。”该现象说明（） A．力的作用是相互的 B．力可以改变物体的形状 C．力可以改变物体的运动状态 D．以上说法都不对 3．（2019?湘潭）《流浪地球》电影中描述到了木星。木星质量比地球大得多，木星对地球的引力大小为F1，地球对木星的引力大小为F2，则F1与F2的大小关系为（） A．F1＜F2B．F1＞F2C．F1＝F2D．无法确定 4．（2019?广州校模拟）下列关于力的说法中不正确的是（） A．力是物体对物体的作用，不仅仅是人对物体的作用 B．如果有一个力产生，一定同时产生一个相互作用力

C．两个物体不接触也能产生力 D．人推墙，墙没有运动起来，也没有发生形变，因此墙没有受到力的作用 5．（2019?邵阳）俗话说“鸡蛋碰石头﹣﹣自不量力”，从物理学角度看（） A．石头对鸡蛋的作用力更大 B．先有石头对鸡蛋的作用力 C．鸡蛋对石头的没有作用力 D．石头和鸡蛋间同时有等大的相互作用力 6．（2019?宜昌）在射箭运动中，以下关于力的作用效果的描述，其中一个与另外三个不同的是（）A．瞄准时，手的拉力把弓拉弯 B．松手后，弓的弹力把箭射出 C．飞行中，重力让箭划出一道弧线 D．中靶时，靶的阻力让箭停止运动 7．（2019?内江）如图所示，坐在船上的人，用力推另只船，船就相互远离而去，这个现象表明力的作用是的，力可以改变物体的状态。 8．（2018?朝阳）观察图中的情况，可以明显说明力能改变物体运动状态的三个图是，明显说明力能使物体发生形变的三个图是。 9．（2017?德州）2017年4月20日，“天舟一号”货运飞船发射升空，22日与“天宫二号”太空舱顺利对接。，对接过程中，“天舟一号”多处向外“喷气”，调节运行姿态，此过程利用的力学知识：。10．（2019?哈尔滨）如图所示，请你画出静止在水平桌面上的茶壶所受力的示意图。（画图时用实心点O表示力的作用点）

因式分解精选例题(附答案)

因式分解例题讲解及练习【例题精选】: (1) 评析:先查各项系数(其它字母暂时不瞧),确定5,15,20得最大公因数就是5,确定系数就是5 ,再查各项就是否都有字母X,各项都有时,再确定X得最低次幂就是几,至此确认提取X2,同法确定提Y,最后确定提公因式5X2Y。提取公因式后,再算出括号内各项。解: = (2) 评析:多项式得第一项系数为负数,应先提出负号,各项系数得最大公因数为3,且相同字母最低次得项就是X2Y 解: = = = (3)(y-x)(c-b-a)-(x-y)(2a+b-c)-(x-y)(b-2a) 评析:在本题中,y-x与x-y都可以做为公因式,但应避免负号过多得情况出现,所以应提取y-x 解:原式=(y-x)(c-b-a)+(y-x)(2a+b-c)+(y-x)(b-2a) =(y-x)(c-b-a+2a+b-c+b-2a) =(y-x)(b-a) （4）(4)把分解因式评析:这个多项式有公因式2x3,应先提取公因式,剩余得多项式16y4-1具备平方差公式得形式解:=2=2= （5）(5)把分解因式评析:首先提取公因式xy2,剩下得多项式x6-y6可以瞧作用平方差公式分解,最后再运用立方与立方差公式分解。

对于x6-y6也可以变成先运用立方差公式分解,但比较麻烦。解: =xy2(x6-y6)= xy2[]= = (6)把分解因式评析:把(x+y)瞧作一个整体,那么这个多项式相当于(x+y)得二次三项式,并且为降幂排列,适合完全平方公式。对于本例中得多项式切不可用乘法公式展开后再分解,而要注意观察分析,善于把(x+y)代换完全平方公式中得a,(6Z)换公式中得解: ==(x+y-6z)2 （7）(7)把分解因式评析:把x2-2y2与y2瞧作两个整体,那么这个多项式就就是关于x2-2y2与y2得二次三项式,但首末两项不就是有理数范围内得完全平方项,不能直接应用完全平方公式,但注意把首项系数提出后,括号里边实际上就就是一个完全平方式。解: = = = （8）(8)分解因式a2-b2-2b-1 评析:初瞧,前两项可用平方差公式分解。采用“二、二”分组,原式=(a+b)(a-b)-(2b+1),此时无法继续分解。再仔细瞧,后三项就是一个完全平方式,应采用“一、三”分组。解:a2-b2-2b-1= a2-(b2-2b+1)=a2-(b+1)2=[a+(b+1)][a-(b+1)]=(a-b-1)(a+b+1) 一般来说,四项式“一、三”分解,最后要用“平方差”。四项式“二、二”分组,只有前后两组出现公因式,才就是正确得分组方案。（9）(9)把a2-ab+ac-bc分解因式

高考排列组合典型例题

高考排列组合典型例题 Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】

排列组合典型例题例1 用0到9这10 个数字．可组成多少个没有重复数字的四位偶数分析：这一问题的限制条件是：①没有重复数字；②数字“0”不能排在千位数上；③个位数字只能是0、2、4、6、8、，从限制条件入手，可划分如下：如果从个位数入手，四位偶数可分为：个位数是“0”的四位偶做，个位数是 2、4、6、8的四位偶数（这是因为零不能放在千位数上）．由此解法一与二．如果从千位数入手．四位偶数可分为：千位数是1、3、5、7、9和千位数是2、4、6、8两类，由此得解法三．如果四位数划分为四位奇数和四位偶数两类，先求出四位个数的个数，用排除法，得解法四．解法1：当个位数上排“0”时，千位，百位，十位上可以从余下的九个数字中任选3个来排列，故有39A 个；当个位上在“2、4、6、8”中任选一个来排，则千位上从余下的八个非零数字中任选一个，百位，十位上再从余下的八个数字中任选两个来排，按乘法原理有281814A A A ??（个）． ∴ 没有重复数字的四位偶数有 2296179250428181439 =+=??+A A A A 个．解法2：当个位数上排“0”时，同解一有39A 个；当个位数上排2、4、6、8中之一时，千位，百位，十位上可从余下9个数字中任选3个的排列数中减去千位数是“0”排列数得：)(283914 A A A -?个 ∴ 没有重复数字的四位偶数有 22961792504)(28391439 =+=-?+A A A A 个．

排列组合专题复习与经典例题详解

排列组合专题复习及经典例题详解 1. 学习目标掌握排列、组合问题的解题策略 2.重点（1）特殊元素优先安排的策略：（2）合理分类与准确分步的策略；（3）排列、组合混合问题先选后排的策略；（4）正难则反、等价转化的策略；（5）相邻问题捆绑处理的策略；（6）不相邻问题插空处理的策略． 3.难点综合运用解题策略解决问题． 4.学习过程: (1)知识梳理 1．分类计数原理（加法原理）：完成一件事，有几类办法，在第一类办法中有1m 种不同的方法，在第2类办法中有2m 种不同的方法……在第n 类型办法中有n m 种不同的方法，那么完成这件事共有n m m m N +++=...21种不同的方法． 2．分步计数原理（乘法原理）：完成一件事，需要分成n 个步骤，做第1步有1m 种不同的方法，做第2步有2m 种不同的方法……，做第n 步有n m 种不同的方法；那么完成这件事共有n m m m N ???=...21种不同的方法．特别提醒：分类计数原理与“分类”有关，要注意“类”与“类”之间所具有的独立性和并列性；分步计数原理与“分步”有关，要注意“步”与“步”之间具有的相依性和连续性，应用这两个原理进行正确地分类、分步，做到不重复、不遗漏． 3．排列：从n 个不同元素中，任取m(m≤n)个元素，按照一定的顺序排成一列，叫做从n 个不同元素中取出m 个元素的一个排列，n m <时叫做选排列，n m =时叫做全排列. 4．排列数：从n 个不同元素中，取出m(m≤n)个元素的所有排列的个数，叫做从n 个不同元素中取出m 个元素的排列数，用符号m n P 表示. 5．排列数公式：）、（+∈≤-= +---=N m n n m m n n m n n n n P m n ,)! (!)1)...(2)(1( 排列数具有的性质：11-++=m n m n m n mP P P 特别提醒：规定0!=1

初中精选数学计算题200道

计算题 c l 1.3 3 +（π+3）o- 3 27 +∣ 3 -2∣ 2. 5x+2 x2+x = 3 x+1 3. 3-x x-4+ 1 4-x=1 4. x2-5x=0 5. x2-x-1=0 6. 化简2 39x +6 x 4-2x 1 x 7. 因式分解x4-8x2y2+16y4 8. 2 2x+1+ 1 2x-1= 5 4x2-1 9. 因式分解（2x+y）2-(x+2y)2 10. 因式分解-8a2b+2a3+8ab2 11. 因式分解a4-16 12. 因式分解3ax2-6axy+8ab2 13. 先化简，再带入求值（x+2）(x-1)-x2-2x+1 x-1,x= 3 14. ( - 3 )o-∣-3∣+(-1)2015+(1 2) -1 15. ( 1 a-1- 1 a2-1 )÷ a2-a a2-1 16. 2(a+1)2+(a+1)(1-2a)

17. (2x-1 x+1-x+1)÷ x-2 x2+2x+1 18. (-3-1)×(- 3 2)2-2 -1÷(- 1 2)3 19. 1 2x-1=2 4 3 - 2 1 x 20. (x+1)2-(x+2)(x-2) 21. sin60°-∣1- 3 ∣+（1 2） -1 22．（-5）16×(-2)15 (结果以幂的形式表示) 23. 若n为正整数且（m n）2=9,求（1 3m 3n）3(m2)2n 24. 因式分解a2+ac-ab-bc 25. 因式分解x2-5x+6 26. 因式分解(x+2)(x+3)+x2-4 27. 因式分解(a2+1)2-4a2 28. -12016+18÷(-3)×∣-1 2∣ 29. 先化简，再求值3(x2+xy-1)-(3x2-2xy),其中x=1，y= - 1 5 30. 计算3-4+5-(-6)-7 31. 计算-12+(-4)2×∣-1 8∣-82÷(-4)3 32.计算20-（-7）-∣-2∣ 33.计算（1 3- 5 9+ 11 12）×(-36)

排列组合典型例题

典型例题一例1 用0到9这10 个数字．可组成多少个没有重复数字的四位偶数？分析：这一问题的限制条件是：①没有重复数字；②数字“0”不能排在千位数上；③个位数字只能是0、2、4、6、8、，从限制条件入手，可划分如下：如果从个位数入手，四位偶数可分为：个位数是“0”的四位偶做，个位数是 2、4、6、8的四位偶数（这是因为零不能放在千位数上）．由此解法一与二．如果从千位数入手．四位偶数可分为：千位数是1、3、5、7、9和千位数是2、4、6、8两类，由此得解法三．如果四位数划分为四位奇数和四位偶数两类，先求出四位个数的个数，用排除法，得解法四．解法1：当个位数上排“0”时，千位，百位，十位上可以从余下的九个数字中任选3个来排列，故有3 A个； 9 当个位上在“2、4、6、8”中任选一个来排，

则千位上从余下的八个非零数字中任选一个，百位，十位上再从余下的八个数字中任选两个来排，按乘法原理有2 8181 4 A A A ??（个）． ∴ 没有重复数字的四位偶数有 2296 179250428181439=+=??+A A A A 个．解法2：当个位数上排“0”时，同解一有3 9 A 个；当个位数上排2、4、6、8中之一时，千位，百位，十位上可从余下9个数字中任选3个的排列数中减去千位数是“0”排列数得：) (28391 4 A A A -?个 ∴ 没有重复数字的四位偶数有 2296 1792504)(28391439=+=-?+A A A A 个．解法3：千位数上从1、3、5、7、9中任选一个，个位数上从0、2、4、6、8中任选一个，百位，十位上从余下的八个数字中任选两个作排列有 2 81 515A A A ??个干位上从2、4、6、8中任选一个，个位数上从余下的四个偶数中任意选一个（包括0在内），百位，十位从余下的八个数字中任意选两个作排列，有 2 81414A A A ??个 ∴ 没有重复数字的四位偶数有

高中排列组合知识点汇总及典型例题(全)

模电基础例题精选

二极管 1?. 本征半导体热激发时的两种载流子分别是、。 2． ?N型半导体多数载流子是 ,少数载流子是。 3.P型半导体多数载流子是 ,少数载流子是。 4.在常温下硅二极管的开启电压约为 V,导通后的正向压降为， 5.在常温下锗二极管的开启电压约为V,导通后的正向压降为 , 6.当PN结外加正向电压时,扩散电流漂移电流,耗尽层 ;当PN结外加反向电压时，扩散电流漂移电流,耗尽层 ; A．大于 B.小于 C. 等于D．变宽E．变窄Ｆ. 不变７．PN结的空间电荷区有哪些称谓？为何这样称谓？二极管有哪些特性?其中最重要的特性是。１、在本征半导体中掺入三价元素后的半导体称为 B、P型半导体 2、N型半导体中少数载流子为 B、空穴 3、P型半导体是Ｃ、中性４、PN结加正向电压时,其正向电流是 A、多数载流子扩散形成的８、稳压二极管是利用PN结的 B、反向击穿特性 9、PN结反向电压的数值增大（小于击穿电压）Ｃ、其反向电流不变 1.15 试判断图1.40中的二极管是否导通,还是截止,并求出两端电压u AO

U0 =8v Ｄ的导通电压为０．7ｖ u０＝1V

6.5电路如图P６.5（a）所示，其输入电压v i１和ｖｉ2的波形如图(b）所示,二极管导通电压V D＝0.7V。试画出输出电压v O的波形，并标出幅值。 v i1/V

解:u O 的波形如解图P1.２所示。 6．8二极管电路如图６.８所示，试判断各图中的二极管是导通还是截止，并求出ＡB 两端电压V ＡB ,设二极管是理想的。解: 图a ：将Ｄ断开,以O 点为电位参考点，D 的阳极电位为-6 V,阴极电位为-1２Ｖ，故 D 处于正向偏置而导通，V AO ＝–6 Ｖ。图b:对D 1有阳极电位为 0Ｖ，阴极电位为-1２Ｖ,故Ｄ1导通,此后使D 2的阴极电位为 0Ｖ，而其阳极为－15 Ｖ，故D 2反偏截止，ＶＡO =0 V 。图ｃ：对D 1有阳极电位为12 V,阴极电位为0 Ｖ，对D 2有阳极电位为12 V,阴极电位为 -6Ｖ．故Ｄ２更易导通,此后使ＶA =－6V;D 1反偏而截止,故V AO ＝-6Ｖ。图P6.5 v R D 1 +V CC （5V ） D 2 v t t v i2/V (a) (b) v o 0.3 0.3 图P6.8 _ V AB D _ R 5k Ω D 2 6V 1212V D 1 + + A A V A B 15V _ D 2 12V D 1 + A V AB 6V R 5k Ω R 5k Ω (a) (b) (c)

(完整版)立体几何典型例题精选(含答案)

F E D C B A 立体几何专题复习热点一：直线与平面所成的角例1．（2014，广二模理 18）如图，在五面体ABCDEF 中，四边形ABCD 是边长为2的正方形， EF ∥平面ABCD ， 1EF =，,90FB FC BFC ?=∠=，3AE =. （1）求证：AB ⊥平面BCF ；（2）求直线AE 与平面BDE 所成角的正切值. 变式1：（2013湖北8校联考）如左图，四边形ABCD 中，E 是BC 的中点，2,1,5,DB DC BC === 2.AB AD ==将左图沿直线BD 折起，使得二面角A BD C --为60,?如右图. （1）求证：AE ⊥平面;BDC （2）求直线AC 与平面ABD 所成角的余弦值. 变式2：[2014·福建卷] 在平面四边形ABCD 中，AB ＝BD ＝CD ＝1，AB ⊥BD ，CD ⊥BD .将△ABD 沿BD 折起，使得平面ABD ⊥平面BCD ，如图1-5所示． (1)求证：AB ⊥CD ； (2)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值．

热点二：二面角例2．[2014·广东卷] 如图1-4，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC＝30°，AF⊥PC于点F，FE∥CD，交PD于点E. (1)证明：CF⊥平面ADF；(2)求二面角D-AF-E的余弦值．变式3：[2014·浙江卷] 如图1-5，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE＝∠BED＝90°，AB＝CD＝2，DE＝BE＝1，AC＝ 2. (1)证明：DE⊥平面ACD；(2)求二面角B-AD-E的大小．变式4：[2014·全国19] 如图1-1所示，三棱柱ABC-A1B1C1中，点A1在平面ABC内的射影D在AC 上，∠ACB＝90°，BC＝1，AC＝CC1＝2. (1)证明：AC1⊥A1B; (2)设直线AA1与平面BCC1B1的距离为3，求二面角A1 -AB -C的大小．

排列组合典型例题

典型例题一例1 用0到9这10 个数字．可组成多少个没有重复数字的四位偶数解法1：当个位数上排“0”时，千位，百位，十位上可以从余下的九个数字中任选3个来排列，故有39A 个；当个位上在“2、4、6、8”中任选一个来排，则千位上从余下的八个非零数字中任选一个，百位，十位上再从余下的八个数字中任选两个来排，按乘法原理有281814 A A A ??（个）． ∴ 没有重复数字的四位偶数有 2296179250428181439 =+=??+A A A A 个．典型例题二例2 三个女生和五个男生排成一排（1）如果女生必须全排在一起，可有多少种不同的排法（2）如果女生必须全分开，可有多少种不同的排法（3）如果两端都不能排女生，可有多少种不同的排法（4）如果两端不能都排女生，可有多少种不同的排法解：（1）（捆绑法）因为三个女生必须排在一起，所以可以先把她们看成一个整体，这样同五个男生合一起共有六个元素，然成一排有66A 种不同排法．对于其中的每一种排法，三个女生之间又都有33A 对种不同的排法，因此共有43203366=?A A 种不同的排法．（2）（插空法）要保证女生全分开，可先把五个男生排好，每两个相邻的男生之间留出一个空档．这样共有4个空档，加上两边两个男生外侧的两个位置，共有六个位置，再把三个女生插入这六个位置中，只要保证每个位置至多插入一个女生，就能保证任意两个女生都不相邻．由于五个男生排成一排有55A 种不同排法，对于其中任意一种排法，从上述六个位置中选出三个来让三个女生插入都有36A 种方法，因此共有144003655 =?A A 种不同的排法．（3）解法1：（位置分析法）因为两端不能排女生，所以两端只能挑选5个男生中的2个，有25A 种不同的排法，对于其中的任意一种排法，其余六位都有66A 种排法，所以共有1440066 25=?A A 种不同的排法．（4）解法1：因为只要求两端不都排女生，所以如果首位排了男生，则未位就不再受条件限制了，这样可有7715A A ?种不同的排法；如果首位排女生，有13A 种排法，这时末位就只能排男生，有15A 种排法，首末两端任意排定一种情况后，

排列&组合计算公式及经典例题汇总

排列组合公式/排列组合计算公式排列A------和顺序有关组合 C -------不牵涉到顺序的问题排列分顺序,组合不分例如把5本不同的书分给3个人,有几种分法. "排列" 把5本书分给3个人,有几种分法"组合" 1．排列及计算公式从n个不同元素中，任取m(m≤n)个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号A(n,m)表示. A(n,m)=n(n-1)(n-2)……(n-m+1)= n!/(n-m)!(规定0!=1). 2．组合及计算公式从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n 个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数.用符号

c(n,m) 表示. c(n,m)=A(n,m)/m!=n!/((n-m)!*m!)；c(n,m)=c(n,n-m); 3．其他排列与组合公式从n个元素中取出r个元素的循环排列数＝A(n,r)/r=n!/r(n-r)!. n个元素被分成k类，每类的个数分别是n1,n2,...nk这n个元素的全排列数为 n!/(n1!*n2!*...*nk!). k类元素,每类的个数无限,从中取出m个元素的组合数为 c(m+k-1,m). 排列（Anm(n为下标，m为上标)） Anm=n×（n-1）....（n-m+1）；Anm=n！/（n-m）！（注：！是阶乘符号）；Ann（两个n分别为上标和下标）=n！；0！=1；An1（n为下标1为上标）=n