坐标旋转公式的推导

坐标旋转变换

翻译自：

翻译：汤永康

出处:

转贴请注明出处

１围绕原点的旋转

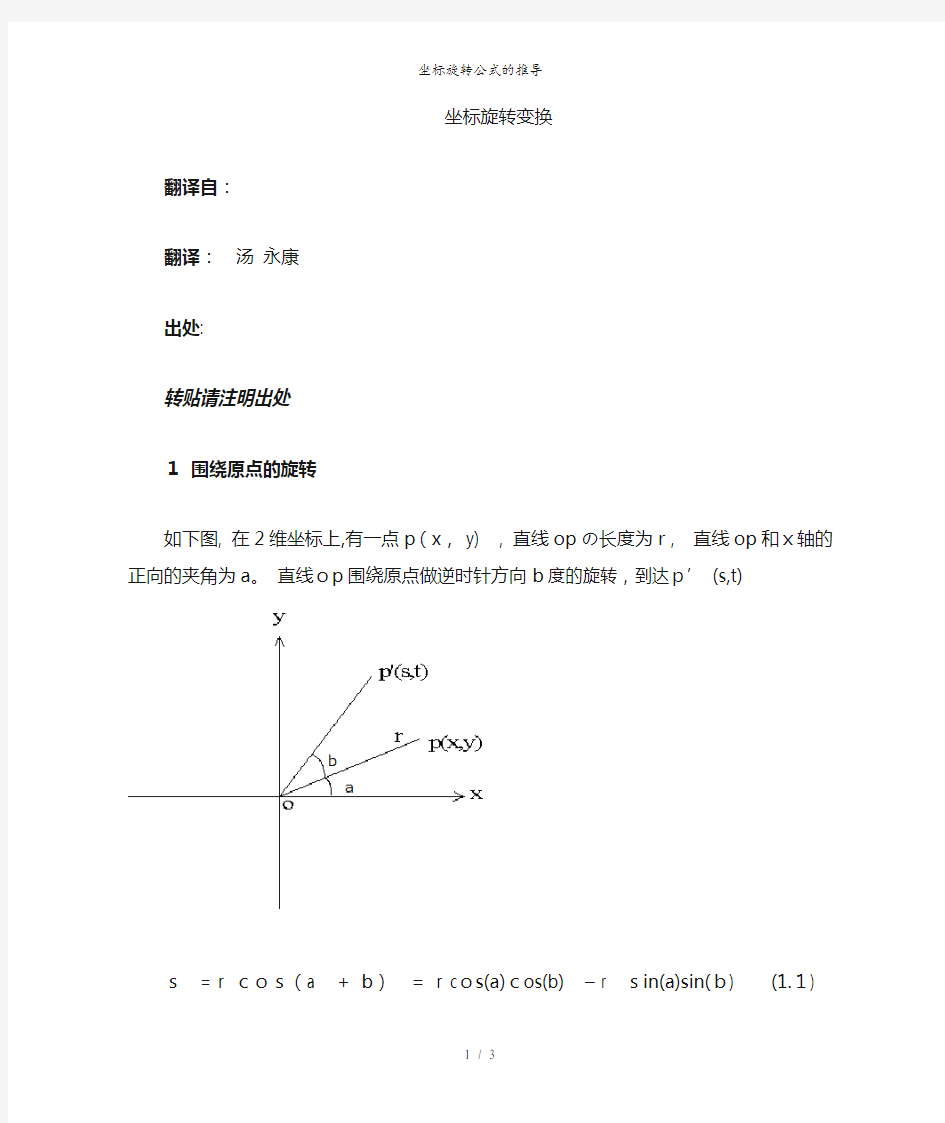
如下图, 在2维坐标上,有一点p（x， y) , 直线opの长度为ｒ, 直线op和ｘ轴的正向的夹角为a。直线ｏp围绕原点做逆时针方向b度的旋转，到达ｐ’

(s,t)

ｓ= r ｃｏｓ（a ＋ b）＝ r cｏs(a)ｃos(b) – r ｓin(a)sin(ｂ) (1.１)

t = r ｓin(ａ + b) = r siｎ(a）ｃos(ｂ) + r coｓ(a) sin（b) (1.2）其中x = ｒcoｓ(a) , y = r sｉｎ(a)

代入(1.１)， (1.２) ,

ｓ＝ｘ cｏs(b) –ｙ siｎ（b) （1.3)

t = ｘｓｉn(b) + y cos(b) (1.4)

用行列式表示如下

２．座标系的旋转

在原坐标系xoy中, 绕原点沿逆时针方向旋转theｔa度, 变成座标系sｏt。设有某点p,在原坐标系中的坐标为 (ｘ, y）, 旋转后的新坐标为(s，t)。

oa = y sin（ｔｈeta) （２．１)

ａs = x cos（theta） (2.2)

综合（2.1），（2.2) ２式

ｓ = ｏｓ= oａ + as = ｘ cos（thｅtａ) ＋y sin（theta)

t ＝ ot = ay –ａb ＝ｙ cｏs（theta) –x ｓｉn(thetａ)

用行列式表达如下

???????＜END>

坐标计算方法

旋转坐标系法求缓和曲线坐标 1、旋转坐标系原理 1.1旋转公式 1cos 1sin 1sin 1cos x x y y x y αααα =-=+ 对于测量坐标系逆时针旋转为α取正值，顺时针为负。例如：原坐标系中的()1,1点，坐标系旋转45 °后，在目标坐标系为(。 1cos 451sin 4501sin 451cos 45x y =*?-*?==*?+*?=

2、利用旋转坐标计算缓和曲线任意点的坐标原理利用缓和曲线坐标公式求 5913 48 16 3711 2610 14034565990401633642240l l l x l A A A l l l y A A A =-+-=-+ 然后旋转坐标轴，γ为方位角，把原坐标系逆时针旋转方位角。 1cos 1sin 1sin 1cos x x y y x y γγγγ =-=+ 3、用旋转坐标系法求曲线坐标已知： ①缓和曲线上任一点离ZH 点的长度：l ②圆曲线的半径：R ③缓和曲线的长度：0l ④过ZH 点的切线方位角：γ ⑤转向角系数：K (1或－1)左转为-1右转为1 计算过程： 3.1、求直缓点ZH 的坐标 3.1.1缓和曲线要素

A =2 03 00 2242240()tan 2 l p R l l m R T R p q α = =- =++ 00cos sin z z x x T y y T γγ =-=- 3.1.2求第一缓和曲线上任意点在原坐标系中的坐标 5913 4816 3711 2610 14034565990401() 633642240l l l x l A A A l l l y K A A A =-+- =-+ 左转为K=-1右转为K=1，因为右转时y1为正，左转时y1为负 3.1.3旋转坐标系 1cos 1sin 1sin 1cos z z x x x y y y x y γγγγ =+-=++ 3.2、求圆曲线上任意点的坐标 3.2.1求圆曲线上任意点在原坐标系上的坐标

初三数学旋转坐标与图形变换

图形的旋转坐标与图形变换 1、（2018武汉模拟）在平面直角坐标系中，将点P （4，-3）绕原点旋转90度得到1P ，则1P 的坐标为________ [解析]：分顺时针和逆时针两种情况旋转，1P 的坐标为（-3，-4）或（3，4） 2、（2018洪泽县模拟）已知点P 的坐标为（1，1），若将点P 绕着原点逆时针旋转45度，得到1P ，则1P 的坐标为________ [解析]：1P 的坐标为（-1，1） 3、（2018杜丹江二模）如图，平面直角坐标系中，等边OAB ?边长为2，点B 在第一象限内，AB//x 轴，若将OAB ?绕点O 旋转120度，再关于y 轴对称后得到O B A 11?，由点1A 的坐标为________ [解析]：分顺时针和逆时针两种情况旋转，),3,1(1 --A 或),0,2(1A 4、（2018杜丹江三模）等边ABC ?如图放置，A （1，1），B （3，1），等边三角形的中心是点D ，若将点D 绕点A 旋转90度后得到点、D ，则、D 的坐标是________ [解析]：)331,2(+ D 顺时针旋转得到)0,331(+、D ，逆时针旋转得到)2,331(-、D

5、（2018杜丹江）如图，ABC ?三个顶点的坐标分别是A （1，-1），B （2，-2），C （4，-1），将ABC ?绕着原点O 旋转75度，得到111C B A ?，则点1B 的坐标为________ [解析]：由点B （2，-2），则OB=2，且OB 与x 轴、y 轴夹角为45度，当点B 绕原点逆时针旋转75度后，与x 轴正向夹角为30度，则点1B 到x 轴y 轴距离分别为6,2，则点)2,6(1B ，同理，当点B 绕原点顺时针旋转时，可得)6,2(1--B 6、（2018邵阳期末）如图，已知A （2，1），现将A 点绕原点O 逆时针旋转90度得到1A ，则1A 的坐标是________ [解析]：)2,1(1-A 7、（2018沙坪坝区期末）如图，平面直角坐标系中，已知点B （-3，2），若将ABO ?绕点O 沿顺时针方向旋转90度得到O B A 11?，则点B 的对应点1B 的坐标是________ [解析]：)3,2(1B

推导坐标旋转公式

推导坐标旋转公式数学知识2010-09-12 21:03:53 阅读151 评论0 字号：大中小订阅在《Flash actionScript 3.0 动画教程》一书中有一个旋转公式： x1=cos(angle)*x-sin(angle)*y; y1=cos(angle)*y+sin(angle)*x; 其中x，y表示物体相对于旋转点旋转angle的角度之前的坐标，x1，y1表示物体旋转angle 后相对于旋转点的坐标从数学上来说，此公式可以用来计算某个点绕另外一点旋转一定角度后的坐标，例如：A（x，y）绕B（a，b)旋转β度后的位置为C（c，d），则x，y，a，b，β，c，d有如下关系式： 1。设A点旋转前的角度为δ，则旋转(逆时针)到C点后角度为δ+β 2。求A，B两点的距离：dist1=|AB|=y/sin(δ)=x/cos(δ) 3。求C，B两点的距离：dist2=|CB|=d/sin(δ+β)=c/cos(δ+β) 4。显然dist1=dist2，设dist1=r所以： r=x/cos(δ)=y/sin(δ)=d/sin(δ+β)=c/cos(δ+β) 5。由三角函数两角和差公式知： sin(δ+β)=sin(δ)cos(β)+cos(δ)sin(β) cos(δ+β)=cos(δ)cos(β)-sin(δ)sin(β) 所以得出：

c=r*cos(δ+β)=r*cos(δ)cos(β)-r*sin(δ)sin(β)=xcos(β)-ysin(β) d=r*sin(δ+β)=r*sin(δ)cos(β)+r*cos(δ)sin(β)=ycos(β)+xsin(β) 即旋转后的坐标c，d只与旋转前的坐标x，y及旋转的角度β有关从图中可以很容易理解出A点旋转后的C点总是在圆周上运动，圆周的半径为|AB|，利用这点就可以使物体绕圆周运动，即旋转物体。上面公式是相对于B点坐标来的，也就是假如B点位（0,0）可以这么做。现在给出可以适合任意情况的公式： x0 = dx * cos(a) - dy * sin(a) y0 = dy * cos(a) + dx * sin(a) 参数解释： x0,y0是旋转后相对于中心点的坐标，也就是原点的坐标，但不是之前点旋转后的实际坐标，还要计算一步，a旋转角度，可以是顺时针或者逆时针。 dx是旋转前的x坐标-旋转后的x坐标 dy是旋转前的y坐标-旋转后的y坐标 x1=b+x0; y1=c+y0; 上面才是旋转后的实际坐标，其中b，c是原点坐标下面是上面图的公式解答： x0=(x-b)*cos(a)-(y-c)*sin(a); y0=(y-c)*cos(a)+(x-b)*sin(a); x1=x0+b; y1=y0+c;

坐标旋转推导

'cos sin 'sin cos x x y y θθθ θ-??????= ? ????????? 其中,x y 表示物体相对于旋转点旋转θ的角度之前的坐标,','x y 表示物体逆时针旋转θ后相对于旋转点的坐标从数学上来说，此公式可以用来计算某个点绕着另外一点旋转一定角度后的坐标，例如：(,)A x y 绕(,)B a b 旋转β角度后的位置为(,)C c d ，则,,,,,,xyab cd β有如下关系式： 1．设A 点旋转前的角度为δ，则旋转(逆时针)到C 点之后角度为δβ+ 2．求A ，B 两点的距离：dist1=|AB|=/()/()y Sin x Cos δδ= 3．求C ，B 两点的距离：dist2=|CB|=/()/()d Sin c Cos δβδβ+=+ 4．显然dist1=dist2，设dist1=R 所以： R=/()/()/()/()y Sin x Cos d Sin c Cos δδδβδβ==+=+ 5．由三角函数两角和差公式知：

()()()()S i n S i n C o s C o s S i n δ βδβδβ+=+ ()()()()C o s C o s C o s S i n S i n δ βδβδδ+=- 所以得出： c=()()()()()()()RCos RCos Cos RSin Sin xCos ySin δβδβδβββ+=-=- d=()()()()()()()RSin RSin Cos RCos Sin yCos xSin δβδβδβββ+=+=+即旋转后的坐标c ，d 只与旋转前的坐标x ，y 及旋转的角度β有关从图中可以很容易理解出A 点旋转后的C 点总是在圆周上运动，圆周的半径为|AB|，利用这点就可以使物体绕圆周运动，即旋转物体。

回转体在卧式加工中心的旋转工作台上任意放置的坐标计算方法

回转体在卧式加工中心的旋转工作台上任意放置的坐标计算方法李超吴建波张强四川宜宾普什模具有限公司 644000 摘要：为了解决大型回转体类零件加工径向孔，在装夹时旋转中心定位困难和容易造成变形、损坏加工表面等问题。充分利用机床NC 程序的公式计算功能，加工零件可以随意地放置在工作台上，利用该功能可将工件的回转中心虚拟到工作台的回转中心（即将工件的回转中心偏移到工作台的回转中心），理论误差可小于0.001mm 。实际应用表明，此方法定位准确可靠，给加工编程带来极大的方便，节省很大的人力物力。关键字：回转体坐标计算方法 1、装夹方法比较 1.1 传统装夹放置方法如图2所示，在回转体上加工6个Φ60大的孔，传统加工方法是把回转体中心放在工作台旋转中心上，再旋转工作台(B 轴)分度加工6个Φ60大的孔，以达到所要加工孔的目的。优点是：(1)加工时易于理解，加工基准能完全与图纸基准重合； (2)编程简单。缺点是：(1)需要将工件的回转中心放置在工作台的旋转中心上，并根据零件的精度要求控制重合误差。 (2)、工件在调整位置时移动较困难，容易损伤工件的外观同时引起变形，影响外形尺寸和表面质量。 (3)、装夹找正时间长，效率低。 60° 6-?60均布图 1 X Z ?1200?1500 800 A A A-A 工件中心和旋转中心重合工作台工件工件第一个孔图1 传统零件放置示意图 1、2新的装夹放置方法只需要将工件随意地放置在工作台上，通过机床NC 程序的公式计算功能，将工件的回转中心偏虚拟到工作台的回转中心即可。如图3所示优点是：(1)、装夹放置位置没有任何限制。 (2)、装夹时间短，效率低。 (3)、不需要专用工装。

平面内坐标旋转公式

平面内坐标旋转公式在网上看到有一个平面内坐标点的旋转公式： x1=cos(angle)*x-sin(angle)*y; y1=cos(angle)*y+sin(angle)*x; 其中x，y表示物体相对于旋转点旋转angle的角度之前的坐标，x1，y1表示物体旋转angle后相对于旋转点的坐标从数学上来说，此公式可以用来计算某个点绕另外一点旋转一定角度后的坐标，例如：A（x，y）绕B（a，b)旋转β度后的位置为C（c，d），则x，y，a，b，β，c，d有如下关系式： 1.设A点旋转前的角度为δ，则旋转(逆时针)到C点后角度为δ+β 2.求A，B两点的距离：dist1=|AB|=y/sin(δ)=x/cos(δ)

3.求C，B两点的距离：dist2=|CB|=d/sin(δ+β)=c/cos(δ+β) 4.显然dist1=dist2，设dist1=r所以： r=x/cos(δ)=y/sin(δ)=d/sin(δ+β)=c/cos(δ+β) 5.由三角函数两角和差公式知： sin(δ+β)=sin(δ)cos(β)+cos(δ)sin(β) cos(δ+β)=cos(δ)cos(β)-sin(δ)sin(β) 所以得出： c=r*cos(δ+β)=r*cos(δ)cos(β)-r*sin(δ)sin(β)=xcos(β)-ysin(β) d=r*sin(δ+β)=r*sin(δ)cos(β)+r*cos(δ)sin(β)=ycos(β)+xsin(β) 即旋转后的坐标c，d只与旋转前的坐标x，y及旋转的角度β有关从图中可以很容易理解出A点旋转后的C点总是在圆周上运动，圆周的半径为|AB|，利用这点就可以使物体绕圆周运动，即旋转物体。

两角和的正余弦公式与旋转坐标

坐标变换是解析几何里非常重要的内容，不过对于中学生来讲，只是学过平移压缩变换，不曾接触旋转变换，未免有些遗憾，老实说个人觉得，旋转变换才是精彩之处。很多参考书提到旋转变换的公式，都是采用复数法，其实大可不必，我们中学其实就已经接触过，那就是三角函数里的两角和正余弦公式：别以为他的作用就只是计算两角和的正余弦。今天你将看到，我们将根据他来推出我们的旋转坐标公式。当然，这里说的旋转都只是说绕坐标原点旋转。至于旋转中心不是原点的情况，其实只需要做个平移变换即可。我们首先要明白的是，一个点和其旋转后的点都是在一个圆上，我们做出这两个点，并且做出这个圆：如图所示，P点绕原点旋转α弧度。在这里仍然遵循基本的法则，逆时针为正，顺时针为负。显然，我们可以设P点坐标为(x,y)=(rcosθ,rsinθ)。那么P'点的坐标就为(x',y')=(rcos(θ+α)，rsin(θ+α)),根据两角和的正余弦公式,P'的坐标就为： P'=(x',y')=(rcosθcosα-rsinθsinα，rsinθcosα+rcosθsinα) =(xcosα-ysinα，xsinα+ycosα)…………………………………………①这个就是我们的旋转坐标变换公式，可以看出，我们压根不用什么复数，很简单的两角和的正余弦公式就搞定，端的是活学活用，好得紧啦！我们来两道例题对其熟悉熟悉。例题1：求点P(1,3)绕坐标原点逆时针旋转45°后的坐标解：根据式子①，设旋转后的坐标为(x,y)，那么有： x=1cos45°-3sin45°=-√2；y=1×s in45°+3cos45°=2√2。即旋转后的坐标为(-√2,2√2) 例题2：点P绕原点旋转30°后，得到的新坐标为P‘=(2,6)，求P点坐标解：将P'点旋转-30°后就得到P点坐标，设P坐标为(x,y),那么根据式子①有： x=2cos(-30°)-6sin(-30°)=3+√3，y=2sin(-30°)+6cos(-30°)=-1+3√3，即P点坐标为(3+√3，-1+3√3). 例题3：已知点P(3,4)绕坐标原点旋转以后的坐标为(√5,2√5),求旋转角度解，这个题很简单，运用向量的夹角公式即可。每个中学生都有着这样的问题：圆锥曲线里的双曲线与初中所学的那个反比例函数是否是同一种类型？这个问题对于每个老师来讲是一个很简单的问题。但是很少有教辅对这一点做说明，我想还是怕提到旋转坐标公式。虽然偶尔有一些题目会用双曲线的定义来提及，但是都始终没有说清他们之间的关系。今天我们有了旋转坐标公式，对这个问题就可以细细阐述了。明天的文章将与大家分享。

向量的应用----求空间坐标旋转变换

向量的应用----求空间坐标旋转变换山石摘要：利用向量的投影意义推导出空间直角坐标转换公式，并举例应用——点绕定直线转动的问题。此方法易理解掌握、计算简单，不仅拓宽了向量知识的应用范围，为解决三维直角坐标转换提供了一种新方法，同时对测绘学、计算机图形学都有借鉴意义。介绍一种利用空间向量求解坐标变换关系的方法，简化了传统的坐标系之间坐标变换关系求解的复杂计算，减小了采样误差对计算结果的影响，为建立各种物体之间的位姿描述提供了有效的数学计算手段。关键词：向量；坐标转换。什么是三维直角坐标转换呢？简单的说：就是空间的点在两个不同空间直角坐标系中的坐标转换关系。求解它的方法多涉及高数内容。笔者经研究发现：利用向量知识也可以求三维直角坐标转换。一．利用向量推导三维直角坐标转换已知空间直角坐标系O XYZ -中一点(,,)P x y z 在另一空间直角坐标系O X Y Z '' ''-的坐标(,,)x y z '''，点O '在坐标系O XYZ -的坐标为000(,,)x y z ，且两个坐标系符合右手旋转规则，如图一，X '轴、Y '轴、Z '轴正方向的单位向量分别为X n → '、Y n →'、Z n →'，设(,,)X X X X n x y z →''''=、Y n → ' (,,)Y Y Y x y z '''=、 Z n → '(,,)Z Z Z x y z '''=。证明：将空间直角坐标系O XYZ -按OO '平移得新空间直角坐标系111O X Y Z '-，（如图一）则点 (,,)P x y z 在111O X Y Z '-的坐标为000(,,)x x y y z z ---。根据向量的投影知识O P '在X n → '上的投影就是点P 在坐标系O X Y Z ''''-中的横坐标，O P '在Y n → '上的投影就是点P 在坐标系O X Y Z ''''-中的纵坐标，O P '在Z n → '上的投影就是点P 在坐标系O X Y Z '' ''-中的竖坐标。所以X X X O P n x O P n n →→ →→ ' '→ ' '?''= =?= 000()()()X X X x x x y y y z z z '''-+-+- 证明： x '=000()()()X X X x x x y y y z z z '''-+-+- y '=000()()()Y Y Y x x x y y y z z z '''-+-+- z '=000()()()Z Z Z x x x y y y z z z '''-+-+- （公式一）

坐标旋转公式的推导

坐标旋转变换翻译自: http://www.metro-hs.ac.jp/rs/sinohara/zahyou_rot/zahyou_rotate.htm 翻译：汤永康出处:https://www.360docs.net/doc/6c10250285.html,/tangyongkang 转贴请注明出处 1 围绕原点的旋转如下图，在2维坐标上，有一点p(x, y) ,直线opの长度为r, 直线op和x轴的正向的夹角为a。直线o p围绕原点做逆时针方向b度的旋转，到达p’ (s,t) s = r cos(a + b) = r cos(a)cos(b) – r sin(a)sin(b) (1.1) t = r sin(a + b) = r sin(a)cos(b) + r cos(a) sin(b) (1.2) 其中 x = r cos(a) , y = r sin(a) 代入(1.1), (1.2) , s = x cos(b) – y sin(b) (1.3) t = x sin(b) + y cos(b) (1.4)

用行列式表示如下 2．座标系的旋转在原坐标系xoy中, 绕原点沿逆时针方向旋转theta度，变成座标系 sot。设有某点p，在原坐标系中的坐标为 (x, y), 旋转后的新坐标为(s, t)。 oa = y sin(theta) (2.1) as = x cos(theta) (2.2) 综合(2.1)，(2.2) 2式 s = os = oa + as = x cos(theta) + y sin(theta) t = ot = ay – ab = y cos(theta) – x sin(theta) 用行列式表达如下

直角坐标与球坐标的换算及坐标的旋转

直角坐标与球坐标的换算及坐标的旋转画地图当然要用球坐标，但是球坐标计算复杂，所以通常要把球坐标转换为直角坐标，便于计算及变换如旋转等。这里首先就要建立直角坐标与球坐标的换算。如下图所示，可得 1.由球坐标转换为直角坐标有： cos cos sin cos sin x r y r z r θφ θφφ ===y 2.反过来有直角坐标转换为球坐标有： tan tan r y x φθ== = 当然也可以用其他函数进行换算。 3.坐标的旋转与物体的旋转。通常从不同的角度观察物体是把物体进行旋转，这样更直观。例如地球的正视图以y 为轴旋转一个角度如以逆时针旋转为正，顺时针旋转为负，如下图以x 为轴旋转α角。这时x 坐标不变。在yz 平面内，设原图形上任一点到x 轴的距离为ρ，幅角为θ则其原坐标为 cos sin y z ρθρθ == 则旋转后有 ''cos()cos cos sin sin cos sin 'sin()sin cos cos sin cos sin x x y y z z z y ρθαρθαρθαααρθαρθαρθααα ==+=-=-=+=+=+ 同理若以y 为轴旋转旋转α角则有：

''cos()cos cos sin sin cos sin 'sin()sin cos cos sin cos sin y y z z z x x z ρθαρθαρθαααρθαρθαρθααα==+=-=-=+=+=+ 若以z 为轴旋转α角则有： ''cos()cos cos sin sin cos sin 'sin()sin cos cos sin cos sin z z x x y y y x ρθαρθαρθαααρθαρθαρθααα==+=-=-=+=+=+ 这样我们便可以吧图形任意旋转，不过还要注意旋转的次序。

旋转体体积一般积分公式的坐标变换法推导

旋转体体积一般积分公式的坐标变换法推导【摘要】根据已有的已知截面面积的几何体体积积分公式，通过坐标变换，推导沿倾斜轴旋转的旋转体体积的一般积分公式，继而推导作为其特殊形式的平面曲线绕坐标轴旋转所得旋转体体积的积分公式，列举公式的应用. 【关键词】坐标变换；旋转体体积；一般积分公式一般高等数学、数学分析教材中，只给由平面曲线绕坐标轴旋转所得旋转体体积的积分公式，但是，根据几何体体积的积分公式可以推证，平面曲线y=f(x)上介于m,n两点间的曲线段绕同平面直线l：ax+by+c=0旋转所得旋转体体积的一般积分公式为： v=π[](a2+b2)3[]2b a ax+bf(x)+c］ 2|af′(x)-b|dx.(a) 其中a,b分别为m,n两点所对应的x值. 依此公式，不仅可简化曲线段绕一般直线旋转所得旋转体体积的计算，同时，坐标轴作为坐标平面直线l的特殊形式，由平面曲线绕坐标轴旋转所得旋转体体积的积分公式，自然也可作为公式(a)的特殊形式而得到.公式(a)的推导有多种方法，通过坐标变换推导，不失为其中方法之一. 一、公式的坐标变换法推导在直线l：ax+by+c=0的任意一条垂线与曲线y=f(x) 一个交点的假定条件下，若b≠0，直线l与y轴的交点为0,-c[]b，

设直线l在坐标系xoy上的倾斜角为θ，则tanθ=-a[]b，且作为更一般的例子，由y=f(x)，x=a，x=b及y=0所围成区域绕y 轴旋转所得旋转体体积公式，也可由(c)推出. ［1］同济大学应用数学系.高等数学（第五版）［m］.北京：高等教育出版社，2002. ［2］复旦大学数学系.数学分析（第三版）［m］.北京：高等教育出版社，2007. ［3］陈抚良,张振兰,黄浩然.解析几何［m］.北京：科学出版社，2005. ［4］龚冬保.高等数学典型题解法、技巧、注释［m］.西安：西安交通大学出版社，2000. ［5］李德新.求旋转体体积的一个公式［j］.高等数学研究，2005(3).

坐标系平移和旋转

坐标系平移和旋转 3.4 平面上的坐标系地理坐标是一种球面坐标。由于地球表面是不可展开的曲面，也就是说曲面上的各点不能直接表示在平面上，因此必须运用地图投影的方法，建立地球表面和平面上点的函数关系，使地球表面上任一点由地理坐标（φ、λ）确定的点，在平面上必有一个与它相对应的点，平面上任一点的位置可以用极坐标或直角坐标表示。平面直角坐标系的建立在平面上选一点O为直角坐标原点，过该点O作相互垂直的两轴X’OX和Y’OY而建立平面直角坐标系，如图5所示。直角坐标系中，规定OX、OY方向为正值，OX、OY方向为负值，因此在坐标系中的一个已知点P，它的位置便可由该点对OX与OY轴的垂线长度唯一地确定，即x=AP，y=BP，通常记为P(x，y)。平面极坐标系（Polar Coordinate）的建立图4-5：平面直角坐标系和极坐标系如图5所示，设O’为极坐标原点，O’O为极轴，P是坐标系中的一个点，则O’P称为极距，用符号ρ表示，即ρ=O’P。∠OO’P为极角，用符号δ表示，则∠OO’P=δ。极角δ由极轴起算，按逆时针方向为正，顺时针方向为负。

极坐标与平面直角坐标之间可建立一定的关系式。由图5可知，直角坐标的x轴与极轴重合，二坐标系原点间距离OO’用Q表示，则有： X=Q–ρcosδ Y=ρsinδ 直角坐标系的平移和旋转坐标系平移如图1所示，坐标系XOY与坐标系X’O’Y’相应的坐标轴彼此平行，并且具有相同的正向。坐标系X’O’Y’是由坐标系XOY平行移动而得到的。设P点在坐标系XOY中的坐标为(x，y)，在X’O’Y’中坐标为(x’，y’)，而(a，b)是O’在坐标系XOY中的坐标，于是： x=x’+a y=y’+b 上式即一点在坐标系平移前后之坐标关系式。图1：坐标平移坐标系旋转如图2所示，如坐标系XOY与坐标系X’O’Y’的原点重合，且对应的两坐标轴夹角为θ，坐标系X’O’Y’是由坐标系XOY以O为中心逆时针旋转θ角后得到的。 x=x’cosθ+y’sinθ

坐标旋转公式的推导

坐标计算方法

初三数学旋转坐标与图形变换

推导坐标旋转公式

坐标旋转推导

回转体在卧式加工中心的旋转工作台上任意放置的坐标计算方法

平面内坐标旋转公式

两角和的正余弦公式与旋转坐标

向量的应用----求空间坐标旋转变换

坐标旋转公式的推导

直角坐标与球坐标的换算及坐标的旋转

最新坐标系平移和旋转

旋转体体积一般积分公式的坐标变换法推导

坐标系平移和旋转