一元连续函数的一个性质及其应用

一元连续函数的一个性质及其应用

叶留青 杨秀芹

焦作师范高等专科学校数学系 河南焦作 454001

树立函数观点，突出函数思想，培养函数思维模式，运用函数方法，是初等数学教育教学的重要内容之一。幂平均不等式实质上是幂函数的一个性质，它是否还可以改进，一般一元连续函数是否也具有类似的性质？我们对此问题进行探讨表明，利用所给出的定理证明不等式时，思路通畅，作题规范，步骤简便，使有些证明难度较大的不等式问题变得比较简单，也加深了学生对函数思想和函数方法的运用和理解，为发现不等式，解决不等式问题开辟了一条新途径。

1.关于一元连续函数的一个性质定理

设()m

f x x =，则幂平均不等式可表示为

（1）()1111n n i i i i f x f x n n ==??

≥ ???∑∑其中0i x >()1,2,

,i n =，1m ≥ （2）()1111n n i i i i f x f x n n ==??

≤ ???

∑∑其中0i x >()1,2,

,i n =，01m <≤

1.1引理 设()f x 是区间Q 上的连续函数，,(1,2,,1)i x Q i n ∈=+，且1231n x x x x +≤≤≤

≤。

用()

n M

表示点()1111,n n i i i i x f x n n ==?? ???

∑∑（下同），则点()1n M +在以点()n M 和点()()11,n n A x f x ++为端

点的线段()

n M A 上。

证明 因为

()()()1

11

11

111111111111n

n

i i i i n n i i i i n n x f x n n x f x n n x f x ==++==++++∑∑∑∑＝()()

()

()

1

1

1

1

1

1

1

11

111

n

n

i i

i i n n i i

i i n n x f x n x f x n n n x f x ==++==++++∑∑∑∑ ＝

()

()

()

()

111

1

1

11

11

n

n

i

i

i i n

n

i

i

i i n n x f x n x f x n n n x f x ====+++∑∑∑∑＝0

基金项目:全国教育科学十五规划课题(FIB030837)子课题,河南省教育厅课程教学改革项目（C2803） 作者简介：叶留青（1965-），男，河南汝南人， 硕士，焦作师专数学系教授，从事数学课程与教学论研究。

所以点()

n M

，()

1n M

+，A 共线。由1231n x x x x +≤≤≤

≤易知1

111

111n n i i n i i x x x n n ++==≤≤+∑∑，故点 (

)

1n M +在线段()

n M

A 上。

1.2 定理 函数()f x 在区间Q 上，

（1）若()f x '是增函数，则对于,(1,2,)i x Q i n ∈=有()1111n n i i i i f x f x n n ==??≥ ???∑∑

（2）若()f x '是减函数，则对于,(1,2,

)i x Q i n ∈=有()1111n n i i i i f x f x n n ==??≤ ???∑∑

（3）若()f x '是常函数，则对于,(1,2,)i x Q i n ∈=有()1111n n i i i i f x f x n n ==??= ???

∑∑

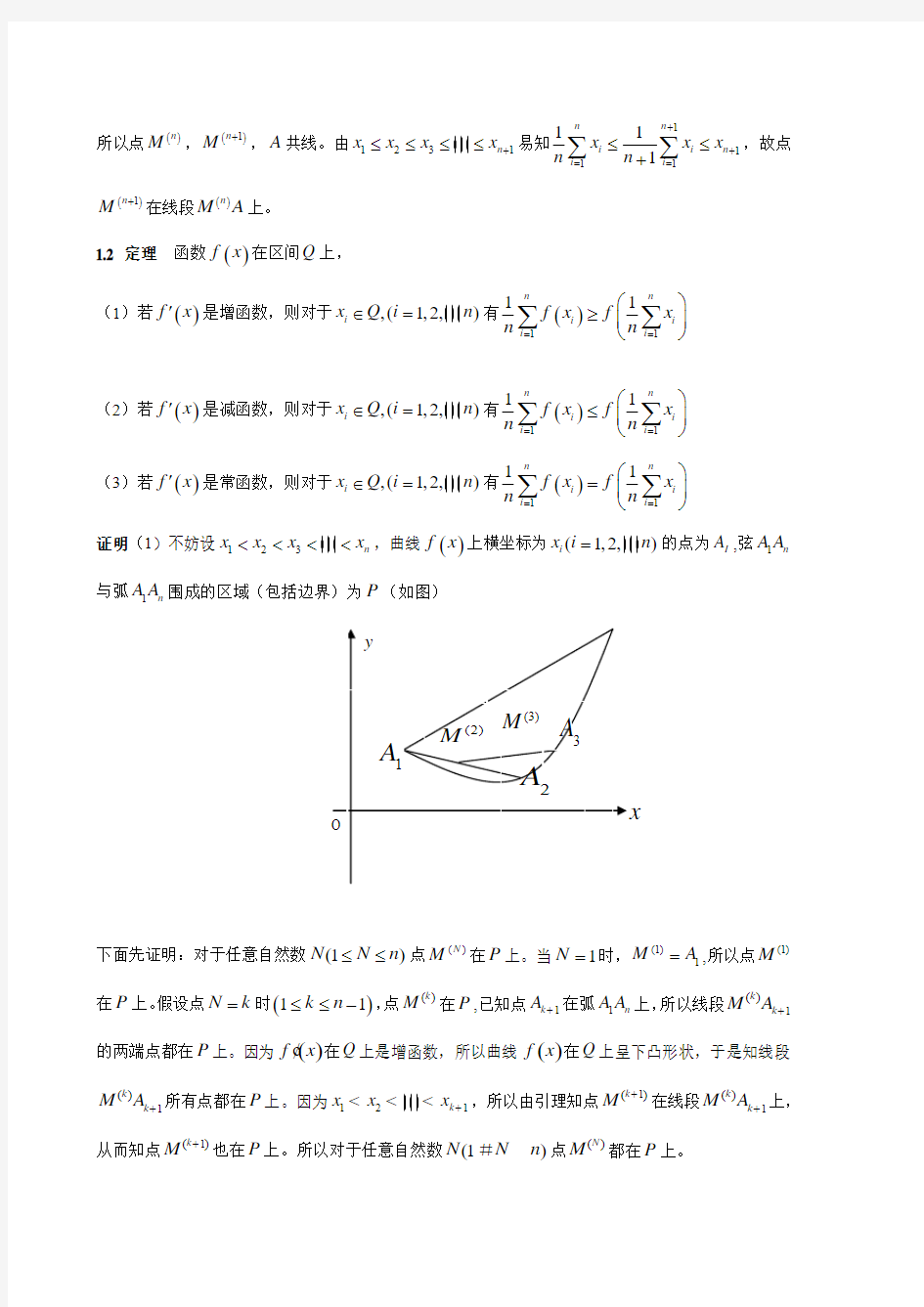
证明（1）不妨设123n x x x x <<<

<，曲线()f x 上横坐标为(1,2,

)i x i n =的点为I A ,弦1n

A A 与弧1n A A 围成的区域（包括边界）为P （如图）

下面先证明：对于任意自然数(1)N N n ≤≤点()

N M 在P 上。当1N =时，(1)

1M

A =,所以点(1)

M 在P 上。假设点N k =时()11k n ≤≤-，点()

k M

在P ,已知点1k A +在弧1n A A 上，所以线段()

1

k k M A +的两端点都在P 上。因为()f x ￠在Q 上是增函数，所以曲线()f x 在Q 上呈下凸形状，于是知线段

()1k

k M A +所有点都在P 上。因为121k x x x +<<

<，所以由引理知点()1k M +在线段()1k k M A +上，

从而知点()

1k M

+也在P 上。所以对于任意自然数(1)N N

n ＃点()N

M 都在P 上。

点()

()11

11,n n n i

i i i M

x f x n n ==骣÷?=÷?÷?桫

邋在P 上，而点1

1

11

,n n i i i i A x f x n n ==骣骣÷琪?÷÷??÷÷??÷

?桫

桫邋在弧1n A A 上，注意到()n A M x x =,于是()

n A M y y 3，即()11

11

n n i i i i f x f x n n ==骣÷?3÷?÷?桫

邋.

同理可证明（2）. （

3

）

因

()f x ￠是常函数，故可设

()f x kx b

=+，于是

()11

11

11

11

()n n

n n i i i i i i i i f x kx b k x b f x n n n n ====

骣骣

鼢珑=+=+=鼢珑鼢珑桫桫

邋邋1A

2.定理应用

一元连续函数的图像或凸或凹或直总是普遍存在的，而高中数学新编教材增加导数内容后，为判断一元连续函数的凸凹性提供了有力工具，这就为运用定理证明不等式，发现不等式，解决不等式问题开辟了新途径。 2.1改进幂平均不等式

长期以来，在应用幂平均不等式时，只考虑幂指数1m 3或01m

f x x =的导数()1

m f x mx

-￠=在()

0,￥上是增函数，由定理知，对于()()0,

,1,2,

,i x i n 违=，有1

1

11m

n n m

i i i i x x n n ==骣÷?3

÷?÷?桫

邋 ()0m <

许多与幂平均不等式有关的命题也应改进。例如文〔2〕给出的经多次推广而得到的一个不等式：若：,,,n x y z R +

?,且2,1m x

y z ?+=则2

3(1)(1)(1)31

m m m n m n n n

n x y z y y z z x x -+++?----中n 和m 的取值范围应改进为n R +?或1n <-；2m 3或0m <。顺便说明一下，该不等式还可以

推广为

若：()1,2,,i x R

i N +

?，n R +

?或1n <-；2m 3或0m <，

1

n

i i x P ==?

，则

12

12

223311(1)(1)(1)m

m m

m n m N n n

n n n

x x x p N x x x x x x N P --++++?

----，因证明思路与文〔2〕中对原不等式的证明类同，故从略。

2.2导出几个重要不等式

由于一元连续函数的导数的单调性与函数图像的凸凹性是等价的，因而根据几个常见函数图像的凹凸性，即可得出下面几个重要不等式

1. 弦平均不等式

若[]2,(21),(1,2,

,),i x k k

i n k z p p ?=?，则有11

11

sin sin n n i i i i x x n n ==骣÷?3÷?÷?桫

邋

若[](21),2,(1,2,

,),i x k

k i n k z p p ?=?，则有11

11

sin sin n n i i i i x x n n ==骣÷?￡÷?÷?桫邋

2 .切平均不等式

若1,(),(1,2,,),2i x k k i n k z p p 骣

÷

??=?÷?÷

?桫，则有1111tan tan n n i i i i x x n n ==骣÷?3÷?÷?桫邋 若1

(),,(1,2,,),2

i x k k i n k z p p 骣÷??=?÷?÷?桫

，则有11

11tan tan n n i i i i x x n n ==骣÷?￡÷?÷?桫

邋

3. 对数平均不等式

若,1,(1,2,

,),i x R a

i n +

?=则

11

11log log n n a i

i i i x x n n ==骣÷?￡÷??÷

桫

邋 ?121

1()n

n n i i x x x x n =￡?

若,1,(1,2,

,),01i x R a

i n a +

?=<<，则

11

11log log n n a i a i i i x x n n ==骣÷?3÷?÷?桫

邋 ?12

1

1()n

n n i i x x x x n =3?

4 指数平均不等式 若,1,(1,2,

,),0i x R a

i n a +

?=>且1a 1，则111

1n

i i

i n

x n

x i a a n ==?3?

2.3简证一类不等式

许多不等式问题，一旦与一元连续函数起来以后，利用所给定理去解决，顺畅，简便，得心应手。

例1 设正数12,,,n a a a 之和为S ，求证：1

(2)1

n

i i i a n

n s a n ==?--?

（1976年英国数学竞赛题）

证明：设()x

f x s x

=-，则()2

()s f x s x ￠=-，当0x s <<时，()f x ￠是增函数，由定理知，当()(0,),1,2,

,i a s i

n ?，且12n a a a s ++

+=时，

1

1

1

111

11n

i

n

i i n i i

i

i s

a a n n

s n s a n s s a n

n ===?

=----???，于是得11n

i i i a n s a n =3--?，故原不等式成立。

例2 设,,a b c R +

? 求证

22

22

a b c a b c

b c a c a b ++++?+++（1998年第二届“友谊杯”国

际数学竞赛题）

证明：设a b c s ++=，则原不等式等价于不等式

2222

a b c s

s a s b s c ++?--- 设2

()x f x s x

=-，则22

2()()x x f x s x s x ￠=+--，在()0,s 上是增函数。因(),,0,a b c s ?，且a b c s ++=，由定理知2

222

1336

3

s a b c s s s a s b s c

s 骣÷?÷?÷

骣?桫÷?÷++??÷÷?---桫-，于是得

2222a b c s

s a s b s c

++?---，故原不等式成立。 例

3

设

12,,

,n a a a R +

?，

12,,2

n a a a s k N k

+++=纬，则有

()1

12

2

121k k k k n k n a a a s s a s a s a n n --+++?

----，该不等式是文〔4〕给出的重要定理，其证明难度较大。

证明：设()k

x f x s x

=-，则12()()k k kx x f x s x s x -￠=+--，在()0,s 上是增函数。因()0,i a s ?，

由定理知

1

121

12

1(1)k

k k k

k n k n s a a a s n s n s a s a s a n n s n

--骣÷?÷?骣÷?桫÷?÷+++

??÷?÷----桫-，于是有

1

12

2

12(1)k k k

k n k n a a a s s a s a s a n n

--+++?----。 例4证明对任意1,1a b >>，有不等式22

811a b b a +?-- （第26届全俄数学竞赛奥林匹克试题） 证明：设a b s +=，则原不等式等价于

22

811

a b s a s b +?----， 设2

()1

x f x s x =--，则22

2()1(1)x x f x s x s x ￠=+----，在()1,1s -上是增函数。由题意知(),1,1a b s ?，由定理知2

222

1221124

1

2

s a b s s s a s b s s 骣÷?÷?÷骣?桫÷?÷+??÷÷?-----桫--，于是得

()

2

222

488112

2

s a b s s a s b s s -+?

+?------，故原不等式成立。

例5 设,,,0a b c R l

+

纬

设123,,b c a

x x x a b c

=

==，则1233x x x ++?，

，

设()f x =

则()f x ￠=

=

()0,￥

上是增函数。因()123,,0,x x x 违，由定理知

1

3

?

?，故原不等式成立。 例6 设0(1,2,

,),1i x i n k >=<，

求证：

1

1

11212121

n

n

n x x x n

kx x x x kx x x x kx n k +

++

?++

+++

++++-+

（数学通报2004.1第1474号问题） 证明：设12n x x x s ++

+=，

原不等式等价于不等式

()()()12

12

1111

n n x x x n

s k x s k x s k x n k ++

+

?+-+-+--+

设()()1x f x s k x =

+-，注意到1k <，则()()()()

2

11

()11k x f x s k x s k x -￠=++-+-，在()0,￥上是增函数。因为12,,

,(0,

)n x x x 违，

由定理知()()()()

1212

11

1111

1n n s x x x n

s n s k x s k x s k x n k s k n

骣÷?÷?+++

?

÷?÷

÷?+-+-+-+-桫+-

于是得

()()()12

12

1111

n n x x x n

s k x s k x s k x n k ++

+

?+-+-+--+，故原不等式成立。

例7 设,,a b c R +

?，且1abc = 求证：()()()3331113

2

a b c b c a c a b ++?+++（36届IMO 试

题）

证明：设1abc =，原不等式等价于不等式2222223

2b c a c a b ab ac bc ab ac bc ++?+++，令

,,ab x bc y ac z ===，则2

22

1x y z a b c =

=，于是原不等式又等价于不等式

22232y z x x z x y y z ++?+++，设2()t f x s t =-，则()

2

2

2()t t f x

s t s t ￠=+--，在()0,￥上是增函数，由定理知(),,0,

x y z 违时

2

22211

33662

3

s y z x s x y z s s x s y s z s 骣÷?÷?÷骣?++桫÷?÷++?=??÷?÷---桫-， 于是得

2223

2

y z x s x s y s z ++?---，故原不等式成立。 例

8 设,,a b g

均为锐角，且满足2

2

2

cos cos cos 1a b g ++=，求证：

2223

cot cot cot 2

a b g ++?

（数学通报839号问题） 证明：原不等式等价于不等式222222

cos cos cos 3

1cos 1cos 1cos 2a b g a b g ++?---，设222

1

2

3c o s ,c o s ,c o s x x x a b g ===，则

222

123cos cos cos 1x x x a b g ++=++=，于是原不

等式等价于不等式：

31212331112x x x x x x ++?---，设()1x f x x =-，则()

2

1

()1f x x ￠=-，由定理知123

3121

23123

11

3

31112

13

x x x x x x x x x x x x ++骣

÷?÷++??÷?÷++---桫-，于是得31212331112x x x x x x +

+?---，故原不等式成立。

例9 设正数,,,a b c d ，满足1ab bc cd da +++=，试证：

33331

3

a b c d b c d a c d a b d a b c +++?++++++++（31届IMO 试题）

证明：设a b c d s +++=，则原不等式等价于不等式

33331

3a b c d s a s b s c s d +++?---- 设3()x f x s x =-，则()

23

2

2()x x f x s x s x ￠=+--，在()0,￥上是增函数。因为,,,(0,)a b c d s ?，由定理知()

2

2

333321444848

4

s a b c d a b c d s s s a s b s c s d s 骣÷?÷?÷骣?+++桫÷?÷+++?=?÷?÷----桫- ()()224()()

()()2()()

4848

12

a c

b d a

c b

d a c b d a c b d ++++++++++=?

1

1212

ab bc cd ad +++==

，于是得，333313a b c d s a s b s c s d +++?----，故原不等式成立。 利用定理还可以证明下列不等式：

1

、证明不等式2

(1)

1(2

2n n n n n 骣++÷

?+

?÷?÷

?桫 2、已知3

3

1,,p q p q R +=?，求证2p q +? 3、设12,,

,,2n a a a R n

+

纬，且121n a a a ++

+=，求证：1121n

i i i

a n

a n =3--?

（1984年巴尔干数学竞赛题）

4、若01

(1,2,,)i a i n <<=且12n a a a a +++=求证

1212

111n n a a a na

a a a n a

+++

?---- （Shopiro 不等式）

5、设,,a b c R +

?，求证

32

a b c b c a c a b ++?+++（1963年莫斯科数学竞赛试题） 6、设,,a b c 是ABC D 的三边，求证：

222

a b c a b c b c a a c b a b c

++?++-+-+-（数学通报

2003.1第36页题） 7、在ABC D 中，求证3

sin

sin sin 2222

A B C ++?（数学通报1995.2第936号问题） 可见，如果说函数单调性常用的话，那么文中函数凹凸性的运用，拓宽了不等式的空间，

也是高等数学增加了导数内容后的必然要求，这为运用定理证明不等式，发现不等式，解决不等式

问题开辟了一条新途径。

参考文献

[1]原北京矿业学院高等数学教研组编著.《数学手册》[M]. 北京：高等教育出版社，1959

[2]宋庆.一个分式不等式的再推广[J].数学通报,2006.5

[3]刘南山.也谈一类竞赛不等式创新证法[J].数学通报,2006.5

[4]徐丹，杨露. 一个不等式的再推广[J].数学通报2001.10

[5]叶留青.大学文科数学.M].山头大学出版社,2005

[6]贾长虹，叶留青.新课程教学中数学应用意识和能力的培养[J].教学与管理,2006（8）