用弹性力学理论分析合理拱轴线

胡文亚1，齐永正2

（1. 中铁四局集团一公司，安徽合肥230041; 2. 合肥工业大学土木建筑工程学院，安徽合肥230009）

摘要：本文从弹性力学的角度用极坐标应力函数法求解出了无铰圆拱在径向均布荷载作用下不

考虑荷载引起的轴向变形情况的应力及内力弹性解，从而证明了结构力学中拱在径向均布荷载作

用下，合理轴线为圆弧，轴力为常数的结论是合理的；文章最后讨论了超静定圆拱在径向均布荷

载下考虑轴向变形的弹性计算方法。

关键词：应力函数法；圆拱；径向均布荷载；轴向变形；弹性解；合理拱轴线

Analysis of appropriate axis of arches using

Mechanical Theory of Elasticity

HU Wen-ya1，QI Yong-zheng2

(1. The 1st engineering Co., Ltd of China Tisiju Civil Engineering Group, Hefei 230041, China; 2. School of Civil

Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:In the paper, accurate stress and internal force elastic solutions of fixed-supported circular arch carrying a radial-uniform-load are obtained without considering axial deformation effects by stress functional method under the point of view on mechanics of elasticity, which prove that the results in the mechanics of structure that appropriate axis of arches carrying a radial-uniform-load is arc, and axial forces is constant, are accurate and efficient. Finally elastic calculation method of statically indeterminate arches carrying a radial-uniform-load are discussed when axial deformation effects are taken into account.

Key words: stress functional method; circular arch; radial-uniform-load; axial deformation; elastic solutions; appropriate axis of arches

0 引言

结构力学教材[1]及大量文章[5~6]用结构力学的方法推导了拱在各种荷载作用下的合理轴线的曲线方程。本文仅以求解等截面圆拱受径向均布荷载产生的弹性应力解为例证明结构力学结论的正确性。设以拱的任一截面左边（或右边）所有外力的合力（包括数量、方向和作用点）作出合力多边形，这个合力多边形称为拱的压力线。当拱的压力线与拱的轴线重合时，各截面的弯矩为零，拱处于无弯矩状态，这时各截面只受轴力作用,材料的使用最经济。在固定荷载下，使拱处于无弯矩状态的轴线称为合理拱轴线。结构力学中推导了拱在均匀水压力作用下的合理轴线（即无弯矩状态）为圆弧，此时拱只受常值轴力的作用，本文从结构力学的结论出发，用弹性力学中的应力函数法求解径向均布荷载作用下圆拱的弹性解，从而验证了结构力学结论的正确性。

作者简介：胡文亚（1974—），男，安徽安庆人，中铁四局集团一公司，工程师

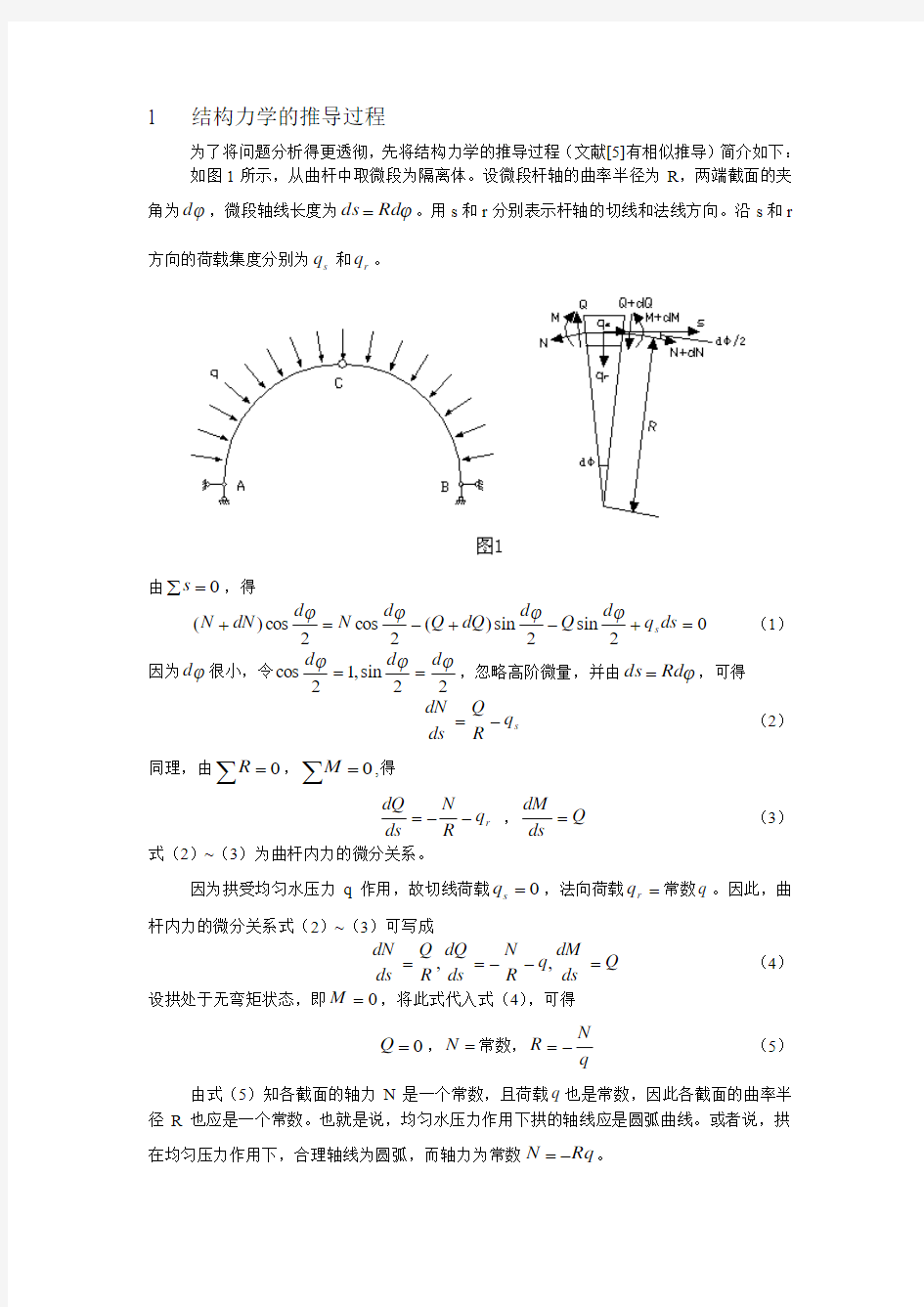
1 结构力学的推导过程

为了将问题分析得更透彻，先将结构力学的推导过程（文献[5]有相似推导）简介如下：如图1所示，从曲杆中取微段为隔离体。设微段杆轴的曲率半径为R ，两端截面的夹角为?d ，微段轴线长度为?Rd ds =。用s 和r 分别表示杆轴的切线和法线方向。沿s 和r 方向的荷载集度分别为s q 和r q 。

由0=∑s ，得

sin 2sin )(2cos 2cos

)(=+-+-=+ds q d Q d dQ Q d N d dN N s ???? （1）因为?d 很小，令2

2sin ,12cos ???d d d ==，忽略高阶微量，并由?Rd ds =，可得 s q R Q ds dN -= （2）同理，由∑=0R ，∑=0M ,得

r q R N ds dQ --= ，Q ds

dM = （3）式（2）~（3）为曲杆内力的微分关系。

因为拱受均匀水压力q 作用，故切线荷载0=s q ，法向荷载=r q 常数q 。因此，曲杆内力的微分关系式（2）~（3）可写成

Q ds

dM q R N ds dQ R Q ds dN =--==,, （4）设拱处于无弯矩状态，即0=M ，将此式代入式（4），可得

0=Q ，=N 常数，q

N R -= （5）由式（5）知各截面的轴力N 是一个常数，且荷载q 也是常数，因此各截面的曲率半径R 也应是一个常数。也就是说，均匀水压力作用下拱的轴线应是圆弧曲线。或者说，拱在均匀压力作用下，合理轴线为圆弧，而轴力为常数Rq N -=。

2 弹性力学应力函数法求解过程

如图2所示，有一两端固定的圆拱，内半径为a 、外半径为b ，受径向均布荷载q 作用，下面求圆拱内的应力（体力不计）。

由于结构的的形状是圆弧形，本文采用极坐标应力函数法[2~3]求解，由应力函数在边界上的性质，知应力函数与?无关[2] ，故取应力函数)(),(ρ?ρU U =。将应力函数代入极坐标形式的双调和方程[2~3]即

0)11(222

2224

=???+???+??=?U U ?ρρρρρ （6）式（6）展开后等号两边乘以4ρ有

022********

=+-+ρρρρρρρρd dU d U d d U d d U d （7）式（7）是Euler （欧拉）方程，其通解为

D C B A U +++=22ln ln )(ρρρρρ （8）

式中A ，B ，C ，D 为积分常数，由边界条件确定。则应力分量表达式为

0)1(2)ln 21(/2)ln 21(/11

2222222=?????-=+++-=??=+++=???+???=?

ρρτρρρ

σρρ?ρρρσρ??ρU C B A U C B A U U （9）

由弹性力学物理方程及几何方程得位移分量为 )1(ln )1(2)31(/)1([--+-++-=ρρρρρB v B v A v u

??ρcos sin /])1(2K I E C v ++-+ （10）

??ρρ??sin cos /4K I H E B u -++=

式中H 、I 、K 为物体的刚体位移，当不考虑荷载引起的轴向变形且不计刚体的位移时，0,0=====K I H B u ?，应力分量表达式（9）及位移分量表达式（10）可简化如下

0,2/,2/22=+-=+=

ρ??ρτρσρσC A C A （11）

E C v A v u /])1(2/)1([ρρρ-++-= （12）

由边界条件q b a -====ρρρρσσ)(,0)(得积分常数为

)

(2,222

2222a b qb C a b q b a A --=-= （13）将式（13）代入式（11）得圆拱的应力分量，即拉梅（Lam é）解为

0),1(),1(22

22222222=+--=--=ρ??ρτρ

σρσa a b qb a a b qb （14）将式（13）代入式（12）得圆拱的位移分量为

0)],()[()

(2222222

=-++--=?ρρρρu a v a a b E qb u （15）因为a ≥ρ，所以?ρσσ,均是压应力，在垂直轴线的截面上只作用有主应力，剪应力为零，其分布图如图3所示。最大压应力发生在内周壁：)/(22

22a b qb --=?σ ，主应力迹线为垂直于轴线的一组径向直线，应力等值线为平行于轴线的一组圆弧[4]，如图4所示。令壁厚a b h -=，则拱每延米宽的横断面面积为a b h -=，乘以式（14）即求得拱的内力为 )1()(22

2++-=-?=ρ

σ?a a b qb a b N （16）

由于垂直轴线的截面上无剪应力，所以该截面上剪力为零。由轴向应力在截面上不是均匀分布，可知当拱壁较厚时，应考虑轴向应力在拱壁中产生的弯矩影响；当拱壁较薄时，可认为

轴向应力沿拱横截面均匀分布。即若拱的中轴线曲率半径R >>（b-a ），则R b a ≈≈≈ρ，代入式（16）得拱的内力为

0,0,==-=M Q Rq N （17）

由式（17）可以看出通过弹性力学的应力解所得出拱的内力与结构力学中推导的结果完全相同，由合理拱轴线的定义即可认为拱在径向均布荷载作用下，圆弧是拱的合理拱轴线，此时拱只受轴力Rq N -=的作用，负号表示压力。从而验证了结构力学的结论。 3 结论及分析

（1）本文中的求解是在假设两端固定的拱不考虑轴向变形下的解，由本文的推导过程可以看出仅由应力边界条件即可求得此状态下的全部积分常数。当考虑轴向变形时积分常数B 将不再为零，此时仅由应力边界条件不能确定全部积分常数，尚需考虑到支座处的位移边界条件。对于两铰拱和无铰拱，由于其位移约束条件不同，其解亦具有一定的差异。由于求解过程非常复杂，本文从略。

（2）结构力学中推导在均匀水压力作用下三铰拱的合理轴线为圆弧。本文用弹性力学应力函数法求解了超静定圆拱假设不考虑轴向变形的弹性解，表明在此荷载下的薄壁圆拱处于无弯矩状态，拱只受常值轴力作用。结构力学中求解等截面圆弧形无铰拱在均匀水压作用下的内力中假设不考虑轴向变形时荷载引起的受力状态为无弯矩状态[1]，因为拱的壁厚与拱的曲率半径相比是非常小的，所以这种假设是合理的。

结构力学中求解单纯由轴向变形引的受力状态——附加内力状态时，从所得结果可知拱内弯矩是沿拱轴线变化的，最大弯矩发生在拱顶和拱脚处。但从弹性力学的应力解答来看，无论是否考虑轴向变形，拱在垂直轴线的截面上都只作用有主应力，剪应力为零，拱内弯矩沿拱轴线是不变的，且值很小。当圆拱承受如图5所示的荷载时，由应力函数在边界上的性质可知些时的应力函数与?有关，可设应力函数为?ρ2cos )(f U =，进

内力解答与结构力学中的解答是相符的。这表明结构力学中用弹性中心法[1]求解超静定拱内力具有一定的局限性。

[参考文献]

[1] 龙驭球,包世华.结构力学教程(上册)[M].高等教育出版社,1993.51—62、212—232.

[2] 吴家龙.弹性力学[M].同济大学出版社,2002.129—201.

[3] 徐秉业,刘信声.应用弹塑性力学[M].清华大学出版社,2001.129—159.

[4] 孙训方,方孝淑.材料力学(下册) [M].高等教育教育出版社,1992.14—17.

[5] 魏德妨,赵继德.三铰拱的合理拱轴线方程[J].曲阳师范大学学报.1994, 20(3):80—83.

[6] 丁大钧.结构机理学——拱[J].工业建筑.1994,(11):54—59.

《弹性力学》、《岩体力学》复习大纲2015

第一章绪论 1-1弹性力学的内容 1-2弹性力学中的几个基本概念 1-3弹性力学中的基本假定习题第二章平面问题的基本理论 2-1平面应力问题与平面应变问题 2-2平衡微分方程 2-3平面问题中一点的应力状态 2-4几何方程刚体位移 2-5物理方程 2-6边界条件 2-7圣维南原理及其应用 2-8按位移求解平面问题 2-9按应力求解平面问题相容方程 2-10常体力情况下的简化应力函数习题第三章平面问题的直角坐标解答 3-1逆解法与半逆解法多项式解答 .3-2矩形梁的纯弯曲 3-3位移分量的求出 3-4简支梁受均布荷载 3-5楔形体受重力和液体压力习题第四章平面问题的极坐标解答 4-1极坐标中的平衡微分方程 4-2极坐标中的几何方程及物理方程 4-3极坐标中的应力函数与相容方程 4-4应力分量的坐标变换式 4-5轴对称应力和相应的位移 4-6圆环或圆筒受均布压力 4-7压力隧洞 4-8圆孔的孔口应力集中 4-9半平面体在边界上受集中力 4-10半平面体在边界上受分布力习题要求：了解弹性力学的基本概念，发展历史与基本假设，理解两类平面问题的解法，掌握三大方程的建立，边界的确定，有限单元法在解弹性力学问题的应用，了解空间问题的求解的方法。

第1章绪论 1.1 岩石与岩体（二者的区别） 1.2 岩体力学的研究任务与内容（岩体的力学特征） 1.3 岩体力学的研究方法 1.4 岩体力学在其他学科中的地位 1.5 岩体力学的发展简史基本要求：了解岩石力学、岩体力学定义及其它们的联系和区别；理解岩石力学的发展、研究对象和研究方法；了解岩石力学研究现状及热点问题。重点与难点：岩石力学的定义、任务、研究方法。第2章岩石的基本物理力学性质 2.1 岩石的基本物理力学性质 2.2 岩石的强度特性 2.3 岩石的变形特性 2.4 岩石的强度理论基本要求：掌握岩石的成分、结构及其力学性质；了解岩石的变形特征和流变性；理解岩石的各种强度及其测定方法。重点与难点：岩石的物理指标、强度与变形特征。第3章岩石动力学基础 3.1 岩石的波动特性 3.2 影响岩体波速的因素 3.3 岩体的其他动力学特性基本要求：理解岩石的波动特性，了解影响岩体波速的因素，了解岩体的其他动力学特性。重点与难点：岩石的动力学特性。第4章岩体的基本力学性能 4.1 岩体结构面的分析 4.2 结构面的变形特性 4.3 结构面的力学效应 4.4 碎块岩体的破坏 4.5岩体的应力－应变分析基本要求：理解岩石和岩体的区别，了解结构面的相关性质，了解岩体的变形特征和强度测定方法，理解岩体的破坏条件及应力-应变分析。重点与难点：理解岩体的相关特性。

弹性力学简明教程(第四版)_习题解答

【2-9】试列出图2-17，图2-18所示问题的全部边界条件。在其端部小边界上，应用圣维南原理列出三个积分的应力边界条件。 x y 2 h 1h b g ρo () 2h b >> h x y l /2/2 h M N F S F 1 q q 图2-17 图2-18 【分析】有约束的边界上可考虑采用位移边界条件，若为小边界也可写成圣维南原理的三个积分形式，大边界上应精确满足公式（2-15）。【解答】图2-17：上（y =0）左(x =0) 右（x =b ） l 0 -1 1 m -1 () x f s () 1g y h ρ+ () 1g y h ρ-+ () y f s 1gh ρ 代入公式（2-15）得 ①在主要边界上x=0，x=b 上精确满足应力边界条件： ()()100(),0;===-+=x xy x x g y h σρτ ()()1b b (),0; ===-+=x xy x x g y h σρτ ②在小边界0y =上，能精确满足下列应力边界条件： () () ,0y xy y y gh σρτ===-= ③在小边界2y h =上，能精确满足下列位移边界条件： ()()2 2 0,0 ====y h y h u v 这两个位移边界条件可以应用圣维南原理，改用三个积分的应力边界条件来代替，当板厚=1δ时，可求得固定端约束反力分别为： 10,,0s N F F gh b M ρ==-=

由于2y h =为正面，故应力分量与面力分量同号，则有： ()()()222 10000 0b y y h b y y h b xy y h dx gh b xdx dx σρστ===?=-???=???=????? ⑵图2-18 ①上下主要边界y=-h/2，y=h/2上，应精确满足公式（2-15） l m x f (s) y f (s) 2h y =- 0 -1 0 q 2 h y = 1 -1q -/2()y y h q σ==-，-/2()0yx y h τ==，/2()0y y h σ==，/21()yx y h q τ==- ②在x =0的小边界上，应用圣维南原理，列出三个积分的应力边界条件：负面上应力与面力符号相反，有 /20/2/2 0/2/20 /2()()()h xy x S h h x x N h h x x h dx F dx F ydx M τσσ=-=-=-?=-??=-???=-???? ③在x=l 的小边界上，可应用位移边界条件0,0====l x l x v u 这两个位移边界条件也可改用三个积分的应力边界条件来代替。首先，求固定端约束反力，按面力正方向假设画反力，如图所示，列平衡方程求反力： 110,x N N N N F F F q l F q l F ''=+=?=-∑ 0,0y S S S S F F F ql F ql F ''=++=?=--∑ 2 211110,'02222 A S S q lh ql M M M F l ql q lh M M F l =+++-=?=---∑ 由于x=l 为正面，应力分量与面力分量同号，故 M ' N F 'S F '

弹性力学基本概念和考点汇总

基本概念：（1）面力、体力与应力、应变、位移的概念及正负号规定（2）切应力互等定理：作用在两个互相垂直的面上，并且垂直于改两面交线的切应力是互等的（大小相等，正负号也相同）。（3）弹性力学的基本假定：连续性、完全弹性、均匀性、各向同性和小变形。（4）平面应力与平面应变；设有很薄的等厚度薄板，只在板边上受有平行于板面并且不沿厚度变化的面力或约束。同时，体力也平行与板面并且不沿厚度方向变化。这时， 0,0,0z zx zy σττ===，由切应力互等，0,0,0z xz yz σττ===，这样只剩下平行于xy 面的三个平面应力分量，即,,x y xy yx σσττ=，所以这种问题称为平面应力问题。设有很长的柱形体，它的横截面不沿长度变化，在柱面上受有平行于横截面且不沿长度变化的面力或约束，同时，体力也平行于横截面且不沿长度变化，由对称性可知，0,0zx zy ττ==，根据切应力互等，0,0xz yz ττ==。由胡克定律， 0,0zx zy γγ==，又由于z 方向的位移w 处处为零，即0z ε=。因此，只剩下平行于xy 面的三个应变分量，即,,x y xy εεγ，所以这种问题习惯上称为平面应变问题。（5）一点的应力状态；过一个点所有平面上应力情况的集合，称为一点的应力状态。（6）圣维南原理；（提边界条件）如果把物体的一小部分边界上的面力，变换为分布不同但静力等效的面力（主失相同，主矩也相同），那么，近处的应力分布将有显著的改变，但是远处

所受到的影响可以忽略不计。（7）轴对称；在空间问题中，如果弹性体的几何形状、约束情况，以及所受的外力作用，都是对称于某一轴（通过该轴的任一平面都是对称面），则所有的应力、变形和位移也就对称于这一轴。这种问题称为空间轴对称问题。一、平衡微分方程： (1) 平面问题的平衡微分方程； 00yx x x xy y y f x y f x y τστσ??++=????++=??（记） (2) 平面问题的平衡微分方程（极坐标）； 10210f f ρρ?ρ? ρ?ρ?ρ? ??σ?τσσ?ρρ??ρ ?σ?ττρ???ρρ -+++=+++= 1、平衡方程仅反映物体部的平衡，当应力分量满足平衡方程，则物体部是平衡的。 2、平衡方程也反映了应力分量与体力（自重或惯性力）的关系。二、几何方程；（1）平面问题的几何方程； x y xy u x v y v u x y εεγ?= ??=???=+ ??（记）（2）平面问题的几何方程（极坐标）；

弹性力学岩石力学

弹性力学基本知识考试一、基本概念： 1. 面力、体力与应力、应变、位移的概念及正负号规定体力是作用于物体体积内的力，以单位体积力来度量，体力分量的量纲为 L -2MT -2 ；面力是作用于物体表面上力，以单位表面面积上的力度量，面力的量纲为 L -1MT -2 ；体力和面力符号的规定为以沿坐标轴正向为正，属外力；应力是作用于截面单位面积的力，属内力，应力的量纲为 L -1MT -2 ，应力符号的规定为：正面正向、负面负向为正，反之为负。（1）切应力互等定理：作用在两个互相垂直的面上，并且垂直于改两面交线的切应力是互等的（大小相等，正负号也相同）。（2）弹性力学的基本假定：连续性、完全弹性、均匀性、各向同性和小变形。平面应力与平面应变；（8分）弹性力学平面问题包括哪两类问题？分别对应哪类弹性体？两类平面问题各有哪些特征？答：弹性力学平面问题包括平面应力问题和平面应变问题两类，两类问题分别对应的弹性体和特征分别为：平面应力问题：所对应的弹性体主要为等厚薄板，其特征是：面力、体力的作用面平行于xy 平面，外力沿板厚均匀分布，只有平面应力分量x σ,y σ,xy τ存在，且仅为x,y 的函数。平面应变问题：所对应的弹性体主要为长截面柱体，其特征为：面力、体力的作用面平行于xy 平面，外力沿z 轴无变化，只有平面应变分量x ε,y ε,xy γ存在，且仅为x,y 的函数。（3）圣维南原理；（提边界条件）如果把物体的一小部分边界上的面力，变换为分布不同但静力等效的面力（主失相同，主矩也相同），那么，近处的应力分布将有显著的改变，但是远处所受到的影响可以忽略不计。（4）轴对称；在空间问题中，如果弹性体的几何形状、约束情况，以及所受的外力作用，都是对称于某一轴（通过该轴的任一平面都是对称面），则所有的应力、变形和位移也就对称于这一轴。这种问题称为空间轴对称问题。

弹性力学简明教程

《弹性力学简明教程》是教育部“十五”国家规划教材。是在第二版的基础上，保持原有的体系和特点，根据教学改革的需要和国家的有关新标准，进行了修订。全书按照由浅入深的原则，安排了平面问题的理论及解答、空间问题的理论及解答和薄板弯曲理论。并着重介绍了弹性力学的数值解法，即差分法、变分法和有限单元法。《弹性力学简明教程》作为弹性力学的入门教材，注重基本理论（基本概念、基本方程和基本解法）的阐述及其应用，以使学生在掌握基本理论的基础上能阅读和应用弹性力学文献，并能初步应用弹性力学的数值解法解决工程实际问题。主要符号表第一章绪论1-1 弹性力学的内容1-2 弹性力学中的几个基本概念1-3 弹性力学中的基本假定习题第二章平面问题的基本理论2-1 平面应力问题与平面应变问题2-2 平衡微分方程2-3 平面问题中一点的应力状态2-4 几何方程刚体位移2-5 物理方程2-6 边界条件2-7 圣维南原理及其应用2-8 按位移求解平面问题2-9 按应力求解平面问题相容方程 2-10 常体力情况下的简化应力函数习题第三章平面问题的直角坐标解答3-1 逆解法与半逆解法多项式解答 .3-2 矩形梁的纯弯曲3-3 位移分量的求出3-4 简支梁受均布荷载3-5 楔形体受重力和液体压力习题

第四章平面问题的极坐标解答4-1 极坐标中的平衡微分方程4-2 极坐标中的几何方程及物理方程4-3 极坐标中的应力函数与相容方程4-4 应力分量的坐标变换式4-5 轴对称应力和相应的位移4-6 圆环或圆筒受均布压力4-7 压力隧洞4-8 圆孔的孔口应力集中4-9 半平面体在边界上受集中力 4-10 半平面体在边界上受分布力习题第五章用差分法和变分法解平面问题5-1 差分公式的推导 5-2 应力函数的差分解5-3 应力函数差分解的实例5-4 弹性体的形变势能和外力势能5-5 位移变分方程5-6 位移变分法5-7 位移变分法的例题习题.. 第六章用有限单元法解平面问题6-1 基本量及基本方程的矩阵表示6-2 有限单元法的概念6-3 单元的位移模式与解答的收敛性6-4 单元的应变列阵和应力列阵6-5 单元的结点力列阵与劲度矩阵6-6 荷载向结点移置单元的结点荷载列阵6-7 结构的整体分析结点平衡方程组6-8 解题的具体步骤单元的划分6-9 计算成果的整理6-10 计算实例6-11 应用变分原理导出有限单元法基本方程习题第七章空间问题的基本理论7-1 平衡微分方程7-2 物体内任一点的应力状态7-3 主应力最大与最小的应力7-4 几何方程及物理方程7-5 轴对称问题的基本方程习题

《弹性力学》试题参考答案

《弹性力学》试题参考答案（答题时间：100分钟）一、填空题（每小题4分） 1．最小势能原理等价于弹性力学基本方程中：平衡微分方程，应力边界条件。 2．一组可能的应力分量应满足：平衡微分方程，相容方程（变形协调条件）。 3．等截面直杆扭转问题中， M dxdy D =?? 2?的物理意义是杆端截面上剪应力对转轴的矩等于杆截面内的扭矩 M 。 4．平面问题的应力函数解法中，Airy 应力函数?在边界上值的物理意义为边界上某一点（基准点）到任一点外力的矩。 5．弹性力学平衡微分方程、几何方程的张量表示为： 0,=+i j ij X σ ，)(2 1,,i j j i ij u u +=ε。二、简述题（每小题6分） 1．试简述力学中的圣维南原理，并说明它在弹性力学分析中的作用。圣维南原理：如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力（主矢与主矩相同），则近处的应力分布将有显著的改变，但远处的应力所受影响可以忽略不计。作用：（1）将次要边界上复杂的面力（集中力、集中力偶等）作分布的面力代替。（2）将次要的位移边界条件转化为应力边界条件处理。 2．图示两楔形体，试分别用直角坐标和极坐标写出其应力函数?的分离变量形式。题二（2）图（a ）???=++= )(),(),(222θθ??f r r cy bxy ax y x （b ）???=+++= )(),(),(3 3223θθ??f r r dy cxy y bx ax y x 3．图示矩形弹性薄板，沿对角线方向作用一对拉力P ，板的几何尺寸如图，材料的弹性模量E 、泊松比 μ 已知。试求薄板面积的改变量S ?。题二（3）图

弹性力学课后习题详解

第一章习题 1-1 试举例证明，什么是均匀的各向异性体，什么是非均匀的各向同性体，什么是非均匀的各向异性体。 1．均匀的各向异性体：如木材或竹材组成的构件。整个物体由一种材料组成，故为均匀的。材料力学性质沿纤维方向和垂直纤维方向不同，故为各向异性的。 2．非均匀的各向同性体：实际研究中，以非均匀各向同性体作为力学研究对象是很少见的，或者说非均匀各向同性体没有多少可讨论的价值，因为讨论各向同性体的前提通常都是均匀性。设想物体非均匀（即点点材性不同），即使各点单独考察都是各向同性的，也因各点的各向同性的材料常数不同而很难加以讨论。实际工程中的确有这种情况。如泌水的水泥块体，密度由上到下逐渐加大，非均匀。但任取一点考察都是各向同性的。再考察素混凝土构件，由石子、砂、水泥均组成。如果忽略颗粒尺寸的影响，则为均匀的，同时也必然是各向同性的。反之，如果构件尺寸较小，粗骨料颗粒尺寸不允许忽略，则为非均匀的，同时在考察某点的各方向材性时也不能忽略粗骨料颗粒尺寸，因此也必然是各向异性体。因此，将混凝土构件作为非均匀各向同性体是很勉强的。 3．非均匀的各向异性体：如钢筋混凝土构件、层状复合材料构件。物体由不同材料组成，故为非均匀。材料力学性质沿纤维方向和垂直纤维方向不同，故为各向异性的。 1-2一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体一般的岩质地基和土质地基能否作为理想弹性体理想弹性体指：连续的、均匀的、各向同性的、完全（线）弹性的物体。一般的混凝土构件（只要颗粒尺寸相对构件尺寸足够小）可在开裂前可作为理想弹性体，但开裂后有明显塑性形式，不能视为理想弹性体。一般的钢筋混凝土构件，属于非均匀的各向异性体，不是理想弹性体。一般的岩质地基，通常有塑性和蠕变性质，有的还有节理、裂隙和断层，一般不能视为理想弹性体。在岩石力学中有专门研究。一般的土质地基，虽然是连续的、均匀的、各向同性的，但通常具有蠕变性质，变形与荷载历史有关，应力-应变关系不符合虎克定律，不能作为理想弹性体。在土力学中有专门研究。 1-3 五个基本假定在建立弹性力学基本方程时有什么用途连续性假定使变量为坐标的连续函数。完全（线）弹性假定使应力应变关系明确为虎克定律。均匀性假定使材料常数各点一样，可取任一点分析。各向同性使材料常数各方向一样，坐标轴方位的任意选取不影响方程的唯一性。小变形假定使几何方程为线性，

弹性力学简明教程(第四版)习题解答

弹性力学简明教程（第四版）习题解答第一章绪论【1-1】试举例说明什么是均匀的各向异性体，什么是非均匀的各向同性体？【分析】均匀的各项异形体就是满足均匀性假定，但不满足各向同性假定；非均匀的各向异性体，就是不满足均匀性假定，但满足各向同性假定。【解答】均匀的各项异形体如：竹材，木材。非均匀的各向同性体如：混凝土。【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体？一般的岩质地基和土质地基能否作为理想弹性体？【分析】能否作为理想弹性体，要判定能否满足四个假定：连续性，完全弹性，均匀性，各向同性假定。【解答】一般的混凝土构件和土质地基可以作为理想弹性体；一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。【1-3】五个基本假定在建立弹性力学基本方程时有什么作用？【解答】（1）连续性假定：假定物体是连续的，也就是假定整个物体的体积都被组成这个物体的介质所填满，不留下任何空隙。引用这一假定后，物体的应力、形变和位移等物理量就可以看成是连续的。因此，建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。完全弹性假定：假定物体是完全弹性的，即物体在对应形变的外力被去除后，能够完全恢复原型而无任何形变。这一假定，还包含形变与引起形变的应力成正比的涵义，亦即两者之间是成线性关系的，即引用这一假定后，应力与形变服从胡克定律，从而使物理方程成为线性的方程，其弹性常数不随应力或形变的大小而变。均匀性假定：假定物体是均匀的，即整个物体是由同一材料组成的，引用这一假定后整个物体的所有各部分才具有相同的弹性，所研究物体的内部各质点的物理性质都是相同的，因而物体的弹性常数不随位置坐标而变化。各向同性假定：假定物体是各向同性的，即物体的弹性在所有各个方向都相同，引用此假定后，物体的弹性常数不随方向而变。小变形假定：假定位移和变形是微小的。亦即，假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸，而且应变和转角都远小于1。这样在建立物体变形以后的平衡方程时，就可以方便的用变形以前的尺寸来代替变形

岩石力学知识点

岩石的结构：岩石中矿物颗粒相互之间的关系，包括颗粒大小，形状，排列结构连接特点及岩石中的微结构面。岩石：由一种或几种矿物按一定的方式结合而成的天然集合体。岩石的结构联结类型：结晶联结、胶结联结碎屑岩胶结类型：基质胶结、接触胶结、孔隙胶结。结晶联结：岩石中矿物颗粒通过结晶相互嵌合在一起。胶结联结：颗粒与颗粒之间通过胶结物在一起的联结。微结构面：是指存在于矿物颗粒内部或矿物颗粒及矿物集合体之间微小的弱面及空隙。解理面：矿物晶体或晶粒受力后沿一定结晶方向分裂成的光滑平面。微裂缝：发育于矿物颗粒内部及颗粒之间的多呈闭合状态的破裂迹线。层理：在垂直方向上岩石成分变化情况。片理：岩石沿平行的平面分裂为薄片的能力。颗粒密度：岩石固体相部分的质量与其体积之比。块状密度：岩石单位体积内的质量。吸水率：岩石试件在大气压条件下自由吸入水的质量与岩样干质量之比。岩石的膨胀性:岩石浸水后体积增大的性质。岩石的软化性:岩石浸水饱和后强度降低的性质。岩石的崩解性：岩石与水相互作用时失去粘结性并变成完全丧失强度的松散物质的性质。体胀系数：温度上升1°所引起的体积增量与其初始体积之比。线胀系数：温度上升1°所引起的长度增量与其初始长度之比。岩石的非均质性：岩石的物理力学性质随空间而变化的一种行为饱和吸水率：岩石在高压或真空条件下吸入水的质量与岩样干质量之比抗冻性：岩石抵抗冻融破坏的能力水理性质：岩石在水溶液作用下表现的物理性质粒度组成：构成砂岩的各种粒组含量，通常以百分数表示岩石的热导率：度量岩石传热导能力的参数圆度：碎屑颗粒表面的光滑程度岩石的变形特征：岩石试件在各种载荷作用下的变形规律，其中包括岩石的弹性变形，塑性变形，粘度流动和破坏规律反映力学属性岩石强度：岩石试件在载荷作用下开始破坏时的最大应力以及应力与破坏之间的关系单轴压缩强度：在单轴压缩载荷作用下所承受的最大压应力岩石的抗压强度：岩石试件在单轴压力下达到破坏的极限值岩石的抗剪强度：岩石抵抗剪切滑动的能力三轴抗压强度：岩石在三向压缩载荷作用下，达到破坏时所承受的最大应力岩石的变形：岩石在任何物理作用因素作用下形状和大小的变化岩石本构关系：岩石应力或应力速度与其应变速率的关系岩石的流变性：是指岩石的应力或应变随时间的变化关系岩石的蠕变：在应力不变的情况下岩石变形随时间增长而增长的现象古地应力：泛指燕山运动以前的地应力，有时也特指某一地质时期以前的地应力原地应力：工程施工开始前存在于岩体中的应力现今地应力：目前存在或正在变化的地应力重力应力：指由于上覆岩层的重力引起的地应力分量，特别指由于上覆岩层的重力所产生的应力扰动应力：是指由于地表或地下加载或解载及开挖等，引起原地应力发生改变所产生的应力

拱桥主要尺寸拟定和拱轴线形选择

第三章拱桥主要尺寸拟定和拱轴线形选择第一节拱桥的总体布置一、确定桥梁的设计标高和矢跨比拱桥的四个主要标高：桥面标高、拱顶底面标高、起拱线标高、基底标高。桥面标高：由两岸线路的纵断面控制，且要保证桥下净空能满足宣泄洪水和通航的要求。拱顶底面标高：由桥面标高减去拱顶填料（包括桥面铺装）厚度和拱圈厚度。起拱线标高：尽量采用低拱脚，但要满足通航净空、排洪、流冰等条件和《桥规》要求。基础底面标高：根据冲刷、基底承载力、冰冻等条件确定。矢跨比的确定：矢跨比的大小与拱脚的水平推力成正比，与拱脚的垂直反力成反比。常用的矢跨比：①圬工拱桥不小于1/8 ②箱形拱不小于1/10 ③钢筋混凝土桁架拱、刚架拱不小于1/12 二、不等跨的处理 1、采用不同的矢跨比 2、采用不同的拱脚标高 3、调整拱上建筑的恒载重量第二节拱轴线形的选择和拱上建筑的布置一、拱轴线形的选择选择拱轴线的原则：尽可能降低由于荷载产生的弯距数值。理想拱轴线：与拱上各种荷载作用下的压力线相吻合。工程上采用的“合理拱轴线”——恒载压力线。圆弧线常用的拱轴线形式抛物线悬链线二、拱上建筑的布置小跨径——实腹式（圆弧线、悬链线）大中跨径——空腹式（悬链线）轻型拱或矢跨比较小的大跨径钢筋混凝土拱——抛物线拱第三节拱圈截面变化规律和截面尺寸的拟定

一、拱圈截面变化规律或在拱脚处：，，则：二、截面尺寸的拟定（一）主拱圈的宽度确定拱圈的宽度取决于桥面净空的宽度。一般均大于，如拱圈的宽度小于，则应验算拱圈的横向稳定性。（二）主拱圈高度的拟定 1、石拱桥 1）中小跨径：

l0——主拱圈净跨径（cm）； d——主拱圈高度（cm）； M——系数，一般取4.5—6，取值随矢跨比的减小而增大； K——荷载系数，对于公路—Ⅰ级为1.0，对于公路—Ⅱ级为1.2。 2、箱形拱、桁架拱和刚架拱桥在确定箱形拱、拱片中距不大于3.0m的桁架拱和刚架拱时，可参考下列经验公式估算拱顶截面主拱圈(肋)的高度：式中：L。——主拱圈净跨径(cm)； a、b——系数，根据主拱圈的构造形式不同分别按表3—3一l采用； K——荷载系数，按表3-3-l采用。 a、b、K系数值

弹性力学简明教程(第四版)-习题解答

【2-9】【解答】图2-17：上（y =0）左(x =0) 右（x =b ） l -1 1 m -1 () x f s () 1g y h ρ+ () 1g y h ρ-+ () y f s 1gh ρ 代入公式（2-15）得 ①在主要边界上x=0，x=b 上精确满足应力边界条件： ()()100(),0;===-+=x xy x x g y h σρτ()()1b b (),0; ===-+=x xy x x g y h σρτ ②在小边界0y =上，能精确满足下列应力边界条件：() () ,0y xy y y gh σρτ===-= ③在小边界2y h =上，能精确满足下列位移边界条件：()()2 2 0,0 ====y h y h u v 这两个位移边界条件可以应用圣维南原理，改用三个积分的应力边界条件来代替，当板厚=1δ时，可求得固定端约束反力分别为： 10,,0s N F F gh b M ρ==-= 由于2y h =为正面，故应力分量与面力分量同号，则有： ()()()22210000 0b y y h b y y h b xy y h dx gh b xdx dx σρστ===?=-???=???=?? ??? ⑵图2-18 ①上下主要边界y=-h/2，y=h/2上，应精确满足公式（2-15） l m x f (s) y f (s) 2h y =- 0 -1 0 q 2 h y = 1 -1q -/2()y y h q σ==-，-/2()0yx y h τ==，/2()0y y h σ==，/21()yx y h q τ==- ②在x =0的小边界上，应用圣维南原理，列出三个积分的应力边界条件：负面上应力

最全面弹性力学基本方程和岩石力学介绍(精华版)

第二章弹性力学的基本原理 §2.1 应力分析 2.1.1 应力与应力张量应力被定义为：用假想截面将物体截开，在截面上一点设 S 的外法 P 的周围取一微元 S , 线为 ν , S 上的力为 T ，如极限存在，则称 T 为 P 点在该截面上的应力矢量。 lim T / S T S 0 (1 ) ( 2) (3 ) 考察三个面为与坐标面平行的截面 (即以 x 1 , x 2 , x 3 三个坐标轴为法线的三个截面 ), T , T , T 分别表示三个截面上的应力矢量。每一个应力矢量又分解为沿三个坐标轴的应力分量，有 (i ) T ij e j (i,j =1,2,3) (2.1) 这里的张量运算形式满足 “求和约定” ，即凡是同一指标字母在乘积中出现两次时， 3 则理解为对所有同类求和，即 ij e j ij e j 应理解为。这样的求和指标 j 称之为假指标或哑指标。由此得到 j 1 九个应力分量表示一点的应力状态，这九个分量组成应力张量： 11 12 13 xx xy xz 或 (2.2) ij 21 22 23 ij yx yy yz 31 32 33 zx zy zz 在本书第一章致第九章，应力分量符号 (正负号 )规定如下：对于正应力，我们规定张应力为正，压应力为负。对于剪应力，如果截面外法向与坐标轴的正方向一致，则沿坐标轴正方向的剪应力为正，反之为负。如果沿截面外法向与坐标轴的正方向相反，则沿坐标轴正方向的剪应力为负。 2.1.2 柯西 (Cauchy)方程记 S 为过 P 点的外法向为 n 的斜截面。外法线 n 的方向可由其方向余弦记为 cos(n , x 1 ), n1 cos(n , x 3 ) 。 cos(n , x 2 ) , 设此斜截面坐标面平行的截面 n3 n2 ABC (即以的面积为 S, 则如图 2.1, 过此点所取的小四面体 OABC 另外三个面为与 x 1 , x 2 , x 3 三个坐标轴为法线的三个截面其面积分别为 ), OBC : S 1 OAC : S 2 OAB : S 3 S S S cos(n , x 1 ) cos(n , x 2 ) cos(n , x 3 ) S S S n1 (2.3) n 2 n3 ( n) 此截面上的应力矢量记为即 T , ( n ) ( n) T T j e j T 。 (2.4) (1) ( 2) , (3) 另外三个面上的应力矢量分别为 T , T 考虑此微元 (四面体 OABC 的平衡，其平衡方程为 1 3 ( n) (1) ( 2 ) ( 3 ) T S T S 1 T S 2 T S 3 f S h 0 (2.5) 1 S 3 其中 f 为作用于此单元上的体力， h 为 O 点至截面 ABC 的垂直距离， h 为此微元的体积。当

(完整)[2018年最新整理]弹性力学简明教程(第四版)-课后习题解答

【3-1】为什么在主要边界（大边界）上必须满足精确的应力边界条件式（2-15），而在小边界上可以应用圣维南原理，用三个积分的应力边界条件（即主矢量、主矩的条件）来代替？如果在主要边界上用三个积分的应力边界条件代替式（2-15），将会发生什么问题？【解答】弹性力学问题属于数学物理方程中的边值问题，而要使边界条件完全得到满足，往往比较困难。这时，圣维南原理可为简化局部边界上的应力边界条件提供很大的方便。将物体一小部分边界上的面力换成分布不同，但静力等效的面力（主矢、主矩均相同），只影响近处的应力分布，对远处的应力影响可以忽略不计。如果在占边界绝大部分的主要边界上用三个积分的应力边界条件来代替精确的应力边界条件（公式2-15），就会影响大部分区域的应力分布，会使问题的解答精度不足。【3-2】如果在某一应力边界问题中，除了一个小边界条件，平衡微分方程和其它的应力边界条件都已满足，试证：在最后的这个小边界上，三个积分的应力边界条件必然是自然满足的，固而可以不必校核。【解答】区域内的每一微小单元均满足平衡条件，应力边界条件实质上是边界上微分体的平衡条件，即外力（面力）与内力（应力）的平衡条件。研究对象整体的外力是满足平衡条件的，其它应力边界条件也都满足，那么在最后的这个次要边界上，三个积分的应力边界条件是自然满足的,因而可以不必校核。【3-3】如果某一应力边界问题中有m 个主要边界和n 个小边界，试问在主要边界和小边界上各应满足什么类型的应力边界条件，各有几个条件？【解答】在m 个主要边界上，每个边界应有2个精确的应力边界条件，公式（2-15），共2m 个；在n 个次要边界上，如果能满足精确应力边界条件，则有2n 个；如果不能满足公式（2-15）的精确应力边界条件，则可以用三个静力等效的积分边界条件来代替2个精确应力边界条件，共3n 个。【3-4】试考察应力函数3 ay Φ=在图3-8所示的矩形板和坐标系中能解决什么问题(体力不计)? 【解答】⑴相容条件: 不论系数a 取何值，应力函数3 ay Φ=总能满足应力函数表示的相容方程，式(2-25). ⑵求应力分量当体力不计时，将应力函数Φ代入公式(2-24)，得 6,0,0x y xy yx ay σσττ==== ⑶考察边界条件上下边界上应力分量均为零，故上下边界上无面力.

弹性理论基础

弹性理论基础产生弹性形变的介质叫弹性介质。（一）各向同性介质和各向异性介质对弹性介质，如果沿不同方向测定的物理性质均相同，称各向同性介质，否则是各向异性介质。（二）均匀介质、层状介质若介质的弹性性质不仅与测定方向无关，而且与坐标位置无关，就称为均匀介质；非均匀介质中，介质的性质表现出成层性，称这种介质为层状介质；其中每一层是均匀介质；不同介质层的分界处称界面（平面或曲面）；两个界面之间的间隔称为该层的厚度。（三）连续介质将速度v是空间连续变化函数的介质定义为连续介质。连续介质是层状介质的一种极限情况。即当层状介质的层数无限增加，每层厚度无限减小，层状介质就过渡为连续介质，如 v=v0 (1+bz)叫线性连续介质。（四）单相介质和双相介质只考虑单一相态的介质称单相介质，由两种相态组成例如一种是固相一种是流相的，称为双相介质。二、弹性模量（一）应力与应变 1.应力：弹性体受力后产生的恢复原来形状的内力称内应力，简称为应力。应力和外力相抗衡，阻止弹性体的形变。对于一个均匀各向同性的弹性圆柱体，设作用于s面上的法向应力为N，若力f在s面上均匀分布，则应力pn定义为 Pn=f/s ，若外力f非均匀分布，则可以取一小面元△S,作用于小面元上的力为△f，则应力定义为（lim(△f/△S)）。因此应力的数学定义为：单位横截面上所产生的内聚力称为内力。根据力的分解定理，可以将力分解成垂直于单元面积的应力—法向应力（正应力）；相切于单元面积的应力—切向应力（剪切应力）。 2.应变：物理定义：弹性体受应力作用，产生的体积和形状的变化称为应变。只发生体积变化而形状不变的应变称正应变；反之，只发生形状变化的应变称切应变。数学定义：弹性理论中，将单位长度所产生的形变称应变。 3.应力与应变的关系：应力与应变成正比关系的物体叫完全弹性体，虎克定律表示了应力与应变之间的线性关系。对于一维弹性体，虎克定律为： F=kx； F: 外力； x: 形变； k: 弹性系数。对于三维弹性体，用广义虎克定律表示应力与应变之间的关系。

弹性力学简明教程_第四章_课后作业题答案

第四章平面问题的极坐标解答【4-8】实心圆盘在r ρ=的周界上受有均布压力q 的作用，试导出其解答。【解答】实心圆盘是轴对称的，可引用轴对称应力解答，教材中的式（4-11），即 2 2(12ln )2(32ln )20A B C A B C ρ?ρ? σρρσρρτ? =+++? ???=-+++?? ?? =?? (a) 首先，在圆盘的周界（r ρ=）上，有边界条件()=r q ρρσ=-，由此得 -q 2 (12ln )2A B C ρσρρ = +++= (b) 其次，在圆盘的圆心，当0ρ→时，式（a ）中ρσ，?σ的第一、第二项均趋于无限大，这是不可能的。按照有限值条件（即，除了应力集中点以外，弹性体上的应力应为有限值。），当=0ρ时，必须有0A B ==。把上述条件代入式（b ）中，得 /2C q =-。所以，得应力的解答为 -q 0ρ?ρ?σστ===。【4-9】半平面体表面受有均布水平力q ，试用应力函数 2(sin 2)ΦρB φC φ=+求解应力分量（图4-15）。【解答】（1）相容条件：将应力函数Φ代入相容方程40?Φ=，显然满足。（2）由Φ求应力分量表达式 =-2sin 222sin 222cos 2B C B C B C ρ?ρ?σ?? σ??τ??+?? =+??=--??

（3）考察边界条件：注意本题有两个?面，即2 π ?=± ，分别为?±面。在?±面上，应力符号以正面正向、负面负向为正。因此，有 2()0,??πσ=±= 得0C =； -q 2 (),ρ??πτ=±= 得2 q B =-。将各系数代入应力分量表达式，得 sin 2sin 2cos 2q q q ρ?ρ?σ?σ?τ? ?=?? =-??=?? 【4-14】设有内半径为r 而外半径为R 的圆筒受内压力q ，试求内半径和外半径的改变量，并求圆筒厚度的改变量。【解答】本题为轴对称问题，只有径向位移而无环向位移。当圆筒只受内压力q 的情况下，取应力分量表达式，教材中式（4-11），注意到B =0。内外的应力边界条件要求 r r ()0,()0;(), ()0 R R q ρ?ρρ?ρρρρρττσσ=======-= 由表达式可见，前两个关于ρ?τ的条件是满足的，而后两个条件要求 r 2 22,20A C q A C R ?+=-??? ?+=??。由上式解得 22 2 ,C () 2() 22 22 qr R qr A R -r R -r =-=。 (a) 把A ，B ，C 值代入轴对称应力状态下对应的位移分离，教材中式（4-12）。 ()()222211cos sin ,(R r )qr R u I K E ρμρμ??ρ?? =-++++??-? ? (b) sin cos 0u H I K ?ρ??=-+=。 (c) 式（c ）中的ρ，?取任何值等式都成立，所以各自由项的系数为零

弹性力学基础知识点复习

固体力学的重要分支，它研究弹性物体在外力和其他外界因素作用下产生的变形和内力，又称弹性理论。它是材料力学、结构力学、塑性力学和某些交叉学科的基础，广泛应用于建筑、机械、化工、航天等工程领域。弹性体是变形体的一种，它的特征为：在外力作用下物体变形，当外力不超过某一限度时，除去外力后物体即恢复原状。绝对弹性体是不存在的。物体在外力除去后的残余变形很小时，一般就把它当作弹性体处理。人类从很早时就已经知道利用物体的弹性性质了，比如古代弓箭就是利用物体弹性的例子。当时人们还是不自觉的运用弹性原理，而人们有系统、定量地研究弹性力学，是从17世纪开始的。弹性力学所依据的基本规律有三个：变形连续规律、应力-应变关系和运动(或平衡)规律，它们有时被称为弹性力学三大基本规律。弹性力学中许多定理、公式和结论等，都可以从三大基本规律推导出来。连续变形规律是指弹性力学在考虑物体的变形时，只考虑经过连续变形后仍为连续的物体，如果物体中本来就有裂纹，则只考虑裂纹不扩展的情况。这里主要使用数学中的几何方程和位移边界条件等方面的知识。

弹性力学所依据的基本规律有三个：变形连续规律、应力-应变关系和运动（或平衡）规律，它们有时被称为弹性力学三大基本规律。弹性力学中许多定理、公式和结论等，都可以从三大基本规律推导出来。 ①变形连续规律弹性力学（和刚体的力学理论不同）考虑到物体的变形，但只限于考虑原来连续、变形后仍为连续的物体，在变形过程中，物体不产生新的不连续面。如果物体中本来就有裂纹，则弹性力学只考虑裂纹不扩展的情况。反映变形连续规律的数学方程有两类：几何方程和位移边界条件。几何方程反映应变和位移的联系，它的力学含义是，应变完全由连续的位移所引起，

2011岩石力学考试试题(含答案)

1、岩体的强度小于岩石的强度主要是由于（）。（ A ）岩体中含有大量的不连续面（ B ）岩体中含有水（ C ）岩体为非均质材料（ D ）岩石的弹性模量比岩体的大 2、岩体的尺寸效应是指（）。（ A ）岩体的力学参数与试件的尺寸没有什么关系（ B ）岩体的力学参数随试件的增大而增大的现象（ C ）岩体的力学参数随试件的增大而减少的现象（ D ）岩体的强度比岩石的小 3 、影响岩体质量的主要因素为（）。（A）岩石类型、埋深（B）岩石类型、含水量、温度（C）岩体的完整性和岩石的强度（D）岩体的完整性、岩石强度、裂隙密度、埋深 4、我国工程岩体分级标准中岩石的坚硬程序确定是按照（）。（A）岩石的饱和单轴抗压强度（B）岩石的抗拉强度（C）岩石的变形模量（D）岩石的粘结力 5、下列形态的结构体中，哪一种具有较好的稳定性？（）（A）锥形（B）菱形（C）楔形（D）方形 6、沉积岩中的沉积间断面属于哪一种类型的结构面？（）（A）原生结构面（B）构造结构面（C）次生结构面 7、岩体的变形和破坏主要发生在（）（A）劈理面（B）解理面（C）结构（D）晶面 8、同一形式的结构体，其稳定性由大到小排列次序正确的是（）（A）柱状>板状>块状（B）块状>板状>柱状（C）块状>柱状>板状（D）板状>块状>柱状 9、不同形式的结构体对岩体稳定性的影响程度由大到小的排列次序为（）（A）聚合型结构体>方形结构体>菱形结构体>锥形结构体（B）锥形结构体>菱形结构体>方形结构体>聚合型结构体（C）聚合型结构体>菱形结构体>文形结构体>锥形结构体（D）聚合型结构体>方形结构体>锥形结构体>菱形结构体 10、岩体结构体是指由不同产状的结构面组合围限起来，将岩体分割成相对的完整坚硬的单无块体，其结构类型的划分取决于（）（A）结构面的性质（B）结构体型式（C）岩石建造的组合（D）三者都应考虑

用弹性力学理论分析合理拱轴线

用弹性力学理论分析合理拱轴线胡文亚1，齐永正2 （1. 中铁四局集团一公司，安徽合肥230041; 2. 合肥工业大学土木建筑工程学院，安徽合肥230009）摘要：本文从弹性力学的角度用极坐标应力函数法求解出了无铰圆拱在径向均布荷载作用下不考虑荷载引起的轴向变形情况的应力及内力弹性解，从而证明了结构力学中拱在径向均布荷载作用下，合理轴线为圆弧，轴力为常数的结论是合理的；文章最后讨论了超静定圆拱在径向均布荷载下考虑轴向变形的弹性计算方法。关键词：应力函数法；圆拱；径向均布荷载；轴向变形；弹性解；合理拱轴线 Analysis of appropriate axis of arches using Mechanical Theory of Elasticity HU Wen-ya1，QI Yong-zheng2 (1. The 1st engineering Co., Ltd of China Tisiju Civil Engineering Group, Hefei 230041, China; 2. School of Civil Engineering, Hefei University of Technology, Hefei 230009, China) Abstract:In the paper, accurate stress and internal force elastic solutions of fixed-supported circular arch carrying a radial-uniform-load are obtained without considering axial deformation effects by stress functional method under the point of view on mechanics of elasticity, which prove that the results in the mechanics of structure that appropriate axis of arches carrying a radial-uniform-load is arc, and axial forces is constant, are accurate and efficient. Finally elastic calculation method of statically indeterminate arches carrying a radial-uniform-load are discussed when axial deformation effects are taken into account. Key words: stress functional method; circular arch; radial-uniform-load; axial deformation; elastic solutions; appropriate axis of arches 0 引言结构力学教材[1]及大量文章[5~6]用结构力学的方法推导了拱在各种荷载作用下的合理轴线的曲线方程。本文仅以求解等截面圆拱受径向均布荷载产生的弹性应力解为例证明结构力学结论的正确性。设以拱的任一截面左边（或右边）所有外力的合力（包括数量、方向和作用点）作出合力多边形，这个合力多边形称为拱的压力线。当拱的压力线与拱的轴线重合时，各截面的弯矩为零，拱处于无弯矩状态，这时各截面只受轴力作用,材料的使用最经济。在固定荷载下，使拱处于无弯矩状态的轴线称为合理拱轴线。结构力学中推导了拱在均匀水压力作用下的合理轴线（即无弯矩状态）为圆弧，此时拱只受常值轴力的作用，本文从结构力学的结论出发，用弹性力学中的应力函数法求解径向均布荷载作用下圆拱的弹性解，从而验证了结构力学结论的正确性。作者简介：胡文亚（1974—），男，安徽安庆人，中铁四局集团一公司，工程师