信号与系统习题问题详解(7-10)

7.22 信号()y t 由两个均为带限的信号1()x t 和2()x t 卷积而成，即

12()()()y t x t x t =* 其中

12()0,1000()0,2000X j X j ωωπωωπ

=>=>

现对()y t 作冲激串采样，以得到

()()()p y t y nT t nT δ+∞

-∞=-∑

请给出()y t 保证能从()p y t 中恢复出来的采样周期T 的围。

解：根据傅立叶变换性质，可得

12()()()Y j X j X j ωωω= 因此，有

当1000ωπ>时，()0Y j ω=

即()y t 的最高频率为1000π，所以()y t 的奈奎施特率为210002000ππ?=，因此最大采样周期3210()2000T s π

π

-=

=，所以当310()T s -<时能保证()y t 从()p y t 中恢复出来。

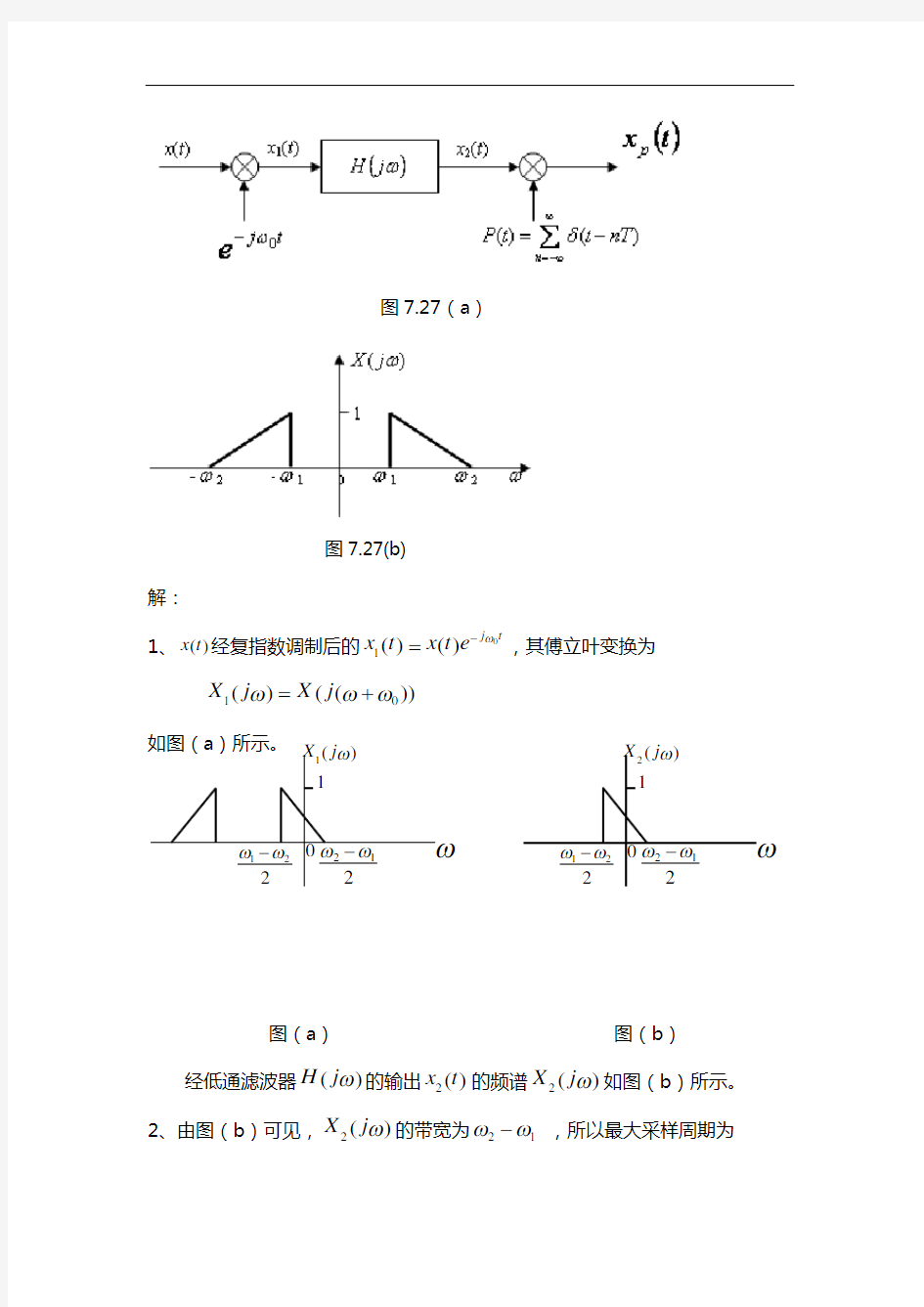
7.27如图7.27（a ）一采样系统，)(t x 是实信号，且其频谱函数为)(ωj X ，如图7.27（b ）。频率0ω选为()2102

1

ωωω+=

，低通滤波器()ωj H 的截至频率为()122

1

ωωω-=

c 。 1. 画出输出()t x 2的频谱()ωj X 2；

2. 确定最大采样周期T ，以使得()t x 可以从()t x p

恢复；

1

()

X j ωω

1

021

2

ωω-122ωω-2()

X j ωω

1

021

2

ωω-122ωω-

图7.27（a ）

图7.27(b) 解：

1、)(t x 经复指数调制后的01()()j t

x t x t e

ω-=，其傅立叶变换为

10()(())X j X j ωωω=+ 如图（a ）所示。

图（a ） 图（b ） 经低通滤波器()H j ω的输出2()x t 的频谱2()X j ω如图（b ）所示。 2、由图（b ）可见，2()X j ω的带宽为21ωω- ，所以最大采样周期为

max 21

2T π

ωω=

-

8.3设()x t 是一实值信号，并有()0X j ω=，2000ωπ>，现进行幅度调制以产生信号()()()sin 2000g t x t t π=，图4-1给出一种解调方法，其中()g t 是输入，()y t 是输出，理想低通滤波器截止频率为2000π，通带增益为2，试确定()y t 。

图4-1

解：()()()()()1

()cos(2000)sin 2000cos(2000)sin 40002

w t g t x t t x t t ππππ===

对 ()w t 进行傅立叶变换 ()()11

()(4000)(4000)44W j X j X j j j ωωπωπ=

--+ 因为()02000, X j ωωπ=>

很明显，()02000, W j ωωπ=≤，所以()w t 通过截止频率为2000π的理想低通滤波器后的输出()0y t =。 9.17

解：系统可以看作是由()1H s 和()2H s 的并联构成

()122

14(2)8

s H s s s =

=++

()cos 2000t π(g t ()

y t

Im

()211

12(1)2

s H s s s =

=++

()()()122

312

1016

s H s H s H s s s +=+=

++ ()2()312

()1016

Y s s H s X s s s +=

=++ 2()(1016)()(312)Y s s s X s s ++=+

求上式反变换，有

2()()()

1016()12()3d y t dy t dx t y t x t dt dt dt

++=+ 9.28考虑一LTI 系统，其系统函数()H s 的零极点图如图9.28所示。 1.指出与该零极点图有关的所有可能的收敛域ROC 。

2.对于1中所标定的每个ROC ，给出有关的系统是否是稳定和/或因果的。

图9.28

解：1. 可能的收敛域ROC 为： （1）Re{}2s <-

（2）2Re{}1s -<<-

)

s （3）1Re{}1s -<< （4）Re{}1s >

2. （1）Re{}2s <-，不稳定和反因果的。 （2）2Re{}1s -<<-，不稳定和非因果的。

（3）1Re{}1s -<<，稳定和非因果的。 （4）Re{}1s >，不稳定和因果的。

9.31有一连续时间LTI 系统，其输入()t x 和输出()y t 由下列微分方程所关联：

22

()()

2()()d y t dy t y t x t dt dt

--= 设()X s 和()Y s 分别是()t x 和()y t 的拉普拉斯变换，()H s 是系统单位冲激响应()h t 的拉普拉斯变换。

1. 求()H s ，画出()H s 的零极点图。

2. 对下列每一种情况求()h t ：

（1）系统是稳定的。（2）系统是因果的。（3）系统既不稳定又不是因果的。 解：

1、对给出的微分方程两边作拉普拉斯变换，得

()()()()22s Y s sY s Y s X s --=

所以得

()2()11()2(2)(1)

Y s H s X s s s s s ===---+ 其零—极点图如图（a ）所示。 图（a ） 2、()2()111111

()2(2)(1)3231

Y s H s X s s s s s s s =

===----+-+

（1）当系统是稳定时，其收敛域为{}12s -

()211

()()33

t t h t e u t e u t -=---

（2）当系统是稳定时，其收敛域为{}2s ?>，所以有

()211

()()33

t t h t e u t e u t -=-

（3）当系统是非因果的和不稳定的时，其收敛域为{}1s ?<-，所以有

()211

()()33t t h t e u t e u t -=--+-

10.18 解：（a ）

()12

1216821139z z H Z z z -----+=-+（此为直接型Ⅱ结构，详见第二章课件分析）

由()12

12

()16821()139

Y Z z z H Z X Z z z -----+==-+得 121221

()(1)()(168)39Y Z z z X Z z z -----+=-+

求上式Z 反变换，得

21

[][1][2][]6[1]8[2]39

y n y n y n x n x n x n -

-+-=--+- （b ）

系统有一个二阶极点1

3

z =

，由于系统是因果的，所以收敛域为 1

3

z >，包括单位圆，故系统是稳定的

10.28已知序列[][][]0.956x

n n n δδ=--

a.求该序列的z 变换()X z 。

b.画出()X z 零极点图。

c.利用考虑极点向量和零点向量沿单位圆横穿一周时的特性，近似画出[]x n 傅里叶变换的模特性。 解： a 、[]x

n 的z 变换为

6

6

60.95

()10.95z X z z z

--=-=，||0z >

b 、由()X z 可知，在0z = 处有一6阶极点， 其零点为

1/63

(0.95)k j k z e

π-= ，0,1,25 k =

其零—极点图如图（a ）所示

图（a ） c 、傅氏变换的幅值近似图如图（b ）所示。

()j X e ω

ω

图（b ）

10.34（P583）有一个因果LTI 系统，其差分方程为

[][][][]121y n y n y n x n =-+-+-

1.求该系统的系统函数，画出()H z 的零极点图，指出收敛域。

2.求系统的单位脉冲响应。

3.判断该系统是不是稳定的？如果是不稳定的，试求一个满足该差分方程的稳定（非因果）单位脉冲响应。 解：

1、1、对所给的差分方程两边进行z 变换，得

121()()()Y z z Y z z Y z X z ---=++

所以得

11212()()()1()()Y z z z H z X z z z z z αα---===----

，1||2

z >

其中，11 1.622α+==

，2

10.622

α-==- 系统函数()H z 的零点为0z = ，极点为1z α= 和2z α= 系统的零极点图如图（a

[]

x n []

y n

图（a ）

2、因为

12()()()

()()22

z

H z z

z α

α=-

-

所以

[]11[][]22n n

h n u n u n ????+-=-

???

???

3、系统是不稳定的，因为系统的收敛域为1||2

z >，不包括单位圆。若要使系

11||2

2

z << 此时有

[]11[1][]22n n

h n u n u n ????

+-=---??????

10.59

图10.59

a.求这个因果滤波器的()H z ，画出零极点图，并指出收敛域。

b.当k 为何值时，该系统是稳定的。

c.如果1k =且对所有的n ，2[]3n

x n ??

= ???

，确定[]y n 。

解：a.由图（1）得

[]

x n []

y n

图（1）

12()()()Y z W z W z =+

1

11()()()3

k W z X z z W z -=-

所以

111()()3k z W z X z -??

+= ???

而

1

21()()4

k W z z W z -=-

得 1

1211()

()4()()()1133k z X z X z Y z W z W z k k z z ---=+=-++ 111()4()()313

k z

Y z k H z z k X z z ---

=

=->+,

（a ） （b ） 图（2）

b ．只有3k <时，收敛域才包含单位圆，系统才能是稳定的。

c. 由于2[]3n

x n ??

= ???

是LTI 系统的特征函数，所以输出

23

2[]()|

3n

z y n H z =

??=? ???

1k =时，代入得

1213112524[]|1312313

n n

z z y n z -=--??

??=?= ? ?????

+