相似中的基本图形反A、蝴蝶型

反A、蝴蝶型训练
一、基本图形解析:
(一)反A型:
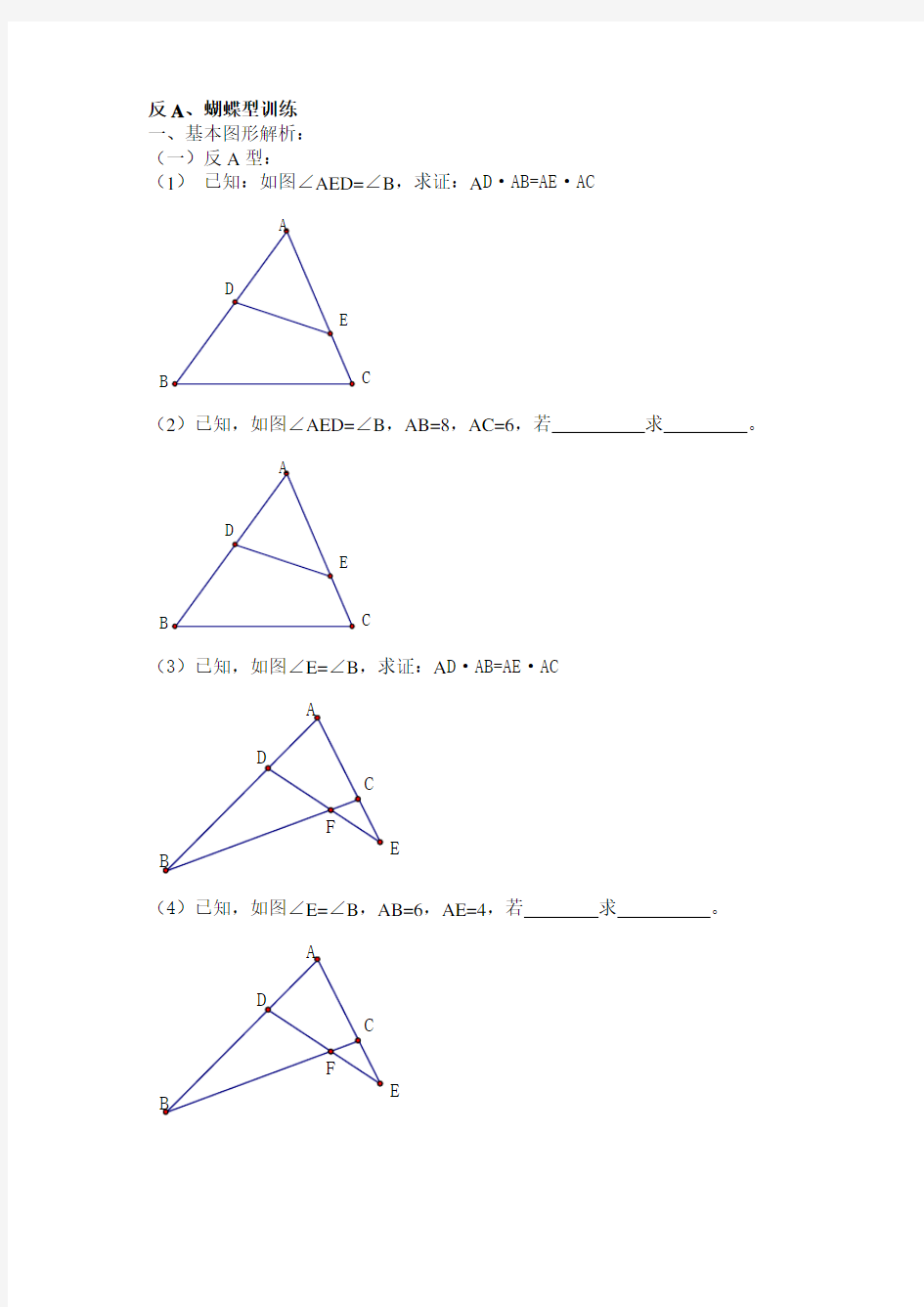
(1)已知:如图∠AED=∠B,求证:A D·AB=AE·AC
B C
(2)已知,如图∠AED=∠B,AB=8,AC=6,若求。
B C
(3)已知,如图∠E=∠B,求证:A D·AB=AE·AC
E
(4)已知,如图∠E=∠B,AB=6,AE=4,若求。
E
(二)蝴蝶型(反8)
(1)已知,如图∠A=∠D,求证:OA·OC=BO·DO
B
(2)已知,如图∠A=∠B,AC=6,BD=8,若求
C
(3)已知,如图∠BAC=∠BDC,求证:∠DAC=∠DBC
C
二、基本图形训练:
1、如图,D、E分别在△ABC的边AB、AC上,若要使△AED∽△ABC,那么只需满足()
A、∠B=∠DAE
B、AD:AB=D E:BC
C、AD:BC=AE:AB
D、AE:AB=AD:AC
C
B
2、如图,点D、E分别在△ABC的边AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为。
3、如图,点D、E分别在△ABC的边AB、AC上的点(DE不平行于BC),当
或或时,△AED∽△ABC。
4、如图,锐角三角形ABC的边AB、AC上高线CE、BF交于点D,图中相似的三角形有对
B C
B
C
5、如图,若∠BEF=∠CDF,则△∽△,△∽△
6、已知AB∥DE,∠AFC=∠E,则图中共有相似三角形()
A.1对B。 2 C、3对D、4对
9题10题11题
7、如图,BE、CD相交于点O,且∠EDO=∠CBO,则图中相似三角形有。
8、如图,若∠B=∠C,则图中的相似三角形有。
12、如图,AD⊥BC于D,CE⊥AB于E交AD于F,图中相似三角形的对数是()A、3 B、4 C、5 D、6
9、如图,直角三角形ABC中,∠C=90,D为AB的中
点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积
为。
10、如图,在三角形ABC中,高BD、CE交于点O,下
列错误的是()
A、C O·CE=CD·CA
B、OE·OC=OD·OB
C、AD·AC=AE·
D、CO·DO=BO·EO
11、如图,在三角形ABC中,AD⊥BC,CE⊥AB
分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4
则CH的长是。
12、如图,∠AOD=900,OA=OB=BC=CD
成立的是()
A、△OAB∽△OCA
B、△OAB∽△ODA
C、△BAC∽△BDA
D、以上结论都不成立
13、矩形ABCD对角线AC、BD交于点O,AB=4,AD=8,
OE⊥BD交AD于E,求DE的长。
14、如图,⊙O的两条弦AB、CD相交于点E,连接AC、BD,证明:A E·BE=CE·DE
15、如图:∠A=∠B,
1)求证:O A·OC=OB·OD;
2)若OD=6,OB=2,AC=7,求OA的长。
16、如图,等边△ABC,点D、E分别在BC、AC
上,且BD=CE,AD与BE相交于点F,
1)试说明△ABD≌△BCE
2)△AEF与△ABE相似吗?说说你的理由。
3)BD2=A D·DF吗?请说明理由。
17、已知,如图,△ABC中,CE⊥AB,BF⊥AC,
求证:△AEF∽△ACB
18、如图,在△ABC中,CD、AE是三角形的两条高1)求证:B D·AB=BE·BC
2)连接DE,求证:DE BE AC AB
19、已知,如图所示,在△ABC中,AB=AC,D为
长线上的点,且AB2=A D·AE,求证:BC平分∠DCE。
20、如图正方形
ABCD中,∠GBH的两边分别与直线AD、CD相交于G、H 两点,且GH=AG+CH
求证:△BEH为等腰直角三角形
21
、CD为Rt△ABC斜边AB上的高,E为CD中点,AE的延长线交BC于F,FG ⊥AB于G,
求证:FG2=C F·
BF
26、如图,直角△ABC,∠C=900,∠BAC=300,BC=6,D为AC边上一点,且AD=2CD,点E从点A出发向终点B运动,∠DEF=300,EF分别交BC、BD于F、M,连接DF 1)当F在BC边上时,求证:BC+CF=BE
2)当F在BC延长线上时,直接写
出BC、CF、BE间的数量关系
3)运动过程中,当CF=3时,求EM
的长。
椭圆中的蝴蝶定理及其应用
2003年北京高考数学卷第18(III)题考查了椭圆内的蝴蝶定理的证明,本文给出了一般圆锥曲线的蝴蝶定理的两种形式,并由它们得到 圆锥曲线的若干性质. 定理1:在圆锥曲线中,过弦AB中点M任作两条弦CD和EF,直线CE与DF 交直线AB于P,Q,则有. 证明:如图1,以M为原点,AB所在的直线为y轴,建立直角坐标系. 设圆锥曲线的方程为(*),设A(0,t),B(0,-t),知t,-t是的两个根,所以. 若CD,EF有一条斜率不存在,则P,Q与A,B重合,结论成立. 若CD,EF斜率都存在,设C(x1,k1x1), D(x2,k1x2),E(x3,k2x3), F(x4,k2x4),P(0,p),Q(0, q),, ,同理, 所以 将代入(*)得,又得 , , 同理 , ,所以,即 .
注:2003年高考 数学北京卷第18 (III)题,就是定理1中取圆锥曲线为椭圆,AB为平行长轴的弦的特殊情形. 定理2:在圆锥曲线中,过弦AB端点的切线交于点M,过M的直线l∥AB,过M任作两条弦CD和EF,直线CE与DF交直线l于P,Q,则有. 证明:如图2,以M为原点,AB所在的直线为y轴,建立直角坐标系. 设圆锥曲线的方程为(*),设A(),B(),则切线MA的方程是,切线MB的方程是 ,得,所以.(下面与定理1的证明相同,略) 特别的,当弦AB垂直圆锥曲线的对称轴时,点M在圆锥曲线的该对称轴上. 性质1:过点M(m,0)做椭圆、双曲线的弦CD,EF是其焦点轴, 则直线CE、DF的连线交点G在直线l:上.特别的,当M为焦点时,l就是准线.当M为准线与焦点轴所在直线的交点时,l就是过焦点的直线. 证明:如图3,过M做直线AB垂直焦点轴所在的直线,直线CE与DF交直线AB于P,Q,则根据定理1,定理2得.
人教版八年级数学上册 第27章 相似专题练习:相似三角形的判定与性质(含答案)
C.∠D=∠AEC D△.ADE∽△CBE c a c c C.AC2=AD·B C D.= 小专题(四)相似三角形的判定与性质 1.(河北中考)如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是(D) ︵︵ A.AE>BE B.AD=BC 1 2 2.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,△ 要使ABC∽△CAD,只要CD 等于(A) b2b2ab a2 A.B.C.D. 3.如图,在四边形ABCD中,AD∥BC,如果添加下列条件,不能使得△ABC∽△DCA成立的是(D) A.∠BAC=∠ADC B.∠B=∠ACD DC AB AC BC 4.(邯郸育华中学月考)如图,在7×12的正方形网格中有一只可爱的小狐狸,算算看画面中由实线组成的相似三角形有(C) A.4对B.3对C.2对D.1对 提示:△ABC∽△FGE△,HIJ∽△HKL. 5.如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B,BC交PD于F,AD 交PC于G,则图中相似三角形有3对. 提示:△BCP∽△PCF△,DAP∽△DPG△,APG∽△BFP.
的延长线于N,则 1 +=1. CD CE, AB-32 6.(河池中考)如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于点M,交AD 1 AM AN 7.(保定高阳章末测试)如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°. (1)求证:△ABD∽△DCE; (2)若BD=3,CE=2,△求ABC的边长. 解:(1)证明:∵△ABC是等边三角形, ∴∠B=∠C=60°. ∴∠BAD+∠ADB=120°. ∵∠ADE=60°, ∴∠ADB+∠EDC=120°. ∴∠DAB=∠EDC. 又∵∠B=∠C=60°, ∴△ABD∽△DCE. (2)∵△ABC是等边三角形, ∴AB=BC. ∴CD=BC-BD=AB-3. ∵△ABD∽△DCE, ∴ AB BD = 即 AB3 =.解得AB=9. 8.(邯郸育华中学月考)如图所示,已知ABCD中,AE∶EB=1∶2. (1)△求AEF△与CDF的周长之比; (2)如果△S AEF =6cm2,求S△CDF.
梯形蝴蝶定理
梯形蝴蝶定理 如上图,在梯形中,存在以下关系: 1.相似图形,面积比等于对应边长比的平方S1:S2=a2/b2 2.S1:S2:S3:S4= a2:b2:ab:ab 3.S3=S4 4.S1×S2=S3×S4(由S1/S3=S4/S2推导出) 5.AO:BO=(S1+S3):(S2+S4) 【例】E是平行四边形ABCD的CD边上的一点,BD、AE相交于点F,已知三角形AFD的面积是6,三角形DEF的面积是4,求四边形BCEF的面积为多少? 【解】如图,由梯形蝴蝶定理可得△BEF面积等于6,而△ABF的面积为6×6÷4=9 因为△BCD面积等于△ABD,所以△BCE面积为9+6-6-4=5 因此所求四边形面积为5+6=11。 蝴蝶定理的证明:
右上角为A,左下角为B S1和S2的的三角形是相似的(AAA)~~~所以面积比=边长比的平方即a2:b2 设梯形高为h,S3+S2=1/2 bh=S4+S2。。。。所以S3=S4 设S3+S1的三角形的AB上的高为h1,可知S3:S1=OB:OA 因为S1和S2的的三角形是相似,S3:S1=OB:OA=b:a 所以S1︰S2︰S3︰S4= a^2︰b^2︰ab︰ab 射影定理 公式: 如图,Rt△ABC中,∠ABC=90°,BD是斜边AC上的高,则有射影定理如下:(1)(BD)^2=AD·DC,(2)(AB)^2=AD·AC ,(3)(BC)^2=CD·CA 。 等积式(4)AB×BC=AC×BD(可用“面积法”来证明) 直角三角形射影定理的证明 射影定理简图(几何画板): (主要是从三角形的相似比推算来的) 证法一 在△BAD与△BCD中,∵∠ABD+∠CBD=90°,且∠CBD+∠C=90°, ∴∠ABD=∠C, 又∵∠BDA=∠BDC=90°
27.1 图形的相似练习题及答案
27.1 图形的相似 一.选择题: 1、下列各组数中,成比例的是( ) A .-7,-5,14,5 B .-6,-8,3,4 C .3,5,9,12 D .2,3,6,12 2、如果x:(x+y)=3:5,那么x:y =( ) A. B. C. D. 3、如图,F 是平行四边形ABCD 对角线BD 上的点,BF ∶FD=1∶3,则BE ∶EC=( ) A 、21 B 、31 C 、32 D 、4 1 4、下列说法中,错误的是( ) (A )两个全等三角形一定是相似形 (B )两个等腰三角形一定相似 (C )两个等边三角形一定相似 (D )两个等腰直角三角形一定相似 5、如图,RtΔABC 中,∠C =90°,D 是AC 边上一点,AB =5,AC =4,若ΔABC ∽ΔBDC , 则CD = . A .2 B .32 C .43 D .9 4 二、填空题 6、已知a =4,b =9,c 是a b 、的比例中项,则c = . 7、如图,要使ΔABC ∽ΔACD ,需补充的条件是 .(只要写出一种) 8、如图,小东设计两个直角,来测量河宽DE ,他量得AD =2m ,BD =3m ,CE =9m ,则河宽DE 为 (第5题) (第7题) 2 3833258
9、一公园占地面积约为8000002m ,若按比例尺1∶2000缩小后,其面积约为 2m . 10、如图,点P 是RtΔABC 斜边AB 上的任意一点(A 、B 两点除外)过点P 作一条直线,使截得的三角形与RtΔABC 相似,这样的直线可以作 条. 三、解答题 11、如图18—95,AB 是斜靠在墙壁上的长梯,梯脚B 距墙80cm ,梯上点D 距墙70cm ,BD 长55cm .求梯子的长.(8分) 12、如图,已知AC ⊥AB ,BD ⊥AB ,AO =78cm ,BO =42cm ,CD =159cm ,求CO 和DO .(8分) (第10题)
相似三角形基本模型及证明
相似三角形基本模型与证明一、基本图形回顾 经典模型
构造相似辅助线——双垂直模型 1.在平面直角坐标系xOy中,点A的坐标为(2,1),正比例函数y=kx的图象与线段OA的夹角是45°,求这个正比例函数的表达式. 2.在△ABC中,AB=,AC=4,BC=2,以AB为边在C点的异侧作△ABD,使△ABD为等腰直角三角形,求线段CD的长. 3.在△ABC中,AC=BC,∠ACB=90°,点M是AC上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB上的P点.求证:MC:NC=AP:PB. 4.如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折B点落在D点的位置,且AD交y轴于点E.那么D点的坐标为 () A. B. C. D.
5.已知,如图,直线y=﹣2x+2与坐标轴交于A、B两点.以AB为短边在第一 象限做一个矩形ABCD,使得矩形的两边之比为1﹕2。 求C、D两点的坐标。 构造相似辅助线——A、X字型 6.如图:△ABC中,D是AB上一点,AD=AC,BC边上的中线AE交CD于F。 求证: 7.四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB。 求证: 8.已知:如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC。求BN:NQ:QM.
9.(1)如图1,点在平行四边形ABCD的对角线BD上,一直线过点P分别交BA,BC的延长线于点Q,S,交于点.求证: (2)如图2,图3,当点在平行四边形ABCD的对角线或的延长线上时,是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图2为例进行证明或说明);
蝴蝶定理的证明及推广
一 蝴蝶定理的证明 (一)运用简单的初中高中几何知识的巧妙证明 蝴蝶定理经常在初中和高中的试卷中出现,于是涌现了很多利用中学简单几何 方法完成蝴蝶定理的方法。 1 带有辅助线的常见蝴蝶定理证明 在蝴蝶定理的证明中有各种奇妙的辅助线,同时诞生了各种美妙的思想,蝴蝶定理在这些辅助线的帮助下,翩翩起舞! 证法1 如图2,作OU AD OV BC ⊥⊥,,则垂足U V ,分别为AD BC 、的中点,且由于 EUO EMO 90∠=∠=? FVO FMO 90∠=∠=? 得M E U O 、、、共圆;M F V O 、、、共圆。 则AUM=EOM MOF MVC ∠∠∠=∠, 又MAD MCB ,U V 、为AD BC 、的中点,从而M U A M V ?? , AUM MVC ∠=∠ 则 EOM MOF ∠=∠,于是ME=MF 。[1] 证法2 过D 作关于直线OM 的对称点D',如图3所示,则 FMD'EMD MD=MD'∠=∠, ○1 联结D'M 交圆O 于C',则C 与C'关于OM 对称,即 PC'CQ =。又 111CFP=QB+PC =QB+CC'+CQ =BC'=BD'C'222 ∠∠()() 故M F B D'、、、四点共圆,即MBF MD'F ∠=∠ 而 M B F E D M ∠=∠ ○2 由○1、○2知,DME D'MF ???,故ME=MF 。 证法3 如图4,设直线DA 与BC 交于点N 。对NEF ?及截线AMB ,NEF ?及截线CMD 分别应用梅涅劳斯定理,有 F M E A N B 1M E A N B F ??=,FM ED NC 1ME DN CF ??= 由上述两式相乘,并注意到
第27章《相似》单元培优检测题(含答案)
第27章《相似》单元培优检测题 一.选择题 1.如图,线段BD,CE相交于点A,DE∥BC.若BC=3,DE=1.5,AD=2,则AB的长为() A.2 B.3 C.4 D.5 2.如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是() A.B.C.D. 3.我国古代数学《九章算术》中,有个“井深几何”问题:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸(1尺=10寸),问井深几何?其意思如图所示,则井深BD的长为() A.12尺B.56尺5寸C.57尺5寸D.62尺5寸 4.如图,以A,B,C为顶点的三角形与以D,E,F为顶点的三角形相似,则这两个三角形的相似比为()
A.2:1 B.3:1 C.4:3 D.3:2 5.如图,线段AB=1,点P1是线段AB的黄金分割点(且AP1<BP1,即P1B2=AP1?AB),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段AP2017的长度是() A.()2017B.()2017C.()2017D.(﹣2)1008 6.如图,在△ABC中,点D,E分别在AB,AC上,若==,DE=3,则BC的值为() A.6 B.8 C.9 D.10 7.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则S △ABE :S △ECF 等于() A.1:2 B.4:1 C.2:1 D.1:4 8.如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作AB的平行线交BC于点F,连接CD,交EF于点K,则下列说法正确的是()
相似三角形的几种基本图形复习
相似三角形的几种基本图形: (1)称为“平行线型”的相似三角形. (2)其中∠1=∠2,则△ADE∽△ABC称为“相交线型”的相似三角形. A B C D A B C D E (3)如图:∠1=∠2,∠B=∠D,则△ADE∽△ABC,称为“旋转型”的相似三角形. (4)一线三等角型
1、矩形ABCD中,把DA沿AF对折,使D与CB边上的点E重合,若 AD=10, AB= 8,则EF=______ 2、如图,在矩形ABCD中,E在AD上,连结BE、EF、BF。已知 AE=4,ED=2,AB=3,若△ABE和△EDF相似,则 DF=__________。 3、如图,在直角梯形ABCD中,AD∥BC,∠B=900,AD=3, BC=6,点P在AB上滑动。若△DAP与△PBC相似,且 AP=4.5 ,求PB的长。
4、如图,在△ABC中,∠C=90°,BC=8,AC=6.点P从点B出发,沿着BC 方向点C以2cm/s的速度移动;点Q从点C出发,沿着CA向点A以1cm/s的速度移动。如果P、Q分别从B、C同时出发,问:经过多少秒时以C、P、Q为顶点的三角形恰好与△ABC相似?
5、如图,菱形ABCD的边长为24厘米,∠A=60°,点P从点A出发沿线路AB→BD作匀速运动,点Q从点D同时出发沿线路DC→CB→BA作匀速运动. (1)求BD的长; (2)已知点P、Q运动的速度分别为4厘米/秒,5厘米/秒,经过12秒后,P、Q分别到达M、N两点,若按角的大小进行分类,请你确定 △AMN是哪一类三角形,并说明理由; (3)设(2)中的点P、Q分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改变为a厘米/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与(2)中的△AMN相似,试求a的值. 如图, □ABCD中, G是AB延长线上一点, DG交AC A B F C D E G
蝴蝶定理的证明
图 5 蝴蝶定理的证明 定理:设M 为圆内弦PQ 的中点,过M 作弦AB 和CD 。设AD 和BC 各相交PQ 于点E 和F ,则M 是EF 的中点。 在蝴蝶定理的证明中有各种奇妙的辅助线,同时诞生了各种美妙的思想,蝴蝶定理在这些辅助线的帮助下,翩翩起舞! 证法1 如图2,作OU AD OV BC ⊥⊥,,则垂足U V ,分别为AD BC 、的中点,且由于 EUO EMO 90∠=∠=? FVO FMO 90∠=∠=? 得M E U O 、、、共圆;M F V O 、、、共圆。 则AUM=EOM MOF MVC ∠∠∠=∠, 又MAD MCB ,U V 、为AD BC 、的中点,从而MUA MVC ??,AUM MVC ∠=∠ 则 EOM MOF ∠=∠,于是ME=MF 。 证法2 过D 作关于直线OM 的对称点D',如图3所示,则 FMD'EMD MD=MD'∠=∠, ○ 1 联结D'M 交圆O 于C',则C 与C'关于OM 对称,即 PC'CQ =。又 111CFP=QB+PC =QB+CC'+CQ =BC'=BD'C'222 ∠∠()() 故M F B D'、、、四点共圆,即MBF MD'F ∠=∠ 而 MBF EDM ∠=∠ ○2 由○1、○2知,DME D'MF ???,故ME=MF 。 证法 3 如图4,设直线DA 与BC 交于点N 。对NEF ?及截线AMB ,NEF ?及截线CMD 分别应用梅涅劳斯定理,有 FM EA NB 1ME AN BF ??=,FM ED NC 1ME DN CF ??= 由上述两式相乘,并注意到 NA ND NC NB ?=? 得 2 2 FM AN ND BF CF BF CF ME AE ED BN CN AE ED ?=???=? ()()()()2 2 22 PM MF MQ MF PM MF PM ME MQ+ME PM ME -= =-+-- 化简上式后得ME=MF 。 [2] 2 不使用辅助线的证明方法 单纯的利用三角函数也可以完成蝴蝶定理的证明。 证法 4 (Steven 给出)如图5,并令 图 2 图 3 图 4
人教版九年级数学下册27章相似教案
第二十七章相似教案 总第11课时 执教人(备课人):虞福中 课题:27.1图形的相似 一、教学目标 1.通过实例知道相似图形的意义. 2.经历观察、猜想和分析过程,知道相似多边形对应角相等,对应边的比相等,反之亦然. 二、教学重点和难点 1.重点:相似图形和相似多边形的意义. 2.难点:探索相似多边形对应角相等,对应边的比相等. 三、教学过程 (一)创设情境,导入新课 师:(出示两张全等的图片)大家看这两个图形,(稍停)这两个图形形状相同,大小也相同,它们叫什么图形? 生:(齐答)叫全等图形. 师:(出示两张相似的图片)大家看这两个图形,(稍停)这两个图形只是形状相同,它们叫什么图形?(稍停)它们叫相似图形.也可以说,这两个图形相似(板书:相似). 师:和全等一样,相似也是两个图形的一种关系.从今天开始我们要学习新的一章,这一章要学的内容就是相似(在“相似”前板书:第二十七章).
(二)尝试指导,讲授新课 师:相似图形在我们的生活中是很常见的,大家把课本翻到第34页,(稍停)34页上有几个图,左上方是用同一张底片洗出的不同尺寸的照片,它们是相似图形;还有大小不同的两个足球,它们也是相似图形;还有一辆汽车和它的模型,它们也是相似图形. 师:看了这些相似图形,哪位同学能给相似图形下一个定义?生:……(让几名同学回答) (师出示下面的板书) 形状相同的两个图形叫做相似图形. 师:请大家一起把相似图形的概念读两遍.(生读) 师:(出示两张全等的图片)全等图形,它们不仅形状相同,而且大小也相同;(出示两张相似的图片)而相似图形,它们只是形状相同,它们的大小可能相同,也可能不相同. 师:明确了相似图形的概念,下面请同学们来举几个相似图形的例子,谁先来说? 生:……(让几位同学说,如果学生说的题材不够广泛,师可以再举几个例子.譬如,放电影时,屏幕上的画面及胶片上的图形是相似图形;实际的建筑物及它的模型是相似图形;复印机把一个图形放大,放大后的图形和原来图形是相似图形) 师:好了,下面请大家做一个练习. (三)试探练习,回授调节 1.下列各组图形哪些是相似图形?
相似三角形知识点梳理
相似三角形知识点大总结 知识点1 有关相似形的概念 (1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形. (2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形.相似多边形对应边长度的比叫做相似比(相似系数). 知识点2 比例线段的相关概念 (1)如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是 n m b a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。 (2)在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称 比例线段. 注:①比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:a d c b =. ②()a c a b c d b d ==在比例式 ::中, a 、d 叫比例外项, b 、 c 叫比例内项, a 、c 叫比例前项,b 、 d 叫比例后项,d 叫第四比例项,如果b=c ,即 a b b d =::那么b 叫做a 、d 的比例中项, 此时有2 b ad =。 (3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =?,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点, (4)其中AB AC 215-=≈0.618AB .即AC BC AB AC == 简记为:1 2 长短==全长 注:黄金三角形:顶角是360 的等腰三角形。黄金矩形:宽与长的比等于黄金数的矩形 知识点3 比例的性质(注意性质立的条件:分母不能为0) (1) 基本性质: ①bc ad d c b a =?=::;②2 ::a b b c b a c =?=?. 注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除 了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=. (2) 更比性质(交换比例的内项或外项): ()() ()a b c d a c d c b d b a d b c a ?=?? ?=?=?? ?=??, 交换内项,交换外项. 同时交换内外项 (3)反比性质(把比的前项、后项交换): a c b d b d a c =?=. (4)合、分比性质:a c a b c d b d b d ±±=?=. 注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间
蝴蝶定理
一、蝴蝶定理的发展历程简介:。 蝴蝶定理最先是作为一个征求证明的问题,刊载于1815年的一份通俗杂志《男士日记》上。由于其几何图形形象奇特、貌似蝴蝶,便以此命名,定理内容:圆O中的弦PQ的中点M,过点M任作两弦AB,CD,弦AD与BC分别交PQ于X,Y,则M为XY之中点。 如图,过圆中弦AB的中点作M引任意两弦CD和EF,连结CF和ED,分别交AB于P、Q,则PM=QM 由于此图形似只蝴蝶飞舞,故此定理因此而得名:蝴蝶定理。此定理早在1815年在英国杂志《男士日记》上见刊,征求证明,有意思的是,迟到1972年以前,人们的证明都并非初等,且十分繁琐。然近些年来,证明者不乏其人,使得这只翩翩起舞的蝴蝶栖止不定,变化多端。笔者结合自己的证明和收集别人的研究,整理证法十种,以飨读者。 证法1 (证∠POM=∠QOM) 作CF、DE的弦心距OG、OH,连OM,则OM⊥AB且OGPM四点共圆。 ∴∠POM=∠PGM…①。同理,∠QOM=∠QHM…② ∵△MFC∽MDE,∴MF﹕FC=MD﹕DE ∴MF﹕2FG=MD﹕2DH,∴MF﹕FG=MD﹕DH ∠F=∠D ∴△MFG∽△MDH,∴∠MGF=∠MHD…③
由①②③得:∠POM=∠QOM ∴PM=QM 证法2 (作△PMD′≌△QM D) 作C关于直线OM的对称点C'连C'M交⊙O于D',则AC弧=BC'弧,MD'=MD,∠PMD'=∠QMD ∠CPM=0.5AF弧+0.5BC'C弧=0.5AF弧+0.5AC弧+0.5CC'弧=0.5FCC'弧=∠FD'M 从而PFD’M四点共圆。 ∴∠PD’M=∠PFM=∠D ∴在△PD’M与△QDM中 ∠PD’M=∠D MD’=MD ∠PMD’=∠QMD ∴△PMD’≌△QMD ∴PM=QM 证法3 (利用梅氏定理) 延长CF、ED相交于G点。
第27章相似测试题
百度文库 1 第27章《相似》单元测试题 一、选择题(每小题 3分, 共 30分) 1、如图, 已知 AB // CD // EF , 那么下列结论正确的是( ) AD BC BC DF A . DF = CE B . CE =AD CD BC CD AD C . EF —BE D . EF —AF 2、已知△ ABC DEF , 且AB : DE=1 : 2,则厶ABC 的面积 与厶DEF 的面积之比为( (A )1 : 2 (B )1 : 4 3、如图,小正方形的边长均为 ) (C )2 : 1 (D )4 : 1 1,则下列图中的三角形(阴影部分) △ ABC 相似的是 ( A , B 两个顶点在x 轴的上方,点 4、如图,△ ABC 中, 的下方作厶ABC 的位似图形,并把△ ABC 的边长放大到原来的 B 的横坐标是 1 a 2 1 应点 C . a 1) a ,则点B 的横坐标是( 1 B . —(a 1) 2 1 D . (a 3) 2 C . C 的坐标是(-1,0).以点C 为位似中心,在 2倍,记所得的像是厶 A'B'C .设点B x 轴 的对 如图,在长为 8 cm 、宽为4 cm 的矩形中,截去 使得留下的矩形 的面积是( 2 A . 2 cm 6、 如图,菱形 5、 个矩形, (图中阴影部分)与原矩形相似,则留下矩形 ) B . 4 cm 2 C . ABC D 中,对角线 2 2 8 cm D . 16 cm MN ,则下列叙述正确的是( A . △ AOM 和厶AON 都是等边三角形 B .四边形MBON 和四边形 C .四边形 AMON 与四边形 D .四边形MBCO 和四边形 7、 如图,在Rt A ABC 中, AC 、BD 相交于点 O , M 、N 分别是边 AB 、AD 的中点,连接 OM 、 ) MODN 都是菱形 ABCD 是位似图形 NDCO 都是等腰梯形 ACB 90° BC 3, AC 4, B O C ON 、 AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( 3 7 25 A . B . C .— 2 6 6 D . 2 D A 8、 美是一种感觉,当人体下半身长与身高的比值越接近时,越给人一种美感. 下半身长x 与身高I 的比值是,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( A . 4cm B . 6cm C . 8cm D . 10cm AO 9、 如图正 方形ABCD 中,E 为AB 的中点,AF 丄DE 于点O ,则DO 等于( 2 5 A .〒 如图,某女士身高 165cm ,
相似三角形经典的基本图形及练习题
D A B C 相似中的基本图形练习 相似三角形是初中数学中重要的内容,应用广泛,可以证明线段的比例式;也可证明线段相等、平行、垂直等;还可计算线段的长、比值,图形面积及比值。 而识别(或构造)A 字型、X 字型、母子相似型、旋转型等基本图形是解证题的关键。 1.A 字型及变形 △ABC 中 , AD=2,BD=3,AE=1 (1)如图1,若DE ∥BC , 求CE 的长 (2)如图2,若∠ADE=∠ACB , 求CE 的长 2. X 字型及变形 (1)如图1,AB ∥CD ,求证:AO :DO=BO :CO (2)如图2,若∠A=∠C ,求证:AO ×DO=BO ×CO 3. 母子相似型及变形 (1)如右图,在△ABC 中, AD 把△ABC 分成两个三角形△BCD 和△CAD ,当∠ACD =∠B 时,说明△CAD 与△ABC 相似。 说明:由于小三角形寓于大三角形中,恰似子依母怀,故被称为“母子三角形” (2)如图, Rt △ABC 中 ,CD ⊥AB, 求证:AC 2=ADxAB,CD 2=ADxBD, 4. 旋转型 如图,若∠ADE=∠B ,∠BAD=∠CAE ,说明△ADE 与△ABC 相似 A D B
练习题 1、如图1,在△ABC 中,中线BE 、CD 相交于点G ,则BC DE = ;S △GED :S △GBC = ; 2、如图2,在△ABC 中, ∠B=∠AED ,AB=5,AD=3,CE=6,则AE= ; 3、如图3,△ABC 中,M 是AB 的中点,N 在BC 上,BC=2AB ,∠BMN=∠C ,则△ ∽△ ,相似比为 , NC BN = ; 4、如图4,在梯形ABCD 中,AD ∥BC ,S △ADE :S △BCE =4:9,则S △ABD :S △ABC = ; 5、如图5,在△ABC 中,BC=12cm ,点D 、F 是AB 的三等分点,点E 、G 是AC 的三等分点,则DE+FG+BC= ; 二、选择题 6、如图,在△ABC 中,高BD 、CE 交于点O ,下列结论错误的是( ) A 、CO ·CE=CD ·CA B 、OE ·OC=OD ·OB C 、AD ·AC=AE ·AB D 、CO ·DO=BO ·EO 7、如图,D 、E 分别是△ABC 的边AB 、AC 上的点, AD BD =CE AE =3, 且∠AED=∠B ,则△AED 与△ABC 的面积比是( ) A 、1:2 B 、1:3 C 、1:4 D 、4:9 8、已知,如图, 在△ABC 中,DE ∥BC ,AD=5,BD=3,求S △ADE :S △ABC 的值。 9、如图,已知在△ABC 中,CD=CE ,∠A=∠ECB ,试说明CD 2 =AD ·BE 。 A B C D E G 图1 A B C D E 图2 A B C M 图3 A B C D E 图4 A B C D F 图5 G E A E C D O A B C D E C A B D E A B C D E
(完整word版)蝴蝶定理的八种证明及三种推广
蝴蝶定理的证明 定理:设M 为圆内弦PQ 的中点,过M 作弦AB 和CD 。设AD 和BC 各相交PQ 于点E 和F ,则M 是EF 的中点。 在蝴蝶定理的证明中有各种奇妙的辅助线,同时诞生了各种美妙的思想,蝴蝶定理在这些辅助线的帮助下,翩翩起舞! 证法1 如图2,作OU AD OV BC ⊥⊥,,则垂足U V ,分别为AD BC 、的中点,且由于 EUO EMO 90∠=∠=? FVO FMO 90∠=∠=? 得M E U O 、、、共圆;M F V O 、、、共圆。 则AUM=EOM MOF MVC ∠∠∠=∠, 又MAD MCB ,U V 、为AD BC 、的中点,从而MUA MVC ??,AUM MVC ∠=∠ 则 EOM MOF ∠=∠,于是ME=MF 。 证法2 过D 作关于直线OM 的对称点D',如图3所示,则 FMD'EMD MD=MD'∠=∠, ○ 1 联结D'M 交圆O 于C',则C 与C'关于OM 对称,即 PC'CQ =。又 111CFP=QB+PC =QB+CC'+CQ =BC'=BD'C'222 ∠∠()() 故M F B D'、、、四点共圆,即MBF MD'F ∠=∠ 而 MBF EDM ∠=∠ ○2 由○1、○2知,DME D'MF ???,故ME=MF 。 证法 3 如图4,设直线DA 与BC 交于点N 。对NEF ?及截线AMB ,NEF ?及截线CMD 分别应用梅涅劳斯定理,有 FM EA NB 1ME AN BF ??=,FM ED NC 1ME DN CF ??= 由上述两式相乘,并注意到 NA ND NC NB ?=? 得 2 2 FM AN ND BF CF BF CF ME AE ED BN CN AE ED ?=???=? ()()()()2 2 22 PM MF MQ MF PM MF PM ME MQ+ME PM ME -= =-+-- 化简上式后得ME=MF 。[2] 2 不使用辅助线的证明方法 单纯的利用三角函数也可以完成蝴蝶定理的证明。 图 2 图 3 图 4
(完整版)人教版第27章相似三角形知识点总结
第27章相似三角形知识点 知识点1 有关相似形的概念 1、形状相同的图形叫相似图形, 2、如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形. 3、相似多边形对应边长度的比叫做相似比(相似系数). 知识点2 比例线段的相关概念 (1)在求线段比时,线段单位要统一。 (2)在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段, 简称比例线段 知识点3 比例的性质(注意性质里的条件:分母不能为0) bc ad d c b a =?=::; a c a b c d b d b d ±±= ?= 知识点4 比例线段的有关定理 1、平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例 已知AD ∥BE ∥CF, 可得 AB DE AB DE BC EF BC EF AB BC BC EF AC DF AB DE AC DF DE EF ===== 或或或或等. 知识点5 相似三角形的概念 对应角相等,对应边成比例的三角形,叫做相似三角形. 相似三角形对应边的比叫做相似比(或相似系数). 相似三角形对应角相等,对应边成比例. 知识点6 三角形相似的判定方法 1、平行法: 平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 2、只看角法(AA ): 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似. 简述为:两角对应相等,两三角形相似. 3、只看边法 (SSS):如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似. (HL)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似. 4、边角组合法(SAS): 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. 简述为:两边对应成比例且夹角相等,两三角形相似 B
初中数学《相似三角形》优秀教案
相似三角形 一、知识概述 (一)相似三角形 1、对应角相等,对应边成比例的两个三角形,叫做相似三角形. 温馨提示: ①当且仅当一个三角形的三个角与另一个(或几个)三角形的三个角对应相等,且三条对应边的比相等时,这两个(或几个)三角形叫做相似三角形,即定义中的两个条件,缺一不可; ②相似三角形的特征:形状一样,但大小不一定相等; ③相似三角形的定义,可得相似三角形的基本性质:对应角相等,对应边成比例,其应用广泛. 2、相似三角形对应边的比叫做相似比. 温馨提示: ①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例. ②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽△ABC的相似比,当且仅当它们全等时,才有k=k′=1. ③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出. 3、如果两个边数相同的多边形的对应角相等,对应边成比例,那么这两个多边形叫做相似多边形. 4、相似三角形的预备定理:如果一条直线平行于三角形的一条边,且这条直线与原三角形的两条边(或其延长线)分别相交,那么所构成的三角形与原三角形相似.
①定理的基本图形有三种情况,如图其符号语言: ∵DE∥BC,∴△ABC∽△ADE; ②这个定理是用相似三角形定义推导出来的三角形相似的判定定理.它不但本身有着广泛的应用,同时也是证明下节相似三角形三个判定定理的基础,故把它称为“预备定理”; ③有了预备定理后,在解题时不但要想到上一节“见平行,想比例”,还要想到“见平行,想相似”. (二)相似三角形的判定 1、相似三角形的判定: 判定定理(1):两角对应相等,两三角形相似. 判定定理(2):两边对应成比例且夹角相等,两三角形相似. 判定定理(3):三边对应成比例,两三角形相似. 温馨提示: ①有平行线时,用上节学习的预备定理; ②已有一对对应角相等(包括隐含的公共角或对顶角)时,可考虑利用判定定理(1)或判定定理(2); ③已有两边对应成比例时,可考虑利用判定定理2或判定定理3.但是,在选择利用判定定理2时,一对对应角相等必须是成比例两边的夹角对应相等. 2、直角三角形相似的判定:斜边和一条直角边对应成比例,两直角三角形相似.
蝴蝶定理的证明及推广
摘要 蝴蝶定理想象洵美,蕴理深刻,近两百年来,关于蝴蝶定理的研究成果不断,引起了许多中外数学家的兴趣。到目前为止,关于蝴蝶定理的证明就有60多种,其中初等证法就有综合证法、面积证法、三角证法、解析证法等。而基于蝴蝶定理的推广与演变,能得到很多有趣与漂亮的结果。 关键词:蝴蝶定理;证明;推广; 一摘要 [1]作者简介:陈富,祖籍江苏泰州,现就读于湖南工业大学机械工程学院机械系。 [2]指导老师简介:刘东南,祖籍湖南邵阳,现任湖南工业大学讲师。
在20世纪20年代时,蝴蝶定理作为一道几何题传到我国中学数学界,严济慈教授在《几何证题法》中有构思奇巧的证明。 如可将蝴蝶定理中的圆“压缩变换”为椭圆,甚至变为双曲线、抛物线、筝形、凸四边形、两直线,都依然成立。另外,如果将蝴蝶定理中的条件一般化,即M 点不再是中点,能得到坎迪定理、若M 、N 点是AB 的三等分点,两次应用坎迪定理,能得到“三翅蝴蝶定理”。 二 蝴蝶定理的证明 (一)运用简单的初中高中几何知识的巧妙证明 蝴蝶定理经常在初中和高中的试卷中出现,于是涌现了很多利用中学简单几何 方法完成蝴蝶定理的方法。 1 带有辅助线的常见蝴蝶定理证明 在蝴蝶定理的证明中有各种奇妙的辅助线,同时诞生了各种美妙的思想,蝴蝶定理在这些辅助线的帮助下,翩翩起舞! 证法1 如图2,作OU AD OV BC ⊥⊥,,则垂足U V ,分别为AD BC 、的中点,且由于 EUO EMO 90∠=∠=? FVO FMO 90∠=∠=? 得M E U O 、、、共圆;M F V O 、、、共圆。 则AUM=EOM MOF MVC ∠∠∠=∠, 又MAD MCB ,U V 、为AD BC 、的中点,从而MUA MVC ?? ,AUM MVC ∠=∠ 则 EOM MOF ∠=∠,于是ME=MF 。[1] 证法2 过D 作关于直线OM 的对称点D',如图3所示,则 FMD'EMD MD=MD'∠=∠, ○1 联结D'M 交圆O 于C',则C 与C'关于OM 对称,即 PC'CQ =。又 111CFP=QB+PC =QB+CC'+CQ =BC'=BD'C'222 ∠∠()() 故M F B D'、、、四点共圆,即MBF MD'F ∠=∠ 而 M B F E D M ∠=∠ ○2 图 2 图 3
27章相似知识点总结
第27章相似形(要求深刻理解、熟练运用)
1.三角形中,作平行线构造相似形和已知中点构造中位线是常用辅助线. 2.相似形有传递性;即:∵Δ1∽Δ2Δ2∽Δ3∴Δ1∽Δ3 四、位似 1、位似图形:如果两个多边形不仅相似,而且对应顶点的连线相交于一点,且每组对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比. 2、掌握位似图形概念,需注意:①位似是一种具有位置关系的相似,所以两个图形是位似图形,必定是相似图形,而相似图形不一定是位似图形;②两个位似图形的位似中心只有一个;③两个位似图形可能位于位似中心的两侧,也可能位于位似中心的同一侧;④位似比就是相似比.利用位似图形的定义可判断两个图形是否位似. 3、位似图形首先是相似图形,所以它具有相似图形的一切性质.位似图形是一种特殊的相似图形,它又具有特殊的性质,位似图形上任意一对对应点到位似中心的距离等于位似比(相似比). 4、利用位似,可以将一个图形放大或缩小.作图时要注意:①首先确定位似中心,位似中心的位置可随意选择; ②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;④符合要求的图形不惟一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形.
第29章投影和视图知识点总结 知识点一:三视图 1.三种视图的内在联系 主视图反映物体的_________;俯视图反映物体的________;左视图反映物体的 _____ __.因此,在画三种视图时,主、俯视图要长对______,主、左视图要高_____ __,俯、左视图要_______. 2.三种视图的位置关系 一般地,首先确定主视图的位置,画出主视图,然后在主视图的______画出俯视图,在主视图的________画出左视图. 3.三种视图的画法 首先观察物体,画出视图的外轮廓线,然后将视图补充完整,其中看得见部分的轮廓线通常画成______线,看不见部分的轮廓线通常画成_______线. 知识点二:平行投影和中心投影 1.太阳光与影子 太阳光线可以看成平行光线,像这样的光线所形成的投影称为______ ___. 物体在太阳光照射的不同时刻,不仅影子的长短在_______,而且影子的方向也在改变.根据不同时刻影长的变换规律,以及太阳东____西______的自然规律,可以判断时间的先后顺序. 分别过每个物体的顶端及其影子的顶端作一条直线,若两直线______,则为平行投影;若两直线_______,则为中心投影,其交点就是光源的位置. 灯光的光线可以看成是从_______发出的(即为点光源),像这样的光线所形成的投影称为中心投影. 中心投影光源的确定:分别过每个物体的顶端及其影子的顶端作一条直线,这两条直线的___________即为光源的位置. 知识点三.视点与盲区 盲区即为视觉看_______的区域.
人教版九年级数学下《第27章相似》专项训练含答案
第27章相似专项训练 专训1证比例式或等积式的技巧 名师点金: 证比例式或等积式,若所遇问题中无平行线或相似三角形,则需构造平行线或相似三角形,得到成比例线段;若比例式或等积式中的线段分布在两个三角形或不在两个三角形中,可尝试证这两个三角形相似或先将它们转化到两个三角形中再证两三角形相似,若在两个明显不相似的三角形中,可运用中间比代换.构造平行线法 1.如图,在△ABC中,D为AB的中点,DF交AC于点E,交BC的延长线于点F, 求证:AE·CF=BF·EC. (第1题) 2.如图,已知△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD =CE,DE交AC于点F, 试证明:AB·DF=BC·EF. (第2题) 三点找三角形相似法 3.如图,在?ABCD中,E是AB延长线上的一点,DE交BC于F. 求证:DC AE = CF AD . (第3题) 4.如图,在△ABC中,∠BAC=90°,M为BC的中点,DM⊥BC交CA的延长线于D,交AB于E. 求证:AM2=MD·ME.
(第4题) 构造相似三角形法 5.如图,在等边三角形ABC中,点P是BC边上任意一点,AP的垂直平分线分别交AB,AC于点M,N. 求证:BP·CP=BM·CN. (第5题) 等比过渡法 6.如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE. 求证:(1)△DEF∽△BDE; (2)DG·DF=DB·EF. (第6题) 7.如图,CE是Rt△ABC斜边上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP于点G,交CE于点D. 求证:CE2=DE·PE. (第7题) 两次相似法 8.如图,在Rt△ABC中,AD是斜边BC上的高,∠ABC的平分线BE交AC
