初中数学经典四边形习题50道
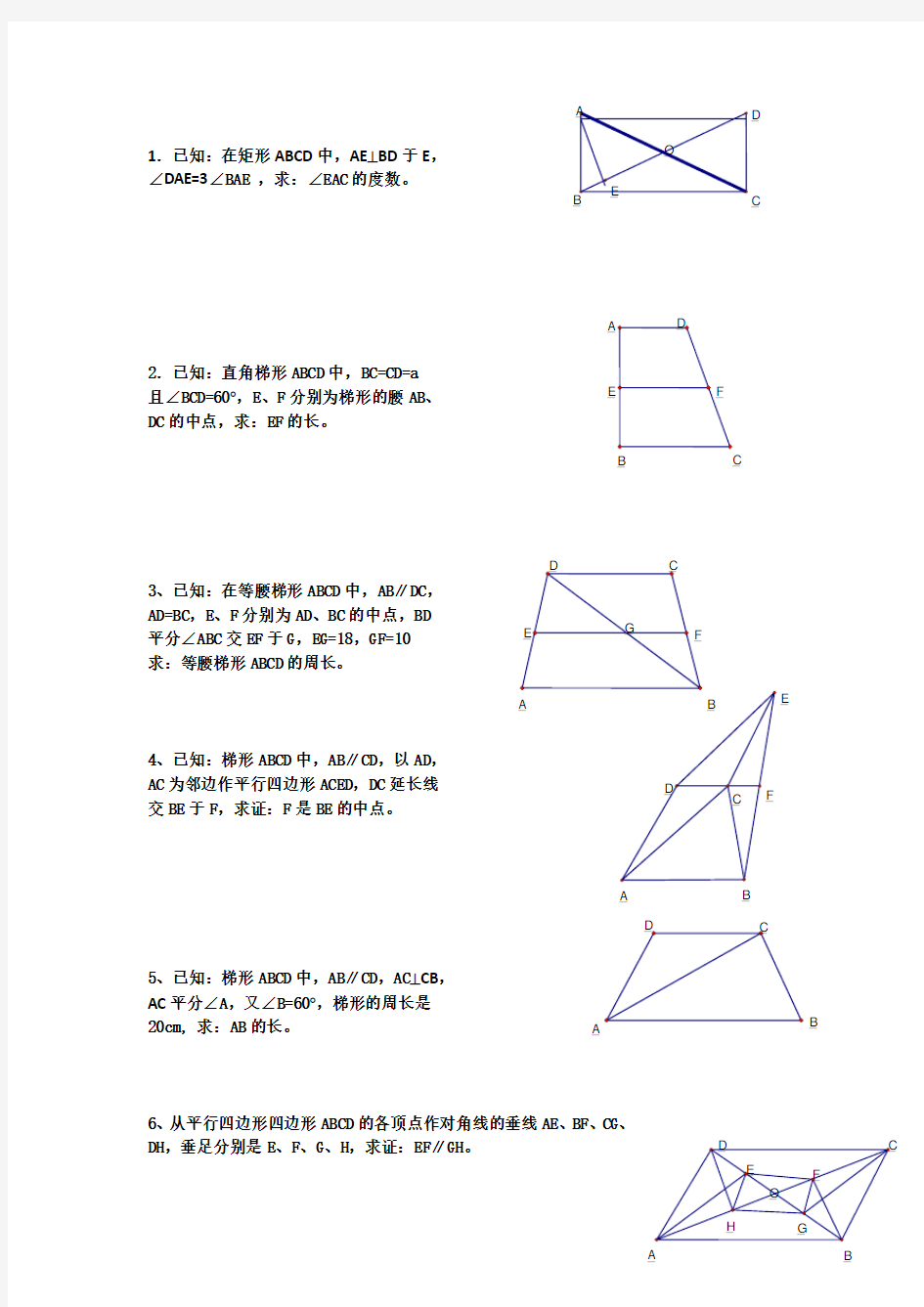
1.已知:在矩形ABCD 中,AE ⊥BD 于E ,
∠DAE=3∠BAE ,求:∠EAC 的度数。
2.已知:直角梯形ABCD 中,BC=CD=a
且∠BCD=60?,E 、F 分别为梯形的腰AB 、 DC 的中点,求:EF 的长。
3、已知:在等腰梯形ABCD 中,AB ∥DC , AD=BC ,E 、F 分别为AD 、BC 的中点,BD
平分∠ABC 交EF 于G ,EG=18,GF=10
求:等腰梯形ABCD 的周长。
4、已知:梯形ABCD 中,AB ∥CD ,以AD , AC 为邻边作平行四边形ACED ,DC 延长线 交BE 于F ,求证:F 是BE 的中点。
5、已知:梯形ABCD 中,AB ∥CD ,AC ⊥CB , AC 平分∠A ,又∠B=60?,梯形的周长是 20cm, 求:AB 的长。
6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、
DH ,垂足分别是E 、F 、G 、H ,求证:EF ∥GH 。
_ D
_ C
_B
_ C
_ A
_ B _ E
_
A _ B
_ A
_ B
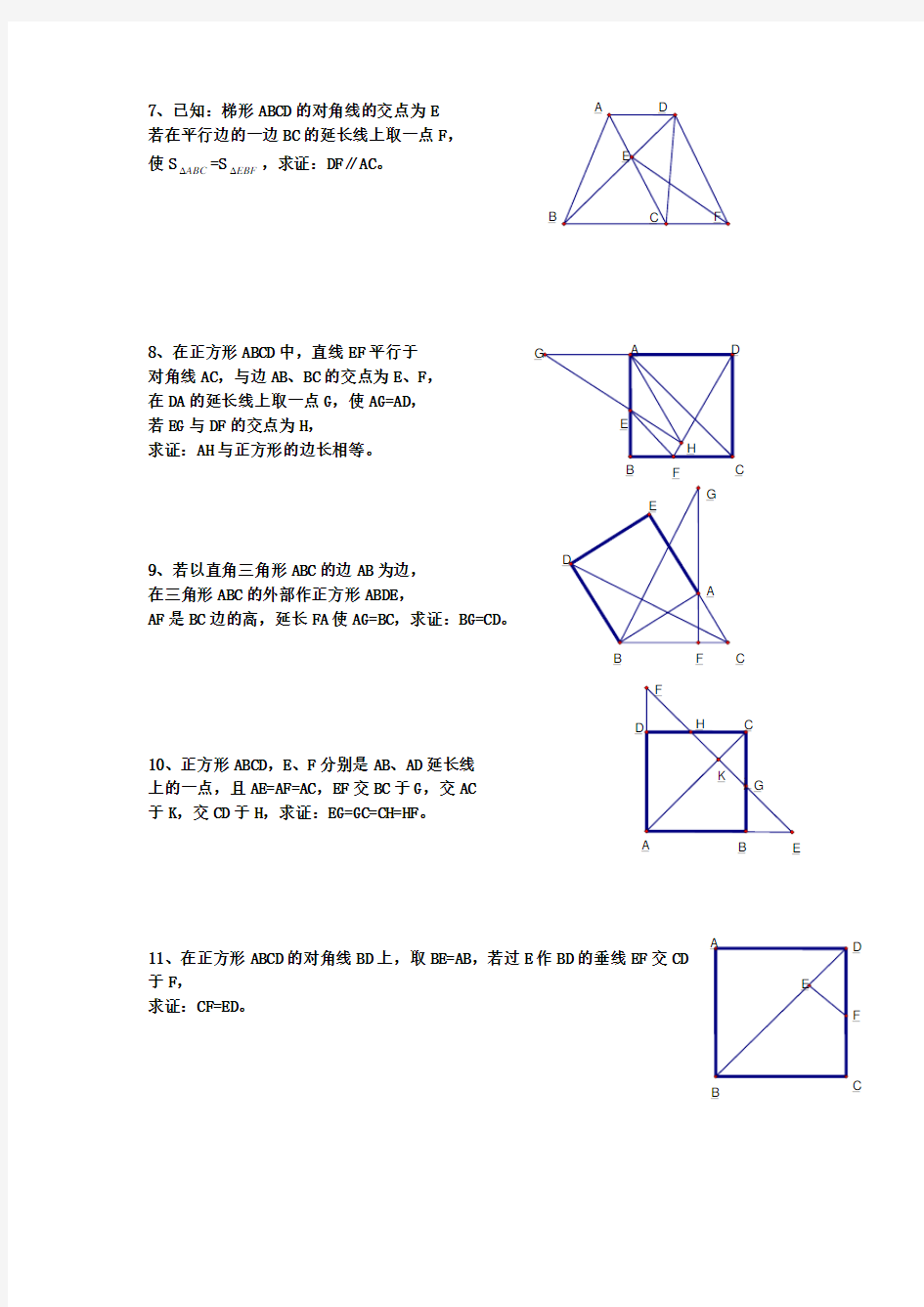
7、已知:梯形ABCD 的对角线的交点为E 若在平行边的一边BC 的延长线上取一点F , 使S ABC ?=S EBF ?,求证:DF ∥AC 。
8、在正方形ABCD 中,直线EF 平行于 对角线AC ,与边AB 、BC 的交点为E 、F , 在DA 的延长线上取一点G ,使AG=AD ,
若EG 与DF 的交点为H ,
求证:AH 与正方形的边长相等。
9、若以直角三角形ABC 的边AB 为边,
在三角形ABC 的外部作正方形ABDE ,
AF 是BC 边的高,延长FA 使AG=BC ,求证:BG=CD 。
10、正方形ABCD ,E 、F 分别是AB 、AD 延长线
上的一点,且AE=AF=AC ,EF 交BC 于G ,交AC
于K ,交CD 于H ,求证:EG=GC=CH=HF 。
11、在正方形ABCD 的对角线BD 上,取BE=AB ,若过E 作BD 的垂线EF 交CD 于F ,
求证:CF=ED 。
_B _
C _B _ F
_ B _ C
_ F
_ C
_ D
_ B
_ F
_ B _A _ E
12、平行四边形ABCD 中,∠A 、∠D 的平分线相交于E ,AE 、DE 与DC 、AB
延长线交于G 、F ,求证:AD=DG=GF=FA 。
13、在正方形ABCD 的边CD 上任取一点E ,延长BC 到F ,使CF=CE , 求证:BE ⊥DF
14、在四边形ABCD 中,AB=CD ,P 、Q 分别是AD 、BC 中点,M 、N 分别是对角线 AC 、BD 的中点,求证:PQ ⊥MN 。
15、平行四边形ABCD 中,AD=2AB , AE=AB=BF 求证:CE ⊥DF 。
16、在正方形ABCD 中,P 是BD 上一点, 过P 引PE ⊥BC 交BC 于E ,过P 引PF ⊥CD 于F ,求证:AP ⊥EF 。
_ F _ G
_ E _ F
_ A
_ B _ C
_ D
_F
17、过正方形ABCD 的顶点B 引对角线AC 的平行线BE , 在BE 上取一点F ,使AF=AC ,若作菱形CAFé, 求证:AE 及AF 三等分∠BAC 。
18、以?ABC 的三边AB 、BC 、CA 分别为边,在BC 的同侧作等边三角形ABD 、
BCE 、CAF ,求证:ADEF 是平行四边形。
19、M 、N 为?ABC 的边AB 、AC 的中点,E 、F 为边AC 的三等分点,
延长ME 、NF 交于D 点,连结AD 、DC ,求证:
⑴BFDE 是平行四边形,
⑵ABCD 是平行四边形。
20、平行四边形ABCD 的对角线交于O ,作OE ⊥BC ,AB=37cm, BE=26cm, EC=14cm,求:平行四边形ABCD 的面积。
21、在梯形ABCD 中,AD ∥BC ,高AE=DF=12cm,两对角线BD=20cm,AC=15cm, 求梯形ABCD 的面积。
22、在梯形ABCD 中,二底AD 、BC 的中点是E 、F ,在EF 上
任取一点O ,
_ B
_ C _ Q
_ E
_ F
_ B
_ C
_ B
_ C
_ N _ B _C
_
E
_ B _ C
_ E _ F
_ B _ C
_ F
求证:S
OAB
?=S
OCD
?
23、平行四边形ABCD中,EF平行于对角线AC,且与AB、BC分别交
于E、F,求证:S
ADE
?=S
CDF
?
24、梯形ABCD的底为AD、BC,
若CD的中点为E求证:S
ABE
?=
2
1
S
ABCD
25、梯形ABCD的面积被对角线BD分成3:7两部分,
求这个梯形被中位线EF分成的两部分的面积的比。
26、在梯形ABCD中,AB∥CD,M是BC边的中点,且MN⊥AD于N,
求证:S
ABCD =MN?AD。
_B_C
_F
_B_C
_A_B
_A_B
27、求证:四边形ABCD 的两条对角线之和小于它的周长而大于它的周长之半。
28、平行四边形ABCD 的对边AB 、CD 的中点为E 、F ,求证:DE 、BF 三等分对角线AC 。
29、证明:顺次连结四边形的各边中点的四边形是平行四边形,其周长等于原四边形的对角线之和。
30、在正方形ABCD 的CD 边上取一点G , 在CG 上向原正方形外作正方形GCEF , 求证:DE ⊥BG ,DE=BG 。
31、在直角三角形ABC 中,CD 是斜边AB
的高,∠A 的平分线AE 交CD 于F ,交BC
于E ,EG ⊥AB 于G ,求证:CFGE 是菱形。
_ B _ C
_ C _ B _ E
_ A _B _D _ G
32、若分别以三角形ABC 的边AB 、AC
为边,在三角形外作正方形ABDE 、ACFG , 求证:BG=EC ,BG ⊥EC 。
33、求证:对角线相等的梯形是等腰梯形。
34、正方形ABCD 中,M 为AB 的任意点,MN ⊥DM ,BN 平分∠CBF , 求证:MD=NM
35、在梯形ABCD 中,AD ∥BC ,AD=12cm ,
BC=28cm ,EF ∥AB 且EF 平分ABCD 的面积,求:BF 的长。
36、平行四边形ABCD 中,E 为AB 上的任一点,
若CE 的延长线交DA 于F ,连结DE ,
求证:S ADE ?=S BEF ?
_ B
_ C
_
_ B _ C
_
F
_D
_ A
_ F
37、过四边形ABCD 的对角线BD 的中点E 作AC 的平行线FEG ,与AB 、AC 的交点分别为 F 、G ,求证:AG 或FC 平分此四边形的面积,
38、若以三角形ABC 的边AB 、AC 为边 向三角形外作正方形ABDE 、ACFG , 求证:S AEG ?=S ABC ?。
39、四边形ABCD 中,M 、N 分别是对角线AC 、BD 的中点,又AD 、BC 相交于点P ,求证:S PMN ?=
4
1
S ABCD 。
40、正方形ABCD 的边AD 上有一点E ,满足BE=ED+DC ,如果M 是AD 的中点, 求证:∠EBC=2∠ABM ,
41、若以三角形ABC 的边AB 、BC 为边向
三角形外作正方形ABDE 、BCFG ,N 为AC 中点,求证:DG=2BN ,BM ⊥DG 。
_ A
_ B
_F
_ A _ B
_ C
_B
_A _ C
_ N
_ B _ C
42、从正方形ABCD的一个顶点C作CE平行于BD,使BE=BD,若BE、CD的交点为F,求证:DE=DF。
43、平行四边形ABCD中,直线FH与AB、CD相交,过A、D、C、B,向FH作垂线,垂足为G、F、E、H,
求证:AG-DF=CE-BH。
44、四边形ABCD中,若∠A=∠C,
求证各角平分线围成的四边形等腰梯形。
45、正方形ABCD中,∠EAF=45?
求证:BE+DF=EF。
46、正方形ABCD中,点P与B、C的
连线和BC的夹角为15?
求证:PA=PD=AD。
_C
_B
_B_
E
_F
_B
_A
47、四边形ABCD 中,AD=BC ,EF 为AB 、DC 的中点的连线,并分别与AD 、BC 延长线交于 M 、N ,求证:∠AME=∠BNE 。
48、正方形ABCD 中,MN ⊥GH , 求证:MN=HG 。
49、正方形ABCD 中,E 是边CD 的中点,F 是线段CE 的中点
求证:∠DAE=2
1
∠BAF 。
50、等腰梯形ABCD 中,DC ∥AB ,AB>CD ,AD=BC ,AC 和BD 交于O , 且所夹的锐角为60?,E 、F 、M 分别为OD 、OA 、BC 的中点。 求证:三角形EFM 为等边三角形。
_A _ B
_ E
_ N
_ C
_ B
_ E
_ A
_ B
人教版八年级下册数学平行四边形知识点归纳及练习
平行四边形复习 | 3.平行四边形的性质: 因为ABCD 是平行四边形 ?????????. 54321)邻角互补()对角线互相平分;()两组对角分别相等;()两组对边分别相等;()两组对边分别平行;( 5.矩形的性质: 因为ABCD 是矩形 ?? ? ??.3; 2;1)对角线相等()四个角都是直角(有通性)具有平行四边形的所( 、 6. 矩形的判定: ??? ?? +边形)对角线相等的平行四()三个角都是直角(一个直角)平行四边形(321四边形ABCD 是矩形. 7.菱形的性质: — 因为ABCD 是菱形 ?? ? ??.321角)对角线垂直且平分对()四个边都相等; (有通性;)具有平行四边形的所( A B D O C C D B A O D A D B C A D B C A D B C O A D B C O
8.菱形的判定: ?? ? ?? +边形)对角线垂直的平行四()四个边都相等(一组邻边等)平行四边形(321四边形四边形ABCD 是菱形. 9.正方形的性质: 因为ABCD 是正方形 ?? ? ??.321分对角)对角线相等垂直且平(角都是直角; )四个边都相等,四个(有通性;)具有平行四边形的所( C D A B (1) A B C D O (2)(3) 10.正方形的判定: ?? ? ? ? ++++一组邻边等矩形)(一个直角)菱形(一个直角一组邻边等)平行四边形(321四边形ABCD 是正方形. (3)∵ABCD 是矩形 又∵AD=AB ∴四边形ABCD 是正方形 11.等腰梯形的性质: 因为ABCD 是等腰梯形 ?? ? ??.321)对角线相等(; )同一底上的底角相等(两底平行,两腰相等;)( 12.等腰梯形的判定: ??? ??+++对角线相等)梯形(底角相等)梯形(两腰相等 )梯形(321四边形ABCD 是等腰梯形 (3)∵ABCD 是梯形且AD ∥BC ∵AC=BD ∴ABCD 四边形是等腰梯形 A B C D O A B C D O C D A B
初中数学最值问题典型例题
初中数学《最值问题》典型例题 一、解决几何最值问题的通常思路 两点之间线段最短; 直线外一点与直线上所有点的连线段中,垂线段最短; 三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值) 是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段. 轴 对 称 最 值 图形 l P B A N M l B A A P B l 原理两点之间线段最短两点之间线段最短三角形三边关系 特征 A,B为定点,l为定直 线,P为直线l上的一 个动点,求AP+BP的 最小值 A,B为定点,l为定直线, MN为直线l上的一条动线 段,求AM+BN的最小值 A,B为定点,l为定直线, P为直线l上的一个动 点,求|AP-BP|的最大值转化 作其中一个定点关于定 直线l的对称点 先平移AM或BN使M,N 重合,然后作其中一个定 点关于定直线l的对称点 作其中一个定点关于定 直线l的对称点 折 叠 最 值 图形 B' N M C A B 原理两点之间线段最短 特征 在△ABC中,M,N两点分别是边AB,BC上的动点,将△BMN沿MN翻折, B点的对应点为B',连接AB',求AB'的最小值. 转化转化成求AB'+B'N+NC的最小值 1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=32,则△PMN 的周长的最小值为. 【分析】作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN 的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解.【解答】解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长. ∵PC关于OA对称, ∴∠COP=2∠AOP,OC=OP 同理,∠DOP=2∠BOP,OP=OD ∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD.
人教版初中数学第十八章平行四边形知识点
第十八章平行四边形 18.1 平行四边形 平行四边形定义:两组对边分别平行的四边形叫做平行四边形. 平行四边形用“□”表示,读作“平行四边形”.平行四边形ABCD 记作“□ABCD”. 18.1.1 平行四边形的性质 平行四边形是中心对称图形,对称中心是两条对角线的交点. 例、已知:□ABCD 求证:AD=BC ,AB=DC ;∠A=∠C ,∠B=∠D. 证明:连接AC ,//,//AD CD AD BC 12,34∴∠=∠∠=∠ 又AC 是△ABC 和△CDA 的公共边, ∴△ABC ≌△CDA , ,,AD CB AB CD B D ∴==∠=∠ 平行四边形性质1:平行四边形的两组对边分别相等. 平行四边形性质2:平行四边形的两组对角分别相等. 例、已知:如图:□ABCD 的对角线AC 、BD 相交于点O. 求证:OA=OC ,OB=OD. 证明:四边形ABCD 是平行四边形 ∴ AD=BC ,AD ∥BC. ∴∠1=∠2,∠3=∠4. ∴△AOD ≌△COB (ASA ). ∴ OA=OC ,OB=OD. 平行线之间的距离定义:若两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离. 平行线之间的距离特征1:平行线之间的距离处处相等. 平行线之间的距离特征2:夹在两条平行线之间的平行线段相等. 平行四边形性质3:平行四边形的两条对角线互相平分. 例、如图,□ ABCD 中,BD ⊥AB ,AB=12cm ,AC=26cm ,求AD 、BD 长.
解:∵四边形ABCD 是平行四边形,∴AO=CO=2 1AC ,OB=OD . ∵BD ⊥AB ,∴在Rt △A BO 中,AB=12cm ,AO=13cm . ∴BO=522=-AB AO .∴BD=2B0=10cm . ∴在Rt △ABD 中,AB=12cm ,BD=10cm . ∴AD=61222=+BD AB (cm). 例、如图,在□ABCD 中,已知对角线AC 和BD 相交于点O ,△AOB 的周长 为25,AB=12,求对角线AC 与BD 的和. 解:∵△AOB 的周长为25, ∴OA+BO+AB=25, 又AB=12,∴AO+OB=25-12=13, ∵平行四边形的对角线互相平分,∴AC+BD=2OA+2OB=2(0A+OB)=2×13=26 18.1.2 平行四边形的判定 平行四边形判定1:两组对边分别平行的四边形是平行四边形. 平行四边形判定2:两组对边分别相等的四边形是平行四边形. 平行四边形判定3:两组对角分别相等的四边形是平行四边形. 平行四边形判定4:两条对角线互相平分的四边形是平行四边形. 平行四边形判定5:一组对边平行且相等的四边形是平行四边形. 中位线:连接三角形两边中点的线段叫做三角形的中位线 三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半. 例、如图,在□ABCD 中,已知点E 和点F 分别在AD 和BC 上,且AE=CF ,连结 CE 和AF ,试说明四边形AFCE 是平行四边形. 证明:∵四边形ABCD 是平行四边形, ∴AD//BC , ∵点E 在AD 上,点F 在BC 上, ∴AE//CF , 又∵AE=CF , ∴四边形AFCE 是平行四边形. 例、如图,E 、F 是四边形ABCD 的对角线AC 上的两点,AF=CE ,DF=BE ,DF ∥BE . 求证:(1)△AFD ≌△CEB . (2)四边形ABCD 是平行四边形.
旋转相似经典例题知识讲解
旋转与全等、相似中的线段数量关系 基本例题:1、如图,△ABC中,∠C=90°.(1)将△ABC绕点B逆时针旋转90,画出旋转后的三角形;(2)若BC=3,AC=4,点A旋转后的对应点为A′,求A′A的长 变式1,如图Rt△AB'C'是由Rt△ABC,绕点A顺时针旋转得到的,连接C C'交AB于E, (1)证明:△CA C'∽△BA B' (2)延长C C'交B B'于F,证明:△CA E∽△FBE 变式2,△ABC绕点B逆时针旋转90°得到△DBE,若恰好得到C、E、D三点共线,则AC、BC、CD的数量关系是 变式3,△ABC绕点B逆时针旋转a°得到△DBE,若恰好得到C、E、D三点共线,则AC、
BC、CD的数量关系是 变式4、Rt△ABC中,AC=BC,∠ACB=∠ADB=90°,连接CD,求:AD、CD、BD的数量关系 变式5、Rt△ABC中,AC=kBC,∠ACB=∠ADB=90°,连接CD,探究:AD、CD、BD的数量关系 变式6、如图,在△OAB和△OCD中,∠A<90°,OB=KOD(K>1),∠AOB=∠COD,∠OAB与∠OCD互补,试探索线段AB与CD的数量关系,并证明你的结论。 变式7.如图AB∥CD,BC∥ED, ∠BCD+∠ACE=180°。 (1)当BC=CD 且∠ACE=90°时如图3探究线段AC和CE之间的数量关系 (2)当BC=CD 时如图2探究线段AC和CE之间的数量关系 (3)当BC=kCD时如图1探究线段AC和CE之间的数量关系(用含k的式子表示) E B C A D C A D B
80中田凌志老师提供 1如图R t △ABC ,∠ACB=90°,AC=3,BC=4,过点B 作直线MN ∥AC,点P 在直线BC 上,∠EPF=∠CAB ,且两边分别交直线AB 于E ,交直线MN 于F 。如图(1)(2)(3)探究PE 与PF 之间的数量关系,并证明 P N M F E C B A _ P _ N _ M _F _E _ C _ B _ A 图1 图2
初中数学10大解题方法及典型例题详解
初中数学10大解题方法及典型例题详解 1、配方法 所谓配方,就是把一个解析式利用恒等变形的方法,把其中的某些项配成一个或几个多项式正整数次幂的和形式。通过配方解决数学问题的方法叫配方法。其中,用的最多的是配成完全平方式。配方法是数学中一种重要的恒等变形的方法,它的应用十分非常广泛,在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它。 例题: 用配方法解方程x2+4x+1=0,经过配方,得到( ) A.(x+2) 2=5 B.(x-2) 2=5 C.(x-2) 2=3 D.(x+2) 2=3 【分析】配方法:若二次项系数为1,则常数项是一次项系数的一半的平方,若二次项系数不为1,则可先提取二次项系数,将其化为1后再计算。【解】将方程x2+4x+1=0, 移向得:x2+4x=-1, 配方得:x2+4x+4=-1+4, 即(x+2) 2=3; 因此选D。 2、因式分解法 因式分解,就是把一个多项式化成几个整式乘积的形式。因式分解是恒等变形的基础,它作为数学的一个有力工具、一种数学方法在代数、几何、三角等的解题中起着重要的作用。因式分解的方法有许多,除中学课本上介绍的提取公因式法、公式法、分组分解法、十字相乘法等外,还有如利用拆项添项、求根分解、换元、待定系数等等。 例题: 若多项式x2+mx-3因式分解的结果为(x-1)(x+3),则m的值为()A.-2 B.2 C.0 D.1 【分析】根据因式分解与整式乘法是相反方向的变形,先将(x-1)(x+3)乘法公式展开,再根据对应项系数相等求出m的值。
【解】∵x2+mx-3因式分解的结果为(x-1)(x+3), 即x2+mx-3=(x-1)(x+3), ∴x2+mx-3=(x-1)(x+3)=x2+2x-3, ∴m=2; 因此选B。 3、换元法 换元法是数学中一个非常重要而且应用十分广泛的解题方法。我们通常把未知数或变数称为元,所谓换元法,就是在一个比较复杂的数学式子中,用新的变元去代替原式的一个部分或改造原来的式子,使它简化,使问题易于解决。 例题: 已知(x2+y2+1)(x2+y2+3)=8,则x2+y2的值为() A.-5或1 B.1 C.5 D.5或-1 【分析】解题时把x2+y2当成一个整体来考虑,再运用因式分解法就比较简单【解】设x2+y2=t,t≥0,则原方程变形得 (t+1)(t+3)=8,化简得: (t+5)(t-1)=0, 解得:t 1=-5,t 2 =1 又t≥0 ∴t=1 ∴x2+y2的值为只能是1. 因此选B. 4、判别式法与韦达定理 一元二次方程ax2+bx+c=0(a、b、c属于R,a≠0)根的判别,△=b2-4ac,不仅用来判定根的性质,而且作为一种解题方法,在代数式变形,解方程(组),解不等式,研究函数乃至几何、三角运算中都有非常广泛的应用。 韦达定理除了已知一元二次方程的一个根,求另一根;已知两个数的和与积,求
初中数学专题典型例题训练
第一讲:实数与代数专题典型例题讲解 一实数 1. 例:在14-和15 -之间,请写出两个有理数: . 2. 有理数2 2 3 1 2, (2), 2, 2 ---- 按从小到大的顺序排列是( ) A .322122< (2) 2-<--<-, B . 223 12< (2) 22 -<--<- C . 22312< (2) 22-<--<-, D . 232 12< 2(2)2 -<--<- 3. 将一刻度尺如图所示放在数轴上 (数轴的单位长度是1CM ),刻度尺上的“0cm ”和 “15cm ”分别对应数轴上的-3.6和x ,则( ) A .9<x <10; B .10<x <11; C .11<x <12; D .12<x <13; 4. 下列说法正确的是( ) A .互为相反数的两个数一定不相等; B .互为倒数的两个数一定不相等; C .互为相反数的两个数的绝对值相等; D .互为倒数的两个数的绝对值相等; 5. 若3x -和7x -是某个实数的平方根,则x = . 6. 若函数()f x 、()g x 满足()()0f x g x +=,当2()f x x x =-+,则函数()g x 的最小值为: 7. 有理数A 、B 、C 在数轴上的位置如图所示,则式子|A |+|B |+|A +B |+|B -C |化简结果为.[ ]. .A .2A +3B -C...B .3B -C..C .B +C....D .C -- 8. 若|A -2|=2-A ,求A 的取值范围。 9. 已知:|x -2|+x -2=0,.求:(1)x +2的最大值; 10. 单项式3x y π - 的系数是_______,次数是_____。 11. 如果21 13 m n a b +--与5 4a b 的同类项,则M =_____,N =_________。 12. 如图.在正方形ABCD 的边长为3,以A 为圆心,2为半径作圆弧.以D 为圆心, 3为半径作圆弧.若图中阴影部分的面积分为S 1、S 2.则S 1-S 2= . 13. 以Rt △ACB 两条直角边为直径向外作半圆,如图,其面积分别为1S 和2S ,若△ABC 的面积为S ,则12,S S 与S 的关系为 . 14. 若2 2(3)16x m x +-+是完全平方式,则m 的值为: . 15. 若m 2+m -1=0,求m 3+2m 2+2015的值. 16. 若0,0,x xy <<则15y x x y -+---=
人教版初中数学第十八章平行四边形知识点
第十八章平行四边形 平行四边形 平行四边形定义:两组对边分别平行的四边形叫做平行四边形. 平行四边形用“□”表示,读作“平行四边形”.平行四边形ABCD记作“□ABCD”. 平行四边形的性质 平行四边形是中心对称图形,对称中心是两条对角线的交点. 例、已知:□ABCD求证:AD=BC,AB=DC;∠A=∠C,∠B=∠D. AD CD AD BC 证明:连接AC,//,// ' ∴∠=∠∠=∠ 12,34 又AC是△ABC和△CDA的公共边, ∴△ABC≌△CDA, AD CB AB CD B D ∴==∠=∠ ,, 平行四边形性质1:平行四边形的两组对边分别相等. 平行四边形性质2:平行四边形的两组对角分别相等. 例、已知:如图:□ABCD的对角线AC、BD相交于点O. 求证:OA=OC,OB=OD. [ 证明:四边形ABCD是平行四边形 ∴ AD=BC,AD∥BC. ∴∠1=∠2,∠3=∠4. ∴△AOD≌△COB(ASA). ∴ OA=OC,OB=OD. 平行线之间的距离定义:若两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离. 平行线之间的距离特征1:平行线之间的距离处处相等. 平行线之间的距离特征2:夹在两条平行线之间的平行线段相等. ' 平行四边形性质3:平行四边形的两条对角线互相平分.
例、如图,□ ABCD 中,BD ⊥AB ,AB=12cm ,AC=26cm ,求AD 、BD 长. 解:∵四边形ABCD 是平行四边形,∴AO=CO=2 1AC ,OB=OD . ∵BD ⊥AB ,∴在Rt △A BO 中,AB=12cm ,AO=13cm . ∴BO=522=-AB AO .∴BD=2B0=10cm . ∴在Rt △ABD 中,AB=12cm ,BD=10cm . ∴AD=61222=+BD AB (cm). ? 例、如图,在□ABCD 中,已知对角线AC 和BD 相交于点O ,△AOB 的周长为25, AB=12,求对角线AC 与BD 的和. 解:∵△AOB 的周长为25, ∴OA+BO+AB=25, 又AB=12,∴AO+OB=25-12=13, ∵平行四边形的对角线互相平分,∴AC+BD=2OA+2OB=2(0A+OB)=2×13=26 平行四边形的判定 平行四边形判定1:两组对边分别平行的四边形是平行四边形. 平行四边形判定2:两组对边分别相等的四边形是平行四边形. / 平行四边形判定3:两组对角分别相等的四边形是平行四边形. 平行四边形判定4:两条对角线互相平分的四边形是平行四边形. 平行四边形判定5:一组对边平行且相等的四边形是平行四边形. 中位线:连接三角形两边中点的线段叫做三角形的中位线 三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半. 例、 如图,在□ABCD 中,已知点E 和点F 分别在AD 和BC 上,且AE=CF ,连结CE 和AF ,试说明四边形AFCE 是平行四边形. 证明:∵四边形ABCD 是平行四边形,
(完整版)初一年级数学经典例题
数学天地: 初一年级数学核心题目赏析 有理数及其运算篇 【核心提示】 有理数部分概念较多,其中核心知识点是数轴、相反数、绝对值、乘方. 通过数轴要尝试使用“数形结合思想”解决问题,把抽象问题简单化.相反数看似简单,但互为相反数的两个数相加等于0这个性质有时总忘记用..绝对值是中学数学中的难点,它贯穿于初中三年,每年都有不同的难点,我们要从七年级把绝对值学好,理解它的几何意义.乘方的法则我们不仅要会正向用,也要会逆向用,难点往往出现在逆用法则方面. 【核心例题】 例1计算:2007 20061 ......431321211?+ +?+?+? 分析 此题共有2006项,通分是太麻烦.有这么多项,我们要有一种“抵消”思想,如能把一些项抵消了,不就变得简单了吗?由此想到拆项,如第一项可拆 成 2 1 11211-=?,可利用通项 ()11111+-=+?n n n n ,把每一项都做如此变形,问题会迎刃而解. 解 原式=)20071 20061(......413131212111-++-+-+-)()()( =20071 20061......41313121211- ++-+-+- =20071 1- =2007 2006 例2 已知有理数a 、b 、c 在数轴上的对应点 分别为A 、B 、C(如右图).化简b c b a a -+-+. 分析 从数轴上可直接得到a 、b 、c 的正负性,但本题关键是去绝对值,所以应判断绝对值符号内表达式的正负性.我们知道“在数轴上,右边的数总比左边的数大”,大数减小数是正数,小数减大数是负数,可得到a-b<0、c-b>0. 解 由数轴知,a<0,a-b<0,c-b>0 所以,b c b a a -+-+= -a-(a-b)+(c-b)= -a-a+b+c-b= -2a+c 例3 计算:?? ? ??-??? ??-????? ??-??? ??-??? ??-211311 (9811991110011)
旋转经典题型
01 分点突破 知识点1中心对称与中心对称图形 1. 图形的是 C 1) 2.(齐齐哈尔屮考)下列汉字或字母既是屮 心对称图形又是轴对称图形的是 知识点2平面直角坐标系与旋转 (阜新屮考)ri 章末复习 旋转 A. Bl cH D Z (济宁中考)下列图形是中心对称 如图,正方形OABC 在平面直角坐标系屮,点 A 的坐标为 (2, 0),将正方形OABC 绕点0顺时针旋转45 0得到正方形 标为( ) OA B' C 则点C'的坐 A. ( .2, .2) C. ( . 2, — . 2) B. (— 2, . 2) D. (2 .2, 2 .2) 3. 4. (宁夏中考)如图,在平面直角坐标系xOy
中,△ A'B'由込ABC绕点P旋转得到,则点P的坐标为 . 5. __________________________ (北京中考)如图,在平面直角坐标系xOy中, 4AOB可以看作是AOCD经过若干次图形的变化(平移、轴对称、旋转)得到的, 写出一种由△ OCD得到△ AOB的过程:
知识点 3 6.(天津 屮考)如图, 将厶 ABC 绕 点B 顺时针 旋转60 ° E 恰好落在AB 的延长线上,连 接AD.下列结论一定正确的是() AC = 5 cm, BC = 12 cm. 将厶ABC 绕点B 顺时针旋转60°得到△ BDE ,连接DC 交AB 于点F,则厶ACF 和厶BDF 的周长之和为 cm. 8?(徐州中考)如图,已知AC 丄BC,垂足为C, AC 二4, BC 二3. 3,将线 段AC 绕 点A 按逆时针方向旋转60°得到线段AD,连接DC, DB. (1)线段 DC 二 4; (2)求线段DB 的长度. 02 中考题型演练 9. (聊城中考)如图,将AABC 绕点C 顺时针旋转,使点B 落在AB 边上点 B'处,此时,点A 的对应点A'恰好落在BC 的延长线上,下列结论错误的是() 得"DBE,点 C 的对应点 旋转屮的让算问题 4 A. Z ABD 二Z E B. Z CBE 二Z C C. AD II BC D. AD =BC E B
初中数学知识要点及典型例题
初中数学知识要点及典型例题 第一章实数 第一讲实数的有关概念 【回顾与思考】 知识点:有理数、无理数、实数、非负数、相反数、倒数、数的绝对值 课标要求: 1.使学生复习巩固有理数、实数的有关概念. 2.了解有理数、无理数以及实数的有关概念;理解数轴、相反数、绝对值等概念,了解数的绝对值的几何意义。 3.会求一个数的相反数和绝对值,会比较实数的大小 4.画数轴,了解实数与数轴上的点一一对应,能用数轴上的点表示实数,会利用数轴比较大小。 考查重点: 1.有理数、无理数、实数、非负数概念; 2.相反数、倒数、数的绝对值概念; 3.在已知中,以非负数a2、|a|、 a (a≥0)之和为零作为条件,解决有关问题。 实数的有关概念
(1)实数的组成 {} ?????????????????????????????????正整数整数零负整数有理数有尽小数或无尽循环小数正分数实数分数负分数正无理数无理数无尽不循环小数 负无理数 (2)数轴:规定了原点、正方向和单位长度的直线叫做数轴(画数轴 时,要注童上述规定的三要素缺一个不可),实数与数轴上的点是一 一对应的。数轴上任一点对应的数总大于这个点左边的点对应的数, (3)相反数 实数的相反数是一对数(只有符号不同的两个数,叫做互为相反 数,零的相反数是零). 从数轴上看,互为相反数的两个数所对应的点关于原点对称. (4)绝对值 ?? ???<-=>=)0()0(0)0(||a a a a a a 从数轴上看,一个数的绝对值就是表示这个数的点与原点的距离 (5)倒数 实数a(a ≠0)的倒数是a 1(乘积为1的两个数,叫做互为倒数); 零没有倒数. 【例题经典】 理解实数的有关概念
人教版八年级数学四边形知识点及练习题带答案
A C B D 第十九章 四边形 一.知识框架 二.知识概念 1.平行四边形定义: 有两组对边分别平行的四边形叫做平行四边形。 2.平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等。平行四边形的对角线互相平分。 3.平行四边形的判定 ○ 1.两组对边分别相等的四边形是平行四边形 ○ 2.对角线互相平分的四边形是平行四边形; ○ 3.两组对角分别相等的四边形是平行四边形; ○ 4.一组对边平行且相等的四边形是平行四边形。 4.三角形的中位线平行于三角形的第三边,且等于第三边的一半。 5.直角三角形斜边上的中线等于斜边的一半。 6.矩形的定义:有一个角是直角的平行四边形。 7.矩形的性质: 矩形的四个角都是直角;矩形的对角线平分且相等。AC=BD 8.矩形判定定理: ○1.有一个角是直角的平行四边形叫做矩形。 ○2.对角线相等的平行四边形是矩形。 ○ 3.有三个角是直角的四边形是矩形。 9.菱形的定义 :邻边相等的平行四边形。
第4题图 O F E D C B A 10.菱形的性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。 11.菱形的判定定理:○ 1.一组邻边相等的平行四边形是菱形。 ○ 2.对角线互相垂直的平行四边形是菱形。 ○ 3.四条边相等的四边形是菱形。 12.S 菱形=1/2×ab (a 、b 为两条对角线) 13.正方形定义:一个角是直角的菱形或邻边相等的矩形。 14.正方形的性质:四条边都相等,四个角都是直角。 正方形既是矩形,又是菱形。 15.正方形判定定理: 1.邻边相等的矩形是正方形。 2.有一个角是直角的菱形是正方形。 16.梯形的定义: 一组对边平行,另一组对边不平行的四边形叫做梯形。 17.直角梯形的定义:有一个角是直角的梯形 18.等腰梯形的定义:两腰相等的梯形。 19.等腰梯形的性质:等腰梯形同一底边上的两个角相等;等腰梯形的两条对角线相等。 20.等腰梯形判定定理:同一底上两个角相等的梯形是等腰梯形。 本章内容是对平面上四边形的分类及性质上的研究,要求学生在学习过程中多动手多动脑,把自己的发现和知识带入做题中。因此教师在教学时可以多鼓励学生自己总结四边形的特点,这样有利于学生对知识的把握。 练习题 一、 选择题(本大题共12小题,每小题2分,共24分) 1.□ABCD 中,∠A 比∠B 大40°,则∠C 的度数为( ) A. 60° B. 70° C. 100° D. 110° 2.□ABCD 的周长为40cm ,△ABC 的周长为25cm ,则对角线AC 长为( ) A. 5cm B. 6cm C. 8cm D. 10cm 3.在□ABCD 中,∠A =43°,过点A 作BC 和CD 的垂线,那么这两条垂线的夹角度为( ) A. 113° B. 115° C. 137° D. 90° 4.如图,在□ABCD 中,EF 过对角线的交点O ,AB =4,AD =3,OF =1.3, 则四边形BCEF 的周长为( ) A. 8.3 B. 9.6 C. 12.6 D. 13.6 5.下列命题:①一组对边平行,另一组对边相等的四边形 是平行四边形;②对角线互相平分的四边形是平行四边形; ③在四边形ABCD 中,AB =AD ,BC =DC ,那么这个四边形ABCD 是平行四边形;④一组对边相等,一组对角相等的四边形是平行四边形.其中正确命题的个数是( )
旋转 典型例题(精品解析)
典型例题一 例 如图,以点O 为旋转中心,将ABC ?顺时针旋转45°,画出图形. 分析 当旋转中心O 在图形之外时,O 是一个孤立的点,没有从O 出发的线段或射线作参照,就无法确定旋转的角度,因此,首先还须将O 与图形上的某点(或某些点)连结起来. 解 如图,连结OA 、OB 、OC .将这三条线段绕O 点分别顺时针旋转45°,得C O B O A O '''、、,则C B A '''?就是按题目要求得到的旋转后的图形. 说明: 图形旋转后的效果有时不像平移那样直观,画图出现错误时可能不易发现,因此画图时要特别细心. 典型例题二 例 如图,正方形ABCD 中,E 是正方形内的一点,把AED ?绕着点A 按逆时针旋转90°,画出旋转后的三角形,并回答: (1)图中有哪些等线段和等角? (2)哪两个三角形形状、大小都一样? 分析 一个图形绕它的对称中心旋转一个角度后,图形中的每一点都绕旋转中心旋转了同样大小的角度.本例中可以发现AD 旋转90°后,刚好与AB 重合,于是将AE 旋转90°到E A '的位置,使?='∠90E EA ,确定点E ',连E B ',则E AB '?就是ADE ?按要求旋转的三角形.(1)(2)中,根据图形旋转的特征,图形从一个位置旋转到另一个位置,形状和大小都没有改变,可确定相等的线段、相等的角以及形状相同的三角形. 答案 (1)相等的线段有:E B DE E A AE CD BC AB AD '='====,,.相等的角有:E E E AB ADE E BA DAE '∠=∠'∠=∠'∠=∠,,.
(2)ADE ?与E AB '?的形状和大小都一样. 典型例题三 例 如图,把一块砖ABCD 直立于地面上,然后将其轻轻推倒.在这个过程中,A 点保持不动,四边形ABCD 旋转到B C D A '''位置. (1)指出在这个过程中的旋转中心,并说出旋转的角度是多大? (2)指出图中的对应线段. 分析(1)由于四边形B C D A '''是由四边形ADCB 旋转得到的,A 点保持不动,所以A 是旋转中心.又由于D A B ',,三点在一条直线上,且AB AD ⊥,所以旋转的角度是90°.(2)由于D C B A ,,,的对应点分别是D C B A ''',,,,所以不难找出图中的对应线段. 答案 (1)A 是旋转中心,旋转的角度是90°. (2)CD BC AD AB ,,,的对应线段分别是D C C B D A B A '''''',,,. 典型例题四 例 (1)把长方形ABCD 绕着顶点A 逆时针旋转60°.如图. (2)把长方形ABCD 绕着长方形内一点P 逆时针旋转60°. 解 (1)①AB 绕A 点逆时针旋转60°到B A '位置,.,60AB B A AB B ='?='∠ ②连结AC ,作.,60AC C A AC C ='?='∠ ③作.,60AD D A AD D ='?='∠ 连结B C C D '''',,则四边形D C B A '''是四边形ABCD 逆时针旋转60°得到的图形. (2)①连结AP ,作?='∠60PA A ,使.AP P A =' ②用同样的方法作出D C B '''、、,连结A D D C C B B A ''''''''、、、.
初中数学几何证明经典题(含答案)
初中几何证明题 经典题(一) 1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO. 求证:CD=GF.(初二) .如下图做GH⊥AB,连接EO。由于GOFE四点共圆,所以∠GFH=∠OEG, 即△GHF∽△OGE,可得EO GF = GO GH = CO CD ,又CO=EO,所以CD=GF得证。 2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150. 求证:△PBC是正三角形.(初二) .如下图做GH⊥AB,连接EO。由于GOFE四点共圆,所以∠GFH=∠OEG, 即△GHF∽△OGE,可得EO GF = GO GH = CO CD ,又CO=EO,所以CD=GF得证。 .如下图做GH⊥AB,连接EO。由于GOFE四点共圆,所以∠GFH=∠OEG, 即△GHF∽△OGE,可得EO GF = GO GH = CO CD ,又CO=EO,所以CD=GF得证。 A P C D B A F G C E B O D
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、 CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . 经典题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二) D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 B
图形旋转练习题(经典题)
图形旋转练习题 1. 如图1,P 是正三角形ABC 内的一点,且PA=6,PB=8,PC=10,求∠APB 的度数。 2. 如图P 是正方形ABCD 内一点,点P 到正方形的三个顶点A 、B 、C 的距离分别为PA=1,PB=2,PC=3。求此正方形ABCD 面积。 A B C D P 3.设点E 、F 分别在正方形ABCD 的边BC 、CD 上滑动且保持∠EAF=450, A P ⊥EF 于点P (1) 求证:AP=AB ,(2)若AB=5,求ΔECF 的周长。 4.如图17,正方形ABCD ,E 、F 分别为BC 、CD 边上一点. (1)若∠EAF=45o.求证:EF=BE+DF . (2)若⊿AEF 绕A 点旋转,保持∠EAF=45o,问⊿CEF 的周长是否随⊿AEF 位置的变化而变化? (3)已知正方形ABCD 的边长为1,如果⊿CEF 的周长为2.求∠EAF 的度数. 5ABC 中,∠ABC=90°,点D 在AC 上,将△ABD 绕顶点B 沿顺时针方向旋转90°后得到△CBE. ⑴求∠DCE 的度数; ⑵当AB=4,AD ∶DC=1∶3时,求DE 的长. F E D C B A A A F P P B B C C
6.如图所示,△ABC 是直角三角形,BC 是斜边,将△ABP 绕点A 逆时针旋转后,使AB 落到AC 上,则P 落到点P '处。如果AP=1,则PP '=___________. 7.如图,四边形ABCD 中,∠BAD=∠C=90o,AB=AD ,AE ⊥BC 于E ,若线段AE=5,则S 四边形ABCD = 。 8.如图所示,已知P 是正方形ABCD 内一点,以B 为 旋转中心,把△PBC 沿逆时针方向旋转90°得到△P BA ',连接PP ', 则∠P PB '的度数是______。 9、如图,将△ABC 绕点A 旋转一定角度后能与△ADE 重合,如果△ABC 的面积是 12cm 2 ,那么△ADE 的面积是 。 10、如图,△ABC 是等边三角形,D 为BC 边上的点,∠BAD =15°, △ABD 经旋转后到达△ACE 的位置,那么旋转角的度数是 . 11、如图,把三角形△ABC 绕着点C 顺时针旋转350,得到△A 'B 'C ,A 'B '交AC 于点D ,若∠A 'DC=900,则∠A 的度数是__________。 E D C B A 11
初中数学最值问题典型例题(含答案分析)
中考数学最值问题总结 考查知识点:1、“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。 (2、代数计算最值问题3、二次函数中最值问题) 问题原型:饮马问题造桥选址问题(完全平方公式配方求多项式取值二次函数顶点)出题背景变式:角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。 解题总思路:找点关于线的对称点实现“折”转“直” 几何基本模型: 条件:如下左图,A、B是直线l同旁的两个定点. 问题:在直线l上确定一点P,使PA PB +的值最小. 方法:作点A关于直线l的对称点A',连结A B'交l于 点P,则PA PB A B' +=的值最小 例1、如图,四边形ABCD是正方形,△ABE是等边三 角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM. (1)求证:△AMB≌△ENB; (2)①当M点在何处时,AM+CM的值最小; ②当M点在何处时,AM+BM+CM的值最小,并说明理由; (3)当AM+BM+CM的最小值为 时,求正方形的边长。 A B A' ′ P l
例2、如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0) (1)求抛物线的解析式 (2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由. (3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线M N∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.
人教版初中数学四边形专项训练及答案
人教版初中数学四边形专项训练及答案 一、选择题 ?绕点A顺时针旋转90?到1.如图,点E是正方形ABCD的边DC上一点,把ADE ?的位置.若四边形AECF的面积为20,DE=2,则AE的长为() ABF A.4 B.25C.6 D.26 【答案】D 【解析】 【分析】 利用旋转的性质得出四边形AECF的面积等于正方形ABCD的面积,进而可求 出正方形的边长,再利用勾股定理得出答案. 【详解】 Q绕点A顺时针旋转90?到ABF ADE ? ?的位置. ∴四边形AECF的面积等于正方形ABCD的面积等于20, ∴==, AD DC 25 Q, DE= 2 ∴?中,2226 Rt ADE AE AD DE =+= 故选:D. 【点睛】 本题主要考查了旋转的性质以及正方形的性质,正确利用旋转的性质得出对应 边关系是解题关键. 2.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为() A.24 B.18 C.12 D.9 【答案】A 【解析】 【分析】易得BC长为EF长的2倍,那么菱形ABCD的周长=4BC问题得解. 【详解】∵E是AC中点,
∵EF ∥BC ,交AB 于点F , ∴EF 是△ABC 的中位线, ∴BC=2EF=2×3=6, ∴菱形ABCD 的周长是4×6=24, 故选A . 【点睛】本题考查了三角形中位线的性质及菱形的周长公式,熟练掌握相关知识是解题的关键. 3.如图,在菱形ABCD 中,点E 在边AD 上,30BE AD BCE ⊥∠=?,.若2AE =,则边BC 的长为( ) A 5 B 6 C 7 D .22【答案】B 【解析】 【分析】 由菱形的性质得出AD ∥BC ,BC=AB=AD ,由直角三角形的性质得出3,在Rt △ABE 中,由勾股定理得:BE 2+22=3)2,解得:2,即可得出结果. 【详解】 ∵四边形ABCD 是菱形, ∴AD BC BC AB =,∥. ∵BE AD ⊥.∴BE BC ⊥. ∴30BCE ∠=?,∴2EC BE =, ∴223AB BC EC BE BE ==-=. 在Rt ABE △中,由勾股定理得)22223BE BE += , 解得2BE =,∴36BC BE == 故选B. 【点睛】 此题考查菱形的性质,含30°角的直角三角形的性质,勾股定理,熟练掌握菱形的性质,由勾股定理得出方程是解题的关键. 4.如图 ,矩形 ABCD 中,AB >AD ,AB =a ,AN 平分∠DAB ,DM ⊥AN 于点 M ,CN ⊥AN 于点 N .则 DM +CN 的值为(用含 a 的代数式表示)( )
初中数学典型例题100道
初中数学典型例题100道(二) 选择填空题150道 一.选择题: 7,如图,直线,点A1坐标为(1,0),过点A1作x的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为(,). 8,在Rt△ABC中,∠C=90°,∠A=30°,BC=2.若将此直角三角形的一条直角边BC或AC与x轴 重合,使点A或点B刚好在反比例函数(x>0)的图象上时,设△ABC在第一象限部分的面 积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小. 9,若不论k为何值,直线y=k(x﹣1)﹣与抛物线y=ax2+bx+c有且只有一个公共点,求a、b、c的值。 10,如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1. ①b2>4ac; ②4a﹣2b+c<0; ③不等式ax2+bx+c>0的解集是x≥3.5; ④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2. 上述4个判断中,正确的是()
A.①②B.①④C.①③④ D.②③④ 二,解答题 4,如图,在平面直角坐标系中,将直线y=kx沿y轴向下平移3个单位长度后恰好经过B(﹣3,0)及y轴上的C点.若抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的右侧),且经过点C,其对称轴与直线BC交于点E,与x轴交于点F. (1)求直线BC及抛物线的解析式; (2)设抛物线的顶点为D,点P在抛物线的对称轴上,若∠APD=∠ACB,求点P的坐标; (3)在抛物线上是否存在点M,使得直线CM把四边形EFOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由. 5,如图,在平面直角坐标系中,抛物线y=ax2﹣3ax﹣4a的图象经过点C(0,2),交x轴于点A、B(A点在B点左侧),顶点为D. (1)求抛物线的解析式及点A、B的坐标; (2)将△ABC沿直线BC对折,点A的对称点为A′,试求A′的坐标; (3)抛物线的对称轴上是否存在点P,使∠BPC=∠BAC?若存在,求出点P的坐标;若不存在,请说明理由.
(整理)中考数学几何图形旋转试题经典问题及解答
几何图形旋转常见问题 一、填空题 1.如图1,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于. 2.如图2,将一块斜边长为12cm,∠B=60°的直角三角板ABC,绕点C沿逆时针方向旋转90°至△A′B′C′的位置,再沿CB向右平移,使点B′刚好落在斜边AB上,那么此三角板向右平移的距离是cm. 3.正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA顺时针连续翻转(如图3所示),直至点P第一次回到原来的位置,则点P运动路径的长为cm. 4.如图4,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD 以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是. 二、解答题 5.如图5-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F. (1) 求证:BP=DP; (2) 如图5-2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明; (3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .
6.如图6-1是一个美丽的风车图案,你知道它是怎样画出来的吗?按下列步骤可画出这个风车图案:在图6-2中,先画线段OA,将线段OA平移至CB处,得到风车的第一个叶 片F 1,然后将第一个叶片OABC绕点O逆时针旋转180°得到第二个叶片F 2 ,再将F 1 、F 2 同时 绕点O逆时针旋转90°得到第三、第四个叶片F 3、F 4 .根据以上过程,解答下列问题: (1)若点A的坐标为(4,0),点C的坐标为(2,1),写出此时点B的坐标; (2)请你在图6-2中画出第二个叶片F 2 ; (3)在(1)的条件下,连接OB,由第一个叶片逆时针旋转180°得到第二个叶片的过程中,线段OB扫过的图形面积是多少? 7.如图7,在直角坐标系中,已知点P 0的坐标为(1,0),将线段OP 按逆时针方向旋转 45°,再将其长度伸长为OP 0的2倍,得到线段OP 1 ;又将线段OP 1 按逆时针方向旋转45°, 长度伸长为OP 1的2倍,得到线段OP 2 ;如此下去,得到线段OP 3 ,OP 4 ,…,OP n (n为正整数). (1)求点P 6 的坐标; (2)求△P 5OP 6 的面积; (3)我们规定:把点P n (x n ,y n )(n=0,1,2,3,…)的横坐标x n 、纵坐标y n 都取绝对值后 得到的新坐标(|x n |,|y n |)称之为点P n 的“绝对坐标”.根据图中点P n 的分布规律,请你猜 想点P n 的“绝对坐标”,并写出来. 8.把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H (如图8).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
