2017年江苏省苏州市中考数学一模试卷

2017年省市中考数学一模试卷

一、选择题本大题共10小题，每小题3分，共30分．

1．（3分）的倒数是（）

A．B．﹣ C．D．﹣

2．（3分）某细胞截面可以近似看成圆，它的半径约为0.000 000787m，则0.000 000787用科学记数法表示为（）

A．7.87×107 B．7.87×10﹣7C．0.787×10﹣7D．7.87×10﹣6

3．（3分）下列运算正确的是（）

A．a2+a3=a5B．a2?a3=a6C．a8÷a4=a2D．（﹣2a2）3=﹣8a6

4．（3分）学校为了解七年级学生参加课外兴趣小组活动情况，随机调查了40名学生，其中，参加书法兴趣小组的有8人，文学兴趣小组的有11人，舞蹈兴趣小组的有9人，其余参加绘画兴趣小组．则参加绘画兴趣小组的频率是（）

A．0.1 B．0.15 C．0.25 D．0.3

5．（3分）小明记录了3月份某一周的最高气温如下表：

日期12日13日14日15日16日17日18日

最高气温（℃）15101314131613

那么7天每天的最高气温的众数和中位数分别是（）

A．13，14 B．13，15 C．13，13 D．10，13

6．（3分）已知点A（﹣1，y1）、B（2，y2），C（3，y3）都在反比例函数y=﹣的图象上，则下列y1、y2、y3的大小关系为（）

A．y1＜y2＜y3 B．y1＞y3＞y2C．y1＞y2＞y3 D．y2＞y3＞y1

7．（3分）如图，△ABC中，AB=AC=15，AD平分∠BAC，点E为AC的中点，连接DE，若△CDE的周长为21，则BC的长为（）

A．16 B．14 C．12 D．6

8．（3分）抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=1，且经过点（3，0），则a﹣b+c的值为（）

A．﹣1 B．0 C．1 D．2

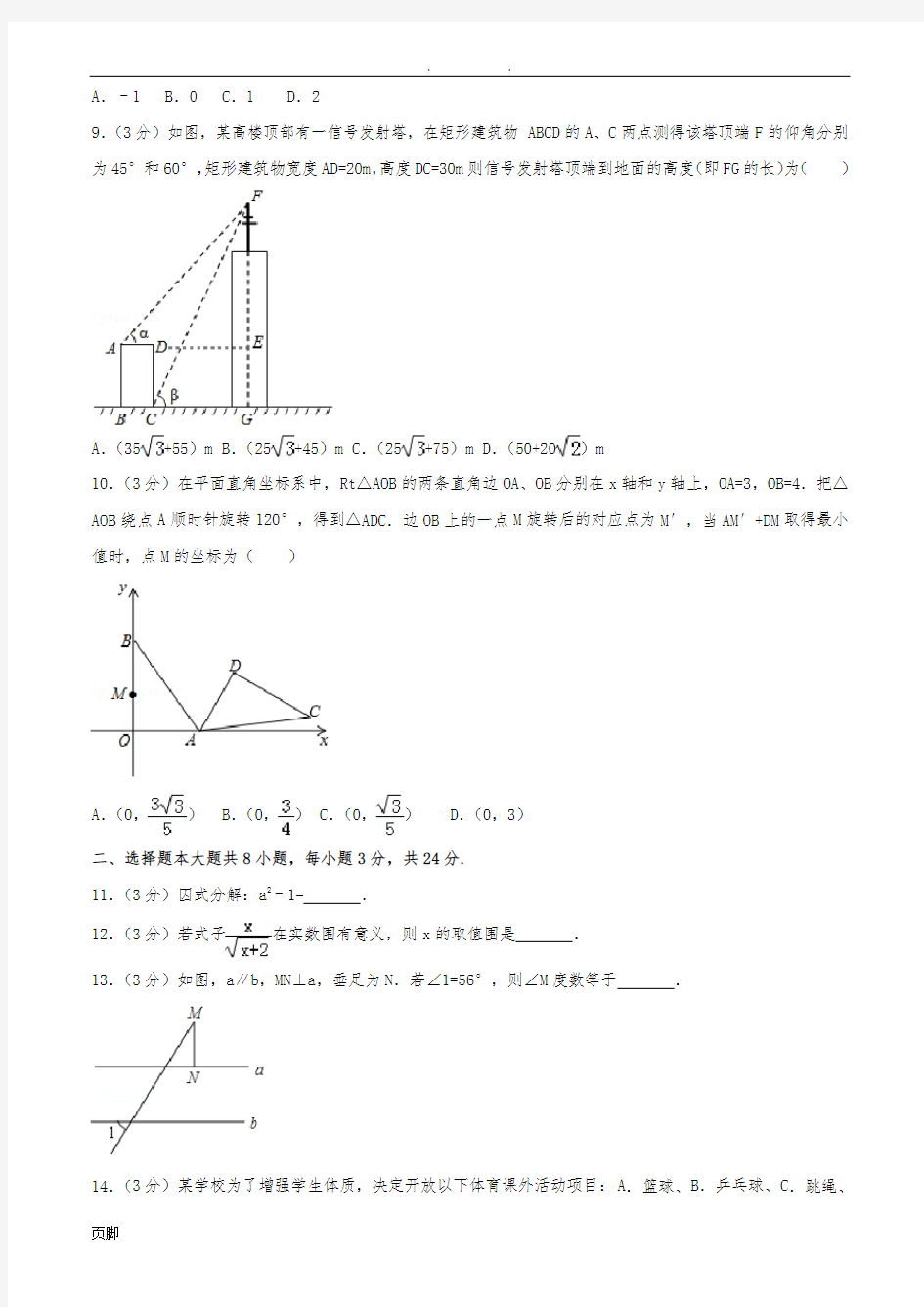
9．（3分）如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°，矩形建筑物宽度AD=20m，高度DC=30m则信号发射塔顶端到地面的高度（即FG的长）为（）

A．（35+55）m B．（25+45）m C．（25+75）m D．（50+20）m

10．（3分）在平面直角坐标系中，Rt△AOB的两条直角边OA、OB分别在x轴和y轴上，OA=3，OB=4．把△AOB绕点A顺时针旋转120°，得到△ADC．边OB上的一点M旋转后的对应点为M′，当AM′+DM取得最小值时，点M的坐标为（）

A．（0，）B．（0，） C．（0，）D．（0，3）

二、选择题本大题共8小题，每小题3分，共24分.

11．（3分）因式分解：a2﹣1= ．

12．（3分）若式子在实数围有意义，则x的取值围是．

13．（3分）如图，a∥b，MN⊥a，垂足为N．若∠1=56°，则∠M度数等于．

14．（3分）某学校为了增强学生体质，决定开放以下体育课外活动项目：A．篮球、B．乒乓球、C．跳绳、

D．踢毽子．为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，其中A所在扇形的圆心角为30°，则在被调查的学生中选择跳绳的人数是．

15．（3分）关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根，则m的取值围是．

16．（3分）如图，矩形ABCD中，AB=4，将矩形ABCD绕点C顺时针旋转90°，点B、D分别落在点B′，D′处，且点A，B′，D′在同一直线上，则tan∠DAD′．

17．（3分）如图，⊙O的半径是2，弦AB和弦CD相交于点E，∠AEC=60°，则扇形AOC和扇形BOD的面积（图中阴影部分）之和为．

18．（3分）如图，在等腰Rt△ABC中，∠ABC=90°，AB=BC=4．点P是△ABC的一点，连接PC，以PC为直角边在PC的右上方作等腰直角三角形PCD．连接AD，若AD∥BC，且四边形ABCD的面积为12，则BP的长为．

三、解答题本大题共10小题，共76分

19．（5分）计算：+|﹣|﹣﹣tan30°．

20．（5分）解不等式组：．

21．（6分）先化简，再求值：（1﹣）÷，其中x=+1．

22．（6分）某班为奖励在校运动会上取得较好成绩的运动员，花了396元钱购买甲、乙两种奖品共30件．其中甲种奖品每件15元，乙种奖品每件12元，求甲、乙两种奖品各买多少件？

23．（8分）九年级（1）班和（2）班分别有一男一女共4名学生报名参加学校文艺汇演主持人的选拔．（1）若从报名的4名学生中随机选1名，则所选的这名学生是女生的概率是．

（2）若从报名的4名学生中随机选2名，用树状图或表格列出所有可能的情况，并求出这2名学生来自同一个班级的概率．

24．（8分）如图，已知Rt△ABD中，∠A=90°，将斜边BD绕点B顺时针方向旋转至BC，使BC∥AD，过点C作CE⊥BD于点E．

（1）求证：△ABD≌△ECB；

（2）若∠ABD=30°，BE=3，求弧CD的长．

25．（8分）如图，在平面直角坐标系中，函数y=（x＞0，k是常数）的图象经过A（2，6），B（m，n），其中m＞2．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，AC与BD交于点E，连结AD，DC，

CB．

（1）若△ABD的面积为3，求k的值和直线AB的解析式；

（2）求证：=；

（3）若AD∥BC，求点B的坐标．

26．（10分）如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC边于点D，交AC边于点E．过点D作⊙O 的切线，交AC于点F，交AB的延长线于点G，连接DE．

（1）求证：BD=CD；

（2）若∠G=40°，求∠AED的度数．

（3）若BG=6，CF=2，求⊙O的半径．

27．（10分）如图，正方形OABC的顶点O在坐标原点，顶点A的坐标为（4，3）

（1）顶点C的坐标为（，），顶点B的坐标为（，）；

（2）现有动点P、Q分别从C、A同时出发，点P沿线段CB向终点B运动，速度为每秒1个单位，点Q沿

折线A→O→C向终点C运动，速度为每秒k个单位，当运动时间为2秒时，以P、Q、C为顶点的三角形是等腰三角形，求此时k的值．

（3）若正方形OABC以每秒个单位的速度沿射线AO下滑，直至顶点C落到x轴上时停止下滑．设正方形OABC在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值围．

28．（10分）如图，在平面直角坐标系中，抛物线y=ax2﹣2ax﹣3a（a＞0）与x轴交于A、B两点（点A在点B左侧），经过点A的直线l：y=kx+b与y轴交于点C，与抛物线的另一个交点为D，且CD=4AC．

（1）直接写出点A的坐标，并用含a的式子表示直线l的函数表达式（其中k、b用含a的式子表示）．（2）点E为直线l下方抛物线上一点，当△ADE的面积的最大值为时，求抛物线的函数表达式；（3）设点P是抛物线对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否为矩形？若能，求出点P的坐标；若不能，请说明理由．

参考答案与试题解析

一、选择题

1． C．2． B．3． D．4． D．5． C．6． B．7．【解答】解：∵AB=AC，AD平分∠BAC，

∴AD⊥BC，

∴∠ADC=90°，

∵点E为AC的中点，

∴DE=CE=AC=．

∵△CDE的周长为21，

∴CD=6，

∴BC=2CD=12．

故选C．

8．【解答】解：∵抛物线y=ax2+bx+c的对称轴为x=1，∴根据二次函数的对称性得：点（3，0）的对称点为（﹣1，0），

∵当x=﹣1时，y=a﹣b+c=0，

∴a﹣b+c 的值等于0．

故选B ．

9．【解答】解：设CG=xm，

由图可知：EF=（x+20）?tan45°，FG=x?tan60°，则（x+20）tan45°+30=xtan60°，

解得x==25（+1），

则FG=x?tan60°=25（+1）×=（75+25）m．

故选C．

10．【解答】解：∵把△AOB绕点A顺时针旋转120°，得到△ADC，点M是BC边上的一点，

∴AM=AM′，

∴AM′+DM的最小值=AM+DM的最小值，作点D关于直线OB的对称点D′，连接AD′交OB 于M，

则AD′=AM′+DM的最小值，

过D作DE⊥x轴于E，

∵∠OAD=120°，

∴∠DAE=60°，

∵AD=AO=3，

∴DE=×3=，AE=，

∴D（，），

∴D′（﹣，），

设直线AD′的解析式为y=kx+b，

∴，

∴，

∴直线AD′的解析式为y=﹣x+，

当x=0时，y=，

∴M（0，），

故选A．

二、填空题

11．（a+1）（a﹣1）．12． x＞﹣2．

13．【解答】解：∵a∥b，∠1=56°，

∴∠2=∠1=56°，

∴∠3=∠2=56°，

∵MN⊥a，

∴∠M=180°﹣∠3﹣90°=180°﹣56°﹣90°=34°．

故答案为：34°．

14．【解答】解：由题意可得，

被调查的学生有：20÷=240（人），

则选择跳绳的有：240﹣20﹣80﹣40=100（人），

故答案为：100人．

15．【解答】解：由题意知，△=4﹣4（m﹣1）≥0，∴m≤2，

故答案为：m≤2．

16．【解答】解：由题意可得：AD∥CD′，

故△ADE∽△D′CB′，

则=，

设AD=x，则B′C=x，DB′=4﹣x，AB=CD′=4，

故=，

解得：x1=﹣2﹣2（不合题意舍去），x2=﹣2+2，则DB′=6﹣2，

则tan∠DAD′===．

故答案为：．

17．【解答】解：连接BC，如图所示：

∵∠CBE+∠BCE=∠AEC=60°，∴∠AOC+∠BOD=120°，

∴扇形AOC与扇形DOB面积的和==，

故答案为：．

18．【解答】解：如图，作PF⊥BC于点F，延长FP 交AD于点E，

∵AD∥BC，

∴∠PFC=∠DEP=90°，

∴∠CPF+∠PCF=90°，

∵∠DPC=90°，

∴∠CPF+∠DPE=90°，

∴∠PCF=∠DPE，

在△PCF和△DPE中，

∵，

∴△PCF≌△DPE（AAS），

∴PF=DE、PE=CF，

设PF=DE=x，则PE=CF=4﹣x，

∵S四边形ABCD=（AD+BC）?AB=12，

∴×（AD+4）×4=12，解得AD=2，

∴AE=BF=2﹣x，

∴FC=BC﹣BF=4﹣（2﹣x）=2+x，

可得2+x=4﹣x，解得x=1，

∴BP==，

故答案为：．

三、解答题

19．【解答】解：+|﹣|﹣﹣tan30°

=3+﹣1﹣

=

20．【解答】解：由①得，x＞﹣1，

由②得，x≤4，

∴不等式组的解集为﹣1＜x≤4．

21．【解答】解：（1﹣）÷

=

=

=，

当x=+1时，原式==．

22．【解答】解：设甲种奖品买了x件，乙种奖品买了y件．

根据题意得：，

解得：．

答：甲种奖品买了12件，乙种奖品买了18件．23．【解答】解：（1）所选的学生性别为女生的概率==，

故答案为：；

（2）画树形图得：

所以共有12种等可能的结果，满足要求的有4种．∴这2名学生来自同一个班级的概率为=．

24．【解答】（1）证明：∵∠A=90°，CE⊥BD，

∴∠A=∠BEC=90°．

∵BC∥AD，

∴∠ADB=∠EBC．

∵将斜边BD绕点B顺时针方向旋转至BC，

∴BD=BC．

在△ABD和△ECB中，

∴△ABD≌△ECB；

（2）∵△ABD≌△ECB，

∴AD=BE=3．

∵∠A=90°，∠BAD=30°，

∴BD=2AD=6，

∵BC∥AD，

∴∠A+∠ABC=180°，

∴∠ABC=90°，

∴∠DBC=60°，

∴弧CD的长为=2π．

25．【解答】解：（1）∵函数y=（x＞0，k是常数）的图象经过A（2，6），

∴k=2×6=12，

∵B（m，n），其中m＞2．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，

∴mn=12①，BD=m，AE=6﹣n，

∵△ABD的面积为3，

∴BD?AE=3，

∴m（6﹣n）=3②，

联立①②得，m=3，n=4，

∴B（3，4）；

设直线AB的解析式为y=kx+b（k≠0），

则，

∴，

∴直线AB的解析式为y=﹣2x+10

（2）∵A（2，6），B（m，n），

∴BE=m﹣2，CE=n，DE=2，AE=6﹣n，

∴DE?AE=2（6﹣n）=12﹣2n，

BE?CE=n（m﹣2）=mn﹣2n=12﹣2n，

∴DE?AE=BE?CE，

∴

（3）由（2）知，，

∵∠AEB=∠DEC=90°，

∴△DEC∽△BEA，

∴∠CDE=∠ABE

∴AB∥CD，∵AD∥BC，

∴四边形ADCB是平行四边形．

又∵AC⊥BD，

∴四边形ADCB是菱形，

∴DE=BE，CE=AE．

∴B（4，3）．

26．

【解答】（1）证明：连接AD，

∵AB为直径，

∴∠ACB=90°，

∴AD⊥BC，

∵AB=AC，

∴BD=CD；

（2）解：连接OD，

∵GF是切线，OD是半径，

∴OD⊥GF，

∴∠ODG=90°，

∵∠G=40°，

∴∠GOD=50°，

∵OB=OD，

∴∠OBD=65°，

∵点A、B、D、E都在⊙O上，

∴∠ABD+∠AED=180°，

∴∠AED=115°；

（3）解：∵AB=AC，

∴∠ABC=∠C，

∵OB=OD，

∴∠ABC=∠ODB，

∴∠ODB=∠C，

∴OD∥AC，

∴△GOD∽△GAF，

∴=，

∴设⊙O的半径是r，则AB=AC=2r，

∴AF=2r﹣2，

∴=，

∴r=3，

即⊙O的半径是3．

27．【解答】解：（1）如图1中，作CM⊥x轴于，AN ⊥x轴于N．连接AC、BO交于点K．

易证△AON≌△COM，可得CM=ON=4，OM=AN=3，

∴C（﹣3，4），∵CK=AK，OK=BK，∴K（，），B（1，7），

故答案为﹣3，4，1，7．

（2）由题意得，AO=CO=BC=AB=5，

当t=2时，CP=2．

①当点Q在OA上时，∵PQ≥AB＞PC，

∴只存在一点Q，使QC=QP．

作QD⊥PC于点D（如图2中），则CD=PD=1，

∴QA=2k=5﹣1=4，

∴k=2．

②当点Q在OC上时，由于∠C=90°所以只存在一点Q，使CP=CQ=2，

∴2k=10﹣2=8，∴k=4．

综上所述，k的值为2或4．

（3）①当点A运动到点O时，t=3．

当0＜t≤3时，设O’C’交x轴于点E，作A’F⊥x轴于点F（如图3中）．

则△A’OF∽△EOO’，

∴==，OO′=t，

∴EO′=t，

∴S=t2．

②当点C运动到x轴上时，t=4

当3＜t≤4时（如图4中），设A’B’交x轴于点F，

则A’O=A′O=t﹣5，

∴A′F=．

∴S=（+t）×5=．

综上所述，S=．

28．【解答】解：（1）令y=0，则ax2﹣2ax﹣3a=0，解得x1=﹣1，x2=3

∵点A在点B的左侧，

∴A（﹣1，0），

如图1，作DF⊥x轴于F，∴DF∥OC，

∴=，

∵CD=4AC，

∴==4，

∵OA=1，

∴OF=4，

∴D点的横坐标为4，

代入y=ax2﹣2ax﹣3a得，y=5a，

∴D（4，5a），

把A、D坐标代入y=kx+b得，

解得，

∴直线l的函数表达式为y=ax+a．

（2）如图2，过点E作EH∥y轴，交直线l于点H，

设E（x，ax2﹣2ax﹣3a），则H（x，ax+a）．

∴HE=（ax+a）﹣（ax2﹣2ax﹣3a）=﹣ax2+3ax+4a，由得x=﹣1或x=4，

即点D的横坐标为4，

∴S△ADE=S△AEH+S△DEH=（﹣ax2+3ax+4a）=﹣a（x﹣）2+a．

∴△ADE的面积的最大值为a，

∴a=，

解得：a=．

∴抛物线的函数表达式为y=x2﹣x﹣．

（3）已知A（﹣1，0），D（4，5a）．

∵y=ax2﹣2ax﹣3a，

∴抛物线的对称轴为x=1，

设P（1，m），

①若AD为矩形的边，且点Q在对称轴左侧时，则AD∥PQ，且AD=PQ，

则Q（﹣4，21a），

m=21a+5a=26a，则P（1，26a），

∵四边形ADPQ为矩形，

∴∠ADP=90°，

∴AD2+PD2=AP2，

∴52+（5a）2+（1﹣4）2+（26a﹣5a）2=（﹣1﹣1）2+（26a）2，

即a2=，

∵a＞0，

∴a=，

∴P1（1，），②若AD为矩形的边，且点Q在对称轴右侧时，则AD∥PQ，且AD=PQ，

则Q（4，5a），

此时点Q与点D重合，不符合题意，舍去；

③若AD是矩形的一条对角线，则AD与PQ互相平分且相等．

∴x D+x A=x P+x Q，y D+y A=y P+y Q，

∴x Q=2，

∴Q（2，﹣3a）．

∴y P=8a

∴P（1，8a）．

∵四边形APDQ为矩形，

∴∠APD=90°

∴AP2+PD2=AD2

∴（﹣1﹣1）2+（8a）2+（1﹣4）2+（8a﹣5a）2=52+（5a）2

即a2=，

∵a＞0，

∴a=

∴P2（1，4）

综上所述，以点A、D、P、Q为顶点的四边形能成为矩形，点P的坐标为（1，）或（1，4）．