二次函数与方程、不等式综合

一、二次函数与一元二次方程的联系

1. 直线与抛物线的交点

（1） y 轴与抛物线2y ax bx c =++得交点为()0c ，

. （2） 与y 轴平行的直线x h =与抛物线2y ax bx c =++有且只有一个交点()

2h ah bh c ++，.

（3） 抛物线与x 轴的交点:二次函数2y ax bx c =++的图像与x 轴的两个交点的横坐标1x 、2x ，是对应一元二次方程20ax bx c ++=的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程

的根的判别式判定：

①有两个交点?0?>?抛物线与x 轴相交；

②有一个交点（顶点在x 轴上）?0?=?抛物线与

x 轴相切； ③没有交点?

0?

. （4） 平行于x 轴的直线与抛物线的交点．可能有

0个交点、1个交点、2个交点.当有2

个交点时，两

交点的纵坐标相等，设纵坐标为k ，则横坐标是2ax bx c k ++=的两个实数根.

（5） 抛物线与x 轴两交点之间的距离．若抛物线2y ax bx c =++与x 轴两交点为()()1200A x B x ，

，，，由于1x 、2x 是方程20ax bx c ++=的两个根，故1212b c

x x x x a

+=-

?=， 12AB x x =-=

=

2. 二次函数常用的解题方法

（1） 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程； （2） 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式； （3） 根据图象的位置判断二次函数2y ax bx c =++中a ，b ，c 的符号，或由二次函数中a ，b ，c 的

符号判断图象的位置，要数形结合； （4） 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴

的一个交点坐标，可由对称性求出另一个交点坐标. （5） 与二次函数有关的还有二次三项式，二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函

数；以0a >时为例，二次函数、二次三项式和一元二次方程之间的内在联系如下： 中考要求

知识点睛

二次函数与方程、不等式综合

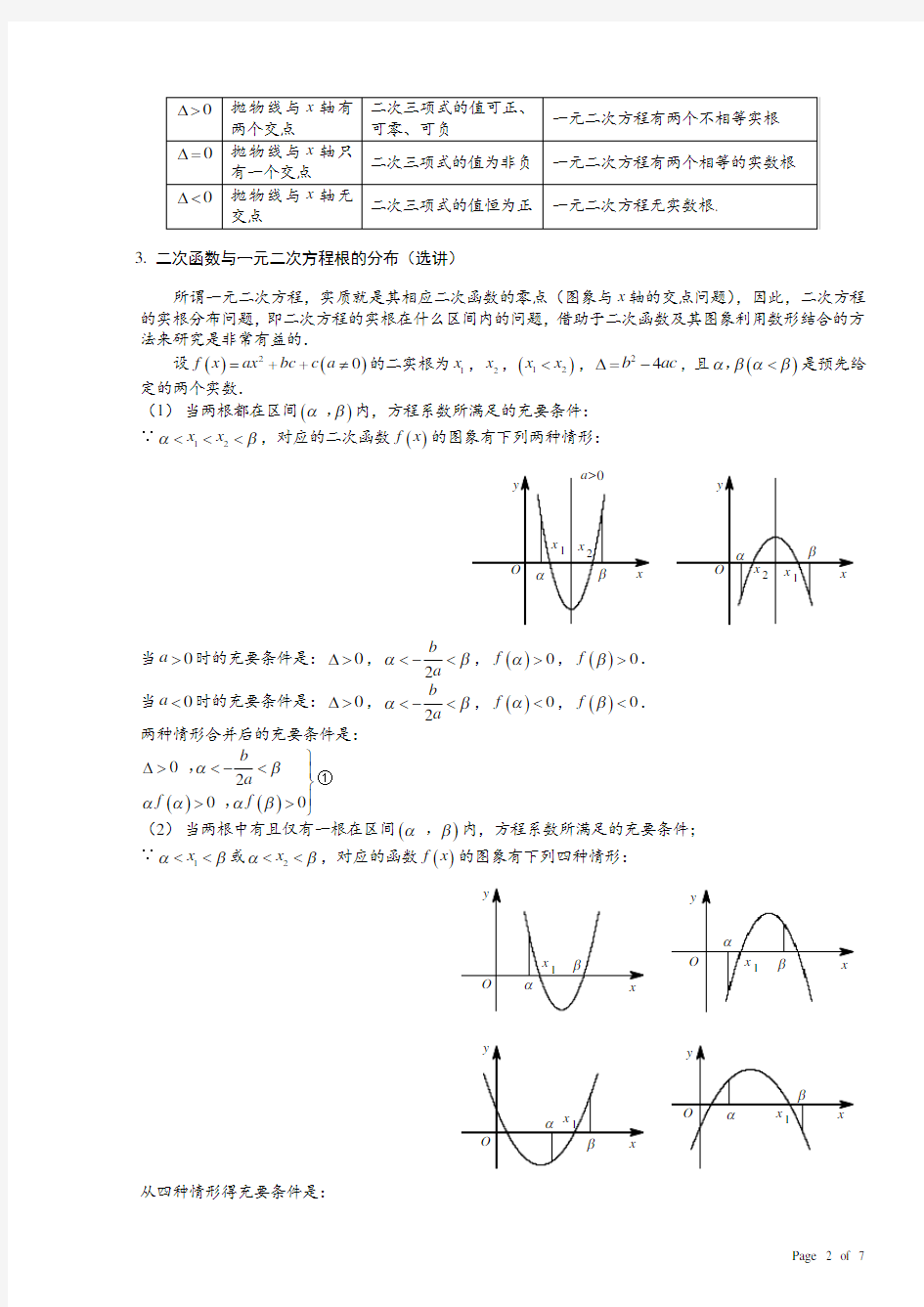
3. 二次函数与一元二次方程根的分布（选讲）

所谓一元二次方程，实质就是其相应二次函数的零点（图象与x 轴的交点问题），因此，二次方程的实根分布问题，即二次方程的实根在什么区间内的问题，借助于二次函数及其图象利用数形结合的方法来研究是非常有益的．

设(

)()20f x ax bc c a =++≠的二实根为1x ，2x ，()12x x <，

24b ac ?=-，且()αβαβ<，是预先给定的两个实数．

（1） 当两根都在区间()αβ，内，方程系数所满足的充要条件： ∵12x x αβ<<<，对应的二次函数()f x 的图象有下列两种情形：

当0a >时的充要条件是：0?>，2b

a αβ<-

<，()0f α>，()0f β>． 当0a <时的充要条件是：0?>，2b

a

αβ<-<，()0f α

<，()0f β<．

两种情形合并后的充要条件是：

()()0200b a f

f αβαααβ?

?><-

??>>?，，①

（2

） 当两根中有且仅有一根在区间()αβ，内，方程系数所满足的充要条件； ∵1x αβ<<或2x αβ<<，对应的函数

()f x 的图象有下列四种情形：

从四种情形得充要条件是：

()()0f f αβ?<②

（3） 当两根都不在区间[]αβ，

内方程系数所满足的充要条件： 当两根分别在区间[]αβ，

的两旁时； ∵12x x αβ<<<对应的函数()f x 的图象有下列两种情形：

当0a >时的充要条件是：()0f α<，()0f β<． 当0a <时充要条件是：()0f α>，()0f β>． 两种情形合并后的充要条件是：

()0f αα<，()0f αβ<③ 当两根分别在区间[]αβ，之外的同侧时：

∵12x x αβ<<<或12x x αβ<<<，对应函数()f x 的图象有下列四种情形：

当12x x α<<时的充要条件是：

0?>，2b

a

α-<，()0f αα>④

当12x x β<<时的充要条件是：

0?>，2b

a

β->，()0f αβ>⑤

（3）区间根定理

如果在区间()a b ，

上有()()0f a f b ?<，则至少存在一个()x a b ∈，，使得()0f x =． 此定理即为区间根定理，又称作勘根定理，它在判断根的位置的时候会发挥巨大的威力．

一、二次函数与方程、不等式综合

【例1】 已知二次函数()2f x x px q =++，且方程()0f x =与()20f x =有相同的非零实根．

（1）求

2

q

p 的值； （2）若()128f =，解方程()0f x =.

【例2】 已知二次函数2y x x a =-+(0)a >，当自变量x 取m 时，其相应的函数值小于0，那么下列结论

中正确的是（ ）

A .1m -的函数值小于0

B .1m -的函数值大于0

C .1m -的函数值等于0

D .1m -的函数值与0的大小关系不确定

【例3】 小明、小亮、小梅、小花四人共同探究代数式245x x -+的值的情况．他们作了如下分工：小明

负责找值为1时x 的值，小亮负责找值为0时x 的值，小梅负责找最小值，小花负责找最大值．几分钟后，各自通报探究的结论，其中错误的是（ ） A.小明认为只有当2x =时，245x x -+的值为1. B.小亮认为找不到实数x ，使245x x -+的值为0.

C.小梅发现245x x -+的值随x 的变化而变化，因此认为没有最小值

D.小花发现当x 取大于2的实数时，245x x -+的值随x 的增大而增大，因此认为没有最大值.

【例4】 已知关于x 的一元二次方程22410x x k ++-=有实数根，k 为正整数.

（1）求k 的值；

（2）当此方程有两个非零的整数根时，将关于x 的二次函数2241y x x k =++-的图象向下平移8个单位，求平移后的图象的解析式；

（3）在（2）的条件下，将平移后的二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余

部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线()1

2

y x b b k =+<与此图

象有两个公共点时，b 的取值范围.

【例5】 已知函数1y x =，22y x bx c =++，αβ，为方程120y y -=的两个根，点()M t T ，

在函数2y 的图象上．

（1）若11

32

αβ==，，求函数2y 的解析式；

（2）在（1）的条件下，若函数1y 与2y 的图象的两个交点为A B ，，当ABM ?的面积为

3

1

12时，求t 的值；

（3）若01αβ<<<，当01t <<时，试确定T αβ，，三者之间的大小关系，并说明理由．

【例6】 已知方程2210x px ++=的两个实根一个小于1，一个大于1，求p 的取值范围．

【例7】 已知方程20x ax b ++=的两根均大于2，求a b ，的关系式． 例题精讲

【例8】 设二次方程()

22120x a x a +-+-=有一根比1大，另一根比1-小，试确定实数a 的范围．

【例9】 若二次方程()22100ax x a -+=>在区间()13，内仅有较大实根，另一根不等于1，求a 的取值范围．

【例10】 已知方程20x bx c ++=有两个实数根s t 、，并且22x t <<，

．证明： （1）4c <； （2）4b c <+．

【例11】 若x 的二次方程242x mx n -+，因为方程()0f x =的解都位于01x <<的范围中，求正整数m n ，的

值．

【例12】 设有整系数二次函数()2f x ax bx c =++，其图像开口方向朝上，且与x 轴有两个交点，分别在

()10-，

、()1+∞，内，且()0f x =的判别式等于5，试求a b c ，，的值．

【例13】 已知方程()210x k x k --+=有两个大于2的实根，求k 的取值范围．

【例14】 若关于x 的二次方程()2271320x p x p p -++--=的两根α、β满足01α<<2β<<，求实数p

的取值范围．

【例15】 方程()211300x x a -++=有两实根，且两根都大于5，证明1

04

a <≤．

【例16】 已知方程240ax x b ++=()0a <的两实根为1x 、2x ，方程230ax x b ++=的两实根为α、β．

（1）若a 、b 均为负整数，且||1αβ-=，求a 、b 的值； （2）若12αβ<<<，12x x <，求证：1221x x -<<<．

【例17】 设a b ，是实数，二次方程20x ax b -+=的一个根属于区间[]11-，

，另一个根属于区间[]12，，求2a b -的取值范围．

【例18】 已知m 、n 均为正整数，若关于x 的方程2420x mx n -+=的两个实数根都大于1且小于2，求m 、

n 的值．

【例19】 实数a 在什么范围内取值时，关于x 的方程2(2)50x a x a --+-=的一个根大于0而小于2，另一

个根大于4而小于6？

【例20】 已知方程20ax bx c ++=有两个不同实根，求证：方程202b ax bx c k x a ?

?++++= ??

?至少有一个根，

在前一个方程的两根之间．（此处0k ≠）

【例21】 试证：若实数a b c ，，满足条件

021a b c

m m m

++=++，这里m 时正数，那么方程20ax bx c ++=有一个根介于0和1之间．

【例22】 阅读材料，解答问题．

例：用图象法解一元二次不等式：2230x x -->． 解：设223y x x =--，则y 是x 的二次函数． ∵10a =>，∴抛物线开口向上．

又∵当0y =时，2230x x --=，解得1213x x =-=，．

∴由此得抛物线223y x x =--的大致图象如图所示． 观察函数图象可知：当1x <-或3x >时，0y >．

∴2230x x -->的解集是1x <-或3x >．

（1）观察图象，直接写出一元二次不等式：2230x x --<的解集是____________； （2）仿照上例，用图象法解一元二次不等式：210x ->．

【例23】 阅读下列内容后，解答下列各题：

几个不等于0的数相乘，积的符号由负因数的个数决定． 例如：考查代数式()()12x x --的值与0的大小

当1x <时，1020x x -<-<，，∴()()120x x --> 当12x <<时，1020x x ->-<，，∴()()120x x --< 当2x >时，1020x x ->->，，∴()()120x x -->

综上：当12x <<时，()()120x x --<；当1x <或2x >时，()()120x x --> （

（2）由上表可知，当x 满足 时，()()()()21340x x x x ++--<； （3）运用你发现的规律，直接写出当x 满足 时，()()()7890x x x -+-<．

【例24】 如图所示，抛物线()20y ax bx c a =++≠与x 轴的两个交点分别为()10A -，

和()20B ，，当0y <时，x 的取值范围是 ．

【例25】 如下右图是抛物线2y ax bx c =++的一部分，其对称轴为直线1x =，若其与x 轴一交点为

()30B ，，则由图象可知，不等式20ax bx c ++>的解集是．

【例26】 解不等式：22x x x -<-<．

【例27】 对于满足04p ≤≤的所有实数p ，求使不等式243x px x p +>+-成立的x 的取值范围．

【例28】 已知二次函数2(1)1y x m x m =-++-

（1）求证：不论m 为任何实数，这个函数的图象与x 轴总有交点，

（2）m 为何实数时，这两个交点间的距离最小？这个最小距离是多少？

【例29】 先阅读理解下面的例题，再按要求解答：

例题：解一元二次不等式290x ->． 解：∵()()2933x x x -=+-，

∴()()330x x +->．

由有理数的乘法法则“两数相乘，同号得正”，有

（1）3030x x +>??->?（2）3030x x +

解不等式组（1），得3x >， 解不等式组（2），得3x <-，

故()()330x x +->的解集为3x >或3x <-， 即一元二次不等式290x ->的解集为3x >或3x <-．

问题：求分式不等式51

023

x x +<-的解集．

【例30】 不

x a +的解为x m >，求m 的最小值． 【例31】