几何最值—折叠求最值(含答案)

学生做题前请先回答以下问题

问题1：几何最值问题的处理思路：

①分析________、_________，寻找__________；

②若属于常见模型、结构，调用模型、结构解决问题；

若不属于常见模型，要结合所求目标，根据___________转化为基本定理或表达为函数解决问题．

转化原则：

尽量减少变量，向________、__________、__________靠拢，或使用同一变量表达所求目标．

问题2：几何最值问题转化为基本定理处理；

基本定理：

①______________________________；

②______________________________；

③______________________________；

④过圆内一点，最长的弦为直径，最短的弦为垂直于直径的弦．

几何最值—折叠求最值

一、单选题(共6道，每道16分)

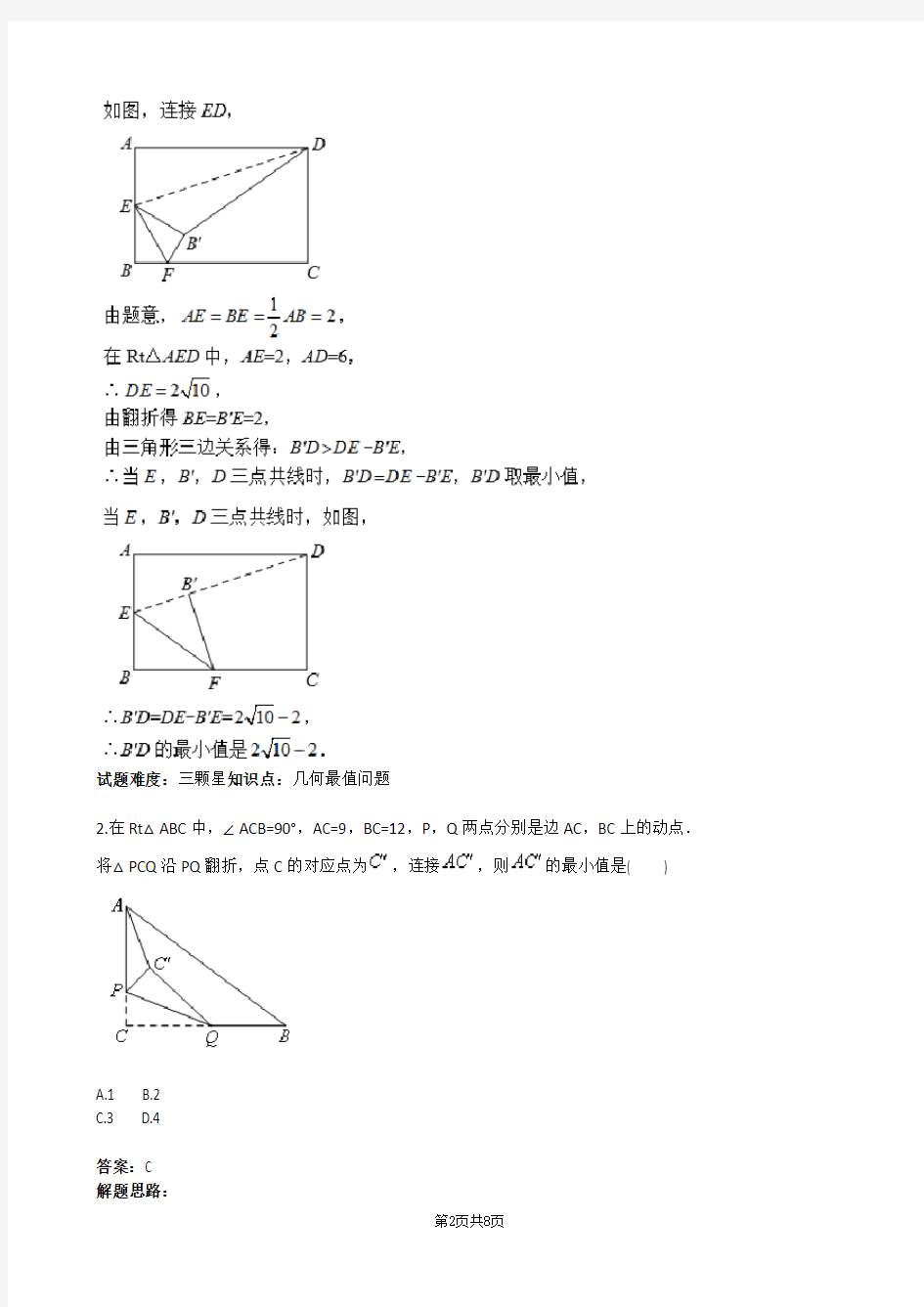
1.如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直

线折叠得到△，连接，则的最小值是( )

A. B.

C. D.4

答案：A

解题思路：

试题难度：三颗星知识点：几何最值问题

2.在Rt△ABC中，∠ACB=90°，AC=9，BC=12，P，Q两点分别是边AC，BC上的动点．将△PCQ沿PQ翻折，点C的对应点为，连接，则的最小值是( )

A.1

B.2

C.3

D.4

答案：C

解题思路：

试题难度：三颗星知识点：几何最值问题

3.如图，在△ABC中，∠BAC=120°，AB=AC=4，M，N分别为边AB，AC上的动点，将△AMN沿MN翻折，点A的对应点为，连接，则长度的最小值为( )

A. B.4

C. D.

答案：D

解题思路：

试题难度：三颗星知识点：翻折变换（折叠问题）

4.如图，在直角梯形ABCD中，AD⊥AB，AB=6，AD=CD=3，点E，F分别在线段AB，AD上，将△AEF沿EF 翻折，点A的落点记为P．当P落在直角梯形ABCD内部时，DP长度的最小值为( )

A.3

B.

C. D.1

答案：C

解题思路：

试题难度：三颗星知识点：翻折变换（折叠问题）

5.动手操作：在矩形纸片ABCD中，AB=5，AD=13．如图所示，折叠纸片，使点A落在BC边上的处，折痕为PQ，当点在BC边上移动时，折痕的端点P，Q也随之移动．若限定点P，Q分别在

AB，AD边上移动（包括端点），设=x，则x的取值范围是( )

A. B.

C. D.

答案：C

解题思路：

试题难度：三颗星知识点：几何最值问题

6.如图，在三角形纸片ABC中，已知∠ABC=90°，BC=5，AB=4，过点A作直线平行于

BC，折叠三角形纸片ABC，使直角顶点B落在直线上的点P处，折痕为MN，当点P在直线上移动时，折痕的端点M，N也随之移动．若限定端点M，N分别在AB，BC边上（包括端点）移动，则线段AP长度的最大值与最小值之差为( )

A. B.4

C.2

D.3

答案：C

解题思路：

试题难度：三颗星知识点：折叠问题（翻折变换）