实际问题与二次函数图形面积问题

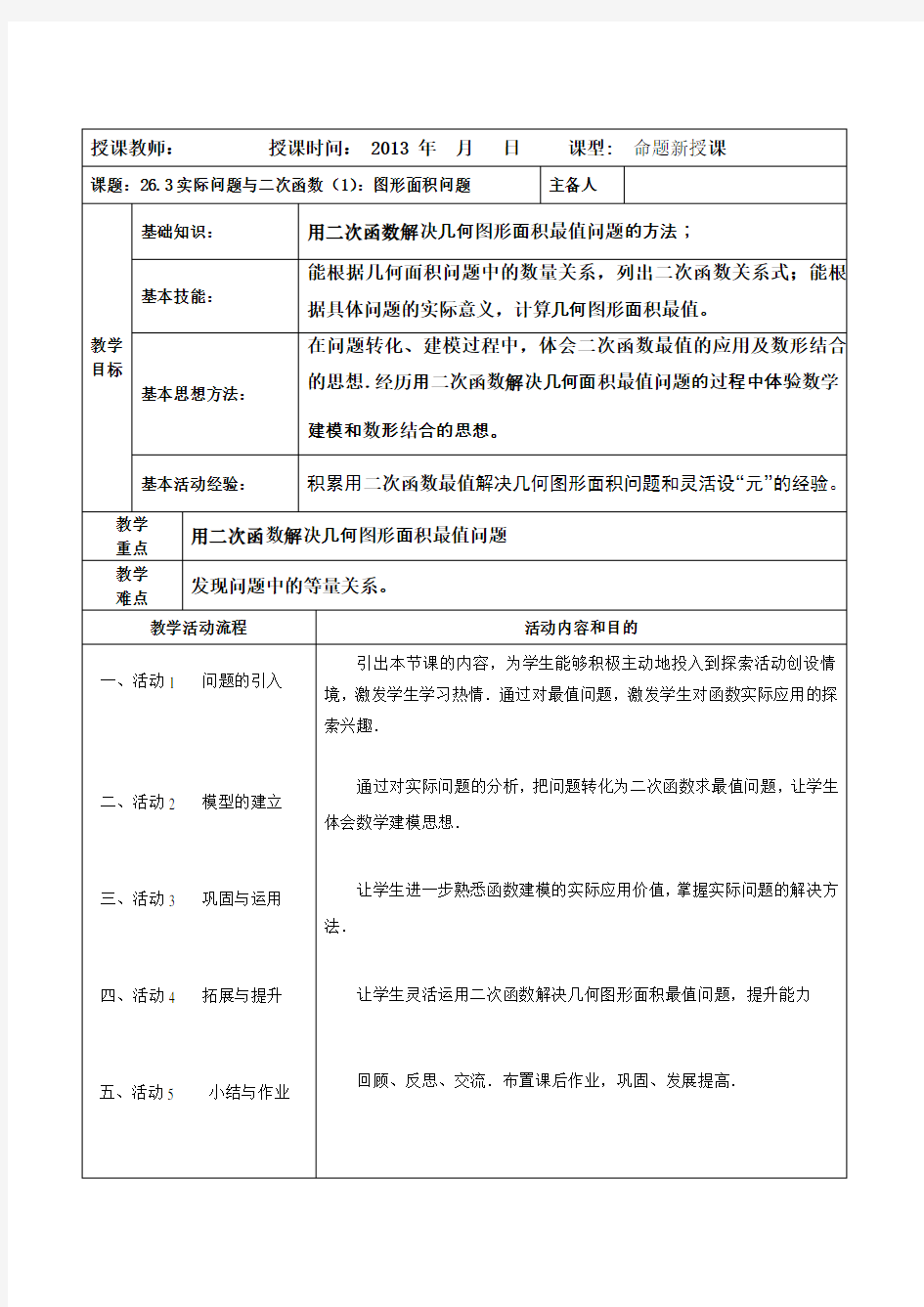
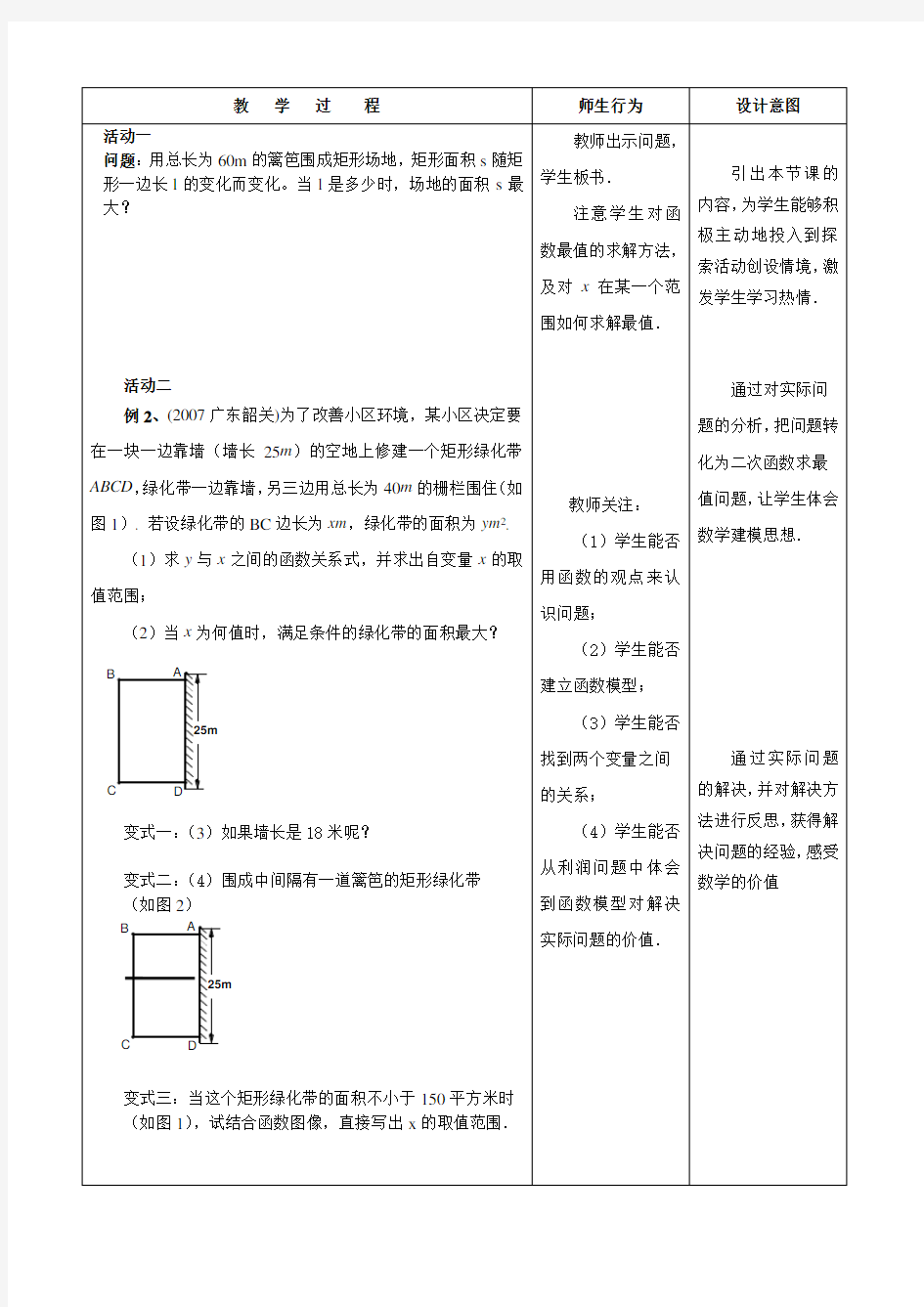
（2011贵州贵阳）

用长度一定的不锈钢材料设计成外观为矩形的框架（如图○1○2○3

中的一种）．

设竖档AB=x米，请根据以上图案回答下列问题：（题中的不

锈钢材料总长度均指各图中所有黑线的长度和，所有横档和竖

档分别与AD、AB平行）

（1）在图○1中，如果不锈钢材料总长度为12米，当x为多少

时，矩形框架ABCD的面积为3平方米？

（2）在图○2中，如果不锈钢材料总长度为12米，当x为多少

时，矩形框架ABCD的面积S最大？最大面积是多少？（

（3）在图○3中，如果不锈钢材料总长度为a米，共有n条竖档，

那么当x为多少时，矩形框架ABCD的面积S最大？最大面

积是多少？

活动四：

1、（2008山东省聊城市）如图，把一张长10cm，宽8cm的矩形硬

纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的

长方体盒子（纸板的厚度忽略不计）．

（1）要使长方体盒子的底面积为48cm2，那么剪去的正方形的边

长为多少？

（2）你感到折合而成的长方体盒子的侧面积会不会有更大的情

况？如果有，请你求出最大值和此时剪去的正方形的边长；如果

没有，请你说明理由；

（3）如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和

2个同样形状、同样大小的矩形，然后折合成一个有盖的长方体

盒子，是否有侧面积最大的情况；如果有，请你求出最大值和此

时剪去的正方形的边长；如果没有，请你说明理由．

教师出示问题，

学生独立解答．

（3）小组交流

教师关注：

（1）学生能否

用函数的观点来认

识问题；

（2）学生能否

建立函数模型；

（3）学生能否

找到两个变量之间

的关系；

（4）学生能否

从利润问题中体会

到函数模型对解决

实际问题的价值．

让学生进一步

熟悉函数建模的实

际应用价值，掌握实

际问题的解决方法．

让学生灵活运

用二次函数解决几

何图形面积最值问

题，提升能力

二次函数与图形面积

二次函数与图形面积涉及图形：三角形、不规则四边形。考查设问：（1）首先求出不规则三角形或者四边形的面积；（2）通过已知图形的面积确定未知三角形的面积；（3）通过未知三角形的面积求点坐标。例1：（2009陕西24题10分）如图，在平面直角坐标系中，OB OA ⊥，且2OB OA =，点A 的坐标(12)-，．（1）求点B 的坐标；（2）求过点A O B 、、的抛物线的表达式；（3）连接AB ，在（2）中的抛物线上求出点P ，使得ABP ABO S S =△△． 24．（本题满分10分）解：（1）过点A 作AF x ⊥轴，垂足为点F ，过点B 作则21AF OF ==，． OA OB ⊥， 90AOF BOE ∴∠+∠=°．又 90BOE OBE ∠+∠=°， AOF OBE ∴∠=∠． Rt Rt AFO OEB ∴△∽△． 2BE OE OB OF AF OA ∴ ===．（第24题）

24BE OE ∴==，． (42)B ∴，． ················································································· （2分）（2）设过点(12)A -，，(42)B ，，(00)O ，的抛物线为2y ax bx c =++． 216420.a b c a b c c -+=??∴++=??=?，，解之，得12320a b c ? =?? ? =-?? =??? ，，． ∴所求抛物线的表达式为213 22 y x x = -． ············································ （5分）（3）由题意，知AB x ∥轴．设抛物线上符合条件的点P 到AB 的距离为d ，则11 22 ABP S AB d AB AF = =△． 2d ∴=． ∴点P 的纵坐标只能是0，或4． ····················································· （7分）令0y =，得 213 022 x x -=．解之，得0x =，或3x =． ∴符合条件的点1(00)P ，，2(30)P ，．令4y =，得 213 4 22 x x -=．解之，得32 x ±= ． ∴符合条件的点33 ( 4)2P ，43(4)2 P +． ∴综上，符合题意的点有四个： 1(00)P ，，2(30)P ，，33 (4)2P ，43(4)2 P +． ···························· （10分）（评卷时，无1(00)P ，不扣分） 1.能够根据二次函数中不同图形的特点选择合适的方法解答图形的面积。

2020二次函数中的面积问题

二次函数——面积问题〖知识要点〗一．求面积常用方法： 1. 直接法（一般以坐标轴上线段或以与轴平行的线段为底边） 2. 利用相似图形，面积比等于相似比的平方 3. 利用同底或同高三角形面积的关系 4. 割补后再做差或做和（三边均不在坐标轴上的三角形及不规则多边形需把图形分解）二．常见图形及公式抛物线解析式y=ax 2 +bx+c (a ≠0) 抛物线与x 轴两交点的距离AB=︱x 1–x 2︱= a ? 抛物线顶点坐标（-a b 2, a b ac 442-）抛物线与y 轴交点（0，c ） “歪歪三角形中间砍一刀” ah S ABC 2 1=?，即三角形面积等于水平宽与铅垂高乘积的一半. y 轴交PCD 的面 3、已知抛物线c bx x y ++=2与y 轴交于点A ，与x 轴的正半轴交于B 、C 两点，且BC=2，S △ABC =3，则b = ， c = ．〖典型例题〗 ● 面积最大问题 1、二次函数c bx ax y ++=2 的图像与x 轴交于点A （-1,0）、B （3 ，0），与y 轴交于点C ，∠ACB=90°. （1）求二次函数的解析式；（2）P 为抛物线X 轴上方一点，若使得△PAB 面积最大，求P 坐标（3）P 为抛物线X 轴上方一点，若使得四边形PABC 面积最大，求P 坐标 (4) P 为抛物线上一点，若使得ABC PAB S S ??=2 1，求P 点坐标。 ● 同高情况下，面积比=底边之比 2．已知：如图，直线y=﹣x +3与x 轴、y 轴分别交于B 、C ，抛物线y=﹣x 2+bx +c 经过点B 、C ，点A 是 B 图1

二次函数与几何综合--面积问题

二次函数与几何综合--面积问题知识点睛 1.“函数与几何综合”问题的处理原则：_________________，__________________． 2.研究背景图形：①研究函数表达式．二次函数关注____________，一次函数关注__________ ． 2___________________________．找特殊图形、特殊位置关系，寻求边长和角度信息． 3．二次函数之面积问题的常见模型①割补求面积——铅垂法： ②转化法——借助平行线转化：若S △ABP =S △ABQ ，若S △ABP =S △ABQ ，当P ，Q 在AB 同侧时，当P ，Q 在AB 异侧时，PQ ∥AB ．AB 平分PQ ．例题示范例1：如图，抛物线y =ax 2+2ax -3a 与x 轴交于A ，B 两点（点A 在点 B 的左侧），与y 轴交于点 C ，且OA =OC ，连接AC ．（1）求抛物线的解析式．（2）若点P 是直线AC 下方抛物线上一动点，求△ACP 面积的最大值．（3）若点E 在抛物线的对称轴上，抛物线上是否存在点F ，使以A ，B ， E ， F 为顶点的四边形是平行四边形？若存在，求出所有满足条件的点F 的坐标；若不存在，请说明理由．第一问：研究背景图形【思路分析】读题标注，注意到题中给出的表达式中各项系数都只含有字母a ，可以求解A (-3，0)，B (1，0)，对称轴为直线x =-1；结合题中给出的OA =OC ，可得C (0，-3)，代入表达式，即可求得抛物线解析式．再结合所求线段长来观察几何图形，发现△AOC 为等腰直角三角形．【过程示范】解：（1）由2 23y ax ax a =+-(3)(1) a x x =+-可知(30)A -，，(10)B ，， ∵OA OC =， ∴(03)C -，，将(03)C -，代入2 23y ax ax a =+-，第二问：铅垂法求面积【思路分析】（1）整合信息，分析特征：由所求的目标入手分析，目标为S △ACP 的最大值，分析A ，C 为定点，P 为动点且P 在1()2 APB B A S PM x x =??-△

九年级数学：二次函数与图形面积

二次函数与图形面积练习题基础题知识点二次函数与平面面积 1．如图，假设篱笆(虚线部分)的长度为16 m ，则所围成矩形ABCD 的最大面积是( ) A ．60 m 2 B ．63 m 2 C ．64 m 2 D ．66 m 2 2．用一根长为40 cm 的绳子围成一个面积为a cm 2的长方形，那么a 的值不可能为( ) A ．20 B ．40 C ．100 D ．120 3．用长8 m 的铝合金条制成使窗户的透光面积最大的矩形窗框(如图)，那么这个窗户的最大透光面积是 ( ) A.6425 m 2 B.43 m 2 C.83 m 2 D ．4 m 2 4．如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止，设小三角形移动的距离为x ，两个三角形重叠面积为y ，则y 关于x 的函数图象是( ) 5．如图，利用一面墙(墙的长度不超过45 m)，用80 m 长的篱笆围一个矩形场地．当AD ＝________时，矩形场地的面积最大，最大值为________． 6．如图，在△ABC 中，∠B ＝90°，AB ＝8 cm ，BC ＝6 cm ，点P 从点A 开始沿AB 向B 点以2 cm/s 的速度移动，点Q 从点B 开始沿BC 向C 点以1 cm/s 的速度移动，如果P ，Q 分别从A ，B 同时出发，当△PBQ 的面积为最大时，运动时间t 为________s.

7．将一根长为20 cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是________ cm2. 8．已知直角三角形两条直角边的和等于20，两条直角边各为多少时，这个直角三角形的面积最大？最大值是多少？ 9．某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形，抽屉底面周长为180 cm，高为20 cm.请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？(材质及其厚度等暂忽略不计)

二次函数与图形面积教案

课题：二次函数与图形面积撰写：陈天灵审核：______ 授课日期：__月__日教学课时：第 6 周第 1 课教学目标知识与技能目标通过本节学习，巩固二次函数y=ax2+bx+c(a≠0）的图象与性质，理解顶点与最值的关系，会求解最值问题。过程与方法目标通过观察图象，理解顶点的特殊性，会把实际问题中的最值转化为二次函数的最值问题，通过动手动脑，提高分析解决问题的能力，并体会一般与特殊的关系，了解数形结合思想、函数思想。情感、态度与价值观目标通过学生之间的讨论、交流和探索，建立合作意识，提高探索能力，激发学习的兴趣和欲望，体会数学在生活中广泛的应用价值。教学重点利用二次函数y=ax2+bx+c(a≠0）的图象与性质，求面积最值问题教学难点对函数图象顶点、端点与最值关系的理解与应用教学过程环节教学内容调整意见复习旧知导入新课1.二次函数y=a(x-h)2+k的图象是一条抛物线，它的对称轴是直线x=h，顶点坐标是 (h，k) 。 2.二次函数的一般式是，它的图像的对称轴是，顶点坐标是 . 当a>0时，开口向向上，有最低点，函数有最小值，是；.当a<0时，开口向向下，有最高点，函数有最大值，是。 3.二次函数y=2(x-3)2+5的对称轴是直线x=3, 顶点坐标是 (3 ，5) 。当x= 3时，y有最小值，是 5 . 4.5详见课件。自学指导阅读教材P49“问题”，解决下面问题。 1、问题1中是通过什么方法来求出小球在运动中的最大高度？ 2.归纳：一般地，当a>0(a<0)时，抛物线y=ax2+bx+c的的顶点是最低 ( 高_)点,当x=________时，二次函数y=ax2+bx+c有最大（小）值________. 阅读教材P49-P50“探究1”，解决下面问题 1.“探究1”中，场地面积S与边长l之间是什么关系？你能写出它们的关系式 c bx ax y+ + =2 a b x 2 - = 直线) 4 4 , 2 ( 2 a b ac a b- - a b ac 4 42 - a b ac 4 42 -

二次函数与几何图形面积

专题3: 二次函数中的面积计算问题例1. 如图，二次函数图象与轴交于A,B两点(A在B的左边)，与轴交于点C，顶点为M ，为直角三角形, 图象的对称轴为直线，点是抛物线上位于两点之间的一个动点，则的面积的最大值为（） A． B． C． D．

练习：1、如图，抛物线y＝－x 2＋bx＋c与x轴交于A(1，0)，B(－3，0)两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由；（3）在（1）中的抛物线上的第二象限内是否存在一点P，使△PBC的面积最大？，若存在，求出点P的坐标及△PBC的面积最大值；若不存在，请说明理由．例2.如图1，抛物线顶点坐标为点C(1，4)，交x轴于点A(3，0)，交y轴于点B. （1）求抛物线和直线AB的解析式；（2）求△CAB的铅垂高CD及S△CAB ；

（3）设点P是抛物线（在第一象限内）上的一个动点，是否存在一点P，使 S△PAB＝ S△CAB，若存在，求出P点的坐标；若不存在，请说明理由. 练习：2、如图，在平面直角坐标系中，Rt△AOB的顶点坐标分别为A（0，2），O（0，0），B（4，0），把△AOB绕点O逆时针方向旋转90°得到△COD（点A转到点C的位置），抛物线y＝ax 2＋bx＋c(a≠0)经过C、D、B三点．（1）求抛物线的解析式；（2）若抛物线的顶点为P，求△PAB的面积；（3）抛物线上是否存在点M，使△MBC的面积等于△PAB的面积？若存在，请求出点M的坐标；若不存在，请说明理由．

中考数学解答专项二次函数与图形面积练习(九大专题)

二次函数与图形面积 1. 已知抛物线y ＝－x 2 ＋bx ＋c 的图象过点A (4，0)、B (1，3)． (1)求抛物线的表达式； (2)求出抛物线的对称轴和顶点坐标； (3)抛物线的对称轴为直线l ，设抛物线上的点P (m ，n )在第四象限，点P 关于直线l 的对称点为E ，点E 关于x 轴的对称点为F ，若以O 、A 、P 、F 四点组成的四边形的面积为20，求m 、n 的值．解：(1)将点A (4，0)、B (1，3)代入抛物线y ＝－x 2 ＋bx ＋c 得???=++-=++-3 10 416c b c b ，解得 ???==0 4 c b ， ∴抛物线的表达式为y ＝－x 2 ＋4x ； (2)对称轴为直线x ＝－b 2a ＝－ () 124 -? ＝2，顶点坐标为(2，4)； (3)抛物线的对称轴为直线x ＝2，设抛物线上的点P (m ，n )在第四象限，则点P 关于直线l 的对称点为E (4－m ，n )，点E 关于x 轴的对称点为F (4－m ，－n )，若以O 、A 、P 、F 四点组成的四边形的面积为20，则S 四边形OPAF ＝S △AOF ＋S △AOP ＝12×4×(－n )＋1 2×4×(－n )＝－4n ＝20，得n ＝－5，将(m ，－5) 代入y ＝－x 2 ＋4x ，解得m ＝5或m ＝－1. ∵点P (m ，n )在第四象限， ∴m ＝5，n ＝－5. 2. 抛物线y ＝ax 2 ＋bx ＋c 经过原点O 、B (1，3)、C (2，2)，与x 轴交于另一点N . (1)求抛物线的表达式； (2)连接BC ，若点A 为BC 所在直线与y 轴的交点，在抛物线上是否存在点P ，使得S △OAP ＝ 8 15 S △ONP ，若存在，请求出点P 的坐标；若不存在，请说明理由．解：(1)将0(0，0)、B (1，3)、C (2，2)三点的坐标分别代入抛物线 y ＝ax 2 ＋bx ＋c ，可得?????==++=++02243c c b a c b a ，解得?? ? ??==-=052c b a ， ∴所求抛物线的表达式为y ＝－2x 2 ＋5x ； (2)存在，

初三二次函数与几何图形面积(有答案)

在动点变化过程中，会产生的几何图形的形状发生改变，由此可引出求该图形的面积，建立面积与动点坐标，或动点的运动时间的函数关系。面积的求法主要有两种：①直接求面积；②割补法求面积；无论哪种求法，都需要用参数表示线段的长度。【例1】（改编题）如图，抛物线233y mx mx =+-（0m >）与y 轴交于点C ,与x 轴交于A 、B 两点，点A 在点B 的左侧，且1 tan 3OCB ∠=． ⑴求此抛物线的解析式； ⑵如果点D 是线段AC 下方抛物线上的动点，设D 点的横坐标为x ，ACD ?的面积为S ，求S 与x 的关系式，并求当S 最大时，点D 的坐标；【答案】⑴239 344 y x x = +- ⑵方法一：如图，连接OD ，可求(40)A -，设点239 (3)44D x x x +-，，则ACD AOD DOC AOC S S S S ????=+- 2139 4(3)244OAD S x x ?=??--+ 1 3()2 OCD S x ?=??- 1 4362 AOC S ?=??= ∴23 62S x x =--，当2x =-时，S 取得最大值为6 此时点D 的坐标为9(2)2 --，方法二：过点D 作DN x ⊥轴于点N ，交AC 于点M 转化：ACD AMD DMC S S S ???=+，下略【注意】本题由综合题改编而来，去掉了平行四边形的存在性问题，就 “三角形的面积与动点之间的关系” 例题精讲二次函数与几何图形面积

的问题，本题具有一定的代表性，给出的两种解法，都是采用的割补法，如果学生程度不怎么好，建议只讲第二种方法。转化的目的：构造水平和竖直方向上的底和高，使求解更方便，更简单【例2】已知：如图，抛物线2334y x =-+与x 轴交于点A 、点B ，与直线3 4 y x b =-+相交于点B 、点C ，直线3 4y x b =-+与y 轴交于点E ． ⑴求直线BC 的解析式． ⑵若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A ，B 重合），同时，点 N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB ?的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB ?的面积最大，最大面积是多少？【答案】⑴33 42 y x =-+ ⑵过点N 作NP ⊥MB 于点P ∵EO ⊥MB ， ∴NP ∥EO ∴△BNP ∽△BEO ∴ BE BN ＝ EO NP 由直线y ＝－43x ＋23可得：E （0，23 ）在△BEO 中，∵OB ＝2，EO ＝23，∴BE ＝2 5 ∴ 252t ＝ 2 3NP ，∴NP ＝56 t ∴S ＝ 21·(4－t )·56t ＝－53t 2＋5 12t ＝－ 53( t －2)2＋5 12 （0＜t ＜4） ∵此抛物线开口向下，∴当t ＝2时，S 最大＝ 5 12 ∴当点M 运动2秒时，△MNB 的面积最大，最大面积是 5 12 【注意】构造在求解三角形面积的时候，如果需要构造三角形的高，应优先考虑，水平和竖直方向进行构造，求高的途径可以有：①相似三角形对边成比例；②锐角三角函数；③勾股定理【例3】如图①，梯形ABCD 中，90C ∠=?．动点E 、F 同时从点B 出发，点E 沿折线BA AD DC --运动到点C 时停止运动，点F 沿BC 运动到点C 时停止运动，它们运动时的速度都是1cm/s ．设E 、 F 出发t s 时，EBF ?的面积为y 2cm ．已知y 与t 的函数图象如图②所示，其中曲线OM 为抛物线的一部分，MN 、NP 为线段．请根据图中的信息，解答下列问题： ⑴梯形上底的长______AD =cm ，梯形ABCD 的面积＝__________cm 2；

二次函数与三角形的面积问题

二次函数与三角形的面积问题【教学目标】 1.能够根据二次函数中不同图形的特点选择合适的方法解答图形的面积。 2.通过观察、分析、概括、总结等方法了解二次函数面积问题的基本类型，并掌握二次函数中面积问题的相关计算，从而体会数形结合思想和转化思想在二次函数中的应用。 3.掌握利用二次函数的解析式求出相关点的坐标，从而得出相关线段的长度，利用割补方法求图形的面积。【教学重点和难点】 1.运用 2铅垂高水平宽? = s； 2.运用y； 3.将不规则的图形分割成规则图形，从而便于求出图形的总面积。【教学过程】类型一：三角形的某一条边在坐标轴上或者与坐标轴平行例1.已知：抛物线的顶点为D（1，-4），并经过点E（4，5），求: （1）抛物线解析式；（2）抛物线与x轴的交点A、B，与y轴交点C；（3）求下列图形的面积△ABD、△ABC、△ABE、△OCD、△OCE。解题思路：求出函数解析式________________；写出下列点的坐标：A______；B_______；C_______；求出下列线段的长：AO________；BO________；AB________；OC_________。求出下列图形的面积△ABD、△ABC、△ABE、△OCD、△OCE。

一般地，这类题目的做题步骤：1.求出二次函数的解析式；2.求出相关点的坐标；3.求出相关线段的长；4.选择合适方法求出图形的面积。变式训练1.如图所示，已知抛物线()02 ≠++=a c bx ax y 与x 轴相交于两点A ()0,1x ， B ()0,2x ()21x x <，与y 轴负半轴相交于点 C ，若抛物线顶点P 的横坐标是1，A 、 B 两点间的距离为4，且△ABC 的面积为6。（1）求点A 和B 的坐标；（2）求此抛物线的解析式；（3）求四边形ACPB 的面积。类型二：三角形三边均不与坐标轴轴平行，做三角形的铅垂高。（歪歪三角形拦腰来一刀）关于2 铅垂高水平宽?= ?S 的知识点：如图1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法：ah S ABC 2 1 =?，即三角形面积等于水平宽与铅垂高乘积的一半. 想一想：在直角坐标系中，水平宽如何求？铅垂高如何求？例2．如图2，抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0)，交y 轴于点B .(1)求抛物线和直线AB 的解析式；(2)点P 是抛物线(在第一象限内)上的一个动点，连结P A ，PB ，当P 点运动到顶点C 时，求△CAB 的铅垂高CD 及CAB S ?；(3)是否存在一点P ，使S △P AB =8 9 S △CAB ，若存在，求出P 点的坐标；若不存在，请说明理由. 解题思路：求出直线AB 的解析式是为了求出D ．点的纵坐标．．．．．D y ；铅垂高，注意线段的长度非负性；分析P 点在直线AB 的上方还是下方? x A B O C y P B C 铅垂高水平宽 h a 图1 图-2 x C O y A B D 1 1

中考数学复习二次函数与三角形的面积问题

中考数学复习二次函数与三角形的面积问题 Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#

二次函数与三角形的面积问题 1.运用2 铅垂高水平宽?=s ； 2.运用y ； 3. 例1.已知：抛物线的顶点为D （1，-4），并经过点E （4，5），求: （1）抛物线解析式；（2）抛物线与x 轴的交点A 、B ，与y 轴交点C ；（3）求下列图形的面积△ABD 、△ABC 、△ABE 、△OCD 、△OCE 。解题思路：求出函数解析式________________；写出下列点的坐标：A______；B_______；C_______；求出下列线段的长：AO________；BO________；AB________；OC_________。求出下列图形的面积△ABD 、△ABC 、△ABE 、△OCD 、△OCE 。一般地，这类题目的做题步骤：1.求出二次函数的解析式；2.求出相关点的坐标；3.求出相关线段的长；4.选择合适方法求出图形的面积。训练1.如图所示，已知抛物线()02≠++=a c bx ax y 与x 轴相交于两点A ()0,1x ， B ()0,2x ()21x x <，与y 轴负半轴相交于点C ，若抛物线顶点P 的横坐标是1，A 、 B 两点间的距离为4，且△ABC 的面积为6。 P

（1）求点A 和B 的坐标；（2）求此抛物线的解析式；（3）求四边形ACPB 的面积。类型二：三角形三边均不与坐标轴轴平行，做三角形的铅垂高。（歪歪三角形拦腰来一刀）关于2铅垂高水平宽?= ?S 的知识点：如图1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高 (h )”.我们可得出一种计算三角形面积的新方法：的一ah S ABC 21=?，即三角形面积等于水平宽与铅垂高乘积半. 想一想：在直角坐标系中，水平宽如何求铅垂高如何求例2．如图2，抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0)，交y 轴于点B .(1)求抛物线和直线AB 的解析式；(2)点P 是抛物线(在第一象限内)上的一个动点，连结PA ，PB ，当P 点运动到顶点C 时，求△CAB 的铅垂高CD 及出 CAB S ?；(3)是否存在一点P ，使S △PAB =89S △CAB ，若存在，求P 点的坐标；若不存在，请说明理由. 标．D y ；解题思路：求出直线AB 的解析式是为了求出D ．点的纵坐．．．．铅垂高D C y y CD -=，注意线段的长度非负性；分析P 点在直线AB 的上方还是下方

中考复习：二次函数与图形面积

二次函数与图形面积 ★1.已知抛物线y ＝－x 2＋bx ＋c 的图象过点A (4，0)、B (1，3)． (1)求抛物线的表达式； (2)求出抛物线的对称轴和顶点坐标； (3)抛物线的对称轴为直线l ，设抛物线上的点P (m ，n )在第四象限，点P 关于直线l 的对称点为E ，点E 关于x 轴的对称点为F ，若以O 、A 、P 、F 四点组成的四边形的面积为20，求m 、n 的值．解：(1)将点A (4，0)、B (1，3)代入抛物线y ＝－x 2＋bx ＋c 得 ?? ?=++-=++-310416c b c b ，解得???==0 4 c b ， ∴抛物线的表达式为y ＝－x 2＋4x ； (2)对称轴为直线x ＝－b 2a ＝－ () 124 -?＝2，顶点坐标为(2，4)； (3)抛物线的对称轴为直线x ＝2，设抛物线上的点P (m ，n )在第四象限，则点P 关于直线l 的对称点为E (4－m ，n )，点E 关于x 轴的对称点为F (4－m ，－n )，若以O 、A 、P 、F 四点组成的四边形的面积为20，则S 四边形OP AF ＝S △AOF ＋S △AOP ＝12×4×(－n )＋12×4×(－n )＝－4n ＝20，得n ＝－5，将(m ，－5)代入y ＝－x 2＋4x ，解得m ＝5或m ＝－1. ∵点P (m ，n )在第四象限， ∴m ＝5，n ＝－5. ★2.如图，抛物线y ＝ax 2＋bx ＋c 经过原点O 、B (1，3)、C (2，2)，

与x 轴交于另一点N . (1)求抛物线的表达式； (2)连接BC ，若点A 为BC 所在直线与y 轴的交点，在抛物线上是否存在点P ，使得S △OAP ＝8 15S △ONP ，若存在，请求出点P 的坐标；若不存在，请说明理由．第2题图解：(1)将0(0，0)、B (1，3)、C (2，2)三点的坐标分别代入抛物线 y ＝ax 2＋bx ＋c ，可得?????==++=++02243c c b a c b a ，解得??? ??==-=052c b a ， ∴所求抛物线的表达式为y ＝－2x 2＋5x ； (2)存在，设BC 所在直线的表达式为y ＝kx ＋b ，将点B 、C 的坐标代入可得 ?? ?+=+=b k b k 223，解得???=-=4 1 b k ，则y ＝－x ＋4. 把x ＝0代入y ＝－x ＋4得y ＝4， ∴点A (0，4)，

二次函数求面积

二次函数中常见图形的面积问题(1) 1、说出如何表示各图中阴影部分的面积？例2.解答下列问题：如图1，抛物线顶点坐标为点C (1，4)，交x 轴于点A (3，0)，交y 轴于点 B . （1）求抛物线和直线AB 的解析式；（2）求△CAB 的铅垂高CD 及S △CAB ；（3）设点P 是抛物线（在第一象限内）上的一个动点，是否存在一点P ，使S △P AB ＝8 9 S △CAB ，若存在，求出P 点的坐标；若不存在，请说明理由. 图五图四图六图二图一图三图2

1．（2013哈尔滨，24，6分）某水渠的横截面呈抛物线形，水面的宽为AB (单位：米)，现以AB 所在直线为x 轴，以抛物线的对称轴为y 轴建立如图所示的平面直角坐标系，设坐标原点为O ，已知AB =8米，设抛物线解析式为y =ax 2-4． (1)求a 的值； (2)点C (-1,m )是抛物线上一点，点C 关于原点O 的对称点为点D ，连接CD 、BC 、BD ，求△BCD 的面积． 2、抛物线322 +--=x x y 与x 轴交与A 、B （点A 在B 右侧），与y 轴交与点C ， D 为抛物线的顶点，连接BD ，CD ，（1）求四边形BOCD 的面积. （2）求△BCD 的面积.（提示：本题中的三角形没有横向或纵向的边，可以通过添加辅助线进行转化，把你想到的思路在图中画出来，并选择其中的一种写出详细的解答过程）

3.已知二次函数322--=x x y 与x 轴交于A 、B 两点（A 在B 的左边），与y 轴交于点C ，顶点为P. （1）求A 、B 、C 、P 的坐标，并求出一个刚刚提出的图形面积；（2）在抛物线上（除点C 外），是否存在点N ，使得ABC NAB S S ??=, 若存在，请写出点N 的坐标；若不存在，请说明理由。变式一：在抛物线的对称轴上是否存点N ，使得ABC NAB S S ??=，若存在直接写出N 的坐标；若不存在，请说明理由.

中考数学专题一(二次函数面积问题)

专题一：二次函数中的面积问题（一）利用割补：将图形割（补）成三角形或梯形面积的和差，其中需使三角形的底边在坐标轴上或平行于坐标轴；（例如以下4、5两图中，连结BD 解法不简便。）例1：如图抛物线与轴交于两点，与轴交于点, （1）k=___-3_____,点的坐标为___(-1,0)___，点的坐标为____(3,0)____；（2）设抛物线的顶点为，求的面积；（3）在轴下方的抛物线上是否存在一点，使四边形的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；解：（2）M （1，-4）； (3)设, ,当m =52时，四边形ABDC 面积最大，为52。练习1、如图，抛物线与轴交于A 、B 两点，与轴交于点C ，抛物线的对称轴交轴于点D ，已知A （﹣1，0），C （0，2）．（1）求抛物线的表达式；（2）点E 是线段BC 上的一个动点，过点E 作轴的垂线与抛物线相交于点F ，当点E 运动到什么位置时，四边形CDBF 的面积最大？求出四边形CDBF 的最大面积及此时E 点的坐标．解：（1）y =-12x 2+3 2 x +2 (2)对称轴x =- b 2a =32,\D (3 2 ,0)，令-12x 2+32x +2=0,x 1=-1,x 2=4,\B (4,0) ,设F (a ,-12a 2+3 2 a +2), y =x 2-2x +k x A ,B y C (0,-3)A B M D BCM x D ABDC S D BCM =S D OCM +S D BOM -S D BOC = 12′3′1+12′3′4-1 2′3′3=3D (m ,m 2-2m -3) S 四边形ABDC =S D AOC +S D BOD +S D COD = 12′1′3+12′|m 2-2m -3|′3+1 2′m ′3=-12m 2+5 2m +3 - b 2a =-52 2′(-12 )=52,0

九年级数学：利用二次函数解决几何图形面积最值问题

九年级数学：利用二次函数解决几何图形面积最值问题知|识|目|标经历利用二次函数的有关性质解决实际问题的过程,会利用二次函数解决几何面积的最值问题．目标会利用二次函数解决面积最值问题例1 教材补充例题将一根长为100 cm的铁丝围成一个矩形框,要想使铁丝框的面积最大,应怎样围？【归纳总结】应用二次函数解决面积最大(小)值问题的步骤 (1)分析题中的变量与常量． (2)根据几何图形的面积公式建立函数模型． (3)结合函数图像及性质,考虑实际问题中自变量的取值范围,求出面积的最大(小)值．例2 教材“复习巩固”第15题针对训练如图5－5－2,在矩形ABCD中,AB ＝6 cm,BC＝12 cm,点P从点A出发沿AB边向点B以1 cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2 cm/s的速度运动,P,Q两点在分别到达B,C 两点后就停止运动,设经过t s时,△PBQ的面积为S cm2. (1)求S与t之间的函数表达式(不需要写出自变量的取值范围)； (2)当t取何值时,S的值最大？最大值是多少？

图5－5－2 【归纳总结】几何问题中应用二次函数时的三个注意点 (1)点在线段上的取值范围． (2)顶点的横坐标、纵坐标必须符合实际意义． (3)自变量和函数值的单位．知识点建立函数模型,解决图形中的最值问题利用二次函数解决几何图形面积最值问题的一般步骤： (1)列：分析几何图形的特点,设出自变量x,根据题中两个变量之间的关系列出二次函数表达式； (2)求：利用公式法或配方法求出其最大(小)值； (3)写：结合相关问题写出结果．如图5－5－3,利用一面墙,其他三边用80 m长的篱笆围一块矩形场地,墙长为30 m,求围成矩形场地的最大面积．图5－5－3 解：设矩形场地的面积为S m2,所围矩形ABCD的边BC为x m. 由题意,得S＝x·1 2 (80－x)＝－ 1 2 (x－40)2＋800, ∴当x＝40时,S最大＝800,符合题意, ∴当所围矩形ABCD的边BC为40 m时,矩形场地的面积最大,最大面积为800 m2. 你认为上述解答有问题吗？若有问题,请说明理由,并给出正确的解答过程．

二次函数中动点图形的面积最值专题

中学复习学案年级：9年级科目：数学执笔：内容：《二次函数中动点图形的面积最值专题一》目标：1.学会用代数法表示与函数图象相关的几何图形的长度，面积 2.能用函数图象的性质解决相关问题重点：二次函数中动点图形的面积最值的一般及特殊解法难点：点的坐标的求法学习过程：一、学前准备：（1）填空如图，抛物线与x 轴交于点A 和点B ，与ｙ轴交于点Ｃ．则点A 坐标为，点B 坐标为，点Ｃ坐标为， ΔＡＢＣ的面积为 . 顶点坐标为，对称轴为 . 直线AC 的解析式为 . (2)观察下列图形，指出如何求出阴影部分的面积小结：规则图形的面积可直接套用公式，不规则图形的面积用割补法。二、“二次函数中动点与图形面积”试题解析例题：如图二次函数43 4312--=x x y 与x 轴交于点C ，与y 轴交于点A ，过点A 作一条直线与x 轴平行，与抛物线交于点B. (1) 求直线AC 的解析式； (2)连接BC ，求ΔABC 的面积. 322++-=x x y

变式1：若抛物线的顶点为B ，求ΔABC 的面积. 变式2：若点B 是线段AC 下方的抛物线上的动点，那么，ΔABC 的面积有最大值吗？如果有，请求出. 最大面积和此时点B 的坐标. 变式3:如图，抛物线中的点A 、B 、C 与例题中的点A 、B 、C 一样，点P 是直线AC 上方抛物线上的动点，是否存在点P ，使ABC PAC S S ??=2，若存在，求出点P 的坐标，若不存在，说明理由. 变式4：若B 、C 是抛物线与x 轴的交点，A 是抛物线与y 轴的交点，点D 是线段AC 上的动点，求四边形ABCD 面积的最大过点D 作x 轴的垂线与抛物线相交于点E ，当点D 运动到什么位置时，四边形ABCE 的面积最大？求最大面积及此时点D 的坐标. 学后反思：归纳“二次函数中动点图形的面积最值”试题解析一般规律：这类问题的特征是要以静代动解题，首先找面积关系的函数解析式，关键是用含x 的代数式表示出相关的线段的长度，若是规则图形则套用公式或用割补法，若为不规则图形则用割补法. 三、自我检测 1.若抛物线62+-=x x y 与x 轴交于A 、B 两点，则AB= ，抛物线与y 轴交于点C ，则C 点的坐标为，△ABC 的面积为 . 2.已知二次函数2 3212-- =x x y 与x 轴交于A 、B 两点，顶点为C ，则△ABC 的面积为 . 3. 已知抛物线322-+=x x y 与x 轴交于A(-3,0)，B(1,0)两点，与y 轴交于点C ，直线y=x+1与抛物线交于E ，F 两点．点Ｐ是直线EF 下方抛物线上的动点，求△PEF 面积的最大值及点P 的坐标. 4.抛物线4524542+-=x x y 在平面直角坐标系中的位置如图，直线454--=x y 与x 轴交于点A(-5,0)，与y 轴交于点B.在抛物线上是否存在一点P ，使得△PAB 的面积

初三二次函数与几何图形面积

【例1】（改编题）如图，抛物线233y mx mx =+-（0m >）与y 轴交于点C ,与x 轴交于A 、B 两点，点A 在点B 的左侧，且1 tan 3OCB ∠=． ⑴求此抛物线的解析式； ⑵如果点D 是线段AC 下方抛物线上的动点，设D 点的横坐标为x ，ACD ?的面积为S ，求S 与x 的关系式，并求当S 最大时，点D 的坐标；例题精讲二次函数与几何图形面积

【例2】已知：如图，抛物线2334y x =-+与x 轴交于点A 、点B ，与直线3 4 y x b =-+相交于点B 、点C ，直线3 4y x b =-+与y 轴交于点E ． ⑴求直线BC 的解析式． ⑵若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A ，B 重合），同时，点 N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB ?的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB ?的面积最大，最大面积是多少？

【例3】如图①，梯形ABCD中，90 ∠=?．动点E、F同时从点B出发，点E沿折线BA AD DC --运 C 动到点C时停止运动，点F沿BC运动到点C时停止运动，它们运动时的速度都是1cm/s．设E、 cm．已知y与t的函数图象如图②所示，其中曲线OM为抛F出发t s时，EBF ?的面积为y2 物线的一部分，MN、NP为线段．请根据图中的信息，解答下列问题： ⑴梯形上底的长______ AD=cm，梯形ABCD的面积＝__________cm2； ⑵当点E在BA、DC上运动时，分别求出y与t的函数关系式（注明自变量的取值范围）； ⑶当t为何值时，EBF ?与梯形ABCD的面积之比为1:2 图①

实际问题与二次函数几何图形的最大面积

22.3实际问题与二次函数-几何图形的最大面积姓名学号评价（A组）一．解答题（共3小题） 1．（2016?内江）某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边的长为x米．（1）若苗圃园的面积为72平方米，求x；（2）若平行与墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；（3）当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围．（B组） 2．（2015?泉州）某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长69米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的面积最大？下面是两位学生争议的情境：请根据上面的信息，解决问题：（1）设AB=x米（x＞0），试用含x的代数式表示BC的长；（2）请你判断谁的说法正确，为什么？（C组） 3．（2015?广西自主招生）如图，要设计一个等腰梯形的花坛，花坛上底120米，下底180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为x米．（1）用含x的式子表示横向甬道的面积；（2）当三条甬道的面积是梯形面积的八分之一时，求甬道的宽；

（3）根据设计的要求，甬道的宽不能超过6米．如果修建甬道的总费用（万元）与甬道的宽度成正比例关系，比例系数是5.7，花坛其余部分的绿化费用为每平方米0.02万元，那么当甬道的宽度为多少米时，所建花坛的总费用最少？最少费用是多少万元？参考答案：一．解答题（共3小题） 1．（2016?内江）某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边的长为x米．（1）若苗圃园的面积为72平方米，求x；（2）若平行与墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；（3）当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围．【解答】解：（1）根据题意得：（30﹣2x）x=72，解得：x=3，x=12， ∵30﹣2x≤18， ∵x=12；（2）设苗圃园的面积为y， ∵y=x（30﹣2x）=﹣2x2+30x， ∵a=﹣2＜0， ∵苗圃园的面积y有最大值， ∵当x=时，即平行于墙的一边长15＞8米，y最大=112.5平方米；（3）由题意得：﹣2x2+30x≥100，解得：5≤x≤10． 2．（2015?泉州）某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长69米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的面积最大？下面是两位学生争议的情境：

中考复习：二次函数与图形面积

二次函数与图形面积 ★1.已知抛物线y＝－x2＋bx＋c的图象过点A(4，0)、B(1，3)． (1)求抛物线的表达式； (2)求出抛物线的对称轴和顶点坐标； (3)抛物线的对称轴为直线l，设抛物线上的点P(m，n)在第四象限，点P关于直线l的对称点为E，点E关于x轴的对称点为F，若以O、A、P、F四点组成的四边形的面积为20，求m、n的值．解：(1)将点A(4，0)、B(1，3)代入抛物线y＝－x2＋bx＋c得，解得， ∴抛物线的表达式为y＝－x2＋4x； (2)对称轴为直线x＝－b 2a ＝－＝2，顶点坐标为(2，4)；(3)抛物线的对称轴为直线x＝2，设抛物线上的点P(m，n)在第四象限，则点P关于直线l的对称点为E(4－m，n)，点E关于x轴的对称点为F(4－m，－n)，若以O、A、P、F四点组成的四边形的面积为20，则S四边形OP AF＝S△AOF＋S△AOP＝1 2×4×(－n)＋1 2×4×(－n)＝－4n＝20，得n＝－5，将(m，－5)代入y＝－x2＋4x，解得m＝5或m＝－1. ∵点P(m，n)在第四象限， ∴m＝5，n＝－5. ★2.如图，抛物线y＝ax2＋bx＋c经过原点O、B(1，3)、C(2，2)， 1 / 10

与x轴交于另一点N. (1)求抛物线的表达式； (2)连接BC，若点A为BC所在直线与y轴的交点，在抛物线上是否，若存在，请求出点P的坐标；若不存在点P，使得S△OAP＝8 15S△ONP 存在，请说明理由．第2题图解：(1)将0(0，0)、B(1，3)、C(2，2)三点的坐标分别代入抛物线 y＝ax2＋bx＋c，可得，解得， ∴所求抛物线的表达式为y＝－2x2＋5x； (2)存在，设BC所在直线的表达式为y＝kx＋b，将点B、C的坐标代入可得，解得，则y＝－x＋4. 把x＝0代入y＝－x＋4得y＝4， ∴点A(0，4)，