附表1华北水利水电学院本科专业设置及学生分布一览表
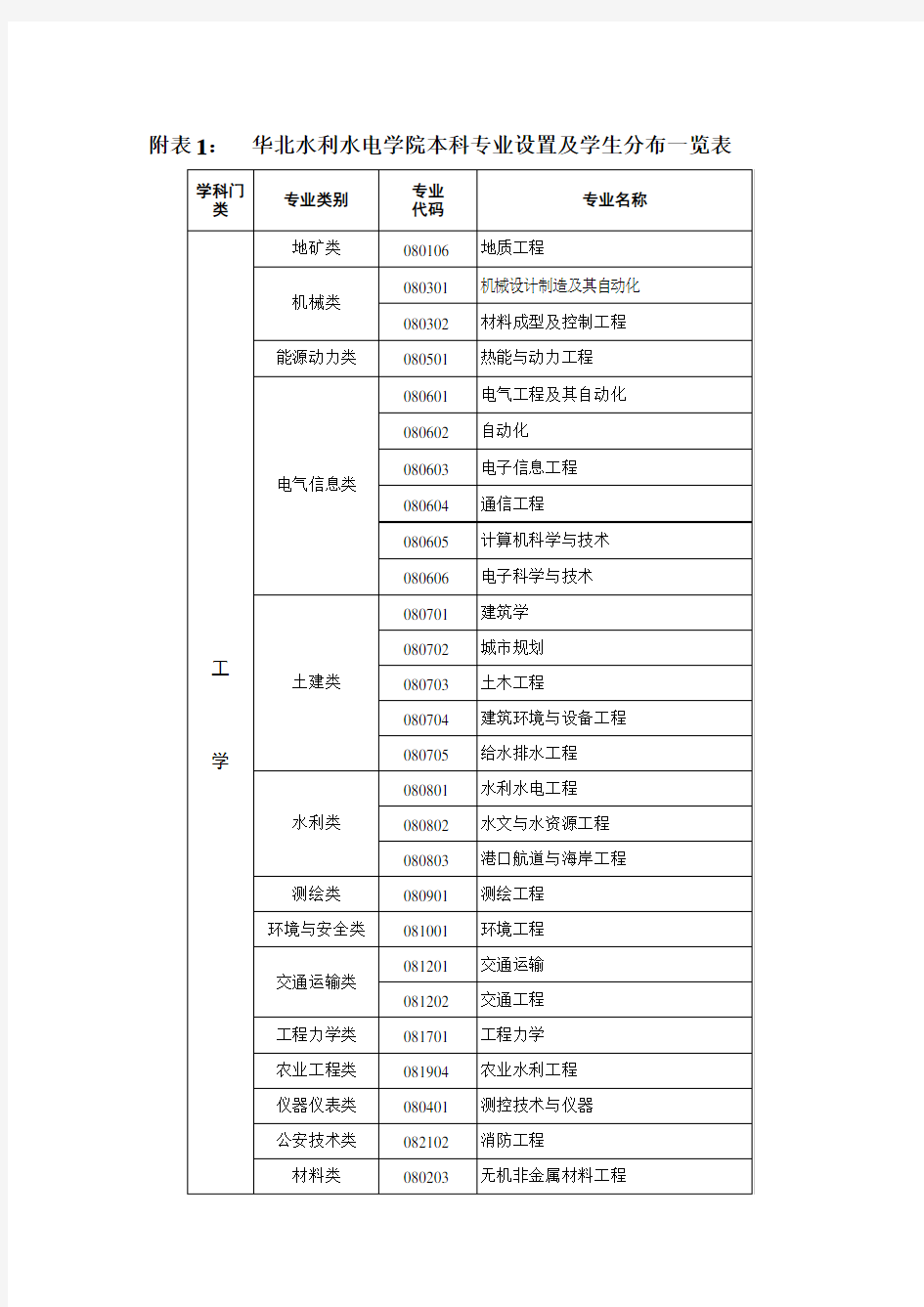

附表1:华北水利水电学院本科专业设置及学生分布一览表
华北水利水电学院本科专业设置及学生分布一览表
标准正态分布表
标准正态分布表 集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-
标准正态分布表
4432198653 1.80.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0.970 6 1.90.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0.975 6 0.976 2 0.976 7 20.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.10.982 1 0.982 6 0.983 0.983 4 0.983 8 0.984 2 0.984 6 0.985 0.985 4 0.985 7 2.20.986 1 0.986 4 0.986 8 0.987 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.989 2.30.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.40.991 8 0.992 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.50.993 8 0.994 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.60.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0.996 1 0.996 2 0.996 3 0.996 4 2.70.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0.997 1 0.997 2 0.997 3 0.997 4 2.80.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0.998 1 2.90.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x00.10.20.30.40.50.60.70.80.9 30.998 7 0.999 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 正态分布概率表 Φ( u ) =
二项分布概念及图表和查表方法
目录 1定义 ?统计学定义 ?医学定义 2概念 3性质 4图形特点 5应用条件 6应用实例 定义 统计学定义 在概率论和统计学中,二项分布是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上,当 时,二项分布就是伯努利分布,二项分布是显著性差异的二项试验的基础。 医学定义 在医学领域中,有一些随机事件是只具有两种互斥结果的离散型随机事件,称为二项分类变量(dichotomous variable),如对病人治疗结果的有效与无效,某种化验结果的阳性与阴性,接触某传染源的感染与未感染等。二项分布(binomial distribution)就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。
考虑只有两种可能结果的随机试验,当成功的概率()是恒定的,且各次试验相互独立,这种试验在统计学上称为伯努利试验(Bernoulli trial)。如果进行次伯努利试验,取得成功次数为 的概率可用下面的二项分布概率公式来描述:P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 式中的n为独立的伯努利试验次数,π为成功的概率,(1-π)为失败的概率,X为在n次伯努里试验中出现成功的次数,表示在n次试验中出现X的各种组合情况,在此称为二项系数(binomial coefficient)。 所以的含义为:含量为n的样本中,恰好有X例阳性数的概率。 概念 二项分布(Binomial Distribution),即重复n次的伯努利试验(Bernoulli Experiment),用ξ表示随机试验的结果。 二项分布公式 如果事件发生的概率是P,则不发生的概率q=1-p,N次独立重复试验中发生K次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k),其中C(n, k) =n!/(k!(n-k)!),注意:第二个等号后面的括号里的是上标,表示的是方幂。 那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p) 期望:Eξ=np; 方差:Dξ=npq; 其中q=1-p 证明:由二项式分布的定义知,随机变量X是n重伯努利实验中事件A发生的次数,且在每次试验中A发生的概率为p。因此,可以将二项式分布分解成n个相互独立且以p为参数的(0-1)分布随机变量之和。 设随机变量X(k)(k=1,2,3...n)服从(0-1)分布,则X=X(1)+X(2)+X(3)....X(n). 因X(k)相互独立,所以期望:
正态分布讲解(含标准表)
2.4正态分布 复习引入: 总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线. 总体密度曲线 b 单位 O 频率/组距 a 它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a,b)内取值的概率等于总体密度曲线,直线x=a,x=b及x轴所围图形的面积. 观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示: 2 2 () 2 , 1 (),(,) 2 x x e x μ σ μσ ? πσ - - =∈-∞+∞ 式中的实数μ、)0 (> σ σ是参数,分别表示总体的平均数与标准差,, ()x μσ ? 的图象为正态分布密度曲线,简称正态曲线. 讲解新课:
一般地,如果对于任何实数a b <,随机变量X 满足 ,()()b a P a X B x dx μσ?<≤=?, 则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2 σ μN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN . 经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位. 说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计. 2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布. 2.正态分布),(2 σ μN )是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值,讨论均值与标准差对于正态曲线的影响
卡方分布表
WORD格式 x 2 分布临界值表(卡方分布) P n' 0.995 0.99 0.975 0.95 0.9 0.75 0.5 0.25 0.1 0.05 0.025 0.01 0.005 1 ????0.0 2 0.1 0.45 1.32 2.71 3.84 5.02 6.6 3 7.88 2 0.01 0.02 0.02 0.1 0.21 0.58 1.39 2.77 4.61 5.99 7.38 9.21 10.6 3 0.07 0.11 0.22 0.35 0.58 1.21 2.37 4.11 6.25 7.81 9.35 11.3 4 12.84 4 0.21 0.3 0.48 0.71 1.06 1.92 3.36 5.39 7.78 9.49 11.14 13.28 14.86 5 0.41 0.55 0.83 1.15 1.61 2.67 4.35 6.63 9.24 11.07 12.83 15.09 16.75 6 0.68 0.8 7 1.24 1.64 2.2 3.45 5.35 7.84 10.64 12.59 14.45 16.81 18.55 7 0.99 1.24 1.69 2.17 2.83 4.25 6.35 9.04 12.02 14.07 16.01 18.48 20.28 8 1.34 1.65 2.18 2.73 3.4 5.07 7.34 10.22 13.36 15.51 17.53 20.09 21.96 9 1.73 2.09 2.7 3.33 4.17 5.9 8.34 11.39 14.68 16.92 19.02 21.67 23.59 10 2.16 2.56 3.25 3.94 4.87 6.74 9.34 12.55 15.99 18.31 20.48 23.21 25.19 11 2.6 3.05 3.82 4.57 5.58 7.58 10.34 13.7 17.28 19.68 21.92 24.72 26.76 12 3.07 3.57 4.4 5.23 6.3 8.44 11.34 14.85 18.55 21.03 23.34 26.22 28.3 13 3.57 4.11 5.01 5.89 7.04 9.3 12.34 15.98 19.81 22.36 24.74 27.69 29.82 14 4.07 4.66 5.63 6.57 7.79 10.17 13.34 17.12 21.06 23.68 26.12 29.14 31.32 15 4.6 5.23 6.27 7.26 8.55 11.04 14.34 18.25 22.31 25 27.49 30.58 32.8 16 5.14 5.81 6.91 7.96 9.31 11.91 15.34 19.37 23.54 26.3 28.85 32 34.27 17 5.7 6.41 7.56 8.67 10.09 12.79 16.34 20.49 24.77 27.59 30.19 33.41 35.72 18 6.26 7.01 8.23 9.39 10.86 13.68 17.34 21.6 25.99 28.87 31.53 34.81 37.16 19 6.84 7.63 8.91 10.12 11.65 14.56 18.34 22.72 27.2 30.14 32.85 36.19 38.58 20 7.43 8.26 9.59 10.85 12.44 15.45 19.34 23.83 28.41 31.41 34.17 37.57 40 21 8.03 8.9 10.28 11.59 13.24 16.34 20.34 24.93 29.62 32.67 35.48 38.93 41.4 22 8.64 9.54 10.98 12.34 14.04 17.24 21.34 26.04 30.81 33.92 36.78 40.29 42.8 23 9.26 10.2 11.69 13.09 14.85 18.14 22.34 27.14 32.01 35.17 38.08 41.64 44.18 24 9.89 10.86 12.4 13.85 15.66 19.04 23.34 28.24 33.2 36.42 39.36 42.98 45.56 25 10.52 11.52 13.12 14.61 16.47 19.94 24.34 29.34 34.38 37.65 40.65 44.31 46.93 26 11.16 12.2 13.84 15.38 17.29 20.84 25.34 30.43 35.56 38.89 41.92 45.64 48.29 27 11.81 12.88 14.57 16.15 18.11 21.75 26.34 31.53 36.74 40.11 43.19 46.96 49.64 28 12.46 13.56 15.31 16.93 18.94 22.66 27.34 32.62 37.92 41.34 44.46 48.28 50.99 29 13.12 14.26 16.05 17.71 19.77 23.57 28.34 33.71 39.09 42.56 45.72 49.59 52.34 30 13.79 14.95 16.79 18.49 20.6 24.48 29.34 34.8 40.26 43.77 46.98 50.89 53.67 40 20.71 22.16 24.43 26.51 29.05 33.66 39.34 45.62 51.8 55.76 59.34 63.69 66.77 50 27.99 29.71 32.36 34.76 37.69 42.94 49.33 56.33 63.17 67.5 71.42 76.15 79.49 60 35.53 37.48 40.48 43.19 46.46 52.29 59.33 66.98 74.4 79.08 83.3 88.38 91.95 70 43.28 45.44 48.76 51.74 55.33 61.7 69.33 77.58 85.53 90.53 95.02 100.42 104.22 80 51.17 53.54 57.15 60.39 64.28 71.14 79.33 88.13 96.58 101.88 106.63 112.33 116.32 90 59.2 61.75 65.65 69.13 73.29 80.62 89.33 98.64 107.56 113.14 118.14 124.12 128.3 100 67.33 70.06 74.22 77.93 82.36 90.13 99.33 109.14 118.5 124.34 129.56 135.81 140.17 专业资料
泊松分布的概念及表和查表方法
目录 1命名原因 2分布特点 3关系 4应用场景 5应用示例 6推导 7形式与性质 命名原因 泊松分布实例
泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)命名的,他在1838年时发表。这个分布在更早些时候由贝努里家族的一个人描述过。 分布特点 泊松分布的概率函数为: 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。 泊松分布的期望和方差均为特征函数为 关系 泊松分布与二项分布 泊松分布 当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦时,就可以用泊松公式近似得计算。 事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。 应用场景 在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性)。 应用示例
二项分布概念及图表和查表方法
二项分布概念及图表 二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。 目录 1 定义 ?统计学定义 ?医学定义 2 概念 3 性质 4 图形特点 5 应用条件 6 应用实例 定义 统计学定义 在概率论和统计学中,二项分布是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上,当 时,二项分布就是伯努利分布,二项分布是显著性差异的二项试验的基础。
医学定义 在医学领域中,有一些随机事件是只具有两种互斥结果的离散型随机事件,称为二项分类变量(dichotomous variable),如对病人治疗结果的有效与无效,某种化验结果的阳性与阴性,接触某传染源的感染与未感染等。二项分布(binomial distribution)就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。 考虑只有两种可能结果的随机试验,当成功的概率()是恒定的,且各次试验相互独立,这种试验在统计学上称为伯努利试验(Bernoulli trial)。如果进行次伯努利试验,取得成功次数为的概率可用下面的二项分布概率公式来描述:P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 二项分布公式 P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k),其中C(n, k) =n!/(k!(n-k)!),注意:第二个等号后面的括号里的是上标,表示的是方幂。
二项分布概念及图表和查表方法
目录 1 定义 ?统计学定义 ?医学定义 2 概念 3 性质 4 图形特点 5 应用条件 6 应用实例 定义 统计学定义 在概率论和统计学中,二项分布是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上,当 时,二项分布就是伯努利分布,二项分布是显著性差异的二项试验的基础。 医学定义 在医学领域中,有一些随机事件是只具有两种互斥结果的离散型随机事件,称为二项分类变量(dichotomous variable),如对病人治疗结果的有效与无效,某种化验结果的阳性与阴性,接触某传染源的感染与未感染等。二项分布(binomial distribution)就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。
考虑只有两种可能结果的随机试验,当成功的概率()是恒定的,且各次试验相互独立,这种试验在统计学上称为伯努利试验(Bernoulli trial)。如果进行次伯努利试验,取得成功次数为的概率可用下面的二项分布概率公式来描述:P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 表示随机试验的结果。 二项分布公式 如果事件发生的概率是P,则不发生的概率q=1-p,N次独立重复试验中发生K次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k),其中C(n, k) =n!/(k!(n-k)!),注意:第二个等号后面的括号里的是上标,表示的是方幂。 那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p) 期望:Eξ=np; 方差:Dξ=npq; 其中q=1-p 证明:由二项式分布的定义知,随机变量X是n重伯努利实验中事件A发生的次数,且在每次试验中A发生的概率为p。因此,可以将二项式分布分解成n个相互独立且以p为参数的(0-1)分布随机变量之和。 设随机变量X(k)(k=1,2,3...n)服从(0-1)分布,则X=X(1)+X(2)+X(3)....X(n). 因X(k)相互独立,所以期望:
泊松分布的概念及表和查表方法
泊松分布的概念及表和查表方法 Poisson分布,是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。 中文名泊松分布外文名poisson distribution 分类数学时间1838年 台译卜瓦松分布提出西莫恩·德尼·泊松 目录 1命名原因 2分布特点 3关系 4应用场景 5应用示例 6推导 7形式与性质
命名原因 泊松分布实例 泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)命名的,他在1838年时发表。这个分布在更早些时候由贝努里家族的一个人描述过。 分布特点 泊松分布的概率函数为: 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。 泊松分布的期望和方差均为特征函数为 关系 泊松分布与二项分布 泊松分布
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦时,就可以用泊松公式近似得计算。 事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。 应用场景 在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性)。 应用示例 泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数,一块产品上的缺陷数,显微镜下单位分区内的细菌分布数等等。 观察事物平均发生m次的条件下,实际发生x次的概率P(x)可用下式表示: 例如采用㎡紫外线照射大肠杆菌时,每个基因组(~4×106核苷酸对)平均产生3个嘧啶二体。实际上每个基因组二体的分布是服从泊松分布的,将取如下形式: …… 是未产生二体的菌的存在概率,实际上其值的5%与采用㎡照射时的大肠杆菌uvrA-株,recA-株(除去既不能修复又不能重组修复的二重突变)的生存率是一致的。由于该菌株每个基因组有一个二体就是致死量,因此就意味着全部死亡的概率。 推导
标准正态分布表(附表1-2)
附表1-2 标准正态分布函数表φ(x ) x0.000.010.020.030.040.050.060.070.080.09 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.60.500 0 0.539 8 0.579 3 0.617 9 0.655 4 0.691 5 0.725 7 0.758 0 0.788 1 0.815 9 0.841 3 0.864 3 0.884 9 0.903 2 0.919 2 0.933 2 0.945 2 0.504 0 0.543 8 0.583 2 0.621 7 0.659 1 0.695 0 0.729 1 0.761 1 0.791 0 0.818 6 0.843 8 0.866 5 0.886 9 0.904 9 0.920 7 0.934 5 0.946 3 0.508 0 0.547 8 0.587 1 0.625 5 0.662 8 0.698 5 0.732 4 0.764 2 0.793 9 0.821 2 0.846 1 0.868 6 0.888 8 0.906 6 0.922 2 0.935 7 0.947 4 0.512 0 0.551 7 0.591 0 0.629 3 0.666 4 0.701 9 0.735 7 0.767 3 0.796 7 0.823 8 0.848 5 0.870 8 0.890 7 0.908 2 0.923 6 0.937 0 0.948 4 0.516 0 0.555 7 0.594 8 0.633 1 0.670 0 0.705 4 0.738 9 0.770 3 0.799 5 0.826 4 0.850 8 0.872 9 0.892 5 0.909 9 0.925 1 0.938 2 0.949 5 0.519 9 0.559 6 0.598 7 0.636 8 0.673 6 0.708 8 0.742 2 0.773 4 0.802 3 0.828 9 0.853 1 0.874 9 0.894 4 0.911 5 0.926 5 0.939 4 0.950 5 0.523 9 0.563 6 0.602 6 0.640 4 0.677 2 0.712 3 0.745 4 0.776 4 0.805 1 0.835 5 0.855 4 0.877 0 0.896 2 0.913 1 0.927 9 0.940 6 0.951 5 0.527 9 0.567 5 0.606 4 0.644 3 0.680 8 0.715 7 0.748 6 0.779 4 0.807 8 0.834 0 0.857 7 0.879 0 0.898 0 0.914 7 0.929 2 0.941 8 0.952 5 0.531 9 0.571 4 0.610 3 0.648 0 0.684 4 0.719 0 0.751 7 0.782 3 0.810 6 0.836 5 0.859 9 0.881 0 0.899 7 0.916 2 0.930 6 0.943 0 0.953 5 0.535 9 0.575 3 0.614 1 0.651 7 0.687 9 0.722 4 0.754 9 0.785 2 0.813 3 0.838 9 0.862 1 0.883 0 0.901 5 0.917 7 0.931 9 0.944 1 0.953 5
二项分布表
附录2 附表 附表1 二项分布表 0{}(1)x k n k n P X x p p k k ?=?? ≤=????? ∑ p n x 0.001 0.002 0.0030.005 0.01 0.02 0.03 0.05 0.10 0.15 0.20 0.25 0.30 2 0 0.9980 0.9960 0.99400.9900 0.9801 0.96040.94090.90250.81000.72250.6400 0.5625 0.4900 2 1 1.0000 1.0000 1.00001.0000 0.9999 0.99960.99910.99750.99000.97750.9600 0.9375 0.9100 3 0 0.9970 0.9940 0.99100.9851 0.9703 0.94120.91270.85740.72900.61410.5120 0.4219 0.3430 3 1 1.0000 1.0000 1.00000.9999 0.9997 0.99880.99740.99280.97200.93930.8960 0.8438 0.7840 3 2 1.0000 1.0000 1.00001.00000.99990.99900.99660.9920 0.9844 0.9730 4 0 0.9960 0.9920 0.98810.9801 0.9606 0.92240.88530.81450.65610.52200.4096 0.3164 0.2401 4 1 1.0000 1.0000 0.99990.9999 0.9994 0.99770.99480.98600.94770.89050.8192 0.7383 0.6517 4 2 1.00001.0000 1.0000 1.00000.99990.99950.99630.98800.9728 0.9492 0.9163 4 3 1.00001.00000.99990.99950.9984 0.9961 0.9919 5 0 0.9950 0.9900 0.98510.9752 0.9510 0.90390.85870.77380.59050.44370.3277 0.2373 0.1681 5 1 1.0000 1.0000 0.99990.9998 0.9990 0.99620.99150.97740.91850.83520.7373 0.6328 0.5282 5 2 1.00001.0000 1.0000 0.99990.99970.99880.99140.97340.9421 0.8965 0.8369 5 3 1.00001.00001.00000.99950.99780.9933 0.9844 0.9692 5 4 1.00000.99990.9997 0.9990 0.9976 6 0 0.9940 0.9881 0.98210.9704 0.9415 0.88580.83300.73510.53140.37710.2621 0.1780 0.1176 6 1 1.0000 0.9999 0.99990.9996 0.9985 0.99430.98750.96720.88570.77650.6554 0.5339 0.4202 6 2 1.0000 1.00001.0000 1.0000 0.99980.99950.99780.98420.95270.9011 0.8306 0.7443 6 3 1.00001.00000.99990.99870.99410.9830 0.9624 0.9295 6 4 1.00000.99990.99960.9984 0.9954 0.9891 6 5 1.00001.00000.9999 0.9998 0.9993 7 0 0.9930 0.9861 0.97920.9655 0.9321 0.86810.80800.69830.47830.32060.2097 0.1335 0.0824 7 1 1.0000 0.9999 0.99980.9995 0.9980 0.99210.98290.95560.85030.71660.5767 0.4449 0.3294 7 2 1.0000 1.00001.0000 1.0000 0.99970.99910.99620.97430.92620.8520 0.7564 0.6471 7 3 1.00001.00000.99980.99730.98790.9667 0.9294 0.8740 7 4 1.00000.99980.99880.9953 0.9871 0.9712 7 5 1.00000.99990.9996 0.9987 0.9962 7 6 1.00001.0000 0.9999 0.9998 8 0 0.9920 0.9841 0.97630.9607 0.9227 0.85080.78370.66340.43050.27250.1678 0.1001 0.0576 8 1 1.0000 0.9999 0.99980.9993 0.9973 0.98970.97770.94280.81310.65720.5033 0.3671 0.2553 8 2 1.0000 1.00001.0000 0.9999 0.99960.99870.99420.96190.89480.7969 0.6785 0.5518 8 3 1.0000 1.00000.99990.99960.99500.97860.9437 0.8862 0.8059 - 262 -
二项分布临界值表
附表1 二项分布临界值表 在p=q=下,x或n–x(不论何者为大)的临界值 n 单侧检验()双侧检验()0.050.010.050.01 55———66—6—7777—8788—98989 10910910 119101011 1210111011 1310121112 1411121213 1512131213 1612141314 1713141315 1813151415 1914151516 2015161517 2115171617 2216171718 2316181719 2417191819
2518191820 2618201920 2719202021 2819212022 2920222122 3020222123
附表2 正态分布概率表 Z F(Z)Z F(Z)Z F(Z)Z F(Z) 0.000.00000.350.27370.700.5161 1.050.7063 0.010.00800.360.28120.710.5223 1.060.7109 0.020.01600.370.28860.720.5285 1.070.7154 0.030.02390.380.29610.730.5346 1.080.7199 0.040.03190.390.30350.740.5407 1.090.7243 0.050.03990.400.31080.750.5467 1.100.7287 0.060.04780.410.31820.760.5527 1.110.7330 0.070.05580.420.32550.770.5587 1.120.7373 0.080.06380.430.33280.780.5646 1.130.7415 0.090.07170.440.34010.790.5705 1.140.7457 0.100.07970.450.34730.800.5763 1.150.7499 0.110.08760.460.35450.810.5821 1.160.7540 0.120.09550.470.36160.820.5878 1.170.7580 0.130.10340.480.36880.830.5935 1.180.7620 0.140.11130.490.37590.840.5991 1.190.7660 0.150.11920.500.38290.850.6047 1.200.7699 0.160.12710.510.38990.860.6102 1.210.7737 0.170.13500.520.39690.870.6157 1.220.7775 0.180.14280.530.40390.880.6211 1.230.7813 0.190.15070.540.41080.890.6265 1.240.7850
标准正态分布表
标准正态分布表 x 0 0、01 0、02 0、03 0、04 0、05 0、06 0、07 0、08 0、09 0 0、500 0 0、504 0 0、508 0 0、512 0 0、516 0 0、519 9 0、523 9 0、527 9 0、531 9 0、535 9 0、1 0、539 8 0、543 8 0、547 8 0、551 7 0、555 7 0、559 6 0、563 6 0、567 5 0、571 4 0、575 3 0、2 0、579 3 0、583 2 0、587 1 0、591 0 0、594 8 0、598 7 0、602 6 0、606 4 0、610 3 0、614 1 0、3 0、617 9 0、621 7 0、625 5 0、629 3 0、633 1 0、636 8 0、640 4 0、644 3 0、648 0 0、651 7 0、4 0、655 4 0、659 1 0、662 8 0、666 4 0、670 0 0、673 6 0、677 2 0、680 8 0、684 4 0、687 9 0、5 0、691 5 0、695 0 0、698 5 0、701 9 0、705 4 0、708 8 0、712 3 0、715 7 0、719 0 0、722 4 0、6 0、725 7 0、729 1 0、732 4 0、735 7 0、738 9 0、742 2 0、745 4 0、748 6 0、751 7 0、754 9 0、7 0、758 0 0、761 1 0、764 2 0、767 3 0、770 3 0、773 4 0、776 4 0、779 4 0、782 3 0、785 2 0、8 0、788 1 0、791 0 0、793 9 0、796 7 0、799 5 0、802 3 0、805 1 0、807 8 0、810 6 0、813 3 0、9 0、815 9 0、818 6 0、821 2 0、823 8 0、826 4 0、828 9 0、835 5 0、834 0 0、836 5 0、838 9 1 0、841 3 0、843 8 0、846 1 0、848 5 0、850 8 0、853 1 0、855 4 0、857 7 0、859 9 0、86 2 1 1、1 0、864 3 0、866 5 0、868 6 0、870 8 0、872 9 0、87 4 9 0、877 0 0、879 0 0、881 0 0、883 0 1、2 0、884 9 0、886 9 0、888 8 0、890 7 0、892 5 0、894 4 0、89 6 2 0、898 0 0、899 7 0、901 5 1、3 0、903 2 0、904 9 0、906 6 0、90 8 2 0、90 9 9 0、911 5 0、913 1 0、914 7 0、916 2 0、917 7 1、4 0、919 2 0、920 7 0、922 2 0、923 6 0、925 1 0、926 5 0、927 9 0、929 2 0、930 6 0、931 9 1、5 0、933 2 0、934 5 0、935 7 0、937 0 0、938 2 0、939 4 0、940 6 0、941 8 0、943 0 0、944 1 1、6 0、945 2 0、946 3 0、947 4 0、948 4 0、949 5 0、950 5 0、951 5 0、952 5 0、953 5 0、953 5 1、7 0、955 4 0、956 4 0、957 3 0、958 2 0、959 1 0、959 9 0、960 8 0、961 6 0、962 5 0、963 3 1、8 0、964 1 0、964 8 0、965 6 0、966 4 0、967 2 0、967 8 0、968 6 0、969 3 0、970 0 0、970 6 1、9 0、971 3 0、971 9 0、972 6 0、973 2 0、973 8 0、974 4 0、975 0 0、975 6 0、976 2 0、976 7 2 0、977 2 0、977 8 0、978 3 0、978 8 0、979 3 0、979 8 0、980 3 0、980 8 0、981 2 0、981 7 2、1 0、982 1 0、982 6 0、983 0 0、983 4 0、983 8 0、984 2 0、984 6 0、98 5 0 0、985 4 0、985 7 2、2 0、98 6 1 0、986 4 0、986 8 0、98 7 1 0、987 4 0、987 8 0、988 1 0、988 4 0、988 7 0、98 9 0 2、3 0、989 3 0、989 6 0、989 8 0、990 1 0、990 4 0、990 6 0、990 9 0、991 1 0、991 3 0、991 6 2、4 0、991 8 0、992 0 0、992 2 0、992 5 0、992 7 0、992 9 0、993 1 0、993 2 0、993 4 0、993 6 2、5 0、993 8 0、994 0 0、994 1 0、994 3 0、994 5 0、994 6 0、994 8 0、994 9 0、995 1 0、995 2 2、6 0、995 3 0、995 5 0、995 6 0、995 7 0、995 9 0、996 0 0、996 1 0、996 2 0、996 3 0、996 4 2、7 0、996 5 0、996 6 0、996 7 0、996 8 0、996 9 0、997 0 0、997 1 0、997 2 0、997 3 0、997 4 2、8 0、997 4 0、997 5 0、997 6 0、997 7 0、997 7 0、997 8 0、997 9 0、997 9 0、998 0 0、998 1 2、9 0、998 1 0、998 2 0、998 2 0、998 3 0、998 4 0、998 4 0、998 5 0、998 5 0、998 6 0、998 6 x 0 0、1 0、2 0、3 0、4 0、5 0、6 0、7 0、8 0、9 3 0、998 7 0、999 0 0、999 3 0、999 5 0、999 7 0、999 8 0、999 8 0、999 9 0、999 9 1、000 0
概率论与数理统计附表1 泊松分布表
附表1 泊松分布表 ()! m P X m e m λλ-==
390.0000070.000056 附录 附录A A1 正态分布函数表 2 2 ()e d(0) 2π t x x t x Φ -∞ =-≥ ? x 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 x 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 0.5000 0.5398 0.5793 0.6179 0.6554 0.6915 0.7257 0.7580 0.7881 0.8159 0.8413 0.8643 0.8849 0.90320 0.91924 0.93319 0.94520 0.95543 0.96407 0.97128 0.97725 0.98214 0.98610 0.98928 0.99180 0.99379 0.99534 0.99653 0.99745 0.99813 0.5040 0.5438 0.5832 0.6217 0.6591 0.6950 0.7291 0.7611 0.7910 0.8186 0.8438 0.8665 0.8869 0.90490 0.92073 0.93448 0.94630 0.95637 0.96485 0.97193 0.9778 0.98257 0.98645 0.98956 0.99202 0.99396 0.99547 0.99664 0.99752 0.99819 0.5080 0.5478 0.5871 0.6255 0.6628 0.6985 0.7324 0.7642 0.7939 0.8212 0.8461 0.8686 0.8888 0.90658 0.92220 0.93574 0.94738 0.95728 0.96562 0.97257 0.97831 0.98300 0.98679 0.98983 0.99224 0.99413 0.99560 0.99674 0.99760 0.99825 0.5120 0.5517 0.5910 0.6293 0.6664 0.7019 0.7357 0.7673 0.7967 0.8238 0.8485 0.8708 0.8907 0.90824 0.92364 0.93699 0.94845 0.95818 0.96638 0.97320 0.97882 0.98341 0.98713 0.99010 0.99245 0.99430 0.99573 0.99683 0.99767 0.99831 0.5160 0.5557 0.5948 0.6331 0.6700 0.7054 0.7389 0.7703 0.7995 0.8264 0.8508 0.8729 0.8925 0.90988 0.92507 0.93822 0.94950 0.95907 0.96712 0.97381 0.97932 0.98382 0.98745 0.99036 0.99266 0.99446 0.99586 0.99693 0.99774 0.99836 0.5199 0.5596 0.5987 0.6368 0.6736 0.7088 0.7422 0.7734 0.8023 0.8289 0.8531 0.8749 0.8944 0.91140 0.92647 0.93943 0.95053 0.95994 0.96784 0.97441 0.97982 0.98422 0.98778 0.99061 0.99286 0.99461 0.99598 0.99702 0.99781 0.99841 0.5239 0.5636 0.6026 0.6406 0.6772 0.7123 0.7454 0.7764 0.8051 0.8315 0.8554 0.8770 0.8962 0.91309 0.92785 0.94062 0.95154 0.96080 0.96856 0.97500 0.98030 0.98461 0.98809 0.99086 0.99305 0.99477 0.99609 0.99711 0.99788 0.99846 0.5279 0.5675 0.6064 0.6443 0.6808 0.7157 0.7486 0.7794 0.8078 0.8340 0.8577 0.8790 0.8980 0.91466 0.92922 0.94179 0.95254 0.96164 0.96926 0.97558 0.98077 0.98500 0.98840 0.99111 0.99324 0.99492 0.99621 0.99720 0.99795 0.99851 0.5319 0.5714 0.6103 0.6480 0.6844 0.7190 0.7517 0.7823 0.8106 0.8365 0.8599 0.8810 0.8997 0.91621 0.93056 0.94295 0.95352 0.96246 0.96995 0.97615 0.98124 0.98537 0.98870 0.99134 0.99343 0.99506 0.99632 0.99728 0.99801 0.99856 0.5359 0.5753 0.6141 0.6517 0.6879 0.7224 0.7549 0.7852 0.8133 0.8389 0.8621 0.8830 0.90147 0.91774 0.93189 0.94408 0.95449 0.96327 0.97062 0.97670 0.98169 0.98574 0.98899 0.99158 0.99361 0.99520 0.99643 0.99737 0.99807 0.99861 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9
