数值线性代数第二版徐树方高立张平文上机习题第二章实验报告

(1)估计5到20阶Hilbert 矩阵的∞数条件数
(2)设n n R A ?∈?????
??
??????
???------=111
1
111110110
01
,先随机地选取n R x ∈,并计算出x A b n =;然
后再用列主元Gauss 消去法求解该方程组,假定计算解为∧
x 。试对n 从5到30估计计算解∧
x 的精度,并且与真实相对误差作比较。
解(1)分析:利用for 使n 从5循环到20,利用()hilb 函数得到Hilbert 矩阵A ;先将算
法2.5.1编制成通用的子程序,利用算法2.5.1编成的子程序)(B opt v =,对T
A B -=求解,
得到∞
-1
A
的一个估计值v v =~
;再利用inf),(A norm 得到∞A ;则条件数
inf),(1
A norm v A A K *==∞∞
-。
另,矩阵A 的∞数条件数可由inf),(A cond 直接算出,两者可进行比较。
程序为
1 算法2.5.1编成的子程序)(B opt v =
function v=opt(B)
k=1;
n=length(B);
x=1./n*ones(n,1); while k==1 w=B*x;
v=sign(w); z=B'*v;
if norm(z,inf)<=z'*x v=norm(w,1); k=0; else
x=zeros(n,1);
[s,t]=max(abs(z)); x(t)=1; k=1; end end end
2 问题(1)求解 ex2_1
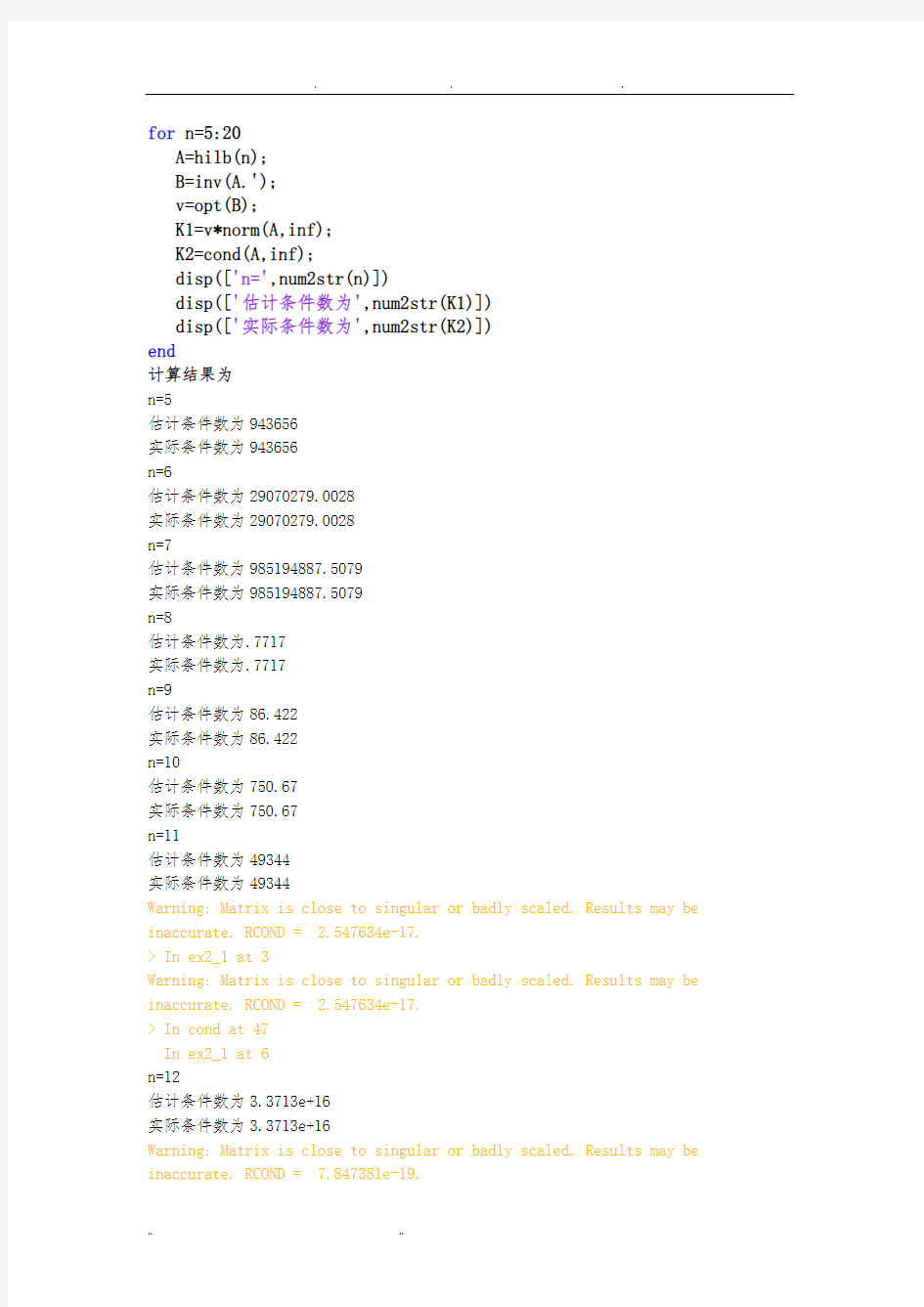
for n=5:20
A=hilb(n);
B=inv(A.');
v=opt(B);
K1=v*norm(A,inf);
K2=cond(A,inf);
disp(['n=',num2str(n)])
disp(['估计条件数为',num2str(K1)])
disp(['实际条件数为',num2str(K2)])
end
计算结果为
n=5
估计条件数为943656
实际条件数为943656
n=6
估计条件数为29070279.0028
实际条件数为29070279.0028
n=7
估计条件数为985194887.5079
实际条件数为985194887.5079
n=8
估计条件数为.7717
实际条件数为.7717
n=9
估计条件数为86.422
实际条件数为86.422
n=10
估计条件数为750.67
实际条件数为750.67
n=11
估计条件数为49344
实际条件数为49344
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.547634e-17.
> In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.547634e-17.
> In cond at 47
In ex2_1 at 6
n=12
估计条件数为3.3713e+16
实际条件数为3.3713e+16
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 7.847381e-19.
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 7.847381e-19.
> In cond at 47
In ex2_1 at 6
n=13
估计条件数为1.5327e+18
实际条件数为1.5327e+18
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.246123e-18.
> In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.246123e-18.
> In cond at 47
In ex2_1 at 6
n=14
估计条件数为4.8374e+17
实际条件数为4.8374e+17
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 8.491876e-19.
> In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 8.491876e-19.
> In cond at 47
In ex2_1 at 6
n=15
估计条件数为4.9674e+17
实际条件数为5.3619e+17
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 9.137489e-19.
> In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 9.137489e-19.
> In cond at 47
In ex2_1 at 6
n=16
估计条件数为8.3166e+17
实际条件数为8.3167e+17
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 6.244518e-19.
> In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 6.244518e-19.
> In cond at 47
n=17
估计条件数为1.093e+18 实际条件数为1.093e+18
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.693737e-19. > In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.693737e-19. > In cond at 47 In ex2_1 at 6 n=18
估计条件数为2.0651e+18 实际条件数为2.7893e+18
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.264685e-19. > In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.264685e-19. > In cond at 47 In ex2_1 at 6 n=19
估计条件数为2.9357e+18 实际条件数为2.9357e+18
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 1.351364e-19. > In ex2_1 at 3
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 1.351364e-19. > In cond at 47 In ex2_1 at 6 n=20
估计条件数为2.674e+18 实际条件数为6.473e+18
结果分析
随着矩阵阶数增加,估计值误差开始出现,20,17,16,15=n 时估计条件数与实际值存在误差;且条件数很大,Hilbert 矩阵为病态的。
解(2)分析:先根据题目要求,利用for 和()rand 使n 从5循环到30,作出A 和随机
的x ,并计算出Ax b =;然后再利用第一章习题中得到的)(],,[A GaussCol P U L =和
),,,,(P U L b A Gauss x =用列主元Gauss 消去法求解该方程组,假定计算解为1x ,得
1*x A b r -=,利用第(1)问所得函数)).'((A inv opt 计算∞
-1A 的一个估计值,利用
inf),(*norm 计算A b r ,,的无穷数,则1x 的相对误差估计为))/norm(b,(A,A.'))*norm )*opt(inv(norm(r,p inf inf inf 1=,真实相对误差为))/norm(x,,norm(x-x p inf inf 12=。
程序为
1 列主元Gauss 消去法求解该方程组的程序为
A 的LU 分解:
function [L,U,P]=GaussCol(A) n=length(A); for k=1:n-1
[s,t]=max(abs(A(k:n,k))); p=t+k-1;
temp=A(k,1:n);
A(k,1:n)=A(p,1:n); A(p,1:n)=temp;
u(k)=p;
if A(k,k)~=0
A(k+1:n,k)=A(k+1:n,k)/A(k,k);
A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); else
break ; end end
L=tril(A); U=triu(A);
L=L-diag(diag(L))+diag(ones(1,n)); P=eye(n); for i=1:n-1
temp=P(i,:);
P(i,:)=P(u(i),:); P(u(i),:)=temp; end end
高斯消去法解线性方程组
function x=Gauss(A,b,L,U,P) if nargin<5
P=eye(length(A));
n=length(A);
b=P*b;
for j=1:n-1
b(j)=b(j)/L(j,j);
b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);
end
b(n)=b(n)/L(n,n);
y=b;
for j=n:-1:2
y(j)=y(j)/U(j,j);
y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);
end
y(1)=y(1)/U(1,1);
x=y;
end
2 问题(2)求解ex2_2
for n=5:30
A=2*eye(n)+tril(-1*ones(n)); A(1:n-1,n)=ones(n-1,1); x=100*rand(n,1);
b=A*x;
[L,U,P]=GaussCol(A); x1=Gauss(A,b,L,U,P);
r=b-A*x1;
p1=norm(r,inf)*opt(inv(A.'))*norm(A,inf)/norm(b,inf); p2=norm(x-x1,inf)/norm(x,inf);
disp(['n=',num2str(n)])
disp(['估计相对误差为',num2str(p1)])
disp(['实际相对误差为',num2str(p2)])
y1(n-4)=p1;y2(n-4)=p2;
end
plot(5:30,y1,5:30,y2)
legend('估计相对误差','实际相对误差')
计算结果为
n=5
估计相对误差为2.8265e-15
实际相对误差为3.1615e-16
n=6
估计相对误差为3.3434e-15
实际相对误差为2.8523e-16
n=7
估计相对误差为9.882e-16
实际相对误差为1.7941e-16
估计相对误差为4.8733e-14 实际相对误差为1.0891e-14 n=9
估计相对误差为2.2282e-14 实际相对误差为3.6143e-15 n=10
估计相对误差为1.5622e-14 实际相对误差为3.9702e-15 n=11
估计相对误差为1.9668e-14 实际相对误差为5.1566e-15 n=12
估计相对误差为4.808e-14 实际相对误差为8.5677e-15 n=13
估计相对误差为2.8696e-13 实际相对误差为4.0392e-14 n=14
估计相对误差为1.5109e-12 实际相对误差为3.8759e-13 n=15
估计相对误差为4.3829e-13 实际相对误差为1.67e-13 n=16
估计相对误差为8.7941e-13 实际相对误差为2.6417e-13 n=17
估计相对误差为2.4842e-12 实际相对误差为5.8841e-13 n=18
估计相对误差为7.6311e-12 实际相对误差为2.4718e-12 n=19
估计相对误差为1.9214e-11 实际相对误差为5.9876e-12 n=20
估计相对误差为5.612e-11 实际相对误差为1.5802e-11 n=21
估计相对误差为1.7181e-11 实际相对误差为2.1433e-12 n=22
估计相对误差为1.0565e-11
实际相对误差为2.8952e-12 n=23
估计相对误差为6.9651e-12 实际相对误差为1.2037e-12 n=24
估计相对误差为3.1487e-10 实际相对误差为1.4479e-10 n=25
估计相对误差为9.884e-10 实际相对误差为2.3499e-10 n=26
估计相对误差为4.1606e-09 实际相对误差为6.3158e-10 n=27
估计相对误差为5.8332e-09 实际相对误差为1.7298e-09 n=28
估计相对误差为3.9754e-09 实际相对误差为6.9346e-10 n=29
估计相对误差为7.8248e-09 实际相对误差为1.4376e-09 n=30
估计相对误差为1.1681e-07 实际相对误差为2.0748e-08
结果分析
n 较小时估计的较好,随着n 的增大估计值误差增大
-8
用MATLAB解决线性代数问题实验报告
实验三使用MATLAB解决线性代数问题学院:数计学院班级:1003班姓名:黄晓丹学号:1051020144 实验目的: 学习MATLAB有关线性代数运算的指令,主要学习运用MATLAB解决矩阵除法,线性方程组的通解,矩阵相似 对角化问题,以及解决投入产出分析等应用问题。 实验内容: 矩阵转置:A=[1 2;3 4];B=[4 3;2 1]; >> A',B' ans = 1 3 2 4 ans = 4 3 3 1 矩阵加减:A-B ans= -3 -1 1 3 矩阵乘法:A*B,A.*B(数组乘法)||比较矩阵乘法与数组乘法的区别ans= 8 5 20 13 ans= 4 6 6 4 矩阵除法:A\B,B./A ans=
-6 -5 5 4 ans= 4 1.5 0.6667 0.25 特殊矩阵生成:zeros(m,n)||生成m行n列的矩阵 ones(m,n)||生成m行n列的元素全为一的矩阵 eye(n)||生成n阶单位矩阵 rand(m,n)||生成m行n列[0 ,1]上均匀分布随 机数矩阵 zeros(2,3) ans = 0 0 0 0 0 0 >> ones(3,3) ans = 1 1 1 1 1 1 1 1 1 >> eye(3)
ans = 1 0 0 0 1 0 0 0 1 >> rand(2,4) ans = Columns 1 through 3 0.9501 0.6068 0.8913 0.2311 0.4860 0.7621 Column 4 0.4565 0.0185 矩阵处理:trace(A)||返回矩阵的迹 diag(A)||返回矩阵对角线元素构成的向量 tril(A)||提取矩阵的下三角部分 triu(A)||提取矩阵的上三角部分 flipud(A)||矩阵上下翻转 fliplr(A)||矩阵左右翻转 reshape(A,m,n)||将矩阵的元素重排成m行n列矩阵A=[1 2 3;4 5 6;7 8 9]; >> t=trace(A),d=diag(A),u=triu(A)
线性代数典型例题
线性代数 第一章 行列式 典型例题 一、利用行列式性质计算行列式 二、按行(列)展开公式求代数余子式 已知行列式412343 344 615671 12 2 D = =-,试求4142A A +与4344A A +. 三、利用多项式分解因式计算行列式 1.计算221 1231223131 5 1319x D x -= -. 2.设()x b c d b x c d f x b c x d b c d x = ,则方程()0f x =有根_______.x = 四、抽象行列式的计算或证明 1.设四阶矩阵234234[2,3,4,],[,2,3,4]A B αγγγβγγγ==,其中234,,,,αβγγγ均为四维列向量,且已知行列式||2,||3A B ==-,试计算行列式||.A B + 2.设A 为三阶方阵,*A 为A 的伴随矩阵,且1 ||2 A = ,试计算行列式1*(3)22.A A O O A -??-??? ?
3.设A 是n 阶(2)n ≥非零实矩阵,元素ij a 与其代数余子式ij A 相等,求行列式||.A 4.设矩阵210120001A ?? ??=?? ????,矩阵B 满足**2ABA BA E =+,则||_____.B = 5.设123,,ααα均为3维列向量,记矩阵 123123123123(,,),(,24,39)A B αααααααααααα==+++++ 如果||1A =,那么||_____.B = 五、n 阶行列式的计算 六、利用特征值计算行列式 1.若四阶矩阵A 与B 相似,矩阵A 的特征值为 1111 ,,,2345 ,则行列式1||________.B E --= 2.设A 为四阶矩阵,且满足|2|0E A +=,又已知A 的三个特征值分别为1,1,2-,试计算行列式*|23|.A E + 第二章 矩阵 典型例题 一、求逆矩阵 1.设,,A B A B +都是可逆矩阵,求:111().A B ---+
线性代数第二章答案
第二章 矩阵及其运算 1 已知线性变换 ?????++=++=++=3 213321232113235322y y y x y y y x y y y x 求从变量x 1 x 2 x 3到变量y 1 y 2 y 3的线性变换 解 由已知 ? ??? ?????? ? ?=???? ??221321323513122y y y x x x 故 ???? ?????? ? ?=???? ??-3211 221323513122x x x y y y ? ??? ?????? ??----=321423736 947y y y ?????-+=-+=+--=3 21332123 211423736947x x x y x x x y x x x y 2 已知两个线性变换 ?????++=++-=+=321332123 11542322y y y x y y y x y y x ?????+-=+=+-=3 233122 11323z z y z z y z z y 求从z 1 z 2 z 3到x 1 x 2 x 3的线性变换 解 由已知 ???? ?????? ? ?-=???? ??221321514232102y y y x x x ??? ? ?????? ??--???? ??-=32131 010 2013514232102z z z ??? ? ?????? ??----=321161109412316z z z
所以有?????+--=+-=++-=3 21332123 2111610941236z z z x z z z x z z z x 3 设???? ??--=111111111A ??? ? ??--=150421321B 求3AB 2A 及A T B 解 ??? ? ??---???? ??--???? ??--=-1111111112150421321111111111323A AB ???? ??----=???? ??---???? ??-=2294201722213211111111120926508503 ??? ? ??-=???? ??--???? ??--=092650850150421321111111111B A T 4 计算下列乘积 (1)??? ? ?????? ??-127075321134 解 ???? ?????? ??-127075321134???? ???+?+??+?-+??+?+?=102775132)2(71112374??? ? ??=49635 (2)???? ??123)321( 解 ??? ? ??123)321((132231)(10)
数值分析实验报告1
实验一误差分析 实验1.1(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 其中ε(1.1)和(1.221,,,a a 的输出b ”和“poly ε。 (1(2 (3)写成展 关于α solve 来提高解的精确度,这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。 实验过程: 程序: a=poly(1:20); rr=roots(a); forn=2:21 n form=1:9 ess=10^(-6-m);
ve=zeros(1,21); ve(n)=ess; r=roots(a+ve); -6-m s=max(abs(r-rr)) end end 利用符号函数:(思考题一)a=poly(1:20); y=poly2sym(a); rr=solve(y) n
很容易的得出对一个多次的代数多项式的其中某一项进行很小的扰动,对其多项式的根会有一定的扰动的,所以对于这类病态问题可以借助于MATLAB来进行问题的分析。 学号:06450210 姓名:万轩 实验二插值法
行列式经典例题
大学-----行列式经典例题 例1计算元素为a ij = | i -j |的n 阶行列式. 解 方法1 由题设知,11a =0,121a =,1,1,n a n =- ,故 01110212 n n n D n n --= -- 1,1,,2 i i r r i n n --=-= 01 1111 111 n ---- 1,,1 j n c c j n +=-= 121 1 021 (1)2(1)020 1 n n n n n n ------=---- 其中第一步用的是从最后一行起,逐行减前一行.第二步用的每列加第n 列. 方法2 01110 212 0n n n D n n --= -- 1 1,2,,111 1111 120 i i r r i n n n +-=----=-- 1 2,,100120 1231 j c c j n n n n +=---= --- =12(1)2(1) n n n ---- 例2. 设a , b , c 是互异的实数, 证明: 的充要条件是a + b + c =0. 证明: 考察范德蒙行列式:
= 行列式 即为y 2前的系数. 于是 = 所以 的充要条件是a + b + c = 0. 例3计算D n = 121 100010n n n x x a a a x a ----+ 解: 方法1 递推法 按第1列展开,有 D n = x D 1-n +(-1) 1 +n a n 1 1111n x x x ----- = x D 1-n + a n 由于D 1= x + a 1,221 1x D a x a -=+,于是D n = x D 1-n + a n =x (x D 2-n +a 1-n )+ a n =x 2 D 2-n + a 1-n x + a n = = x 1 -n D 1+ a 2x 2 -n + + a 1-n x + a n =111n n n n x a x a x a --++++ 方法2 第2列的x 倍,第3列的x 2 倍, ,第n 列的x 1 -n 倍分别加到第1列上 12 c xc n D += 21121 10010000n n n n x x x a xa a a x a -----++
线性代数第二章矩阵试题及答案
第二章矩阵 一、知识点复习 1、矩阵的定义 由m n个数排列成的一个m行n列的表格,两边界以圆括号或方括号,就成为一个m n型矩阵。例如 2 -1 0 1 1 1 1 1 0 2 2 5 4 -2 9 3 3 3 -1 8 是一个45矩阵. 一个矩阵中的数称为它的元素,位于第i行第j列的数称为(i,j)位元素。 元素全为0的矩阵称为零矩阵,通常就记作0。 两个矩阵A和B相等(记作A=B),是指它的行数相等,列数也相等(即它们的类型相同),并且对应的元素都相等。 2、 n阶矩阵与几个特殊矩阵 行数和列数相等的矩阵称为方阵,行列数都为n的矩阵也常常叫做n阶矩阵。 n阶矩阵的从左上角到右下角的对角线称为主对角线。 下面列出几类常用的n阶矩阵,它们都是考试大纲中要求掌握的. 对角矩阵: 对角线外的的元素都为0的n阶矩阵. 单位矩阵: 对角线上的的元素都为1的对角矩阵,记作E(或I). 数量矩阵: 对角线上的的元素都等于一个常数c的对角矩阵,它就是c E. 上三角矩阵: 对角线下的的元素都为0的n阶矩阵. 下三角矩阵: 对角线上的的元素都为0的n阶矩阵. 对称矩阵: 满足A T=A矩阵,也就是对任何i,j,(i,j)位的元素和(j,i)位的元素总是相等的n阶矩阵. 反对称矩阵:满足A T=-A矩阵.也就是对任何i,j,(i,j)位的元素和(j ,i)位的元素之和总等于0的n阶矩阵.反对称矩阵对角线上的元素一定都是0.) 正交矩阵:若AA T=A T A=E,则称矩阵A是正交矩阵。 (1)A是正交矩阵?A T=A-1 (2)A是正交矩阵?2 A=1 阶梯形矩阵:一个矩阵称为阶梯形矩阵,如果满足: ①如果它有零行,则都出现在下面。 ②如果它有非零行,则每个非零行的第一个非0元素所在的列号自上而下严 格单调递增。 把阶梯形矩阵的每个非零行的第一个非0元素所在的位置称为台角。 每个矩阵都可以用初等行变换化为阶梯形矩阵,这种运算是在线性代数的各类 计算题中频繁运用的基本运算,必须十分熟练。 请注意:一个矩阵用初等行变换化得的阶梯形矩阵并不是唯一的,但是其非零 行数和台角位置是确定的。 3、矩阵的线形运算 (1)加(减)法:两个m n的矩阵A和B可以相加(减),得到的和(差)仍是m n 矩阵,记作A+B (A-B),运算法则为对应元素相加(减). (2)数乘: 一个m n的矩阵A与一个数c可以相乘,乘积仍为m n的矩阵, 记作c A,运算法则为A的每个元素乘c. 这两种运算统称为线性运算,它们满足以下规律: ①加法交换律:A+B=B+A. 2加法结合律:(A+B)+C=A+(B+C). ③加乘分配律:c(A+B)=c A+c B.(c+d)A=c A+d A. ④数乘结合律: c(d)A=(cd)A. ⑤ c A=0 c=0 或A=0. 4、矩阵乘法的定义和性质 (1)当矩阵A的列数和B的行数相等时,则A和B可以相乘,乘积记作AB. AB的行数和A相等,列数和B相等. AB的(i,j)位元素等于A的第i个行向量 和B的第j个列向量(维数相同)对应分量乘积之和.
线性代数课后习题答案(陈维新)
第一章 行列式 习题1.1 1. 证明:(1)首先证明)3(Q 是数域。 因为)3(Q Q ?,所以)3(Q 中至少含有两个复数。 任给两个复数)3(3,32211Q b a b a ∈++,我们有 3 )()3()3)(3(3)()()3()3(3)()()3()3(2121212122112121221121212211b a a b b b a a b a b a b b a a b a b a b b a a b a b a +++=++-+-=+-++++=+++。 因为Q 是数域,所以有理数的和、差、积仍然为有理数,所以 ) 3(3)()3()3)(3()3(3)()()3()3()3(3)()()3()3(2121212122112121221121212211Q b a a b b b a a b a b a Q b b a a b a b a Q b b a a b a b a ∈+++=++∈-+-=+-+∈+++=+++。 如果0322≠+b a ,则必有22,b a 不同时为零,从而0322≠-b a 。 又因为有理数的和、差、积、商仍为有理数,所以 )3(33) (3)3() 3)(3()3)(3(3 32 2 22212122222121222222112211Q b a b a a b b a b b a a b a b a b a b a b a b a ∈--+--= -+-+= ++。 综上所述,我们有)3(Q 是数域。 (2)类似可证明)(p Q 是数域,这儿p 是一个素数。 (3)下面证明:若q p ,为互异素数,则)()(q Q p Q ?。 (反证法)如果)()(q Q p Q ?,则q b a p Q b a +=? ∈?,,从而有 q ab qb a p p 2)()(222++==。 由于上式左端是有理数,而q 是无理数,所以必有02=q ab 。 所以有0=a 或0=b 。 如果0=a ,则2 qb p =,这与q p ,是互异素数矛盾。 如果0=b ,则有 a p =,从而有“有理数=无理数”成立,此为矛盾。 所以假设不成立,从而有)()(q Q p Q ?。
数值线性代数第二版徐树方高立张平文上机习题第一章实验报告(供参考)
上机习题 1.先用你所熟悉的的计算机语言将不选主元和列主元Gauss 消去法编写成通用的子程序;然后用你编写的程序求解84阶方程组;最后将你的计算结果与方程的精确解进行比较,并就此谈谈你对Gauss 消去法的看法。 Sol : (1)先用matlab 将不选主元和列主元Gauss 消去法编写成通用的子程序,得到P U L ,,: 不选主元Gauss 消去法:[])(,A GaussLA U L =得到U L ,满足LU A = 列主元Gauss 消去法:[])(,,A GaussCol P U L =得到P U L ,,满足LU PA = (2)用前代法解()Pb or b Ly =,得y 用回代法解y Ux =,得x 求解程序为()P U L b A Gauss x ,,,,=(P 可缺省,缺省时默认为单位矩阵) (3)计算脚本为ex1_1 代码 %算法(计算三角分解:Gauss 消去法) function [L,U]=GaussLA(A) n=length(A); for k=1:n-1 A(k+1:n,k)=A(k+1:n,k)/A(k,k); A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); end
U=triu(A); L=tril(A); L=L-diag(diag(L))+diag(ones(1,n)); end %算法计算列主元三角分解:列主元Gauss消去法) function [L,U,P]=GaussCol(A) n=length(A); for k=1:n-1 [s,t]=max(abs(A(k:n,k))); p=t+k-1; temp=A(k,1:n); A(k,1:n)=A(p,1:n); A(p,1:n)=temp; u(k)=p; if A(k,k)~=0 A(k+1:n,k)=A(k+1:n,k)/A(k,k); A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); else break; end end L=tril(A);U=triu(A);L=L-diag(diag(L))+diag(ones(1,n));
(完整版)线性代数重要知识点及典型例题答案
线性代数知识点总结 第一章 行列式 二三阶行列式 N 阶行列式:行列式中所有不同行、不同列的n 个元素的乘积的和 n n n nj j j j j j j j j n ij a a a a ...)1(21212121) ..(∑-= τ (奇偶)排列、逆序数、对换 行列式的性质:①行列式行列互换,其值不变。(转置行列式T D D =) ②行列式中某两行(列)互换,行列式变号。 推论:若行列式中某两行(列)对应元素相等,则行列式等于零。 ③常数k 乘以行列式的某一行(列),等于k 乘以此行列式。 推论:若行列式中两行(列)成比例,则行列式值为零; 推论:行列式中某一行(列)元素全为零,行列式为零。 ④行列式具有分行(列)可加性 ⑤将行列式某一行(列)的k 倍加到另一行(列)上,值不变 行列式依行(列)展开:余子式ij M 、代数余子式ij j i ij M A +-=)1( 定理:行列式中某一行的元素与另一行元素对应余子式乘积之和为零。 克莱姆法则: 非齐次线性方程组 :当系数行列式0≠D 时,有唯一解:)21(n j D D x j j ??==、 齐次线性方程组 :当系数行列式01≠=D 时,则只有零解 逆否:若方程组存在非零解,则D 等于零 特殊行列式: ①转置行列式:33 23133222123121 11333231232221 131211 a a a a a a a a a a a a a a a a a a → ②对称行列式:ji ij a a = ③反对称行列式:ji ij a a -= 奇数阶的反对称行列式值为零 ④三线性行列式:33 31 2221 13 1211 0a a a a a a a 方法:用221a k 把21a 化为零,。。化为三角形行列式 ⑤上(下)三角形行列式:
数值分析实验报告1
实验一 误差分析 实验(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 )1.1() ()20()2)(1()(20 1∏=-=---=k k x x x x x p 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 )2.1(0 )(19=+x x p ε 其中ε是一个非常小的数。这相当于是对()中19x 的系数作一个小的扰动。我们希望比较()和()根的差别,从而分析方程()的解对扰动的敏感性。 实验内容:为了实现方便,我们先介绍两个Matlab 函数:“roots ”和“poly ”。 roots(a)u = 其中若变量a 存储n+1维的向量,则该函数的输出u 为一个n 维的向量。设a 的元素依次为121,,,+n a a a ,则输出u 的各分量是多项式方程 01121=+++++-n n n n a x a x a x a 的全部根;而函数 poly(v)b =
的输出b 是一个n+1维变量,它是以n 维变量v 的各分量为根的多项式的系数。可见“roots ”和“poly ”是两个互逆的运算函数。 ;000000001.0=ess );21,1(zeros ve = ;)2(ess ve = ))20:1((ve poly roots + 上述简单的Matlab 程序便得到()的全部根,程序中的“ess ”即是()中的ε。 实验要求: (1)选择充分小的ess ,反复进行上述实验,记录结果的变化并分析它们。 如果扰动项的系数ε很小,我们自然感觉()和()的解应当相差很小。计算中你有什么出乎意料的发现表明有些解关于如此的扰动敏感性如何 (2)将方程()中的扰动项改成18x ε或其它形式,实验中又有怎样的现象 出现 (3)(选作部分)请从理论上分析产生这一问题的根源。注意我们可以将 方程()写成展开的形式, ) 3.1(0 ),(1920=+-= x x x p αα 同时将方程的解x 看成是系数α的函数,考察方程的某个解关于α的扰动是否敏感,与研究它关于α的导数的大小有何关系为什么你发现了什么现象,哪些根关于α的变化更敏感 思考题一:(上述实验的改进) 在上述实验中我们会发现用roots 函数求解多项式方程的精度不高,为此你可以考虑用符号函数solve 来提高解的精确度,这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。
《经济数学》线性代数学习辅导与典型例题解析
《经济数学》线性代数学习辅导及典型例题解析 第1-2章行列式和矩阵 ⒈了解矩阵的概念,熟练掌握矩阵的运算。 矩阵的运算满足以下性质 ⒉了解矩阵行列式的递归定义,掌握计算行列式(三、四阶)的方法;掌握方阵乘积行列式定理。 是同阶方阵,则有: 若是阶行列式,为常数,则有: ⒊了解零矩阵,单位矩阵,数量矩阵,对角矩阵,上(下)三角矩阵,对称矩阵,初等矩阵的定义及性质。
⒋理解可逆矩阵和逆矩阵的概念及性质,掌握矩阵可逆的充分必要条件。 若为阶方阵,则下列结论等价 可逆满秩存在阶方阵使得 ⒌熟练掌握求逆矩阵的初等行变换法,会用伴随矩阵法求逆矩阵,会解简单的矩阵方程。 用初等行变换法求逆矩阵: 用伴随矩阵法求逆矩阵:(其中是的伴随矩阵) 可逆矩阵具有以下性质: ⒍了解矩阵秩的概念,会求矩阵的秩。 将矩阵用初等行变换化为阶梯形后,所含有的非零行的个数称为矩阵的秩。 典型例题解析 例1 设均为3阶矩阵,且,则。 解:答案:72 因为,且
所以 例2设为矩阵,为矩阵,则矩阵运算()有意义。 解:答案:A 因为,所以A可进行。 关于B,因为矩阵的列数不等于矩阵的行数,所以错误。 关于C,因为矩阵与矩阵不是同形矩阵,所以错误。 关于D,因为矩阵与矩阵不是同形矩阵,所以错误。 例3 已知 求。 分析:利用矩阵相乘和矩阵相等求解。 解:因为 得。
例4 设矩阵 求。 解:方法一:伴随矩阵法 可逆。 且由 得伴随矩阵 则=
方法二:初等行变换法 注意:矩阵的逆矩阵是唯一的,若两种结果不相同,则必有一个结果是错误的或两个都是错误的。 例4 设矩阵 求的秩。 分析:利用矩阵初等行变换求矩阵的秩。 解: 。
线性代数第二章答案
第二章 矩阵及其运算 1 已知线性变换 ?????++=++=++=3 21332123 2113235322y y y x y y y x y y y x , 求从变量x 1 x 2 x 3到变量y 1 y 2 y 3的线性变换 解 由已知 ? ??? ?????? ? ?=???? ??22 1321323513122y y y x x x 故 ???? ?????? ? ?=???? ??-3211 221323513122x x x y y y ? ??? ?????? ??----=321423736 947y y y ?????-+=-+=+--=3 21332123 211423736947x x x y x x x y x x x y 2 已知两个线性变换 ?????++=++-=+=3 2133 2123 11542322y y y x y y y x y y x ?????+-=+=+-=3 233122 11323z z y z z y z z y 求从z 1 z 2 z 3到x 1 x 2 x 3的线性变换 解 由已知 ???? ?????? ? ?-=???? ??221321514232102y y y x x x ??? ? ?????? ??--???? ??-=32131 010 2013514232102z z z ??? ? ?????? ??----=32 1161109412316z z z
所以有?????+--=+-=++-=3 2133 2123 2111610941236z z z x z z z x z z z x 3 设???? ??--=111111111A ??? ? ??--=150421321B 求3AB 2A 及A T B 解 ??? ? ??---???? ??--???? ??--=-1111111112150421321111111111323A AB ???? ??----=???? ??---???? ??-=2294201722213211111111120926508503 ??? ? ??-=???? ??--???? ??--=092650850150421321111111111B A T 4 计算下列乘积 (1)??? ? ?????? ??-127075321134 解 ???? ?????? ??-127075321134???? ???+?+??+?-+??+?+?=102775132)2(71112374?? ? ? ??=49635 (2)???? ??123)321( 解 ??? ? ??123)321((132231)(10)
数值线性代数第二版徐树方高立张平文上机习题第三章实验报告
数值线性代数第二版徐树方高立张平文上机习题第三章实验报告
第三章上机习题 用 你所熟悉的的计算机语言编制利用QR 分解 求解线性方程组和线性最小二乘问题的通用子程序,并用你编制的子程序完成下面的计算任务: (1)求解第一章上机习题中的三个线性方程组,并将所得的计算结果与前面的结果相比较,说明各方法的优劣; (2)求一个二次多项式+bt+c y=at 2 ,使得在残向量 的2范数下最小的意义下拟合表3.2中的数据; (3)在房产估价的线性模型 11 1122110x a x a x a x y ++++= 中,11 2 1 ,,,a a a 分别表示税、浴室数目、占地面积、车库数目、房屋数目、居室数目、房龄、建筑类型、户型及壁炉数目,y 代表房屋价格。现根据表3.3和表3.4给出的28组数据,求出模型中参数的最小二乘结果。
(表3.3和表3.4见课本P99-100) 解 分析: (1)计算一个Householder 变换H : 由于T T vv I ww I H β-=-=2,则计算一个Householder 变换H 等价于计算相应的 v 、β。其中 ) /(2,||||12v v e x x v T =-=β。 在实际计算中, 为避免出现两个相近的数出现的情形,当0 1 >x 时, 令 2 12 221||||)(-x x x x v n +++= ; 为便于储存,将v 规格化为1 /v v v =,相应的,β变为)/(22 1 v v v T =β 为防止溢出现象,用∞ ||||/x x 代替 (2)QR 分解: 利用Householder 变换逐步将n m A n m ≥?,转化为上三 角矩阵A H H H n n 11 -=Λ,则有
数值线性代数二版徐树方高立张平文上机习题第三章实验报告
- 1 - 第三章上机习题 用你所熟悉的的计算机语言编制利用QR 分解求解线性方程组和线性最小二乘问题的 通用子程序,并用你编制的子程序完成下面的计算任务: (1)求解第一章上机习题中的三个线性方程组,并将所得的计算结果与前面的结果相比较,说明各方法的优劣; (2)求一个二次多项式+bt+c y=at 2 ,使得在残向量的2范数下最小的意义下拟合表3.2中的数据; (3)在房产估价的线性模型 111122110x a x a x a x y ++++= 中,1121,,,a a a 分别表示税、浴室数目、占地面积、车库数目、房屋数目、居室数目、房龄、建筑类型、户型及壁炉数目,y 代表房屋价格。现根据表3.3和表3.4给出的28组数据,求出模型中参数的最小二乘结果。 (表3.3和表3.4见课本P99-100) 解 分析: (1)计算一个Householder 变换H : 由于T T vv I ww I H β-=-=2,则计算一个Householder 变换H 等价于计算相应的v 、β。其中)/(2,||||12v v e x x v T =-=β。 在实际计算中, 为避免出现两个相近的数出现的情形,当01>x 时,令2 12221||||) (-x x x x v n +++= ; 为便于储存,将v 规格化为1/v v v =,相应的,β变为)/(221v v v T =β 为防止溢出现象,用∞||||/x x 代替 (2)QR 分解: 利用Householder 变换逐步将n m A n m ≥?,转化为上三角矩阵A H H H n n 11 -=Λ,则有
?? ? ???=0R Q A ,其中n H H H Q 21=,:),:1(n R Λ=。 在实际计算中,从n j :1=,若m j <,依次计算)),:((j m j A x =对应的)1()1()~ (+-?+-k m k m j H 即对应的j v ,j β,将)1:2(+-j m v j 储存到),:1(j m j A +,j β储存到)(j d ,迭代结束 后再次计算Q ,有??? ? ?? ??=-~001 j j j H I H ,n H H H Q 21=(m n =时1-21n H H H Q =) (3)求解线性方程组b Ax =或最小二乘问题的步骤为 i 计算A 的QR 分解; ii 计算b Q c T 11=,其中):1(:,1n Q Q = iii 利用回代法求解上三角方程组1c Rx = (4)对第一章第一个线性方程组,由于R 的结果最后一行为零,故使用前代法时不计最后一行,而用运行结果计算84x 。 运算matlab 程序为 1 计算Householder 变换 [v,belta]=house(x) function [v,belta]=house(x) n=length(x); x=x/norm(x,inf); sigma=x(2:n)'*x(2:n); v=zeros(n,1); v(2:n,1)=x(2:n); if sigma==0 belta=0; else alpha=sqrt(x(1)^2+sigma); if x(1)<=0 v(1)=x(1)-alpha; else v(1)=-sigma/(x(1)+alpha); end belta=2*v(1)^2/(sigma+v(1)^2); v=v/v(1,1); end end
线性代数行列式经典例题
线性代数行列式经典例题 例1计算元素为a ij = | i -j |的n 阶行列式. 解 方法1 由题设知,11a =0,121a =,1,1,n a n =- ,故 01110212 n n n D n n --= -- 1,1,,2 i i r r i n n --=-= 01 1111 111 n ---- 1,,1 j n c c j n +=-= 121 1 021 (1)2(1)020 1 n n n n n n ------=---- 其中第一步用的是从最后一行起,逐行减前一行.第二步用的每列加第n 列. 方法2 01110 212 0n n n D n n --= -- 1 1,2,,111 1111 120 i i r r i n n n +-=----=-- 1 2,,100120 1231 j c c j n n n n +=---= --- =12(1)2(1) n n n ---- 例2. 设a , b , c 是互异的实数, 证明: 的充要条件是a + b + c =0. 证明: 考察范德蒙行列式:
= 行列式 即为y 2前的系数. 于是 = 所以 的充要条件是a + b + c = 0. 例3计算D n = 121 100010n n n x x a a a x a ----+ 解: 方法1 递推法 按第1列展开,有 D n = x D 1-n +(-1) 1 +n a n 1 1111n x x x ----- = x D 1-n + a n 由于D 1= x + a 1,221 1x D a x a -=+,于是D n = x D 1-n + a n =x (x D 2-n +a 1-n )+ a n =x 2 D 2-n + a 1-n x + a n = = x 1 -n D 1+ a 2x 2 -n + + a 1-n x + a n =111n n n n x a x a x a --++++ 方法2 第2列的x 倍,第3列的x 2 倍, ,第n 列的x 1 -n 倍分别加到第1列上 12 c xc n D += 21121 10010000n n n n x x x a xa a a x a -----++
线性代数第二章习题答案
习 题 2-1 1.由6名选手参加乒乓球比赛,成绩如下:选手1胜选手2、4、5、6而负于选手3;选手2胜选手4、5、6而负于选手1、3;选手3胜选手1、2、4而负于选手5、6;选手4胜选手5、6而负于选手1、2、3;选手5胜选手3、6而负于选手1、2、4;选手6胜选手2而负于选手1、3、4、5.若胜一场得1分,负一场得0分,使用矩阵表示输赢状况,并排序. 解: ????? ?? ? ? ? ??000010 100100110000001011 1110001110106543216 54321,选手按胜多负少排序为:6,5,4,3,2,1. 2.设矩阵???? ??-=???? ?? +-=2521 ,03231 z x y x B A ,已知B A =,求z y x ,,. 解:由于B A =得?????=-=+=-0253223z x y x ,解得:?? ? ??===211 z y x 。 习 题 2-2 1.设???? ??=0112A ,??? ? ??-=4021B ,求 (1)B A 52-; (2)BA AB -; (3)2 2B A -. 解:(1)??? ? ??--=???? ??--???? ??=???? ??--???? ??=-202892001050224402150112252B A ; (2)???? ??--=???? ??--???? ??--=???? ?????? ??--???? ??-???? ??=-2592041021820112402140210112BA AB ; (3)??? ? ??--=???? ??-???? ??=???? ??-???? ??--???? ?????? ??=-152441606112254021402101120112B A 22. 2.已知????? ??--=230412301321A ,??? ? ? ??---=052110 35123 4B ,求B A 23-. 解:??? ? ? ??----????? ??--=052110351234223041230 13 21 323B -A ??? ? ? ??----=????? ??----????? ??--=61941016151055011010422061024686901236903963 3.设??? ? ? ??----=????? ??=101012121234,432112 122121B A ,求
考研线性代数重点内容和典型题型
考研线性代数重点内容和典型题型 线性代数在考研数学中占有重要地位,必须予以高度重视.线性代数试题的特点比较突出,以计算题为主,证明题为辅,因此,专家们提醒广大的xx年的考生们必须注重计算能力.线性代数在数学一、二、三中均占22%,所以考生要想取得高分,学好线代也是必要的。下面,就将线代中重点内容和典型题型做了总结,希望对xx年考研的同学们学习有帮助。 行列式在整张试卷中所占比例不是很大,一般以填空题、选择题为主,它是必考内容,不只是考察行列式的概念、性质、运算,与行列式有关的考题也不少,例如方阵的行列式、逆矩阵、向量组的线性相关性、矩阵的秩、线性方程组、特征值、正定二次型与正定矩阵等问题中都会涉及到行列式.如果试卷中没有独立的行列式的试题,必然会在其他章、节的试题中得以体现.行列式的重点内容是掌握计算行列式的方法,计算行列式的主要方法是降阶法,用按行、按列展开公式将行列式降阶.但在展开之前往往先用行列式的性质对行列式进行恒等变形,化简之后再展开.另外,一些特殊的行列式(行和或列和相等的行列式、三对角行列式、爪型行列式等等)的计算方法也应掌握.常见题型有:数字型行列式的计算、抽象行列式的计算、含参数的行列式的计算.关于每个重要题型的具体方法以及例题见《xx 年全国硕士研究生入学统一考试数学120种常考题型精解》。 矩阵是线性代数的核心,是后续各章的基础.矩阵的概念、运算及理论贯穿线性代数的始终.这部分考点较多,重点考点有逆矩阵、
伴随矩阵及矩阵方程.涉及伴随矩阵的定义、性质、行列式、逆矩阵、秩及包含伴随矩阵的矩阵方程是矩阵试题中的一类常见试题.这几年还经常出现有关初等变换与初等矩阵的命题.常见题型有以下几种:计算方阵的幂、与伴随矩阵相关联的命题、有关初等变换的命题、有关逆矩阵的计算与证明、解矩阵方程。 向量组的线性相关性是线性代数的重点,也是考研的重点。xx 年的考生一定要吃透向量组线性相关性的概念,熟练掌握有关性质及判定法并能灵活应用,还应与线性表出、向量组的秩及线性方程组等相联系,从各个侧面加强对线性相关性的理解.常见题型有:判定向量组的线性相关性、向量组线性相关性的证明、判定一个向量能否由一向量组线性表出、向量组的秩和极大无关组的求法、有关秩的证明、有关矩阵与向量组等价的命题、与向量空间有关的命题。 往年考题中,方程组出现的频率较高,几乎每年都有考题,也是线性代数部分考查的重点内容.本章的重点内容有:齐次线性方程组有非零解和非齐次线性方程组有解的判定及解的结构、齐次线性方程组基础解系的求解与证明、齐次(非齐次)线性方程组的求解(含对参数取值的讨论).主要题型有:线性方程组的求解、方程组解向量的判别及解的性质、齐次线性方程组的基础解系、非齐次线性方程组的通解结构、两个方程组的公共解、同解问题。 特征值、特征向量是线性代数的重点内容,是考研的重点之一,题多分值大,共有三部分重点内容:特征值和特征向量的概念及计算、
数值分析实验报告
实验五 解线性方程组的直接方法 实验5.1 (主元的选取与算法的稳定性) 问题提出:Gauss 消去法是我们在线性代数中已经熟悉的。但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss 消去法作为数值算法的稳定性呢?Gauss 消去法从理论算法到数值算法,其关键是主元的选择。主元的选择从数学理论上看起来平凡,它却是数值分析中十分典型的问题。 实验内容:考虑线性方程组 编制一个能自动选取主元,又能手动选取主元的求解线性方程组的Gauss 消去过程。 实验要求: (1)取矩阵?? ? ?? ?? ?????????=????????????????=1415157,6816816816 b A ,则方程有解T x )1,,1,1(* =。取n=10计算矩阵的 条件数。让程序自动选取主元,结果如何? (2)现选择程序中手动选取主元的功能。每步消去过程总选取按模最小或按模尽可能小的元素作为主元,观察并记录计算结果。若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。 (3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用。 (4)选取其他你感兴趣的问题或者随机生成矩阵,计算其条件数。重复上述实验,观察记录并分析实验结果。 思考题一:(Vadermonde 矩阵)设 ?? ??????????????????????=? ? ? ?????????????=∑∑∑∑====n i i n n i i n i i n i i n n n n n n n x x x x b x x x x x x x x x x x x A 0020 10022222121102001111 ,, 其中,n k k x k ,,1,0,1.01 =+=, (1)对n=2,5,8,计算A 的条件数;随n 增大,矩阵性态如何变化? (2)对n=5,解方程组Ax=b ;设A 的最后一个元素有扰动10-4,再求解Ax=b (3)计算(2)扰动相对误差与解的相对偏差,分析它们与条件数的关系。 (4)你能由此解释为什么不用插值函数存在定理直接求插值函数而要用拉格朗日或牛顿插值法的原因吗? 相关MATLAB 函数提示: zeros(m,n) 生成m 行,n 列的零矩阵 ones(m,n) 生成m 行,n 列的元素全为1的矩阵 eye(n) 生成n 阶单位矩阵 rand(m,n) 生成m 行,n 列(0,1)上均匀分布的随机矩阵 diag(x) 返回由向量x 的元素构成的对角矩阵 tril(A) 提取矩阵A 的下三角部分生成下三角矩阵
