2012年全国各地市中考数学模拟试题分类汇编55动态综合型问题

D
图4
M 动态综合型问题
一、选择题
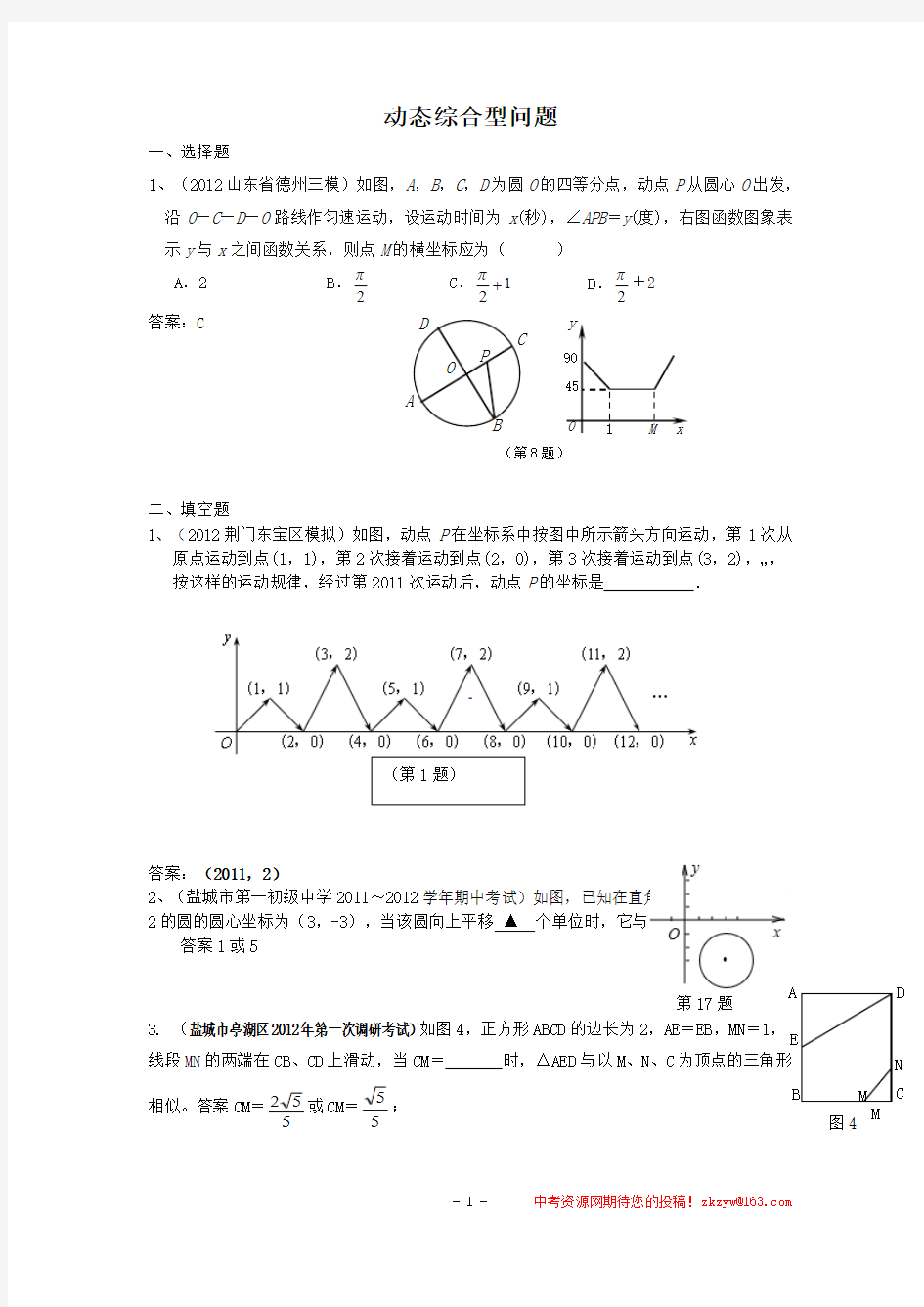
1、(2012山东省德州三模)如图,A ,B ,C ,D 为圆O 的四等分点,动点P 从圆心O 出发,沿O —C —D —O 路线作匀速运动,设运动时间为x (秒),∠APB =y (度),右图函数图象表示y 与x 之间函数关系,则点M 的横坐标应为( )
A .2
B .2π
C .12π+
D .2π
+2
答案:C
二、填空题
1、(2012荆门东宝区模拟)如图,动点P 在坐标系中按图中所示箭头方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P 的坐标是 .
答案:(2011,2)
2、(盐城市第一初级中学2011~2012学年期中考试)如图,已知在直角坐标系中,半径为2的圆的圆心坐标为(3,-3),当该圆向上平移 ▲ 个单位时,它与x 轴相切.
答案1或5
3. (盐城市亭湖区2012年第一次调研考试)如图4,正方形ABCD 的边长为2,AE =EB ,MN =1,线段MN 的两端在CB 、CD 上滑动,当CM = 时,△AED 与以M 、N 、C 为顶点的三角形
相似。答案CM =5
52或CM =55
;
(第8题)
第17题
4、(2012石家庄市42中二模)如图,矩形ABCD 的边AB 在y
轴上,AB 的中点与原点重合,AB =2,AD =1,过定点Q (2,0)和动点P (0,a )的直线与矩形ABCD 的边有公共点,
则a 的取值范围是____________. 答案:-2≤a ≤2
5、(2012年浙江省金华市一模)如图,直角梯形OABC
的直角顶点是坐标原点,边OA ,OC 分别
在X 轴,y 轴的正半轴上。OA ∥BC ,D 是BC 上一点,1
4
BD OA =
=AB =3, ∠OAB =45°,E ,F 分别是线段OA ,AB 上的两个动点,且始终保持∠DEF =45°,设OE =x ,AF =y ,则y 与x 的
函数关系式为
,如果△AEF 是等腰三角形时。将△AEF 沿EF 对
折得△A ′
EF 与五边形OEFBC 重叠部分的面积
。
答案:21
3y x x =-, 1, 214,12。
1. 解答题
1河南省信阳市二中).(11分)已知抛物线c bx ax y ++=2的顶点为(1,0),且经过点(0,1).
(1)求该抛物线对应的函数的解析式;
(2)将该抛物线向下平移)0(>m m 个单位,设得到的抛物线的顶点为A ,与x 轴的两个交点为B 、C ,若△ABC 为等边三角形.
①求m 的值;
②设点A 关于x 轴的对称点为点D ,在抛物线上是否存在点P ,使四边形CBDP 为菱形?
若存在,写出点P 的坐标;若不存在,请说明理由.
答案:.解:(1)由题意可得,0,
1,21.
a b c b
a
c ++=-==???
????解得1,2,1.a b c ==-=?????
∴抛物线对应的函数的解析式为2
21y x x =-+.………………………………3分 (2)①将2
21y x x =-+向下平移m 个单位得:2
21y x x =-+-m =2
(1)x m --,可知
A (1,-m ),B
0),C
0),BC
6分
由△ABC
2
m =,由m >0,解得m =3.…………7分
②不存在这样的点P . ……………………………………………………………8分 ∵点D 与点A 关于x 轴对称,∴D (1,3).由①得BC
CBDP 为菱形,需DP ∥BC ,DP =BC .
由题意,知点P 的横坐标为
当x
=1+22
21y x x =-+-m =2
22x x --
=2
(12(1293+-+-=≠,故不存在这样的点P .……………………………………………………………………11分
2(2012年4月韶山市初三质量检测)如图,矩形ABCD 中,点P 是线段AD 上一动点,O 为BD 的中点, PO 的延长线交BC 于Q. (1)求证:△ P O D ≌ △Q O B ;
(2)若AD=8厘米,AB=6厘米,P 从点A 出发,以1厘米/秒的速度向D 运动(不与D 重合).设点P 运动时间为t 秒,请用t 表示PD 的长;并求t 为何值时,四边形
P B Q D 是菱形.
【答案】(1)证明: 四边形ABCD 是矩形, ∴AD∥BC, ∴∠PDO=∠QBO,又OB=OD ,∠POD=∠QOB, ∴△POD≌△QOB
(2)解法一: PD=8-t
∵四边形ABCD 是矩形,∴∠A=90°,
∵AD=8cm,AB=6cm ,∴BD=10cm,∴OD=5cm. 当四边形PBQD 是菱形时, PQ⊥BD,∴∠POD=∠A,又∠ODP=∠ADB, ∴△ODP∽△ADB, ∴
OD AD PD BD =,即58
810
t =-,
解得74t =
,即运动时间为7
4
秒时,四边形PBQD 是菱形. 解法二:PD=8-t
当四边形PBQD 是菱形时,PB=PD=(8-t)cm ,
∵四边形ABCD 是矩形,∴∠A=90°,在RT△ABP 中,AB=6cm ,
∴222
AP AB BP +=, ∴2
2
2
6(8)t t +=-,
解得74t =,即运动时间为7
4
秒时,四边形PBQD 是菱形.
3(2012年中考数学新编及改编题试卷)开口向下的抛物线)4)(1(-+=x x a y 与x 轴的交点为A 、B (A 在B 的左边),与y 轴交于点C 。连结AC 、BC 。[来源:中.考.资.源.网] (1) 若△ABC 是直角三角形(图1)。求二次函数的解析式;
(2) 在(1)的条件下,将抛物线沿y 轴的负半轴向下平移k (k >0)个单位, 使平移后的抛物线与坐标轴只有两个交点。求k 的值。
(3) 当点C 坐标为(0,4)时(图2),P 、Q 两点同时从C 点出发,点P 沿折线C →O →B 运动到点B ,点Q 沿抛物线(在第一象限的部分)运动到点B ,若P 、Q 两点的运动速度相同,请问谁先到达点B ?请说明理由.(参考数据:6.313= 4.529=)
答案:
抛物线)4)(1(-+=x x a y 与x 轴的交点为A (-1,0)、B (4,0) (1) 若△ABC 是直角三角形,只有∠ACB =900
。[来源:学&科&网] 由题易得△ACO ∽△COB ∴
BO CO CO AO = ∴4
1CO
CO =
∴2=CO ∵抛物线开口向下 ∴C (0,2) 把 C (0,2)代入得 2)40)(10(=-+a 2
1
-
=a )4)(1(2
1
-+-=x x y
(2)由 )4)(1(2
1
-+-
=x x y 可得 抛物线的顶点为(23,8
25
), 点C (0,2)
当点C 向下平移到原点时,
平移后的抛物线与坐标轴只有两个交点 ∴2=k 当顶点向下平移到x 轴时,
平移后的抛物线与坐标轴只有两个交点 ∴8
25
=
k (3)当点C 为(0,4)时,抛物线的解析式为)4)(1(-+-=x x y 抛物线的顶点为D (23,4
25) 连结DC 、DB
∵D (23,4
25
) B (4,0) C (0,4)
∴CD =7.21343)4425(
)2
3(22
==-+ DB =75.6294
5
)425(
)2
3
4(22==+- ∴CD +DB =2.7+6.75=9.45 ∵CO +OB =4+4=8 ∴DB +DC >CO +OB
D
由函数图像可知第一象限内的抛物线的长度比CD +DB 还要长 所以第一象限内的抛物线的长度要大于折线C →O →B 的长度 所以点P 先到达点B
4、(2012年北京中考数学模拟试卷)如图9所示,OAB ?是边长为32+
的等边三角形,
其中O 是坐标原点,顶点A 在x 轴的正方向上,将OAB ?折叠,使点B 落在边OA 上,记为B ',折痕为EF 。
(1)设B O '的长为x ,E B O '?的周长为c ,求c 关于x 的函数关系式. (2)当E B '//y 轴时,求点B '和点E 的坐标. (3)当B '在OA 上运动但不与O 、A 重合时,能否使
F B E '?成为直角三角形?若能,请求出点B '的坐标;若不能,请说明理由.
(1)解:∵B '和B 关于EF 对称,∴B 'E =BE ,
∴OE E B B O y +'+'==OE BE B O ++' =OB x +=32++x . (2)解:当E B '//y 轴时,∠O B E '=90°。
∵△OAB 为等边三角形,∴∠EO B '=60°,O B '=2
1
EO 。 设a B O =',则OE =a 2。
在Rt △OE B '中,tan ∠EO B '=
O
B E
B '', ∴B 'E =B 'Otan ∠EO B '=a 3 ∵B 'E + OE =BE +OE =2+3,∴1=a , ∴B '(1,0),E (1,3)。
(图9)
(3)答:不能。
理由如下:∵∠E B'F=∠B=60°,
∴要使△E B'F成为直角三角形,则90°角只能是∠B'EF或
∠B'FE。
假设∠B'EF=90°,
∵△F B'E与△FBE关于FE对称,
∴∠BEF=∠B'EF=90°,
∴∠BE B'=180°,
则B'、E、B三点在同一直线上,B'与O重合。
这与题设矛盾。
∴∠B'EF≠90°。
即△E B'F不能为直角三角形。
同理,∠B'FE=90°也不成立。
∴△E B'F不能成为直角三角形。
5、(2012年北京市延庆县一诊考试)在平面直角坐标系xOy中,已知二次函数y1=ax2+3x+c 的图像经过原点及点A(1,2),
与x轴相交于另一点B。
(1)求:二次函数y1的解析式及B点坐标;
(2)若将抛物线y1以x=3为对称轴向右翻折后,得到一个新的二次函数y2,已知二次函数y2与x轴交于两点,其中右边的交点为C点. 点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D、点E、点F也随之运动);
①当点E在二次函数y1的图像上时,求OP的长。
解:(1)二次函数y1=-x2+3x
如图3:当点P 、点N 重合时,有OP +CN =6,则有
如图4:当点P 、点Q 重合时,有OP +CQ =6,则有
6、(2012年山东泰安模拟)如图,已知抛物线C 1:5)2(2
--=x a y 的顶点为P ,与x 轴相交于A 、B 两点(点A 在点B 的左边),点A 的横坐标是1-. (1)求p 点坐标及a 的值;
(2)如图(1),抛物线C 2与抛物线C 1关于x 轴对称,将抛物线C 2向左平移,平移后的抛物线记为C 3,C 3的顶点为M ,当点P 、M 关于点A 成中心对称时,求C 3的解析式
k h x a y +-=2)(;
(3)如图(2),点Q 是x 轴负半轴上一动点,将抛物线C 1绕点Q 旋转180°后得到抛物线C 4.抛物线C 4的顶点为N ,与x 轴相交于E 、F 两点(点E 在点F 的左边),当以点P 、
N 、E 为顶点的三角形是直角三角形时,求顶点N 的坐标.
1、解:(1)由抛物
线
C 1:
5)2(2--=x a y 得顶点P 的坐标(2,5)
∵点A (-1,0)在抛物线C 1上∴9
5
a =
. t+2t+45t=6,t=
30
19
t+2t=6,
t=2
(2)连接PM ,作PH ⊥x 轴于H ,作MG ⊥x 轴于G .. ∵点P 、M 关于点A 成中心对称, ∴PM 过点A ,且PA =MA .. ∴△PAH ≌△MAG .. ∴MG =PH =5,AG =AH =3. ∴顶点M 的坐标为(4-,5)
∵抛物线C 2与C 1关于x 轴对称,抛物线C 3由C 2平移得到 ∴抛物线C 3的表达式5)4(9
5
2++-=x y .
(3)∵抛物线C 4由C 1绕x 轴上的点Q 旋转180°得到 ∴顶点N 、P 关于点Q 成中心对称. 由(2)得点N 的纵坐标为5.
设点N 坐标为(m ,5),作PH ⊥x 轴于H ,
作NG ⊥x 轴于G ,作PR ⊥NG 于R .∵旋转中心Q 在x 轴上, ∴EF =AB =2AH =6.
∴EG =3,点E 坐标为(3m -,0),H 坐标为(2,0),R 坐标为(m ,-5). 根据勾股定理,得
,104m 4m PR NR PN 2
222+-=+= 50m 10m HE PH PE 2222+-=+= 3435NE 222=+=
①当∠PNE =90o时,PN 2
+ NE 2
=PE 2
,解得m =344-,∴N 点坐标为(3
44
-,5) ②当∠PEN =90o时,PE 2
+ NE 2
=PN 2
,解得m =310-,∴N 点坐标为(3
10-,5). ③∵PN >NR =10>NE ,∴∠NPE ≠90o 综上所得,当N 点坐标为(3
44
-,5)或(310-,5)时,以点P 、N 、E 为顶点的三角形是
直角三角形.
7、[河南开封2012年中招第一次模拟](9分)刘卫同学在一次课外活动中,用硬纸片做了两个直角三角形,在Rt△ABC 中∠B=90°,∠A=30°,BC=6cm ;Rt△FDE 中∠D=90°,∠E=45°,DE=4cm 。如图是刘卫同学所做的一个实验,他将Rt△FDE 的直角边DE 与Rt△ABC 的斜边AC 重合在一起,并将△FDE 沿AC 的方向移动,在移动过程中,D 、E 两点始终在AC 边上(移动开始时点D 与点E 重合)。
(1)在△FDE 沿AC 方向移动的过程中,刘卫同学发现:
F 、C 两点间的距离逐渐 ;(填“不变”、“变大”或“变小”) (2)刘卫同学经过进一步的研究,编制了如下问题:
问题①:当△FDE 移动到什么位置时,即AD 的长为多少时,F 、C 的连线与AB 平行? 问题②:当△FDE 移动到什么位置时,即AD 的长为多少时,以线段AD 、FC 、BC 的长度为三边长的三角形能构成直角三角形?(请完成解答过程。)
答案:
8(2012年福建福州质量检查)(满分13分)如图,在△ABC 中,AB =AC =10cm ,BC =16cm ,
DE =4cm .动线段DE (端点D 从点B 开始)沿BC 边以1cm/s 的速度向点C 运动,当端点E 到
达点C 时运动停止.过点E 作EF ∥AC 交AB 于点F (当点E 与点C 重合时,EF 与CA 重合),连接DF ,设运动的时间为t 秒(t ≥0).
F
(1) 直接写出用含t 的代数式表示线段BE 、EF 的长;
(2) 在这个运动过程中,△DEF 能否为等腰三角形?若能,请求出t 的值;若不能,请说明理由;
(3) 设M 、N 分别是DF 、EF 的中点,求整个运动过程中,MN 所扫过的面积. 答案:解:(1) BE =(t +4)cm , 222222222222222222222 1分
EF =5
8
(t +4)cm . 2222222222222222222222 4分
(2) 分三种情况讨论:
① 当DF =EF 时,
A
B (D )
C
E
F
A
B
C
D
E
F
A
B
C
D E
F
A
B
C
D
E
M
P
F
N L
K
B
C
D
E
第21题图
有∠EDF =∠DEF =∠B , ∴ 点B 与点D 重合,
∴ t =0. 222222222 5分 ② 当DE =EF 时,[来源:学.科.网] ∴4=5
8
(t +4),
解得:t =12
5. 2222222 7分
③ 当DE =DF 时,
有∠DFE =∠DEF =∠B =∠C , ∴△DEF ∽△ABC .
∴DE AB =EF BC ,即410=5
8(t +4)
16, 解得:t =156
25
. 222222 9分
综上所述,当t =0、125或156
25秒时,△DEF 为等腰三角形.
(3) 设P 是AC 的中点,连接BP , ∵ EF ∥AC , ∴ △FBE ∽△ABC . ∴ EF AC =BE BC , ∴ EN CP =
BE
BC
. 又∠BEN =∠C , ∴ △NBE ∽△PBC ,
∴ ∠NBE =∠PBC . 2222222222222222222222222 10分 ∴ 点N 沿直线BP 运动,MN 也随之平移.
如图,设MN 从ST 位置运动到PQ 位置,则四边形PQST 是平行四边形. 222 11分 ∵ M 、N 分别是DF 、EF 的中点,∴ MN ∥DE ,且ST =MN =1
2
DE =2.
分别过点T 、P 作TK ⊥BC ,垂足为K ,PL ⊥BC ,垂足为L ,延长ST 交PL 于点R ,则四边形TKLR 是矩形,
当t =0时,EF =58(0+4)=52,TK =12EF 2sin∠DEF =12352335=3
4;
当t =12时,EF =AC =10,PL =12AC 2sin C =1231033
5
=3.
∴PR =PL -RL =PL -TK =3-34=9
4.
∴S □PQST =ST 2PR =2394=9
2
.
∴整个运动过程中,MN 所扫过的面积为92cm 2
. 22222222222222 13分
9、(2012年浙江丽水一模)平面直角坐标系中,平行四边形ABOC 如图放置,点A 、C 的坐标分别为(0,3)、(-1,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形'''A B OC 。
(1)若抛物线过点C ,A ,A',求此抛物线的解析式;
(2)求平行四边形ABOC 和平行四边形'''A B OC 重叠部分△'OC D 的周长;
(3)点M 是第一象限内抛物线上的一动点,间:点M 在何处时△AMA'的面积最大?最大面积是多少?并求出此时点M 的坐标。
[来源:学#科#网Z#X#X#K]
答案:
解:(1)∵平行四边形'''OC B A 由ABOC 旋转得到,且点A 的坐标为(0,3), 点A'的坐标为(3,0)。
所以抛物线过点C(-1,0),A(0,3),A' (3,0)设抛物线的解析式为2
(0)y ax bx c a =++≠,可得
03930
a b c c a b c -+=??=??++=?
解得123a b c =-??=??=?
∴过点C ,A ,A'的抛物线的解析式为2
23y x x =-++。 (2)因为AB ∥CO ,所以∠OAB=∠AOC=90°。
∴OB ==,又'OC D OCA B ∠=∠=∠.
'C OD BOA ∠=∠,∴BOA OD C ∽△△'又'1OC OC ==,
∴
''=BOA C OD OC OB ?=
?的周长的周长又△ABO 的周长为4 ∴'C OD ?。
(3)连接OM ,设M 点的坐标为()m n ,,
第1题图
∵点M 在抛物线上,∴223n m m =-++。 ∴'''AMA AMO OMA AOA S S S S ????=+-
=111393
''()(3)222222OA m OA n OA OA m n m n ?+?-?=+-=+- =2233327(3)()2228
m m m =--=--+
因为03m <<,所以当32
m =时,15
4n =。△AMA ’的面积有最大值
所以当点M 的坐标为(31524,)时,△AMA ’的面积有最大值,且最大值为27
8
。
10(2012年浙江金华一模)如图,在平面直角坐标系xOy 中,△ABC 的A 、B 两个顶点在x 轴上,顶点C 在y 轴的负半轴上.已知OA :OB =1:5,OB =OC ,△ABC 的面积15ABC S ?=,抛物线2
(0)y ax bx c a =++≠经过A 、B 、C 三点. (1)求此抛物线的函数表达式; (2)点P (2,-3)是抛物线对称轴上的一点,在线段OC 上有一动点M ,以每秒2个单位的速度从O 向C 运动,(不与点O ,C 重合),过点M 作MH ∥BC ,交X 轴于点H ,设点M 的运动时间为t 秒,试把⊿PMH 的面积S 表示成t 的函数,当t 为何值时,S 有最大值,并求出最大值;
(3)设点E 是抛物线上异于点A ,B 的一个动点,过点E 作x 轴的平行线交抛物线于另一点F . 以EF 为直径画⊙Q ,则在点E 的运动过程中,是否存在与x 轴相切的⊙Q ?若存在,求出此时点E 的坐标;若不存在,请说明理由。
第1题答案图
答案:
(1)542
--=x x y (4分)
(2).由题意可求得直线BC :y =x -5 ∵M (0,-2t ) 直线MH 平行于直线BC ∴直线MH 为y =x -2t
设直线MH 与对称轴交与点D ,点D 的坐标为(2,2-2t ) ∴DP =5-2t ∴ S △pmh =
2132t (5-2t )=—2t 2
+5t (0<t <25 当t =45时,S 有最大值是8
25 (8分)
(3)当点E 在x 轴下方且对称轴右侧时坐标为(
237
3+, 2371-)
当点E 在x 轴下方且对称轴左侧时坐标为(
237
5-, 2371-)
当点E 在x 轴上方且对称轴右侧时坐标为(
237
5+, 2371+)
当点E 在x 轴上方且对称轴左侧时坐标为(
2
37
3-, 2371+)(12分)
11、(2012年浙江金华五模)如图,Rt ABC ?在平面直角坐标系中,BC 在X 轴上,B (﹣1,0)、
A (0,2),, AC ⊥A
B .
(1)求线段OC 的长.
(2)点P 从B 点出发以每秒4个单位的速度沿x 轴正半轴运动,点Q 从A 点出发沿线.段.AC 以5个单位每秒速度向点C 运 动,当一点停止运动,另一点也随之停止,设△CPQ 的面 积为S ,两点同时运动,运动的时间为t 秒,求S 与t 之间关系式,并写出自变量取值范围.
(3)Q 点沿射线AC 按原速度运动,⊙G 过A 、B 、Q 三点,是否有这样的t 值使点P 在⊙G 上、如果有求t 值,如果没有说明理由。
答案:(1)利用AOB COA ?? 即可求得OC =4. (2)ⅰ 当P 在BC 上,Q 在线段AC 上时,(5
04
t )过点Q 作QD ⊥BC , 如图所示,则,
且CQ =,54CP t =-, 由CQD CAO ?? 可得2QD t =-,所以11(54)(2)22
s CP QD t t ==-- 即213252s t t =-+(5
04
t )
ⅱ 当P 在BC 延长线上,Q 在线段AC 上时(
5
24
t ),过点Q 作QD ⊥BC , 如图所示,则,
且CQ =,45CP t =-, 由CQD CAO ?? 可得2QD t =-,所以11(45)(2)22
s CP QD t t ==-- 即213252s t t =-+-(5
24
t ) ⅲ 当5
4
t =
或2t =时C 、P 、Q 都在同一直线上。 (3)若点P 在圆G 上,因为AC ⊥AB ,所以BQ 是直径,所以BPQ Rt ∠=∠,即P Q B C ⊥,
则2
2
2
2
2
BP PQ BQ BA AQ +==+,
得
)2
2
22
42t t +-=+
解得112t =
,21
6
t =-(不合题意,舍去)
y
x
C
B
O
x
y
D C
B
O
P
x
y
D
C
B
O
P
所以当t =
1
2
时,点P 在圆G 上. (也可以在(2)的基础上分类讨论,利用相似求得)
12、(2012山东省德州二模)如图,在等腰梯形ABCD 中,AB ‖CD,已知6=AB ,22=BC ,
?=∠45DAB ,以AB 所在直线为x 轴,A 为坐标原点,建立直角坐标系,将等腰梯形ABCD
绕A 点按顺时针方向旋转?90得到等腰梯形OEFG (O 、E 、F 、G 分别是A 、B 、C 、D 旋转后的对应点)(如图).
⑴在直线DC 上是否存在一点P ,使E FP ?为等腰三角形,若存在,写出出P 点的坐标,若不存在,请说明理由.
⑵将等腰梯形ABCD 沿x 轴的正半轴平行移动,设移动后的x OA =(0 答案:1)P (-2,2),P (0,2) ………………………………………………2分 2)①当0<x ≤2时,y=4 1x 2 2; …………………………………………4分 当2≤x ≤4时;y=- 41x 2 +2x-2 ………………………………………………6分 当4≤x ≤6时;y=-21x 2 +4x-6 ………………………………………………8分 ②当0<x ≤2时,y=4 1x 2 当x =2时,y 最大=1, …………………9分 当2≤x ≤4时;y=-41x 2+2x-2=-4 1(x -4)2 +2 当x =4时,y 最大= 2 …………………………10分 当4≤x ≤6时;y=- 21x 2+4x-6=-2 1 (x -4)2+2 当x =4时,y 最大=2 ………………第28题图 11分 综上可知:当x =4时,重叠部分的面积y 最大=2 ……………………12分 13、(2012荆门东宝区模拟)如图,将—矩形OABC 放在直角坐际系中,O 为坐标原点.点 A 在x 轴正半轴上.点E 是边A B 上的—个动点(不与点A 、B 重合),过点E 的反比例函 数(0)k y x x = >的图象与边BC 交于点F . (1)若△OAE 、△OCF 的而积分别为12S S 、.且12=2S S +,求k 的值. (2)若OA =2,0C =4,问当点E 运动到什么位置时,四边形OAEF 的面积最大,其最大值 为多少? (第1题) 答案:解:(1) 222 k k +=,2k =。 (2)当点E 运动到AB 的中点时,四边形OAEF 的面积最大,最大值是5. 14(2012昆山一模) 如图(1),Rt △ABC 中,∠C =90°,AC =12,BC =5,点M 在边AB 上,且AM =6. (1)动点D 在边AC 上运动,且与点A 、C 均不重合,设CD =x . ①设△ABC 与△ADM 的面积之比为y ,求y 与x 之间的函数关系式,并写出自变量的 取值范围. ②当x 取何值时,△ADM 是等腰三角形?写出你的理由; (2)如图(2),以图(1)中的BC 、CA 为一组邻边的矩形ACBE 中,动点D 在矩形边上运动 一周,能使△ADM 是以∠AMD 为顶角的等腰三角形共有几个?(直接写出结果,不必说明理由) 答案: 15、(2012年,瑞安市模考)如图,直线l1与坐标轴分别交于点A、B,经过原点的直 线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3, 15 4 ),且OA=8. 在直线AB上取点P,过点P作y轴的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t. (1)求直线l1的解析式; (2)当点P在线段AC上时,试探求正方形PQEF与△ACD重叠部分(阴影部分)的面积的最大值; (3)设点M坐标为 9 (4,) 2 ,在点P的运动过程中,当点M在正方形PQEF内部时,请直接写 出的取值范围. 答案:(1) 6 4 3 + - =x y ;…4分 (第2题) Q 2019-2020 年中考数学模拟试题分类汇编- 实验与操作 一、选择题 1. ( 2010 年河南省南阳市中考模拟数学试题)将如图①的矩形ABCD纸片沿 EF 折叠得到图②,折叠后 DE 与 BF 相交于点 P,如果∠ BPE=130°,则∠ PEF的度数为 ( ) A. 60°B.65°C . 70°D . 75° E D A E A B C B P D F F ①② C 答: B 2.( 2010 年河南中考模拟题 4)分别剪一些边长相同的①正三角形,②正方形,③正五边形,如果用其 中一种正多边形镶嵌,可以镶嵌成一个平面图案的有( ) A. ①② B. ②③ C.①③ D.①②③都可以 答案: A 3.(2010 年西湖区月考)有一张矩形纸片 ABCD,其中 AD=4cm,上面有一个以 AD为直径的半园,正好与对 边 BC相切,如图 ( 甲). 将它沿 DE折叠,是 A 点落在 BC上,如图 ( 乙 ). 这时,半圆还露在外面的部分 ( 阴影部分 ) 的面积是() A. (π -2 3 )cm2 B. (1 3 2 π +) cm 2 C. (4 3 2 π -) cm 3 D. (2 π+ 3 )cm2 3 答案: C 4. ( 2010 河南模拟)某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案,你认为符合条件的是() A正三角形B正五边形C等腰梯形D菱形 答案: D 5. ( 2010 年广西桂林适应训练)、在1, 2,3, 4,, 999, 1000,这 1000 个自然数中,数字“0”出现的次数一共是()次. A.182 B.189 C.192 D.194 答案: C ①② 综合性问题 一、选择题 1.(2018·湖北省孝感·3分)如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(﹣1)EF.其中正确结论的个数为() A.5 B.4 C.3 D.2 【分析】①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°,据此可判断;②求出∠AFP和∠FAG度数,从而得出∠AGF度数,据此可判断;③证△ADF≌△BAH即可判断;④由∠AFG=∠CBG=60°、∠AGF=∠CGB 即可得证;⑤设PF=x,则AF=2x、AP==x,设EF=a,由△ADF≌△BAH知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得=,从而得出a与x的关系即可判断. 【解答】解:∵△ABC为等边三角形,△ABD为等腰直角三角形, ∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°, ∴△CAD是等腰三角形,且顶角∠CAD=150°, ∴∠ADC=15°,故①正确; ∵AE⊥BD,即∠AED=90°, ∴∠DAE=45°, ∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°, ∴∠AGF=75°, 由∠AFG≠∠AGF知AF≠AG,故②错误; 记AH与CD的交点为P, 由AH⊥CD且∠AFG=60°知∠FAP=30°, 则∠BAH=∠ADC=15°, 在△ADF和△BAH中, ∵, ∴△ADF≌△BAH(ASA), ∴DF=AH,故③正确; ∵∠AFG=∠CBG=60°,∠AGF=∠CGB, ∴△AFG∽△CBG,故④正确; 在Rt△APF中,设PF=x,则AF=2x、AP==x, 设EF=a, ∵△ADF≌△BAH, ∴BH=AF=2x, △ABE中,∵∠AEB=90°、∠ABE=45°, ∴BE=AE=AF+EF=a+2x, ∴EH=BE﹣BH=a+2x﹣2x=a, ∵∠APF=∠AEH=90°,∠FAP=∠HAE, ∴△PAF∽△EAH, ∴=,即=, 整理,得:2x2=(﹣1)ax, 由x≠0得2x=(﹣1)a,即AF=(﹣1)EF,故⑤正确; 故选:B. 【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握等腰三角形与等边三角形的性质、全等三角形与相似三角形的判定与性质等知识点. 2.(2018·山东潍坊·3分)如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米秒的速度自A点出发 2015 年全国中考数学试题分类汇编————压轴题 1. 在平面直角坐标系xOy 中,抛物线的解析式是y = 1 x2 +1,点 C 的坐标为 (–4, 0),平行4 四边形 OABC 的顶点 A,B 在抛物线上, AB 与 y 轴交于点M,已知点 Q(x,y)在抛物线上,点 P(t ,0)在 x 轴上 . (1)写出点 M 的坐标; (2)当四边形 CMQP 是以 MQ , PC 为腰的梯形时 . ①求 t 关于 x 的函数解析式和自变量x 的取值范围; ②当梯形 CMQP 的两底的长度之比为1: 2 时,求t 的值 . 11 x210 1 4 (1)M(0,2)(2)1AC:y= 2 x+1.PQ // MC.x t= 2 2.如图,已知在矩形 ABCD 中, AB= 2, BC= 3, P 是线段 AD 边上的任意一点(不含端点 A、 D ),连结 PC,过点 P 作 PE⊥ PC 交 AB 于 E (1)在线段 AD 上是否存在不同于 P 的点 Q,使得 QC⊥ QE?若存在,求线段 AP 与AQ 之间的数量关系;若不存在,请说明理由; ( 2)当点 P 在 AD 上运动时,对应的点 E 也随之在AB 上运动,求BE 的取值范围. A P D E B C (3 )存在,理由如下: 如图 2 ,假设存在这样的点Q,使得 QC ⊥ QE. 由( 1)得:△ PAE ∽ △ CDP , ∴ , ∴ , ∵QC ⊥ QE ,∠ D= 90°, ∴∠ AQE +∠ DQC = 90 °,∠ DQC +∠ DCQ = 90 °, ∴∠ AQE= ∠DCQ. 又∵∠ A=∠ D=90°, ∴△ QAE ∽ △ CDQ , ∴ , ∴ ∴ , 即, ∴ , ∴ , ∴. ∵AP≠ AQ,∴ AP + AQ = 3.又∵AP≠ AQ,∴AP≠,即 P 不能是 AD 的中点,∴当P是 AD 的中点时,满足条件的Q点不存在, 综上所述,的取值范围7 ≤< 2;8 3.如图,已知抛物线y=-1 x2+ x+ 4 交x 轴的正半轴于点 A ,交y 轴于点 B .2 ( 1)求 A 、B 两点的坐标,并求直线( 2)设 P( x,y)( x> 0)是直线为对角线作正方形 PEQF,若正方形( 3)在( 2)的条件下,记正方形 AB 的解析式; y= x 上的一点, Q 是 OP 的中点( O 是原点),以PQ PEQF 与直线AB 有公共点,求x 的取值范围; PEQF 与△ OAB 公共部分的面积为S,求 S 关于 x 的函 数解析式,并探究S 的最大值. (1) 令 x=0, 得 y=4 即点 B 的坐标为 (0,4) 令y=0, 得(-1/2)x2+x+4=0 则x2-2x-8=0 ∴x=-2 或 x=4 ∴点 A 的坐标为 (4,0) 直线 AB 的解析式为 (y-0)/(x-4)=(4-0)/(0-4) ∴y=-x+4 (2) 由(1),知直线AB的解析式为y=-x+4 二次函数 一、选择题 1.(2010年山东宁阳一模)在平面直角坐标系中,先将抛物线22-+=x x y 关于x 轴作轴对称变换,再将所得抛物线关于y 轴作轴对称变换,经过两次变换后所得的新抛物线解析式为( ) A .22+--=x x y B .22-+-=x x y C .22++-=x x y D .22++=x x y 答案:C 2.(2010年江西省统一考试样卷)若抛物线y =2x 2 向左平移1个单位,则所得抛物线是( ) A .y =2x 2 +1 B .y =2x 2 -1 C .y =2(x +1)2 D .y =2(x -1)2 答案:C 3. (2010年河南中考模拟题1)某校运动会上,某运动员掷铅球时,他所掷的铅球的高 与水平 的距离 ,则该运动员的成绩是( ) A. 6m B. 10m C. 8m D. 12m 答案:D 4.(2010年河南中考模拟题4)二次函数2 y ax bx c =++(0a ≠)的图象 如图所示,则正确的是( ) A .a <0 B .b <0 C .c >0 D .以答案上都不正确 答案:A 5.(2010年河南中考模拟题3)已知二次函数y=ax 2 +bx+c 的图像如图所 示,则下列条件正确的是( ) A .ac <0 B.b 2 -4ac <0 C. b >0 D. a >0、b <0、c >0 答案:D 6.(2010年江苏省泰州市济川实验初中中考模拟题)抛物线y =ax 2 +bx +c 上部分点的横坐标x ,纵坐标 y 的对应值如表所示. 给出下列说法:①抛物线与y 轴的交点为(0,6); ②抛物线的对称轴是在y 轴的右侧; ③抛物线一定经过点(3,0); ④在对称轴左侧,y 随x 增大而减小. x … -3 -2 -1 0 1 … y … -6 0 4 6 6 … y x O x= 1 中考数学真题汇编:平移与旋转 一、选择题 1.下列图形中,可以看作是中心对称图形的是() A. B. C. D. 【答案】A 2.在平面直角坐标系中,点关于原点对称的点的坐标是() A. B. C. D. 【答案】C 3.在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为() A.(4,-3) B.(-4,3) C.(-3,4) D.(-3,-4) 【答案】B 4.如图,在平面直角坐标系中,的顶点在第一象限,点,的坐标分别为、, ,,直线交轴于点,若与关于点成中心对称,则 点的坐标为() A. B. C. D. 【答案】A 5.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是() A. 55° B. 60° C. 65° D. 70° 【答案】C 6.下列图形中,既是轴对称又是中心对称图形的是() A. B. C. D. 【答案】B 7.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系如图,在平面上取定一点称为极点;从点出 发引一条射线称为极轴;线段的长度称为极径点的极坐标就可以用线段的长度以及从 转动到的角度(规定逆时针方向转动角度为正)来确定,即或或 等,则点关于点成中心对称的点的极坐标表示不正确的是( ) A. B. C. D. 【答案】D 8.如图,点是正方形的边上一点,把绕点顺时针旋转到的位置, 若四边形的面积为25,,则的长为() A. 5 B. C. 7 D. 【答案】D 9.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是() A. 主视图 B. 左视图 C. 俯视图 D. 主视图和左视图 【答案】C 10.如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分 三角形的面积为4.若,则等于() A. 2 B. 3 C. D. 【答案】A 11.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0, ).现将该三角板向右平移使点A与点O重合,得到△OCB’,则点B的对应点B’的坐标是() A. (1,0) B. (,) C. (1,) D. (-1,) 【答案】C 12.如图,直线都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为,对角线AC 在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移 A B C D P E 2015年全国中考数学试题分类汇编————压轴题 1. 在平面直角坐标系xOy 中,抛物线的解析式是y = 2 4 1x +1,点C 的坐标为(–4,0),平行四边形OABC 的顶点A ,B 在抛物线上,AB 与y 轴交于点M ,已知点Q (x ,y )在抛物线上,点P (t ,0)在x 轴上. (1) 写出点M 的坐标; (2) 当四边形CMQP 是以MQ ,PC 为腰的梯形时. ① 求t 关于x 的函数解析式和自变量x 的取值范围; ② 当梯形CMQP 的两底的长度之比为1:2时,求t 的值. (1)M(0,2)(2)1AC:y= 21x+1.PQ // MC.t x x --+0 14 12 =21 2. 如图,已知在矩形ABCD 中,AB =2,BC =3,P 是线段AD 边上的任意一点(不含端点 A 、D ),连结PC , 过点P 作PE ⊥PC 交A B 于E (1)在线段AD 上是否存在不同于P 的点Q ,使得QC ⊥QE ?若存在,求线段AP 与AQ 之间的数量关系;若不存在,请说明理由; (2)当点P 在AD 上运动时,对应的点E 也随之在AB 上运动,求BE 的取值范围. (3)存在,理由如下: 如图2,假设存在这样的点Q ,使得QC ⊥QE. 由(1)得:△PAE ∽△CDP , ∴ , ∴ , ∵QC ⊥QE ,∠D =90 ° , ∴∠AQE +∠DQC =90 ° ,∠DQC +∠DCQ =90°, ∴∠AQE=∠DCQ. 又∵∠A=∠D=90°, ∴△QAE ∽△CDQ , ∴ , ∴ ∴ , 即 , ∴ , ∴ , ∴ . ∵AP≠AQ ,∴AP +AQ =3.又∵AP≠AQ ,∴AP≠ ,即P 不能是AD 的中点, ∴当P 是AD 的中点时,满足条件的Q 点不存在, 综上所述, 的取值范围8 7 ≤ <2; 3.如图,已知抛物线y =-1 2 x 2+x +4交x 轴的正半轴于点A ,交y 轴于点B . (1)求A 、B 两点的坐标,并求直线AB 的解析式; (2)设P (x ,y )(x >0)是直线y =x 上的一点,Q 是OP 的中点(O 是原点),以PQ 为对角线作正方形PEQF ,若正方形PEQF 与直线AB 有公共点,求x 的取值范围; (3)在(2)的条件下,记正方形PEQF 与△OAB 公共部分的面积为S ,求S 关于x 的函数解析式,并探究S 的最大值. (1)令x=0,得y=4 即点B 的坐标为(0,4) 令y=0,得(-1/2)x2+x+4=0 则x2-2x-8=0 ∴x=-2或x=4 ∴点A 的坐标为(4,0) 直线AB 的解析式为 (y-0)/(x-4)=(4-0)/(0-4) ∴y=-x+4 (2)由(1),知直线AB 的解析式为y=-x+4 2020年广东各地区中考数学试题分类汇编——函数 1、(佛山)15.如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在 函数()的图象上,则点E的坐标是(,). 2、(肇庆)9.在直角坐标系中,将点P(3,6)向左平移4个单位长度, 再向下平移8个单位长度后,得到的点位于() A.第一象限 B.第二象限 C.第三象限D.第四象限 3、(茂名)9.已知反比例函数=(≠0)的图象,在每一象限内,的值随值的增 大而减少,则一次函数=-+的图象不经过() A.第一象限B.第二象限C.第三象限D.第四象限 4、(梅州)5.一列货运火车从梅州站出发,匀加速行驶一段时间后开始匀速行驶,过了 一段时间,火车到达下一个车站停下,装完货以后,火车又匀加速行驶,一段时间后再次开始匀速行驶,那么可以近似地刻画出火车在这段时间内的速度变化情况的是 () 5、(湛江)8.函数的自变量的取值范围是() A. B. C. D. 6、(湛江)11.已知三角形的面积一定,则它底边上的高与底边之间的函数关系 的图象大致是() 1 y x =0 x> y x a a y x y a x a 1 2 y x = - x 2 x=2 x≠2 x≠-2 x> a h a O A B C E F D x y 第15题图 h h h h A . B . C . D . 7、(湛江)12. 如图2所示,已知等边三角形ABC 的边长为,按图中所示的规律,用个这样的三角形镶嵌而成的四边形的周长是( ) A. B. C. D. 8、(梅州)10. 函数的自变量的取值范围是_____. 9、(梅州)12. 已知直线与双曲线的一个交点A 的坐标为(-1,-2).则=_____;=____;它们的另一个交点坐标是______. 10、(东莞)7.经过点A (1,2)的反比例函数解析式是_____ _____; 11、(佛山)22.某地为四川省汶川大地震灾区进行募捐,共收到粮食100吨,副食品54 吨. 现计划租用甲、乙两种货车共8辆将这批货物全部运往汶川,已知一辆甲种货车同时可装粮食20吨、副食品6吨,一辆乙种货车同时可装粮食8吨、副食品8吨. (1) 将这些货物一次性运到目的地,有几种租用货车的方案? (2) 若甲种货车每辆付运输费1300元,乙种货车每辆付运输费1000元,要使运输总 费用最少,应选择哪种方案? 12008 20082009 201020111 1-=x y x mx y =x k y = m k 图2 C A B ┅┅ 有理数一、选择题 1.(2016·天津北辰区·一摸)计算 1 1 2 --的结果等于() (A)1 2 (B) 1 2 - (C)3 2 (D) 3 2 - 答案:D 2.(2016·天津北辰区·一摸)据报道,2015年国内生产总值达到677 000亿元,677 000用科学记数法表示应为(). (A)6 0.67710 ?(B)5 6.7710 ? (C)4 67.710 ?(D)3 67710 ? 答案:B 3.(2016·天津南开区·二模)﹣2的绝对值是() A.2B.﹣2C.D. 考点:实数的相关概念 答案:A 试题解析:﹣2的绝对值是2,即|﹣2|=2.故选:A. 4.(2016·天津南开区·二模)下列各数中是有理数的是() A.B.4π C.sin45°D. 考点:实数及其分类 答案:D 试题解析:A、==3,是无理数;B、4π是无理数;C、sin45°=是无理数; D、==2,是有理数;故选D. 5.(2016·天津南开区·二模)2014年3月5日,李克强总理在政府工作报告中指出:2013年全国城镇新增就业人数约13100000人,创历史新高,将数字13100000用科学记数法表示为() A.13.1×106B.1.31×107 C.1.31×108D.0.131×108 考点:科学记数法和近似数、有效数字 答案:B 试题解析:13100000=1.31×107 6.(2016·天津市和平区·一模)计算(﹣3)﹣(﹣5)的结果等于() A.﹣2 B.2 C.﹣8 D.15 【考点】有理数的减法. 【分析】根据有理数的减法法则:减去一个数等于加上这个数的相反数. 【解答】解:(﹣3)﹣(﹣5)=(﹣3)+5=5﹣3=2, 故选:B. 河北 周建杰 分类 (2008年南京市)27.(8分)如图,已知O 的半径为6cm ,射线PM 经过点O ,10cm OP =, 射线PN 与 O 相切于点Q .A B ,两点同时从点P 出发, 点A 以5cm/s 的速度沿射线PM 方向运动,点B 以4cm/s 的速度沿射线PN 方向运动.设运动时间为t s . (1)求PQ 的长; (2)当t 为何值时,直线AB 与O 相切? 以下是河南省高建国分类: (2008年巴中市)已知:如图14,抛物线2 334 y x =- +与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线3 4y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式. (2)求ABC △的面积. (3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积 最大,最大面积是多少? 答 以下是湖北孔小朋分类: 21.(2008福建福州)(本题满分13分) 如图,已知△ABC 是边长为6cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 匀速运动,其中点P 运动的速度是1cm/s ,点Q 运动的速度是2cm/s ,当点Q 到达 A B Q O P N M 点C 时,P 、Q 两点都停止运动,设运动时间为t (s ),解答下列问题: (1)当t =2时,判断△BPQ 的形状,并说明理由; (2)设△BPQ 的面积为S (cm 2),求S 与t 的函数关系式; (3)作QR //BA 交AC 于点R ,连结PR ,当t 为何值时,△APR ∽△PRQ ? (2008年贵阳市)15.如图4,在126 的网格图中(每个小正方形的边长均为1个单位),A 的半径为1,B 的半径为2,要使A 与静止的B 相切,那么A 由图示位置需向右平移个单位. 以下是江西康海芯的分类: 1.(2008年郴州市)如图10,平行四边形ABCD 中,AB =5,BC =10,BC 边上的高AM =4, E 为 BC 边上的一个动点(不与B 、C 重合).过E 作直线AB 的垂线,垂足为 F .FE 与DC 的延长线相交于点 G ,连结DE ,DF .. (1) 求证:ΔBEF ∽ΔCEG . (2) 当点E 在线段BC 上运动时,△BEF 和△CEG 的周长之间有什么关系?并说明你的理由. (3)设BE =x ,△DEF 的面积为 y ,请你求出y 和x 之间的函数关系式,并求出当x 为何值时,y 有最大值,最大值是多少? 10分 辽宁省 岳伟 分类 2008年桂林市 如图,平面直角坐标系中,⊙A的圆心在X轴上,半径为1,直线L为y=2x-2,若⊙A沿X轴向右运动,当⊙A与L有公共点时,点A移动的最大距离是( ) A B (图4) 上海市各区2018届九年级中考二模数学试卷精选汇编:压轴题专题 宝山区、嘉定区 25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分) 在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10=OA ,12=AC ,AC ∥OB ,联结AB . (1)如图8,求证: AB 平分OAC ∠; (2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在如图9中画出 点M 的位置并求CM 的长; (3)如图10 ,点D 在弦AC 上,与点A 不重合,联结OD 与弦 AB 交于点E ,设点D 与点C 的 距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围. 25.(1)证明:∵AO 、BO 是圆O 的半径 ∴BO AO =…………1分 ∴B OAB ∠=∠…………1分 ∵AC ∥OB ∴B BAC ∠=∠…………1分 ∴BAC OAB ∠=∠ ∴AB 平分OAC ∠…………1分 (2)解:由题意可知BAM ∠不是直角, 所以△AMB 是直角三角形只有以下两种情况: ?=∠90AMB 和?=∠90ABM ① 当?=∠90AMB ,点M 的位置如图9-1……………1分 过点O 作AC OH ⊥,垂足为点H 图8 图10 图8 ∵OH 经过圆心 ∴AC HC AH 2 1 = = ∵12=AC ∴6==HC AH 在Rt △AHO 中,2 2 2 OA HO AH =+ ∵10=OA ∴8=OH ∵AC ∥OB ∴?=∠+∠180OBM AMB ∵?=∠90AMB ∴?=∠90OBM ∴四边形OBMH 是矩形 ∴10==HM OB ∴4=-=HC HM CM ……………2分 ②当?=∠90ABM ,点M 的位置如图9-2 由①可知58=AB ,55 2cos = ∠CAB 在Rt △ABM 中,55 2 cos ==∠AM AB CAB ∴20=AM 8=-=AC AM CM ……………2分 综上所述,CM 的长为4或8. 说明:只要画出一种情况点M 的位置就给1分,两个点都画正确也给1分. (3)过点O 作AB OG ⊥,垂足为点G 由(1)、(2)可知,CAB OAG ∠=∠sin sin 由(2)可得:5 5 sin = ∠CAB ∵10=OA ∴52=OG ……………1分 ∵AC ∥OB ∴ AD OB AE BE = ……………1分 又BE AE -=58,x AD -=12,10=OB ∴ x BE BE -= -1210 58 ∴x BE -=22580 ……………1分 ∴52225 802121?-?=??=x OG BE y ∴x y -= 22400 ……………1分 自变量x 的取值范围为120<≤x ……………1分 图10 份全国中考数学真题汇编 100份全国中考数学真题汇编 一、选择题 1;如图.在△ABC 中,∠B=90°, ∠A=30°,AC=4cm ,将△ABC 绕顶点C 顺时针方向旋转至△A ′B ′C ′的位置,且A 、C 、B ′三点在同一条直线上,则点A 所经过的最短路线的长为( ) A. B. 8cm C. 163cm π D. 8 3 cm π 【答案】D 2. 如图2,AB 切⊙O 于点B ,OA =23,AB =3,弦BC ∥OA ,则劣弧 ⌒BC 的弧长为( ). A .3 3π B .32π C .π D .32π 图2 【答案】A 3. (2011山东德州7,3分)一个平面封闭图形内(含边界)任意两点距离的最大值称 为该图形的“直径”,封闭图形的周长与直径之比称为图形的“周率”,下面四个平面 B′ A′ C B A (第11题图) 图形(依次为正三角形、正方形、正六边形、圆)的周率从左到右依次记为1a ,2a ,3a , 4a ,则下列关系中正确的是 (A )4a >2a >1a (B )4a >3a >2a (C )1a >2a >3a (D )2a >3a >4a 【答案】B 4. (2011山东济宁,9,3分)如图,如果从半径为9cm 的圆形纸片剪去1 3 圆周的一 个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( ) A .6cm B .35cm C .8cm D .53cm 【答案】B 5. (2011山东泰安,14 ,3分)一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( ) A.5π B. 4π C.3π D.2π 【答案】C 6. (2011山东烟台,12,4分)如图,六边形ABCDEF 是正六边形,曲线 FK 1K 2K 3K 4K 5K 6K 7……叫做“正六边形的渐开线”,其中1FK ,12K K ,23K K ,34K K ,45K K , 56K K ,……的圆心依次按点A ,B ,C ,D ,E ,F 循环,其弧长分别记为l 1,l 2,l 3,l 4, l 5,l 6,…….当AB =1时,l 2 011等于( ) (第9题) 剪 2020年全国中考数学试题分类汇编————压轴题 1.(2020年浙江杭州) 在平面直角坐标系xOy 中,抛物线的解析式是y = 2 4 1x +1,点C 的坐标为(–4,0),平行四边形OABC 的顶点A ,B 在抛物线上,AB 与y 轴交于点M ,已知点Q (x ,y )在抛物线上,点P (t ,0)在x 轴上. (1) 写出点M 的坐标; (2) 当四边形CMQP 是以MQ ,PC 为腰的梯形时. ① 求t 关于x 的函数解析式和自变量x 的取值范围; ② 当梯形CMQP 的两底的长度之比为1:2时,求t 的值. (第24题) 2.(2020年浙江湖州)如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、 D),连结PC,过点P作PE⊥PC交AB于E (1)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由; (2)当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围. B C 第25题 3.(2020年浙江嘉兴市)如图,已知抛物线y=-1 2 x2+x+4交x轴的正半轴于点A,交y轴于点B. (1)求A、B两点的坐标,并求直线AB的解析式; (2)设P(x,y)(x>0)是直线y=x上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF,若正方形PEQF与直线AB有公共点,求x的取值范围; (3)在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值. 4.(2020年浙江金华)如图,P为正方形ABCD的对称中心,A(0,3),B(1,0),直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以2个单位每秒速度运动,运动时间为t。求:Array(1)C的坐标为▲; (2)当t为何值时,△ANO与△DMR相似? (3)△HCR面积S与t的函数关系式; 并求以A、B、C、R为顶点的四边形是梯形 时t的值及S的最大值。 2010全国各地中考模拟数学试题汇编 压轴题 1.(2010年广州中考数学模拟试题一)如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。 (1)当点C在第一象限时,求证:△OPM≌△PCN; (2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围; (3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。 答案:(1)∵OM∥BN,MN∥OB,∠AOB=900, ∴四边形OBNM为矩形。 ∴MN=OB=1,∠PMO=∠CNP=900 ∵AM PM AO BO =,AO=BO=1, ∴AM=PM。 ∴OM=OA-AM=1-AM,PN=MN-PM=1-PM, ∴OM=PN, ∵∠OPC=900, ∴∠OPM+CPN=900, 又∵∠OPM+∠POM=900∴∠CPN=∠POM,∴△OPM≌△PCN. (2)∵AM=PM=APsin450= 2 m 2 , ∴NC=PM= 2 m 2 ,∴BN=OM=PN=1- 2 m 2 ; ∴BC=BN-NC=1- 2 m 2 - 2 m 2 =12m - A B C N P M O x y x=1 第1题图 (3)△PBC可能为等腰三角形。 ①当P与A重合时,PC=BC=1,此时P(0,1) ②当点C在第四象限,且PB=CB时, 有BN=PN=1- 2 2 m, ∴BC=PB=2PN=2-m, ∴NC=B N+BC=1- 2 2 m+2-m, 由⑵知:NC=PM= 2 2 m, ∴1- 2 2 m+2-m= 2 2 m,∴m=1. ∴PM= 2 2 m= 2 2 ,BN=1- 2 2 m=1- 2 2 , ∴P( 2 2 ,1- 2 2 ). ∴使△PBC为等腰三角形的的点P的坐标为(0,1)或( 2 2 ,1- 2 2 ) 2. (2010年广州中考数学模拟试题(四))关于x的二次函数y=-x2+(k2-4)x+2k-2以y 轴为对称轴,且与y轴的交点在x轴上方. (1)求此抛物线的解析式,并在直角坐标系中画出函数的草图; (2)设A是y轴右侧抛物线上的一个动点,过点A作AB垂直x轴于点B,再过点A作x轴的平行线交抛物线于点D,过D点作DC垂直x轴于点C, 得到矩形ABCD.设矩形ABCD 的周长为l,点A的横坐标为x,试求l关于x的函数关系式; (3)当点A在y轴右侧的抛物线上运动时,矩形ABCD能否成为正方形.若能,请求出此时正方形的周长;若不能,请说明理由. 2020年中考数学试题分类汇编之十一 四边形 一、选择题 1.(2020广州)如图5,矩形ABCD 的对角线AC ,BD 交于点O ,6AB =,8BC =,过点O 作OE ⊥AC ,交AD 于点E ,过点E 作EF ⊥BD ,垂足为F ,则OE EF +的值为( * ). (A ) 485 (B )325 (C )24 5 (D ) 12 5 【答案】C 2.(2020陕西)如图,在?ABCD 中,AB =5,BC =8.E 是边BC 的中点,F 是?ABCD 内一点,且∠BFC =90°.连接AF 并延长,交CD 于点G .若EF ∥AB ,则DG 的长为( ) A . B . C .3 D .2 【解答】解:∵E 是边BC 的中点,且∠BFC =90°, ∴Rt △BCF 中,EF =BC =4, ∵EF ∥AB ,AB ∥CG ,E 是边BC 的中点, ∴F 是AG 的中点, ∴EF 是梯形ABCG 的中位线, ∴CG =2EF ﹣AB =3, 又∵CD =AB =5, ∴DG =5﹣3=2, 故选:D . 图5 O F E D C B A 3.(2020乐山)如图,在菱形ABCD 中,4AB =,120BAD ∠=?,O 是对角线BD 的中点,过点O 作OE CD ⊥ 于点E ,连结OA .则四边形AOED 的周长为( ) A. 9+ B. 9+ C. 7+ D. 8 【答案】B 【详解】∵四边形ABCD 是菱形,O 是对角线BD 的中点, ∵AO∵BD , AD=AB=4,AB∵DC ∵∵BAD=120o, ∵∵ABD=∵ADB=∵CDB=30o, ∵OE∵DC , ∵在RtΔAOD 中,AD=4 , AO=1 2 AD =2 ,= 在RtΔDEO 中,OE= 1 2 OD =,3=, ∵四边形AOED 的周长为 故选:B. 4.(2020贵阳)菱形的两条对角线长分别是6和8,则此菱形的周长是( ) A. 5 B. 20 C. 24 D. 32 【答案】B 【详解】解:如图所示,根据题意得AO =1842 ?=,BO =1 632?=, ∵四边形ABCD 是菱形, ∵AB =BC =CD =DA ,AC∵BD , ∵∵AOB 是直角三角形, ∵AB 5==, ∵此菱形的周长为:5×4=20. 故选:B . 2019年全国各地中考数学试卷试题分类汇编 第2章 实数 一、选择题 1. (2018,1,3分)如在实数0,-3,3 2 - ,|-2|中,最小的是( ). A .3 2- B . - 3 C .0 D .|-2| 【答案】B 2. (2018市,1,3分)四个数-5,-0.1,1 2,3中为 无理数的是( ). A. -5 B. -0.1 C. 1 2 D. 3 【答案】D 3. (2018滨州,1,3分)在实数π、13 、 2、sin30°,无理 数的个数为( ) A.1 B.2 C.3 D.4 【答案】B 4. (2018,2,3分)(-2)2 的算术平方根是( ). A . 2 B . ±2 C .-2 D . 2 【答案】A 5. (2018,8,3分)已知实数m 、n 在数轴上的对应点的位置如图所示,则下列判断正确的是 (A)0>m (B)0 【答案】D · 10. (20181,3)如计算:-1-2= A.-1 B.1 C.-3 D.3 【答案】C 11. (2018滨州,10,3分)在快速计算法中,法国的“小 九九”从“一一得一”到“五五二十五”和我国的“小九九”算法是完全一样的,而后面“六到九”的运算就改用手势了.如计算8×9时,左手伸出3根手指,右手伸出4根手指,两只手伸出手指数的和为7,未伸出手指数的积为2,则8×9=10×7+2=72.那么在计算6×7时,左、右手伸出 的 手 指 数 应 该 分 别 为 ( ) A.1,2 B.1,3 C.4,2 D.4,3 【答案】A 12. (2018,10,3分)计算()221222 -+---1 (-) =( ) A .2 B .-2 C .6 D .10 【答案】A 13. (2018,6,3分)定义一种运算☆,其规则为a☆b=1a + 1 b ,根据这个规则、计算2☆3的值是 动态问题 一、选择题 1.(2010年河南省南阳市中考模拟数学试题)如图1,在直角梯形ABCD 中,∠B=90°,DC ∥AB ,动点P 从B 点出发,沿折线B →C →D →A 运动,设点P 运动的路程为x ,△ABP 的面积为y ,如果关于x 的函数y 的图像如图2所示,则△ABC 的面积为( ) A .10 B .16 C .18 D .32 答:B 2.( 2010年山东菏泽全真模拟1)如图所示:边长分别为1和2的两个正方形,其一边在同一水平线上, 小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t ,大正方形内除去小正方形部分的面积为S (阴影部分),那么S 与t 的大致图象应为( ) 答案:A 3.如图,点A 是y 关于x 的函数图象上一点.当点A 沿图象运动,横坐标增加5时,相应的纵坐标( ) A.减少1. B.减少3. C.增加1. D.增加3. 答案:A 4.(2010年河南中考模拟题5)如图,A ,B ,C ,D 为圆O 的四等分点,动点P 从圆心O 出发,沿O —C —D —O 路线作匀速运动,设运动时间为x (秒),∠APB =y (度),右图函数图象表示y 与x 之间函数关系,则点M 的横坐标应为( ) O 4 9 14 x y 图2 D C P B A 图1 t O S t O S t O S t O S A. B. C. D. A.2 B . 2 π C .1 2 π + D. 2 π +2 答案:C 5.(2010年杭州月考)如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点, 且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是() 答案:A 6.(2010 河南模拟)如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图像是( ) 答案:C 7.(2010年中考模拟)(北京市)如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C 数关系式在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函 的图象大致是() D B C O A 90 1 M x y 45 O P 全国各地2018年中考数学真题汇编(含答案) 实数与代数式(选择+填空28题) 一、选择题 1. (2018山东潍坊)( ) A. B. C. D. 【答案】B 2.(2018四川内江)已知:,则的值是() A. B. C. 3 D. -3 【答案】C 3.按如图所示的运算程序,能使输出的结果为的是() A. B. C. D. 【答案】C 4.下列无理数中,与最接近的是() A. B. C. D. 【答案】C 5.四个数0,1,,中,无理数的是() A. B.1 C. D.0 【答案】A 6.下列计算正确的是() A. B. C. D. 【答案】D 7.估计的值在() A. 5和6之间 B. 6和7之间 C. 7和8之间 D. 8和9之间 【答案】D 8.我国南宋数学家杨辉所著的《详解九章算术》一书中,用下图的三角形解释二项式 的展开式的各项系数,此三角形称为“杨辉三角”. 根据“杨辉三角”请计算的展开式中从左起第四项的系数为() A. 84 B. 56 C. 35 D. 28 【答案】B 9.如果规定[x]表示不大于x的最大整数,例如[2.3]=2,那么函数y=x﹣[x]的图象为() A. B. C. D. 【答案】A 10.某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合),现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚 图钉(例如,用9枚图钉将4张作品钉在墙上,如图),若有34枚图钉可供选用,则最多可以展示绘画作品( ) A. 16张 B. 18张 C. 20张 D. 21张 【答案】D 11.把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为() A. 12 B. 14 C. 16 D. 18 【答案】C 12.在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到,第2次移动到……,第n 次移动到,则△的面积是() A.504 B. C. D. 【答案】A 13.将全体正奇数排成一个三角形数阵 1 3 5 7 9 11 2019-2020年中考数学试题分类汇编 统计 一.选择题 1.(2015安徽)某校九年级(1)班全体学生2015年初中毕业体育考试的成绩统计如下表: 根据上表中的信息判断,下列结论中错误..的是 A .该班一共有40名同学 B .该班学生这次考试成绩的众数是45分 C .该班学生这次考试成绩的中位数是45分 D .该班学生这次考试成绩的平均数是45分 2.(2015广东) 3. 一组数据2,6,5,2,4,则这组数据的中位数是 A.2 B.4 C.5 D.6 【答案】B. 【解析】由小到大排列,得:2,2,4,5,6,所以,中位数为4,选B 。 3.(孝感)今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量, 对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为 20 18 17 10 15 10,,,,,.对于这组数据,下列说法错误..的是 A .平均数是15 B .众数是10 C .中位数是17 D .方差是 3 44 4.(湖南常德)某村引进甲乙两种水稻良种,各选6块条件相同的实验田,同时播种并核定 亩产,结果甲、乙两种水稻的平均产量均为550kg/亩,方差分别为2 141.7S 甲= ,2 433.3S 乙=,则产量稳定,适合推广的品种为: A 、甲、乙均可 B 、甲 C 、乙 D 、无法确定 【解答与分析】这是数据统计与分析中的方差意义的理解,平均数相同时,方差越小越稳定: 答案为B 5.(衡阳)在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,50,55,这组数据的众数和中位数分别是( C ). A .50元,30元 B .50元,40元 C .50元,50元 D .55元,50元 6. )(2015?益阳)某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动中考数学模拟题分类汇编实验及操作.doc
2018中考数学试题分类汇编 压轴题(全)
全国中考数学试题分类汇编.docx
2020年中考数学模拟试题分类汇编--二次函数
2019年全国各地中考数学真题汇编:平移与旋转(含答案)
全国中考数学试题分类汇编
中考数学试题分类汇编——函数
2020年中考数学模拟试题汇编:有理数-最新整理
数学中考试题分类汇编 动态专题
上海市各区2018届中考数学二模试卷精选汇编压轴题专题(有答案)
份全国中考数学真题汇编
2020年全国中考数学分类汇编(压轴题)
2010全国各地中考数学模拟试题汇编压轴题
2020年中考数学试题分类汇编: 四边形(含答案解析)
2019年全国各地中考数学试卷试题分类汇编
2020年中考数学模拟试题分类汇编--动态专题
全国各地2018年中考数学真题汇编(含答案)
2019-2020年中考数学试题分类汇编 统计
