中考数学压轴题之二次函数(中考题型整理,突破提升)附详细答案

一、二次函数真题与模拟题分类汇编(难题易错题)
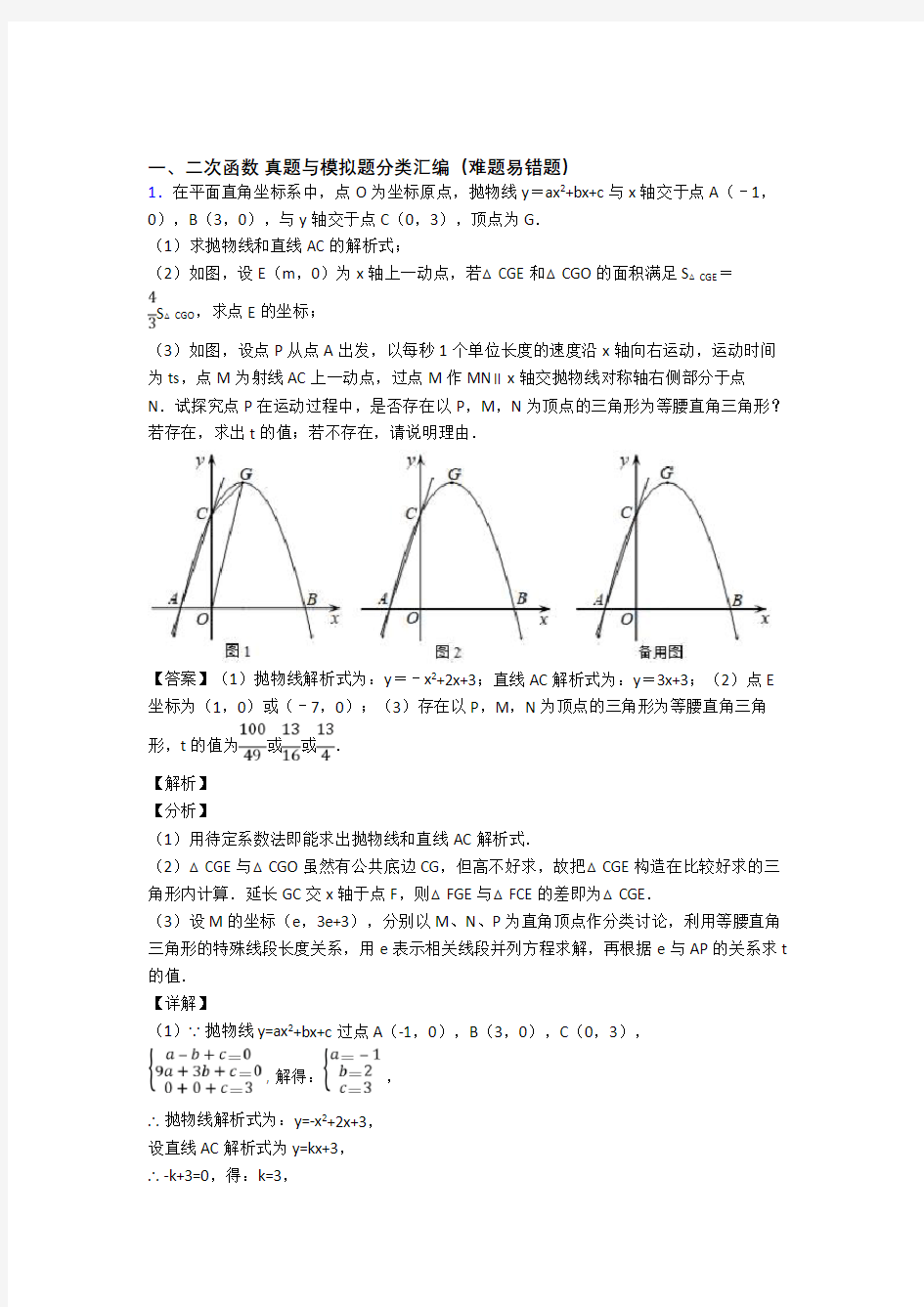
1.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,3),顶点为G.
(1)求抛物线和直线AC的解析式;
(2)如图,设E(m,0)为x轴上一动点,若△CGE和△CGO的面积满足S△CGE=
S△CGO,求点E的坐标;
(3)如图,设点P从点A出发,以每秒1个单位长度的速度沿x轴向右运动,运动时间为ts,点M为射线AC上一动点,过点M作MN∥x轴交抛物线对称轴右侧部分于点N.试探究点P在运动过程中,是否存在以P,M,N为顶点的三角形为等腰直角三角形?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)抛物线解析式为:y=﹣x2+2x+3;直线AC解析式为:y=3x+3;(2)点E 坐标为(1,0)或(﹣7,0);(3)存在以P,M,N为顶点的三角形为等腰直角三角
形,t的值为或或.
【解析】
【分析】
(1)用待定系数法即能求出抛物线和直线AC解析式.
(2)△CGE与△CGO虽然有公共底边CG,但高不好求,故把△CGE构造在比较好求的三角形内计算.延长GC交x轴于点F,则△FGE与△FCE的差即为△CGE.
(3)设M的坐标(e,3e+3),分别以M、N、P为直角顶点作分类讨论,利用等腰直角三角形的特殊线段长度关系,用e表示相关线段并列方程求解,再根据e与AP的关系求t 的值.
【详解】
(1)∵抛物线y=ax2+bx+c过点A(-1,0),B(3,0),C(0,3),
, 解得:,
∴抛物线解析式为:y=-x2+2x+3,
设直线AC解析式为y=kx+3,
∴-k+3=0,得:k=3,
∴直线AC解析式为:y=3x+3.
(2)延长GC交x轴于点F,过G作GH⊥x轴于点H,
∵y=-x2+2x+3=-(x-1)2+4,
∴G(1,4),GH=4,
∴S△CGO=OC?x G=×3×1=,
∴S△CGE=S△CGO=×=2,
①若点E在x轴正半轴上,
设直线CG:y=k1x+3,
∴k1+3=4 得:k1=1,
∴直线CG解析式:y=x+3,
∴F(-3,0),
∵E(m,0),
∴EF=m-(-3)=m+3,
∴S△CGE=S△FGE-S△FCE=EF?GH-EF?OC=EF?(GH-OC)=(m+3)?(4-3)=,
∴=2,解得:m=1,
∴E的坐标为(1,0).
②若点E在x轴负半轴上,则点E到直线CG的距离与点(1,0)到直线CG距离相等,即点E到F的距离等于点(1,0)到F的距离,
∴EF=-3-m=1-(-3)=4,
解得:m=-7 即E(-7,0),
综上所述,点E坐标为(1,0)或(-7,0).
(3)存在以P,M,N为顶点的三角形为等腰直角三角形,
设M(e,3e+3),则y N=y M=3e+3,
①若∠MPN=90°,PM=PN,如图2,过点M作MQ⊥x轴于点Q,过点N作NR⊥x轴于点R,
∵MN∥x轴,
∴MQ=NR=3e+3,
∴Rt△MQP≌Rt△NRP(HL),
∴PQ=PR,∠MPQ=∠NPR=45°,
∴MQ=PQ=PR=NR=3e+3,
∴x N=x M+3e+3+3e+3=7e+6,即N(7e+6,3e+3),∵N在抛物线上,
∴-(7e+6)2+2(7e+6)+3=3e+3,
解得:e1=-1(舍去),e2=?,
∵AP=t,OP=t-1,OP+OQ=PQ,
∴t-1-e=3e+3,
∴t=4e+4=,
②若∠PMN=90°,PM=MN,如图3,
∴MN=PM=3e+3,
∴x N=x M+3e+3=4e+3,即N(4e+3,3e+3),
∴-(4e+3)2+2(4e+3)+3=3e+3,
解得:e1=-1(舍去),e2=?,
∴t=AP=e-(-1)=?+1=,
③若∠PNM=90°,PN=MN,如图4,
∴MN=PN=3e+3,N (4e+3,3e+3), 解得:e=?
,
∴t=AP=OA+OP=1+4e+3=
,
综上所述,存在以P ,M ,N 为顶点的三角形为等腰直角三角形,t 的值为或
或
.
【点睛】
本题考查了待定系数法求函数解析式,坐标系中三角形面积计算,等腰直角三角形的性质,解一元二次方程,考查了分类讨论和方程思想.第(3)题根据等腰直角三角形的性质找到相关线段长的关系是解题关键,灵活运用因式分解法解一元二次方程能简便运算.
2.(2017南宁,第26题,10分)如图,已知抛物线2239y ax ax a =--与坐标轴交于A ,B ,C 三点,其中C (0,3),∠BAC 的平分线AE 交y 轴于点D ,交BC 于点E ,过点D 的直线l 与射线AC ,AB 分别交于点M ,N .
(1)直接写出a 的值、点A 的坐标及抛物线的对称轴;
(2)点P 为抛物线的对称轴上一动点,若△PAD 为等腰三角形,求出点P 的坐标; (3)证明:当直线l 绕点D 旋转时,
11AM AN
+均为定值,并求出该定值.
【答案】(1)a =13
-,A 30),抛物线的对称轴为x 32)点P 的坐标为3034);(3)32
. 【解析】
试题分析:(1)由点C 的坐标为(0,3),可知﹣9a =3,故此可求得a 的值,然后令y =0得到关于x 的方程,解关于x 的方程可得到点A 和点B 的坐标,最后利用抛物线的对称性
可确定出抛物线的对称轴;
(2)利用特殊锐角三角函数值可求得∠CAO =60°,依据AE 为∠BAC 的角平分线可求得∠DAO =30°,然后利用特殊锐角三角函数值可求得OD =1,则可得到点D 的坐标.设点P 的
,a ).依据两点的距离公式可求得AD 、AP 、DP 的长,然后分为AD =PA 、AD =DP 、AP =DP 三种情况列方程求解即可;
(3)设直线MN 的解析式为y =kx +1,接下来求得点M 和点N 的横坐标,于是可得到AN 的长,然后利用特殊锐角三角函数值可求得AM 的长,最后将AM 和AN 的长代入化简即可.
试题解析:(1)∵C (0,3),∴﹣9a =3,解得:a =13
-.
令y =0得:290ax a --=,∵a ≠0,∴290x --=,解得:x =
x =∴点A 0),B (0),∴抛物线的对称轴为x
(2)∵OA OC =3,∴tan ∠CAO ∴∠CAO =60°.
∵AE 为∠BAC 的平分线,∴∠DAO =30°,∴DO =1,∴点D 的坐标为(0,1).
设点P a ).
依据两点间的距离公式可知:AD 2=4,AP 2=12+a 2,DP 2=3+(a ﹣1)2. 当AD =PA 时,4=12+a 2,方程无解.
当AD =DP 时,4=3+(a ﹣1)2,解得a =0或a =2(舍去),∴点P 0).
当AP =DP 时,12+a 2=3+(a ﹣1)2,解得a =﹣4,∴点P ,﹣4).
综上所述,点P 04).
(3)设直线AC 的解析式为y =mx +3,将点A 的坐标代入得:30+=,解得:
m ∴直线AC 的解析式为3y =+. 设直线MN 的解析式为y =kx +1.
把y =0代入y =kx +1得:kx +1=0,解得:x =1k -,∴点N 的坐标为(1
k
-,0),
∴AN =1
k
-
.
将3y =+与y =kx +1联立解得:x
,∴点M .
过点M 作MG ⊥x 轴,垂足为G .则AG
∵∠MAG =60°,∠AGM =90°,∴AM =2AG =4
233k +-=2323
k k --,
∴
11AM AN +=323231k k k k -+-- =33232k k --=3(31)2(31)
k k -- =3
2. 点睛:本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,分类讨论是解答问题(2)的关键,求得点M 的坐标和点N 的坐标是解答问题(3)的关键.
3.如图,某足球运动员站在点O 处练习射门,将足球从离地面0.5m 的A 处正对球门踢出(点A 在y 轴上),足球的飞行高度y(单位:m )与飞行时间t(单位:s )之间满足函数关系y =at 2+5t +c ,已知足球飞行0.8s 时,离地面的高度为3.5m . (1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m )与飞行时间t(单位:s )之间具有函数关系x =10t ,已知球门的高度为2.44m ,如果该运动员正对球门射门时,离球门的水平距离为28m ,他能否将球直接射入球门?
【答案】(1)足球飞行的时间是8
5
s 时,足球离地面最高,最大高度是4.5m ;(2)能. 【解析】
试题分析:(1)由题意得:函数y=at 2+5t+c 的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣
t 2+5t+,当t=时,y 最大
=4.5;
(2)把x=28代入x=10t 得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得
到他能将球直接射入球门.
解:(1)由题意得:函数y=at 2+5t+c 的图象经过(0,0.5)(0.8,3.5), ∴
,
解得:,
∴抛物线的解析式为:y=﹣t2+5t+,
∴当t=时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,
∴他能将球直接射入球门.
考点:二次函数的应用.
4.如图,抛物线y=ax2+bx(a≠0)过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,是否存在这样的点P,使得△ABP的面积为△ABC面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由;
(4)若点M在直线BH上运动,点N在x轴正半轴上运动,当以点C,M,N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
【答案】(1)y=-x2+4x;(2)C(3,3),面积为3;(3)P的坐标为(5,-5);
(4)5
2
或5.
【解析】
试题分析:(1)利用待定系数法进行求解即可;
(2)先求出抛物线的对称轴,利用对称性即可写出点C的坐标,利用三角形面积公式即可求面积;
(3)利用三角形的面积以及点P所处象限的特点即可求;
(4)分情况进行讨论,确定点M、N,然后三角形的面积公式即可求.
试题解析:(1)将A(4,0),B(1,3)代入到y=ax2+bx中,得
1640
3
a b
a b
+=
?
?
+=
?
,解
得
1
4
a
b
=-
?
?
=
?
,
∴抛物线的表达式为y=-x2+4x.
(2)∵抛物线的表达式为y=-x2+4x,∴抛物线的对称轴为直线x=2.
又C,B关于对称轴对称,∴C(3,3).∴BC=2,∴S△ABC=1
2
×2×3=3.
(3)存在点P.作PQ⊥BH于点Q,设P(m,-m2+4m).∵S△ABP=2S△ABC,S△ABC=3,∴S△ABP=6.
∵S△ABP+S△BPQ=S△ABH+S梯形AHQP
∴6+1
2×(m-1)×(3+m2-4m)=
1
2
×3×3+
1
2
×(3+m-1)(m2-4m)
整理得m2-5m=0,解得m1=0(舍),m2=5,∴点P的坐标为(5,-5).
(4)5
2
或5.
提示:①当以M为直角顶点,则S△CMN=5
2
;
②当以N为直角顶点,S△CMN=5;
③当以C为直角顶点时,此种情况不存在.
【点睛】本题是二次函数的综合题,主要考查待定系数法求解析式,三角形面积、直角三角形的判定等,能正确地根据题意确定图形,分情况进行讨论是解题的关键.
5.在平面直角坐标系xOy中(如图).已知抛物线y=﹣1
2
x2+bx+c经过点A(﹣1,0)和
点B(0,5
2
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时
针方向旋转90°,点C落在抛物线上的点P处.(1)求这条抛物线的表达式;
(2)求线段CD 的长;
(3)将抛物线平移,使其顶点C 移到原点O 的位置,这时点P 落在点E 的位置,如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求点M 的坐标.
【答案】(1)抛物线解析式为y=﹣12x 2+2x+5
2
;(2)线段CD 的长为2;(3)M 点的坐标为(0,72)或(0,﹣7
2
). 【解析】
【分析】(1)利用待定系数法求抛物线解析式;
(2)利用配方法得到y=﹣
12(x ﹣2)2+9
2
,则根据二次函数的性质得到C 点坐标和抛物线的对称轴为直线x=2,如图,设CD=t ,则D (2,9
2
﹣t ),根据旋转性质得∠PDC=90°,
DP=DC=t ,则P (2+t ,
92﹣t ),然后把P (2+t ,92﹣t )代入y=﹣12x 2+2x+5
2
得到关于t 的方程,从而解方程可得到CD 的长;
(3)P 点坐标为(4,
92),D 点坐标为(2,5
2
),利用抛物线的平移规律确定E 点坐标为(2,﹣2),设M (0,m ),当m >0时,利用梯形面积公式得到12?(m+5
2
+2)?2=8
当m <0时,利用梯形面积公式得到12?(﹣m+5
2
+2)?2=8,然后分别解方程求出m 即可得到对应的M 点坐标.
【详解】(1)把A (﹣1,0)和点B (0,
52)代入y=﹣1
2
x 2+bx+c 得 1
0252b c c ?--+=????=??
,解得252b c =??
?=??,
∴抛物线解析式为y=﹣
12x 2+2x+5
2
; (2)∵y=﹣12(x ﹣2)2+9
2
,
∴C(2,9
2
),抛物线的对称轴为直线x=2,
如图,设CD=t,则D(2,9
2
﹣t),
∵线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处,∴∠PDC=90°,DP=DC=t,
∴P(2+t,9
2
﹣t),
把P(2+t,9
2
﹣t)代入y=﹣
1
2
x2+2x+
5
2
得﹣
1
2
(2+t)2+2(2+t)+
5
2
=
9
2
﹣t,
整理得t2﹣2t=0,解得t1=0(舍去),t2=2,∴线段CD的长为2;
(3)P点坐标为(4,9
2
),D点坐标为(2,
5
2
),
∵抛物线平移,使其顶点C(2,9
2
)移到原点O的位置,
∴抛物线向左平移2个单位,向下平移9
2
个单位,
而P点(4,9
2
)向左平移2个单位,向下平移
9
2
个单位得到点E,
∴E点坐标为(2,﹣2),设M(0,m),
当m>0时,1
2
?(m+
5
2
+2)?2=8,解得m=
7
2
,此时M点坐标为(0,
7
2
);
当m<0时,1
2
?(﹣m+
5
2
+2)?2=8,解得m=﹣
7
2
,此时M点坐标为(0,﹣
7
2
);
综上所述,M点的坐标为(0,7
2
)或(0,﹣
7
2
).
【点睛】本题考查了二次函数的综合题,涉及到待定系数法、抛物线上点的坐标、旋转的性质、抛物线的平移等知识,综合性较强,正确添加辅助线、运用数形结合思想熟练相关知识是解题的关键.
6.在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),
如图,直线y=1
4
x与抛物线交于A、B两点,直线l为y=﹣1.
(1)求抛物线的解析式;
(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.
【答案】(1)抛物线的解析式为y=1
4
x2﹣x+1.(2)点P的坐标为(
28
13
,﹣1).(3)
定点F的坐标为(2,1).
【解析】
分析:(1)由抛物线的顶点坐标为(2,0),可设抛物线的解析式为y=a(x-2)2,由抛物线过点(4,1),利用待定系数法即可求出抛物线的解析式;
(2)联立直线AB与抛物线解析式成方程组,通过解方程组可求出点A、B的坐标,作点B关于直线l的对称点B′,连接AB′交直线l于点P,此时PA+PB取得最小值,根据点B的坐标可得出点B′的坐标,根据点A、B′的坐标利用待定系数法可求出直线AB′的解析式,再利用一次函数图象上点的坐标特征即可求出点P的坐标;
(3)由点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标
特征,即可得出(1-1
2
-
1
2
y0)m2+(2-2x0+2y0)m+x02+y02-2y0-3=0,由m的任意性可得出关
于x0、y0的方程组,解之即可求出顶点F的坐标.详解:(1)∵抛物线的顶点坐标为(2,0),
设抛物线的解析式为y=a(x-2)2.
∵该抛物线经过点(4,1),
∴1=4a,解得:a=1
4
,
∴抛物线的解析式为y=1
4(x-2)2=
1
4
x2-x+1.
(2)联立直线AB与抛物线解析式成方程组,得:
214
1
14y x y x x ?????-+??
==,解得:11114x y ?????==,2241x y ??
?==, ∴点A 的坐标为(1,
1
4
),点B 的坐标为(4,1). 作点B 关于直线l 的对称点B′,连接AB′交直线l 于点P ,此时PA+PB 取得最小值(如图1所示).
∵点B (4,1),直线l 为y=-1, ∴点B′的坐标为(4,-3).
设直线AB′的解析式为y=kx+b (k≠0), 将A (1,
1
4
)、B′(4,-3)代入y=kx+b ,得: 1443k b k b ?+??
?+-?==,解得:1312
43k b ?
-??????
==, ∴直线AB′的解析式为y=-1312x+43
, 当y=-1时,有-1312x+4
3
=-1, 解得:x=
28
13
, ∴点P 的坐标为(
28
13
,-1). (3)∵点M 到直线l 的距离与点M 到点F 的距离总是相等, ∴(m-x 0)2+(n-y 0)2=(n+1)2, ∴m 2-2x 0m+x 02-2y 0n+y 02=2n+1. ∵M (m ,n )为抛物线上一动点,
∴n=1
4
m2-m+1,
∴m2-2x0m+x02-2y0(1
4
m2-m+1)+y02=2(
1
4
m2-m+1)+1,
整理得:(1-
1
2
-
1
2
y0)m2+(2-2x0+2y0)m+x02+y02-2y0-3=0.
∵m为任意值,
∴
00
22
000
11
10
22
2220
230
y
x y
x y y
?
--
?
?
-+
?
?+--
?
?
=
=
=
,
∴0
2
1
x
y
?
?
?
=
=
,
∴定点F的坐标为(2,1).
点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、轴对称中的最短路径问题以及解方程组,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数解析式;(2)利用两点之间线段最短找出点P的位置;(3)根据点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征,找出关于x0、y0的方程组.
7.如图,已知抛物线2
y ax bx c
=++的顶点为()
4,3
A,与y轴相交于点()
0,5
B-,对称轴为直线l,点M是线段AB的中点.
(1)求抛物线的表达式;
(2)写出点M的坐标并求直线AB的表达式;
(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.
【答案】(1)2
1
45
2
=-+-
y x x;(2)()
2,1-
M,25
y x
=-;(3)点P、Q的坐标分别为()
6,1或()
2,1、()
4,3
-或()
4,1.
【解析】
【分析】
(1)函数表达式为:()2
43y a x ==+,将点B 坐标代入上式,即可求解; (2)()4,3A 、()0,5B -,则点()2,1-M ,设直线AB 的表达式为:5y kx =-,将点
A 坐标代入上式,即可求解;
(3)分当AM 是平行四边形的一条边、AM 是平行四边形的对角线两种情况,分别求解即可. 【详解】
解:(1)函数表达式为:()2
43y a x ==+, 将点B 坐标代入上式并解得:12
a =-, 故抛物线的表达式为:2
1452
=-
+-y x x ; (2)()4,3A 、()0,5B -,则点()2,1-M , 设直线AB 的表达式为:5y kx =-,
将点A 坐标代入上式得:345k =-,解得:2k =, 故直线AB 的表达式为:25y x =-; (3)设点()4,Q s 、点21,452P m m m ??-
+- ???
, ①当AM 是平行四边形的一条边时,
点A 向左平移2个单位、向下平移4个单位得到M ,
同样点21,452P m m m ??
-+-
???
向左平移2个单位、向下平移4个单位得到()4,Q s , 即:24m -=,2
14542
m m s -
+--=, 解得:6m =,3s =-,
故点P 、Q 的坐标分别为()6,1、()4,3-; ②当AM 是平行四边形的对角线时, 由中点定理得:424m +=+,2
131452
m m s -=-+-+, 解得:2m =,1s =,
故点P 、Q 的坐标分别为()2,1、()4,1;
故点P 、Q 的坐标分别为()6,1,()4,3-或()2,1、()4,3-,()2,1或()4,1. 【点睛】
本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图象的面积计算等,其中(3),要主要分类求解,避免遗漏.
8.抛物线与x轴交于A,B两点(OA<OB),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<2).
①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时,的值最小,求出这个最小值并写出此时点E,P的坐标;
②在满足①的条件下,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
【答案】(1)A(2,0),B(4,0),C(0,2);(2)①t=1时,有最小值1,此时OP=2,OE=1,∴E(0,1),P(2,0);②F(3,2),(3,7).
【解析】
试题分析:(1)在抛物线的解析式中,令y=0,令x=0,解方程即可得到结果;
(2)①由题意得:OP=2t,OE=t,通过△CDE∽△CBO得到,即,求得
有最小值1,即可求得结果;
②存在,求得抛物线的对称方程为x=3,设F(3,m),当△EFP为直角三角形时,①当∠EPF=90°时,②当∠EFP=90°时,③当∠PEF=90°时,根据勾股定理列方程即可求得结果.
试题解析:(1)在抛物线的解析式中,令y=0,即,解得:,,∵OA<OB,∴A(2,0),B(4,0),在抛物线的解析式中,令x=0,得y=2,∴C(0,2);
(2)①由题意得:OP=2t,OE=t,∵DE∥OB,∴△CDE∽△CBO,∴,即
,∴DE=4﹣2t,
∴===,∵0<t<2,始终为正数,且t=1
时,有最大值1,∴t=1时,有最小值1,即t=1时,有最小值1,此时OP=2,OE=1,∴E(0,1),P(2,0);
②存在,∵抛物线的对称轴方程为x=3,设F(3,m),∴,
=,=,
当△EFP为直角三角形时,
①当∠EPF=90°时,,即,解得:m=2,
②当∠EFP=90°时,,即,解得;m=0或m=1,不合题意舍去,∴当∠EFP=90°时,这种情况不存在,
③当∠PEF=90°时,,即,解得:m=7,综上所述,F(3,2),(3,7).
考点:1.二次函数综合题;2.动点型;3.最值问题;4.二次函数的最值;5.分类讨论;6.压轴题.
9.如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.
(1)求这个二次函数的表达式;
(2)点P是直线BC下方抛物线上的一动点,求△BCP面积的最大值;
(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值.
【答案】(1)这个二次函数的表达式是y=x2﹣4x+3;(2)S△BCP最大=27
8
;(3)当△BMN
是等腰三角形时,m22,1,2.
【解析】
分析:(1)根据待定系数法,可得函数解析式;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PE的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;
(3)根据等腰三角形的定义,可得关于m的方程,根据解方程,可得答案.
详解:(1)将A (1,0),B (3,0)代入函数解析式,得
30
9330
a b a b ++??
++?==, 解得14
a b ??
-?=
=,
这个二次函数的表达式是y=x 2-4x+3; (2)当x=0时,y=3,即点C (0,3),
设BC 的表达式为y=kx+b ,将点B (3,0)点C (0,3)代入函数解析式,得
30
k b b +??
?==, 解这个方程组,得
1
3k b -???
== 直线BC 的解析是为y=-x+3, 过点P 作PE ∥y 轴
,
交直线BC 于点E (t ,-t+3), PE=-t+3-(t 2-4t+3)=-t 2+3t , ∴S △BCP =S △BPE +S CPE =12(-t 2+3t )×3=-32(t-3
2)2+278
,
∵-
32<0,∴当t=3
2时,S △BCP 最大=
278
. (3)M (m ,-m+3),N (m ,m 2-4m+3) MN=m 2-3m ,2|m-3|,
当MN=BM 时,①m 22(m-3),解得2, ②m 22m-3),解得2 当BN=MN 时,∠NBM=∠BMN=45°, m 2-4m+3=0,解得m=1或m=3(舍) 当BM=BN 时,∠BMN=∠BNM=45°,
-(m 2-4m+3)=-m+3,解得m=2或m=3(舍), 当△BMN 是等腰三角形时,m 的值为2,-2,1,2.
点睛:本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用面积的和差得出二次函数,又利用了二次函数的性质,解(3)的关键是利用等腰三角形的定义得出关于m 的方程,要分类讨论,以防遗漏.
10.如图,△ABC 的顶点坐标分别为A (﹣6,0),B (4,0),C (0,8),把△ABC 沿直线BC 翻折,点A 的对应点为D ,抛物线y=ax 2﹣10ax+c 经过点C ,顶点M 在直线BC 上.
(1)证明四边形ABCD 是菱形,并求点D 的坐标; (2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P ,使得△PBD 与△PCD 的面积相等?若存在,直接写出点P 的坐标;若不存在,请说明理由. 【答案】(1)详见解析
(2)2
2y x 4x 85
=
-+ (3)详见解析 【解析】 【分析】
(1)根据勾股定理,翻折的性质可得AB=BD=CD=AC ,根据菱形的判定和性质可得点D 的坐标.
(2)根据对称轴公式可得抛物线的对称轴,设M 的坐标为(5,n ),直线BC 的解析式为y=kx+b ,根据待定系数法可求M 的坐标,再根据待定系数法求出抛物线的函数表达式. (3)分点P 在CD 的上面下方和点P 在CD 的上方两种情况,根据等底等高的三角形面积相等可求点P 的坐标: 设P 22x,
x 4x 85??-+ ???
,
当点P 在CD 的上面下方,根据菱形的性质,知点P 是AD 与抛物线2
2y x 4x 85
=-+的交点,由A,D 的坐标可由待定系数法求出AD 的函数表达式:1
y x 32
=+,二者联立可得P 1(
529
,48
); 当点P 在CD 的上面上方,易知点P 是∠D 的外角平分线与抛物线2
2y x 4x 85
=
-+的交点,此时,∠D 的外角平分线与直线AD 垂直,由相似可知∠D 的外角平分线PD 的斜率等于-2,可设其为y 2x m =-+,将D (10,8)代入可得PD 的函数表达式:y 2x 28=-+,与抛物线2
2y x 4x 85
=-+联立可得P 2(﹣5,38). 【详解】
(1)证明:∵A (﹣6,0),B (4,0),C (0,8), ∴AB=6+4=10
,AC 10==.∴AB=AC .
由翻折可得,AB=BD ,AC=CD .∴AB=BD=CD=AC .∴四边形ABCD 是菱形. ∴CD ∥AB .
∵C (0,8),∴点D 的坐标是(10,8).
(2)∵y=ax 2﹣10ax+c ,∴对称轴为直线10a
x 52a
-=-=. 设M 的坐标为(5,n ),直线BC 的解析式为y=kx+b ,
∴4k b 0b 8+=??
=?,解得k 2
b 8=-??=?
.
∴直线BC 的解析式为y=﹣2x+8.
∵点M 在直线y=﹣2x+8上,∴n=﹣2×5+8=﹣2. ∴M (5,,-2).
又∵抛物线y=ax 2﹣10ax+c 经过点C 和M ,
∴25a 50a c 2c 8-+=-??=?,解得2a 5c 8
?
=?
??=?.
∴抛物线的函数表达式为2
2y x 4x 85
=
-+. (3)存在.点P 的坐标为P 1(
529
,48
),P 2(﹣5,38)
