概率论重点及课后题答案2

第2章 条件概率与独立性

一、大纲要求

（1）理解条件概率的定义.

（2）掌握概率的加法公式、乘法公式，会应用全概率公式和贝叶斯公式.

（3）理解事件独立性的概念，掌握应用事件独立性进行概率计算.

（4）了解独立重复试验概型，掌握计算有关事件概率的方法，熟悉二项概率公式的应用.

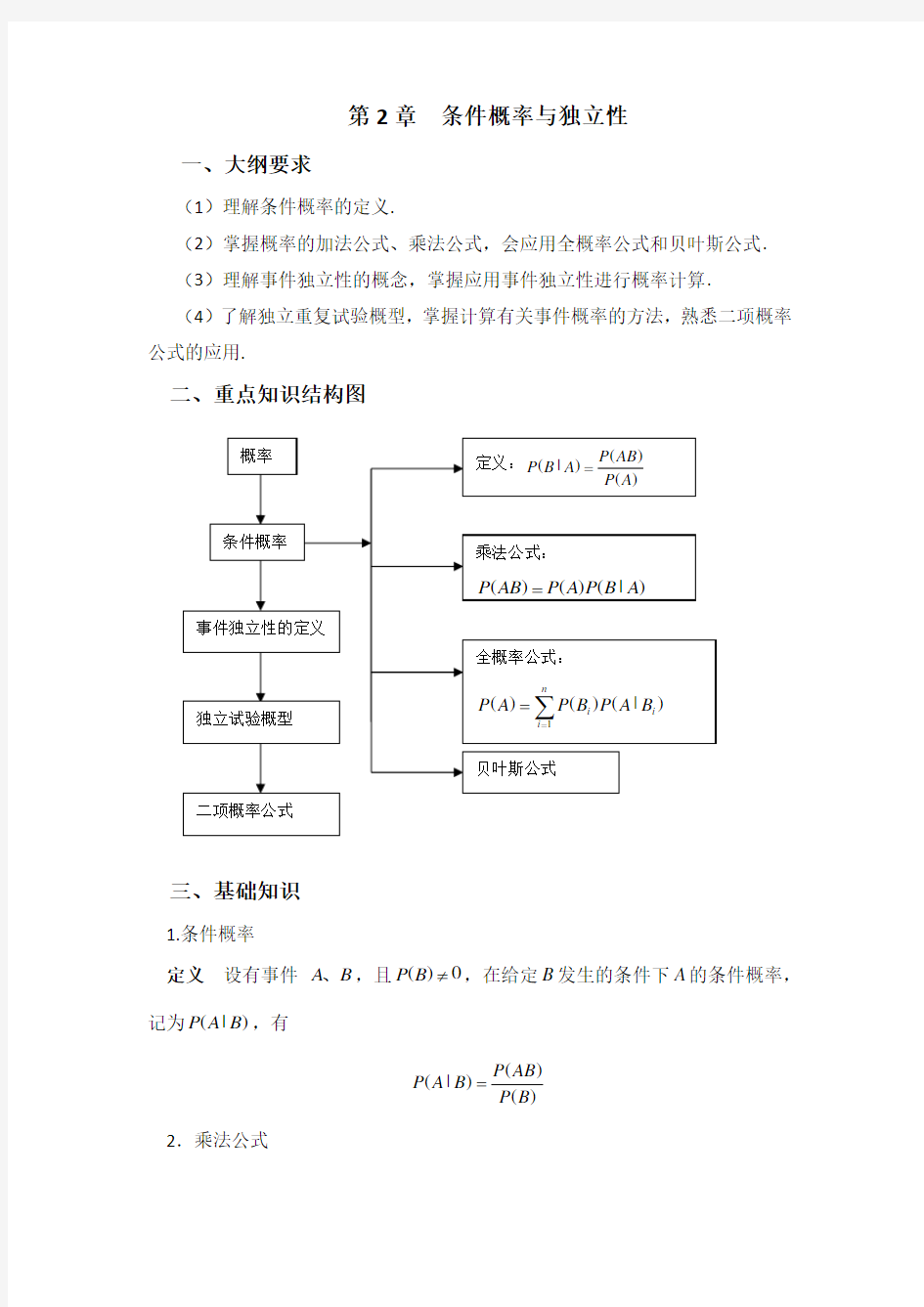
二、重点知识结构图

三、基础知识

1.条件概率

定义 设有事件 A B 、，且()0P B ≠，在给定B 发生的条件下A 的条件概率，记为(|)P A B ，有

()(|)()

P AB P A B P B =

2．乘法公式

定理 若对于任意事件A B 、，都有()0,()0P A P B >> ，则

()()(|)()(|)P AB P A P B A P B P A B ==

这个公式称为乘法定理.

乘法定理可以推广到有限多个随机事件的情形.

定理 设12,,,n A A A L 为任意n 个事件（2n ≥），且 121()0n P A A A ->L ，则有

121121312121()()(|)(|)(|)n n n n P A A A A P A P A A P A A A P A A A A --=L L L

3．全概率公式

定理 设12,,B B L 为一列（有限或无限个）两两互不相容的事件，有

1i i B

∞==Ω∑ ()0(1,2,)i P B i >=L

则对任一事件A ，有1()()(|)i i i P A P B P A B ∞

==∑.

4.贝叶斯公式

定理 设12,,B B L 为一系列（有限或无限个）两两互不相容的事件，有

1i i B

∞==Ω∑ ()0(1,2,)i P B i >=L

则对任一具有正概率的事件A ，有

1

()(|)

(|)()(|)k k k j j

j P B P A B P B A P B P A B ∞==∑ 5.事件的相互独立性

定义 若两事件A B 、满足 ，则称A B 、（或B A 、）相互独立，简称独立.

定理 若四对事件;;A B A B A B A B 、、 、；、 中有一对是相互独立的，则另外三

对事件也是相互独立的.即这四对事件或者都相互独立，或者都相互不独立.

定义 设12n A A A L ，，，是n 个事件，若对所有可能的组合1i j k n ≤<<<≤L 成

立：

()()()i j i j P A A P A P A = （共2n C 个）

()()()()i j k i j k P A A A P A P A P A = （共3n C 个）

M

1212()()()()n n P A A A P A P A P A =L L （共n n C 个）

则称 12,,n A A A L 相互独立.

定理 设n 个事件12,,n A A A L 相互独立，那么，把其中任意m （1m n ≤≤）个事件相应换成它们的对立事件，则所得的n 个事件仍然相互独立.

6. 重复独立试验，而且这些重复试验具备：（1）每次试验条件都相同，因此各次试验中同一个事件的出现概率相同；（2）各次试验结果相互独立；满足这两个条件的 n 次重复试验，称为n 重独立试验.

定理 （二项概率公式）设在一次试验中，事件A 出现的概率为()(01)P A p p =<<，则在n 重伯努利试验中，事件A 恰好出现k 次的概率()n P k 为

()(0,1,2,,)k k n k n n P k C p q k n -==L

式中，1()q p P A =-=

四、典型例题

例1 掷两颗骰子，在第一枚骰子出现的点数被3整除的条件下，求两枚骰子出现的点数大于8的概率.

解 同时掷两枚骰子，样本空间所包含的样本点数总数为6636n =?=.若设 A ={第一枚骰子出现的点数能被3整除}，则第一枚骰子出现3点或者6点，此时事件A 所包含的样本数为2612k =?=.设B ={两枚骰子出现的点数之和大于8}，则AB ={（3,6），（6,3），（6,4），（6,5），（6,6）}，故

121()363P A ==， 5()36

P AB =， ()5(|)()12P AB P B A P A == 例2 袋子有50个乒乓球，其中20个是黄球，30个是白球，现有两人依次随机地从袋子中各取一球，然后不放回，求两人取得黄球的概率.

解 设 i A ={第i 个人摸到黄球} (1,2)i =，则

1202()505

P A == 22112111922032()(|)()(|)()4954955P A P A A P A P A A P A =+=

?+?= 例3 对一个目标依次进行三次对立的射击，设第一、二、三次射击命中概率分别为0.4，0.5，0.7，试求：（1）三次射击击中恰好有一次命中的概率；（2）三次射击中至少有一次命中的概率.

解 设 i A ={第 次命中}， B ={恰有一次命中}，C ={至少有一次命中}，则

（1） 123123123()()()()P B P A A A P A A A P A A A =++

0.40.50.30.60.50.30.60.50.70.36=??+??+??=

（2）123()1()10.60.50.30.91P C P A A A =-=-??=

例 4 设三次独立试验中事件A 出现的概率相等，若已知A 至少出现一次的概率为19/27，求事件A 在一次试验中出现的概率.

解 由于33319{1}1{0}1(1)27P k P k p ≥=-==--= 解得13

p = 例5 掷三枚均匀骰子，设A ={三枚骰子掷出的点数中至少有两枚一样}， B ={至少有一枚骰子掷出1}，问A B 、是否独立？

解 考虑(|)P A B ，若B 发生，则三枚骰子不出现1点，那么只有5种可能性发生（2,3,4,5,6），比不知B 发生时可能取的点数（1,2,3,4,5,6）少了一个，从5个数字取3个（可重复取），其中有两个一样的可能性，应比6个数字中取3个时有两个一样的可能性要大些，即()(|)P A P A B <.由此可以推出()(|)P A P A B >，故A B 、不独立.

例6 若某种病菌在人口中的带病概率为0.83.当检查时，带菌者未必检出阳性反应，而不带菌者也可能呈阳性反应，假设

(|)0.99P =阳性带菌，(|)0.01P =阴性带菌

(|)0.05P =阳性不带菌， (|)0.95P =阴性不带菌

设某人检出阳性，问：他“带菌”的概率是多少？

解 设A ={某人检出阳性}，1B ={带菌}，2B ={不带菌}

由题设知1212()0.83,()10.830.17,(|)0.99,(|)0.05P B P B P A B P A B ==-===，故所求的概率为

111121

()()(|)

(|)()()(|)j

j j P AB P B P A B P B A P A P B P A B ===∑

0.830.990.980.830.990.170.05

?==?+?

例7 甲、乙两人独立地对同一个目标射击一次，其命中率分别为0.6和0.5，现已知目标被命中，求它是甲射中的概率.

解 设A ={甲射击一次命中目标}，B ={乙射击一次命中目标}，则所求概率为

((()(|(()()()

P A A B P A P A A B P A B P A P B P AB =+-I U U U ）)）=） 0.60.750.60.50.60.5

==+-? 例8 已知男子中有5%是色盲患者，女子中有0.25%是色盲患者，若从男女人数相等的人群中随机地挑选一人，恰好是色盲患者，问此人是男性的概率是多少？

解 设A ={抽到一名男性}；B ={抽到一名女性}；C ={抽到一名色盲患者}，由全概率公式得

11()(|)()(|)()5%0.25% 2.625%22

P C P C A P A P C B P B =+=?+?= 1()()(|)5% 2.5%2

P AC P A P C A ==?= 由贝叶斯公式得

()20(|)()21

P AC P A C P C ==

例9 有两箱相同种类的零件，第一箱装50个，其中10个一等品；第二箱装30个，其中18个一等品.今从两箱中任取一箱，然后从该箱中取零件两次，每次任选一个，均不放回抽样，试求：（1）第一次取到的零件是一等品的概率；

（2）第一次取到的零件是一等品的条件下，第二次取到的也是一等品的概率.

解 （1）设i A ={在第i 次中取到一等品}（1,2i =） ，i B ={挑到第i 箱}，则

111112211181()(|)()(|)()0.452302

P A P A B P B P A B P B =+=?+?= （2）由于 1212111222()(|)()(|)()P A A P A A B P B P A A B P B =+

191171810.194549229302

=??+??= 故 12211()0.194(|)0.485()0.4

P A A P A A P A === 例10 设()0.10,(|)0.90,(|)0.20P A P B A P B A ===，求 (|)P A B

解 由于()()()()P B P AB AB P AB P AB ==+U

()(|)()(|)P A P B A P A P B A =+

0.100.90(10.10)0.200.27=?+-?=

故 ()()(|)0.100.901(|)()()0.273

P AB P A P B A P A B P B P B ?==== 例11 某商店成箱出售玻璃杯，每箱20个，假设各箱有0，1，2个残次品的概率依次为0.8,0.1,0.1.一顾客欲购买一箱玻璃杯，在购买时，售货员任取一箱，而顾客开箱随机地察看4个，如无残次品，则买下该箱玻璃杯；否则退回.试求

（1）顾客买下该箱玻璃杯的概率α；（2）在顾客买下的一箱玻璃杯中，确实没有残次品的概率β.

解 设A ={顾客买下玻璃杯}，i B ={箱中有i 只残次品}（i =0,1,2） ，由题意可知，012()0.8,()()0.1P B P B P B ===，则

441918012442020412(|)1,(|),(|)519

C C P A B P A B P A B C C =====

（1）由全概率公式，得

2012448()()(|)0.810.10.80.10.94319475

i i i P A P B P A B α====?+?+?

?≈∑ （2）由贝叶斯公式，得

000()(|)0.81(|)0.848448()

475

P B P A B P B A P A β?===≈ 五、课本习题全解

2-1 （1）()()()()0.50.40.10.8;P A B P A P B P AB =+-=+-=U

（2）()0.1(|)0.25;()0.4

P AB P A B P B === （3）()0.1(|)0.2;()0.5P AB P B A P A =

== （4）()()()0.50.12(|)0.66671()10.43()

P AB P A P AB P A B P B P B --====≈-- 2-2 因为A B 、是独立事件，所以有

()()(),()()(),()()()P AB P A P B P AB P A P B P AB P A P B ===

（1）()()()(|)0.3;()()

P AB P A P B P A B P B P B === （2）()1()1()()10.70.40.72;P A B P A B P A P B =-=-=-?=U U

（3）()()()(|)0.4;()()

P AB P A P B P B A P A P A === （4）()()()(|)0.7()()P AB P A P B P A B P B P B =

== 2-3 因为AB A A B ??U ，所以()()()P AB P A P A B ≤≤U

又因为()()()()P A B P A P B P AB =+-U ，所以

()()()()()P AB P A P A B P A P B ≤≤≤+U

当A B ?时，第一个不等式中的等号成立；

当B A ?时，第二个不等式中的等号成立；

当AB =?时，第三个不等式中的等号成立.

2-4 证明 (())()()()()P A B C P AC BC P AC P BC P ACBC ==+-U U

(()())()()()P A P B P C P AB P C =+-

(()()())()P A P B P AB P C =+-

()()P A B P C =U

()()()()()()P ABC P A P B P C P AB P C ==

(())()()()()P A B C P ABC P A P B P C -==

()()()()P AB P C P A B P C ==-

所以，A B A B AB -U 、、分别与C 独立

2-5 设A ={射手击中目标}，

1A ={第一次击中目标}，2A ={第二次击中目标}，3A ={第三次击中目标}.有题意可知，0.6100

k =，即60k =； 1112233()()()(|)()(|)()(|)P A P A P A P A A P A P A A P A P A A =+++

6060600.60.40.410.832150150200

??=+?+?-?= ??? 2-6 设1A ={投掷两颗骰子的点数之和为偶数}，设2A ={投掷两颗骰子的点数之和为奇数}，1B ={点数和为8}，2B ={点数和为6}

（1）1166111111113333

11166

5

()5(|)()18C C P A B P B A C C C C P A C C ===+； （2）116622221111333321166

62

()12(|)()

18C C P A B P B A C C C C P A C C ?===+；

（3）1166222221166

62

()12(|)21()21

C C P A B P A B P B C C ?=== 2-7 设A ={此密码能被他们译出}，则

141421()0.6553534

P A =+?+??= 2-8 1110101101()1(|),1()10C C P AB P B A P A C === 111010111010

1

()1(|)6()6

C C P AB P A B P B C C === 2-9 设A ={第一次取得的全是黄球}，B ={第二次取出黄球、白球各一半}，则

5552010155103025

()0.1,(|)C C C P A P B A C C === 所以 5551015201052530

()()(|)C C C P AB P A P B A C C == 2-10 设1A ={第一次取得的是黄球}，2A ={第二次取得的是黄球}，3A ={第三次取得的是白球}，则

1111213121112(),(|),(|)b b c a a b a b c a b c

C C C P A P A A P A A A C C C ++++++=== 所以 123121312()()(|)(|)P A A A P A P A A P A A A =

1111112b b c a a b a b c a b c

C C C C C C ++++++=g g 2b b c a a b a b c a b c

+=+++++g g 2-11 设A ={这批货获得通过}，B ={样本中恰有一台次品}，A ={这批空调设备退货}；D ={第一次抽的是合格品}，E ={第二次抽的是合格品}

（1）67661474()()(|);70691610

P A P D P E D ==?=

（2）673367134()()(|)()(|);706970691610

P B P D P E D P D P E D =+=?+?= （3）136()1()1610

P A P A =-= 2-12 设A ={选出的产品是次品}，1B ={产品是由 厂生产}，B ={选出的产品是正品}

（1）118241300042();3000C P A C +== （2）11811182418(|);42

C P B A C +== （3）117821117821761782(|)2958

C P B B C +== 2-13 设A ={检验为次品}，B ={实际为正品}

（1）()5%90%95%1%0.0545P A =?+?=；

（2）()(|)95%1%(|)0.1743()0.0545

P B P A B P B A P A ?=== 2-14 设A ={这位学生选修了会计}，B ={这位学生是女生}

（1）()()(|)0.66%0.036P AB P B P A B ==?=；

（2）()()(|)0.490%0.36P AB P B P A B ==?=；

（3）((())()()P A P A B B P AB P AB =+=+）

()(|)()(|)P B P A B P B P A B =+

0.66%0.410%0.076=?+?=

2-15 设A ={此人被诊断为患肺癌}，B ={此人确实患肺癌}

（1）()98%3%(|)0.7519;()98%3%97%1%

P AB P B A P A ?===?+? （2）()(|)3%2%(|)0.0001;2%3%97%99%()

P B P A B P B A P A ?===?+? （3）对于被检查者，若被查出患肺癌，可不必过于紧张，还有约25%的可能没有患肺癌，可积极准备再做一次检查.对地区医疗防病结构而言，若检查结

果是未患肺癌，则被检查者基本上是没有患肺癌的.

2-16 设A ={收到信息为0}，B ={发送信息为0}，则有

(0.7(10.02)0.30.010.689P A =?-+?=）

(0.7(10.02)0.686P AB =?-=）

所以 (0.686686(|()0.689689

P AB P B A P A ==））= 2-17 设1A ={这批计算机是畅销品}，2A ={这批计算机销路一般}，3A ={这批计算机是滞销品}，B ={试销期内能卖出200台以上}.根据题意有

123()0.5,()0.3,()0.2P A P A P A ===

123(|)0.9,(|)0.5,(|)0.3P B A P B A P B A ===

（1）1111112233()((|(|)()((|((|((|P A B P A P B A P A B P B P A P B A P A P B A P A P B A ==++）））））））） 0.50.90.726;0.50.90.30.50.20.1

?==?+?+? （2）22()0.15(|)0.242;()0.62

P A B P A B P B === （3）33()0.02(|)0.032;()0.62P A B P A B P B =

== （4）33(|)1(|)10.0320.968P A B P A B =-=-=

2-18 设A ={硬币抛掷出现正面}，i B ={硬币是第i 个硬币} （i =1,2,3,4,5），B ={抛掷又出现字面}

（1）125()()()()P A P AB P AB P AB =+++L

112255()(|)()(|)()(|)P B P A B P B P A B P B P A B =+++L

11111311101;545254552

=?+?+?+?+?=

（2）11()(|)0()P AB P B A P A ==， 2211()145(|)1()10

2

P AB P B A P A ?===， 3311()125(|)1()52P AB P B A P A ?=== ， 4431()345(|)1()10

2

P AB P B A P A ?===， 551

()25(|)1()

52

P AB P B A P A === ； （3）1111332()0010.75104521045

P B =?+?+?+?+?= 2-19 设1A ={一人击中}，2A ={两人击中}，3A ={三人击中}，B ={飞机被击落}.根据题意有

1()0.40.5(10.7)0.60.50.30.60.50.70.36,P A =??-+??+??=

2()0.40.5(10.7)0.40.50.370.60.50.70.41,P A =??-+??+??=

3()0.40.50.70.14,P A =??=

123(|)0.2,(|)0.6,(|)1P B A P B A P B A ===

所以 112233()()(|)()(|)()(|)P B P A P B A P A P B A P A P B A =++

0.360.20.410.60.1410.458=?+?+?=

2-20 设A ={这批元件能出厂}，则

495()(4%0.0596%0.99)0.050.999999P A ??=?+?+?+?+ ???

4940.050.9998

98???+? ??? 0.8639=

2-21 （1）设A ={这批产品经检验为合格品}，则

1205124175()0.960.060.960.060.960.063252516162222P A ??=??+?+?+?+?+? ???

0.757=

（2）设B ={产品真是合格品}，则

12012170.960.960.96()3251622(|)0.982()0.757

P AB P B A P A ????+?+? ???=== 六、自测题及答案

1 设A 与B 为两事件，若()0P A >，且(|)()P B A P B = ，则A 与B .

2 设事件A 与B 满足()0.5P A =，()0.6P B =，(|)0.8P B A = ，则 ()P A B =U .

3 假设一批产品中一、二、三等品各占60%、30%和10%，从中任取一件，结果不是三等品，则取到的是一等品的概率为（ ）.

（A ）23 (B) 13 (C) 35 (D)25

4.每次试验成功的概率为p （01p <<），重复进行试验直到第n 次才取得r （1r n <<）次成功的概率是（ ）

（A ）(1)r r n r n C p p -- （B ）11(1)

r r n r n C p p ---- （C ）(1)r n r p p -- （D ）111(1)r r n r n C p

p ----- 5．设事件A 与B 为互不相容事件，且()0P A > ，()0P B >，则命题正确的是（ ）

（A ）()0P AB = （B ）(|)1P B A = （C ）A 与B 独立 （D ）A 与B 不独立

6. 设 A B 、为任意两个事件，且 A B ?，()0P B > ，则下列成立的是（ ）

（A ）()(|)P A P A B < （B ）()(|)P A P A B ≤

（C ） ()(|)P A P A B > （D ）()(|)P A P A B ≥

7.设A B 、 满足(|)1P B A =，则（ ）

（A ）A 是必然事件（B ）(|)0P B A =（C ）A B ?（D ）()()P A P B ≤

8将一枚硬币独立地掷两次，设1A ={掷第一次出现正面}，2A ={掷第二次出现正

面}，3A ={正、反面各出现一次}，4A ={正面出现两次}，则事件（ ）

（A ）123,,A A A 相互独立 （B ）234,,A A A 相互独立

（C ）123,,A A A 两两独立 （D ）234,,A A A 两两独立

9.设A B 、是两事件，且 0()1P A <<，()0P B > ，(|)(|)P B A P B A = ，则必有（ ）

（A ）(|)(|)P A B P A B = （B ）(|)(|)P A B P A B ≠

（C ）()()()P AB P A P B = （D ）()()()P AB P A P B ≠

10．设(),()P A a P B b == . 试证明：1(|)a b P A B b

+-≥ 11．现有两种报警系统A 与B ，每种系统单独使用时，系统A 有效的概率为0.92，系统B 有效的概率为0.93.在A 失灵的条件下，B 有效的概率为0.85.试求：

（1）在B 失灵的条件下，A 有效的概率；

（2）这两个系统至少有一个有效的概率.

12．设有分别来自三个地区的10名、15名、25名考生的报名表，其中女生的报名表分别为3份、7份和5份，随机地取一个地区的报名表，从中先后抽出2份，试求：（1）求先抽到的一份是女生报名表的概率p ；（2）已知后抽到的一份是男生报名表，求先抽到的一份是女生报名表的概率q .

13．甲袋中有9个白球和1个黑球，乙袋中有10个白球，每次从甲、乙两袋中随机地各抽取一球交换放入另一袋中，这样进行了三次，求黑球出现在甲袋中的概率.

【答案】

1．相互独立

2．由()(|),()0.5()

P AB P B A P A P A ==得 ()(|)()0.80.50.4P AB P B A P A ==?=

于是 ()()()()0.50.60.40.7P A B P A P B P AB =+-=+-=U

3．A

设i A ={抽到i 等品}（i =1,2,3），有 123()0.6,()0.3,()0.1P A P A P A ===，故

1311333()()0.62(|)1()10.13

()P A A P A P A A P A P A =

===-- 4． C 设A ={第n 次才取得r 次成功}；B ={前1n -次试验中有1r -次成功}； C ={第n 次成功}；则 A BC =，又因为B 与C 相互独立，由伯努利公式

()(1)k k n k n n P k C p p -=- (0,1,2,,)k n =L ，得

11111()()()()(1)(1)

r r n r r r n r n n P A P BC P B P C C p p p C p p -------===-=- 5．由于AB =?，故 ()0P AB =，又因为()()0P A P B >，即()()()P AB P A P B ≠ .因此，A 与 B 一定不独立.

又由于 ()()()()0(|)1()()()

P AB P A P AB P A P B A P A P A P A --=

=== 所以应选B 项和D 项.

6.由于A B ? ，故AB A =,()1P B ≤,因此有 ()()(|)()()()

P AB P A P A B P A P B P B ==≥ 所以应选 B 项.当()1P B =时，A 项不成立；当()1P B <时， C 项和D 项不成立.

7.由于(|)1P B A =,即()()P AB P A =,因此，A B ?，故()()P A P B ≤,应选D 项.

8.由于12341111(),(),(),()2224P A P A P A P A ====且121(),4P A A = 131(),4

P A A = 231(),4P A A = 241(),4

P A A =123()0,P A A A =所以有 1212()()()P A A P A P A =， 1313()()()P A A P A P A =

2323()()()P A A P A P A = ， 2424()()()P A A P A P A ≠

123123()()()()P A A A P A P A P A ≠

故123,,A A A 两两独立但不相互独立，234,,A A A 不相互独立，更不相互独立，故选C 项. 9. ()()()(|)()(|)(|)()()1()()

P AB P AB P AB P A B P B P B A P B A P A P A P A P A =?=?=- ()(1(|))()()()()()1()()1()P AB P A B P B P AB P B P AB P A P A P A P A --?

=?=-- 从最后一式解出()()()P AB P A P B =,故选C 项.

10. 由()()()()P A B P A P B P AB =+-U ,0()1P A B ≤≤U ,得

()()1()P A P B P AB +-≤ 又因为()()()1(|)()()

P AB P A P B P A B P B P B +-=≥，故 1(|)a b P A B b

+-≥ 11．由于()()()(|)0.851()()

P BA P B P AB P B A P A P A -===-，因此 ()()0.85(1())0.930.850.080.862P AB P B P A =-?-=-?=

(1) ()()()0.920.862(|)0.8286;1()0.07()

P AB P A P AB P A B P B P B --===≈- (2) ()()()()0.920.930.8620.988P A B P A P B P AB =+-=+-=U

12.设 i H ={报名表是第 i 区考生}（i =1,2,3），j A ={第j 次抽到的报名表是男生表}（j =1,2），有

1()(1,2,3),3i P H i == 11217(|)(|)10

P A H P A H == 12228(|)(|)15P A H P A H ==，132320(|)(|)25

P A H P A H == （1）3111

137529()()(|)310152590i i i p P A P H P A H =??===?++= ???∑

（2） 121377(|)10930

P A A H =?= 122788(|)151430

P A A H =?= 1235201(|)25246P A A H =

?= 3221

1782061()()(|)310302590i i i P A P H P A H =??==?++= ???∑ 3

12121

17852()()(|)33030309i i i P A A P H P A A H =??==?++= ???∑ 因此 121222

()209(|)61()

6190

P A A q P A A P A ==== 13.设i A ={ i 次交换后黑球出现在甲袋中}（i =1,2,3），i A ={ 次交换后黑球出现在乙袋中} （i =1,2,3），则

21211219911()()(|)()(|)0.8210101010P A P A P A A P A P A A =+=?+?= 323223291()()(|)()(|)0.820.180.7561010P A P A P A A P A P A A =+=?+?=