数值分析分段线性插值样条插值Runge函数Newton-Lagrange-Chebyshev插值多项式Runge现象matlab源程序代码

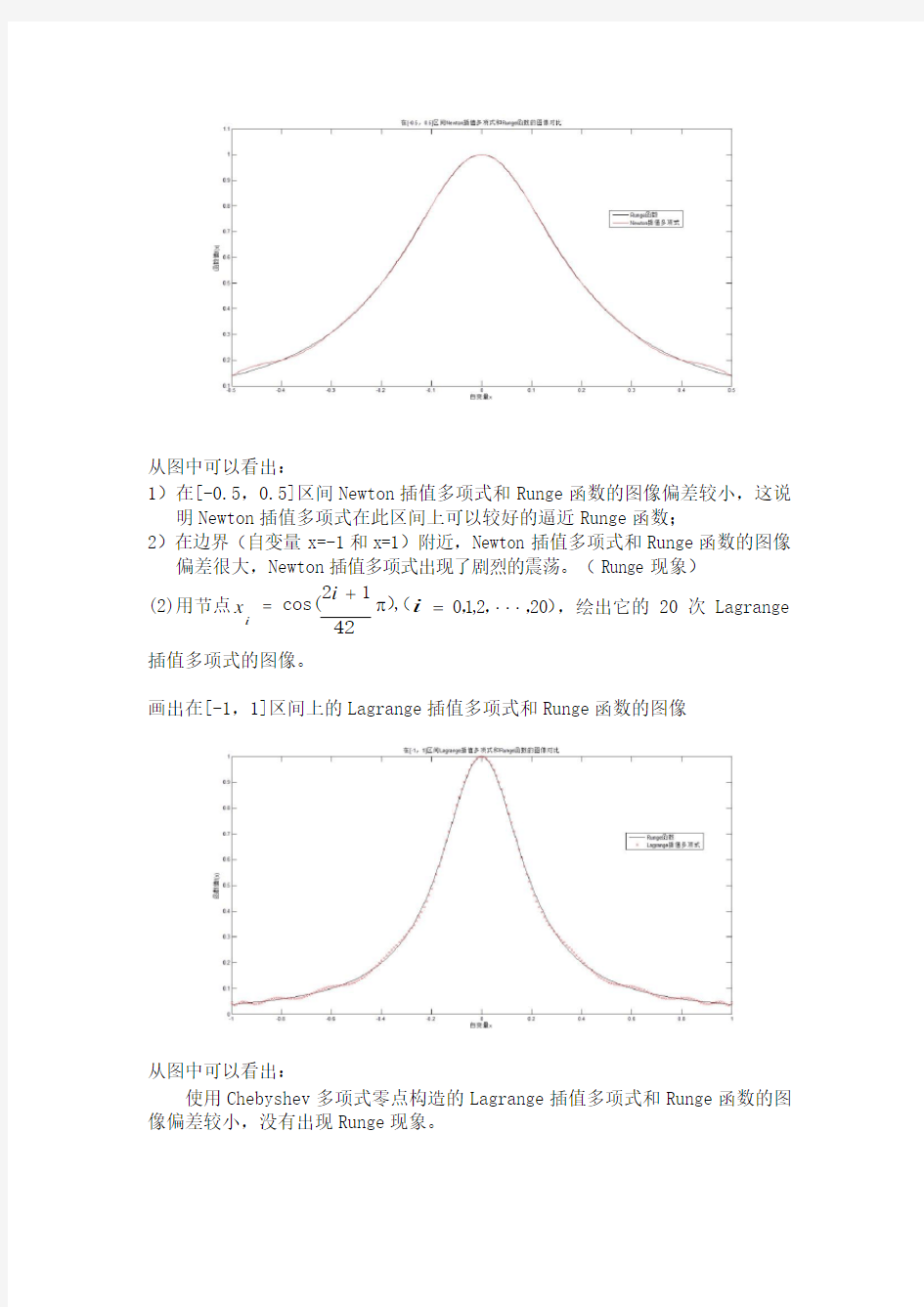
题目1：对R unge 函数R(x ) =

1

在区间[-1,1]作下列插值逼近，并和

x 2

R(x)的图像进行比较，并对结果进行分析。

= -1 + ih,h= 0.1,0 ≤ i≤ 20 绘出它的20 次Newton 插值(1)用等距节点x i

多项式的图像。

分别画出在[-1，1]区间，[-0.7，0.7]区间和[-0.5，0.5]区间上的 Newton 插值多项式和R unge 函数的图像

从图中可以看出： 1）在[-0.5，0.5]区间 N ewton 插值多项式和 R unge 函数的图像偏差较小，这说 明 Newton 插值多项式在此区间上可以较好的逼近 R unge 函数； 2）在边界（自变量 x =-1 和 x =1）附近，Newton 插值多项式和 R unge 函数的图像 偏差很大，Newton 插值多项式出现了剧烈的震荡。（Runge 现象） (2)用节点 x = cos(2i + 1 π）（, i = 0，1,2，? ? ? ，20），绘出它的 20 次 Lagrange

i 42 插值多项式的图像。

画出在[-1，1]区间上的 L agrange 插值多项式和 R unge 函数的图像

从图中可以看出：

使用 C hebyshev 多项式零点构造的 L agrange 插值多项式和 R unge 函数的图 像偏差较小，没有出现 R unge 现象。

(3)用等距节点 x i 的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的分段线性插值函数

画出在[-1，1]区间上分段线性插值函数和 R unge 函数的图像

从图中可以看出：

使用分段线性插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象，只在自变量 x =0 处有稍许偏差。 (4)用等距节点 x i 函数的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的三次自然样条插值

画出在[-1，1]区间上三次自然样条插值函数和 R unge 函数的图像

从图中可以看出：

使用三次自然样条插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象。

题目2：对函数：

在区间[-1,1]作下列插值逼近，并和被插值函数的图像进行比较，并对结果进行分析。

= -1 + ih,h= 0.1,0 ≤ i≤ 20 绘出它的20 次N ewton 插值多(1)用等距节点x i

项式的图像。

分别画出在[-1，1]区间，[-0.8，0.8]区间和[-0.6，0.6]区间上的 Newton 插值多项

式和R unge 函数的图像

从图中可以看出：

Newton 插值多项式和 Runge 函数的图像在[-1，1]区间上整体偏差都比较 大，尤其是在边界（自变量 x=-1 和 x=1）附近，Newton 插值多项式出现了剧烈 的震荡。（Runge 现象） (2)用节点 x = cos(2i + 1 π）（, i = 0，1,2，? ? ? ，20），绘出它的 20 次 L agrange 插

i 42 值多项式的图像。

画出在[-1，1]区间上的 L agrange 插值多项式和 R unge 函数的图像

从图中可以看出：

1）使用 C hebyshev 多项式零点构造的 L agrange 插值多项式和 R unge 函数的 图像偏差较小，没有出现 R unge 现象。

2）使用 C hebyshev 多项式零点构造的 L agrange 插值多项式相比使用等距节 点构造的 Newton 插值多项式要好得多，但在自变量 x=0 附近，Lagrange 插值多 项式有稍许偏差。

(3)用等距节点 x i 数的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的分段线性插值函

画出在[-1，1]区间上分段线性插值函数和 R unge 函数的图像

从图中可以看出：

使用分段线性插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象，只在自变量 x =0 附近处有稍许偏差。 (4)用等距节点 x i 函数的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的三次自然样条插值

画出在[-1，1]区间上三次自然样条插值函数和 R unge 函数的图像

从图中可以看出：

使用三次自然样条插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象，只在自变量 x =0 附近有稍许偏差。

分析与小结：

1）使用等距节点的高次插值多项式会出现 Runge 现象，插值函数和被插值函数的偏差较大，精度不高。

2）使用C hebyshev 多项式零点作为插值节点构造的L agrange 插值多项式，将会消除R unge 现象，可以提高精度。

3）使用分段线性插值函数可以有效的提高精度，但是插值函数不够光滑，只能保证连续性。

4）使用三次自然样条插值函数具有较高的精度，同时插值函数也有一定的光滑性，至少是C2 的。

5）对于被插值函数有间断的情况，插值函数在间断点附近仍有稍许偏差，例如题目2中的被插值函数在自变量x=0 处有间断。

Matlab的源程序代码:

题目1:

Lagrange.m

%Lagrange插值多项式

for i=1:21

x(i)=cos((2*(i-1)+1)*pi/42);

end

n=length(x);

for i=1:n

y(i)=1/(1+25*x(i)*x(i));

end

%构造插值基函数

syms z;

temp=1;

for i=1:n

lx=1;

for j=1:n

if i~=j

temp=(z-x(j))/(x(i)-x(j));

lx=lx*temp;

end

end

l(i)=lx;

end

%插值多项式

L=0;

for i=1:n