人教版高一数学必修3第一章算法初步课时练习题及答案

第一章算法初步
测试一算法与程序框图概念
Ⅰ学习目标
1.了解算法思想及算法的意义.
2.了解框图的概念,明确框图符号的意义.
Ⅱ基础性训练
一、选择题
1.下列程序框通常用来表示赋值、计算功能的是()
(A)(B) (C) (D)
2.算法的有穷性指的是()
(A)算法是明确和有效的(B)算法能够在有限步内完成
(C)算法的每个操作步骤是可执行的(D)用数字进行四则运算的有限过程3.对算法理解正确的是( )
(A)一种解题方法(B)基本运算及规定的运算顺序构成的完整的解题步骤
(C)计算的方法(D)一种语言程序
4.算法中,每一步的结果有()
(A)一个或两个(B)任意多个(C)确定的一个(D)两个
*5.有一堆形状大小相同的珠子,其中只有一粒重量比其他的珠子重,其余所有珠子重量相同.一个同学利用科学的算法,仅两次利用天平就找出了这颗最重的珠子,则这堆珠子最多有()
(A)6粒(B)7粒(C)8粒(D)9粒
二、填空题
6.完成不等式2x+3<3x+2的算法过程:
(1)将含x的项移项至不等式的左边,将常数项移至不等式的右边,得____________;
(2)在不等式两边同时除以x的系数,得____________.
7.阅读流程图(图1),试写出流程图所给出的算法含义:__________________.
图1
8.写出图2中顺序框图的运算结果____________.
图2
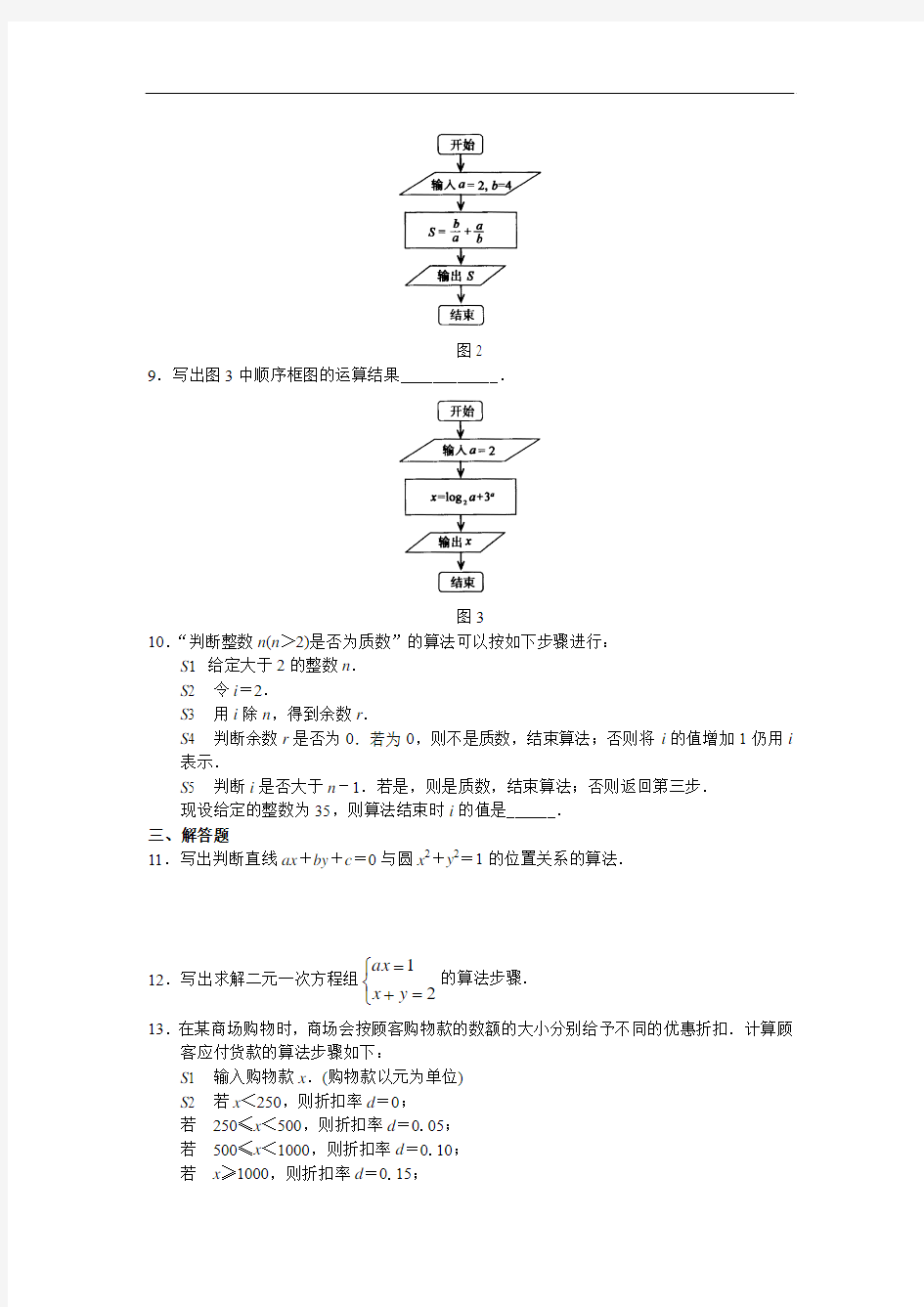
9.写出图3中顺序框图的运算结果____________.
图3
10.“判断整数n (n >2)是否为质数”的算法可以按如下步骤进行:
S 1 给定大于2的整数n . S 2 令i =2.
S 3 用i 除n ,得到余数r .
S 4 判断余数r 是否为0.若为0,则不是质数,结束算法;否则将i 的值增加1仍用i 表示.
S 5 判断i 是否大于n -1.若是,则是质数,结束算法;否则返回第三步. 现设给定的整数为35,则算法结束时i 的值是______. 三、解答题
11.写出判断直线ax +by +c =0与圆x 2+y 2=1的位置关系的算法.
12.写出求解二元一次方程组??
?=+=2
1
y x ax 的算法步骤.
13.在某商场购物时,商场会按顾客购物款的数额的大小分别给予不同的优惠折扣.计算顾
客应付货款的算法步骤如下:
S 1 输入购物款x .(购物款以元为单位) S 2 若x <250,则折扣率d =0;
若 250≤x <500,则折扣率d =0.05; 若 500≤x <1000,则折扣率d =0.10; 若 x ≥1000,则折扣率d =0.15;
S3 计算应付货款T=x(1-d);
S4 输出应付货款T.
现已知某顾客的应付货款是882元,求该顾客的购物款是多少元.
14.输入直角三角形两直角边长度,输出第三条边长度,画出此题的顺序框图.
测试二 程序框图(一)
Ⅰ 学习目标
理解三种逻辑结构,会读逻辑框图,尝试写出程序框图.
Ⅱ 基础性训练
一、选择题
1.程序框图中“处理框”的功能是( ) (A)赋值 (B )计算 (C)赋值或计算 (D )判断某一条件是否成立
2.尽管算法千差万别,但程序框图按其逻辑结构分类只有( ) (A)2类 (B )3类 (C )4类 (D )5类
3.程序框图如图1所示,输出的结果为( )
图1
(A)2,5 (B)4,7 (C)2,4 (D)1,2
4.程序框图如图2所示,输出的结果为( )
图2
(A)2 (B )9 (C )3 (D )1 5.程序框图如图3所示,当a =1,b =-3时输出的结果为( ) (A)0,-1
(B)2,-4
(C )21-
,4
3- (D )-2,4
图3
二、填空题
6.用流程图表示求解不等式ax >b (a ≠0)的算法时,判断框内的内容可以是_________. 7.在表示求解一元二次方程的算法中,需要使用选择结构,因为__________________. 8.如图4,当a =-1时,框图的输出结果是______.
图4
9.如图5,框图的输出结果是______.
图5
10.如图6所示框图,设火车托运重量为p (kg )的行李时,每千克的费用标准为
???>-+?≤=,
)kg 30)(30(5.0303.0,)kg 30(3.0P P P P
y 则图中①②处分别填的内容为:①______;②
________________.
图6
三、解答题
11.已知函数f(x)=|x-3|,程序框图(图7)表示的是给出x值,求相应函数值的算法.请将该框图补充完整.写出①②两处应填的内容.
图7
12.观察所给算法的流程框图(图8),说明它表示的函数.如果输入数字1,则输出的数字是什么?
图8
Ⅲ拓展性训练
13.设计一个求任意实数的绝对值的算法,并画出流程图.
14.已知三个实数a,b,c,试给出寻找这三个数中最大数的一个算法,并画出该算法的流程图.
测试三 程序框图(二)
Ⅰ 学习目标
理解三种逻辑结构,会读逻辑框图,尝试写出程序框图.
Ⅱ 基础性训练
一、选择题
1.下列关于框图的逻辑结构说法正确的是( )
(A)用顺序结构画出“求点到直线的距离”的程序框图是唯一的 (B)条件结构中不含顺序结构 (C)条件结构中一定含有循环结构 (D)循环结构中一定包含条件结构
2.已知函数?
??>-≤=,0,,
0,)(x x x x x f 在由给定的自变量x 计算函数值f (x )的算法中,应该至少包
含以下基本逻辑结构中的( )
(A)顺序结构、循环结构 (B )条件结构、循环结构 (C)顺序结构、条件结构 (D )顺序结构、循环结构 3.下列四个说法中正确的有( ) ①任意一个算法都离不开顺序结构
②算法程序框图中,根据条件是否成立有不同的流向 ③循环体是指按照一定条件,反复执行某一处理步骤
④循环结构中一定有条件结构,条件结构中一定有循环结构 (A)1个 (B )2个 (C )3个 (D )4个 4.要解决下面四个问题,只用顺序结构画不出其流程图的是( ) (A)计算1+2+…+10的值 (B )当圆的面积已知时,求圆的周长 (C)给定一个数x ,求其绝对值 (D )求函数f (x )=x 3-3x 的值 5.算法:S 1 m =a ;
S 2 若b <m ,则m =b ; S 3 若c <m ,则m =c ; S 4 若d <m ,则m =d ; S 5 输出m . 则输出的m 为( )
(A)a ,b ,c ,d 中的最小值 (B )a ,b ,c ,d 中的最大值 (C)d (D )a 二、填空题
6.程序框图中的“处理框”的功能是____________.
7.有如图1所示的程序框图,该程序框图表示的算法功能是____________.
图1
8.如图2所示是求小于等于1000所有正偶数的和的程序框图,则空白处①应为_________;
②应为___________.
图2
9.如图3所示表示的是计算前10个奇数倒数之和的算法的程序框图,其中判断框内应填入的条件是___________.
图3
三、解答题https://www.360docs.net/doc/d210859679.html,新课标第一网
10.给出如图4所示的程序框图.在执行上述框图表达的算法后,输出的S,i的值分别是多少?
图4
11.写出表示解方程ax+b=0(a,b为常数)的一个程序框图.
Ⅲ拓展性训练
12.设计求S=1+3+5+…+2007和T=1×3×5×…×2007的一个算法,并画出相应的流程图.
13.某工厂2004年的生产总值为200万元,技术革新后,预计以后每年的生产总值比上一年增加5%,问最早需要到哪一年年生产总值超过300万元,写出算法并画出相应的程序框图.
测试四 算法语言
Ⅰ 学习目标
了解算法语言,尝试用算法语言实现一些算法.
Ⅱ 基础性训练
1.编写一个输入底面边长和侧棱长,求正四棱锥体积的程序.
2.已知函数f (x )=2x -3,编写一段程序,用来求f [f (x )]的值.(其中,x 值由用户输入)
3.给出三个正数a ,b ,c ,问能否构成一个三角形,若能则求其面积.请设计一个程序解决该问题. (注:已知三角形三边分别为a ,b ,c ,则其面积))()((c p b p a p p S ---=,其中p
=
2
c
b a ++)
4.已知等式“□3×6528=3□×8256”中,方框内是同一个数字,请设计程序,用尝试的方法求出满足等式的一个数字.
5.请编写一个程序,计算1!+2!+3!+4!+ (100)
(注:其中4!=1×2×3×4,5!=1×2×3×4×5,...,100!=1×2×3× (100)
Ⅲ 拓展性训练
6.已知数列{a n }满足:a 1=1,a 2=3,对于任意的n ≥3,有a n =3a n -1-2a n -2.求该数列的前n 项和.
7.写出一个用二分法求方程x 3+x 2-2x -2=0在某个区间上的近似解的程序.要求:初始区间和计算精度都能在运行中指定.
8.求二次函数在给定区间上的最值.
测试五 逻辑框图综合测试
一、选择题 1.找出乘积为528的两个相邻偶数,流程图如图1,其中填充①②处语句正确的选择是( )
图1
(A)S =i *(i +2),输出i ,i -2 (B)S =i *i +2,输出i ,i -2 (C)S =i *(i +2),输出i ,i +2 (D)S =i *(i -2),输出i +2,i
2.如图2所示的算法流程图中,第三个输出的数是( )
图2
(A)1
(B )
2
3 (C )2 (D )
2
5 3.阅读流程图3,若输入的a ,b ,c 分别为21,32,75,则输出的a ,b ,c 分别是( )
图3
(A)75,21,32 (B )21,32,75 (C )32,21,75 (D )75,32,21
4.如图4,程序框图所进行的求和运算是( )
图4
(A)101211+++
(B)1814121+++
(C)2014121+++
(D)19
1311+++
5.如果如图5程序框图的输出结果为-18,那么在判断框①中表示的“条件”应该是( )
图5
(A)i ≥9
(B)i >9 (C)i ≥8 (D)i >11
6.函数??
?
??<=>-=0,1.0,00,1x x x y 求值的程序框图如图6所示,则空白处需要填的语句为:
①_________;②_________;③_________.
图6
7.如图7是一个算法的程序框图,当输入的值为5时,则其输出的结果是______.
图7
8.阅读流程图8填空:①最后一次输出的i=______;②一共输出i的个数为______个.
图8
9.分别写出图9和图10的运行结果:图9______;图10______.
图9 图10
参考答案 第一章 算法初步
测试一
1.C 2.B 3.B 4.C 5.D
6.-x <-1,x >1 7.已知一个数的13%,求这个数 8.2
5
9.10 10.5 11.S 1 求出原点到直线ax +by +c =0的距离2
2
||b
a c d +=
.
S 2 比较d 与圆的半径r =1的大小,
若d >r ,则直线与圆相离;若d =r ,则直线与圆相切;若d <r ,则直线与圆相交.
12.S 1 判断a 是否为0,若是,则执行S 4,若不是,则执行S 2.
S 2 解出a
x 1=. S 3 将a x 1=
代入x +y =2,解出a
y 12-=. S 4 输出方程组的解.
若a =0,则输出“方程组无解”;否则,输出方程组的解???
????
-==.12,1a y a
x
13.解:设该顾客的购物款为x 元.
根据题意,x >882.
如果x <1000,则0.9x =882,解得x =980;
如果x ≥1000,则0.85x =882,解得x ≈1037.65; 所以,该顾客的购物款是980元或1037.65元. 14.
测试二
1.C 2.B 3.A 4.B 5.C 6.a >0,或a <0
7.当方程根的判别式?≥0时,方程有实根;当方程根的判别式?<0时,方程没有实根. 8.“是负数” 9.12,21 10.①0.3*p ②0.3*30+0.5*(p —30). 11.x <3,y =x -3.或x ≤3,y =x -3.
12.流程框图表示的是下面的函数:
??
???-<--=->+=3
,213,
73,21x x x x x y 输出的数字是3. 13.S 1 输入x
S 2 如果x ≥0,则y ←x ;否则y ←-x S 3 输出y .
14.S 1 输入a ,b ,c
S 2 x ←a
S 3 如果b >x ,则x ←b ;否则,执行S 4 S 4 如果c >x ,则x ←c ;否则,执行S 5 S 5 输出
x
测试三
1.D 2.C 3.C 4.C 5.A 6.赋值或计算 7.从小到大连续n 个正整数乘积大于1000时,计算出最小的自然数n .或其他等价的回答. 8.S =S +i ,i =i +2 9.n ≤10? 10.3205,51 11.
12.S1赋值S=1,T=1
S2 赋值i=3
S3赋值S=S+i,赋值T=T×i
S4 赋值i=i+2
S5 若i≤2007,则执行S3
S6输出S,T.
13.S1 赋值n=0,a=200,r=0.05
S2 年增量T=ar
S3年产量a=a+T
S4 若a≤300,那么n=n+2,重复执行S2
S5N=2004+n
S6 输出N.
测试四算法语言1.a=input("底面边长a=");
1=input("侧棱长l=");
//注:这里应该对输入数据的合理性作出判别.
h=sqrt(1^2-(sqrt(2)/2*a)^2); //计算棱锥的高V=a^2*h/3; //计算棱锥的体积
disp(V,"正四棱锥的体积为");
2.[法一]
x=input("x=");
y=2*x-3; //计算y=f(x)
y=2*y-3; //计算y=f(f(x))
disp(y);
[法二]
//定义函数f(x)=2*x-3
function y=f(x)
y=2*x-3;
endfunction
//下面可直接调用f(x)
x=input("x=");
y=f(f(x)); //与代数中的表达方式一样
disp(y);
3.disp("请输入三角形的三条边长:");
a=input("a=");
b=input("b=");
c=input("c=");
if(a+b>c)&(a+c>b)&(b+c>a)then
p=(a+b+c)/2;
S=sqrt(p*(p-a)*(p-b)*(p-c));
disp(S,"三角形面积为");
else
disp("不能构成三角形!");
end;
4.for i=1∶9
if((10*i+3)*6528==(30+i)*8256)then
disp(i,"这个数字是:");
break;
end;
end;
5.[法一]用for语句实现
S=0;
an=1;
for i=1∶100
an=an*i;
S=S+an;
end;
disp(S,"1!+2!+3!+…+100!=");
[法二]用while语句实现
S=0;
an=1;
i=1
while i<=100
an=an*i;
S=S+an;
i=i+1;
end;
disp(S,"1!+2!+3!+…+100!=");
6.a_n_2=1;
a_n_1=3;
n=input("要求前多少项的和呢?请输入n=");
S=0;
//如果只要求前1项或2项的和,则不需要用到递推关系
if(n==1)then
S=a_n_2;
elseif(n==2)then
S=a_n_2+a_n_1;
end;
https://www.360docs.net/doc/d210859679.html,新课标第一网
//如果n大于2,则要用递推关系
i=3;
while(i<=n)
a_n=3*a_n_1-2*a_n_2;//先由递推关系求出下一项
S=S+a_n; //然后累加到和S中
a_n_2=a_n_1; //原来的第(n-1)项在下一轮循环中将变成第(n-2)项a_n_1=a_n; //原来的第n项在下一轮循环中将变成第(n-1)项
i=i+1; //项的脚标增1(表示下一轮循环要计算下一项了) end;
printf("前%d项和为:%d",int(n),int(S));
7.//定义函数f(x)=x^3+x^2-2x-2
//方程f(x)=0有三个实数解:-sqrt(2),-1,sqrt(2)
function y=f(x)
y=x^3+x^2-2*x-2;
endfunction
https://www.360docs.net/doc/d210859679.html,新课标第一网
//用户输入初始区间的左右端点
disp("请输入实根所在初始区间[a,b]:");
a=input("a=");
b=input("b=");
ya=f(a);
yb=f(b);
//用户输入计算精度
d=abs(input("请输入计算精度(输入的越小精度越高,但计算花费的时间就越多):"));
//下面通过二分法求符合精度的近似解
x=0;
err=%f;
while(abs(b-a)>=d)
x=(a+b)/2;
y=f(x);
if(y==0)then break;end; //若此时x的值正好是方程的解,则退出循环
if(y*ya<0)then
b=x;
yb=f(b);
elseif(y*yb<0)then
a=x;
ya=f(a);
else
err=%t;
break;
end;
end;
if(err==%t)then
disp("计算中出现问题,可能是在您输入的初始区间中没有实根.");
else
printf("方程的近似解为:x=%f.",x);
end;
8.[法一]
disp("请依次输入f(x)=ax^2+bx+c的系数");
a=input("a=");
if(a==0)then
disp("系数a不能为0!");
abort;
end;
b=input("b=");
c=input("c=");
disp("请输入区间的左右端点:");
x1=input("x1=");
x2=input("x2=");
if(x1>=x2)then begin
disp("区间端点输入错误!");
abort;
end;
x0=-b/(2*a); //对称轴
if(a>0)then //如果开口朝上
if(x0<x1)then //如果对称轴在给定区间的左侧,则
min_v=a*x1^2+b*x1+c; //在x=x1处取得最小值
max_v=a*x2^2+b*x2+c; //在x=x2处取得最大值
elseif(x0<(x1+x2)/2)then //如果对称轴在区间[x1,x2]的左半部分,则min_v=a*x0^2+b*x0+c; //在顶点处取得最小值
max_v=a*x2^2+b*x2+c; //在x=x2处取得最大值
elseif(x0<x2)then //如果对称轴在区间[x1,x2]的右半部分,则min_v=a*x0^2+b*x0+c; //在顶点处取得最小值
max_v=a*x1^2+b*x1+c; //在x=x1处取得最大值
else //如果对称轴在区间[x1,x2]右侧,则
min_v=a*x2^2+b*x2+c; //在x=x2处取得最小值
min_v=a*x1^2+b*x1+c; //在x=x1处取得最大值
end;
else //如果开口朝下
if(x0<x1)then //如果对称轴在给定区间的左侧,则
max_v=a*x1^2+b*x1+c; //在x=x1处取得最大值
min_v=a*x2^2+b*x2+c; //在x=x2处取得最小值
elseif(x0<(x1+x2)/2)then //如果对称轴在区间[x1,x2]的左半部分,则max_v=a*x0^2+b*x0+c; //在顶点处取得最大值
min_v=a*x2^2+b*x2+c; //在x=x2处取得最小值
elseif(x0<x2)then //如果对称轴在区间[x1,x2]的右半部分,则max_v=a*x0^2+b*x0+c; //在顶点处取得最大值
min_v=a*x1^2+b*x1+c; //在x=x1处取得最小值
else //如果对称轴在区间[x1,x2]右侧,则
max_v=a*x2^2+b*x2+c; //在x=x2处取得最大值
min_v=a*x1^2+b*x1+c; //在x=x1处取得最小值
end;
end;
printf("最小值=%f,\n最大值=%f",min_v,max_v);
[法二]
(为[法一]的简化版)
a=input("a=");
b=input("b=");
c=input("c=");
x1=input("x1=");
x2=input("x2=");
x0=-b/(2*a); //对称轴
if(x0<x1)then //如果对称轴在给定区间的左侧,则
人教版高中(必修3)第一章算法初步 1.1.1 算法的概念 学案
第一章算法初步 §1.1算法与程序框图 1.1.1算法的概念 【明目标、知重点】 1.通过解二元一次方程组的方法,体会算法的基本思想. 2.了解算法的含义和特征. 3.会用自然语言表述简单的算法. 【填要点、记疑点】 1.算法的概念 2 计算机解决任何问题都要依赖于算法,只有将解决问题的过程分解为若干个明确的步骤,即算法,并用计算机能够接受的“语言”准确地描述出来,计算机才能够解决问题.【探要点、究所然】 [情境导学]赵本山和宋丹丹的小品《钟点工》中有这样一个问题:宋丹丹:要把大象装入冰箱,总共分几步?哈哈哈哈,三步.第一步,把冰箱门打开;第二步,把大象装进去;第三步,把冰箱门带上. 探究点一算法的概念 思考1一个大人和两个小孩一起渡河,渡口只有一条小船,每次只能渡1个大人或两个小孩,他们三人都会划船,但都不会游泳.试问他们怎样渡过河去?请写出一个渡河方案.答第一步,两个小孩同船过河去; 第二步,一个小孩划船回来; 第三步,一个大人划船过河去; 第四步,对岸的小孩划船回来; 第五步,两个小孩同船渡过河去.
小结 广义地说,算法就是做某一件事的步骤或程序.菜谱是做菜肴的算法,洗衣机的使用说明书是操作洗衣机的算法.在数学中,主要研究计算机能实现的算法,即按照某种步骤一定可以得到结果的解决问题的程序. 思考2 在初中,对于解二元一次方程组你学过哪些方法?解二元一次方程组 ????? x -2y =-1 ①2x +y =1 ②的具体步骤是什么? 答 解二元一次方程组有加减消元法和代入消元法. 解方程组的步骤: 方法一 第一步,②-①×2得5y =3.③ 第二步,解③得y =35 . 第三步,将y =35代入①,得x =15 . 第四步,得方程组的解为??? x =15,y =35. 方法二 第一步,①+②×2,得5x =1.③ 第二步,解③,得x =15. 第三步,②-①×2,得5y =3.④ 第四步,解④,得y =35 . 第五步,得方程组的解为??? x =15, y =35. 思考3 写出求方程组????? A 1x + B 1y + C 1=0 ①A 2x +B 2y +C 2=0 ②(A 1B 2-B 1A 2≠0)的解的算法. 答 第一步,②×A 1-①×A 2,得(A 1B 2-A 2B 1)y +A 1C 2-A 2C 1=0.③ 第二步,解③,得y =A 2C 1-A 1C 2A 1B 2-A 2B 1 . 第三步,将y =A 2C 1-A 1C 2A 1B 2-A 2B 1代入①,得x =-B 2C 1+B 1C 2A 1B 2-A 2B 1 . 第四步,得方程组的解为????? x =-B 2C 1+B 1C 2A 1B 2-A 2B 1, y =A 2C 1-A 1 C 2A 1B 2-A 2B 1.
必修3算法初步知识总结
必修3算法初步知识总结 1:算法的概念 (1)算法概念:在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成. (2)算法的特点: ①有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的. ②确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可. ③顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个 步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题. ④不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法. ⑤普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计 算器计算都要经过有限、事先设计好的步骤加以解决. 2:程序框图 (1)程序框图基本概念: ①程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及 文字说明来准确、直观地表示算法的图形。 一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。 ②构成程序框的图形符号及其作用 程序框名称功能 起止框表示一个算法的起始和结束,是任何流程图不可少的。 输入、输出框表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。
处理框赋值、计算,算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。 判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”。 学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下: 1、使用标准的图形符号。 2、框图一般按从上到下、从左到右的方向画。 3、除判断框外,大多数流程图符号只有一个进入点和一个退出点。判断框具有超过一个退出点的唯一符号。 4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。 5、在图形符号内描述的语言要非常简练清楚。 3:算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。 (1)顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。 顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤。如在示意图中,A框和B框是依次执行的,只有在执行完A 框指定的操作后,才能接着执行B框所 指定的操作。 (2)条件结构:条件结构是指在算法中通过对条件的判断根据条件是否成立而选择不同流向的 算法结构。 条件P是否成立而选择执行A框或B框。无论P条件是否成立,只能执行A 框或B框之一,不可能同时执行 A框和B框,也不可能A框、B框都不执行。一个判断结构可以有多个判断框。(3)循环结构:在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构。循环结构又称重复结构,循环结构可细分为
高一数学必修三《算法初步》单元测试题
一、单项选择题(共12小题,每小题5分,共60分) 1. 算法的有穷性是指() A. 算法必须包含输出 B. 算法中每个操作步骤都是可执行的 C. 算法的步骤必须有限 D. 以上说法均不正确 【答案】C 【解析】 试题分析:所谓算法有穷性是指一个算法应包含有限的操作步骤,即在执行有限操作后算法结束,从而可得结论. 解:一个算法必须在有限步内结束,简单的说就是没有死循环 即算法的步骤必须有限 故选C. 点评:本题主要考查了算法的特点,属于基本概念的考查,是容易题. 2.2.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( ) A. 一个算法只能含有一种逻辑结构 B. 一个算法最多可以包含两种逻辑结构 C. 一个算法必须含有上述三种逻辑结构 D. 一个算法可以含有上述三种逻辑结构的任意组合 【答案】D 【解析】 分析:根据算法中三种逻辑结构的定义,顺序结构是最基本的结构,每个算法一定包含顺序结构,选择结构是算法中出现分类讨论时使用的逻辑结构,循环结构一定包含一个选择结构,从而即可得出答案. 详解:算法有三种逻辑结构, 最基本的是顺序结构, 一个算法一定包含有顺序结构,但是可以含有三种逻辑结构的任意组合. 故选:D. 点睛:本题考查的知识点是算法的概念及算法的特点,是对概念的直接考查,属基础题,熟练掌握相关概念是解答本题的关键.
3.3.下列给出的赋值语句中正确的是() A. B. C. D. 【答案】B 【解析】 【分析】 根据赋值语句定义判断选择. 【详解】赋值语句一般格式是:变量=表达式(或变量),所以选B. 【点睛】赋值语句用符号“=”表示,其一般格式是变量=表达式(或变量),其作用是对程序中的变量赋值; 4.4.程序执行后输出的结果是() A. -1 B. 0 C. 1 D. 2 【答案】B 【解析】 试题分析:开始满足,第一次循环:; 满足,第二次循环:; 满足,第三次循环:; 满足,第四次循环:; 满足,第五次循环:; 此时不满足,结束循环,所以输出n的值为0。
必修3知识点总结:第一章_算法初步
高中数学必修3知识点总结 第一章算法初步 1.1.1算法的概念 1、算法概念: 在数学上,现代意义上的“算法”通常是指能够用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成. 2. 算法的特点: (1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的. (2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不理应是模棱两可. (3)顺序性与准确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能实行下一步,并且每一步都准确无误,才能完成问题. (4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题能够有不同的算法. (5)普遍性:很多具体的问题,都能够设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决. 1.1.2程序框图 1、程序框图基本概念: (一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。 一个程序框图包括以下几部分:表示相对应操作的程序框;带箭头的流程线;程序框外必要文字说明。(二)构成程序框的图形符号及其作用
学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下: 1、使用标准的图形符号。 2、框图一般按从上到下、从左到右的方向画。 3、除判断框外,绝大部分流程图符号只有一个进入点和一个退出点。判断框具有超过一个退出点的唯一符号。 4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。 5、在图形符号内描述的语言要非常简练清楚。 (三)、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。 1、顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序实行的, 顺序结构在程序框图中的体现就是用流程线将程序框自上而 下地连接起来,按顺序执行算法步骤。如在示意图中,A 框和B 框是依次执行的,只有在执行完A 框指定的操作后,才能接着执 行B 框所指定的操作。 2、条件结构: 条件结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构。 条件P 是否成立而选择执行A 框或B 框。无论 P 条件是否成立,只能执行A 框或B 框之一,不可能同时执行A 框和B 框,也不可能A 框、B 框都不执行。一个判断结构能够有多个判断框。 3、循环结构:在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构。循环结构又称重复结构,循环结构可细分为两类: (1)、一类是当型循环结构,如下左图所示,它的功能是当给定的条件P 成立时,执行A 框,A 框执行完毕后,再判断条件P 是否成立,如果仍然成立,再执行A 框,如此反复执行A 框,直到某一次条件P 不成立为止,此时不再执行A 框,离开循环结构。 (2)、另一类是直到型循环结构,如下右图所示,它的功能是先执行,然后判断给定的条件P 是否成立,如果P 仍然不成立,则继续执行A 框,直到某一次给定的条件P 成立为止,此时不再执行A 框,离开循环结构。 当直到型循环结构
高一数学必修三算法初步知识点
高一数学必修三算法初步知识点 【一】 (1)算法概念:在数学上,现代意义上的“算法”通常是指能够 用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是 明确和有效的,而且能够在有限步之内完成. (2)算法的特点: ①有限性:一个算法的步骤序列是有限的,必须在有限操作之后 停止,不能是无限的. ②确定性:算法中的每一步应该是确定的并且能有效地执行且得 到确定的结果,而不理应是模棱两可. ③顺序性与准确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只 有执行完前一步才能实行下一步,并且每一步都准确无误,才能完成 问题. ④不性:求解某一个问题的解法不一定是的,对于一个问题能够 有不同的算法. ⑤普遍性:很多具体的问题,都能够设计合理的算法去解决,如 心算、计算器计算都要经过有限、事先设计好的步骤加以解决。 【二】 (1)顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序实行的,它是由若干个依次执行的处 理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。 顺序结构在程序框图中的体现就是用流程线将程序框自上而下地 连接起来,按顺序执行算法步骤。如在示意图中,A框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所
指定的操作。 (2)条件结构:条件结构是指在算法中通过对条件的判断根据条 件是否成立而选择不同流向的 算法结构。 条件P是否成立而选择执行A框或B框。无论P条件是否成立, 只能执行A框或B框之一,不可能同时执行 A框和B框,也不可能A框、B框都不执行。一个判断结构能够 有多个判断框。 (3)循环结构:在一些算法中,经常会出现从某处开始,按照一 定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行 的处理步骤为循环体,显然,循环结构中一定包含条件结构。循环结 构又称重复结构,循环结构可细分为两类: ①一类是当型循环结构,如下左图所示,它的功能是当给定的条 件P成立时,执行A框,A框执行完毕后,再判断条件P是否成立,如果仍然成立,再执行A框,如此反复执行A框,直到某一次条件P不 成立为止,此时不再执行A框,离开循环结构。 ②另一类是直到型循环结构,如下右图所示,它的功能是先执行,然后判断给定的条件P是否成立,如果P仍然不成立,则继续执行A 框,直到某一次给定的条件P成立为止,此时不再执行A框,离开循 环结构。 注意:1循环结构要在某个条件下终止循环,这就需要条件结构 来判断。所以,循环结构中一定包含条件结构,但不允许“死循环”。 2在循环结构中都有一个计数变量和累加变量。计数变量用于记 录循环次数,累加变量用于输出结果。计数变量和累加变量一般是同 步执行的,累加一次,计数一次。 【三】
必修三算法初步知识点
第一章算法初步 1.1.1算法的概念 1、算法概念: 在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成. 2. 算法的特点: (1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的. (2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可. (3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题. (4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法. (5)普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决. 1.1.2程序框图 1、程序框图基本概念: (一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。 一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。 (二)构成程序框的图形符号及其作用
学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下:1、使用标准的图形符号。2、框图一般按从上到下、从左到右的方向画。3、除判断框外,大多数流程图符号只有一个进入点和一个退出点。判断框具有超过一个退出点的唯一符号。 4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。 5、在图形符号内描述的语言要非常简练清楚。(三)、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。 1、顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。 下地连接起来,按顺序执行算法步骤。如在示意图中,A框和B 框是依次执行的,只有在执行完A框指定的操作后,才能接着执 行B框所指定的操作。 2、条件结构: 条件结构是指在算法中通过对条件的判断 根据条件是否成立而选择不同流向的算法结构。 条件P是否成立而选择执行A框或B框。无论P条件是否成立,只能执行A框或B框之一, 不可能同时执行A框和B框,也不可能A框、B框都不执行。一个判断结构可以有多个判断 框。 3、循环结构:在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理 步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含 条件结构。循环结构又称重复结构,循环结构可细分为两类: (1)、一类是当型循环结构,如下左图所示,它的功能是当给定的条件P成立时,执行A 框,A框执行完毕后,再判断条件P是否成立,如果仍然成立,再执行A框,如此反复执 行A框,直到某一次条件P不成立为止,此时不再执行A框,离开循环结构。
高中数学必修三《算法初步》练习题(精选.)
高中数学必修三《算法初步》练习题 一、选择题 1.下面对算法描述正确的一项是 ( ) A .算法只能用伪代码来描述 B .算法只能用流程图来表示 C .同一问题可以有不同的算法 D .同一问题不同的算法会得到不同的结果 2.程序框图中表示计算的是 ( ). A . B C D 3 将两个数8,17a b ==交换,使17,8a b ==, 下面语句正确一组是 ( ) A B C D . 4. 计算机执行下面的程序段后,输出的结果是( ) 1a = 3b = a a b =+ b a b =- PRINT a ,b A .1,3 B .4,1 C .0,0 D .6,0 5.当2=x 时,下面的程序运行后输出的结果是 ( ) A .3 B .7 C .15 D .17 6. 给出以下四个问题: ①输入一个数x , 输出它的相反数 ②求面积为6的正方形的周长 ③输出三个数,,a b c 中的最大数 ④求函数1,0 ()2,0x x f x x x -≥?=?+10
B. i<8 C. i<=9 D. i<9 9. INPUT 语句的一般格式是( ) A. INPUT “提示内容”;表达式 B.“提示内容”;变量 C. INPUT “提示内容”;变量 D. “提示内容”;表达式 10.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( ) A . 一个算法只能含有一种逻辑结构 B. 一个算法最多可以包含两种逻辑结构 C. 一个算法必须含有上述三种逻辑结构 D. 一个算法可以含有上述三种逻辑结构的任意组合 11. 如右图所示的程序是用来 ( ) A .计算3×10的值 B .计算93的值 C .计算103的值 D .计算12310???????的值 12. 把88化为五进制数是( ) A. 324(5) B. 323(5) C. 233(5) D. 332(5) 13.下列判断正确的是 ( ) A.条件结构中必有循环结构 B.循环结构中必有条件结构 C.顺序结构中必有条件结构 D.顺序结构中必有循环结构 14. 如果执行右边的框图, 输入N =5,则输出的数等于( ) A .5 4 B.4 5 C. 6 5 D. 56 15.某程序框图如图所示,现输入如下四个函数, 其中可以输出的函数是 ( ) A .2()f x x = B .1 ()f x x = C .()ln 26f x x x =+- D . ()f x x = 二、填空题:
高中数学必修三 算法初步综合测试题
第一章 算法初步 一、选择题 1.如果输入3n ,那么执行右图中算法的结果是( ). A .输出3 B .输出4 C .输出5 D .程序出错,输不出任何结果 2.算法: 第一步,m = a . 第二步,b <m ,则m = b . 第三步,若c <m ,则m = c . 第四步,输出 m . 此算法的功能是( ). A .输出a ,b ,c 中的最大值 B .输出a ,b ,c 中的最小值 C .将a ,b ,c 由小到大排序 D .将a ,b ,c 由大到小排序 3.右图执行的程序的功能是( ). A .求两个正整数的最大公约数 B .求两个正整数的最大值 C .求两个正整数的最小值 D .求圆周率的不足近似值 4.下列程序: INPUT “A =”;1 A =A *2 A =A *3 A =A *4 A =A *5 第一步,输入n . 第二步,n =n +1. 第三步,n =n +1. 第四步,输出n . (第1题) (第2题) (第3题)
PRINT A END 输出的结果A是(). A.5 B.6 C.15 D.120 5.下面程序输出结果是(). A.1,1 B.2,1 C.1,2 D.2,2 6.把88化为五进制数是(). A.324(5)B.323(5)C.233(5)D.332(5) 7.已知某程序框图如图所示,则执行该程序后输出的结果是(). A.1-B.1 C.2 D. 1 2 (第5题) 开始 a =2,i=1 i≥2 010 1 1 a a =- i=i+1 结束 输出a 是 否 (第7题)
8.阅读下面的两个程序: 甲乙 对甲乙两程序和输出结果判断正确的是(). A.程序不同,结果不同B.程序不同,结果相同 C.程序相同,结果不同D.程序相同,结果相同 9.执行右图中的程序,如果输出的结果是4,那么输入的 只可能是(). A.-4 B.2 C.2 或者-4 D.2或者-4 10.按照程序框图(如右图)执行,第3个输出的数是(). A.3 B.4 C.5 D.6 (第8题) (第9题)
高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例B卷
高中数学人教新课标A版必修3 第一章算法初步 1.3算法案例B卷姓名:________ 班级:________ 成绩:________ 一、选择题 (共6题;共12分) 1. (2分)如果执行框图,输入N=5,则输出的数等于() A . B . C . D . 2. (2分) (2018高二上·南山月考) 1037和425的最大公约数是() A . 9 B . 3 C . 51
D . 17 3. (2分) (2018高二上·铜仁期中) 用“辗转相除法”求得和的最大公约数是() A . B . C . D . 4. (2分) (2016高一下·邯郸期中) 下列各数中,最小的数是() A . 75 B . 111111(2) C . 210(6) D . 85(9) 5. (2分)按流程图的程序计算,若开始输入的值为,则输出的的值是() A . 6 B . 21 C . 156 D . 231 6. (2分)运行如图所示的程序框图,若输出的结果为,则判断框内可以填()
A . B . C . D . 二、单选题 (共2题;共4分) 7. (2分) (2019高二上·齐齐哈尔期末) 根据秦九韶算法求时的值,则为() A . B . C . D . 8. (2分) (2017高一下·郴州期中) 下列各数中最小的数是()
A . 85(9) B . 210(6) C . 1000(4) D . 111111(2) 三、填空题 (共4题;共4分) 9. (1分)将二进制数101101(2)化为八进制数,结果为________ . 10. (1分)用更相减损术求152与92的最大公约数时,需要做减法的次数是________. 11. (1分)已知f(x)=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时,f(x)=________. 12. (1分)请将以下用“更相减损术”求两个正整数a,b的最大公约数的程序补充完整: INPUT “a,b=”;a,b WHILE a<>b IF a>b THEN a=a-b ELSE ________ END IF WEND PRINT a END 四、解答题 (共1题;共5分) 13. (5分)(1)将101111011(2)转化为十进制的数;
高二数学必修三之算法初步
高二数学必修三之算法初步
高中数学必修三第一章算法初步 一、选择题 1.右面的程序框图,如果输入三个实数,,a b c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下 面四个选项中的() (A)c x>(B)x c>(C)c b>(D)b c> 2.图1是某县参加2007年高考的学生身高条形统计图,从左
到右的各条形表示的学生人数依次记为A 1、A 2 、…、A 10 (如A 2表示身高(单位:cm)[) 150,155内的学生人数)。图2是统 计图1中身高在一定范围内学生人数的一个算法 流程图。现要统计身高在160~180cm(含160cm,不含180cm))的学生人数,那么在流程图中的判断框内应填写的条 件是() A. 6 i< B. 7 i< C. 8 i< D. 9 i< 3.如果执行下左图的程序框图,那么输出的S=()A.2450 B.2500 C.2550 D.2652
4.阅读(上页右边图)的程序框图,若输入的n是100,则输出的变量S和T的值依次是() (A)2500,2500(B)2550,2550(C)2500,2550(D)2550,2500 二、填空题 1.阅读图3的程序框图,若输入4 n=,则输出a=, m=,6 i=.(注:框图中的赋值符号“=”也可以写成“←” 或“:=”)
2.某地区为了解7080 -岁的老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表: 在上述统计数据的分析中一部分计算见算法流程图,则输出的S的值为. 3.执行右边的程序框图,若0.8 n= p=,则输出的______. 各地市高三调研考试 一、选择题 1.【2008年3月济宁市高三复习第一阶段质量检测】如下左图,
高中数学必修三算法初步测试题
1a = 3b = a a b =+ b a b =- PRINT a ,b IF 10a < THEN 2y a =* else y a a =* i=1 s=0 WHILE i<=4 s=s*x+1 i=i+1 WEND PRINT s END 必修三算法初步综合测试题 一、选择题 1.下面对算法描述正确的一项是:( ) A .算法只能用自然语言来描述 B .算法只能用图形方式来表示 C .同一问题可以有不同的算法 D .同一问题的算法不同,结果必然不同 2.用二分法求方程022 =-x 的近似根的算法中要用哪种算法结构( ) A .顺序结构 B .条件结构 C .循环结构 D .以上都用 3.将两个数8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( ) 4.计算机执行下面的程序段后,输出的结果是( ) A .1,3 B .4,1 C .0,0 D .6,0 5.当3=a 时,下面的程序段输出的结果是( ) A .9 B .3 C .10 D .6 6.用“辗转相除法”求得459和357的最大公约数是( ) A .3 B .9 C .17 D .51 7.当2=x 时,下面的程序段结果是 ( ) A .3 B .7 C .15 D .17 8.对赋值语句的描述正确的是 ( ) ①可以给变量提供初值 ②将表达式的值赋给变量
③可以给一个变量重复赋值 ④不能给同一变量重复赋值 A .①②③ B .①② C .②③④ D .①②④ 9.下列给出的赋值语句中正确的是( ) A .4M = B .M M =- C .3B A == D .0x y += 10.给出以下四个问题, ①x , 输出它的相反数. ②求面积为6的正方形的周长. ③求三个数,,a b c 中输入一个数的最大数. ④求函数1,0 ()2,0x x f x x x -≥?=? +
高中数学必修三《算法初步》练习题(内含答案)[1]
2、基本算法语句: ①输入语句。输入语句的格式:INPUT “提示内容”;变量 ②输出语句。输出语句的一般格式:PRINT“提示内容”;表达式 ③赋值语句。赋值语句的一般格式:变量=表达式 ④条件语句。 (1)“IF—THEN—ELSE”语句 格式: IF 条件THEN 语句1 ELSE 语句2 END IF ⑤循环语句。 (1)当型循环语句 当型(WHILE型)语句的一般格式为:WHILE 条件 循环体 WEND (2)“IF—THEN”语句 格式: IF 条件THEN 语句 END IF (2)直到型循环语句 直到型(UNTIL型)语句的一般格式为:DO 循环体 LOOP UNTIL 条件
高中数学必修三《算法初步》练习题 一、选择题 1.下面对算法描述正确的一项是 ( ) A .算法只能用伪代码来描述 B .算法只能用流程图来表示 C .同一问题可以有不同的算法 D .同一问题不同的算法会得到不同的结果 2.程序框图中表示计算的是 ( ). A . B C D 3 将两个数 8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( ) A B C D . 4. 计算机执行下面的程序段后,输出的结果是( ) 1a = 3b = a a b =+ b a b =- PRINT a ,b A .1,3 B .4,1 C .0,0 D .6,0 5.当2=x 时,下面的程序运行后输出的结果是 ( ) A .3 B .7 C .15 D .17 6. 给出以下四个问题: ①输入一个数x , 输出它的相反数 ②求面积为6的正方形的周长 ③输出三个数,,a b c 中的最大数 ④求函数1,0 ()2,0 x x f x x x -≥?=?+
最全高中数学必修三知识点总结归纳(经典版)
最全高中数学 必修三知识点总结归纳(经典版)
第一章算法初步 1.1.1算法的概念 1、算法概念: 在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成. 2. 算法的特点: (1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的. (2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可. (3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题. (4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法. (5)普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决. 1.1.2程序框图 1、程序框图基本概念: (一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。 一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
(二)构成程序框的图形符号及其作用 学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下: 1、使用标准的图形符号。2、框图一般按从上到下、从左到右的方向画。3、除判断框外,大多数流程图符号只有一个进入点和一个退出点。判断框具有超过一个退出点的唯一符号。4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。5、在图形符号内描述的语言要非常简练清楚。 (三)、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。 1、顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。 顺序结构在程序框图中的体现就是用流程线将程序框自上而 下地连接起来,按顺序执行算法步骤。如在示意图中,A 框和B 框是依次执行的,只有在执行完A 框指定的操作后,才能接着执 行B 框所指定的操作。 2、条件结构: 条件结构是指在算法中通过对条件的判断 根据条件是否成立而选择不同流向的算法结构。
人教新课标A版高中数学必修3第一章算法初步1.3算法与案例同步测试C卷
人教新课标A版高中数学必修3 第一章算法初步 1.3算法与案例同步测试C卷姓名:________ 班级:________ 成绩:________ 一、单选题 (共15题;共30分) 1. (2分) (2016高一下·太康开学考) 把十进制数2016化为八进制数的末尾数字是() A . 0 B . 3 C . 4 D . 7 2. (2分)在下列各数中,最大的数是() A . 85(9) B . 210(5) C . 68(8) D . 11111(2) 3. (2分)十进制数2015等值于八进制数为() A . 3737 B . 737 C . 03737 D . 7373 4. (2分)用秦九韶算法求f(x)=3x5+8x4﹣3x3+5x2+12x﹣6,当x=2时,V3的值为() A . 55 B . 56
C . 57 D . 58 5. (2分)已知f(x)=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时,v3的值为() A . 27 B . 11 C . 109 D . 36 6. (2分) (2019高二上·尚志月考) 用秦九韶算法求多项式在 时的值时,其中的值为() A . B . C . D . 7. (2分)二进制数1011(2)化为十进制数的结果为() A . 11 B . 9 C . 19 D . 13 8. (2分) (2016高一下·邵东期末) 下列各数中最小的是() A . 85 B . 210(6)
D . 101011(2) 9. (2分) (2017高二上·宁城期末) 已知f(x)=5x5+4x4+3x3+2x2+x+1,若用秦九韶算法求f(5)的值,下面说法正确的是() A . 至多4乘法运算和5次加法运算 B . 15次乘法运算和5次加法运算 C . 10次乘法运算和5次加法运算 D . 至多5次乘法运算和5次加法运算 10. (2分)用秦九韶算法计算f(x)=x6﹣12x5+60x4﹣160x3+240x2﹣192x+64的值时,当x=2时,v4的值为() A . 0 B . 80 C . -80 D . -32 11. (2分) (2016高二上·孝感期中) 用秦九昭算法计算多项式f(x)=2x6+5x5+6x4+23x3﹣8x2+10x﹣3,x=﹣4时,V3的值为() A . ﹣742 B . ﹣49 C . 18 D . 188 12. (2分) 1001101(2)与下列哪个值相等() A . 113(8)
高中数学人教A版必修三 第一章 算法初步 5
学业分层测评(五) 输入语句、输出语句和赋值语句 (建议用时:45分钟) [学业达标] 一、选择题 1.下列给出的输入、输出语句正确的是() ①输入语句:INPUT a,b,c,d,e; ②输入语句:INPUT X=1; ③输出语句:PRINT A=4; ④输出语句:PRINT 10,3*2,2/3. A.①②B.②③ C.③④D.①④ 【解析】②③中对变量赋值是错误的. 【答案】 D 2.赋值语句“x=x+1”的正确解释为() A.x的值与x+1的值可能相等 B.将原来x的值加上1后,得到的值替换原来x的值C.这是一个错误的语句 D.此表达式经过移项后,可与x=x-1功能相同 【答案】 B 3.下面的程序输出的结果是()
x=6 y=3 x=x/3 y=4*x+1 PRINT x+y END A.27 B.9 C.2+25 D.11 【解析】该程序的运行过程是x=6,y=3,x=6÷3=2,y=4×2+1=9,x+y=2+9=11.所以输出11. 【答案】 D 4.下列程序执行后,变量a、b的值分别为() 【导学号:28750014】 a=15 b=20 a=a+b b=a-b a=a-b PRINT a,b A.20,15 B.35,35 C.5,5 D.-5,-5 【解析】根据赋值语句的意义,先把a+b=35赋给a,然后把a-b=35-20赋给b,最后再把a-b=35-15=20赋给a. 【答案】 A 5.输出语句:PRINT 4+5,其输出的结果是() A.4B.5
C.9 D.20 【解析】4+5=9,故输出的结果是9. 【答案】 C 二、填空题 6.执行程序PRINT (3+5)*2的结果为________. 【解析】输出语句有计算功能,故结果为8*2=16. 【答案】16 7.下面一段程序执行后的结果为________. A=20 A=A*5 A=A+6 PRINT A END 【解析】A=20×5=100,A=100+6=106. 【答案】106 8.下面程序的功能是求所输入的两个正数的平方和,已知最后输出的结果是3.46,则此程序中,①处应填________;②处应填________. 【解析】由于程序的功能是求所输入的两个正数的平方和,所
人教A版高中数学必修三练习:第一章算法初步分层训练进阶冲关1.3算法案例Word版含答案
分层训练·进阶冲关 A组基础练(建议用时20分钟) 1.在对16和12求最大公约数时,整个操作如下:16-12=4,12-4=8,8-4=4.由此可以看出12和16的最大公约数是 ( A ) A.4 B.12 C.16 D.8 2.在m=nq+r(0≤r 6.用秦九韶算法求n次多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0的值,当 x=x0时,求f(x0)需要算乘方、乘法、加法的次数分别为( C ) A.,n,n B.n,2n,n C.0,n,n D.0,2n,n 7.用更相减损术求36与134的最大公约数时,第一步应为先除以2,得到18与67. 8.用辗转相除法求294和84的最大公约数时,需要做除法的次数是2. 9.三位七进制数表示的最大的十进制数是342. 10.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为3,3,则输出v的值为 48. 11.将1234(5)转化为八进制数. 【解析】先将1234(5)转化为十进制数: 1234(5)=1×53+2×52+3×51+4×50=194. 算法初步章节复习 一.知识梳理 1、算法的特征: ①有限性:算法执行的步骤总是有限的,不能无休止的进行下去 ②确定性:算法的每一步操作内容和顺序必须含义确切 ③可行性:算法的每一步都必须是可执行的,即每一步都可以通过手工或者机器在一定时间内可以完成 2、程序框图的三种基本逻辑结构:顺序结构、条件结构和循环结构。 3、基本语句: 输入语句:INPUT “提示内容”;变量,兼有赋值功能 输出语句:PRINT “提示内容”;表达式,兼有计算功能 赋值语句:变量=表达式,兼有计算功能 条件语句:IF 条件THEN IF 条件THEN 语句体语句体 ELSE END IF 语句体 END IF 循环语句:(1)当型(WHILE型)循环:(2)直到型(UNTIL型)循环: WHILE 条件DO 循环体循环体 WEND LOOP UNTIL 条件 4.常用符号 运算符号:加____,减____,乘____,除____,乘方______,整数取商数____,求余数_______. 逻辑符号:且AND,或OR,大于>,等于=,小于<,大于等于>=,小于等于<=,不等于<>. 常用函数:绝对值ABS(),平方根SQR() 5.算法案例 (1) 辗转相除法和更相减损术: 辗转相除法和更相减损术都是求两个正整数的最大公约数的方法 (2) 秦九韶算法:是求多项式值的优秀算法. 二、习题精练 1.将两个数A =9,B =15交换使得A =15,B =9下列语句正确的一组是( ) A. B. C. D. 2、如图所示程序,若输入8时,则下图程序执行后输出的结果是 ( ) A 、0.5 B 、0.6 C 、0.7 D 、0.8 3. 上图程序运行后输出的结果为 ( ) A. 50 B. 5 C. 25 D. 0 4、上图程序运行后的输出结果为 ( ) A.17 B.19 C.21 D.23 5、如右图所示,对甲乙两程序和输出结果判断正确的是 ( ) A .程序不同结果不同 B.程序不同,结果相同 C .程序相同结果不同 D .程序同,结果 6.下列各数中最小的数是 ( ) A .(9)85 B .(6)210 C .(4)1000 D .(2)111111 7.二进制数111011001001 (2)对应的十进制数是 ( ) A .3901 B .3902 C .3785 D .3904 8、下面的问题中必须用条件结构才能实现的个数是 ( ) (1)已知三角形三边长,求三角形的面积; (2)求方程ax+b=0(a,b 为常数)的根; (3)求三个实数a,b,c 中的最大者; (4)求1+2+3+…+100的值。 A .4个 B . 3个 C . 2个 D . 1个高中数学必修三算法初步复习(含答案)
