勾股定理证明方法及习题全解

勾股定理练习题
一、基础达标:
1. 下列说法正确的是( )
A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;
B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;
C.若 a 、b 、c 是Rt△ABC 的三边,,则a 2+b 2=c 2;
D.若 a 、b 、c 是Rt△ABC 的三边,,则a 2+b 2=c 2.
2. Rt △ABC 的三条边长分别是、、,则下列各式成立的是( )
A . B. C. D.
3. 如果Rt △的两直角边长分别为k 2-1,2k (k >1),那么它的斜边长是( )
A 、2k
B 、k+1
C 、k 2-1
D 、k 2+1 4. 已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0
,则
90=∠A 90=∠C a b c c b a =+c b a >+c b a <+222c b a =+
它的形状为( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形 5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A .121
B .120
C .90
D .不能确定 6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 33 7.※直角三角形的面积为S ,斜边上的中线长为d ,则这个三角形周长为( )
(A
2d (B
d (C
)2d (D
)d
8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )
A :3
B :4
C :5
D :
7
9.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )
A .17 B.3 C.17或3 D.以上都不对
10.已知a 、b 、c 是三角形的三边长,
如果满足2(6)100
a c --=则三角形的形状是( )
A :底与边不相等的等腰三角形
B :等边三角形
C :钝角三角形
D :直角三角形 11.斜边的边长为,一条直角边长为的直角三角形的面积是 .
12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 13. 一个直角三角形的三边长的平方和为200,则斜边长为 14.一个三角形三边之比是,则按角分类它是 三角形. 15. 一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是___.
16. 在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____.
cm 17cm 86:8:10
17.若三角形的三个内角的比是,最短边长为,最长边长为,则这个三角形三个角度数分别是 ,另外一边的平方是 .
18.如图,已知中,,,
,以直角边为直径作半圆,则
这个半圆的面积是 .
19. 一长方形的一边长为,面积为
,
那么它的一条对角线长是 .
二、综合发展:
1.如图,一个高、宽的大门,需要在对角线的顶点间加固一个木条,求木条的长.
2、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?
3:2:1cm 1cm 2ABC ??=∠90C 15=BA 12=AC BC cm 32
12cm 4m 3m
A
B
A
E
B
3.一个三角形三条边的长分别为,,,这个三角形最长边上的高是多少?
4.如图,要修建一个育苗棚,棚高h=3m ,棚宽a=4m ,棚的长为12m ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
5.如图,有一只小鸟在一棵高13m 的大树树梢上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?
cm 15cm 20cm
25
15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方m 处,过了2s 后,测得小汽车与车速检测仪间距离为m ,这辆小汽车超速了吗?
答案:
一、基础达标
1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.
答案: D.
2. 解析:本题考察三角形的三边关系和勾股定理.
答案:B.
3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然
后再求它的周长. 答案:C .
4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角
形的外部,有两种情况,分别求解. 答案:C.
5. 解析: 勾股定理得到:,另一条直角边是15,
所求直角三角形面积为.答案: .
6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.
7030502
2215817=-2
1
158602cm ??=2
60cm
小汽车
小汽车
观测点
答案:,,直角,斜,直角.
7. 解析:本题由边长之比是 可知满足勾股定理,即是直角三角形.答案:直角. 8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:、、
,3.
9. 解析:由勾股定理知道:,所以以直角边为直径的半圆面积为10.125π.答案:10.125π.
10. 解析:长方形面积长×宽,即12长×3,长,所以一条对角线长为5.
答案:. 二、综合发展
11. 解析:木条长的平方=门高长的平方+门宽长的平方.
答案:.
12解析:因为,所以这三角形是直角三角形,设最长边(斜边)上的高为
,由直角三角形面积关系,可得,∴.答案:12cm
13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助
勾股定理求出.
答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,
所以矩形塑料薄膜的面积是:5×20=100(m 2
) .
14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解. 答案:6.5s . 15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >km/h . 答案:这辆小汽车超速了.
222c b a =+c 6:8:10?30?60?902
2222291215=-=-=AC AB BC 9=BC 4=cm 55m 2
22252015=+xcm 111520252
2
x ??=??12=x 70
勾股定理的发现和证明-
勾股定理的发现和证明 中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话: 周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?” 商高回答说:“数的产生来源于对方和圆这些形体饿认识。其中有一条原理:当直角三角形‘矩’得到的一条直角边‘勾’等于3,另一条直角边‘股’等于4的时候,那么它的斜边‘弦’就必定是5。这个原理是大禹在治水的时候就总结出来的呵。” 从上面所引的这段对话中,我们可以清楚地看到,我国古代的人民早在几千年以前就已经发现并应用勾股定理这一重要懂得数学原理了。稍懂平面几何饿读者都知道,所谓勾股定理,就是指在直角三角形中,两条直角边的平方和等于斜边的平方。如图所示,我们 图1 直角三角形 用勾(a)和股(b)分别表示直角三角形得到两条直角边,用弦(c)来表示斜边,则可得: 勾2+股2=弦2 亦即: a2+b2=c2
勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年首先发现的。其实,我国古代得到人民对这一数学定理的发现和应用,远比毕达哥拉斯早得多。如果说大禹治水因年代久远而无法确切考证的话,那么周公与商高的对话则可以确定在公元前1100年左右的西周时期,比毕达哥拉斯要早了五百多年。其中所说的勾3股4弦5,正是勾股定理的一个应用特例(32+42=52)。所以现在数学界把它称为勾股定理,应该是非常恰当的。 在稍后一点的《九章算术一书》中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说;“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”把这段话列成算式,即为: 弦=(勾2+股2)(1/2) 亦即: c=(a2+b2)(1/2) 中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。在这幅“勾股圆方图”中,以弦为边长得到正方形ABDE是由4个相等的直角三角形再加上中间的那个小正方形组成的。每个直角三角形的面积为ab/2;中间懂得小正方形边长为b-a,则面积为(b-a)2。于是便可得如下的式子: 4×(ab/2)+(b-a)2=c2 化简后便可得: a2+b2=c2 亦即: c=(a2+b2)(1/2)
勾股定理的证明方法探究
a2+c2=b2,c=b2-a2!=42-32!=!7(cm).二、忽视定理成立的条件例2在边长都是整数的△ABC 中,AB>AC,如果AC=4cm,BC=3cm,求AB的长.误解:由“勾3股4弦5”知 AC=4cm,BC=3cm,AB>AC,∴AB=5cm.剖析:这种解法受“勾3股4弦5”思维定势的影响,见题中有BC=3,AC=4,就认为AB=5,而忘记了“勾3股4弦5”是在直角三角形的条件下才成立,而本题中没有指明是直角三角形,因此,只能用三角形三条边之间的关系来解。 欧几里得在他的《几何原本》中给出了勾股定理的推广定理:“直角三角形斜边上的一个直边形,其面积为两直角边上两个与之相似的直边形面积之和”。 从上面这一定理可以推出下面的定理:“以直角三角形的三边为直径作圆,则以斜边为直径所作圆的面积等于以两直角边为直径所作两圆的面积和”。 勾股定理还可以推广到空间:以直角三角形的三边为对应棱作相似多面体,则斜边上的多面体的表面积等于直角边上两个多面体表面积之和。 若以直角三角形的三边为直径分别作球,则斜边上的球的表面积等于两直角边上所作二球表面积之和。 总之,在勾股定理探索的道路上,我们走向了数学殿堂。
我们都喜欢把日子过成一首诗,温婉,雅致;也喜欢把生活雕琢成一朵花,灿烂,美丽。可是,前行的道路有时会曲折迂回,让心迷茫无措。生活的上空有时会飘来一场风雨,淋湿了原本热情洋溢的心。 不是每一个人都能做自己想做的事情,也不是每一个人都能到达想去的远方。可是,既然选择了远方,便只有风雨兼程。也许生活会辜负你,但你不可以辜负生活。 匆匆忙忙地奔赴中,不仅要能在阳光下灿烂,也要能在风雨中奔跑!真正的幸福不是拥有多少财富,而是在前行中成就一个优秀的自己! 生命没有输赢,只有值不值得。坚持做对的事情,就是值得。不辜负岁月,不辜负梦想,就是生活最美的样子。 北大才女陈更曾说过:“即使能力有限,也要全力以赴,即使输了,也要比从前更强,我一直都在与自己比,我要把最美好的自己,留在这终于相逢的决赛赛场。” 她用坚韧和执着给自己的人生添上了浓墨重彩的一笔。 我们都无法预测未来的日子是阳光明媚,还是风雨如晦,但前行路上点点滴滴的收获和惊喜,都是此生的感动和珍藏。 有些风景,如果不站在高处,你永远欣赏不到它的美丽;脚下有路,如果不启程,你永远无法揭晓远方的神秘。 我们踮起脚尖,是想离太阳更近一点儿;我们努力奔跑,是想到达远方欣赏最美的风景。 我们都在努力奔跑,我们都是追梦人!没有伞的时候,学会为自己撑伞;没有靠山的时候,学会自己屹立成一座伟岸的山! 远方有多远?多久能达到?勇敢往前冲的人,全世界都会向他微笑。相信,只要启程,哪怕会走许多弯路,也会有到达的那一天。
勾股定理9种证明(有图)
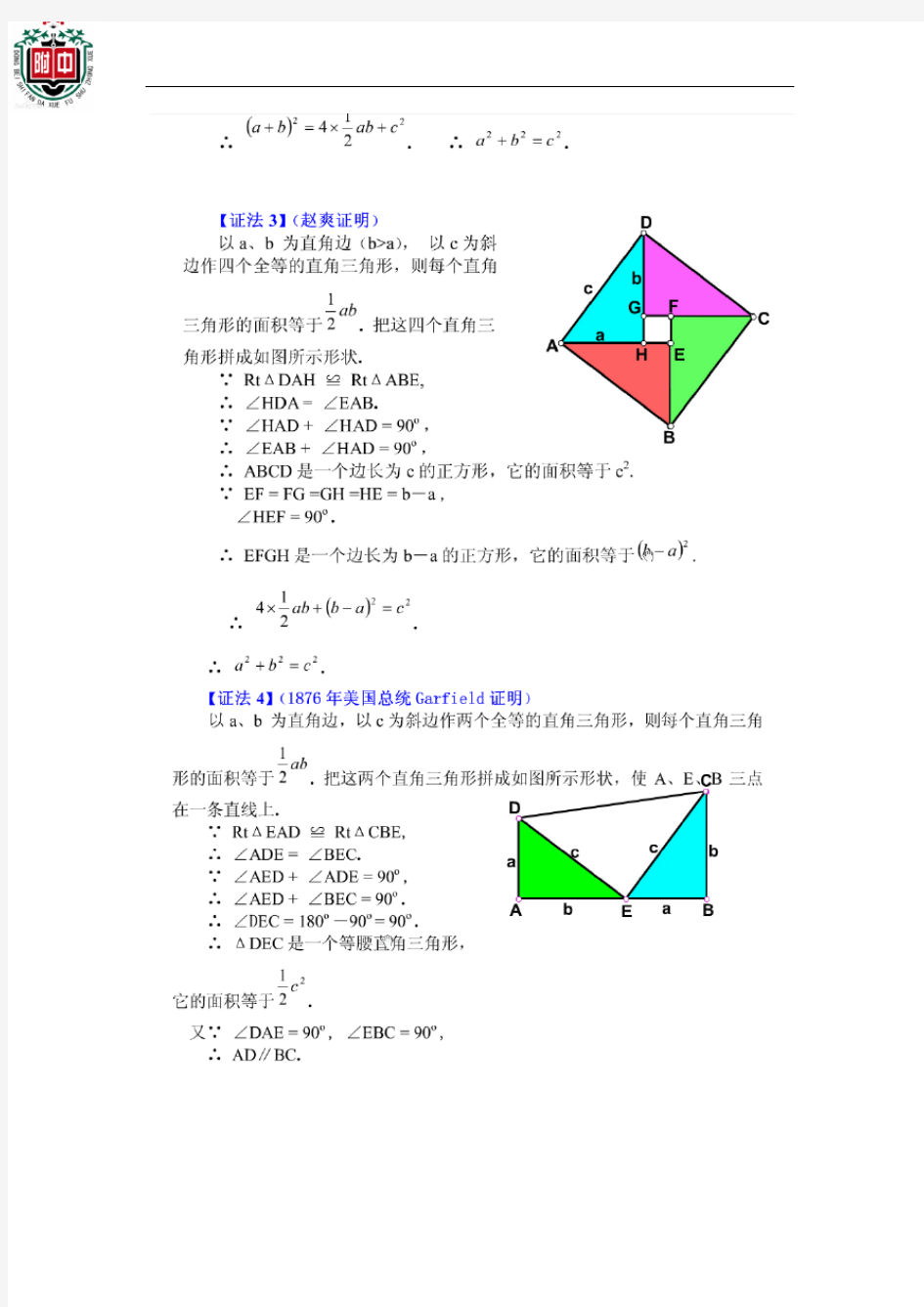
勾股定理的9种证明(有图) 【证法1】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面 积等于ab 21 . 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、 F 、C 三点在一条直线上,C 、 G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF. ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA. ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +. ∴ ()2 22 14c ab b a +?=+. ∴ 2 22c b a =+. 【证法2】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P. ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ ∴ ∠EGF = ∠BED , ∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180o―90o= 90o.
勾股定理经典例题(含答案)
类型一:勾股定理的直接用法 1、在Rt△ABC中,∠C=90° (1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a. 思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。 解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b= (2) 在△ABC中,∠C=90°,a=40,b=9,c= (3) 在△ABC中,∠C=90°,c=25,b=15,a= 举一反三 【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少? 【答案】∵∠ACD=90° AD=13, CD=12 ∴AC2 =AD2-CD2 =132-122 =25 ∴AC=5 又∵∠ABC=90°且BC=3 ∴由勾股定理可得 AB2=AC2-BC2 =52-32 =16 ∴AB= 4 ∴AB的长是4. 类型二:勾股定理的构造应用 2、如图,已知:在中,,,. 求:BC的长. 思路点拨:由条件,想到构造含角的直角三角形,为此作于D,则有 ,,再由勾股定理计算出AD、DC的长,进而求出BC的 长. 解析:作于D,则因, ∴(的两个锐角互余) ∴(在中,如果一个锐角等于, 那么它所对的直角边等于斜边的一半). 根据勾股定理,在中, . 根据勾股定理,在中,
. ∴. 举一反三【变式1】如图,已知:,,于P. 求证:. 解析:连结BM,根据勾股定理,在中, . 而在中,则根据勾股定理有 . ∴ 又∵(已知), ∴. 在中,根据勾股定理有 , ∴. 【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。 分析:如何构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于点E,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。 解析:延长AD、BC交于E。 ∵∠A=∠60°,∠B=90°,∴∠E=30°。 ∴AE=2AB=8,CE=2CD=4, ∴BE2=AE2-AB2=82-42=48,BE==。 ∵DE2= CE2-CD2=42-22=12,∴DE==。 ∴S四边形ABCD=S△ABE-S△CDE=AB2BE-CD2DE= 类型三:勾股定理的实际应用(一) 用勾股定理求两点之间的距离问题3、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了 到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。(1)
勾股定理的证明的方法
【】() 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三 个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上, B 、F 、 C 三点在一条直线上,C 、G 、 D 三点在一条直线上. ∵ Rt ΔHA E ≌ R t ΔEBF,
∴∠AHE = ∠BEF. ∵∠AEH + ∠AHE = 90o, ∴∠AEH + ∠BEF = 90o. ∴∠HEF = 180o―90o= 90o.∴四边形EFGH是一个边长为c的正方形. 它的面积等于c2. ∵ RtΔGDH ≌ RtΔHAE, ∴∠HGD = ∠EHA. ∵∠HGD + ∠GHD = 90o, ∴∠EHA + ∠GHD = 90o. 又∵∠GHE = 90o, ∴∠DHA = 90o+ 90o= 180o. ∴ ABCD是一个边长为a + b的正方形,它的面积等于()2b a+. ∴()2 2 2 1 4c ab b a+ ? = + . ∴2 2 2c b a= +. 【证法3】(赵爽证明) 以a、b 为直角边(b>a),以c为斜边作四个全等直角三角形,则每个直角 三角形的面积等于 ab 2 1 . 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE, ∴∠HDA = ∠EAB.
勾股定理毕达哥拉斯定理及各种证明方法
勾股定理(毕达哥拉斯定理) 勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。勾股定理是余弦定理的一个特例。勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。“勾三股四弦五”是勾股定理最基本的公式。勾股数组方程a 2+b 2=c 2的正整数组(a ,b ,c )。(3,4,5)就是勾股数。也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a 2+b 2=c 2,即直角三角形两直角边的平方和等于斜边的平方。 勾股定理 命题1如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么 。 勾股定理的逆定理 命题2如果三角形的三边长a ,b ,c 满足 ,那么这个三角形是直角三角形。 【证法1】(赵爽证明) 以a 、b 为直角边(b>a ),以c 为斜边作四个全等的直角三角形,则每 个直角三角形的面积等于2 1ab.把这四个直角三角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB. ∵∠HAD+∠HAD=90o,∴∠EAB+∠HAD=90o, ∴ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵EF=FG=GH=HE=b―a,∠HEF=90o. ∴EFGH 是一个边长为b―a 的正方形,它的面积等于. ∴ ∴. 【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a+b ,所以面积相等. 即,整理得. 【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵RtΔEAD≌RtΔCBE,∴∠ADE=∠BEC. ∵∠AED+∠ADE=90o,∴∠AED+∠BEC=90o.∴∠DEC=180o―90o=90o. ∴ΔDEC 是一个等腰直角三角形,它的面积等于 .又∵∠DAE=90o,∠EBC=90o,∴AD∥BC.∴ ABCD 是一个直角梯形,它的面积等于
勾股定理逆定理八种证明方法
勾股定理逆定理八种证 明方法 集团标准化小组:[VVOPPT-JOPP28-JPPTL98-LOPPNN]
证法1 作四个的直角三角形,把它们拼成如图那样的一个多边形,使D、E、F在一条上(设它们的两条直角边长分别为a、b ,斜边长为c.)。过点C作AC的延长线交DF于点P. ∵ D、E、F在一条直线上,且RtΔGEF ≌ RtΔEBD, ∴ ∠EGF = ∠BED, ∵ ∠EGF + ∠GEF =90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180°―90°= 90° 又∵ AB = BE = EG = GA = c, ∴ ABEG是一个边长为c的正方形。 ∴ ∠ABC + ∠CBE = 90° ∵ RtΔABC ≌ RtΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90° 即∠CBD= 90° 又∵ ∠BDE = 90°,∠BCP = 90°,BC = BD = a. ∴ BDPC是一个边长为a的正方形。 同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则 证法2 作两个的直角三角形,设它们的两条直角边长分别为a、b(b>a),做一个边长为c的正方形。斜边长为c. 再把它们拼成如图所示的多边形,使E、A、C 三点在一条直线上. 过点Q作QP∥BC,交AC于点P. 过点B作BM⊥PQ,垂足为M;再过点F作FN⊥PQ,垂足为N. ∵ ∠BCA = 90°,QP∥BC, ∴ ∠MPC = 90°, ∵ BM⊥PQ, ∴ ∠BMP = 90°, ∴ BCPM是一个矩形,即∠MBC =90°。 ∵ ∠QBM + ∠MBA = ∠QBA = 90°,∠ABC + ∠MBA = ∠MBC = 90°, ∴ ∠, 又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c, ∴ RtΔBMQ ≌ RtΔBCA. 同理可证RtΔQNF ≌ RtΔAEF.即 证法3 作两个全等的直角三角形,同证法2,再作一个边长为c的正方形。把它们拼成如图所示的多边形. 分别以CF,AE为边长做正方形FCJI和AEIG, ∵EF=DF-DE=b-a,EI=b, ∴FI=a, ∴G,I,J在同一直线上, ∵CJ=CF=a,CB=CD=c,∠CJB = ∠CFD = 90°,
勾股定理五种证明方法
勾股定理五种证明方法 【证法1】 做 8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 214214222?+=?++, 整理得 222c b a =+. 【 证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角 形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点 在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +. ∴ ()2 2214c ab b a +?=+. ∴ 222c b a =+. 【证法3】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为
勾股定理的证明
勾股定理的证明 【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 2 142 142 2 2 ? +=? ++, 整理得 2 2 2 c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角 形的面积等于ab 2 1. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF , ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE , ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于() 2 b a +. ∴ () 2 2 2 14c ab b a +? =+. ∴ 2 2 2 c b a =+. D G C F A H E B a b c a b c a b c a b c b a b a b a b a c b a c b a c b a c b a c b a c b a
勾股定理和三角形证明相关习题
勾股定理及三角形证明相关测试题 1.已知a 、b 、c 是?ABC 三边长,则2)(c b a --+c b a -+的值是( ) A.2a B.2b C.2c D.2(a-c) 2.如图所示,AB=BC=CD=DE=1,AB ⊥BC,AC ⊥CD,AD ⊥DE,则AE=( ) A.1 B.2 C.3 D.2 3.如图在棱长为1的正方体ABCD-A 1B 1C 1D 1中,一只蚂蚁从点A 出发,沿正方体表 面爬行到面对对角线A 1B 上的一点P ,再沿截面A 1BCD 1,则整个过程中蚂蚁爬行 的最短路程为( ) A.2 B.2 62+ C.2+2 D.22+ 4.下列4个命题中正确的个数是( ) (1)两边及第三边上的中线对应相等的两个三角形全等 (2)两边及第三边上的高线对应相等的两个三角形全等 (3)直角三角形两条边的长分别为3和4,则第三边边长为5. (4)如果a ≥0,那么(a )2=a. A.1 B.2 C.3 D.4
5.若一个直角三角形的三边长为a,b,c,且a2=9,b2=16,则c2= . 6.已知一个直角三角形的两条直角边长为5cm,12cm,则第三边长为 . 7.如图,一棵大树在一次强台风中离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为 m 8.如图,这是某种牛奶的长方体包装盒,长、宽、高分别为5cm,4cm、12cm,插吸管处的出口到相邻两边的距离都是1cm,为了设计配套的直吸管,要求插入碰到底面后,外露的吸管长度要在3cm至5cm间(包括3cm与5cm,不计吸管粗细及出口大小)则设计的吸管总长度L的范围是 . 9.如图,在?ABC中,AB=3+1,AC=6,BC=2,求?ABC三个内角的度数.
勾股定理的证明方法
【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即 a^2+b^2+4*(ab/2)=c^2+4*(ab/2), 整理得到:a^2+b^2=c^2。 【证法2】 以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于 ab/2.把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上. ∵ RtΔHAE ≌ RtΔEBF, ∴∠AHE = ∠BEF. ∵∠AEH + ∠AHE = 90o, ∴∠AEH + ∠BEF = 90o. ∴∠HEF = 180o―90o= 90o. ∴四边形EFGH是一个边长为c的 正方形. 它的面积等于c^2. ∵ RtΔGDH ≌ RtΔHAE, ∴∠HGD = ∠EHA. ∵∠HGD + ∠GHD = 90o, ∴∠EHA + ∠GHD = 90o. 又∵∠GHE = 90o, ∴∠DHA = 90o+ 90o= 180o. ∴ ABCD是一个边长为a + b的正方形,它的面积等于(a+b)^2. ∴(a+b)^2=c^2+4*(ab/2),∴ a^2+b^2=c^2。
【证法3】 以a、b 为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab/2. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE, ∴∠HDA = ∠EAB. ∵∠HAD + ∠HAD = 90o, ∴∠EAB + ∠HAD = 90o, ∴ ABCD是一个边长为c的正方形,它的面积等于c^2. ∵ EF = FG =GH =HE = b―a , ∠HEF = 90o. ∴ EFGH是一个边长为b―a的正方形,它的面积等于(b-a)^2. ∴(b-a)^2+4*(ab/2)=c^2,∴ a^2+b^2=c^2。 【证法4】 以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab/2. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上. ∵ RtΔEAD ≌ RtΔCBE, ∴∠ADE = ∠BEC.
勾股定理试题分类
勾股定理试题分类 Company number:【0089WT-8898YT-W8CCB-BUUT-202108】
《数学》八年级下册第十七章 勾股定理 【题型一】勾股定理的验证与证明 1.如图,每个小正方形的边长是1,图中三个正方形的面积分别是S1、 S2、S3,则它们的面积关系是,直角△ABC的三边的关系是. 参考答案:用数方格的方法或用面积公式计算三个正方形面积,得出S1+S2=S3,从而得到:AB2+BC2=AC2. 2.如图,每个小正方形的边长是1,图中三个正方形的面积分别是S1、 S2、S3,则它们的面积关系是,直角△ABC的三边的关系是. 参考答案:对于S3显然用数方格的方法不合适,利用“相减法”或“相加法”用面积公式计算三个正方形面积,得出 S1+S2=S3,从而得到:AB2+BC2=AC2. 3.如图,是由四个全等的Rt△拼成的图形,你能用它证明勾股定理吗 参考答案:由S大正方形=4S Rt△+S小正方形,得 c2=4× 1 2 ab+(b-a)2 ∴a2+b2=c2. 4.如图,是由四个全等的Rt△拼成的图形,你能用它证明勾股定理吗 参考答案:由S大正方形=4S Rt△+S小正方形,得 (a+b)2=4× 1 2 ab+c2 ∴a2+b2=c2. 5.如图,已知∠A=∠B=90°且△AED≌△BCE,A、E、B在同一直线上.根据此图证明勾股定理. 参考答案:先证明△DCE是等腰直角三角形,再根据梯形面积为三个三角形面积之和得 1 2(a+b)2=2× 1 2 ab+ 1 2 c2, ∴a2+b2=c2. 6.如图,一个直立的火柴盒倒下来就可以证明勾股定理,请你根据图形,设计一种证明方法. 参考答案:方法类似第5题. 7.(2011温州)我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1—1).图1—2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图1—2中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是 . 参考答案:10 3 8.(2010 湖北孝感)[问题情境 ] B A a 图2 图1 c b a
勾股定理(毕达哥拉斯定理)及各种证明方法
勾股定理(毕达哥拉斯定理) 是一个,是人类早期发现并证明的重要数学定理之一,用思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。是的一个特例。约有400种证明方法,是数学定理中证明方法最多的之一。“”是勾股定理最基本的公式。勾股数组方程a 2+b 2=c 2的正整数组(a ,b ,c )。(3,4,5)就是。也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a 2+b 2=c 2,即直角三角形两直角边的平方和等于斜边的平方。 勾股定理 命题1如果的两条直角边长分别为a ,b ,斜边长为c ,那么 。 勾股定理的逆定理 命题2如果的三边长a ,b ,c 满足 ,那么这个三角形是直角三角形。 【证法1】(赵爽证明) 以a 、b 为直角边(b>a ),以c 为斜边作四个全等的直角三角形,则每 个直角三角形的面积等于2 1ab.把这四个直角三角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB. ∵∠HAD+∠HAD=90o,∴∠EAB+∠HAD=90o, ∴ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵EF=FG=GH=HE=b―a,∠HEF=90o. ∴EFGH 是一个边长为b―a 的正方形,它的面积等于. ∴ ∴. 【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a+b ,所以面积相等. 即,整理得. 【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵RtΔEAD≌RtΔCBE,∴∠ADE=∠BEC. ∵∠AED+∠ADE=90o,∴∠AED+∠BEC=90o.∴∠DEC=180o―90o=90o. ∴ΔDEC 是一个等腰直角三角形,它的面积等于 .又∵∠DAE=90o,∠EBC=90o,∴AD∥BC.∴ ABCD 是一个直角梯形,它的面积等于 ∴.∴.
勾股定理16种证明方法
v1.0 可编辑可修改 【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C 、G 、 D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.
v1.0 可编辑可修改 ∴∠HGD = ∠EHA. ∵∠HGD + ∠GHD = 90o, ∴∠EHA + ∠GHD = 90o. 又∵∠GHE = 90o, ∴∠DHA = 90o+ 90o= 180o. ∴ ABCD是一个边长为a + b的正方形,它的面积等于()2b a+. ∴()2 2 2 1 4c ab b a+ ? = + . ∴2 2 2c b a= +. 【证法3】(赵爽证明) 以a、b 为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角 三角形的面积等于 ab 2 1 . 把这四个直角三 角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE, ∴∠HDA = ∠EAB. ∵∠HAD + ∠HAD = 90o, ∴∠EAB + ∠HAD = 90o, ∴ ABCD是一个边长为c的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a , ∠HEF = 90o. ∴ EFGH是一个边长为b―a的正方形,它的面积等于()2a b-. ∴ ()2 2 2 1 4c a b ab= - + ? .
(完整版)勾股定理解答证明题
《勾股定理》证明解答题练习 1、在ABC ?中,AC AB =,D 为BC 边上任一点,求证:DC BD AD AB ?=-2 2 2、已知:如图,在ABC Rt ?中,ο 90=∠C ,D 是AC 的中点,AB ED ⊥于E 求证:(1)2 2 2 43BD BC AB =+ (2)2 2 2 BC AE BE =- 3、如图,在ABC ?中,ο 90=∠C ,13=AB ,12=BC ,BC BD 2 1 = (1)AD 的长. (2)ABD ?的面积. 4、求边长为a 的等边三角形的高和面积 2 5、如图,有一个直角三角形纸片,两直角边AC=6cm ,BC=8cm ,现将直角边AC 沿直线AD 折叠, 3 使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗? B C A C B B C
6、若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状. 7、已知:如图, ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A。 求:BD的长。(8分) 8、甲、乙两船同时从港口A出发,甲船一12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行。2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小时多少海里?9.如图所示,四边形ABCD中,AB=4,BC=3,AD=13,CD=12,∠B=90°,?求该四边形的面积. B C A D 10.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积. 11.如图,某购物中心在会十.一间准备将高5 m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱? 5m 13m 8m 20m
勾股定理逆定理八种证明方法
证法1 作四个全等的直角三角形,把它们拼成如图那样的一个多边形,使D、E、F在一条直线上(设它们的两条直角边长分别为a、b ,斜边长为c.)。过点C作AC 的延长线交DF于点P. ∵ D、E、F在一条直线上,且RtΔGEF ≌ RtΔEBD, ∴∠EGF = ∠BED, ∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180°―90°= 90° 又∵ AB = BE = EG = GA = c, ∴ ABEG是一个边长为c的正方形。 ∴ ∠ABC + ∠CBE = 90° ∵ RtΔABC ≌ RtΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90° 即∠CBD= 90° 又∵ ∠BDE = 90°,∠BCP = 90°,BC = BD = a. ∴ BDPC是一个边长为a的正方形。 同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则 证法2 作两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),做一个边长为c的正方形。斜边长为c. 再把它们拼成如图所示的多边形,使E、A、C三点在一条直线上. 过点Q作QP∥BC,交AC于点P. 过点B作BM⊥PQ,垂足为M;再过点F作FN⊥PQ,垂足为N. ∵ ∠BCA = 90°,QP∥BC, ∴ ∠MPC = 90°, ∵ BM⊥PQ, ∴ ∠BMP = 90°, ∴ BCPM是一个矩形,即∠MBC = 90°。 ∵ ∠QBM + ∠MBA = ∠QBA = 90°,∠ABC + ∠MBA = ∠MBC = 90°, ∴ ∠, 又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c, ∴ RtΔBMQ ≌ RtΔBCA. 同理可证RtΔQNF ≌ RtΔAEF.即 证法3 作两个全等的直角三角形,同证法2,再作一个边长为c的正方形。把它们拼成如图所示的多边形. 分别以CF,AE为边长做正方形FCJI和AEIG, ∵EF=DF-DE=b-a,EI=b, ∴FI=a, ∴G,I,J在同一直线上,
勾股定理的证明方法
勾股定理的证明方法 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】
勾股定理的证明方法 勾股定理是初等几何中的一个基本定理。这个定理有十分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴趣,因为这个定理太贴近人们的生活实际,以至于古往今来,下至平民百姓,上至帝王总统都愿意探讨和研究它的证明.下面结合几种图形来进行证明。 一、传说中毕达哥拉斯的证法(图1) 左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为、,斜边为的直角三角形拼成的。右边的正方形是由1个边长为的正方形和4个直角边分别为、,斜边为的直角三角形拼成的。因为这两个正方形的面积相等(边长都是),所以可以列出等式 ,化简得。 在西方,人们认为是毕达哥拉斯最早发现并证明这一定理的,但遗憾的是,他的证明方法已经失传,这是传说中的证明方法,这种证明方法简单、直观、易懂。 二、赵爽弦图的证法(图2) 第一种方法:边长为的正方形可以看作是由4个直角边分别为、,斜边为的直
角三角形围在外面形成的。因为边长为的正方形面积加上4个直角三角形的面积等于外围正方形的面积,所以可以列出等式,化简得。 第二种方法:边长为的正方形可以看作是由4个直角边分别为、,斜边为的 角三角形拼接形成的(虚线表示),不过中间缺出一个边长为的正方形“小洞”。 因为边长为的正方形面积等于4个直角三角形的面积加上正方形“小洞”的面积,所以可以列出等式,化简得。 这种证明方法很简明,很直观,它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神,是我们中华民族的骄傲。 三、美国第20任总统茄菲尔德的证法(图3) 这个直角梯形是由2个直角边分别为、,斜边为的直角三角形和1个直角边为 的等腰直角三角形拼成的。因为3个直角三角形的面积之和等于梯形的面积,所以可以列出等式,化简得。
勾股定理(毕达哥拉斯定理)及各种证明方法
勾股定理(毕达哥拉斯定理)及 各种证明方法 勾股定理(毕达哥拉斯定理) 勾股定理是一个初等几何定理,是人类早期 发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。勾股定理是余弦定理的一个特例。勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。“勾三股四弦五”是勾股定理最基本的公式。勾股数组方程a2 + b2= c 2的正整数组(a, b, c)。(3,4,5)就是勾股数。也就是说,设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2,即直角三角形两直角边的平方和
等于斜边的平方。 勾股定理 命题1如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么”+b— 勾股定理的逆定理 命题2如果三角形的三边长a,b,c满足 = 3,那么这个三角形是直角三角形。
【证法1】(赵爽证明) 全等的直角三角形,则每个直角三角形的面积等 V Rt △ DAH 今 Rt △ ABE, A ZHDA = ZEAB ? ??? ZHAD + ZHAD = 90°, :. ZEAB + ZHAD = 【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边 长分别为a 、b,斜边长为c,再做三个边长分别 以a 、b 为直角边(b>a ), 以c 为斜边作四个 于冲 把这四个直角三角形拼成如图所示形状 . 90°,
为a、b、c的正方形,把它们像上图那样拼 成两个正方形?从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即,整理得宀F八 【证法3】(1876年美国总统Garfield 证明)以a、b为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于 >.把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上? ??? Rt △ EAD也Rt △ CBE,「? / ADE = / BEC. ??? / AED + / ADE = 90o,二 / AED + / BEC = 90o.二 / DEC = 180c—90o= 90o. ??? △ DEC是一个等腰直角三角形,它的面积等于
勾股定理16种经典证明方法
ab c ab b a 2 1421422 2 ?+=?++ 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21 . 把这四个直角三 角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2 . ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +.
∴ ()2 22 4c ab b a +?=+. ∴ 2 22c b a =+. 【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角 三角形的面积等于ab 21 . 把这四个直角三 角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB . ∵ ∠HAD + ∠HAD = 90o, ∴ ∠EAB + ∠HAD = 90o, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2 . ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90o. ∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2 a b -. ∴ ()2 2 214c a b ab =-+?. ∴ 2 22c b a =+. 【证法4】(1876年美国总统Garfield 证明) 以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21 . 把这两个直角三 角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC . ∵ ∠AED + ∠ADE = 90o, ∴ ∠AED + ∠BEC = 90o. ∴ ∠DEC = 180o―90o= 90o. ∴ ΔDEC 是一个等腰直角三角形, 它的面积等于2 21c .
八年级数学上册第一章勾股定理探索勾股定理勾股定理的发现与证明素材新版北师大
勾股定理的发现与证明 中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话: 周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地的数据呢?” 商高回答说:“数的产生来源于对方和圆这些形体的认识。其中有一条原理:当直角三角形的一条直角边‘勾’等于3,另一条直角边‘股’等于4的时候,那么它的斜边‘弦’就必定是5。这个原理是大禹在治水的时候就总结出来的呵。” 从上面所引的这段对话中,我们可以清楚地看到,我国古代的人民早在几千年以前就已经发现并应用勾股定理这一重要的数学原理了。稍懂平面几何的读者都知道,所谓勾股定理,就是指在直角三角形中,两条直角边的平方和等于斜边的平方。 勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年首先发现的。其实,我国古代得到人民对这一数学定理的发现和应用,远比毕达哥拉斯早得多。如果说大禹治水因年代久远而无法确切考证的话,那么周公与商高的对话则可以确定在公元前1100年左右的西周时期,比毕达哥拉斯要早了五百多年。其中所说的勾3股4弦5,正是勾股定理的一个应用特例(32+42=52)。所以现在数学界把它称为勾股定理,应该是非常恰当的。 在稍后一点的《九章算术一书》中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说;“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合的方法,给出了勾股定理的详细证明。 赵爽的这个证明可谓别具匠心,极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。以后的数学家大多继承了这一风格并且代有发展。例如稍后一点的刘徽在证明勾股定理时也是用的以形证数的方法,只是具体图形的分合移补略有不同而已。 中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位。尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义。事实上,
