中考数学专题复习一线三角三等角型

“一线三等角”基本图形解决问题

三角形相似在整个初中数学中有着重要的地位，在学习三角形相似形时，我们从复杂图形中分离出基本数学模型，对分析问题、解决问题有化繁为简的效果。在近几年的中考题中，经常可以看到“一线三等角”的数学模型，所谓“一线三等角”是指在一条直线上出现了三个角相等。所以，只要见到一条直线上出现了三个等角，往往都存在这样的模型，也会存在相似三角形，当出现了有相等边的条件之后，相似就转化为全等了，综合性题目往往就会把相似和全等的转化，作为出题的一种形式，需要大家注意。本文将重点对这一基本图形进行探讨。通过对题目的有效分解，打破同学们对综合题的畏惧心理，让同学们加深对于题目条件的使用：条件用完，即使题目没有求解完毕，也得到相应的分数，提高问题解决的能力，在这个师生共同探讨的过程中鼓励学生尝试解题，并加强题后反思，培养他们解题的能力。 一、知识梳理：

（1）四边形ABCD 是矩形，三角板的直角顶点M 在BC 边上运动，直角边分别与射线BA 、射线CD 交于E 、F ，在运动过程中，△EBM ∽△MCF.

（2）如图1：已知三角形ABC 中，AB=AC,∠ADE=∠B,那么一定存在的相似三角形有 △ABD ∽△DEC. 如图2：已知三角形ABC 中，AB=AC,∠DEF=∠B,那么一定存在的相似三角形有△DBE ∽△ECF.

（图1） （图2） 二、【例题解析】

【例1】(2014四川自贡）阅读理解： 如图1，在四边形ABCD 的边AB 上任取一点E （点E 不与点A 、点B 重合），分别连接ED ，EC ，可以把四边形ABCD 分成三个三角形，如果其中有两个三角形相似，我们就把E 叫做四边形ABCD 的边AB 上的相似点；如果这三个三角形都相似，我们就把E 叫做四边形ABCD 的边AB 上的强相似点．解决问题：

（1）如图1，∠A=∠B=∠DEC=55°，试判断点E 是否是四边形ABCD 的边AB 上的相似点，并说明理由；

（2）如图2，在矩形ABCD 中，AB=5，BC=2，且A ，B ，C ，D 四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD 的边AB 上的一个强相似点E ；

3

21F

D B M C

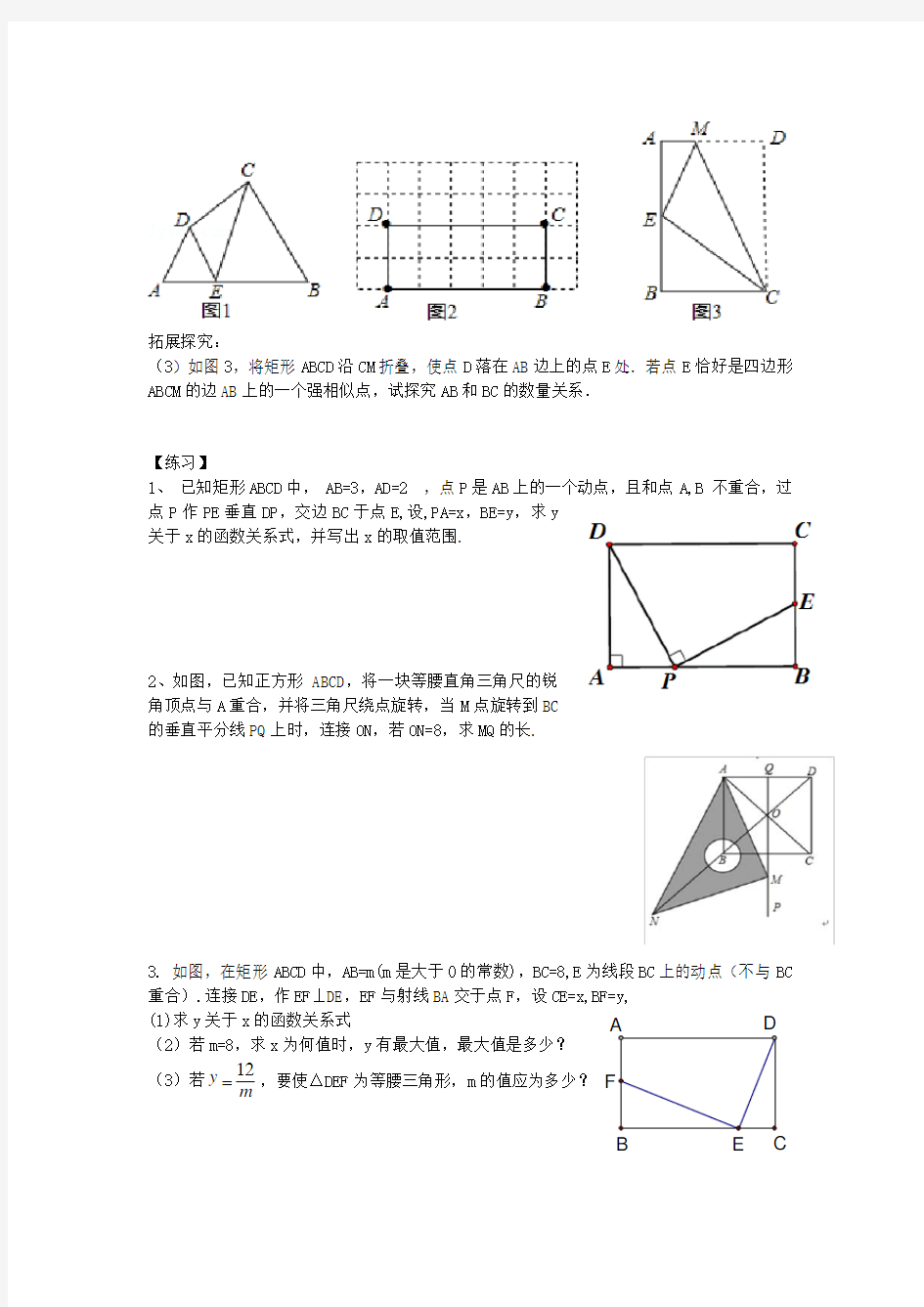
拓展探究：

（3）如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB和BC的数量关系．

【练习】

1、已知矩形ABCD中， AB=3，AD=2，点P是AB上的一个动点，且和点A,B 不重合，过点P作PE垂直DP，交边BC于点E,设,PA=x，BE=y，求y

关于x的函数关系式，并写出x的取值范围.

2、如图，已知正方形ABCD，将一块等腰直角三角尺的锐

角顶点与A重合，并将三角尺绕点旋转，当M点旋转到BC

的垂直平分线PQ上时，连接ON，若ON=8，求MQ的长.

3. 如图，在矩形ABCD中，AB=m(m是大于0的常数)，BC=8,E为线段BC上的动点（不与BC 重合）.连接DE，作EF⊥DE，EF与射线BA交于点F，设CE=x,BF=y,

(1)求y关于x的函数关系式

（2）若m=8，求x为何值时，y有最大值，最大值是多少？

（3）若

12

y

m

，要使△DEF为等腰三角形，m的值应为多少？

A

B E

【例2】等边△ABC 边长为6，P 为BC 边上一点，∠MPN =60°，且PM 、PN 分别于边AB 、AC

交于点E 、F .

（1）如图1，当点P 为BC 的三等分点，且PE ⊥AB 时，判断△EPF 的形状；

（2）如图2，若点P 在BC 边上运动，且保持PE ⊥AB ，设BP =x ，四边形AEPF 面积的y ，

求y 与x 的函数关系式，并写出自变量x 的取值范围；

（3）如图3，若点P 在BC 边上运动，且∠MPN 绕点P 旋转，当CF =AE =2时，求PE 的长.

图1 图2 图3

分析过程：（1）△EPF 为等边三角形. （2）设BP=x ，则CP ＝6－x. 由题意可 △BEP 的面积为

238x .△CFP 的面积为

23(6)2

x -.△ABC 的面积为93. 设四边形AEPF 的面积为y. ∴93y =-

238x 23(6)2x --=25

363938

x x -+-. 自变量x 的取值范围为3＜x ＜6. （3）可证△EBP ∽△PCF.∴

BP BE

CF CP

=

.设BP=x ， 则 (6)8x x -=. 解得 124,2x x ==.∴ PE 的长为4或23.

【练习】.如图，在△ABC 中，AB =AC =5cm ，BC =8，点P 为BC 边上一动点（不与点B 、C 重合），过点P 作射线PM 交AC 于点M ，使∠APM =∠B ； （1）求证：△ABP ∽△PCM ；

（2）设BP =x ，CM =y ．求 y 与x 的函数解析式，并写出自变量的取值范围． （3）当△APM 为等腰三角形时，求PB 的长．

（4) 当点D 是BC 的中点时，试说明△ADE 是什么三角形，并说明理由．

A P M

【例3】在ABC ?中，O BC AC C ,3,4,90===∠o

是AB 上的一点，且

5

2

=AB AO ，点P 是AC 上的一个动点，OP PQ ⊥交线段BC 于点Q ，（不与点B,C 重合），已知AP=2，求CQ

【练习】在直角三角形ABC 中，D BC AB C ,,90==∠o

是AB 边上的一点，E 是在AC 边上的一个动点，（与A,C 不重合），DF DE DF ,⊥与射线BC 相交于点F. (1)、当点D 是边AB 的中点时，求证：DF DE = (2)、当m DB

AD

=，求DF DE 的值

【例4】如图，抛物线y=ax 2

+bx+c 经过点A(﹣3，0)，B(1.0)，C(0，﹣3)．

(1)求抛物线的解析式；

(2)若点P 为第三象限内抛物线上的一点，设△PAC 的面积为S ，求S 的最大值并求出此时点P 的坐标；

(3)设抛物线的顶点为D ，DE ⊥x 轴于点E ，在y 轴上是否存在点M ，使得△ADM 是直角三角形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．

答案：(1)y=x2+2x ﹣3；(2)S 有最大值827，点P 的坐标为（23-，4

15-）； (3)M 的坐标为（0，

23）或（0，2

7

-）或（0，﹣1）或（0，﹣3）.

课后作业：

1. 已知：如图，在△ABC 中，5==AC AB ，6=BC ，点D 在边AB 上，AB DE ⊥，

点E 在边BC 上．又点F 在边AC 上，且B DEF ∠=∠． (1) 求证：△FCE ∽△EBD ； (2) 当点D 在线段AB 上运动时，是否有可能使EBD FCE S S ??=4．

如果有可能，那么求出BD 的长．如果不可能请说明理由．

2. 如图，在△ABC 中，AB =AC =5，BC =6，P 是BC 上一点，且BP =2，将一个大小与∠B 相等

的角的顶点放在P 点，然后将这个角绕P 点转动，使角的两边始终分别与AB 、AC 相交，交点为D 、E 。

（1）求证△BPD ∽△CEP

（2）是否存在这样的位置，△PDE 为直角三角形？若存在，求出

BD 的长；若不存在，说明理由。

3. 如图，在△ABC 中，AB =AC =5，BC =6，P 是BC 上的一个动点(与B 、C 不重合)，PE ⊥AB

与E ，PF ⊥BC 交AC 与F ，设PC =x ，记PE =1y ，PF =2y （1）分别求1y 、2y 关于x 的函数关系式

（2）△PEF 能为直角三角形吗?若能，求出CP 的长，若不能，请说明理由。

4. 如图，在△ABC 中，AB =AC =5，BC =6，P 是BC 上的一个动点(与

B 、

C 不重合)，PE ⊥AB 与E ，PF ⊥BC 交AC 与F ，设PC =x ，△PEF 的面积为y

（1）写出图中的相似三角形不必证明；

（2）求y 与x 的函数关系式，并写出x 的取值范围；

（3）若△PEF 为等腰三角形，求PC 的长。

C

P

E

A

F

P

E A

D P

E A

F

A B C

D E F

5. 已知在等腰三角形ABC 中，4,6AB BC AC ===，D 是AC 的中点，E 是BC 上的动点（不与B 、C 重合），连结DE ，过点D 作射线DF ，使EDF A ∠=∠，射线DF

交射线EB 于点F ，交射线AB 于点H .

（1）求证：CED ?∽ADH ?； （2）设,EC x BF y ==. ①用含x 的代数式表示BH ；

②求y 关于x 的函数解析式，并写出x 的定义域.

6. 已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2．

（1）如图8，P 为AD 上的一点，满足∠BPC ＝∠A ． ①求证；△ABP ∽△DPC ②求AP 的长．

（2）如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么

①当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；

②当CE ＝1时，写出AP 的长（不必写出解题过程）．

H A

B

C

D

E

F

C

答案： 1. 解：（1）∵AB =AC ∴∠B =∠C

∵∠BED +∠DEF =∠C +∠EFC =90°又∵B DEF ∠=∠∴∠BED =∠EFC ∴△FCE ∽△EBD

（2）∵BD =x ，BE =

x 35，x EC 3

56-= ∵△FCE ∽△EBD ∴

2

)(BD

EC S S BED FEC =??若EBD FCE

S S ??=4∴4)35

6(

2=-x

x

∴1118=x ∴311

36

356>=-

x ∴BD 不存在 2. 解：（1）∵AB =AC ∴∠B =∠C

∵∠DPC =∠DPE +∠EPC =∠B +∠BDP ∴∠EPC =∠BDP ∴△ABD ∽△DCE （2）∵∠DPE =∠B ≠90°

若∠PDE=90°，在Rt△ABH 和Rt△PDE 中

∴cos ∠ABH =cos ∠DPE =53==PE PD AB BH ∴53

==PC BD PE PD

∵PC =4 ∴5

12

=BD

若∠PED=90°在Rt△ABH 和Rt△PDE 中

∴cos ∠ABH =cos ∠PED =

53==PD PE AB BH ∴35

==PC BD PE PD ∵PC =4 ∴53

20

>=BD （舍去）

综上所述，BD 的长为5

12

3. 解：（1）52454)6(541+-=-=x x y 、x y 3

4

2=

（2）∵∠FPE =∠B ≠90°

若∠PFE =90°，在Rt△ABH 和Rt△PFE 中 ∴cos ∠ABH =cos ∠FPE =

53==PE PF AB BH ∴

5

3

12=y y ∴535

245434=

+-x x ∴17

27

=x 若∠PEF =90°，在Rt△ABH 和Rt△PFE 中 ∴cos ∠ABH =cos ∠FPE =

53

==PE PF AB BH ∴

3

512=y y ∴355

245434=+-x x

∴3=x 4. 解：（1）△PEB ∽△EPC （2）∵PC =x ∴x PF 34=

，)6(54x PE -=，)6(25

1654x EP EH -== P E

A

D

H C

P E

A B

D

H

C

P

E

A B F

H

C

P

E

A

B

F

H C E A

B

F

H

M

∴)6(75

32)6(2516342121x x x x EH PF y -=-??=??=

即x x y 25

64

75322+-=)30(≤

（3）当PE =PF 时，△EPC ≌△PEB ，PC =BE =x ，536=-x x ∴4

9

=x

当PE =EF 时，x PF PH 3221==，cos ∠EPH =cos B ，53)6(5

432=-x x

∴43108=x

当FE =PF 时，)6(5

2

21x EP PM -==， cos ∠FPM =cos B ，533

4)

6(52

=-x x ∴2=x 综上所述，PC 的长分别为49=x 、43

108

、2

5. 解：（1）∵AB BC =,∴A C ∠=∠∵CDE EDF A H ∠+∠=∠+∠

又EDF A ∠=∠,∴CDE H ∠=∠CED ∴?∽ADH ?

（2）①∵CED ?∽ADH ?，∴CE CD

AD AH

=

∵D 是AC 的中点，6AC =，∴3AD CD ==，又 ∵,4CE x AB ==

∴当H 点在线段AB 的延长线上时，

334x BH =

+，∴9

4BH x

=- 当H 点在线段AB 上时，334x BH =-，∴9

4BH x

=-

②过点D 作DG ∥AB ,交BC 于点G

∴12

DG CG CD AB BC AC ===，∴2,2DG BG == ∴当H 点在线段AB 的延长线上时，∴BH BF

GD GF

=

，∴94

22y x y -=-∴18890924x y x x -??

=

<< ?-??

当H 点在线段AB 上时，∴

BH BF

GD GF

=，∴942

2

y

x y -=

+∴81894924x y x x -??

=

≤< ?-??