三视图还原

三视图问题
解决三视图问题,尤其是一些比较复杂的三视图还原问题,需要极强的空间想象能力.这给好多同学(包括一些空间想象能力挺强的同学)造成了一定的压力,如果在高考中碰到一个稍有些不常规的三视图,绝对会给在高考中以数学成绩为倚傍的同学设置了一道拦路虎,要是稍微一心慌,那我们与这一道5分题就失之交臂了,也会给后面的答题造成心理影响.比如2014年全国1卷第12题,当时就将相当大一部分同学斩于马下.本文就三视图还原总结为“三线交汇得顶点”现从这道高考题入手.
2014年高考全国I 卷理科第12题:如图,网格纸上小正方形
的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各
条棱中,最长的棱的长度是()
A.B.6 C.D.4
正确答案是B.
解:由三视图可知,原几何体的长、宽、高均为4,所以我们可用一个正
方体作为载体对三视图进行还原.先画出一个正方体,如图(1):
第一步,根据正视图,在正方体中画出正视图上的四个顶点的原象所在
的线段,这里我们用红线表示.如图(2),即正视图的四个顶点必定是由图
中红线上的点投影而成的.
第二步,侧视图有三个顶点,画出它们的原象所在的线段,
用蓝线表示,如图(3).
第三步,俯视图有三个顶点,画出它们的原象所在的线段,
用绿线表示,如图(4).
最后一步,三种颜色线的公共点(只有两种颜色线的交点不
行)即为原几何体的顶点,连接各顶点即为原几何体,如图(5).至
此,易知哪条棱是最长棱,求出即可
大家是不是体会到了用这种方法还原三视图的妙处呢?这种方法的核心其实就是七个字:“三线交汇疑似点,虚实搭配真顶点”.这样是不是比我们以前那种天马行空的遐想接地气一些呢?由此,我们在三视图还原上就可以七字真言扫天下了.
此方法更适用于解决三棱锥的问题,画直观图后需要验证一下是否符合。
由三视图画直观图的方法
由立体图形的三视图想象直观图一向是诸多考试的必考项目,而这也
恰好是很多空间想象能力不足的同学的噩梦.其实利用三视图的原理可以
很有效的帮助直观图的建立,下面结合一例说明这一方法,
三视图选自2015年北京市东城区高三一模理科数学选择第7小题.
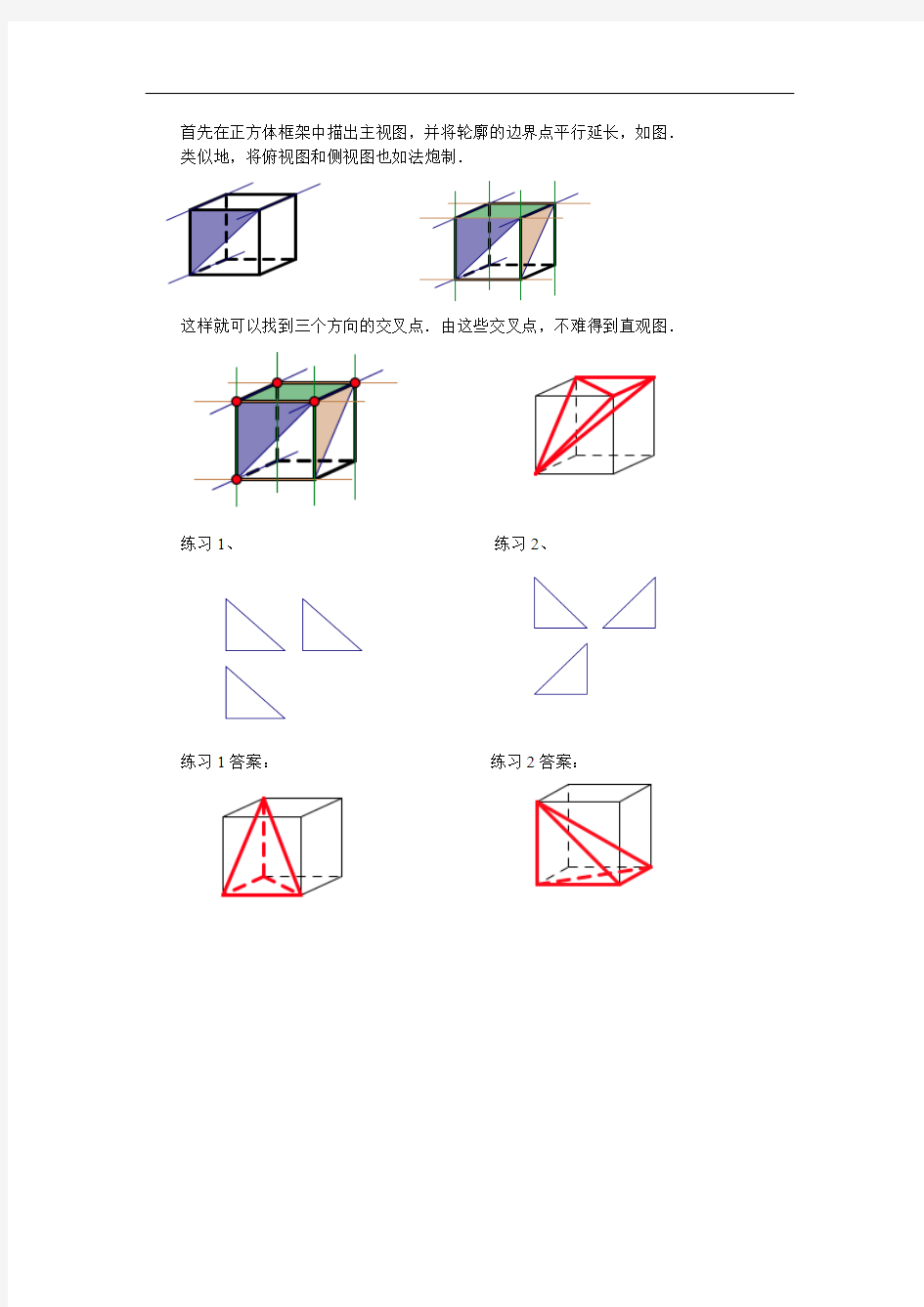
首先在正方体框架中描出主视图,并将轮廓的边界点平行延长,如图.类似地,将俯视图和侧视图也如法炮制.
这样就可以找到三个方向的交叉点.由这些交叉点,不难得到直观图.
练习1、练习2、
练习1答案:练习2答案:
(完整版)(经典)高考数学三视图还原方法归纳
高考数学三视图还原方法归纳 方法一:还原三步曲 核心内容: 三视图的长度特征——“长对齐,宽相等,高平齐” ,即正视图和左视图一样高,正视图和俯视图一样长,左视图和俯视图一样宽。 还原三步骤: (1)先画正方体或长方体,在正方体或长方体地面上截取出俯视图形状; (2)依据正视图和左视图有无垂直关系和节点,确定并画出刚刚截取出的俯视图中各节点处垂直拉升的线条(剔除其中无需垂直拉升的节点,不能确定的先垂直拉升),由高平齐确定其长短; (3)将垂直拉升线段的端点和正视图、左视图的节点及俯视图各个节点连线,隐去所有的辅助线条便可得到还原的几何体。 方法展示 1)将如图所示的三视图还原成几何体 还原步骤: ①依据俯视图,在长方体地面初绘ABCDE如图; ②依据正视图和左视图中显示的垂直关系,判断出在节点A、B、C、D 处不可能有垂直拉升的线条,而在E 处必有垂直拉升的线条ES,由正视图和侧视图中高度,确定点S 的位置;如图 ③将点S 与点ABCD分别连接,隐去所有的辅助线条,便可得到还原的几何体S-ABCD如图所示:
答案: 21+ 3 计算过程 经典题型: 例题 1:若某几何体的三视图,如图所示,则此几何体的体积等于( )cm3 。 例题 2:一个多面体的三视图如图所示,则该多面体的表面积为( 解答:(24)
步骤如下: 第一步:在正方体底面初绘制ABCDEFMN如图; 第二步:依据正视图和左视图中显示的垂直关系,判断出节点E、F、M、N 处不可能有垂直拉升的线条,而在点A、B、C、D处皆有垂直拉升的线条,由正视图和左视图中高度及节点确定点G,G',B',D',E',F 地位置如图; 第三步:由三视图中线条的虚实,将点G与点E、F分别连接,将G'与点E'、F'分别连接,隐去所有的辅助线便可得到还原的几何体,如图所示。 例题3:如图所示,网格纸上小正方形的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是()
三视图还原技巧
三视图还原解读 解决三视图问题,尤其是一些比较复杂的三视图还原问题,需要极强的空间想象能力.这给好多同学(包括一些空间想象能力挺强的同学)造成了一定的压力,如果在高考中碰到一个稍有些不常规的三视图,绝对会给在高考中以数学成绩为倚傍的同学设置了一道拦路虎,要是稍微一心慌,那我们与这一道5分题就失之交臂了,也会给后面的答题造成心理影响.比如2014年全国1卷第12题,当时就将相当大一部分同学斩于马下.本文就三视图还原总结为“三线交汇得顶点”现从这道高考题入手. 2014年高考全国I 卷理科第12题:如图,网格纸上小正方形 的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各 条棱中,最长的棱的长度是() A.B.6 C.D.4 正确答案是B. 解:由三视图可知,原几何体的长、宽、高均为4,所以我们可用一个正 方体作为载体对三视图进行还原.先画出一个正方体,如图(1): 第一步,根据正视图,在正方体中画出正视图上的四个顶点的原象所在 的线段,这里我们用红线表示.如图(2),即正视图的四个顶点必定是由图 中红线上的点投影而成的. 第二步,侧视图有三个顶点,画出它们的原象所在的线段, 用蓝线表示,如图(3). 第三步,俯视图有三个顶点,画出它们的原象所在的线段, 用绿线表示,如图(4). 最后一步,三种颜色线的公共点(只有两种颜色线的交点不 行)即为原几何体的顶点,连接各顶点即为原几何体,如图(5).至 此,易知哪条棱是最长棱,求出即可 大家是不是体会到了用这种方法还原三视图的妙处呢?这种方法的核心其实就是七个字:“三线交汇得顶点”.这样是不是比我们以前那种天马行空的遐想接地气一些呢?由此,我们在三视图还原上就可以七字真言扫天下了. 此方法更适用于解决三棱锥的问题,画直观图后需要验证一下是否符合。 由三视图画直观图的方法 由立体图形的三视图想象直观图一向是诸多考试的必考项目,而这也 恰好是很多空间想象能力不足的同学的噩梦.其实利用三视图的原理可以 很有效的帮助直观图的建立,下面结合一例说明这一方法, 三视图选自2015年北京市东城区高三一模理科数学选择第7小题.
三视图还原大招秒杀技巧
大招一:三视图还原之两大核心方法 方法一:“三线交汇得定点”(三线法) 如图:网格纸上小正方形的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是() 【答案】B 【解析】由三视图可知,原几何体的长、宽、高均为4,所以我们可以用一个正方体作为载体对三视图进行还原,先画出一个正方体,如图(1) 图(1) 第一步,根据正视图,在正方体中画出正视图上的四个顶点的原像所在的线段,如图(2)。 图(2)
第二步:侧视图有三个顶点,画出他们的原像所在的线段,如图(3) 图(3) 第三步:俯视图有三个顶点,画出他们的原像所在的线段,如图(4) 图(4) 最后一步,如图5,至此,易知哪条棱是最长的棱,求出即可。 图(5)
方法二 通过三视图在长方体中排除不符合的点(排点法) 已知一个三棱锥的三视图如图所示,他们都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )个。 【答案】4 【解析】第一步:画出一个长方体(或正方体)。 其中是否是为正方形或长方形,根据三视图中的各边长度来决定。 第二步:把俯视图画在底面。 (1) 底面是一个三角形,其中有三个点,分别为B,C,D 三个点,标 出这三个点。 (2) 对应的标出,B D ,,,C ,三个点,即这六个点是我们的研究对象。 正视图、俯视图出现的交点也是研究对象。 第三步:研究正视图和侧视图
(1)把正视图放在矩形中发现,B,,, C即为无关 C两点空缺,B,,,点,则把这两点画掉。 正视图 (2) 正视图中左上点其实代表正方体中的,,D A线,这条线只有,D点 是我们的研究对象,即,D点为有关点,则留下,D点。 (3)正视图中的左下点其实代表正方体中的A-D这条线,这条线只有D点事我们的研究对象,即D为有关点,则留下D点。 (4)同理,正视图中右下角这个点代表正方体中的B-C这条线,B,C 两点都可能存在,即为可能点,则分析B,C两点。 侧视图 同理:观察侧视图,注意侧视图的方位,“左里右外”方法和观察正视图的方法一样。 四个点逐个分析,最后留下有关点,该题有关点为,D,B,C,D四个点。第四步:分别连接相邻的点(原先俯视图画出的点及提高到上面的点),原俯视图上的点B,C,D及提高点,D,按顺序连接得到下图:
(完整版)三视图还原技巧
核心内容: 三视图的长度特征——“长对齐,宽相等,高平齐”,即正视图和左视图一样高,正视图和俯视图一样长,左视图和俯视图一样宽。 还原三步骤: (1)先画正方体或长方体,在正方体或长方体地面上截取出俯视图形状;(2)依据正视图和左视图有无垂直关系和节点,确定并画出刚刚截取出的俯视图中各节点处垂直拉升的线条(剔除其中无需垂直拉升的节点,不能确定的先垂直拉升),由高平齐确定其长短; (3)将垂直拉升线段的端点和正视图、左视图的节点及俯视图各个节点连线,隐去所有的辅助线条便可得到还原的几何体。 方法展示 (1)将如图所示的三视图还原成几何体。 还原步骤: ①依据俯视图,在长方体地面初绘ABCDE如图; ②依据正视图和左视图中显示的垂直关系,判断出在节点A、B、C、D处不可能有垂直拉升的线条,而在E处必有垂直拉升的线条ES,由正视图和侧视图中高度,确定点S的位置;如图
③将点S与点ABCD分别连接,隐去所有的辅助线条,便可得到还原的几何体S-ABCD如图所示: 经典题型: 例题1:若某几何体的三视图,如图所示,则此几何体的体积等于()cm3。 解答:(24) 例题2:一个多面体的三视图如图所示,则该多面体的表面积为()
答案:21+3 计算过程: 步骤如下: 第一步:在正方体底面初绘制ABCDEFMN 如图; 第二步:依据正视图和左视图中显示的垂直关系,判断出节点E 、F 、M 、N 处不可能有垂直拉升的线条,而在点A 、B 、C 、D 处皆有垂直拉升的线条,由正视图和左视图中高度及节点确定点''''',,,,,F E D B G G 地位置如图; 第三步:由三视图中线条的虚实,将点G 与点E 、F 分别连接,将'G 与点'E 、'F 分别连接,隐去所有的辅助线便可得到还原的几何体,如图所示。
三视图还原万能方法
三视图还原 ——七字真言闯天下 一、首先要掌握简单几何体的三视图。 正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆台和球的三视图分别是什么要熟悉掌握。 二、掌握简单组合体的组合形式。 简单组合体主要有拼接和挖去两种形式。 三、三视图之间的关系。 几何体的长:正视图、俯视图的长; 几何体的宽:俯视图的高、侧视图的长; 几何体的高:正视图、侧视图的高。 (口诀:主俯定长,俯左定宽,主左定高)(下面) 左视左侧(后面)正视左侧 (左面)正视右侧 (右面)左视右侧(前面) (下面) 四、清楚三视图各个线段说表示几何体位置,如上图所表示。 五、由三视图画出直观图的步骤和思考方法。 1、组合类题型,往往很简单,基本可以通过简单想象直接还原; 2、有两个视角为三角形,为椎体特征。选择底面还原(求体积可不用还原); 3、凡是想不出来的,可用七字真言还原。(不到万不得已,不用此法) 前面 俯视左侧 (左面)
【类型一】:(三线交汇得顶点,四顶相连无悬念)
例2: 练习1练习2 类型二】: (三线交汇得顶点,各顶必在其中选、多顶可能用不完,个中取舍是关键。)例3:
连接这五个点的四棱锥,不满足俯视图。 而顶点又必须在这五点交点中, 所以当点数超过4个,可能不需要全部连接, 则这些点有所取舍。 第一取舍法:俯视图看到的面不可以为上面四个点构成的整个四边形,而是中间有一条折痕,故只能说左半边三角形乡下折。即舍弃前面左上方的点。 故得, 第二取舍法:正视图看,已标记下面的点必不可少; 从俯视图看,上面有3个点必不可少; 又不能全部连接,故只能舍弃前面左上方的点。 第三取舍法:口诀:实线两端的点保留,虚线两端的点待定。 从俯视图一看,便知道答案了。 第四取舍法:见下文。 【类型三】:(八点齐飞,直观图不唯一) 例4 此题八点齐飞,通过类型二中的第三取舍法,我们很容易就能还原出来。 答案见下一页,先试试再翻页吧
三视图还原几何体的方法
三视图还原——xyz 定位法 一、首先要掌握简单几何体的三视图。 正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆台和球的三视图分别是什么要熟悉掌握。 二、掌握简单组合体的组合形式。 简单组合体主要有拼接和挖去两种形式。 三、三视图之间的关系。 几何体的长:正视图、俯视图的长; 几何体的宽:俯视图的高、侧视图的长; 几何体的高:正视图、侧视图的高。 (口诀:主俯定长,俯左定宽,主左定高)(下面) 左视左侧(后面)正视左侧 (左面)正视右侧 (右面)左视右侧(前面) (下面) 四、清楚三视图各个线段说表示几何体位置,如上图所表示。 五、由三视图画出直观图的步骤和思考方法。 1、组合类题型,往往很简单,基本可以通过简单想象直接还原; 2、有两个视角为三角形,为椎体特征。选择底面还原(求体积可不用还原); 3、凡是想不出来的,可用xyz 坐标定位法还原。 前面 俯视左侧 (左面)
【类型一】:(三线交汇) 例2:
【类型二】: 例3: 连接这五个点的四棱锥,不满足俯视图。 而顶点又必须在这五点交点中, 所以当点数超过4个,可能不需要全部连接, 则这些点有所取舍。 第一法:俯视图看到的面不可以为上面四个点构成的整个四边形,而是中间有一条折痕,故只能说左半边三角形乡下折。即舍弃前面左上方的点。 故得, 第二:唯一法:正视图看,已标记下面的点必不可少;从俯视图看,上面有3个点必不可少;故只能舍弃前面左上方的点。 第三:口诀:实线两端的点保留,虚线两端的点待定。从俯视图一看,便知道答案了。取舍关键:墙角点是取舍的备选。 练习
【类型三】:(八点齐飞,直观图不唯一) 例4 此题八点齐飞,通过类型二中的第三取舍法,我们很容易就能还原出来。 答案: 然而,我们发现这个三视图也可以看成,是上图中的三棱锥与另外一个三棱锥组合而成。如下图所示:M为顶点的三棱锥(四种)与上图的组合。 同理,还有其他两种形式,此处就不一一画图了。 由此得出,上题中的三视图至少有5种不同的直观图。 【三视图题目几点技巧】 1,部分椎体求体积,直接用公式(可以不还原) 2,斜二测画法与原图面积比例为定值(可以不还原) 3,三视图中,和视线垂直的线段,长度不变。 【反思】 对棱相等的四面体求体积,最简单的方法,就是放回长方体中。
三视图技巧
高中数学 | 三视图还原——七字真言闯天下 2016-01-20 07:29 解决三视图问题,尤其是一些比较复杂的三视图还原问题,需要极强的空间想象能力.这给好多同学(包括一些空间想象能力挺强的同学)造成了一定的压力,如果在高考中碰到一个稍有些不常规的三视图,绝对会给在高考中以数学成绩为倚傍的同学设置了一道拦路虎,要是稍微一心慌,那我们与这一道分题就失之交臂了,也会给后面的答题造成心理影响.比如2014年全国1卷第12题,当时就将相当大一部分同学斩于马下.今天小编就带领大家为曾经在类似这样的三视图还原问题上折戟沉沙的同学报仇雪恨.我们的口号是“七字真言扫天下,不破胡虏誓不归.”就从这道高考题入手吧. 2014年高考全国 I 卷理科第12题(选择压轴题): 如图,网格纸上小正方形的边长为,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是() A. B. C. D. 正确答案是 B. 解由三视图可知,原几何体的长、宽、高均为,所以我们可用一个正方体作为载体对三视图进行还原. 先画出一个正方体,如图(1): 第一步,根据正视图,在正方体中画出正视图上的四个顶点的原象所在的线段,这里我们用红线表示.如图(2),即正视图的四个顶点必定是由图中红线上的点投影而成的.
第二步,左视图有三个顶点,画出它们的原象所在的线段,用蓝线表示,如图(3). 第三步,俯视图有三个顶点,画出它们的原象所在的线段,用绿线表示,如图(4). 最后一步,三种颜色线的公共点(只有两种颜色线的交点不行)即为原几何体的顶点,连接各顶点即为原几何体,如图(5).至此,易知哪条棱是最长棱,求出即可. 大家是不是体会到了用这种方法还原三视图的妙处呢?这种方法的核心其实就是七个字:“三线交汇得顶点”.这样是不是比我们以前那种天马行空的遐想接地气一些呢?由此,我们在三视图还原上就可以七字真言扫天下了. 注一此方法更适用于解决三棱锥的问题,画直观图后需要验证一下是否符合.注二参考文章: 下面给出一道练习. 如图,网格纸上的小正方形的边长为,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为______. 答案是. 提示如图.
三视图还原几何体的方法
三视图还原为几何体的基础知识 一、 首先要掌握简单几何体的三视图。 正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆台和球的三视图分别是什么要熟悉掌握。 二、 掌握简单组合体的组合形式。 简单组合体主要有拼接和挖去两种形式。 三、 三视图之间的关系。 正视图的高是几何体的高,长是几何体的长;俯视图的长是几何体的长,宽是几何体的宽;侧视图的高是几何体的高,宽是几何体的宽。 四、清楚三视图各个线段说表示几何体位置,如上图所表示。 五、由三视图画出直观图的步骤和思考方法。
1、首先看俯视图,根据俯视图画出几何体地面的直观图 2、观察正视图和侧视图找到几何体前、后、左、右的高度。 3、画出整体,让后再根据三视图进行调整。 三视图还原为几何体的方法要点 1.熟悉正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆 台和球的三视图和还原图的转换。 2.要熟悉立体图当中底面形状为三角形、正方形、梯形、多边形、圆形的画法, 立体图的底面按照俯视图的外框用虚线画,一般后方都要向右偏,如正方形画成平行四边形、圆形画成椭圆形等 3.不能将后面的线重叠,画的时候不要把前后的2点画在一个L形直角上 4.俯视图中间是虚线说明立体图上面打下面小。 三视图还原为几何体的方法 1.首先根据俯视图确定立体图底面图形,用虚线画好; 2.根据正视图确定上顶点在左边还是右边 3.根据左视图确定上顶点在立体图的里面还是外面 4.连接顶点和底面的各点,有多个顶点时的原则是先连接各 顶点同一侧的底面点,再参考正视图中间连线情况连接顶点与另一侧的底面点; 5.根据三视图验证立体图,将立体图中能看到部分虚线画实 五、举例说明: 例如1(2011年天津高考试题)
高中数学 立体几何 10.三视图技巧
高中数学 | 三视图还原——七字真言闯天下 解决三视图问题,尤其是一些比较复杂的三视图还原问题,需要极强的空间想象能力.这给好多同学(包括一些空间想象能力挺强的同学)造成了一定的压力,如果在高考中碰到一个稍有些不常规的三视图,绝对会给在高考中以数学成绩为倚傍的同学设置了一道拦路虎,要是稍微一心慌,那我们与这一道分题就失之交臂了,也会给后面的答题造成心理影响.比如2014年全国1卷第12题,当时就将相当大一部分同学斩于马下.今天小编就带领大家为曾经在类似这样的三视图还原问题上折戟沉沙的同学报仇雪恨.我们的口号是“七字真言扫天下,不破胡虏誓不归.”就从这道高考题入手吧. 2014年高考全国 I 卷理科第12题(选择压轴题): 如图,网格纸上小正方形的边长为 ,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是( ) A .26 B .6 C .24 D .4 正确答案是 B . 解由三视图可知,原几何体的长、宽、高均为 ,所以我们可用一个正方体作为载体对三视图进行还原. 先画出一个正方体,如图(1):
第一步,根据正视图,在正方体中画出正视图上的四个顶点的原象所在的线段,这里我们用红线表示.如图(2),即正视图的四个顶点必定是由图中红线上的点投影而成的. 第二步,左视图有三个顶点,画出它们的原象所在的线段,用蓝线表示,如图(3). 第三步,俯视图有三个顶点,画出它们的原象所在的线段,用绿线表示,如图(4). 最后一步,三种颜色线的公共点(只有两种颜色线的交点不行)即为原几何体的顶点,连接各顶点即为原几何体,如图(5).至此,易知哪条棱是最长棱,求出即可.
三视图还原
每日一题[280] 三视图还原——七字真言闯天下2015年10月26日 大雨瓢泼 数海拾贝 解决三视图问题,尤其是一些比较复杂的三视图还原问题,需要极强的空间想象能力.这给好多同学(包括一些空间想象能力挺强的同学)造成了一定的压力,如果在高考中碰到一个稍有些不常规的三视图,绝对会给在高考中以数学成绩为倚傍的同学设置了一道拦路虎,要是稍微一心慌,那我们与这一道分题就失之交臂了,也会给后面的答题造成心理影响.比如2014年全国1卷第12题,当时就将相当大一部分同学斩于马下.今天小编就带领大家为曾经在类似这样的三视图还原问题上折戟沉沙的同学报仇雪恨.我们的口号是“七字真言扫天下,不破胡虏誓不归.”就从这道高考题入手吧. 2014年高考全国 I 卷理科第12题(选择压轴题): 如图,网格纸上小正方形的边长为,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是( ) A . B . C . D .正确答案是 B. 5162 √6 42 √4
解 由三视图可知,原几何体的长、宽、高均为,所以我们可用一个正方体作为载体对三视图进行还原. 先画出一个正方体,如图(1): 第一步,根据正视图,在正方体中画出正视图上的四个顶点的原象所在的线段,这里我们用红线表示.如图(2),即正视图的四个顶点必 定是由图中红线上的点投影而成的. 第二步,左视图有三个顶点,画出它们的原象所在的线段,用蓝线表 示,如图(3). 第三步,俯视图有三个顶点,画出它们的原象所在的线段,用绿线表 示,如图(4). 最后一步,三种颜色线的公共点(只有两种颜色线的交点不行)即为原几何体的顶点,连接各顶点即为原几何体,如图(5).至此,易知哪条棱是最长棱,求出即可. 4
立体几何之三视图高效还原法:拔高法,解题神级方法!
同学们,今天我们来讲一下立体几何里面的三视图,其实三视图主要考察点是空间想象,如果同学们的空间想象能力比较强,如果你能快速还原出对应的立体图形,那么这道问题就马上解决,它无非就是考察几个点: 1、让你判断其形状; 2、由两个试图读出另一视图; 3、考察的综合运算——让你去求多面体棱长最大值、求体积或者表面积。 对于这些问题,你只要把立体图形还原出来,这个题目没有任何难度了。 那么有的同学空间想象稍微偏弱,那种问题就不会得到快速解决,那么怎样快速准确还原对应的三视图呢?方法有很多种,可以是凭你的空间想象直接去还原;三线交汇、或者正方体切等方法,但是我给同学们讲,这些方法都不能最高效、最准确的还原三视图,如果你所有的立体图形都用三线交汇、或者正方体切等方法,我告诉大家就想小题大做了,你会发现解题会比较困难。 那么我今天给大家讲一种方法叫——拔高法,它能够还原90%以上的三视图,还有10%是偏难的要用别的方法:六字箴言——先去除再确定,就能够把所有的三视图题快速准确还原出来,这个方法我以后再给大家讲。 首先,我们来看一下拔高法的步骤: 1、拔高法最主要的就是俯视图,是三视图的根基,首先标出俯视图的所有节点;画出俯视图所对应的直观图; 2、由主、侧视图的左、中、右找出所被拔高的点。 什么意思?那我们先来看一道题,大家要好好理解,好好掌握,只要理解透彻以后,再解题可能就10来秒一道题,是非常快速,而且非常准确。
好,我们先将俯视图作底座,这个最重要: (请注意:我们先只画俯视图外轮廓的直观图,至于哪个虚线那个实线,我们先不管它,先都画成虚线。最终哪个需要是实线,到后面再看)。 ③然后由俯视图看主视图,我们在俯视图和主视图上都标出它们相对应的节点左、中、右。
几何体的三视图还原几何体的方法
1.三视图的关键 一、三视图之间的关系 正视图的高是几何体的高,长是几何体的长; 俯视图的长是几何体的长,宽是几何体的宽; 侧视图的高是几何体的高,宽是几何体的宽。
2.草稿纸 D1 A1A1 1 C C B 1 A1 1 A C C 1 A1 1 A C C
3.构造法 还原步骤 1.先俯视图:根据俯视图画出几何体地面的直观图 2.再正视图:长和高 3.后左视图:宽和高 4. 画整体,再调整。 5. 难点在于实线和虚线例: 解: 1 A A D 1 1 C C C 1 A A 1 A 1 C C C 正视图 左视图 俯视图
4.逐点法(分类讨论) 还原步骤 1. 在每个图上标序号,1,2,3,4,… 2. 通过构造法,每个点的投影逐一讨论 3. 如果 A 点和 B 点的投影相同的,请分类讨论:有 A 无 B 、有 B 无 A 、有 A 有 B 4. 如果 A 点和 B 点的投影不同的,那么该投影的产生必定有 A 和 B 分别作用改进了“构造法”对于“异型”的高难度想象 第一步:我们处理俯视图的序号 4,2,用铅笔,在长方体描粗的点 D 点投影为序号 4, B 点投影为序号 2 D → 4 B → 2 1 A D → 4 或 者 1 B → 2 1 A D , D → 4 或 者 1 B → 2 1 A C C C 结合正视图,序号 1,3 是有 A ,C 的投影,因此
A 1 1 1 A A 情况一的正视图不满足,舍去 情况二、情况三的正视图满足,保留 D 1 1 情况二的俯视图有虚线,保留,情况三的俯视图没虚线,舍去 1 1 所以情况二正确。
三视图还原法
三视图是高中立体几何的基本内容,是培养高中生空间观念的主要内容。纵观近几年的高考,有关三视图的考察逐年稳定,几乎成为各个卷型的必考题之一。这种题型的本质即为由三视图还原直观图,考察知识单一,目标明确,属于基础题目。但从得分情况来看,并不乐观。王坤通过调查发现:学生在由三视图还原直观图时,没有认真分析三个图形的特征,即开始还原;还原时,不根据图形特征考虑还原方法;不清楚三视图是怎么形成的;进行检验时,不画出还原后的几何体的三视图对照原三视图,只画一个或两个视图。要解决这些问题,就必须明确的给出由三视图还原直观图的方法,让学生有迹可循,有规可依。下面就以2012—2016年高考题为例,从不同角度进行分析, 一、割补法 1、(2014高考安徽卷文第8题)一个多面体的三视图如图所示,则多面体的体积是( ) A.233 B.476 C. 6 D. 7 分析:在三视图问题中,如果其中有正方形出现,我们就可以考虑采取用切割正方体的办法。具体做法: 如图,我们先画出正方体,然后将三视图中出现的线画在正方体上,注意点的位置,以及实线画在前面的面,虚线画在后面的面上,最后按照所画的线进行切割,就可以得到我们所需要的几何体的形状,并且由于该几何体边长均有正方体有关,所以很容易求出体积. 解析:如图1第一步先做出正方体并画出正视图中实线与虚线(实线画在前面的面,虚线画在后面的面上),同理做出其它面上的线可得图2,最后我们切割可得所求几何体. 由三视图可得,该多面体的的直观图是一个正方体1111ABCD A B C D -挖去左下角三棱锥EFG A -和右 上角三棱锥''''G F E C -,如下图,则多面体的体积3 2311121312222=?????-??=V ,故选A. 2、(2015高考新课标2理6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去
(完整word)MS01三视图还原之俯视图拔高法
三视图还原之俯视图拔高法 鳖臑:没有鳖臑就制作不出一桌满汉全席似的.下面看它的俯视图拔高法画出直观图; 画弧+连线 拔高 阳马:90 年代全国卷考过一道试题:四棱锥的四个侧面最多有几个直角三角形?嘿嘿,这就是考阳马那! 阳马就是底面为矩形而四个侧面都是直角三角形的四棱锥。 壍堵:正方体(长方体)沿着其对角面"一分为二"就得到两个壍堵. 例1:(2018?浙江)某几何体的三视图如图所示(单位:)cm ,则该几何体的体积(单位:3)cm 是( ) A .2 B .4 C .6 D .8 A .1 B .2 C .3 D .4 秒杀秘籍:盖房子模型——俯视图拔高 一个例题模型的三视图核心——俯视图,代表着地基,三视图可以从俯视图开始,采用画弧、连线、拔高。 画弧:这个是根据工程制图的重要定理,就是俯视图和左视图可以通过90°弧线连接,找到相对应点; 连线:这就是确定各个位置,即主视图和俯视图的重垂线连接,主视图与左视图的水平线连接定位; 拔高:各点定位找好后,在俯视图上能拔高的直接立起来,俯视图转化成斜二测图形,并形成直观图。 画弧 连线 拔高 墙角体的俯视图拔高法:先画弧将俯视图与左视图连接,并将俯视图的三点用数字标记出来;接着将主视图和俯视图连接,发现数字1和2所在的这条重垂线可以拔高,在不知道确切能拔高的点之前,标记上问好,而数字3所在的中垂线看主视图,明显没有高度,不能拔高,标记上Χ;最后判别1和2,通过弧线可知2和3这条线可以拔高,故在2位置标记上〇,而1所在的弧线是不能拔高,故标记上Χ。最后画出直观的墙角体。
例3:(2015?安徽)一个四面体的三视图如图所示,则该四面体的表面积是() 去底座拔高法:主视图和左视图都有的矩形部分叫做底座,故可以在三视图还原时不予考虑,最后加上去这个底座,也就是一个长方体部分,需要注意的是矩形必须为实线。 例5:(2017?新课标Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( ) A. 1 B. 1 C. 1 D.1
三视图还原实物图“五步走”
三视图还原直观图“五步走” 石门县第一中学415300陈锦鑫 三视图是高中立体几何中的一个重要知识点,也是今后进一步学习机械制图、建筑制图等的必修课,三视图也是近几年高考必考的知识点。主要题型就是给出几何体的三视图,计算几何体的面积和体积等相关量。学生丢分的主要原因是不能由三视图还原为几何体,画出相应的直观图。本文通过一道例题介绍一种将三视图还原成实物图的方法。 如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,将该三视图还原成实物图 第一步:根据三视图中三种视图的长与宽,作一个与正视图等长等高,与俯视图等宽的长方体。 例如本例中需要作一个边长为2的正方体ABCD-A’B’C’D’,如图。 第二步:根据三视图中的正视图对长方体切割。 例如本例中由正视图知道,原几何体只能在三棱柱ADD’-BCC’范围内,因此将三棱柱 AA’D’-BB’C’部分截掉,如图。 第三步:根据三视图中的侧视图对剩余几何体切割。 例如本例中由侧视图知道,原几何体只能在四棱锥C’-ABCD范围内,因此将三棱锥D’-ADC’部分截掉,如图。
第四步:根据三视图中的俯视图对剩余几何体切割。 ,同时结合三种视图需要将例如本例中由俯视图知道,原几何体在底面上的投影为BCD 三棱锥C’-ABDC部分截掉,得到三棱锥C’-BCD,如图。 第五步:根据三种视图多边形内部的实线或虚线对剩余几何体切割。 例如本例中正视图、俯视图中均有一条虚线,三视图的虚线表示虚线所在的位置有立体图形的轮廓线,只是在观察者所在的位置看不到。根据正视图、俯视图中知点E为三棱锥C’-BCD 中BC边的中点,连接ED、EC’,ED、EC’是立体图形的轮廓线,因此我们需要将截掉三棱锥C’-ECD,得到三棱锥C’-BDE即为三视图所对应的实物图。
