概率论与数理统计基础

第 1 章概率论与数理统计基础
1.1 概率论基础
一、随机事件与概率
1.随机事件--简称事件自然界中的事件可分为必然事件、不可能事件和
随机事件三种:
①必然事件(U):指在一定条件下必然发生的事件,如“ 1atm下水
加热至100 C时沸腾”是必然事件。
②不可能事件(V):指在一定条件下不发生的事件,如“ 1atm下水
加热至50C时沸腾”是不可能事件。
③随机事件(A B……):指一定条件下,可能发生,也可能不发生的
事件。
2.概率与频率
对每一次试验而言,随机事件是否发生是带有偶然性的。但在大量重复试验下,并把这些试验结果综合在一起,就可以看出支配这些偶然性的某种必然规律性来。实践证明,随机事件发生的可能性大小是它本身所固有的属性,不随人们的主观意愿而转移,并且这种属性可以通过大量试验来认识。
为便于研究,我们将随机事件A发生的可能性的大小用一个数值p
来表示,并把这个数值p叫做事件A的概率。记作:
P (A)= P
为了确定事件A的概率p,首先必须说明频率的概念。
设A为某试验可能出现的随机事件,在同样条件下,该试验重复做n 次,事件A出现了口次(0< me n),则称m为A在这n次试验中出现的频数,称m/n为A在这n次试验中出现的频率。(见书上表 1-1 )
频率 m/n 本身不是常数,它与试验次数 n 有关, 随着试验次数 n 的增加,频
率总是在某一常数附近摆动,而且 n 愈大,频率与这个常数的偏差往往愈小,这种性质叫做频率的稳定性。这个常数是
客观存在的,与所做的若干次具体试验无关,它反映了事件本身所蕴含的规律性,反映了事件出现的可能性大小。
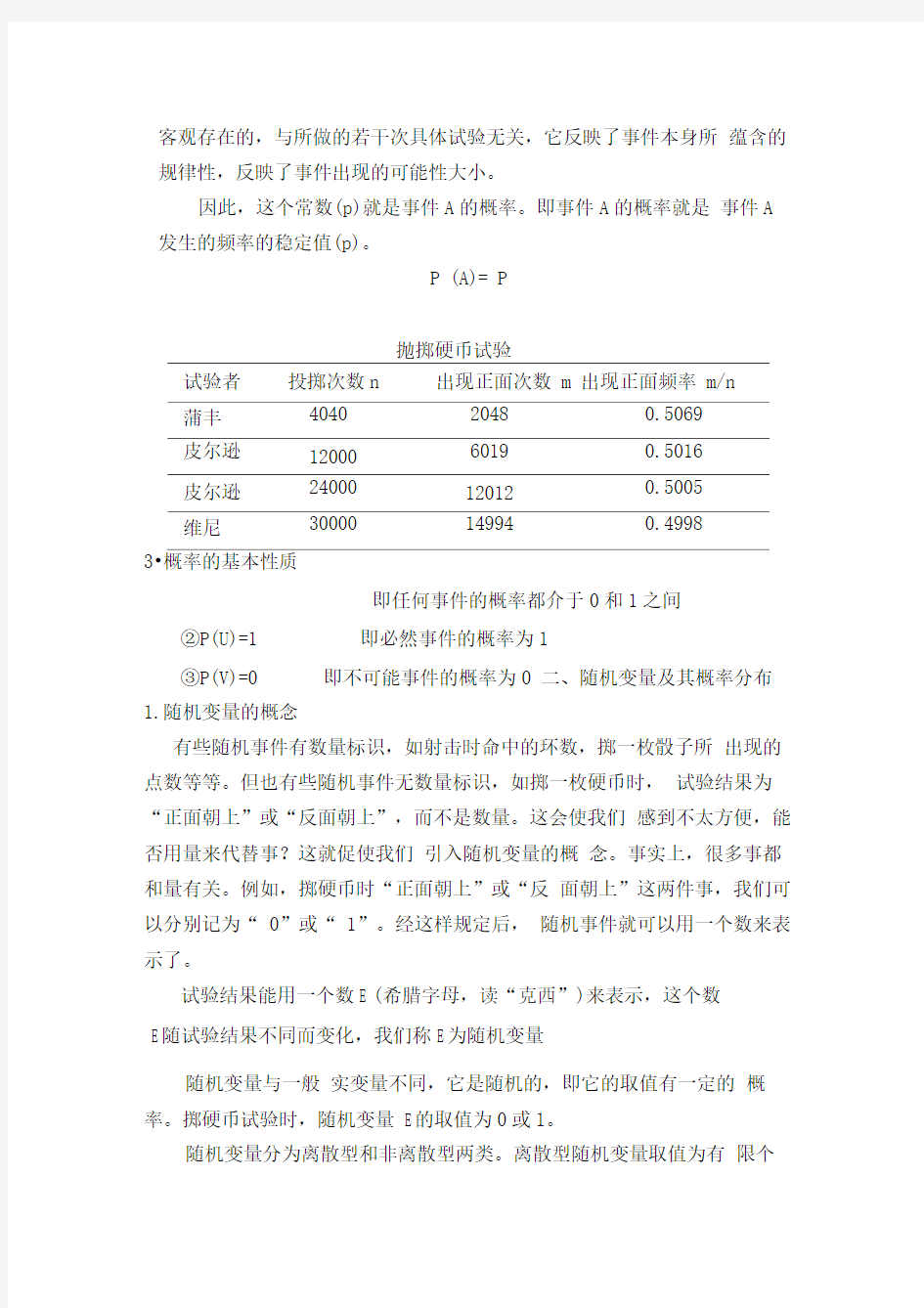
因此,这个常数(p)就是事件A的概率。即事件A的概率就是事件A 发生的频率的稳定值(p)。
P (A)= P
抛掷硬币试验
3?概率的基本性质
即任何事件的概率都介于0和1之间
②P(U)=1 即必然事件的概率为1
③P(V)=0 即不可能事件的概率为0 二、随机变量及其概率分布
1.随机变量的概念
有些随机事件有数量标识,如射击时命中的环数,掷一枚骰子所出现的点数等等。但也有些随机事件无数量标识,如掷一枚硬币时,试验结果为“正面朝上”或“反面朝上”,而不是数量。这会使我们感到不太方便,能否用量来代替事?这就促使我们引入随机变量的概念。事实上,很多事都和量有关。例如,掷硬币时“正面朝上”或“反面朝上”这两件事,我们可以分别记为“ 0”或“ 1”。经这样规定后,随机事件就可以用一个数来表示了。
试验结果能用一个数E (希腊字母,读“克西”)来表示,这个数
E随试验结果不同而变化,我们称E为随机变量
随机变量与一般实变量不同,它是随机的,即它的取值有一定的概率。掷硬币试验时,随机变量E的取值为0或1。
随机变量分为离散型和非离散型两类。离散型随机变量取值为有限个
或无限可列个。非离散型随机变量的取值不能---------- 列举出来,情
况比较复杂,其中最重要的,在实际中最常见的是连续型随机变量。 2.随
机变量的概率分布
(1)离散型随机变量
掌握离散型随机变量的变化规律,除了要了解它的取值以外,更重要的是还要了解它取各可能值的概率是多少。
例如,要检验一批产品的质量,从中任意抽取 5件,仅仅知道次品数E 的可能取值(0, 1, 2, 3, 4, 5)还不够,还应当知道“次品数为0”的概率有多大,“次品数为1”的概率有多大,……,“次品数为5”的概率有多大,只有这样才能对产品中的次品情况有一个较全面的了解。
设离散型随机变量E的所有可能取值为x o, X1,……,X k,……, E取各个可能值的概率为
P( X k) = p(xj (k=0,1,2 ……) (1-1 ) 则称式(1- 1)为离散型随机变量E的概率分布或分布律(也称概率函数),若
将其用表格形式表示,则为
E X0 X1 ..... - X k ....... (1-2 )
p p(x 0) P(X1 )……P(X k) ……
若用图形表示,则如课本上的图1-1所示。
1. 1
丨
1 1
丨]
ffild离散型随机变fltlK率分布
由概率的基本性质可知,概率分布具有以下性质:
(i ) 0 < p(X k) < 1 (k=0,1,2 ……)
(ii)二p( xQ =1
k =0
这两条性质可以作为检验一张表能否成为一个离散型随机变量的分布律的条件。
(2)连续型随机变量的分布密度
离散型随机变量的概率分布的变化规律可以用分布律来描述,但是这种方法不适用于连续型随机变量,因为后者的取值无法一一列举出来,因此不能用分布律的形式来描述。对这类随机变量的概率分布规律的描述通常是以研究“随机变量在某个区间上取值的概率”来实现的。为此,我们引入
概率分布密度函数的概念。
定义:若随机变量E的分布函数F(x)恰好是某个非负函数p(x) 在(-X, x)上的积分,即
X
F(x) = p(x)dx
a
则称E为连续型随机变量,称 p (x)为E的概率分布密度函数(简称为分布密度或密度函数)。称E的分布为连续型分布。
分布密度函数p (x)具有以下性质:
(i ) p (x )> 0
-bo
(ii ) .p(x)dx=1
这两条性质可以作为判断一个函数是否可以作为一个连续型随机变量的分布密度的条件。
b
(iii ) P (av gw b)二p(x)dx= F(b)- F(a)
a
显然,一旦知道了分布密度 p (x),即可求出E在任何实数区间
(a, b]上取值的概率,即(a (iv )在p (x)的连续点处,有F(x) = p(x)。 概率分布密度函数p (x)的图形如图1— 2所示。 3. 随机变量的分布函数 若E 是一个随机变量,x 是任意实数,函数 F (x ) = P( E < x) 称为随机变量E 的概率分布函数,简称分布函数 对离散型随机变量E ,分布 函数为 F (x ) = P ( E < x )= ' p(X k ), (k=0,1,2, ............ ;- *vxv+x ) X k 空 如图1-3所示。 Fg j 1 ? ---- 1 「 0 ---- < 1 ;I 1 Xj M o x 3 勒 阳 X _____________ El-3离fft 型分布函敢 jj 对连续型随机变量E , p(x)为其分布密度,则分布函数为 x F (x ) = P ( E < x ) = . p(x)dx (— oo V X V+K ) 如图1-4所示
