半角模型专题专练
半角模型例题
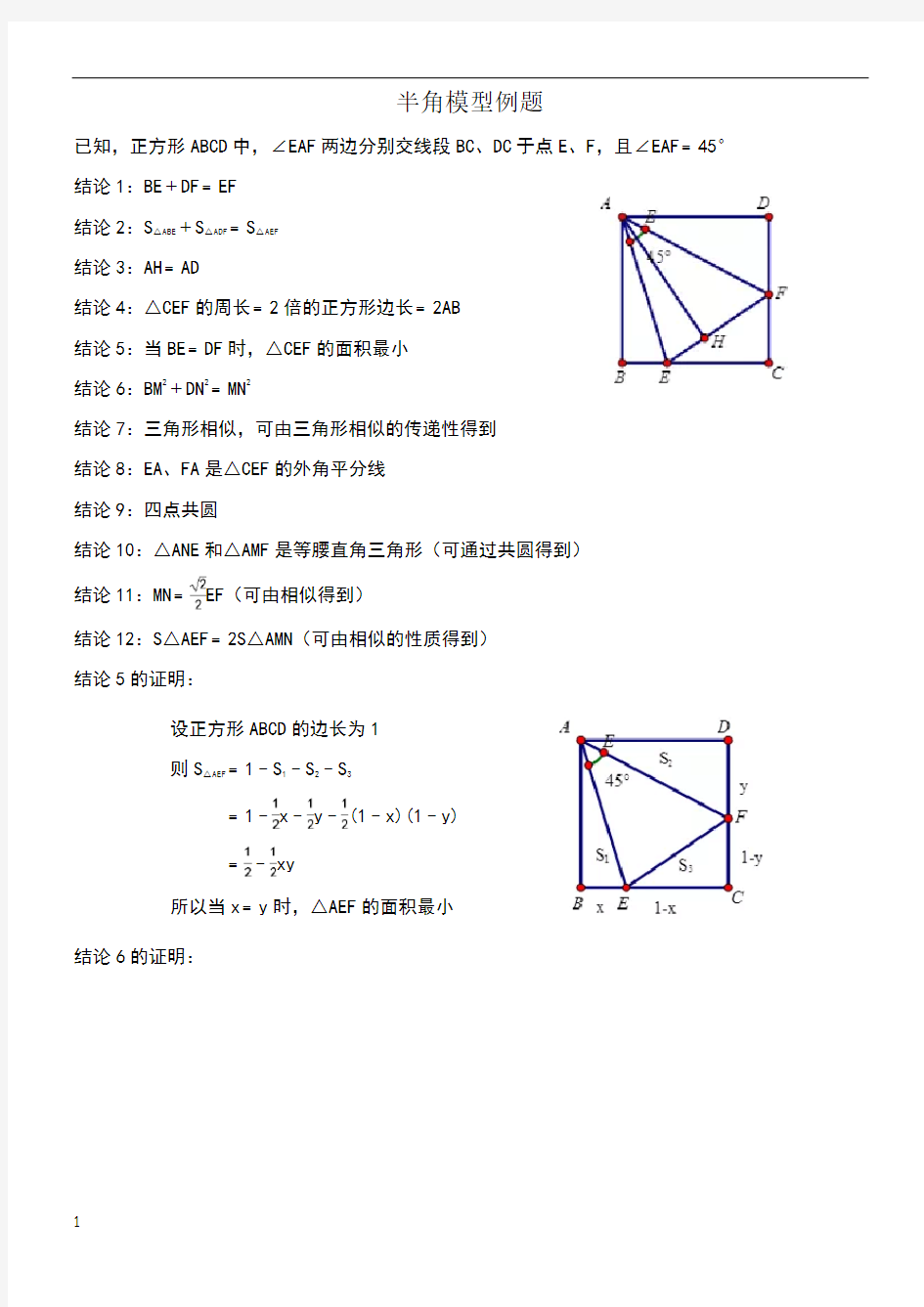
已知,正方形ABCD 中,∠EAF 两边分别交线段BC 、DC 于点E 、F ,且∠EAF ﹦45° 结论1:BE ﹢DF ﹦EF 结论2:S △ABE ﹢S △ADF ﹦S △AEF 结论3:AH ﹦AD
结论4:△CEF 的周长﹦2倍的正方形边长﹦2AB 结论5:当BE ﹦DF 时,△CEF 的面积最小 结论6:BM 2﹢DN 2﹦MN 2
结论7:三角形相似,可由三角形相似的传递性得到 结论8:EA 、FA 是△CEF 的外角平分线 结论9:四点共圆
结论10:△ANE 和△AMF 是等腰直角三角形(可通过共圆得到) 结论11:MN ﹦EF (可由相似得到)
结论12:S △AEF ﹦2S △AMN (可由相似的性质得到) 结论5的证明:
设正方形ABCD 的边长为1 则S △AEF ﹦1﹣S 1﹣S 2﹣S 3
﹦1﹣x ﹣y ﹣(1﹣x)(1﹣y) ﹦﹣xy
所以当x ﹦y 时,△AEF 的面积最小
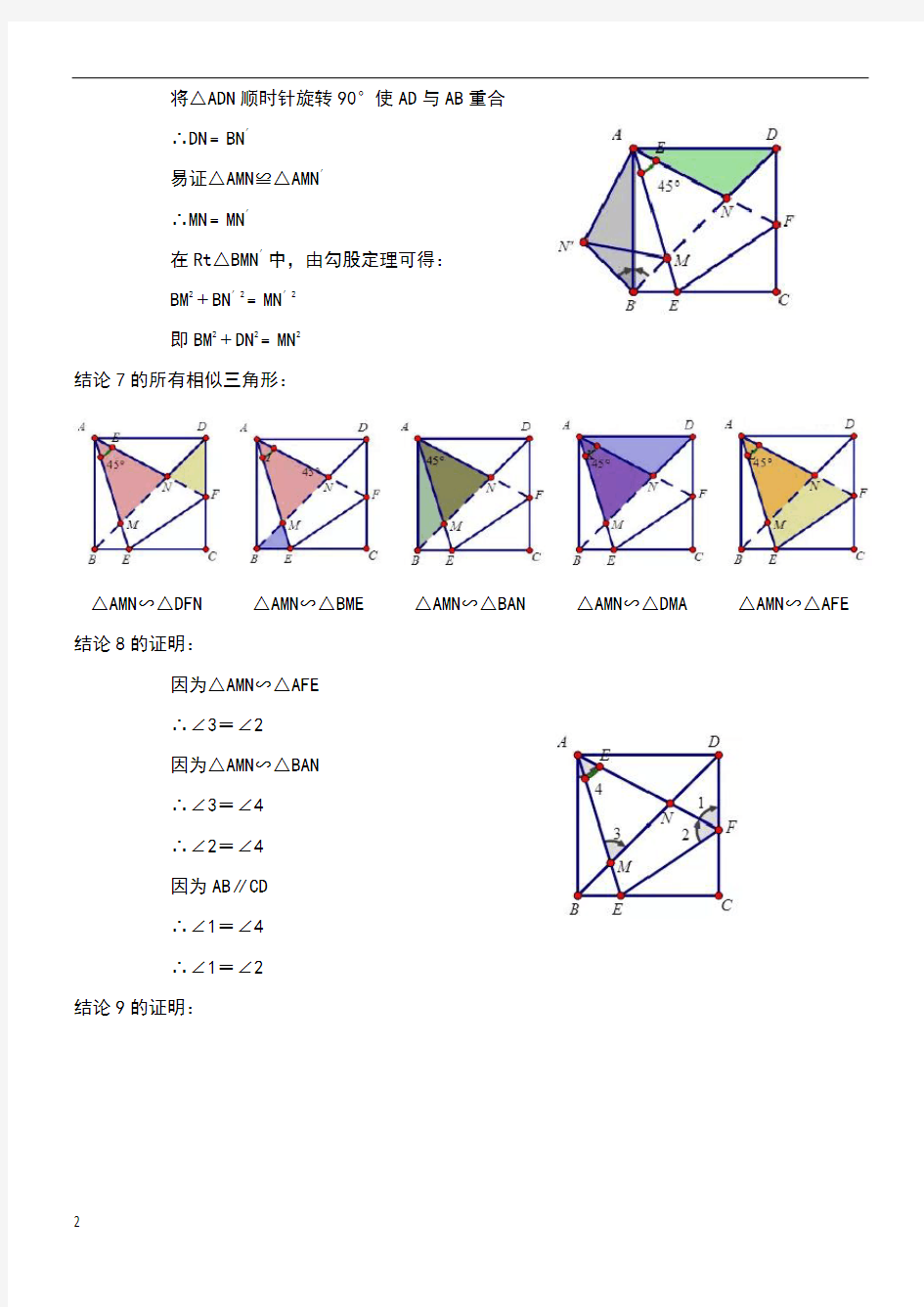
结论6的证明:
将△
ADN顺时针旋转
90°使AD
与
AB重合
∴DN﹦BN′
易证△AMN≌△AMN′
∴MN﹦MN′
在Rt△BMN′中,由勾股定理可得:
BM2﹢BN′2﹦MN′2
即BM2﹢DN2﹦MN2
结论7的所有相似三角形:
△AMN∽△DFN △AMN∽△BME△AMN∽△BAN△AMN∽△DMA△AMN∽△AFE 结论8的证明:
因为△AMN∽△AFE
∴∠3=∠2
因为△AMN∽△BAN
∴∠3=∠4
∴∠2=∠4
因为AB∥CD
∴∠1=∠4
∴∠1=∠2
结论9的证明:
因为∠EAN ﹦∠EBN =45° ∴A 、B 、E 、N 四点共圆(辅圆定理:共边同侧等顶角) 同理可证C 、E 、N 、F 四点共圆 A 、M 、F 、D 四点共圆 C 、E 、M 、F 四点共圆
**必会结论-------- 图形研究正方形半角模型
已知:正方形ABCD ,E 、F 分别在边BC 、CD 上,且
?=∠45EAF ,AE 、AF 分别交BD 于H 、G ,连EF .
一、全等关系
(1)求证:①EF BE DF =+;②DG 2﹢BH 2﹦HG 2;③AE 平分BEF ∠,AF 平分DFE ∠. 二、相似关系
(2)求证:①DG CE 2=;②BH CF 2=;③HG EF 2=. (3)求证:④DH BG AB ?=2;⑤HG BG AG ?=2;⑥2
1=?CF DF CE BE . 三、垂直关系
(4)求证:①EG AG ⊥;②FH AH ⊥;③BE
AB HCF =∠tan . (5)、和差关系
求证:①BE DG BG 2=-;②DH DF AD 2=+; ③||2||DG BH DF BE -=-.
例1、在正方形ABCD中,已知∠MAN﹦45°,若M、N分别在边
CB、DC的延长线上移动,
①.试探究线段MN、BM 、DN之间的数量关系.
②.求证:AB=AH.
例2、在四边形ABCD中,∠B+∠D﹦180°,AB=AD,若E、F分别
在边BC、CD上,且满足EF=BE +DF.
求证:∠EAF=∠BAD
例3、在△ABC中,AB=AC,∠BAC=2∠DAE=120°,若BD=5,
CE=8,求DE的长。
例4、请阅读下列材料:
已知:如图1在Rt ABC
DAE
=,点D、E分别为线段BC上两动点,若45
∠=?.探
BAC
?中,90
∠=?,AB AC
究线段BD、DE、EC三条线段之间的数量关系.
小明的思路是:把AEC
?,连结E D',
?绕点A顺时针旋转90?,得到ABE'
使问题得到解决.请你参考小明的思路探究并解决下列问题:
(1)猜想BD、DE、EC三条线段之间存在的数量关系式,并对你的猜想给予证明;
(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图2,其它条件不变,⑴中探究的结论是否发生改变请说明你的猜想并给予证明.
图1
A
B
C
D
E
图2
A
B C
D
E
例5、探究:
(1)如图1,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,试判断BE 、DF 与EF 三条线段之间的数量关系,直接写出判断结果: ;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF=2
1
∠BAD ”,则(1)问中的结论是否仍然成立若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AE F 绕点A 逆时针旋转,当点分别E 、F 运动到BC 、CD 延长线上时, 如图3所示,其它条件不变,则(1)问中的结论是否发生变化若变化,请给出结论并予以证明..
练习巩固1:
如图,在四边形ABCD 中,∠B ﹦∠D ﹦90°,AB ﹦AD ,若E 、F 分别在边BC 、CD 上的点,且∠EAF =∠BAD . 求证:EF=BE +DF.
练习巩固2:
如图,在五边形ABCDE 中,AB ﹦BC ﹦CD ﹦DE ﹦EA , ∠CAD =∠BAE ,求∠BAE 的度数
练习巩固3:
已知:正方形ABCD 中,45MAN ∠=,绕点A 顺时针旋转,它的两边分别交CB 、DC (或它们的延长线)于点M 、N .
(1)如图1,当MAN ∠绕点A 旋转到BM DN =时,有BM DN MN +=.当MAN ∠ 绕点A 旋转到
BM DN ≠时,如图2,请问图1中的结论还是否成立如果成立,请给予证明,如果不成立,请说明理由;
(2)当MAN ∠绕点A 旋转到如图3的位置时,线段BM DN ,和MN 之间有怎样的等量关系请写出你的猜想,并证明.
N
M
D
C
B
A
N
M
C
D
B
A
N
M D C
B
A
练习巩固4
(1)如图,在四边形ABCD 中,AB ﹦AD ,∠B ﹦∠D ﹦90°,E 、F 分别是边BC 、CD 上的点,且∠EAF =∠BAD . 求证:EF BE FD =+;
E
F
D
C
B
A
v1.0 可编辑可修改
(2) 如图在四边形ABCD 中,AB ﹦AD ,∠B ﹢∠D ﹦180°,E 、F 分别是边BC 、CD 上的点,且∠EAF =∠BAD ,(1)中的结论是否仍然成立不用证明.
E
F
D C
B
A
(3) 如图,在四边形ABCD 中,AB ﹦AD ,∠B ﹢∠ADC ﹦180°,E 、F 分
别是边BC 、CD 延长线上的点,且∠EAF =∠BAD ,(1)中的结论是否仍然成立若成立,请证明;若不成立,请写出它们之间的数量关系,并
证明.
E
F D
C
B
A
(4)如图①,将边长为4cm 的正方形纸片ABCD 沿EF 折叠(点E 、F 分别在边AB 、CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 交于点P ,连接EP . (1)如图②,若M 为AD 边的中点,
①△AEM 的周长﹦ cm ;
②求证:EP ﹦AE ﹢DP ;
(2)随着落点M 在AD 边上取遍所有的位置(点M 不与A 、D 重合),△PDM 的周长是否发生变化请说明理由.
(5).如图17,正方形ABCD ,E 、F 分别为BC 、CD 边上一点. (1)若∠EAF ﹦45o.求证:EF ﹦BE ﹢DF .
(2)若△AEF 绕A 点旋转,保持∠EAF ﹦45o,问⊿CEF 的周长是否随△AEF 位置的变化而变化
(3)已知正方形ABCD 的边长为1,如果⊿CEF 的周长为2.求∠EAF 的度数.
F
E D
C
B
A
图17
练习巩固5、
如图,已知在正方形ABCD 中,∠MAN ﹦45°,连接BD 与AM ,AN 分别交于E 、F 两点。 求证:(1)MN ﹦MB ﹢DN ;
(2)点A 到MN 的距离等于正方形的边长; (3)CMN 的周长等于正方形ABCD 边长的2倍; (4)
=
ABCD CMN S 2AB
S MN
; (5)若∠MAB ﹦20°,求∠AMN ; (6)若(
)
∠=ααMAB 0
45,求∠AMN ;
(7)=+222EF EB DF ;
(8)AEN 与AFM 是等腰三角形; (9)
=
AEF AMN
S 1S
2
。 练习巩固6、
在等边ABC ?的两边AB ,AC 所在直线上分别有两点M N D ,,为ABC ?外一点,且60MDN ∠=?,
120BDC ∠=?,BD CD =,探究:当点M N ,
分别爱直线AB AC ,上移动时,BM BN MN ,,之间的数量关系及AMN ?的周长Q 与等边ABC ?的周长L 的关系.
图①
M N
D
C
B
A
图②
M N
D C
B
A N
图③M
D C
B
A
(1)如图①,当点M N ,在边AB AC ,上,且DM DN =时,BM NC MN ,,之间的数量关系式_________;此时
Q
L
=__________ (2)如图②,当点M N ,在边AB AC ,上,且DM DN ≠时,猜想(1)问的两个结论还成立吗写出你的
(3)如图③,当点M N ,分别在边AB CA ,的延长线上时,若AN x =,则Q =_________(用x L ,表示) 练习巩固7、
如图所示,△ABC 是边长为1的等边三角形,△BDC 是顶角为120°的等腰三角形,以D 为顶点作一个60°的∠MDN ,点M ,N 分别在AB ,AC 上,求△AMN 的周长
练习巩固8、
如图,在正方形ABCD 中,BE=3,EF ﹦5,DF ﹦4,求∠BAE ﹢∠DCF 为多少度。
巩固练习9、
如图1,Rt△ABC≌Rt△EDF,∠ACB﹦∠F﹦90°,∠A﹦∠E﹦30°。△EDF 绕着边AB 的中点D 旋转,DE ,DF 分别交线段..AC 于点M ,K .
(1)①如图2、图3,当∠CDF ﹦0° 或60°时,AM ﹢CK_______MK(填“>”,“<”或“=”). ②如图4,当∠CDF ﹦30° 时,AM ﹢CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF <60°时,AM ﹢CK_______MK ,证明你所得到的结论. (3)如果222AM CK MK =+,请直接写出∠CDF 的度数和AM
MK 的值.
中考数学 几何专题——半角模型
几何模型之半角模型 一、旋转性质 1.图形对应边相等(易得等腰,且等腰均相似) 2.对应角相等 3.对应点与旋转中心连线构成旋转角,旋转角处处相等 二、半角模型 半角模型(90°含45°) 条件模型结论 ①等腰直角△ABC; ②∠DAE=45° DE2=BD2+CE2 ①等腰直角△ABC; ②∠DAE=45° DE2=BD2+CE2 ①正方形ABCD; ②∠EAF=45°①EF=BE+DF; ②△CEF的周长是正方形周长的一半; ③点A到EF的距离等于正方形的边长. ①正方形ABCD; ②∠EAF=45°EF=DF-BE 三、模型演练 1.如图,在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF、AE、AF,过A作AH⊥EF 于点H.若EF=BF+DF.那么下列结论:①AE平分∠BEF;②FH=FD; ③∠EAF=45°;④S△E A F=S△A B E+S△A D F;⑤△CEF的周长为2.其中正确结论的 是.
2.在Rt△ABC中,AB=AC,D?E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A 顺时针旋转90°后,得到△AFB,连接EF,下列结论①△AEF≌△AED;②∠AED=45°; ③BE+DC=DE;④BE2+DC2=DE2,其中正确的是() A.②④ B.①④ C.②③ D.①③ 3如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长. 4.如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=25.若∠EOF=45°,则F点的坐标是. 5.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交
半角模型收集专练
半角模型例题 已知,正方形ABCD 中,∠EAF 两边分别交线段BC 、DC 于点E 、F ,且∠EAF ﹦45° 结论1:BE ﹢DF ﹦EF 结论2:S △ABE ﹢S △ADF ﹦S △AEF 结论3:AH ﹦AD 结论4:△CEF 的周长﹦2倍的正方形边长﹦2AB 结论5:当BE ﹦DF 时,△CEF 的面积最小 结论6:BM 2﹢DN 2﹦MN 2 结论7:三角形相似,可由三角形相似的传递性得到 结论8:EA 、FA 是△CEF 的外角平分线 结论9:四点共圆 结论10:△ANE 和△AMF 是等腰直角三角形(可通过共圆得到) 结论11:MN ﹦√2 2EF (可由相似得到) 结论12:S △AEF ﹦2S △AMN (可由相似的性质得到) 结论5的证明: 设正方形ABCD 的边长为1 则S △AEF ﹦1﹣S 1﹣S 2﹣S 3 ﹦1﹣1 2x ﹣1 2y ﹣1 2(1﹣x)(1﹣y) ﹦1 2﹣12xy 所以当x ﹦y 时,△AEF 的面积最小 结论6的证明:
将△ADN 顺时针旋转90°使AD 与AB 重合 ∴DN ﹦BN ′ 易证△AMN ≌△AMN ′ ∴MN ﹦MN ′ 在Rt △BMN ′中,由勾股定理可得: BM 2﹢BN ′2﹦MN ′2 即BM 2﹢DN 2﹦MN 2 结论7的所有相似三角形: △AMN ∽△DFN △AMN ∽△BME △AMN ∽△BAN △AMN ∽△DMA △AMN ∽△AFE 结论8的证明: 因为△AMN ∽△AFE ∴∠3=∠2 因为△AMN ∽△BAN ∴∠3=∠4 ∴∠2=∠4 因为AB ∥CD ∴∠1=∠4 ∴∠1=∠2 结论9的证明:
中考数学压轴题专项汇编专题15角含半角模型
专题15 角含半角模型 破题策略 1.等腰直角三角形角含半角 如图,在△ABC中,AB=AC,∠BAC=90°,点D,E在BC上且∠DAE=45° (1)△BAE∽△ADE∽△CDA (2)BD2+CE2=DE2. B C 证明(1)易得∠ADC=∠B+∠BAD=∠EAB, 所以△BAE∽△ADE∽△CD A. (2)方法一(旋转法):如图1,将△ABD绕点A逆时针旋转90°得到△ACF,连结EF. B C 则∠EAF=∠EAD=45°,AF=AD, 所以△ADE∽△FAE (SAS). 所以DE=EF. 而CF=BD,∠FCE=∠FCA+∠ACE=90°, 所以BD2+CE2=CF2+CE2=EF2=DE2. 方法二(翻折法):如图2,作点B 关于AD 的对称点F,连结AF,DF,EF. B C 因为∠BAD+∠EAC=∠DAF+∠EAF, 又因为∠BAD=∠DAF, 则∠FAE=∠CAE,AF=AB=AC, 所以△FAE∽△CAE(SAS). 所以EF=E C.
而DF=BD,∠DFE=∠AFD+∠AFE=90°, 所以BD2+EC2=FD2+EF2=DE2. 【拓展】①如图,在△ABC中,AB=AC,∠BAC=90°,点D在BC 上,点E在BC的延长线上,且∠DAE=45°,则BD2+CE2=DE2. D 可以通过旋转、翻折的方法来证明,如图: D D ②将等腰直角三角形变成任意的等腰三角形:如图,在△ABC中,AB=AC,点D,E在 BC上,且∠DAE=1 2 ∠BAC,则以BD,DE,EC为三边长的三角形有一个内角度数为180° -∠BA C. B 可以通过旋转、翻折的方法将BD,DE,EC转移到一个三角形中,如图: B B
半角模型题
半角模型题 Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998
半角模型 例1(海淀201405-8) 如图,点P 是以O 为圆心, AB 为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P 重合, 当此三角板绕点P 旋转时,它的斜边和直角边所在的直线与直径AB 分别 相交于C 、D 两点.设线段AD 的长为x ,线段BC 的长为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是 A B C D 例2.(海201311-24).已知在ABC △中, 90=∠ACB ,26==CB CA , AB CD ⊥于D ,点E 在直线CD 上,CD DE 2 1=,点F 在线段AB 上,M 是DB 的中点,直线AE 与直线CF 交于N 点. (1)如图1,若点E 在线段CD 上,请分别写出线段AE 和CM 之间的位置关系和数量关系:___________,___________; (2)在(1)的条件下,当点F 在线段AD 上,且2AF FD =时,求证: 45=∠CNE ; (3)当点E 在线段CD 的延长线上时,在线段AB 上是否存在点F ,使得 45=∠CNE .若存在,请直接写出AF 的长度;若不存在,请说明理由. D C B A N F E C B A
24. (本小题满分8分) (1)AE ⊥CM ,AE =CM (2)如图,过点A 作AG ⊥AB ,且AG =BM,,连接CG 、FG ,延长AE 交CM 于H . ∵ 90=∠ACB ,26==CB CA , ∴∠CAB =∠CBA =45°, 12. ∴∠GAC =∠MBC =45°. ∵AB CD ⊥, ∴CD=AD=BD =162 AB =. ∵ M 是DB 的中点, ∴3BM DM ==. ∴3AG =. ∵2AF FD =, ∴4 2.AF DF ==, ∴+2+3=5.FM FD DM == ∵AG ⊥AF , ∴FG = ∴.FG FM = 在△CAG 和△CBM 中, ∴△CAG ≌△CBM . ∴CG =CM ,ACG BCM ∠=∠. ∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠=.在△FCG 和△FCM 中, ∴△FCG ≌△FCM . ∴FCG FCM ∠=∠. ∴45FCH ∠=. 由(1)知AE ⊥CM , ∴90CHN ∠= ∴ 45=∠CNE . (3)存在. AF =8. 例3.(平谷201405-24)(1)如图1,点E 、F 分别是正方形ABCD 的边BC 、CD 上的点,∠EAF =45°,连接EF , 则EF 、BE 、FD 之间的数量关系是:EF =BE +FD .连结BD ,交AE 、AF 于点M 、N ,且MN 、BM 、DN 满足222DN BM MN +=,请证明这个等量关系;
专题20 半角模型(解析版)
中考常考几何模型 专题20 半角模型 倍长中线或类中线(与中点有关的线段)构造全等三角形 如图①: (1)∠2=2 1 ∠AOB ;(2)OA=OB 。 如图②: 连接 FB ,将△FOB 绕点 O 旋转至△FOA 的位置,连接 F ′E 、FE ,可得△OEF ′≌△OEF 。 模型精练 1.(2019秋?九龙坡区校级月考)如图.在四边形ABCD 中,∠B +∠ADC =180°,AB =AD ,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =1 2 ∠BAD ,求证:EF =BE ﹣FD . 【点睛】在BE 上截取BG ,使BG =DF ,连接AG .根据SAA 证明△ABG ≌△ADF 得到AG =AF ,∠BAG =∠DAF ,根据∠EAF =1 2∠BAD ,可知∠GAE =∠EAF ,可证明△AEG ≌△AEF ,EG =EF ,那么EF =
GE =BE ﹣BG =BE ﹣DF . 【解析】证明:在BE 上截取BG ,使BG =DF ,连接AG . ∵∠B +∠ADC =180°,∠ADF +∠ADC =180°, ∴∠B =∠ADF . 在△ABG 和△ADF 中, {AB =AD ∠B =∠ADF BG =DF , ∴△ABG ≌△ADF (SAS ), ∴∠BAG =∠DAF ,AG =AF . ∴∠BAG +∠EAD =∠DAF +∠EAD =∠EAF =1 2∠BAD . ∴∠GAE =∠EAF . 在△AEG 和△AEF 中, {AG =AF ∠GAE =∠EAF AE =AE , ∴△AEG ≌△AEF (SAS ). ∴EG =EF ,
中考数学必会几何模型:半角模型
半角模型 已知如图:①∠2=1 2 ∠AOB;②OA=OB. O A B E F 1 23 连接FB,将△FOB绕点O旋转至△FOA的位置,连接F′E,FE,可得△OEF≌△OEF′ 43 2 1 F' F E B A O 模型分析 ∵△OBF≌△OAF′, ∴∠3=∠4,OF=OF′. ∴∠2=1 2 ∠AOB, ∴∠1+∠3=∠2 ∴∠1+∠4=∠2 又∵OE是公共边, ∴△OEF≌△OEF′. (1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点; (2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系; (3)常见的半角模型是90°含45°,120°含60°. 模型实例 例1 已知,正方形ABCD中,∠MAN=45°,它的两边分别交线段CB、DC于点M、N.(1)求证:BM+DN=MN. (2)作AH⊥MN于点H,求证:AH=AB.
证明:(1)延长ND 到E ,使DE=BM , ∵四边形ABCD 是正方形,∴AD=AB . 在△ADE 和△ABM 中, ?? ? ??=∠=∠=BM DE B ADE AB AD ∴△ADE ≌△ABM . ∴AE=AM ,∠DAE=∠BAM ∵∠MAN=45°,∴∠BAM+∠NAD=45°. ∴ ∠MAN=∠EAN=45°. 在△AMN 和△AEN 中, ?? ? ??=∠=∠=AN AN EAN M AN EA M A ∴△AMN ≌△AEN . ∴MN=EN . ∴BM+DN=DE+DN=EN=MN . (2)由(1)知,△AMN ≌△AEN . ∴S △AMN =S △AEN . 即EN AD 2 1 MN AH 21?=?. 又∵MN=EN , ∴AH=AD . 即AH=AB .
半角模型专题专练复习进程
半角模型专题专练
半角模型例题 已知,正方形ABCD 中,∠EAF 两边分别交线段BC 、DC 于点E 、F ,且∠EAF ﹦45° 结论1:BE ﹢DF ﹦EF 结论2:S △ABE ﹢S △ADF ﹦S △AEF 结论3:AH ﹦AD 结论4:△CEF 的周长﹦2倍的正方形边长﹦2AB 结论5:当BE ﹦DF 时,△CEF 的面积最小 结论6:BM 2﹢DN 2﹦MN 2 结论7:三角形相似,可由三角形相似的传递性得到 结论8:EA 、FA 是△CEF 的外角平分线 结论9:四点共圆 结论10:△ANE 和△AMF 是等腰直角三角形(可通过共圆得到) 结论11:MN ﹦√2 2EF (可由相似得到) 结论12:S △AEF ﹦2S △AMN (可由相似的性质得到) 结论5的证明: 设正方形ABCD 的边长为1 则S △AEF ﹦1﹣S 1﹣S 2﹣S 3 ﹦1﹣12x ﹣12y ﹣1 2(1﹣x)(1﹣y) ﹦1 2﹣1 2xy 所以当x ﹦y 时,△AEF 的面积最小 结论6的证明: 将△ADN 顺时针旋转90°使AD 与AB 重合 ∴DN ﹦BN ′ 易证△AMN ≌△AMN ′ ∴MN ﹦MN ′ 在Rt △BMN ′中,由勾股定理可得: BM 2﹢BN ′2﹦MN ′2 即BM 2﹢DN 2﹦MN 2 结论7的所有相似三角形:
△AMN ∽△DFN △AMN ∽△BME △AMN ∽△BAN △AMN ∽△DMA △AMN ∽△AFE 结论8的证明: 因为△AMN ∽△AFE ∴∠3=∠2 因为△AMN ∽△BAN ∴∠3=∠4 ∴∠2=∠4 因为AB ∥CD ∴∠1=∠4 ∴∠1=∠2 结论9的证明: 因为∠EAN ﹦∠EBN =45° ∴A 、B 、E 、N 四点共圆(辅圆定理:共边同侧等顶角) 同理可证C 、E 、N 、F 四点共圆 A 、M 、F 、D 四点共圆 C 、E 、M 、F 四点共圆 **必会结论-------- 图形研究正方形半角模型 已知:正方形ABCD ,E 、F 分别在边BC 、CD 上,且?=∠45EAF ,AE 、AF 分别交BD 于H 、G ,连EF . 一、全等关系 (1)求证:①EF BE DF =+;②DG 2﹢BH 2﹦HG 2;③AE 平分BEF ∠,AF 平分DFE ∠. 二、相似关系 (2)求证:①DG CE 2=;②BH CF 2=;③HG EF 2=. (3)求证:④DH BG AB ?=2;⑤HG BG AG ?=2;⑥21=?CF DF CE BE . 三、垂直关系 (4)求证:①EG AG ⊥;②FH AH ⊥;③BE AB HCF =∠tan . (5)、和差关系 求证:①BE DG BG 2=-;②DH DF AD 2=+; ③||2||DG BH DF BE -=-.
专题05倍半角模型巩固练习(提优)含答案及解析-冲刺中考数学几何专项复习
倍半角模型巩固练习(提优) 1.如图,在正方形ABCD中,点E、F分别在BC、AB上,且∠FDE=45o,连接DE、DF、EF,试探究EF、AF、CE之间的数量关系. 2.如图,在△ABC中,AB=AC,∠BAC=90o,点D在CB的延长线上,连接AD,EA ⊥AD,∠ACE=∠ABD. (1)求证:AD=AE; (2)点F为CD的中点,AF的延长线交BE于点G,求∠AGE的度数. 3.如图,在平行四边形ABCD中,AE⊥BC于点E,CE=CD,点F为CE的中点,点G
为CD上的一点,连接DF、EG、AG,∠1=∠2. (1)若CF=2,AE=3,求BE的长; (2)求证:∠CEG=∠AGE. 4.如图,在正方形ABCD中,E为AD边上的中点,过点A作AF⊥BE交CD边于点F,M是AD边上一点,且BM=DM+CD. (1)求证:点F是CD边上的中点; (2)求证:∠MBC=2∠ABE. 5. 如图,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF, 垂足为点M,BE=3,,求MF的长.
6. 如图,在△ABC中,∠ACB=90o,D是AB边上的一点,M是CD的中点,若∠AMD =∠BMD.求证:∠CDA=2∠ACD. 倍半角模型巩固练习(提优) 1.如图,在正方形ABCD中,点E、F分别在BC、AB上,且∠FDE=45o,连接DE、DF、EF,试探究EF、AF、CE之间的数量关系. 【解答】EF=AF+CE,证明见解析 【解析】如图,将△DCE绕着点D顺时针旋转90o得到△DGA.
∵∠EDC+∠ADF+∠FDE=90o,∠FDE=45o,∴∠EDC+∠ADF=45o, 又∵旋转,∴DE=DG,∠GDA=∠EDC,∴∠GDA+∠ADF=∠GDF=∠FDE=45o, 在△DGF与△DEF中,DF=DF,∠GDF=∠EDF,DG=DE,∴△DGF≌△DEF,∴EF=GF=GA+AF, ∵旋转,∴GA=CE,∴EF=AF+CE. 2.如图,在△ABC中,AB=AC,∠BAC=90o,点D在CB的延长线上,连接AD,EA ⊥AD,∠ACE=∠ABD. (1)求证:AD=AE; (2)点F为CD的中点,AF的延长线交BE于点G,求∠AGE的度数. 【解答】(1)见解析;(2)∠AGE=90o 【解析】(1)证明:∵EA⊥AD,∴∠DAE=∠90o,∴∠DAB+∠BAE=90o, ∵∠BAC=90o,∴∠CAE+∠BAE=90o,∴∠DAB=∠CAE, ∵∠ACE=∠ABD,AB=AC,∴△ADB≌△ACE,∴AD=AE; (2)如图,延长AG至点H,使得FH=FA.
八上培优半角模型精修订
八上培优半角模型 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
八上培优5 半角模型方法:截长补短 图形中,往往出现90°套45°的情况,或者120°套60°的情况。还有2α套α的情况。求证的结论一般是线段的和与差。解决的方法是:截长补短构造全等三角形。旋转移位造全等,翻折分割构全等。截长法,补短法。 勤学早和新观察均有专题。勤学早在第49页,新观察在第34页,新观察培优也有涉及,在第27页2两个例题,29页有习题。这些题大同小异,只是图形略有变化而已。证明过程一般要证明两次全等。 下面是新观察第34页1~4题 1.如图,四边形ABCD中,∠A=∠C=90゜,∠D=60゜,AB=BC,E、F,分别在AD、CD 上,且∠EBF=60゜.求证:EF=AE+CF. 2.如图2,在上题中,若E、F分别在AD、DC的延长线上,其余条件不变,求证: AE=EF+CF. 3.如图,∠A=∠B=90°, CA=CB=4, ∠ACB=120°,∠ECF=60°,AE=3, BF=2, 求五边形ABCDE的面积.
A C B F E A C B F E D 4.如图1.在四边形ABCD中.AB=AD,∠B+∠D=180゜,E、F分别是边BC、CD上的点,且∠BAD=2∠EAF. (1)求证:EF=BE+DF; (2)在(1)问中,若将△AEF绕点A逆时针旋转,当点E、F分别运动到BC、CD延长线上时,如图2所示,试探究EF、BE、DF之间的数量关 系. 3.如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
半角模型专题--优选专练.doc
半角模型例题 已知,正方形 ABCD中,∠ EAF两边分别交线段 BC、 DC于点 E、F,且∠ EAF﹦ 45°结论 1:BE﹢ DF﹦EF 结论 2:S△ABE﹢ S△ADF﹦S△AEF 结论 3:AH﹦ AD 结论 4:△ CEF的周长﹦ 2 倍的正方形边长﹦ 2AB 结论 5:当 BE﹦DF时,△ CEF的面积最小 22 2 结论 6:BM﹢DN﹦MN 结论 7:三角形相似,可由三角形相似的传递性得到 结论 8:EA、 FA是△ CEF的外角平分线 结论 9:四点共圆 结论 10:△ ANE和△ AMF是等腰直角三角形(可通过共圆得到) 结论 11: MN﹦EF(可由相似得到) 结论 12: S△ AEF﹦2S△ AMN(可由相似的性质得到) 结论 5 的证明: 设正方形 ABCD的边长为 1 则S△AEF﹦1﹣S1﹣S2﹣ S3 ﹦1﹣ x﹣ y﹣ (1 ﹣x)(1 ﹣y) ﹦﹣ xy 所以当 x﹦y 时,△ AEF的面积最小 结论 6 的证明: 将△ ADN顺时针旋转 90°使 AD与 AB重合 ′ ∴DN﹦ BN ′ 易证△ AMN≌△ AMN ′ ∴MN﹦ MN ′ 在 Rt△BMN中,由勾股定理可得: 2′ 2′2 BM﹢BN ﹦MN 22 2 即 BM﹢DN﹦MN 结论 7 的所有相似三角形: △ AMN∽△ DFN△AMN∽△ BME△AMN∽△ BAN△ AMN∽△ DMA△AMN∽△ AFE
结论 8 的证明: 因为△ AMN∽△ AFE ∴∠ 3=∠ 2 因为△ AMN∽△ BAN ∴∠ 3=∠ 4 ∴∠ 2=∠ 4 因为 AB∥CD ∴∠ 1=∠ 4 ∴∠ 1=∠ 2 结论 9 的证明: 因为∠ EAN﹦∠ EBN= 45° ∴A、B、E、N 四点共圆(辅圆定 理:共边同侧等顶角) 同理可证 C、E、N、F 四点共圆 A、M、 F、 D 四点共圆 C、E、 M、 F 四点共圆 **必会结论 --------图形研究正方形半角模型 已知:正方形 ABCD ,E、F分别在边 BC 、 CD 上,且 EAF 45 ,AE、AF分别交BD于H、 G ,连EF. 一、全等关系 ()求证:① 2 2 2 平分,平分 DF BE EF ;②DG﹢ BH﹦ HG;③AE BEF AF DFE . 1 二、相似关系 (2)求证:①CE 2DG ;② CF 2 BH ;③ EF 2HG . (3)求证:④AB2 BG DH ;⑤ AG 2 BG HG ;⑥BE DF 1 . CE CF 2 三、垂直关系 (4)求证:①AG EG ;②AH FH ;③tan HCF AB . (5) 、和差关系 BE 求证:① BG DG 2BE ;② AD DF 2DH ; ③ | BE DF | 2 | BH DG | .
2.角含半角模型
角含半角模型 破题策略 1. 等腰直角三角形角含半角 如图,在△ABC 中,AB =AC ,∠BAC =90°,点D ,E 在BC 上且∠DAE =45° (1) △BAE ∽△ADE ∽△CDA (2)BD 2+CE 2=DE 2 . 45° E A B C D 证明(1)易得∠ADC =∠B +∠BAD =∠EAB , 所以△BAE ∽△ADE ∽△CD A . (2)方法一(旋转法):如图1,将△ABD 绕点A 逆时针旋转90°得到△ACF ,连结EF . 45° F E A B C D 则∠EAF =∠EAD =45°,AF =AD , 所以△ADE ∽△FAE ( SAS ). 所以DE = EF . 而CF =BD ,∠FCE =∠FCA +∠ACE =90°, 所以BD 2+ CE 2=CF 2+CE 2=EF 2=DE 2 . 方法二(翻折法):如图2,作点B 关于AD 的对称点F ,连结AF ,DF ,EF . 45° E A B C D 因为∠BAD +∠EAC =∠DAF +∠EAF , 又因为∠BAD =∠DAF , 则∠FAE =∠CAE ,AF =AB =AC , 所以△FAE ∽△CAE (SAS ). 所以EF = E C .
而DF =BD , ∠DFE =∠AFD + ∠AFE =90°, 所以BD 2+ EC 2= FD 2+ EF 2= DE 2 . 【拓展】①如图,在△ ABC 中,AB =AC ,∠BAC =90°,点D 在BC 上,点E 在BC 的 延长线上,且∠DAE =45°,则BD 2+CE 2=DE 2 . E D 可以通过旋转、翻折的方法来证明,如图: E A D F E A D ②将等腰直角三角形变成任意的等腰三角形:如图,在△ABC 中,AB =AC ,点D ,E 在 BC 上,且∠DAE =1 2 ∠BAC ,则以BD ,DE ,EC 为三边长的三角形有一个内角度数为180° -∠BA C . B 可以通过旋转、翻折的方法将BD ,DE ,EC 转移到一个三角形中,如图: B C E B D
人教版八年级下册第18章平行四边形——弦图模型和半角模型专题(Word版,无答案)
一 ) 弦图模型 基本图形】已知正方形 ABCD,过 B,D 两点分别向过点 C 的直线作垂线 , 垂足分别为点 E,F, 则△ BCE ≌△ CDF h, 正方形 ABCD 的四 个顶点分 (1) 当 a=45 °时, 求△EAD 的面积 (2) 当 a=30 °时, 求△EAD 的面积 (3) 当0° 变式训练 】如图,分别以 ABC 的AC 和BC 为一边,在ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半. 4.如图,直角梯形ABCD 中,AD/BC,∠ADC=90°,是AD 的垂直平分线,交AD 于点M,以腰AB 为边作正方形ABFE,EP⊥l 于点P. 求证:2EP+AD=2CD 二)半角模型 半角模型【用旋转和对称(翻折)的方法解决问题】基本结论:在正方形ABCD中,若M、N 分别在边BC、CD上移动,且满足MN=BM+ DN,则有以下基本结论(需记忆):① . ∠MAN4=5°;② . C CMN 2AB;③ . AM、AN分别平分 ∠BMN和∠DNM. 同样,在正方形ABCD中,若已知∠MAN4=5°,则会有:① . MN=B+MD N; ②C CMN 2AB;③.AM、AN分别平分∠BMN 和∠DNM④; 若继续作AH⊥MN于点H, 则有AH=AB. F 倍半角模型知识精讲 一、二倍角模型处理方法 1. 作二倍角的平分线,构成等腰三角形. 例:如图,在△ABC中,∠ABC=2∠C,作∠ABC的平分线交AC于点D,则∠DBC=∠C,DB=DC,即△DBC是等腰三角形. 2. 延长二倍角的一边,使其等于二倍角的另一边,构成两个等腰三角形. 例:如图,在△ABC中,∠B=2∠C,延长CB到点D,使得BD=AB,连接AD,则△ABD、△ADC都是等腰三角形. 例题:如图,在△ABC中,∠C=2∠A,AC=2BC,求证:∠B=90o. 【解答】见解析 【证法一】如图1,作∠C的平分线CE交AB于点E,过点E作ED⊥AC于点D. 则∠ACE=∠A,AE=CE, ∵AE=EC,ED⊥AC,∴CD=AC, 又∵AC=2BC,∴CD=CB,∴△CDE≌△CBE,∴∠B=∠CDE=90o; 【证法二】如图2,延长AC到点D,使得CD=CB,连接BD,取AC的中点E,连接BE. 由题意可得EC=CD=BC,∠DBE=90o, ∵CD=CB,∠D=∠CBD,∴∠ACB=2∠D, ∵∠ACB=2∠A,∠A=∠D,∴AB=BD, 又∵AE=DC,∴△ABE≌△DBC,∴∠ABE=∠DBC,∴∠ABC=∠EBD=90o. 【证法三】如图3,作∠C的平分线CD,延长CB到点E,使得CE=AC,∴AC=BC+BE. ∵AC=2BC,∴BC=BE,在△ACD与△ECD中,AC=EC,∠ACD=∠ECD,CD=CD, ∴△ACD≌△ECD,∴∠A=∠E, 又∵∠DCB=∠DCA=∠A,∴∠E=∠DCB,∴DC=DE,∴∠ABC=90o. 二、倍半角综合 1. 由“倍”造“半” 已知倍角求半角,将倍角所在的直角三角形相应的直角边顺势延长即可. 如图,若,则() 2. 由“半”造“倍” 正方形角含半角模型提升 例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG . 例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积 例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,?垂足为M ,AM AB =,则有EF BE DF =+,为什么 例4. 如图,在正方形ABCD 的BC 、CD 边上取E 、F 两点,使45EAF ∠=o ,AG EF ⊥于G . 求证:AG AB = 例5.(1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点 O ,90AOF ?∠=. 求证:BE CF =. (2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点 O ,90FOH ?∠=,4EF =.求GH 的长. 【双基训练】 1. 如图6,点A 在线段BG 上,四边形ABCD 与DEFG 都是正方形,?其边长分别为3cm 和5cm ,则CDE ?的面积为________2cm . (6) (7) 2.你可以依次剪6张正方形纸片,拼成如图7所示图形.?如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,?那么正方形⑤的面积为________. 3.如图9,已知正方形ABCD 的面积为35平方厘米,E 、F 分别为边AB 、BC 上的点.AF 、CE 相交于G ,并且ABF ?的面积为14平方厘米,BCE ?的面积为5平方厘米,?那么四边形BEGF 的面积是________. 4. 如图,A 、B 、C 三点在同一条直线上,2AB BC =。分别以 AB 、BC 为边作正方形ABEF 和正方形BCMN ,连接FN , EC 。 求证:FN EC =。 5.如图 ,ABCD 是正方形.G 是BC 上的一点,DE AG ⊥于 E ,BF AG ⊥于 F . (1)求证:ABF DAE △≌△; (2)求证:DE EF FB =+. 【纵向应用】 6. 在正方形ABCD 中,12∠=∠.求证:BE OF 2 1 = 7. 在正方形ABCD 中,12∠=∠.AE DF ⊥,求证:CE OG 2 1= 8. 如图13,点E 为正方形ABCD 对角线BD 上一点, EF BC ⊥, EG CD ⊥ 求证:AE FG ⊥ 9.已知:点E 、F 分别正方形ABCD 中AB 和BC 的中点,连接AF 和DE 相交于点G , 图2 D G A E B C F 13 A D E F C G B 半角模型 例1(如图,点P 是以O 为圆心, AB 为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P 重合, 当此三角板绕点P 旋转时,它的斜边和直角边所在的直线与直径AB 分别相交于C 、D 两点.设线段AD 的长为x ,线段BC 的长为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是 A B CD 例2.已知在ABC △中, 90= ∠ACB ,26==CB CA ,AB CD ⊥于D ,点E 在直线 CD 上,CD DE 2 1 = ,点F 在线段AB 上,M 是 DB 的中点,直线AE 与直线CF 交于N 点. (1)如图1,若点E 在线段CD 上,请分别写出线段AE 和CM 之间的位置关系和数量关系:___________ ,___________; (2)在(1)的条件下,当点F 在线段AD 上,且2AF FD =时,求证: 45=∠CNE ; (3)当点E 在线段CD 的延长线上时,在线段AB 上是否存在点F ,使得 45=∠CNE .若存在,请直接写出AF 的长度;若不存在,请说明理由. D C B A N M F E D C B A 24. (本小题满分8分) (1)AE ⊥CM ,AE =CM (2)如图,过点A 作AG ⊥AB ,且AG =BM,,连接CG 、FG ,延长AE 交CM 于H . ∵ 90=∠ACB ,26==CB CA , ∴∠CAB =∠CBA =45°, 12. ∴∠GAC =∠MBC =45°. ∵AB CD ⊥, ∴CD=AD=BD =1 62 AB =. ∵M 是DB 的中点, ∴3BM DM ==. ∴3AG =. ∵2AF FD =, ∴4 2.AF DF ==, ∴+2+3=5.FM FD DM == ∵AG ⊥AF , ∴FG = ∴.FG FM = 在△CAG 和△CBM 中, CA CB CAG CBM AG BM =?? ∠=∠??=? ,, , ∴△CAG ≌△CBM . ∴CG =CM ,ACG BCM ∠=∠. ∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠= .在△FCG 和△FCM 中, CG CM FG FM CF CF =?? =??=? ,, , ∴△FCG ≌△FCM . ∴FCG FCM ∠=∠. ∴45FCH ∠= . 由(1)知AE ⊥CM , ∴90CHN ∠= ∴ 45=∠CNE . (3)存在. AF =8. 中考数学几何模型5:角含半角模型TH 名师点睛拨开云雾开门见山角含半角模型,顾名思义即一个角包含着它的一半大小的角。它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。 类型一:等腰直角三角形角含半角模型 (1)如图,在△ABC中,AB=AC,∠BAC=90°,点D,E在BC上,且∠DAE=45°,则:BD2+CE2=DE2. 图示(1)作法1:将△ABD旋转90°作法2:分别翻折△ABD,△ACE (2)如图,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E在BC延长线上,且∠DAE=45°,则:BD2+CE2=DE2. 图示(2) (3)如图,将等腰直角三角形变成任意等腰三角形时,亦可以进行两种方法的操作处理.. 任意等腰三角形 类型二:正方形中角含半角模型 (1)如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,连接EF,过点A作AG⊥于EF于点G,则:EF=BE+DF,AG=AD. 图示(1)作法:将△ABE绕点A逆时针旋转90° (2)如图,在正方形ABCD中,点E,F分别在边CB,DC的延长线上,∠EAF=45°,连接EF,则:EF=DF-BE. 图示(2)作法:将△ABE绕点A逆时针旋转90° (3)如图,将正方形变成一组邻边相等,对角互补的四边形,在四方形ABCD中,AB=AD,∠BAD+∠ C=180°,点E,F分别在边BC,CD上,∠EAF=1 2 ∠BAD,连接EF,则:EF=BE+DF. 图示(3)作法:将△ABE绕点A逆时针旋转∠BAD的大小 中考数学几何模型5:角含半角模型st ●模型1:截长补短模型●模型2:共顶点模型●模型3:对角互补模型●模型:4:中点模型●模型5:角含半角模型 ●模型6:弦图模型 ●模型7:轴对称最值模型 ●模型8:费马点最值模型 ●模型9:隐圆模型 ●模型10:胡不归最值模型 ●模型11:阿氏圆最值模型 ●模型12:主从联动模型 名师点睛拨开云雾开门见山角含半角模型,顾名思义即一个角包含着它的一半大小的角。它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。 类型一:等腰直角三角形角含半角模型 (1)如图,在△ABC中,AB=AC,∠BAC=90°,点D,E在BC上,且∠DAE=45°,则:BD2+CE2=DE2. 图示(1)作法1:将△ABD旋转90°作法2:分别翻折△ABD,△ACE (2)如图,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E在BC延长线上,且∠DAE=45°,则:BD2+CE2=DE2. 图示(2) (3)如图,将等腰直角三角形变成任意等腰三角形时,亦可以进行两种方法的操作处理.. 任意等腰三角形 类型二:正方形中角含半角模型 (1)如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,连接EF,过点A作AG⊥于EF于点G,则:EF=BE+DF,AG=AD. 图示(1)作法:将△ABE绕点A逆时针旋转90° (2)如图,在正方形ABCD中,点E,F分别在边CB,DC的延长线上,∠EAF=45°,连接EF,则:EF=DF-BE. 图示(2)作法:将△ABE绕点A逆时针旋转90° (3)如图,将正方形变成一组邻边相等,对角互补的四边形,在四方形ABCD中,AB=AD,∠BAD+∠ C=180°,点E,F分别在边BC,CD上,∠EAF=1 2 ∠BAD,连接EF,则:EF=BE+DF. 图示(3)作法:将△ABE绕点A逆时针旋转∠BAD的大小 几何图形之半角模型 主题半角模型 教学内容 教学目标 1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。 2.掌握正方形的性质定理1和性质定理2。 3.正确运用正方形的性质解题。 4.通过四边形的从属关系渗透集合思想。 5.通过理解四种四边形内在联系,培养学生辩证观点。 知识结构 正方形的性质 因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形, 所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。 正方形性质定理1:正方形的四个角都是直角,四条边相等。 正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。 说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。 小结: (1)正方形与矩形,菱形,平行四边形的关系如上图 (2)正方形的性质: ①正方形对边平行。 ②正方形四边相等。 ③正方形四个角都是直角。 ④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。 典型例题精讲 例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG . 【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM . 而BM=BD-DM=2 2-2=2(2-1), ∴AG=BM=2(2-1). 例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积 【解析】:过P 作EF AB ⊥于F 交DC 于E . 设PF x =,则10EF x =+,1 (10)2 BF x =+. 由2 22PB PF BF =+. 可得:2 221 10 (10)4 x x =++. 故6x =. 2 16256ABCD S ==. 例3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥, ?垂足为M ,AM AB =,则有EF BE DF =+,为什么 【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可. 理由:连结AE 、AF . 由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用, ∴△ABE ≌△AME . ∴BE=ME . 同理可得,△ADF ≌△AMF . ∴DF=MF . ∴EF=ME+MF=BE+DF . D C B A M N 图2A M B D C N 1图B A C D M N 第九章 半角模型 模型1 倍长中线或类中线(与中点有关的线段)构造全等三角形 已知如图: ② ∠2=12∠AOB ; ②OA=OB 。 连接F ′B ,将△FOB 绕点O 旋转 至△FOA 的位置,连接F ′E 、FE , 可得△OEF ′≌△OEF 。 模型分析 (1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点; (2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系; (3)常见的半角模型是90°含45°,120°含60°。 模型实例 例1.如图,已知正方形ABCD 中,∠MAN=45°,它的两边分别交线段CB 、DC 于点M 、N 。 (1)求证:BM+DN=MN ; (2)作AH ⊥MN 于点H ,求证:AH=AB 。 例2.在等边△ABC 的两边AB 、AC 上分别有两点M 、N ,D 为△ABC 外一点, 且∠MDN=60°,∠BDC=60°,BD=DC 。探究:当M 、N 分别在线段AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系。 (1)如图①,当DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; (2)如图②,当DM ≠DN 时,猜想(1)问的结论还成立吗?写出你的猜想 并加以证明。 例3.如图,在四边形ABCD 中,∠B+∠ADC=180°,E 、F 分别是BC 、CD 延长 A F E B C D A B C D M N 2图A D B E C 图1D C E B A 线上的点,且∠EAF=12∠BAD 。求证:EF=BE-FD 。 热搜精练 1.如图,正方形ABCD ,M 在CB 延长线上,N 在DC 延长线,∠MAN=45°。 求证:MN=DN-BM 。 2.已知,如图①,在Rt △ABC 中,∠BAC=90°,AB=AC ,点D 、E 分别为线段 BC 上两动点,若∠DAE=45°。探究线段BD 、DE 、EC 三条线段之间的数量 关系。小明的思路是:把△AEC 绕点A 顺时针旋转90°,得到△ABE ′,连接E ′D ,使问题得劲解决。请你参考小明的思路探究并解决以下问题: (1)猜想BD 、DE 、EC 三条线段之间的数量关系式,并对你的猜想给予证明; (2)当动点E 在线段BC 上,动点D 运动到线段CB 的延长线上时,如图②, 其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明。 3.已知,在等边△ABC 中,点O 是边AC 、BC 的垂直平分线的交点,M 、N 分别在直线AC 、BC 上,且∠MON=60°。 (1)如图①,当CM=CN 时,M 、N 分别在边AC 、BC 上时,请写出AM 、CN 、MN倍半角模型知识精讲
2018年初中数学突破中考压轴题几何模型之正方形的半角模型教案
半角模型题
第5讲角含半角模型(解析版)
第5讲角含半角模型(原卷版) 2020年中考数学几何模型能力提升篇(全国通用)
人教版中考数学压轴题解题模型----几何图形之半角模型(含解析)
9第九章 半角模型 初中几何专题提高讲义
