初中几何证明题绝对经典

(如图2)
C (如图3)
C
(如图1)
几何证明
1.点A 、B 、C 在同一直线上,在直线AC 的同侧作ABE ?和BCF ?,连接AF ,CE .取AF 、CE 的中点M 、N ,连接BM ,BN ,MN .
(1)若ABE ?和FBC ?是等腰直角三角形,且090=∠=∠FBC ABE (如图1),则MBN ?是三角形.
(2)在ABE ?和BCF ?中,若BA =BE ,BC =BF ,且α=∠=∠FBC ABE ,(如图2),则MBN ?是
三角形,且=∠MBN .
(3)若将(2)中的ABE ?绕点B 旋转一定角度,(如同3),其他条件不变,那么(2)中的结论是否成立?若成立,给出你的证明;若不成立,写出正确的结论并给出证明.
2.如图,将一三角板放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B,另一边与射线DC 相交于Q .探究:设A 、P 两点间的距离为x .
(1)当点Q 在边CD 上时,线段PQ 与PB 之间有怎样的数量关系?试证明你的猜想;
(2)当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 与x 之间的函数关系,并写出函数自变量x 的取值范围;
(3)当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置.并求出相应的x 值,如果不可能,试说明理由.
Q P D C B
A
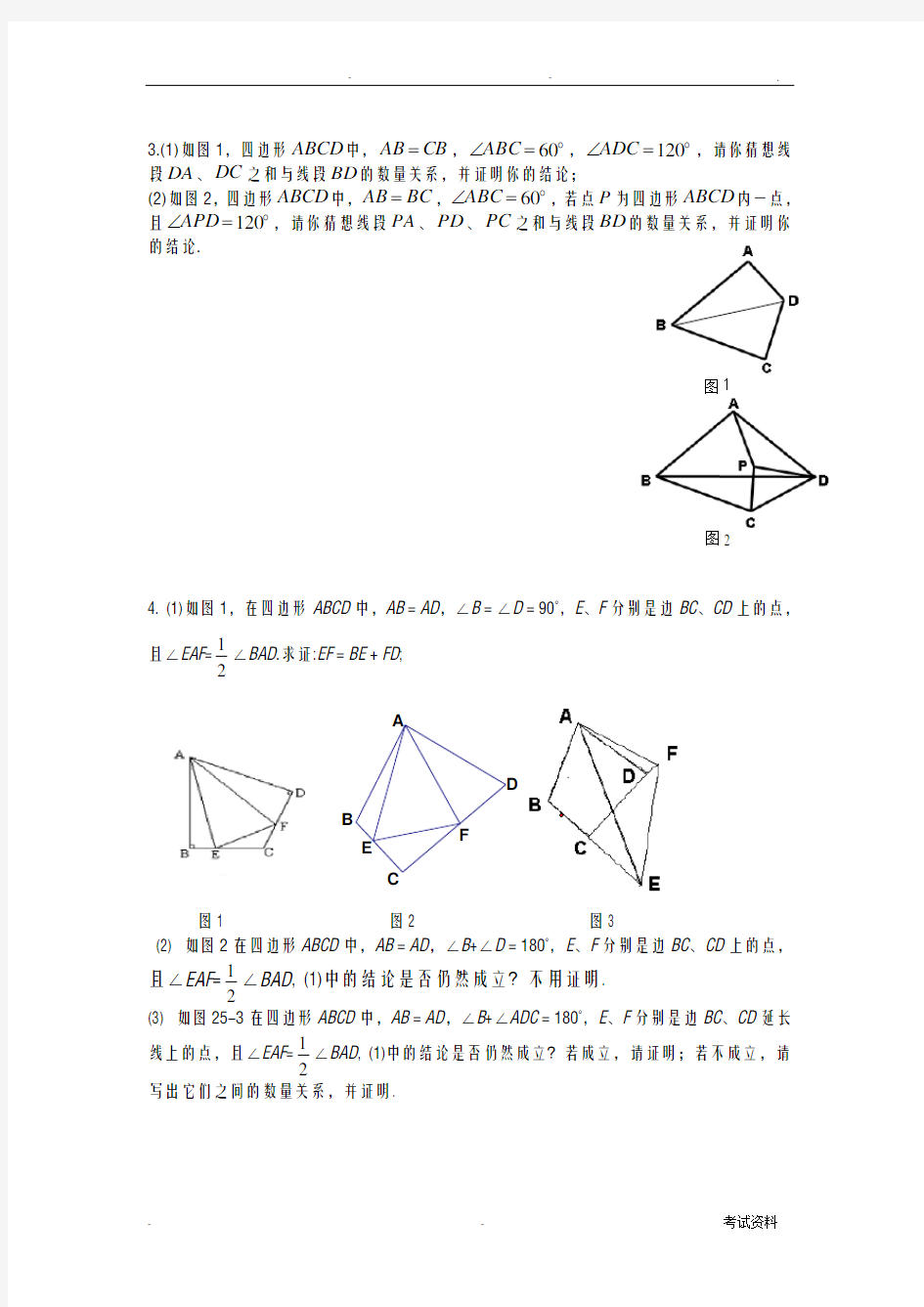
3.(1)如图1,四边形ABCD 中,CB AB =,?=∠60ABC ,?=∠120ADC ,请你猜想线段DA 、DC 之和与线段BD 的数量关系,并证明你的结论;
(2)如图2,四边形ABCD 中,BC AB =,?=∠60ABC ,若点P 为四边形ABCD 内一点,且?=∠120APD ,请你猜想线段PA 、PD 、PC 之和与线段BD 的数量关系,并证明你的结论.
4. (1)如图1,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E 、F 分别是边BC 、CD 上的点,且∠EAF =
1
2
∠BAD .求证:EF =BE +FD ; F
E
D
C
B A
图1 图2 图3
(2) 如图2在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,
且∠EAF =
1
2
∠BAD , (1)中的结论是否仍然成立?不用证明. (3) 如图25-3在四边形ABCD 中,AB =AD ,∠B +∠ADC =180°,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =
1
2
∠BAD , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
图2
图1
5.以ABC ?的两边AB 、AC 为腰分别向外作等腰Rt ABD ?和等腰Rt ACE ?,
90,BAD CAE ∠=∠=?连接DE ,M 、N 分别是BC 、DE 的中点.探究:AM 与DE 的位置及
数量关系.
(1)如图①当ABC ?为直角三角形时,AM 与DE 的位置关系是, 线段AM 与DE 的数量关系是;
(2)将图①中的等腰Rt ABD ?绕点A 沿逆时针方向旋转?θ(0<θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.
6.如图,在平面直角坐标系中,矩形AOBC 在第一象限内,E 是边OB 上的动点(不包括端点),作∠AEF = 90?,使EF 交矩形的外角平分线BF 于点F ,设C (m ,n ).
(1)若m = n 时,如图,求证:EF = AE ;
(2)若m ≠n 时,如图,试问边OB 上是否还存在点E ,使得EF = AE ?若存在,请求出点E 的坐标;若不存在,请说明理由.
(3)若m = tn (t >1)时,试探究点E 在边OB 的何处时,使得EF =(t + 1)AE 成立?并求出点E 的坐标.
x
O
E B
A
y C
F
x
O
E B
A
y
C
F x
O E
B
A
y
C
F
7.如图1,已知∠ABC =90°,△ABE 是等边三角形,点P 为射线BC 上任意一点(点P 与点B 不重合),连结AP ,将线段AP 绕点A 逆时针旋转60°得到线段AQ ,连结QE 并延长交射线
BC 于点F .
(1)如图2,当BP =BA 时,∠EBF =°,猜想∠QFC =°;
(2)如图1,当点P 为射线BC 上任意一点时,猜想∠QFC 的度数,并加以证明;(3)已
知线段AB =32,设BP =x ,点Q 到射线BC 的距离为y ,求y 关于x 的函数关系式.
8. 如图,直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,已知AD =AB =3,BC =4,动点P 从B 点出发,沿线段BC 向点C 作匀速运动;动点Q 从点D 出发,沿线段DA 向点A 作匀速运动.过Q 点垂直于AD 的射线交AC 于点M ,交BC 于点N .P 、Q 两点同时出发,速度都为每秒1个单位长度.当Q 点运动到A 点,P 、Q 两点同时停止运动.设点Q 运动的时间为t 秒. (1)求NC ,MC 的长(用t 的代数式表示);
(2)当t 为何值时,四边形PCDQ 构成平行四边形?
(3)是否存在某一时刻,使射线QN 恰好将△ABC 的面积和周长同时平分?若存在,求出此时t 的值;若不存在,请说明理由;
(4)探究:t 为何值时,△PMC 为等腰三角形?
图1
A
C
B
E
Q
F P 图2
A
B
E Q
P
F C
(如图3)
C
1、解:(1)等腰直角 (2)等腰α (3)结论仍然成立
证明:在ABF EBC ??和中,
BA BE ABF EBC BF BC =??
∠=∠??=?
∴△ABF ≌△EBC. ∴AF=CE. ∠AFB=∠ECB ∵M,N 分别是AF 、CE 的中点, ∴FM=CN. ∴△MFB ≌△NCB. ∴BM=BN. ∠MBF=∠NBC
∴∠MBN=∠MBF+∠FBN=∠FBN+∠NBC=∠FBC= 2、解:(1)PQ =PB
过P 点作MN ∥BC 分别交AB 、DC 于点M 、N 在正方形ABCD 中,AC 为对角线 ∴AM =PM 又∵AB =MN ∴MB=PN ∵∠BPQ =900
∴∠BPM +∠NPQ =900 又∵∠MBP +∠BPM =900
∴∠MBP =∠N PQ ∴Rt △MBP ≌Rt △NPQ, ∴PB =PQ
(2)∵S 四边形PBCQ =S △PBC +S △PCQ
N M
Q P
D
C
B
A
∵AP =x ∴AM =
2
2
x ∴CQ=CD -2NQ =1-2x 又∵S △PBC =
21BC ·BM =21·1·(1-22x )= 21
-4
2x
S △PCQ =
21CQ ·PN=2
1
(1-2x )·(1-22x )
=22
1x -x 423+21
∴S 四边形PBCQ =22
1
x -2x +1 . (0≤x ≤22)
(3)△PCQ 可能成为等腰三角形.
① 当点P 与点A 重合时,点Q 与点D 重合,
PQ=QC ,此时,x=0.
② 当点Q 在DC 的延长线上,且CP=CQ 时, 有:QN=AM=PM=
x 2
2
,CP=2-x , CN=
CP 22=1-x 2
2 CQ=QN -CN =x 22-(1-x 2
2) =2x -1
∴当2-x =x 2-1时 ,x =1
3、解:(1)如图1,延长CD 至E ,使DA DE =.
可证明EAD ?是等边三角形. 联结AC ,可证明BAD ?≌CAE ?. 故BD CE CD DE CD AD ==+=+.
N M Q
P
D
C
B
A
