八年级上数学全等三角形典型例题一

全等三角形典型例题：

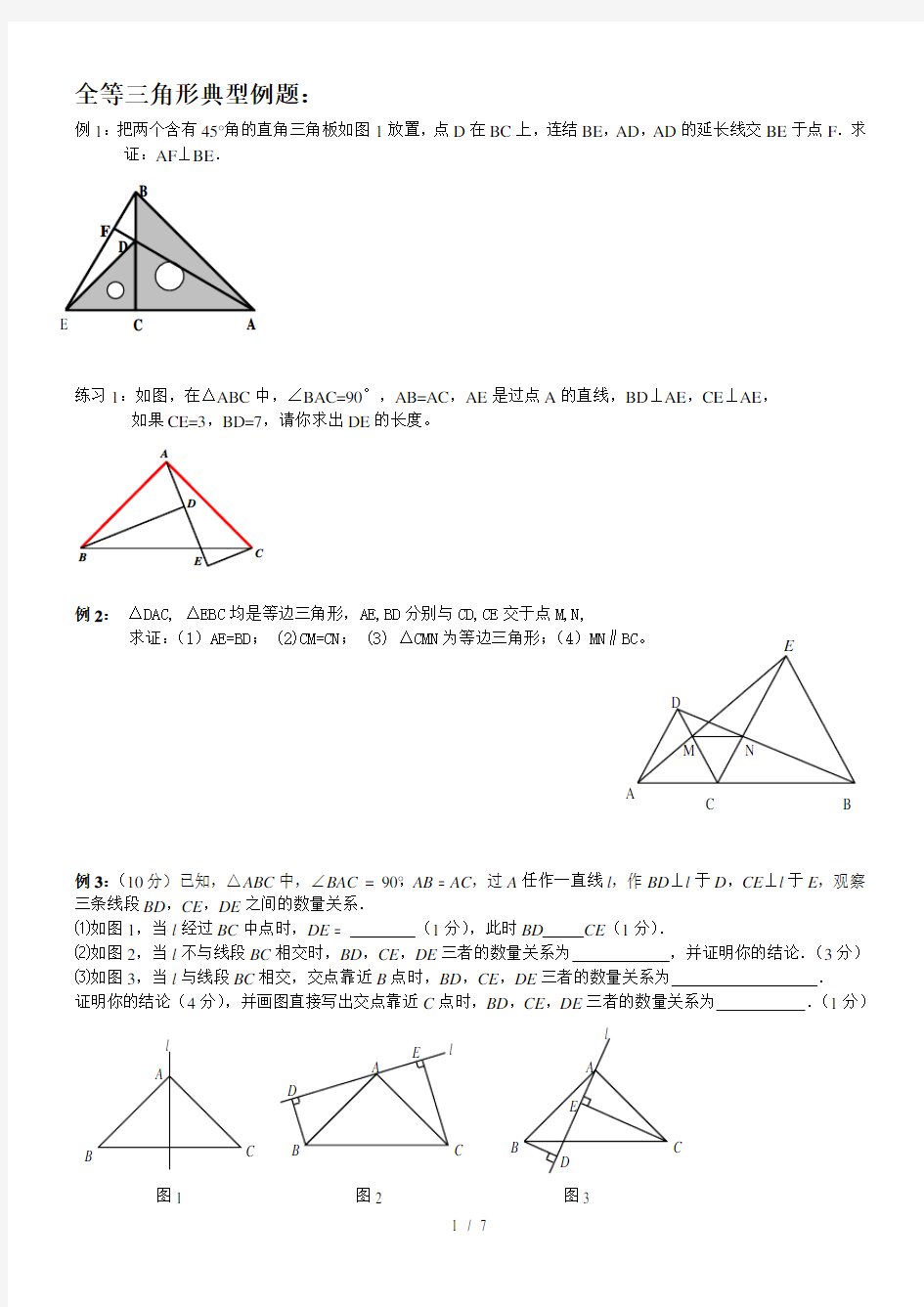
例1：把两个含有45°角的直角三角板如图1放置，点D 在BC 上，连结BE ，AD ，AD 的延长线交BE 于点F ．求

证：AF ⊥BE ．

练习1：如图，在△ABC 中，∠BAC=90°，AB=AC ，

AE 是过点A 的直线，BD ⊥AE ，CE ⊥AE ，

如果CE=3，BD=7，请你求出DE 的长度。

例2： △DAC, △EBC 均是等边三角形，AE,BD 分别与CD,CE 交于点M,N,

求证：（1）AE=BD ； (2)CM=CN ； (3) △CMN 为等边三角形；（4）MN ∥BC 。

例3：（10分）已知，△ABC 中，∠BAC = 90°，AB = AC ，过A 任作一直线l ，作BD ⊥l 于D ，CE ⊥l 于E ，观察三条线段BD ，CE ，DE 之间的数量关系．

⑴如图1，当l 经过BC 中点时，DE = （1分），此时BD CE （1分）．

⑵如图2，当l 不与线段BC 相交时，BD ，CE ，DE 三者的数量关系为 ，并证明你的结论．（3分） ⑶如图3，当l 与线段BC 相交，交点靠近B 点时，BD ，CE ，DE 三者的数量关系为 ． 证明你的结论（4分），并画图直接写出交点靠近C 点时，BD ，CE ，DE 三者的数量关系为 ．（1分）

图1 图2 图3

C

B A l B C

A B C D

E l A B C l

E D

练习1：以直角三角形ABC的两直角边AB、BC为一边，分别向外作等边三角形△ABE和等边△BCF，连结EF、EC。试说明：（1）EF＝EC；（2）EB⊥CF

B

A

F

E

练习2：

如图（1）A、E、F、C在同一直线上，AE=CF，过E、F分别作DE⊥AC，BF⊥AC若AB=CD，G是EF的中点吗？请证明你的结论。

若将⊿ABC的边EC经AC方向移动变为图（2）时，其余条件不变，上述结论还成立吗？为什么？

例四：如图1，已知，AC ⊥CE ，AC=CE ， ∠ABC=∠CDE=90°，

问BD=AB+ED 吗?

[分析] ：

（1）凡是题中的垂直往往意味着会有一组90°角，得到一组等量关系；

（2）出现3个垂直，往往意味着要运用同（等）角的余角相等，得到另一组等量关系； （3）由全等得到边相等之后，还要继续往下面想，这几组相等的边能否组合在一起：

如如图6，除了得到三组对应边相等之外，还可以得到AC=BD 。

解答过程：得到△ABC ≌CDE 之后，可得到BC=DE ，AB=CD ∴ BC+CD=DE+AB （等式性质） 即：BD=AB+DE

[变形1]：如图7， 如果△ABC ≌△CDE ，请说明AC 与CE 的关系。 [注意]：两条线段的关系包括：大小关系（相等，一半，两倍之类）

位置关系（垂直，平行之类）

[变形2]：如图，E 是正方形ABCD 的边DC 上的一点，过点A 作FA ⊥AE 交CB 的延长线于点F ， 求证：DE=BF

[分析]：注意图形中有多个直角，利用同角的余角相等或等式性质可到一组锐角相等。

图6

C

图

5

C

图7

F

E

[变形3]：如图8，在△ABC 中，∠BAC=90°，AB=AC ，AE 是过点A 的直线，

BD ⊥AE ，CE ⊥AE ，

如果CE=3，BD=7，请你求出DE 的长度。

[分析

] ：说明相等的边所在的三角形全等，

题中“AB=AC ”，发现：AB 在Rt △ABD 中，AC 在Rt △CAE 中， 所以尝试着去找条件，去说明它们所在的两个Rt △全等（如图9） 于是：已经存在了两组等量关系：AB=AC ，直角=直角， 再由多个垂直利用同角的余角相等，得到第三组等量关系。

解：由题意可得：在Rt △ABD 中，∠1+∠ABD=90°（直角三角形的两个锐角互余） 又∵ ∠BAC=90°（已知）， 即∠1+∠CAE=90° ∴ ∠ABD=∠CAE （等角的余角相等） 故在△ABD 与△CAE 中，

∠BDA=∠AEC=90°（垂直定义）

∠ABD=∠CAE （已求）

AB=AC （已知）

∴ △ABD ≌△CAE （AAS ） ∴ AE=BD=7，AD=EC=3 （全等三角形的对应边相等） ∴ DE=AE -AD =7-3=4

[变形4]：在△ABC 中，∠ACB= 900，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E 。 （1）当直线MN 绕点C 旋转到图9的位置时，△ADC ≌△CEB ，且 DE=AD+BE 。你能说出其中的道理吗？ （2）当直线MN 绕点C 旋转到图10的位置时， DE =AD-BE 。说说你的理由。

（3）当直线MN 绕点C 旋转到图11

C

C

等腰三角形、等边三角形的全等问题：

[必备知识]：

如右图，由∠1=∠2，可得∠CBE=∠DBA ；反之，也成立。

例五：已知在△ABC 中，AB=AC ，在△ADE 中，AD=AE ，且∠1=∠2，请问BD=CE 吗？

[分析]这类题目的难点在于，需要将本来就存在于同一个三角形中的一组相等的边， 分别放入两个三角形中，看成是一组三角形的对应边，

∴ 题目中所给的△ABC 与△ADE 是用来干扰你的思路的，应该去想如何把两组相等的边联系到一起， 加上所求的“BD=CE ”，你会发现BD 在△ABD 中，CE 在△ACE 中，

这样一来，“AB=AC ”可以理解为：AB 在△ABD 中，AC 在△ACE 中，它们是一组对应边；

“AD=AE ”可以理解为：AD 在△ABD 中，AE 在△ACE 中，它们是一组对应边；

所以只需要说明它们的夹角相等即可。

关键还是在于：说明“相等的边（角）所在的三角形全等” 解： ∵ ∠1=∠2（已知）

∴ ∠1+∠CAD=∠2+∠CAD （等式性质）

即： ∠BAD=∠CAE ∴ 在△ABD 与△ACE 中，

AB=AC （已知） ∠BAD=∠CAE （已求） AD=AE

∴ △ABD ≌△ACE （SAS ）

∴ BD=CE （全等三角形的对应边相等）

[变形1]：如图14，已知∠BAC=∠DAE ，∠1=∠2，BD=CE ，

A

B

E

图13

A

D

请说明△ABD ≌△ACE.吗？为什么？

[分析]：例三是两组边相等，放入一组三角形中，利用SAS 说明全等， 此题是两组角相等，那么该如何做呢?

[变形2]：过点A 分别作两个大小不一样的等边三角形，连接BD ，CE ，请说明它们相等。

[分析]：此题实际上是例三的变形，只不过将等腰三角形换成了等边三角形，只要你根据所求问题，把BD 看成在△ABD 的一边，CE 看成△ACE 的一边，自然就得到了证明的方向。 解：∵△ABC 与△ADE 是等边三角形，

∴ AB=AC ， AD=AE ∠BAC=∠DAE=60° ∴ ∠BAC+∠CAD=∠DAE+∠CAD （等式性质） 即： ∠BAD=∠CAE

[变形3]：如图16—18，还是刚才的条件，把右侧小等边三角形的位置稍加变化，，连接BD ，CE ，请说明它们

这里仅以图17进行说明

解：∵ △ABC 与△ADE 是等边三角形， ∴ AB=AC ， AD=AE

∠BAC=∠DAE=60°

∴∠BAC -∠CAD=∠DAE -∠CAD 【仅这步有差别】

即：∠BAD=∠BAD=∠CAE ∴ 在△ABD 与△ACE 中，

AB=AC （已知）

∠BAD=∠CAE （已求） AD=AE

∴ △ABD ≌△ACE （SAS ）

∴ BD=CE （全等三角形的对应边相等）

B

图15

C

B

A

B

B

B

A

图17

图16，图18的类型，请同学们自己去完成

[变形4]：如图，四边形ABCD 、DEFG 都是正方形，连接AE 、CG ，AE 与CG 相交于点M ，CG 与AD 相交于

点N ．求证：CG AE ；

[分析]：和上面相比，只不过等边三角形换成正方形，60

例六： 如图，△ABC 中，∠C=90°，

AB=2AC ，M 是AB 的中点，点N 在BC 上，MN ⊥AB.

求证：AN 平分∠BAC.

[分析

]：要说明AN 平分∠BAC ，必须说明两角相等，∴可以说明△AMN ≌△CAN 而题中已有了一组直角相等，一组公共边（斜边）

结合题目中条件，比较容易找到一边直角边相等，从而利用HL 定理得到全等。

[变形1]：在Rt △ABC 中，已知∠A=90°，DE ⊥BC 于E 点，如果AD=DE ，BD=CD ，求∠C 的度数

B

C

B