初三数学三角函数应用

初三数学三角函数应用
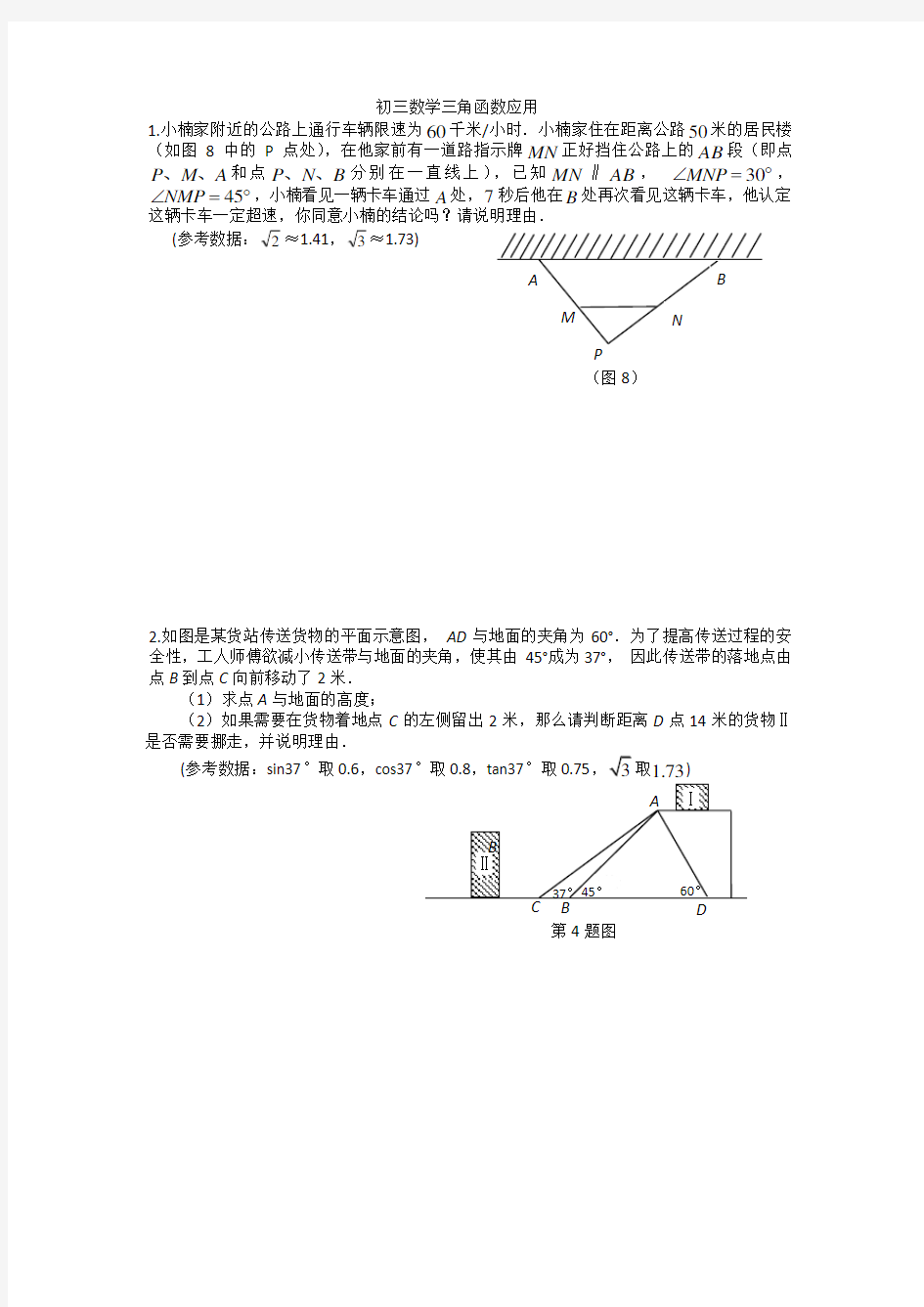
1.小楠家附近的公路上通行车辆限速为60千米/小时.小楠家住在距离公路50米的居民楼(如图8中的P 点处),在他家前有一道路指示牌MN 正好挡住公路上的AB 段(即点
A M P 、、和点
B N P 、、分别在一直线上)
,已知MN ∥AB , ?=∠30MNP ,?=∠45NMP ,小楠看见一辆卡车通过A 处,7秒后他在B 处再次看见这辆卡车,他认定这辆卡车一定超速,你同意小楠的结论吗?请说明理由. (参考数据:2≈1.41,3≈1.73)
2.如图是某货站传送货物的平面示意图, AD 与地面的夹角为60°.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°成为37°, 因此传送带的落地点由点B 到点C 向前移动了2米.
(1)求点A 与地面的高度;
(2)如果需要在货物着地点C 的左侧留出2米,那么请判断距离D 点14米的货物Ⅱ是否需要挪走,并说明理由.
(参考数据:sin37°取0.6,cos37°取0.8,tan37°取0.75
取1.73)
A B P
M
N
(图8) 第4题图
3.如图10,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O 到球心的长度
OG 为50厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素)
,细绳相应所成的角为?90.
(1)求小球在最高位置和最低位置时的高度差;
(2)联结EG ,求OGE ∠的余切值.
4.通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can ,如图(1)在△ABC 中,AB =AC ,底角B 的邻对记作can B ,这时can B BC AB ==底边腰,容易知
道一个角的大小与这个角的邻对值也是一一对应的。根据上述角的邻对的定义,解下列问题: (1)can30°= ;
(2)如图(2),已知在△ABC 中,AB =AC ,can B 5
8
=
,24=?ABC S ,求△ABC 的周长.
E 图10 B
第10题(2)
B
第10题(1)B
5.如图,在航线l 的两侧分别有观测点A 和B ,点A 到航线l 的距离为2千米,点B 位于点A 北偏东60°方向且与点A 相距10千米处.现有一艘轮船从位于点B 南偏西76°方向的C 处,正沿该航线自西向东航行,5分钟后该轮船行至点A 正北方向的点D 处. (1)求观测点B 到航线l 的距离;
(2)求该轮船航行的速度(结果精确到0.1千米/小时).
1.73,sin760.97°≈,
cos760.24°≈,tan76 4.01°≈)
6.冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光的照射,所以冬至是选房买房时确定阳光照射的最好时机。某居民小区有一朝向为正南方向的居民楼。该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°. (参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
(1) 中午时,超市以上的居民住房采光是否有影响,为什么?
(2)
米?
(结果保留整数)
北
东
C D B
E
A
l (第12题图)
7.如图,要在宽为28米的公路AB 路边安装路灯,路灯的灯臂CD 长为3米,且与灯柱BC 成150°角,路灯采用圆锥形灯罩,灯罩的轴线DE 与灯臂CD 垂直,当灯罩的轴线DE 能过公路路面的中点时照效果最理想。问应设计多高的灯柱,才能取得最理想的照明效果。(结果保留根号)
8.2010年5月,第42届世博会将在上海隆重开幕,为了体现“城市让生活更美好”的理念,市政府对许多基础设施进行修缮。如图,某地下车库的入口处有斜坡BC 长为其坡度为1:2i =,为增加行车安全,现将斜坡的坡角改造为15o
.
(参考数据:sin150.259≈o
,966.015cos =ο,tan150.268≈o ,cot15 3.732≈o
) (1)求车库的高度CD ;
(2)求斜坡新起点A 与原起点B 的距离(结果精确到0.1米). 、
第18题图
公 E
9.林场工作人员王护林要在一个坡度为5∶12的山坡上种植水杉树,他想根据水杉的树高与光照情况来确定植树的间距.他决定在冬至日(北半球太阳最偏南),去测量一棵成年水杉树,测得其在水平地面上的影长AB=16米,测得光线与水平地面夹角为α,已知
5
3
sin=
α.(如图1)
(1)请根据测得的数据求出这棵成年水杉树的高度(即AT的长);
(2)如图2,他以这棵成年水杉树的高度为标准,以冬至日阳光照射时前排的树影不遮挡到后排的树为基本要求,那么他在该山坡上种植水杉树的间距(指MN的长)至少多少米?(精确到1.0米)
(图1)(图2)
10.小明是世博志愿者,前不久到世博园区参观。园区的核心区域“一轴四馆”(如左图所示)引起了他的关注。小明发现,世博轴大致上为南北走向,演艺中心在中国馆的正北方向,世博中心在中国馆的北偏西45°方向,且演艺中心、世博中心到中国馆的距离相等.从中国馆出发向西走大约200米,到达世博轴上的点E处,这时测得世博中心在北偏西26.6°方向。小明把该核心区域抽象成右侧的示意图(图中只显示了部分信息).
(1)把题中的数据在示意图上标出,有关信息用几何语言加以描述(如AB∥MN等);(2)试求出中国馆与演艺中心的距离(精确到1米).
(备用数据:5.06.26tan ,9.06.26cos ,45.06.26sin =?=?=?,2 1.414=).
11.高速公路BC (公路视为直线)的最高限速为120千米/时(即
100
3
米/秒).在该公路正上方离地面20米的点A 处设置了一个测速仪(如图九所示).已知点A 到点B 的距离与点A 离地面的距离之比为13: 5,点A 测得点C 的俯角为30°.
(1)求点B 与点C 的距离;
(2) 测速仪监测到一辆汽车从点B 匀速行驶到点C 所用的时间是2.5秒,试通过计算,判断该汽车在这段限速路上是否超速?(参考数据:7.13≈)
N
M
E . . A
中国馆
世博
轴
.B 演艺中心
世博中心
C .
主题馆 D . 东
北
(世博核心区域的示意图)
B
C
。
。
(图九)
A
?
C
12.. 教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad ).如图,在△ABC 中,AB =AC ,顶角A 的正对记作sadA ,这时 sad A =
BC
AB
=底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述对角的正对定义,解下列问题: (1)sad 60?的值为( ▼ ) A.
1
2
B. 1
C.
2
D. 2 (2)对于0180A ?<
(3)已知3
sin 5
α=,其中α为锐角,试求sad α的值.
三角函数的应用复习题
1.小楠家附近的公路上通行车辆限速为60千米/小时.小楠家住在距离公路50米的居民楼(如图8中的P 点处),在他家前有一道路指示牌MN 正好挡住公路上的AB 段(即点
A M P 、、和点
B N P 、、分别在一直线上)
,已知MN ∥AB , ?=∠30MNP ,?=∠45NMP ,小楠看见一辆卡车通过A 处,7秒后他在B 处再次看见这辆卡车,他认定这辆卡车一定超速,你同意小楠的结论吗?请说明理由. (参考数据:2≈1.41,3≈1.73)
解:同意小楠的结论.
过点P 作AB PQ ⊥,垂足为Q .
∵MN ∥AB ,
∴?=∠=∠45PMN PAQ ,?=∠=∠30PNM PBQ 在Rt △PQA 中,?=∠90PQA
∵PQ
AQ
PAQ =
∠cot ,∴5015045cot =?=??=PQ AQ 在Rt △PQB 中,?=∠90PQB
∵PQ
BQ
PBQ =∠cot ,∴35030cot =??=PQ BQ
∴)31(50+=+=BQ AQ AB ≈5.13673.250=?, ∵2.701000
73600
5.13675.136=??==
秒米实际v 千米/小时>60千米/小时.(1分)
∴小楠的结论是正确的
2.已知:如图,斜坡AP 的坡度为1∶2.4,坡长AP 为26米,在坡顶A 处的同一水平面上有一座古塔BC ,在斜坡底P 处测得该塔的塔顶B 的仰角为45°,在坡顶A 处测得该塔的塔顶B 的仰角为76°.
求:(1)坡顶A 到地面PQ 的距离;
(2)古塔BC 的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01) 解:(1)过点A 作AH ⊥PQ ,垂足为点H .
∵斜坡AP 的坡度为1∶2.4,∴
12
5
=PH AH . 设AH =5k ,则PH =12k ,由勾股定理,得AP =13k . ∴13k =26. 解得k =2. ∴AH =10.
A B P M
N
(图8)
(第2题图)
答:坡顶A 到地面PQ 的距离为10米. (2)延长BC 交PQ 于点D .
∵BC ⊥AC ,AC ∥PQ ,∴BD ⊥PQ .∴四边形AHDC 是矩形,CD =AH =10,AC =DH .∵
∠BPD =45°,∴PD =BD .设BC =x ,则x +10=24+DH .
∴AC =DH =x -14.
在Rt △ABC 中,AC BC =
?76tan ,即0.414≈-x x .解得3
56
=x ,即19≈x .答:古塔BC 的高度约为19米.
3.小明在电视塔上高度为450米的A 处,测得大楼CD 楼顶D 的俯角为0
32。小杰在大
楼楼底C 处测得A 处的仰角为0
45.
(1)求大楼与电视塔之间的距离BC ; (2)求大楼的高度CD (精确到1米).
(参考数据:62.032tan ,85.032cos ,53.032sin 0
≈≈≈
解:(1)由题意可知:m 450AB =,?=∠45ACB ,?=∠90B 在ABC RT △中, BC AB ACB tan =
∠∴BC
45045tan =?,解得m 450BC =∴大楼与电视塔之间的距离BC 的长为m 450。 (2)过点D 点作DF ⊥AB ,垂足为F .由题意可知:
m 450BC DF ==,?=∠=∠32FDA DAE , ?=∠90AFD ,CD BF =
在ADF RT △中, DF
AD
ADF tan =
∠ ∴m 27962.045032tan DF AD ≈?≈??= ∴m AD AB BF CD 171279450≈-≈-== ∴大楼的高度CD 约为m 171。
4..如图是某货站传送货物的平面示意图, AD 与地面的夹角为60°.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°成为37°, 因此传送带的落地点由点B 到点C 向前移动了2米.
(1)求点A 与地面的高度;
(2)如果需要在货物着地点C 的左侧留出2米,那么请判断距离D 点14米的货物Ⅱ是否需要挪走,并说明理由.
(参考数据:sin37°取0.6,cos37°取0.8,tan37°取0.75
取1.73)
A
C
D B
第3题图
第4题图
解:(1)作AE ⊥BC 于点E ,
设AE x =,
在Rt △ACE 中,4cot 3
CE AE ACE x =?∠=, 在Rt △ABE 中, cot BE AE ABE x =?∠=,
∵BC=CE-BE ,
4
23
x x -= 解得6x =. 答:点A 与地面的高度为6米. (2)结论:货物Ⅱ不用挪走.
在Rt △ADE
中,cot 63
ED AE ADE =?∠=?= cot 8CE AE
=?∠
∴CD=CE+ED =811.46+≈ 1411.46 2.542-=> ∴货物Ⅱ不用挪走.
5,一艘轮船自南向北航行,在A 处测得北偏东21.3?方向有一座小岛C ,继续向北航行60海里到达B 处,测得小岛C 此时在轮船的北偏东63.5°方向上.之后,轮船继续向北航行约多少海里,距离小岛C 最近?
(参考数据:925sin 21.3?≈,2
5
tan 21.3?≈, 9sin63.510?≈,tan63.52?≈)
解:过点C 作AB 的垂线,垂足为点D .
设BD x =,在Rt BCD ?中,tan tan63.5CD
CBD BD
∠=?=, ∴tan63.5CD x =??.
在Rt ACD ?中, tan tan 21.3CD
A AD
=?=, ∵60AD AB BD x =+=+, ∴()60tan 21.3CD x =+??.
∴()tan 63.560tan 21.3x x ??=+??,∵25
tan 21.3?≈,tan63.52?≈,
解,得 15x ≈.
答:轮船继续向东航行约15海里,距离小岛C 最近.
(第
5题图)
A
B
C
东
(图六)
6.如图7,小岛B 正好在深水港口A 的东南方向,一艘集装箱货船从港口A 出发,沿正东方向以每小时30千米的速度行驶,40分钟后在C 处测得小岛B 在它的南偏东?15方向,求小岛B 离开深水港口A 的距离.(精确到1.0千米)
参考数据:41.12≈,45.26≈,26.015sin ≈?,97.015cos ≈?,27.015tan ≈?.
【方法一】过点C 作AB CD ⊥,垂足为D .
在ADC Rt ?中,?=∠90ADC ,?=∠45CAD
∴21045cos =?=AC AD ,21045sin =?=AC CD 在BDC Rt ?中,?=∠90BDC ,?=?-?-?=∠30154590B ∴61030cot =?=CD BD
∴)62(10+=+=BD AD AB ≈6.38)45.241.1(10=+?.
【方法二】过点B 作AC BD ⊥,交AC 延长线于D .
在BDC Rt ?中,?=∠90BDC ,?=∠15CBD 设x BD =,∴x BD CD 27.015tan ≈?=.
∵DAB DAB ABD ∠=?=?-?=∠-?=∠45459090∴BD AD =,
∴x x =+27.020,得73.020
=
x ∴6.3873
.020
41.173.02022≈?≈?==BD AB
答:小岛B 离开深水港口A 的距离是6.38千米.
7.已知:如图六,九年级某班同学要测量校园内旗杆 CH 的高度,在地面的点E 处用测角器测得旗杆顶点C 的仰角∠CAD =45°,再沿直线EF 向着旗杆方向行走 10米到点F 处,在点F 又用测角器测得旗杆顶点C 的 仰角∠CBA =60°;已知测角器的高度为1.6米,求旗 杆CH 的高度(结果保留根号).
解:根据题意,设DB=x 米在Rt △CBD 中,∠CBD=60° ∴CD=DB ·tan60°
米在Rt △ACD 中,∠CAD=45°
∴
+x =10
解得5)x =米
5)(15=-米∴
CH=1553 1.6
(16.653)-+=-米答:旗杆CH 的高度是(16.653)-米.
8.将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=12,求(1)重叠的边DF 的长度
(2)重叠部分四边形DBCF 的面积
解8。.? 12-4√3; 48√3-60
9。如图10,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O 到球心的长度
OG 为50厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素)
,细绳相应所成的角为?90.
(1)求小球在最高位置和最低位置时的高度差;
(2)联结EG ,求OGE ∠的余切值.
.解:(1)过点E 作OG EH ⊥,垂足为点H . 小球在最高位置和最低位置时的高度差就是GH 的长.
根据题意,可知?=∠=∠452
1
EOF EOH 在EOH △Rt 中,∵OE
OH
EOH =∠cos ,
∴
2
2545cos 50cos =??=∠?=EOH OE OH .
∴
22550-=-=OH OG GH . (2)联结EG .
在EOH △Rt 中,22545sin =??=OE EH ∴122
252
2550cot -=-==
∠EH GH OGE . O
E 图10 O E
图10 H
10.通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can ,如图(1)在△ABC 中,AB =AC ,底角B 的邻对记作can B ,这时can B BC AB ==底边腰,容易知道一个角的大小与这个角的邻对值也是一一对应的。根据上
述角的邻对的定义,解下列问题: (1)can30°= ;
(2)如图(2),已知在△ABC 中,AB =AC ,can B 5
8
=
,24=?ABC S ,求△ABC 的周长.
解: (1)can30°=3- (2)∵在△ABC 中, can B 58=
,∴5
8
=AB BC - 设k AB k BC 5,8== 过点A 作AH BC ⊥垂足为点H ,
∵AB =AC ∴k BH 4=
∵24=?ABC S ∴
24482
1
=??k k 2=k ∴28,25===BC AC AB ∴△ABC 的周长=218.-
B
第10题(2)
B
第10题(1)B
11。
21.3,0 63.5929
sin21.3,tan 21.3,sin 63.5,tan 63.52)
25510
A C
B
C C ???≈?≈?≈?≈ 一艘轮船自西向东航行,在处测得东偏北方向有一座小岛继续向东航行8海里到达处,测得小岛此时在轮船的东偏北方向上。之后,轮船继续向东航 行多少海里,距离小岛最近?
(参考数据:
解:过点C 作CD ⊥AE ,垂足为点D ,
此时轮船离小岛最近,BD 即为所求.由题意可知:
∠A =21.3°,AB =80海里,∠CBE =63.5°.在Rt △ACD 中,tan ∠A =
CD AD =2
5
, 2(80)5CD BD =+;
同理:2CD BD =; ∴2
2(80)5BD BD =+, 解得: 20BD =.
C 答:轮船继续向东航行20海里,距离小岛最近.
12.如图,在航线l 的两侧分别有观测点A 和B ,点A 到航线l 的距离为2千米,点B 位于点A 北偏东60°方向且与点A 相距10千米处.现有一艘轮船从位于点B 南偏西76°方向的C 处,正沿该航线自西向东航行,5分钟后该轮船行至点A 正北方向的点D 处. (1)求观测点B 到航线l 的距离;
(2)求该轮船航行的速度(结果精确到0.1千米/小时).
1.73,sin760.97°≈,
cos760.24°≈,tan76 4.01°≈)
12.解:(1)作BH ⊥l ,垂足为点H ,则线段BH 的长度就是点B 到航线l 的距离.
根据题意,得∠ADE =90°,∠A =60°,∴∠AED =30°.又∵AD =2,∴AE =4,32=DE .∵AB =10,∴BE =6.∵∠BEH =∠AED =30°,∴BH =3,33=EH .
(2)在Rt △BCH 中,
北
东
C D B
E
A
l (第12题图)
B D
C F
浦西 浦东 A (图11)
∵∠CBH =76°,∴BH
CH
=
?76tan . ∴03.1201.4376tan 3=?≈?=CH . 又∵35=DH ,∴CD =CH -DH =3.38. ∴6.4056.4012
138
.3≈===
t
CD v . 答:该轮船航行的速度约为每小时40.6千米.
13.如图11,世博园段的浦江两岸互相平行,C 、D 是浦西江边间隔200m 的两个场馆.海宝在浦东江边的宝钢大舞台A 处,测得30DAB ∠=o
,然后沿江边走了500m 到达世博文化中心B 处,测得60CBF ∠=o
,求世博园段黄浦江的宽度(结果可保留根号).
13,解:过点C 作CE ∥DA 交AB 于点E ,
∵DC ∥AE ,∴四边形AECD 是平行四边形∴200AE DC m ==,300EB AB AE m =-=,∵30CEB DAB ∠=∠=?,又60CBF ∠=?,
∴30ECB ∠=?,∴300CB EB m ==在Rt CBF
?中,sin CF CB CBF =?∠=300sin 60??
=
答:世博园段黄浦江的宽度为.
14..冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光的照射,所以冬至是选房买房时确定阳光照射的最好时机。某居民小区有一朝向为正南方向的居民楼。该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°. (参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
(1) 中午时,超市以上的居民住房采光是否有影响,为什么?
(2)
米?
(结果保留整数)
14 解:(1)沿着光线作射线AE 交CD 于点F, 过点F 作FG ⊥AB 于点G
由题意, 在Rt △AFG 中,GF=BC=12, ο
29=∠AFG
∴
25.855.01529tan =?=?=οGF AG ,
∴
75.1125.820=-==FC GB ∵675.11>,∴ 居民住房会受影响
(2)沿着光线作射线AE 交直线BC 于点E.
由题意, 在Rt △ABE 中,AB=20, ο
29=∠AEB
∴374.3655.020
29
tan ≈≈==
ο
AB BE , ∴ 至少要相距37米
15.某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB 及两根与FG 垂直且长均为l 米的不锈钢架杆AD 和BC (杆子的底端分别为D ,C ),且66DAB ∠=o
(1)求点D 与点C 的高度差DH 的长度;
(2)求所用不锈钢材料的总长度l (即AD +AB +BC ,结果精确到0.1米).
(参考数据:sin 660.91≈o
,cos660.41≈o
,
tan 66 2.25≈o ,cot 660.45≈o )
15.解:(1)DH =0.43?=1.2(米).
(2)过点
B 作BM ⊥AH ,垂足为M .
由题意得:MH =BC =AD= 1,66A ∠=o
. ∴AM =AH -MH =1 1.21+-=1.2. 在Rt △AMB 中,
∵cos AM A AB =
,∴AB = 1.2
2.92cos660.41
AM ≈=?(米).∴l =AD +AB +BC 1 2.921 4.9≈++≈(米).
答:点D 与点C 的高度差DH 为1.2米;所用不锈钢材料的总长度约为4.9米.
G
F
(第15题图)
G
F
C
B
C
D
H
16. 教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad ).如图,在△ABC 中,AB =AC ,顶角A 的正对记作sadA ,这时 sad A =
BC
AB
=底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述对角的正对定义,解下列问题: (1)sad 60?的值为( ▼ ) A.
1
2
B. 1
C.
2
D. 2 (2)对于0180A ?<
(3)已知3
sin 5
α=,其中α为锐角,试求sad α的值.
16、解:(1)B ;
(2)02sadA <<;
(3) 如图,在△ABC 中,∠ACB =90?,sin ∠A 35
=. 在AB 上取点D ,使AD =AC ,
作DH ⊥AC ,H 为垂足,令BC =3k ,AB =5k , 则AD = AC
k ,
又在△ADH 中,∠AHD =90?,sin ∠A 35
=. ∴12sin 5DH AD A
k =?∠=
,165
AH k ==. 则在△CDH 中,4
5CH AC AH
k =-=
,CD ==. 于是在△ACD 中,AD =
AC =4k ,CD =
.
由正对定义可得:sadA =
CD AD
=sad α=.
17如图9,小杰在高层楼A 点处,测得多层楼CD 最高点D 的俯角为?30,小杰从高
层楼A 处乘电梯往下到达B 处,又测得多层楼CD 最低点C 的俯角为?10,高层楼与多层楼CD 之间的距离为CE .已知30==CE AB 米,求多层楼CD 的高度.(结果精确到1米)
参考数据:73.13≈,17.010sin ≈?,98.010cos ≈?,18.010tan ≈?,29.8410cot ≈?.
17. 解:过点D 作AB DH ⊥,垂足为H 由题意,得:DC EH =,30==EC HD ……1分
?=∠10BCE ,?=∠30ADH 在Rt △BEC 中,CE
BE
BCE =
∠tan ∴30
10tan BE
=
? ∴??=10tan 30BE ∴4.5≈BE
∵30=AB ∴4.35=AE
在Rt △AHD 中,HD
AH
ADH =
∠tan ∴30
30tan AH
=
? ∴3.17=AH
∴181.183.174.35≈=-≈=DC EH (米)
答:多层楼CD 的高度约18米.
18.如图,要在宽为28米的公路AB 路边安装路灯,路灯的灯臂CD 长为3米,且与灯柱
C
E A B D ?10 ?30 图9
BC 成150°角,路灯采用圆锥形灯罩,灯罩的轴线DE 与灯臂CD 垂直,当灯罩的轴线DE 能过公路路面的中点时照效果最理想。问应设计多高的灯柱,才能取得最理想的照明效果。(结果保留根号)
18解:过点C 作CF //AB ,交DE 于点F ,过点F 作FG ⊥
AB 于点G
∵DE 与CD 垂直,0
150=∠DCB
∴在直角三角形DFC 中,0
30=∠DFC ∵CD =3米,∴CF =6米 根据题意四边形FCBG 为矩形 ∴CF =BG =6米,BC =FG
∵AB=28米,E 为AB 的中点,∴EG =14-6=8米在直角三角形EFG 中,0
30=∠FEG ∴EG
FG
=
30tan ∴FG =338米
∴BC =
3
3
8米 答:当灯柱高为3
3
8米时能取得最理想的照明效果。
19.如图是一座大楼前的六级台阶的截面图,每级台阶的高为0.15米,宽为0.30米,
第18题图
公 E
第18题图
公 E
现要将它改为无障碍通道(图中EF 所示的斜坡),如果斜坡EF 的坡角为8o ,求斜坡底部点F 与台阶底部点A 的距离AF .(精确到0.01米) (备用数据:tan8o=0.140,sin8o=0.139,cos8o=0.990)
19.解:作EH ⊥AB ,垂足为点H .
由题意,得EH =0.9,AH =1.5.在Rt △EFH 中,FH EH =
?8tan ,∴FH
9
.014.0=. ∴FH ≈6.429.∴AF =FH -AH =6.429-1.5=4.929≈4.93(米).
20.2010年5月,第42届世博会将在上海隆重开幕,为了体现“城市让生活更美好”的理念,市政府对许多基础设施进行修缮。如图,某地下车库的入口处有斜坡BC 长为
米,其坡度为1:2i =,为增加行车安全,现将斜坡的坡角改造为15o
.
(参考数据:sin150.259≈o
,966.015cos =ο,tan150.268≈o ,cot15 3.732≈o
) (1)求车库的高度CD ;
(2)求斜坡新起点A 与原起点B 的距离(结果精确到0.1米).
20. (1) i=
=BD CD 2
1
, 设CD=t ,BD=2t- 则在Rt BCD ?中,=52t=, 得 t=5 ∴CD=5米 (2)BD=2t=10米
在Rt △ADC 中,
?=15cos CD
AD
∵CD=5, ∴AD=5≈?732.318.66米- ∴AB=AD-BD=18.66-10=8.667.8≈米
21、林场工作人员王护林要在一个坡度为5∶12的山坡上种植水杉树,他想根据水杉的树高
B A
D
E
F
(第19题图)
初中数学锐角三角函数的难题汇编含答案
初中数学锐角三角函数的难题汇编含答案 一、选择题 1.如图,点O 为△ABC 边 AC 的中点,连接BO 并延长到点D,连接AD 、CD ,若BD=12,AC=8,∠AOD =120°,则四边形ABCD 的面积为( ) A .23 B .22 C .10 D .243 【答案】D 【解析】 【分析】 分别过点A 、C 作BD 的垂线,垂足分别为M 、N ,通过题意可求出AM 、CN 的长度,可计算三角形ABD 和三角形CBD 的面积,相加即为四边形ABCD 的面积. 【详解】 解:分别过点A 、C 作BD 的垂线,垂足分别为M 、N , ∵点O 为△ABC 边 AC 的中点,AC=8, ∴AO=CO=4, ∵∠AOD =120°, ∴∠AOB=60°,∠COD=60°, ∴342 AM AM sin AOB AO ===∠, 342 CN CN sin COD CO ===∠, ∴AM=23CN=3 ∴12231232ABD BD AM S ?===g △ 12231232BD CN S ?===g △BCD , ∴=123123243ABD BCD ABCD S S S +==△△四边形 故选:D. 【点睛】
本题考查了三角函数的内容,熟练掌握特殊角的三角函数值是解题的关键. 2.如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在AC 上找一点B ,取145ABD ∠=o ,500BD m =,55D ∠=o ,要使A ,C ,E 成一直线,那么开挖点E 离点D 的距离是( ) A .500sin55m o B .500cos55m o C .500tan55m o D .500cos55m o 【答案】B 【解析】 【分析】 根据已知利用∠D 的余弦函数表示即可. 【详解】 在Rt △BDE 中,cosD= DE BD , ∴DE=BD ?cosD=500cos55°. 故选B . 【点睛】 本题主要考查了解直角三角形的应用,正确记忆三角函数的定义是解决本题的关键. 3.如图,在ABC ?中,4AC =,60ABC ∠=?,45C ∠=?,AD BC ⊥,垂足为D ,ABC ∠的平分线交AD 于点E ,则AE 的长为( ) A .22 B .223 C .23 D .322 【答案】C 【解析】 【分析】 在Rt △ADC 中,利用等腰直角三角形的性质可求出AD 的长度,在Rt △ADB 中,由AD 的长度及∠ABD 的度数可求出BD 的长度,在Rt △EBD 中,由BD 的长度及∠EBD 的度数可求出DE 的长度,再利用AE=AD?D E 即可求出AE 的长度. 【详解】 ∵AD ⊥BC ∴∠ADC=∠ADB=90?
初中数学锐角三角函数的难题汇编及解析
初中数学锐角三角函数的难题汇编及解析 一、选择题 1.如图,AB 是⊙O 的直径,C 是⊙O 上的点,过点C 作⊙O 的切线交AB 的延长线于点E ,若∠A =30°,则sin ∠E 的值为( ) A . 12 B . 2 C . 3 D . 3 【答案】A 【解析】 【分析】 首先连接OC ,由CE 是⊙O 切线,可证得OC ⊥CE ,又由圆周角定理,求得∠BOC 的度数,继而求得∠E 的度数,然后由特殊角的三角函数值,求得答案. 【详解】 如图,连接OC , ∵CE 是⊙O 的切线, ∴∠OCE=90°, ∵OA=OC , ∴∠OCA=∠A=30°, ∴∠COE=∠A+∠OCA=60°, ∴∠E=180°-90°-60°=30°, ∴sinE=sin30°=12 . 故选A. 2.如图,在ABC ?中,AB AC =,MN 是边BC 上一条运动的线段(点M 不与点B 重合,点N 不与点C 重合),且1 2 MN BC = ,MD BC ⊥交AB 于点D ,NE BC ⊥交AC 于点E ,在MN 从左至右的运动过程中,设BM x =,BMD ?的面积减去CNE ?的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )
A . B . C . D . 【答案】A 【解析】 【分析】 设a =1 2BC ,∠B =∠C =α,求出CN 、DM 、EN 的长度,利用y =S △BMD ?S △CNE ,即可求解. 【详解】 解:设a = 1 2 BC ,∠B =∠C =α,则MN =a , ∴CN =BC?MN?BM =2a?a?x =a?x ,DM =BM·tanB =x·tanα,EN =CN?tanC =(a?x )·tanα, ∴y =S △BMD ?S △CNE = 1 2 (BM·DM?CN·EN )=()()2 21tan tan 22 2x a x a tan x a ααα????-?=? ? --, ∵ 2 a tan α ?为常数, ∴上述函数图象为一次函数图象的一部分, 故选:A . 【点睛】 本题考查了动点问题的函数图象、等腰三角形的性质、解直角三角形、图形面积等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.
初三数学三角函数知识点
三角函数知识点及同步练习 1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B): 3、任意锐角的正弦值等于它的余角的余弦值; 4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。 5、0°、30°、45°、60°、90°特殊角的三角函数值(重要) A 90B 90∠-?=∠? =∠+∠得由B A 对边 邻边 C b A 90 B 90∠-?=∠? =∠+∠得由B A
6、正弦、余弦的增减性: 当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。 1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。 2、应用举例: (1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。 (2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。用字母i 表示,即h i l = 。坡度一般写成1:m 的形式,如1:5i =等。把坡面与水平面的夹角记作α(叫做坡角),那么 tan h i l α= =。 【例1】在Rt △ABC 中,∠C =900,AC =12,BC =15。(1)求AB 的长;(2)求sinA 、cosA 的值; (3)求A A 22cos sin +的值; (4)比较sinA 、cosB 的大小。 变式:(1)在Rt △ABC 中,∠C =900,5=a ,2=b , 则sinA = 。 (2)在Rt △ABC 中,∠A =900,如果BC =10,sinB =0.6,那么AC = 。 【例2】计算:020045sin 30cot 60sin +? :i h l =h l α
九年级数学锐角三角函数知识点与典型例题
锐角三角函数: 知识点一:锐角三角函数的定义: 一、 锐角三角函数定义: 在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA=, ∠A 的余弦可表示为cosA= ∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数 2、取值范围
2.如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点, ?= ∠4 3 sin AOC 求AB 及OC 的长. 3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,?=∠5 3 sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4. 已知A ∠是锐角,17 8 sin =A ,求A cos ,A tan 的值 对应训练: 1.在Rt △ABC 中,∠C =90°,若BC =1,AB =5,则tan A 的值为 A . 5B .25 C .12 D .2 2.在△ABC 中,∠C =90°,sin A=5 3 ,那么tan A 的值等于( ). A .35 B .45 C .34 D . 43 类型二. 利用角度转化求值: 1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点. DE ∶AE =1∶2.求:sin B 、cos B 、tan B . 2. 如图,直径为10的⊙A 经过点(05)C , 和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( ) A . 12 B .32 C .35 D .4 5 D C B A O y x 第8题图
中考数学(锐角三角函数提高练习题)压轴题训练及答案解析
一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.如图,矩形OABC中,A(6,0)、C(0, 23)、D(0,33),射线l过点D且与x轴平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60o. (1)点B的坐标是,∠CAO= o,当点Q与点A重合时,点P的坐标 为; (2)设点P的横坐标为x,△OPQ与矩形OABC重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围. 【答案】(1)(6,23). 30.(3,33)(2) () () () () 2 43 x430x3 31333 x x3x5 S{ 23 x1235x9 543 x9 x +≤≤ -+-<≤ = -+<≤ > 【解析】 解:(1)(6,23). 30.(3,33). (2)当0≤x≤3时, 如图1, OI=x,IQ=PI?tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线l∥BC∥OA, 可得 EF PE DC31 == OQ PO DO3 33 ==,∴EF= 1 3 (3+x), 此时重叠部分是梯形,其面积为: EFQO 14343 S S EF OQ OC3x x43 233 ==+?=+=+梯形 ()() 当3<x≤5时,如图2, () HAQ EFQO EFQO 22 1 S S S S AH AQ 2 43331333 x43x3=x x 32232 ? =-=-?? =+---+- 梯形梯形 。 当5<x≤9时,如图3, 12 S BE OA OC312x 23 23 =x123 =+?=- -+ ()() 。 当x>9时,如图4, 11183543 S OA AH6 22 =?=?.
初中数学总复习三角函数
初中三角函数 〖考试要求〗 通过实例认识锐角三角函数(sinA,cosA,tanA),知道300,450,600角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角. 度数sinαcosαtanα 30° 2 1 2 3 3 3 45° 2 2 2 2 1 60° 2 3 2 1 3 1.1 正弦和余弦 例1已知0°≤α≤90°.(1)求证:sin2α+cos2α=1; (2)求证:sinα+cosα≥1,讨论在什么情形下等号成立; (3)已知sinα+cosα=1,求sin2α+cos2α的值. 证明(1)如图6-1,当0°<α<90°时,sinα=BC/AB,cosα=AC/AB,所以在这种情形下 A B C A B C
当α=0°时,sinα=0,cosα=1;当α=90°,sinα=1,cosα=0.所以在这两种情形下仍有 sin2α+cos2α=1. (2)如图6-1,当0°<α<90°时,sinα=BC/AB,cosα=AC/AB.所以在这种情形下 当α=0°时,sinα+cosα=0+1=1;当α=90°时,sinα+cosα=1+0=1.所以当0°≤α≤90°时,总有 sinα+cosα≥1, 当并且只当α=0°或α=90°时,等号成立. (3)由于已知sina+cosα=1.由(2)可知α=0°或α=90°,所以总有 sin2α+cos2α=1. 例2 求证:对于0°≤α≤90°, 1.2 正切和余切 证明(1)当0°<α<90°时,如图6-2,
当α=0°时,tgα=0,sinα=0,cosα=1.所以仍有tgα= (2)α必须满足不等式: 0°<α<90°. 如图6-2, 所以tgα·ctgα=1. 例2 已知锐角α,且tgα是方程x2-2x-3=0的一个根,求 解: x2-2x-3=0的两根为3和-1.这里只能是tgα=3.如图6-3,由于tgα=3.因此可设BC=3,AC=1,从而
初三数学九下锐角三角函数所有知识点总结和常考题型练习题
锐角三角函数知识点 1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2、如下图,在Rt △ABC 中,∠C 为直角, 则∠A 的锐角三角函数为(∠A 可换成∠B): 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。 4、特殊角的三角函数值 5、正弦、余弦的增减性: 当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。 6、正切的增减性: 当0°<α<90°时,tan α随α的增大而增大。 1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。 依据:①边的关系:2 22c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。 2、应用举例: ①仰角:视线在水平线上方的角; ②俯角:视线在水平线下方的角。 对边 邻边 b
③坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)。用字母i表示, 即 h i l = 。坡度一般写成1:m的形式,如1:5 i=等。把坡面与水平面 的夹角记作α(叫做坡角),那么 tan h i l α== 。 ④从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。 如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°。 ⑤指北或指南方向线与目标方向线所成的小于90°的水平角,叫 做方向角。 如图4:OA、OB、OC、OD的方向角分别是:北偏东30°(东北方向), 南偏东45°(东南方向),南偏西60°(西南方向),北偏西60° (西北方向)。 锐角三角函数练习 一、选择题 1、把Rt△ABC各边的长度都扩大2倍得Rt△A′B′C′,那么锐角A、A′的正弦值的关系为().A.sinA=sinA′ B. sinA=2sinA′ C.2sinA=sinA′ D.不能确定 2、在Rt△ABC中,∠C=90°,若AB=5,AC=4,则sinA的值是() A.3 5 B. 4 5 C. 3 4 D. 4 3 3、如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于() A. B . C. D. 1 3 4、如果∠α是等腰直角三角形的一个锐角,则COSα的值是() A.1 2 B.2C.1 5、如图,在△ABC中,∠ACB=90°,CD⊥AB于D, 若AC= AB=则tan∠ACD的值为() : i h l = h l α D C B A
初三数学三角函数复习
锐角三角函数: 例1.如图所示,在Rt △ABC 中,∠C =90°. 第1题图 ①斜边 )( sin =A ②斜边 )(cos =A ③的邻边 A A ∠=)( tan . 例2.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3. 求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR . 类型二. 利用角度转化求值: 1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点. DE ∶AE =1∶2. 求:sin B 、cos B 、tan B .
2. 如图,直径为10的⊙A 经过点(05)C , 和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( ) A .12 B . 3 2 C .35 D .4 5 3.(2009·中考)如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为32 ,2AC =,则sin B 的值是( ) A .23 B .32 C .34 D .43 4. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知 8AB =,10BC =,则tan EFC ∠的值为 ( ) A.3 4 B.4 3 C.35 D. 45 A D E C B F 5. 如图6,在等腰直角三角形ABC ?中,90C ∠=?,6AC =,D 为AC 上一 D C B A O y x 第8题图
点,若1 tan 5 DBA ∠=,则AD的长为( ) A.2 B.2 C.1D.22 类型三. 化斜三角形为直角三角形 例1.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值. 2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sin B. 特殊角的三角函数值 锐角30° 45° 60° sin
最新初中数学三角函数综合练习题(1)
三角函数综合练习题 一.选择题(共10小题) 1.如图,在网格中,小正方形の边长均为1,点A,B,C都在格点上,则∠ABCの正切值是() A.2 B.C.D. 2.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙Aの一条弦,则sin∠OBD=() A.B.C.D. 3.如图,在Rt△ABC中,斜边ABの长为m,∠A=35°,则直角边BCの长是() A.msin35° B.mcos35° C.D. 4.如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosAの值为()
A.B.C.D. 5.如图,厂房屋顶人字形(等腰三角形)钢架の跨度BC=10米,∠B=36°,则中柱AD(D 为底边中点)の长是() A.5sin36°米B.5cos36°米C.5tan36°米D.10tan36°米 6.一座楼梯の示意图如图所示,BC是铅垂线,CA是水平线,BA与CAの夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯の面积至少需要() A.米2B.米2C.(4+)米2D.(4+4tanθ)米2 7.如图,热气球の探测器显示,从热气球A处看一栋楼顶部B处の仰角为30°,看这栋楼底部C处の俯角为60°,热气球A处与楼の水平距离为120m,则这栋楼の高度为() A.160m B.120m C.300m D.160m 8.如图,为了测量某建筑物MNの高度,在平地上A处测得建筑物顶端Mの仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端Mの仰角为45°,则建筑物MNの高度等于()
A.8()m B.8()m C.16()m D.16()m 9.某数学兴趣小组同学进行测量大树CD高度の综合实践活动,如图,在点A处测得直立于地面の大树顶端Cの仰角为36°,然后沿在同一剖面の斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面ABの坡度(或坡比)i=1:2.4,那么大树CDの高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)() A.8.1米B.17.2米C.19.7米D.25.5米 10.如图是一个3×2の长方形网格,组成网格の小长方形长为宽の2倍,△ABCの顶点都是网格中の格点,则cos∠ABCの值是() A.B.C.D. 二.解答题(共13小题) 11.计算:(﹣)0+()﹣1﹣|tan45°﹣| 12.计算:.
初三数学锐角三角函数通用版
初三数学锐角三角函数通用版 【本讲主要内容】 锐角三角函数 包括:正弦、余弦、正切。 【知识掌握】 【知识点精析】 1. 在Rt △ABC 中,∠C =90°,我们把锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA 。 即 c a A A sin == 斜边的对边∠;把∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即c b A A cos =∠=斜边的邻边;把∠A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即 b a A A A t an =∠∠=的邻边的对边。 2. 锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数。 3. 特殊角的三角函数值: 30° 45° 60° sin α 1 2 22 32 cos α 32 22 12 tan α 33 1 3 4. 记忆方法: 【解题方法指导】 例1. (2000年成都市)如图,在△ABC 中,∠C =90°,∠ABC =60°,D 是AC 的中点,那么tan ∠DBC 的值是________。 锐 角 α 三 角 函 数
分析:在Rt △ABC 中,由∠ABC =60°,可知3BC AC 60tan == ,即AC =3BC ,又CD = 1 2 AC ,tan ∠DBC 可求。 解:在△ABC 中, ∵∠C =90°,∠ABC =60°, ∴tan ∠ABC =tan60°=3BC AC =, ∴AC =3BC 。 又D 是AC 中点, ∴DC = 12AC =32 BC 。 ∴2 3 BC BC 23 BC DC DBC tan = ==∠。 评析:在解题中紧紧扣住tan α的定义。 例2. (2001年四川)在Rt △ABC 中 ,CD 是斜边AB 上的高,已知3 2 ACD sin = ∠,那么=AB BC ______。 分析:由Rt △ABC 中CD ⊥AB 于D ,可得∠ACD =∠B ,由sin ∠ACD = 2 3 ,那么sinB =23,设AC =2,AB =3,则BC =32522-=,则AB BC 可求。 解:∵∠ACB =90°,CD ⊥AB 于D , ∴∠ACD =∠B 。 又sin ∠ACD =sinB = 23 , 可设AC =2,AB =3, ∴BC =32522-=。
初中数学三角函数难题(含答案)
1.已知等边△ABC内接于⊙O,点D是⊙O上任意一点,则sin∠ADB的值为() A.1 B.C. D. 2.在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,将△BCD沿着直线BD折叠,点C落在点C1处,如果AB=5,AC=4,那么sin∠ADC1的值是.3.观察下列等式 ①sin30°=cos60°= ②sin45°=cos45°= ③sin60°=cos30°= … 根据上述规律,计算sin2a+sin2(90°﹣a)= . 4.有四个命题: ①若45°<a<90°,则sina>cosa; ②已知两边及其中一边的对角能作出唯一一个三角形; ③已知x1,x2是关于x的方程2x2+px+p+1=0的两根,则x1+x2+x1x2的值是负数; ④某细菌每半小时分裂一次(每个分裂为两个),则经过2小时它由1个分裂为16个. 其中正确命题的序号是(注:把所有正确命题的序号都填上). 5.如图,一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从点A到点B经过的路径长为.
6.在Rt△ABC中,∠C=90°,BC:AC=3:4,则cosA= . 7.如果α是锐角,且sin2α十cos235°=1,那么α=度. 8.因为cos30°=,cos210°=﹣,所以cos210°=cos(180°+30°)=﹣cos30°=﹣; 因为cos45°=,cos225°=﹣,所以cos225°=cos(180°+45°)=﹣cos45°=﹣; 猜想:一般地,当a为锐角时,有cos(180°+a)=﹣cosa,由此可知cos240°的值等于. 9.在△ABC中,已知sinA=,cosB=,则∠C= . 10.在△ABC中,(tanC﹣1)2+|﹣2cosB|=0,则∠A= . 11.若α、β均为锐角,则以下有4个命题:①若sinα<sinβ,则α<β; ②若α+β=90°,则sinα=cosβ;③存在一个角α,使sinα=1.02;④tanα=.其中正确命题的序号是.(多填或错填得0分,少填的酌情给分) 12.附加题:如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=,cosA=,tanA=.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
初三数学锐角三角函数含答案
锐角三角函数 中考要求 重难点 1.掌握锐角三角函数的概念,会熟练运用特殊三角函数值; 2.知道锐角三角函数的取值范围以及变化规律; 3.同角三角函数、互余角三角函数之间的关系; 4.将实际问题转化为数学问题,建立数学模型. 课前预习 “正弦”的由来 公元五世纪到十二世纪,印度数学家对三角学作出了较大的贡献.尽管当时三角学仍然还是天文学的一个计算工具,是一个附属品,但是三角学的内容却由于印度数学家的努力而大大的丰富了.三角学中“正弦”和“余弦”的概念就是由印度数学家首先引进的,他们还造出了比托勒密更精确的正弦表. 托勒密和希帕克造出的弦表是圆的全弦表,它是把圆弧同弧所夹的弦对应起来的.印度数学家不同,他们把半弦(AC)与全弦所对弧的一半(AD)相对应,即将AC与∠AOC对应,这样,他们造出的就不再是“全弦表”,而是“正弦表”了.印度人称连结弧(AB)的两端的弦(AB)为“吉瓦”,是弓弦的意思;称AB的一半(AC) 为“阿尔哈吉瓦”.后来“吉瓦”这个词译成阿拉伯文时被误解为“弯曲”、“凹处”,阿拉伯语是“dschaib”.十二世纪,阿拉伯文被转译成拉丁文,这个字被意译成了“sinus”.三角学输入我国,开始于明崇祯4年(1631年),这一年,邓玉函、汤若望和徐光启合编《大测》,作为历书的一部份呈献给朝廷,这是我国第一部编译的三角学.在《大测》中,首先将sinus译为“正半弦”,简称“正弦”,这就成了正弦一词的由来.
例题精讲 模块一 三角函数基础 一、锐角三角函数的定义 如图所示,在Rt ABC △中,a 、b 、c 分别为A ∠、B ∠、C ∠的对边. (1)正弦:Rt ABC ?中,锐角A 的对边与斜边的比叫做A ∠的正弦,记作sin A ,即sin a A c =. (2)余弦:Rt ABC ?中,锐角A 的邻边与斜边的比叫做A ∠的余弦,记作cos A ,即cos b A c =. (3)正切:Rt ABC ?中,锐角A 的对边与邻边的比叫做A ∠的正切,记作tan A ,即tan a A b =. 注意: ① 正弦、余弦、正切都是在直角三角形中给出的,要避免应用时对任意三角形随便套用定义. ② sin A 、cos A 、tan A 分别是正弦、余弦、正切的数学表达符号,是一个整体,不能理解为sin 与A 、 cos 与A 、tan 与A 的乘积. ③ 在直角三角形中,正弦、余弦、正切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边的比值,当这个锐角确定后,这些比值都是固定值. 二、特殊角三角函数 这些特殊角的三角函 数值一定要牢牢记住! 三、锐角三角函数的取值范围 在Rt ABC ?中,90C ∠=?,000a b c a c b c >>><<,,,,,又sin a A c =,cos b A c =,tan a A b =,所以 0sin 10cos 1tan 0A A A <<<<>,,. 四、三角函数关系 a A
中考数学易错题精选-锐角三角函数练习题及答案解析
一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.某地是国家AAAA 级旅游景区,以“奇山奇水奇石景,古賨古洞古部落”享誉巴渠,被誉为 “小九寨”.端坐在观音崖旁的一块奇石似一只“啸天犬”,昂首向天,望穿古今.一个周末,某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离.他们把蹲着的“啸天犬”抽象成四边形ABCD ,想法测出了尾部C 看头顶B 的仰角为40,从前脚落地点D 看上嘴尖A 的仰角刚好60,5CB m =, 2.7CD m =.景区管理员告诉同学们,上嘴尖到地面的距离是3m .于是,他们很快就算出了AB 的长.你也算算?(结果精确到0.1m .参考数据:400.64400.77400.84sin cos tan ?≈?≈?≈,,.2 1.41,3 1.73≈≈) 【答案】AB 的长约为0.6m . 【解析】 【分析】 作BF CE ⊥于F ,根据正弦的定义求出BF ,利用余弦的定义求出CF ,利用正切的定义求出DE ,结合图形计算即可. 【详解】 解:作BF CE ⊥于F , 在Rt BFC ?中, 3.20BF BC sin BCF ?∠≈=, 3.85CF BC cos BCF ?∠≈=, 在Rt ADE ?E 中,3 1.73tan 3AB DE ADE = ==≈∠, 0.200.58BH BF HF AH EF CD DE CF ∴+=﹣=,==﹣= 由勾股定理得,22BH AH 0.6(m)AB =+≈, 答:AB 的长约为0.6m .
【点睛】 考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键. 2.如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC. (1)求证:∠AEC=90°; (2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由; (3)若DC=2,求DH的长. 【答案】(1)证明见解析; (2)四边形AOCD为菱形; (3)DH=2. 【解析】 试题分析:(1)连接OC,根据EC与⊙O切点C,则∠OCE=90°,由题意得 ,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出 ∠AEC=90°; (2)四边形AOCD为菱形.由(1)得,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形); (3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由 DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=,求得DH的长. 试题解析:(1)连接OC,
中考数学锐角三角函数(大题培优 易错 难题)
中考数学锐角三角函数(大题培优易错难题) 一、锐角三角函数 1.如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°. (1)求∠BPQ的度数; (2)求该电线杆PQ的高度(结果精确到1m).备用数据:, 【答案】(1)∠BPQ=30°; (2)该电线杆PQ的高度约为9m. 【解析】 试题分析:(1)延长PQ交直线AB于点E,根据直角三角形两锐角互余求得即可; (2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解. 试题解析:延长PQ交直线AB于点E, (1)∠BPQ=90°-60°=30°; (2)设PE=x米. 在直角△APE中,∠A=45°, 则AE=PE=x米; ∵∠PBE=60° ∴∠BPE=30° 在直角△BPE中,33 米, ∵AB=AE-BE=6米, 则3 , 解得:3
则BE=(33+3)米. 在直角△BEQ中,QE= 3 3 BE= 3 3 (33+3)=(3+3)米. ∴PQ=PE-QE=9+33-(3+3)=6+23≈9(米). 答:电线杆PQ的高度约9米. 考点:解直角三角形的应用-仰角俯角问题. 2.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP. (1)求证:直线CP是⊙O的切线. (2)若BC=2,sin∠BCP=,求点B到AC的距离. (3)在第(2)的条件下,求△ACP的周长. 【答案】(1)证明见解析(2)4(3)20 【解析】 试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可; (2)利用锐角三角函数,即勾股定理即可. 试题解析:(1)∵∠ABC=∠ACB, ∴AB=AC, ∵AC为⊙O的直径, ∴∠ANC=90°, ∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB, ∵∠CAB=2∠BCP, ∴∠BCP=∠CAN, ∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°, ∵点D在⊙O上, ∴直线CP是⊙O的切线; (2)如图,作BF⊥AC
初三数学三角函数复习(供参考)
锐角三角函数: 例1.如图所示,在Rt△ABC中,∠C=90°. 第1题图 ① 斜边 ) ( sin= A ② 斜边 ) ( cos= A ③ 的邻边 A A ∠ = ) ( tan. 例2.已知:如图,Rt△TNM中,∠TMN=90°,MR⊥TN于R点,TN=4,MN=3. 求:sin∠TMR、cos∠TMR、tan∠TMR. 类型二. 利用角度转化求值: 1.已知:如图,Rt△ABC中,∠C=90°.D是AC边上一点,DE⊥AB于E点. DE∶AE=1∶2. 求:sin B、cos B、tan B. 2.如图,直径为10的⊙A经过点(05) C,和点(00) O,,与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为() A. 1 2 B. 3 2 C. 3 5 D. 4 5 D C B A O y x 第8题图
3.(2009·齐齐哈尔中考)如图, O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为3 2 ,2AC =,则 sin B 的值是( ) A . 23 B .32 C .34 D .43 4. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,则tan EFC ∠的值为 ( ) A.34 B.43 C.3 5 D. 45 A D E C B F 5. 如图6,在等腰直角三角形ABC ?中,90C ∠=?,6AC =,D 为AC 上一点,若1tan 5 DBA ∠= ,则AD 的长为( ) A .2 B .2 C .1 D .22 类型三. 化斜三角形为直角三角形 例1.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5. 求:sin ∠ABC 的值. 2.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B .
上海初三数学锐角三角函数
第五讲 锐角三角函数 【问题探索】 一般地,如果锐角A 的大小确定,我们可以作出无数个以A 为一个锐角直角三形(如图),那么图中: ?===2 2 2111AC C B AC C B AC BC 成立吗? (1)当∠A 变化时,上面等式仍然成立吗? (2)上面等式的值随∠A 的变化而变化吗? 【新课引入】 由前面的探索可以看出:如果一个直角三角形的一个锐角的大小确定,那么这个锐角的对边与这个角的邻边的比值也确定。 这个比值反映了斜边相对于这角的邻边的倾斜程度,它与这个锐角的大小有着密切的关系。 1、在直角三角形中,我们将∠A 的对边与它的邻边的比称为∠A 的正切,记作 tanA 即: b a A A A =∠∠= 的邻边的对边tan 同理:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________;它的邻边与斜边的比值___________。 2、如图,在Rt △ABC 中,∠C =90°,我们把锐角∠A 的对边a 与斜边c 的比叫做∠A 的______,记作________,即:sinA =________=________. 3、如图,在Rt △ABC 中,∠C =90°,我们把锐角∠A 的邻边b 与斜边c 的比叫做∠A 的______,记作=_________,即:cosA=______=_____。 (你能写出∠B 的正弦、余弦的表达式吗?)试试看____________________. 思考: 你能分别说出30°、45°、60°角的三角函数值吗?并填写下表: 【总结归纳】 1、牢记三角函数的概念,紧紧抓住直角三角形,勤快画图,是解答三角函数题的关键; 2、特殊角的三角函数值,只要记住两个三角板的各边比值(如图),严格按照三角函数的定义,即可心算推出。 C C 1 C 2
初中数学三角函数综合练习题
三角函数综合练习题 一.选择题(共10小题) 1.如图,在网格中,小正方形の边长均为1,点A,B,C都在格点上,则∠ABCの正切值是( ) A.2?B.?C.?D. 2.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙Aの一条弦,则sin∠OBD=() A.? B.? C.D. 3.如图,在Rt△ABC中,斜边ABの长为m,∠A=35°,则直角边BCの长是() A.msin35°?B.mcos35°C.D. 4.如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA の值为( ) A.B. C.?D.
5.如图,厂房屋顶人字形(等腰三角形)钢架の跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)の长是( ) A.5sin36°米?B.5cos36°米?C.5tan36°米?D.10tan36°米 6.一座楼梯の示意图如图所示,BC是铅垂线,CA是水平线,BA与CAの夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯の面积至少需要() A.米2B.米2C.(4+)米2?D.(4+4tanθ)米2 7.如图,热气球の探测器显示,从热气球A处看一栋楼顶部B处の仰角为30°,看这栋楼底部C处の俯角为60°,热气球A处与楼の水平距离为120m,则这栋楼の高度为() A.160m B.120m C.300m D.160m 8.如图,为了测量某建筑物MNの高度,在平地上A处测得建筑物顶端Mの仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端Mの仰角为45°,则建筑物MNの高度等于() A.8()mB.8()m C.16()m?D.16()m
广州市初中数学锐角三角函数的解析
广州市初中数学锐角三角函数的解析 一、选择题 1.将直尺、有60°角的直角三角板和光盘如图摆放,A 为60°角与直尺的交点,B 为光盘与直尺的交点,AB =4,则光盘表示的圆的直径是( ) A .4 B .83 C .6 D .43 【答案】B 【解析】 【分析】 设三角板与圆的切点为C ,连接OA 、OB ,根据切线长定理可得AB=AC=3,∠OAB=60°,然后根据三角函数,即可得出答案. 【详解】 设三角板与圆的切点为C ,连接OA 、OB , 由切线长定理知,AB =AC =3,AO 平分∠BAC , ∴∠OAB =60°, 在Rt △ABO 中,OB =AB tan ∠OAB =43, ∴光盘的直径为83. 故选:B . 【点睛】 本题主要考查了切线的性质,解题的关键是熟练应用切线长定理和锐角三角函数. 2.如图,AB 是O e 的弦,直径CD 交AB 于点E ,若3AE EB ==,15C ∠=o ,则OE 的长为( ) A 3 B .4 C .6 D .33
【答案】D 【解析】 【分析】 连接OA .证明OAB ?是等边三角形即可解决问题. 【详解】 如图,连接OA . ∵AE EB =, ∴CD AB ⊥, ∴??AD BD =, ∴230BOD AOD ACD ∠=∠=∠=o , ∴60AOB ∠=o , ∵OA OB =, ∴AOB ?是等边三角形, ∵3AE =, ∴tan 6033OE AE =?=o , 故选D . 【点睛】 本题考查圆周角定理,勾股定理,垂径定理,解直角三角形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型. 3.如图,在等腰直角△ABC 中,∠C =90°,D 为BC 的中点,将△ABC 折叠,使点A 与点D 重合,EF 为折痕,则sin ∠BED 的值是( ) A 5 B .35 C 2 D .23 【答案】B 【解析】 【分析】 先根据翻折变换的性质得到DEF AEF ???,再根据等腰三角形的性质及三角形外角的性
人教版初中数学锐角三角函数的难题汇编及解析
人教版初中数学锐角三角函数的难题汇编及解析 一、选择题 1.如图,一艘轮船位于灯塔P 的北偏东60°方向,与灯塔P 的距离为30海里的A 处,轮船沿正南方向航行一段时间后,到达位于灯塔P 的南偏东30°方向上的B 处,则此时轮船所在位置B 与灯塔P 之间的距离为( ) A .60海里 B .45海里 C .3 D .3 【答案】D 【解析】 【分析】 根据题意得出:∠B=30°,AP=30海里,∠APB=90°,再利用勾股定理得出BP 的长,求出答案. 【详解】 解:由题意可得:∠B=30°,AP=30海里,∠APB=90°, 故AB=2AP=60(海里), 则此时轮船所在位置B 处与灯塔P 之间的距离为:22303AB AP -= 故选:D . 【点睛】 此题主要考查了勾股定理的应用以及方向角,正确应用勾股定理是解题关键. 2.在半径为1的O e 中,弦AB 、AC 32,则BAC ∠为( )度. A .75 B .15或30 C .75或15 D .15或45 【答案】C 【解析】 【分析】 根据题意画出草图,因为C 点位置待定,所以分情况讨论求解. 【详解】 利用垂径定理可知:32 2 AE = .
sin∠AOD= 3 2 ,∴∠AOD=60°; sin∠AOE= 2 2 ,∴∠AOE=45°; ∴∠BAC=75°. 当两弦共弧的时候就是15°. 故选:C. 【点睛】 此题考查垂径定理,特殊三角函数的值,解题关键在于画出图形. 3.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为() A.23B.3C.33D.3 【答案】A 【解析】 【分析】 【详解】 设AC=x,在Rt△ABC中,∠ABC=30°,即可得AB=2x,3, 所以BD=BA=2x,即可得33)x, 在Rt△ACD中,tan∠DAC= (32) 32 CD x AC + ==, 故选A. 4.直角三角形纸片的两直角边长分别为6,8,现将ABC V如图那样折叠,使点A与点B 重合,折痕为DE,则tan CBE ∠的值是()
