超松弛迭代法求解泊松方程

计算流作业
1. 题目
对1512cm cm ?的矩形平板,假设板表面绝热,仅在四条边有热流通过,
且导热系数为常数。设一条15cm 边温度保持为100?,其余三条边温度为20?。
计算板内稳定的温度场并绘出等温线。采用迭代法计算时,采用不同的松弛
因子,并比较收敛速度,观察在不同的网格尺度下,最佳松弛因子的变化。
2. 理论基础
超松弛SOR 迭代法迭代公式为:
11212,,1,1,,1,1,2(1)(())2(1)m m m m m m i j i j i j i j i j i j i j x ω
ψωψψψβψψζβ++++-+-=-++++-+
3. 结果分析
计算时取,x y 方向网格数分别为(4,5),(8,10),(32,40),松弛因子取值范围
为1.0,1.0475,1.095, 1.95。控制固定余量为510-
3.1 温度场
网格尺度为0.5dx dy cm ==时,最佳松弛因子下的平板温度场分布结果基本
上是对称的。
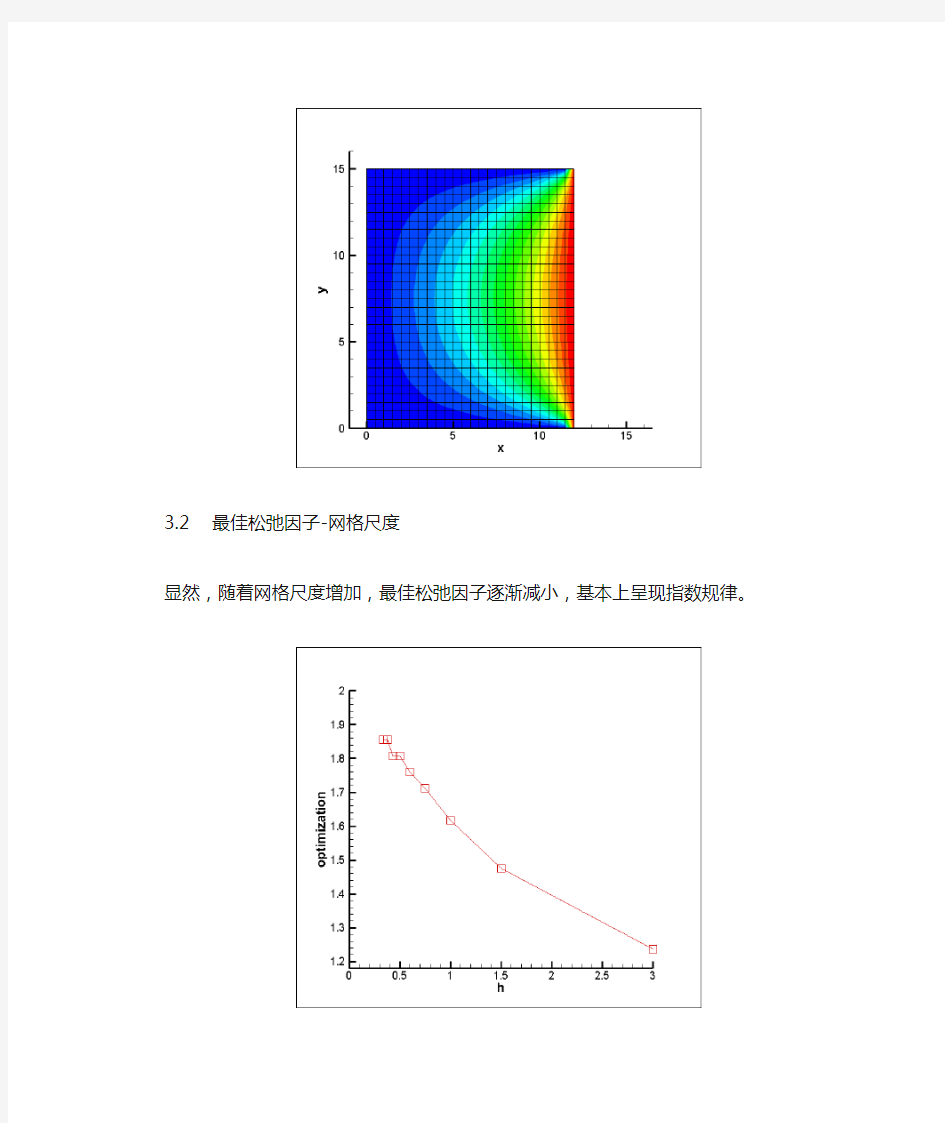
3.2最佳松弛因子-网格尺度
显然,随着网格尺度增加,最佳松弛因子逐渐减小,基本上呈现指数规律。
4.附件
!初始温度分布
subroutine initial(tt_in,nx_in,ny_in)
implicit none
integer::i,j
integer,intent(in)::nx_in,ny_in !横纵网格数
real(kind=8),dimension(0:nx_in,0:ny_in)::tt_in !温度矩阵
tt_in=0.
tt_in(0,0:ny_in)=20.
tt_in(nx_in,0:ny_in)=100.
tt_in(1:(nx_in-1),0)=20.
tt_in(1:(nx_in-1),ny_in)=20.
do i=1,nx_in-1
do j=1,ny_in-1
tt_in(i,j)=60.
end do
end do
end subroutine initial
!超松弛迭代法
subroutine sor(tt_sor,nx_sor,ny_sor,ome,be)
implicit none
integer::i,j
integer,intent(in)::nx_sor,ny_sor !横纵网格数
real(kind=8),dimension(0:nx_sor,0:ny_sor)::tt_sor !温度
real(kind=8),intent(in)::ome,be !松弛因子,网格参数h
real(kind=8)::tem1
do i=1,nx_sor-1
do j=1,ny_sor-1
tem1=tt_sor(i+1,j)+tt_sor(i-1,j)+be**2*(tt_sor(i,j+1)+tt_sor(i,j-1)) tt_sor(i,j)=(1-ome)*tt_sor(i,j)+ome*tem1/2./(1+be**2)
end do
end do
end subroutine sor
program poisson
implicit none
integer::i,j,k,l
integer,parameter::numk=8 !计算时取的网格大小种类数
real(kind=8),allocatable,dimension(:,:)::tem !温度
integer::numx,numy !横纵网格数
real(kind=8),parameter::lx=12.,ly=15. !计算域长宽
integer,parameter::nw=20 !计算时omega取值的数目
integer,dimension(nw)::ncell !存储同一omega下迭代需要的步数 real(kind=8)::om,bt !松弛因子,网格参数h
real(kind=8)::dx,dy !横纵方向上的网格参数
integer::ct !中间变量
real(kind=8)::w_opt !最佳松弛因子
integer,parameter::status=-1 !状态变量.1-计算不同网格尺度下的最佳松弛因子
!-1-计算特定尺度,取最佳松弛因子时得到的最终温度分布
open(unit=15,file='poisson.dat')
open(unit=16,file='poisson2.txt')
write(16,'("title = data")')
write(16,'("variables = x,y,t")')
write(16,'("zone i=",i4,3x,"j=",i4)')8,nw
do l=1,8
numx=4*l
numy=5*l
dx=lx/numx
dy=ly/numy
bt=dx/dy
allocate(tem(0:numx,0:numy))
ct=10**10
do k=1,nw
om=1.+0.95*dble(k)/dble(nw)
call caclulate_w(tem,numx,numy,om,ncell(k),bt)
write(16,'(1x,d15.5,3x,d15.5,3x,i10)')l,om,ncell(k) if(ncell(k) ct=ncell(k) w_opt=om end if end do if(status==1) then write(15,'(1x,d15.5,3x,d15.5)')dx,w_opt else if(status==-1 .and. l==6) then write(15,'("title = data")') write(15,'("variables = x,y,t")') write(15,'("zone i=",i4,3x,"j=",i4)')numx+1,numy+1 call caclulate_w(tem,numx,numy,w_opt,ct,bt) do j=0,numy do i=0,numx write(15,*)i*dx,j*dy,tem(i,j) end do end do end if deallocate(tem) end do end program poisson !计算特定网格和松弛因子下的温度 subroutine caclulate_w(tt,nx,ny,omega,nncell,beta) implicit none integer::i,j integer,intent(in)::nx,ny !横纵网格数 real(kind=8)::error=1.d-5 !误差限 integer,intent(out)::nncell !存储迭代次数 real(kind=8)::omega,etem,beta !etem-两次计算间的平均误差 real(kind=8),dimension(0:nx,0:ny)::tem0 !存储上一次计算得到的温 度矩阵 real(kind=8),dimension(0:nx,0:ny)::tt !温度矩阵 etem=1.d10 nncell=0 call initial(tt,nx,ny) do while(etem>error) nncell=nncell+1 tem0=tt call sor(tt,nx,ny,omega,beta) etem=0. do i=1,nx-1 do j=1,ny-1 etem=etem+(tt(i,j)-tem0(i,j))**2 end do end do etem=sqrt(etem) end do end subroutine caclulate_w 拉普拉斯方程 拉普拉斯方程又名调和方程、位势方程,是一种偏微分方程。因为由法国数学家拉普拉斯首先提出而得名。求解拉普拉斯方程是电磁学、天文学和流体力学等领域经常遇到的一类重要的数学问题,因为这种方程以势函数的形式描写了电场、引力场和流场等物理对象(一般统称为“保守场”或“有势场”)的性质。 拉普拉斯方程表示液面曲率与液体压力之间的关系的公式。一个弯曲的表面称为曲面,通常用相应的两个曲率半径来描述曲面,即在曲面上某点作垂直于表面的直线,再通过此线作一平面,此平面与曲面的截线为曲线,在该点与曲线相重合的圆半径称为该曲线的曲率半径R1。 通过表面垂线并垂直于第一个平面再作第二个平面并与曲面相交,可得到第二条截线和它的曲率半径R2,用 R1与R2可表示出液体表面的弯曲情况。若液面是弯曲的,液体内部的压力p1与液体外的压力p2就会不同,在液面两边就会产生压力差△P= P1- P2,其数值与液面曲率大小有关,可表示为:▽p=γ(1/R1+1/R2)式中γ是液体表面张力。该公式成为拉普拉斯方程。 在数理方程中 拉普拉斯方程拉普拉斯方程为:Δ u=d^2u/dx^2+d^2u/dy^2=0,其中Δ为拉普拉斯算子,此处的拉普拉斯方程为二阶偏微分方程。三维情况下,拉普拉斯方程可由下面的形式描述,问题归结为求解对实自变量x、y、z二阶可微的实函数φ:其中Δ称为拉普拉斯算子. 拉普拉斯方程的解称为调和函数。 如果等号右边是一个给定的函数f(x, y, z),即: 则该方程称为泊松方程。拉普拉斯方程和泊松方程是最简单的椭圆型偏微分方程。偏微分算子或Δ(可以在任意维空间中定义这样的算子)称为拉普拉斯算子,英文是 Laplace operator或简称作Laplacian。 狄利克雷问题 拉普拉斯方程的狄利克雷问题可归结为求解在区域D内定义的函数φ,使得在D的边界上等于某给定的函数。为方便叙述,以下采用拉普拉斯算子应用的其中一个例子——热传导问题作为背景进行介绍:固定区域边界上的温度(是边界上各点位置坐标的函数),直到区域内部热传导使温度分布达到稳定,这个温度分布场就是相应的狄利克雷问题的解。 %%%% 真解 u=sin(pi*x)*sin(pi*y) %%% %%%% 方程 -Laplace(u)=f %%%%%% %%%% f=2*pi^2*sin(pi*x)*sin(pi*y) %%%%%% %%%%difference code for elliptic equations with constant coefficient %%%%% %clear all %clc N=20; h=1/N; S=h^2; x=0:h:1; y=0:h:1; %%% Stiff matrix A=zeros((N-1)^2,(N-1)^2); for i=1 A(i,i)=4/h^2; A(i,i+1)=-1/h^2; A(i,i+(N-1))=-1/h^2; end for i=N-1 A(i,i-1)=-1/h^2; A(i,i)=4/h^2; A(i,2*i)=-1/h^2; %A(i,i+(N-1))=-1/h^2 end for i=(N-2)*(N-1)+1 A(i,i-(N-1))=-1/h^2; A(i,i)=4/h^2; A(i,i+1)=-1/h^2; end for i=(N-1)^2 A(i,i-(N-1))=-1/h^2; A(i,i)=4/h^2; A(i,i-1)=-1/h^2; end for n=2:N-2 i=(N-2)*(N-1)+n; A(i,i-(N-1))=-1/h^2; A(i,i-1)=-1/h^2; A(i,i)=4/h^2; A(i,i+1)=-1/h^2; end for i=2:N-2 A(i,i-1)=-1/h^2; A(i,i)=4/h^2; A(i,i+1)=-1/h^2; A(i,i+(N-1))=-1/h^2; end for m=1:N-3 i=m*(N-1)+1; A(i,i-(N-1))=-1/h^2; A(i,i)=4/h^2; A(i,i+1)=-1/h^2; A(i,i+(N-1))=-1/h^2; end for m=2:N-2 i=m*(N-1); A(i,i-(N-1))=-1/h^2; A(i,i-1)=-1/h^2; A(i,i)=4/h^2; A(i,i+(N-1))=-1/h^2; end % for m=1:N-3 % i=m*(N-1)+(N-1); % A(i,i-(N-1))=-1/h^2; % A(i,i-1)=-1/h^2; % A(i,i)=4/h^2; % A(i,i+(N-1))=-1/h^2; % end for m=1:N-3 for n=2:N-2 i=m*(N-1)+n; A(i,i-(N-1))=-1/h^2; A(i,i-1)=-1/h^2; A(i,i)=4/h^2; A(i,i+1)=-1/h^2; A(i,i+(N-1))=-1/h^2; end end %%% Right term F=zeros((N-1)^2,1); for m=0:N-2 for n=1:N-1 i=m*(N-1)+n; M A T L A B编程求解二维 泊松方程 %%%% 真解 u=sin(pi*x)*sin(pi*y) %%% %%%% 方程 -Laplace(u)=f %%%%%% %%%% f=2*pi^2*sin(pi*x)*sin(pi*y) %%%%%% %%%%difference code for elliptic equations with constant coefficient %%%%% %clear all %clc N=20; h=1/N; S=h^2; x=0:h:1; y=0:h:1; %%% Stiff matrix A=zeros((N-1)^2,(N-1)^2); for i=1 A(i,i)=4/h^2; A(i,i+1)=-1/h^2; A(i,i+(N-1))=-1/h^2; end for i=N-1 A(i,i-1)=-1/h^2; A(i,i)=4/h^2; A(i,2*i)=-1/h^2; %A(i,i+(N-1))=-1/h^2 end for i=(N-2)*(N-1)+1 A(i,i-(N-1))=-1/h^2; A(i,i)=4/h^2; A(i,i+1)=-1/h^2; end for i=(N-1)^2 A(i,i-(N-1))=-1/h^2; A(i,i)=4/h^2; A(i,i-1)=-1/h^2; end for n=2:N-2 i=(N-2)*(N-1)+n; A(i,i-(N-1))=-1/h^2; A(i,i-1)=-1/h^2; A(i,i)=4/h^2; A(i,i+1)=-1/h^2; end 拉普拉斯方程和泊松方程 摘要:拉普拉斯方程,又名调和方程、位势方程,是一种偏微分方程。因为由法国数学家拉普拉斯首先提出而得名。求解拉普拉斯方程是电磁学、天文学和流体力学等领域经常遇到的一类重要的数学问题,因为这种方程以势函数的形式描写了电场、引力场和流场等物理对象的性质。 关键词:分离变量电磁场拉普拉斯 简史 1777年,拉格朗日研究万有引力作用下的物体运动时指出:在引力体系中,每一质点的质量m k除以它们到任意观察点P的距离r k,并且把这些商加在一起,其总和 即P点的势函数,势函数对空间坐标的偏导数正比于在 P点的质点所受总引力的相应分力。1782年,P.S.M.拉普拉斯证明:引力场的势函数满足偏微分方程: ,叫做势方程,后来通称拉普拉斯方程。1813年,S.D.泊松撰文指出,如 果观察点P在充满引力物质的区域内部,则拉普拉斯方程应修改为,叫做泊松方程,式中ρ为引力物质的密度。文中要求重视势函数 V在电学理论中的应用,并指出导体表面为等热面。 静电场的泊松方程和拉普拉斯方程 若空间分区充满各向同性、线性、均匀的媒质,则从静电场强与电势梯度的关系E=-V高斯定理微分式,即可导出静电场的泊松方程: 式中ρ为自由电荷密度,纯数εr为各分区媒质的相对介电常数,真空介电常数εo=8.854×10-12法/米。在没有自由电荷的区域里,ρ=0,泊松方程就简化为拉普拉斯方程。在各分区的公共界面上,V满足边值关系, , 式中i ,j 指分界面两边的不同分区,σ 为界面上的自由电荷密度,n 表示边界面上的内法 线方向。 边界条件和解的唯一性 为了在给定区域内确定满足泊松方程以及边值关系的解,还需给定求解区域边界上的物 理情况,此情况叫做边界条件。有两类基本的边界条件:给定边界面上各点的电势,叫做狄 利克雷边界条件;给定边界面上各点的自由电荷 ,叫做诺埃曼边界条件。 静电场的唯一性定理: 设区域V 内给定自由电荷分布)(x ,在V 内电势满足泊松方程 或拉普拉斯方程,在V 的边界S 上给定电势 ,或V 边界上给定电势的法线方向偏导数 ,则V 内场(静电场)唯一确定。 除了静电场之外,在电学、磁学、力学、热学等领域还有许多服从拉普拉斯方程的势场。 各类物理本质完全不同的势场如果具有相似的边界条件,则因拉普拉斯方程解的唯一性,任 何一个势场的解,或该势场模型中实验测绘的等热面或流线图,经过对应物理量的换算之后,可以通用于其他的势场。 静磁场的泊松方程和拉普拉斯方程 在SI 制中,静磁场满足的方程为 ,式中j 为传导电流密度。第一式表明静磁 场可引入磁矢势r)描述: 。 在各向同性、线性、均匀的磁媒质中,传导电流密度j 0的区域里,磁矢势满足的方程 为 。 选用库仑规范,,则得磁矢势A 满足泊松方程 ,式中纯数μr 为媒质的相对磁导率, 真空磁导率μo =1.257×10-6亨/米。在传导电流密度j=0的区域里,上 式简化为拉普拉斯方程 。 拉普拉斯方程和泊松方程 摘要:拉普拉斯方程,又名调和方程、位势方程,是一种偏微分方程。因为由法国数学家拉普拉斯首先提出而得名。求解拉普拉斯方程是电磁学、天文学和流体力学等领域经常遇到的一类重要的数学问题,因为这种方程以势函数的形式描写了电场、引力场和流场等物理对象的性质。 关键词:分离变量 电磁场 拉普拉斯 简史 1777年,拉格朗日研究万有引力作用下的物体运动时指出:在引力体系中,每一质点的质量m k 除以它们到任意观察点P 的距离r k ,并且把这些商加在一起,其总和 m k r k n k=1 = V x ,y ,z 即P 点的势函数,势函数对空间坐标的偏导数正比于在 P 点的质点所受总引力的相应分力。1782年,P.S.M.拉普拉斯证明:引力场的势函数满足偏微分方程: ?2V ?x +?2V ?y +?2V ?z =0,叫做势方程,后来通称拉普拉斯方程。1813年,S.D.泊松撰文指出, 如果观察点P 在充满引力物质的区域内部,则拉普拉斯方程应修改为?2V ?x 2 + ?2V ?y 2 + ?2V ?z 2 =?4πρ, 叫做泊松方程,式中ρ为引力物质的密度。文中要求重视势函数 V 在电学理论中的应用,并指出导体表面为等热面。 静电场的泊松方程和拉普拉斯方程 若空间分区充满各向同性、线性、均匀的媒质,则从静电场强与电势梯度的关系E=-?V 高斯定理微分式??E =ρ/εr ε0,即可导出静电场的泊松方程:?2V ?x 2+?2V ?y 2+?2V ?z 2=?2V =?ρ/εr ε0 式中ρ为自由电荷密度,纯数 εr 为各分区媒质的相对介电常数,真空介电常数εo =8.854×10-12 法/米。在没有自由电荷的区域里,ρ=0,泊松方程就简化为拉普拉斯方程?2V =0 。 在各分区的公共界面上,V 满足边值关系V i =V j , ε0εri ?V ?n i ?ε0εrj ?V ?n j =??, 五点差分格式求解泊松方程的第一边值问题(可编辑)五点差分格式求解泊松方程的第一边值问题 摘要:给出了二维泊松方程在单位正方形上的五点差分格式。并运用线性方程组的古典迭代解法??Jacobi迭代求解出在区域上的数值解。最终绘制数值解的图形。 关键字:泊松方程五点差分格式 Jacobi迭代 有限差分法的介绍 有限差分法是求解偏微分方程的主要数值解法之一;其基本思想是把连续问题离散化,即对求解区域做网格剖分,用有限个网格点代替连续区域;其次将微分算子离散化,从而把微分方程组的问题化为线性方程组的求解问题,解方程组就可以得到原问题在离散点上的近似解。 差分法的步骤:1 对求解域做网格剖分 2 插值函数的选择 3 方程组的建立 4 方程组的求解 五点差分格式的构造 二维泊松方程: 在单位正方形上,在正方形边界上的边界条件.在正方形网格上,就是在上离散化,.对于N3如图1所示: 图1 沿方向分别用二阶中心差商代替 2.1 2.2 1、2式相加可得差分方程: 2.3 利用Taylor展式 可得差分算子的截断误差 其中是方程2.3的光滑解。 由于差分方程2.3中只出现在及其四个邻点上的值见图1的中间的粗的点,所以称为五点差分格式。 由边界条件知道,因而2.3式确定了一组具有个未知量的个线性方程。对应的系数矩阵为对称、不可约对角占优,且对角元为正,因而系数矩阵非奇异,且为对称正定阵。 三、方程组的求解 我们已经知道,利用差分方法解椭圆型方程边值问题归结为解大型线性代数方程组的问题。因为差分格式产生的大型线性代数方程组的系数矩阵中非零元素占的比例小,分布很有规律性。而且通过数值线性代数的学习,我们知道对于大型的稀疏矩阵来说,迭代法是比较好的选择,其程序实现比较简单,迭代过程能自动校正计算过程中的偶然误差,要求计算机的存储相对较少。 本文采用了线性方程组古典迭代解法??Jacobi迭代求解由五点差分格式得到的线性方程组。以下对Jacobi迭代作简要的介绍: 给定3.1 令3.2 其中 3.3 那么3.1可以写成,3.4 其中.若给定初始向量,并代入3.4的右端,就可以计算出一个新的向量,即, 泊松方程和拉普拉斯方程 势函数的一种二阶偏微分方程。广泛应用于电学、磁学、力学、热学等多种热场的研究与计算。 简史 1777年,拉格朗日研究万有引力作用下的物体运动时指出:在引力体系中,每一质点 的质量m k除以它们到任意观察点P的距离r k,并且把这些商加在一起,其总和 即P点的势函数,势函数对空间坐标的偏导数正比于在 P点的质点所 受总引力的相应分力。1782年,P.S.M.拉普拉斯证明:引力场的势函数满足偏微分方程: ,叫做势方程,后来通称拉普拉斯方程。1813年,S.-D.泊松撰文 指出,如果观察点P在充满引力物质的区域内部,则拉普拉斯方程应修改为 ,叫做泊松方程,式中ρ为引力物质的密度。文中要求重视势 函数 V在电学理论中的应用,并指出导体表面为等热面。 静电场的泊松方程和拉普拉斯方程 若空间分区充满各向同性、线性、均匀的媒质,则从静电场强与电势梯度的关系E=-墷V和高斯定理微分式,即可导出静电场的泊松方程: , 式中ρ为自由电荷密度,纯数εr为各分区媒质的相对介电常数,真空介电常数εo=8.854 ×10-12法/米。在没有自由电荷的区域里,ρ=0,泊松方程就简化为拉普拉斯方程。在各分区的公共界面上,V满足边值关系, , 式中i,j指分界面两边的不同分区,σ为界面上的自由电荷密度,n表示边界面上的内法线方向。 边界条件和解的唯一性 为了在给定区域内确定满足泊松方程以及边值关系的解,还需给定求解区域边界上的物理情况,此情况叫做边界条件。有两类基本的边界条件:给定边界面上各点的电势,叫做狄 利克雷边界条件;给定边界面上各点的自由电荷,叫做诺埃曼边界条件。 边界几何形状较简单区域的静电场可求得解析解,许多情形下它们是无穷级数,稍复杂的须用计算机求数值解,或用图解法作等势面或力线的场图。 除了静电场之外,在电学、磁学、力学、热学等领域还有许多服从拉普拉斯方程的势场。各类物理本质完全不同的势场如果具有相似的边界条件,则因拉普拉斯方程解的唯一性,任何一个势场的解,或该势场模型中实验测绘的等热面或流线图,经过对应物理量的换算之后,可以通用于其他的势场。 静磁场的泊松方程和拉普拉斯方程 在SI制中,静磁场满足的方程为 式中j为传导电流密度。第一式表明静磁场可引入磁矢势r)描述:。 在各向同性、线性、均匀的磁媒质中,传导电流密度j 0的区域里,磁矢势满足的方程为 选用库仑规范,墷?r)=0,则得磁矢势r)满足泊松方程, 式中纯数μr 为媒质的相对磁导率,真空磁导率μo=1.257×10-6亨/米。在传导电流密度j=0的区域里,上式简化为拉普拉斯方程?2Α=0。 Topic 2: Elliptic Partial Di?erential Equations Lecture 2-4: Poisson’s Equation: Multigrid Methods Wednesday, February 3, 2010 Contents 1 Multigrid Methods 2 Multigrid method for Poisson’s equation in 2-D 3 Simple V ?cycle algorithm 4 Restricting the Residual to a Coarser Lattice 2 3 5 7 1 MULTIGRID METHODS 5 Prolongation of the Correction to the Finer Lattice 6 Cell-centered and Vertex-centered Grids and Coarsenings 7 Boundary points 8 Restriction and Prolongation Operators 9 Improvements and More Complicated Multigrid Algorithms 8 8 11 11 15 1 Multigrid Methods The multigrid method provides algorithms which can be used to accelerate the rate of convergence of iterative methods, such as Jacobi or Gauss-Seidel, for solving elliptic partial di?erential equations. Iterative methods start with an approximate guess for the solution to the di?erential equation. In each iteration, the di?erence between the approximate solution and the exact solution is made smaller. One can analyze this di?erence or error into components of di?erent wavelengths, for example by using Fourier analysis. In general the error will have components of many di?erent wavelengths: there will be 泊松方程是数学中一个常见于静电学、机械工程和理论物理的偏微分方程。是因法国数学家、几何学家及物理学家泊松而得名的。 泊松首先在无引力源的情况下得到泊松方程,△Φ=0(即拉普拉斯方程);当考虑引力场时,有△Φ=f(f为引力场的质量分布)。后推广至电场磁场,以及热场分布。该方程通常用格林函数法求解,也可以分离变量法,特征线法求解。 方程的叙述 泊松方程为在这里代表的是拉普拉斯算子,而f和可以是在流形上的实数或复数值的方程。当流形属于欧几里得空间,而拉普拉斯算子通常表示为,因此泊松方程通常写成在三维 直角坐标系,可以写成如果有恒等于0,这个方程就会变成一个齐次方程,这个方程称作“拉普拉斯方程”。 泊松方程可以用格林函数来求解;如何利用格林函数来解泊松方程可以参考屏蔽泊松方程。有很多种数值解。像是松弛法,不断回圈的代数法,就是一个例子。 泊松方程数学表达 通常泊松方程表示为 这里代表拉普拉斯算子,f为已知函数,而为未知函数。当f=0时,这个方程被称为拉普拉斯方程。 为了解泊松方程我们需要更多的信息,比如狄利克雷边界条件: 其中为有界开集。 这种情况下利用基础函数构建泊松方程的解,拉普拉斯方程的 基础函数为: 其中为n维欧几里得空间中单位球面的体积,此时可通过卷积得到的解。 为了使方程满足上述边界条件,我们使用格林函数 为一个校正函数,它满足通常情况下是依赖于。 通过可以给出上述边界条件的解 其中表示上的曲面测度。 此方程的解也可通过变分法得到。 泊松方程应用 在静电学很容易遇到泊松方程。对于给定的f找出φ是一个很实际的问题,因为我们经常遇到给定电荷密度然后找出电场的问题。在国际单位制(SI)中:此代表电势(单位为伏 [整理]拉普拉斯方程 拉普拉斯方程 求助编辑百科名片 拉普拉斯方程 拉普拉斯方程(Laplace'sequation),又名调和方程、位势方程,是一种偏微分方程。因为由 法国数学家拉普拉斯首先提出而得名。求解拉普拉斯方程是电磁学、天文学和流体力学等领 域经常遇到的一类重要的数学问题,因为这种方程以势函数的形式描写了电场、引力场和流 场等物理对象(一般统称为“保守场”或“有势场”)的性质。 目录 拉普拉斯方程(Laplace equation) 在数理方程中狄利克雷问题诺伊曼边界条件拉普拉斯方程的解二维拉普拉斯方程解析函数 三维情况下 二维拉普拉斯方程解析函数 在流场中的应用在电磁学中的应用三维拉普拉斯方程基本解 格林函数 在流场中的应用拉普拉斯人物介绍展开 拉普拉斯方程(Laplace equation) 在数理方程中狄利克雷问题诺伊曼边界条件拉普拉斯方程的解二维拉普拉斯方程解析函数 三维情况下 二维拉普拉斯方程解析函数 在流场中的应用在电磁学中的应用三维拉普拉斯方程基本解 格林函数 在流场中的应用 拉普拉斯人物介绍 展开 编辑本段拉普拉斯方程(Laplace equation) 拉普拉斯方程表示液面曲率与液体压力之间的关系的公式。一个弯曲的表面称为曲面,通常用相应的两个曲率半径来描述曲面,即在曲面上某点作垂直于表面的直线,再通过此线作一平面,此平面与曲面的截线为曲线,在该点与曲线相重合的圆半径称为该曲线的曲率半径R1。通过表面垂线并垂直于第一个平面再作第二个平面并与曲面相交,可得到第二条截线和它的曲率半径R2,用 R1与R2可表示出液体表面的弯曲情况。若液面是弯曲的,液体内部的压力p1与液体外的压力p2就会不同,在液面两边就会产生压力差?P= P1- P2,其数值与液面曲率大小有关,可表示为:?p=γ(1/R1+1/R2)式中γ是液体表面张力。该公式成为拉普拉斯方程。 在数理方程中 拉普拉斯方程为:Δu=d^2u/dx^2+d^2u/dy^2=0,其中Δ 为拉普拉斯算子,此处的拉普拉斯方程为二阶偏微分方程。三维情况下,拉普拉斯方程可由下面的形式描述,问题归结为求解对实自变量x、y、z二阶可微的实函数φ : 其中Δ 称为拉普拉斯算子. 拉普拉斯方程的解称为调和函数。 拉普拉斯方程(Laplace's equation),又名调和方程、位势方程,是一种偏微分方程。定义 三维情况下,拉普拉斯方程可由下面的形式描述,问题归结为求解对实自变量x、y、z二阶可微的实函数φ : 上面的方程常常简写作: 或 其中div表示矢量场的散度(结果是一个标量场),grad表示标量场的梯度(结果是一个矢量场),或者简写作: Δφ = 0 其中Δ称为拉普拉斯算子. 拉普拉斯方程的解称为调和函数。 如果等号右边是一个给定的函数f(x, y, z),即: 则该方程称为泊松方程。拉普拉斯方程和泊松方程是最简单的椭圆型偏微分方程。偏微分算子或Δ(可以在任意维空间中定义这样的算子)称为拉普拉斯算子,英文是Laplace operator或简称作Laplacian。 拉普拉斯方程的狄利克雷问题可归结为求解在区域D内定义的函数φ,使得φ在D的边界上等于某给定的函数。为方便叙述,以下采用拉普拉斯算子应用的其中一个例子——热传导问题作为背景进行介绍:固定区域边界上的温度(是边界上各点位置坐标的函数),直到区域内部热传导使温度分布达到稳定,这个温度分布场就是相应的狄利克雷问题的解。 拉普拉斯方程的诺伊曼边界条件不直接给出区域D边界处的温度函数φ本身,而是φ沿D 的边界法向的导数。从物理的角度看,这种边界条件给出的是矢量场的势分布在区域边界处的已知效果(对热传导问题而言,这种效果便是边界热流密度)。 拉普拉斯方程的解称为调和函数,此函数在方程成立的区域内是解析的。任意两个函数,如果它们都满足拉普拉斯方程(或任意线性微分方程),这两个函数之和(或任意形式的线性组合)同样满足前述方程。这种非常有用的性质称为叠加原理。可以根据该原理将复杂问题的已知简单特解组合起来,构造适用面更广的通解。拉普拉斯方程
MATLAB编程求解二维泊松方程
MATLAB编程求解二维泊松方程doc资料
泊松方程和拉普拉斯方程
泊松方程和拉普拉斯方程
五点差分格式求解泊松方程的第一边值问题(可编辑)
泊松方程拉普拉方程
二维泊松方程很基础详细的求解过程
泊松方程
[整理]拉普拉斯方程
拉普拉斯方程、水平集方法等
