对称变换(2)
对称变换⑵
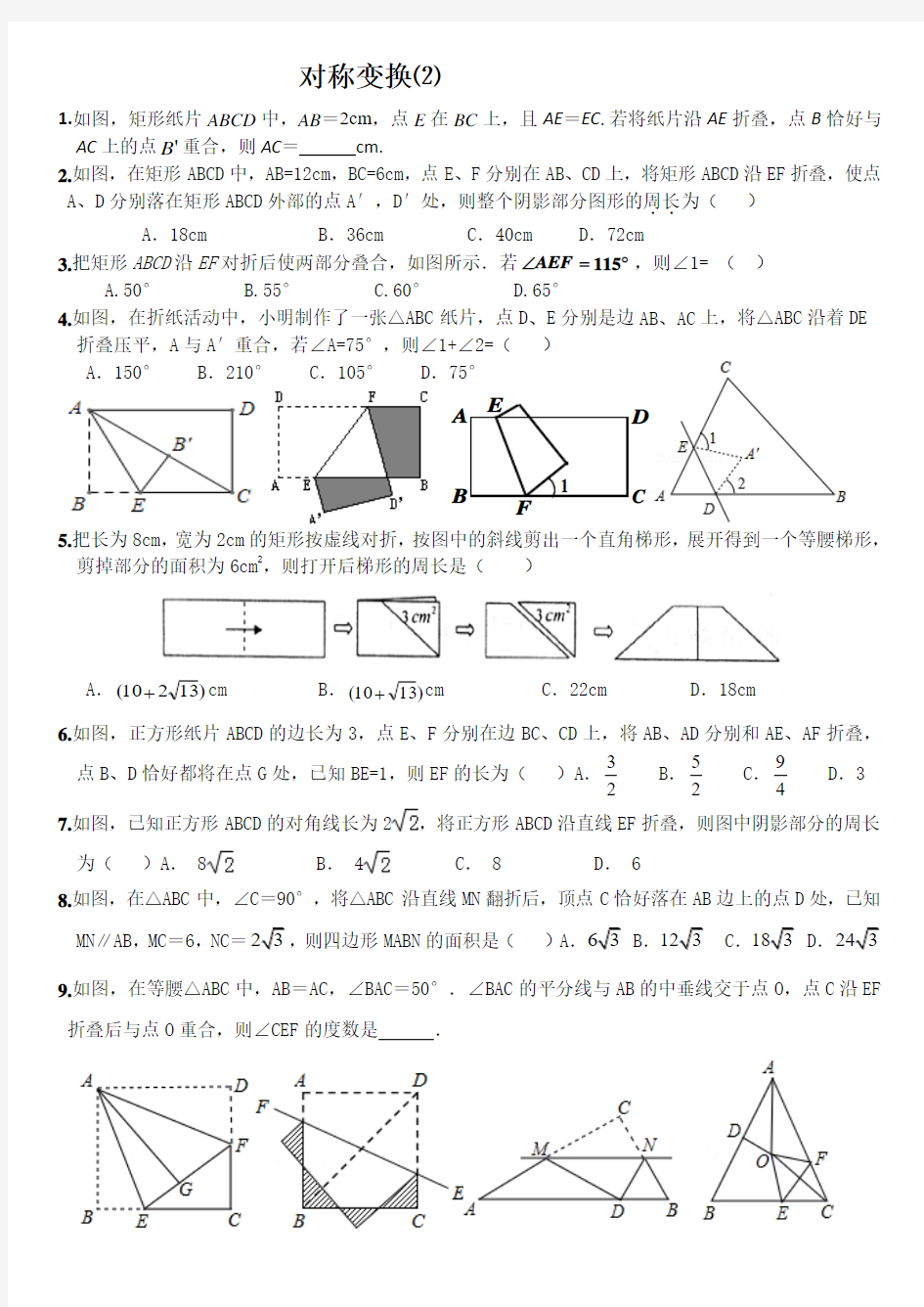
1.如图,矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点'B重合,则AC=cm.
2.如图,在矩形ABCD中,AB=12cm,BC=6cm,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点
A、D分别落在矩形ABCD外部的点A′,D′处,则整个阴影部分图形的周长
..为()
A.18cm B.36cm C.40cm D.72cm
3.把矩形ABCD沿EF对折后使两部分叠合,如图所示.若115
AEF
∠=?,则∠1=()
A.50°
B.55°
C.60°
D.65°
4.如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE
折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=()
A.150°B.210°C.105°D.75°
5.把长为8cm,宽为2cm的矩形按虚线对折,按图中的斜线剪出一个直角梯形,展开得到一个等腰梯形,剪掉部分的面积为6cm2,则打开后梯形的周长是()
A.)
13
2
10
(+cm B.)
13
10
(+cm C.22cm D.18cm
6.如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别和AE、AF折叠,点B、D恰好都将在点G处,已知BE=1,则EF的长为()A.
3
2
B.
5
2
C.
9
4
D.3 7.如图,已知正方形ABCD的对角线长为2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为()A. 8 B. 4C. 8 D. 6
8.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC =23,则四边形MABN的面积是()A .63 B .123C .183D .243 9.如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF 折叠后与点O重合,则∠CEF的度数是.
1
A
B
D
C
E
F
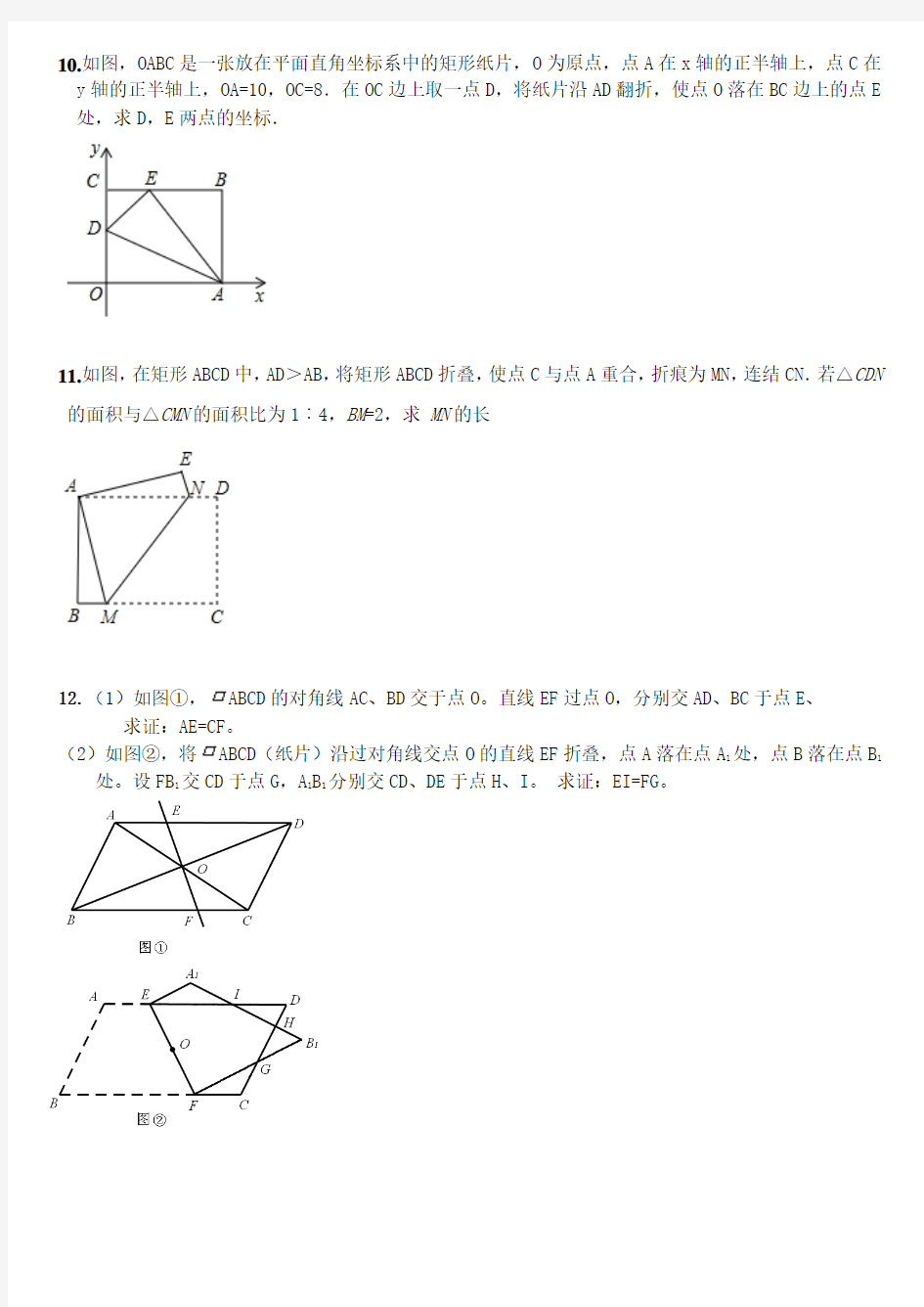
10.如图,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA=10,OC=8.在OC 边上取一点D ,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处,求D ,E 两点的坐标.
11.如图,在矩形ABCD 中,AD >AB ,将矩形ABCD 折叠,使点C 与点A 重合,折痕为MN ,连结CN .若△CDN 的面积与△CMN 的面积比为1︰4,BM =2,求 MN 的长
12.(1)如图①,ABCD 的对角线AC 、BD 交于点O 。直线EF 过点O ,分别交AD 、BC 于点E 、
求证:AE=CF 。
(2)如图②,将ABCD (纸片)沿过对角线交点O 的直线EF 折叠,点A 落在点A 1处,点B 落在点B 1
处。设FB 1交CD 于点G ,A 1B 1分别交CD 、DE 于点H 、I 。 求证:EI=FG 。
13.如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
13.如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.(1)求证:四边形AFCE为菱形;(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.
14.如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;(2)求AG的值;(3)求EF的长.
15.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
①求证:△ABG≌△AFG;②求BG的长;③求证:AG∥CF;
A'D'处,且A'D'经过B,EF 16.如图,菱形纸片ABCD中,∠A=600,将纸片折叠,点A、D分别落在,
D'⊥CD、FD=1时,求CF的长
为折痕,当F
超经典二次函数图象的平移和对称变换总结
二次函数图象的几何变换 内容基本要求略高要求较高要求二次函数 1.能根据实际情境了解二次函数 的意义; 2.会利用描点法画出二次函数的 图像; 1.能通过对实际问题中的情境分 析确定二次函数的表达式; 2.能从函数图像上认识函数的性 质; 3.会确定图像的顶点、对称轴和 开口方向; 4.会利用二次函数的图像求出二 次方程的近似解; 1.能用二次函数 解决简单的实际 问题; 2.能解决二次函 数与其他知识结 合的有关问题; (1)具体步骤: 先利用配方法把二次函数化成2 () y a x h k =-+的形式,确定其顶点(,) h k,然后做出二次函数 2 y ax =的图像,将抛物线2 y ax =平移,使其顶点平移到(,) h k.具体平移方法如图所示: (2)平移规律:在原有函数的基础上“左加右减”. 二、二次函数图象的对称变换 二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x轴对称 2 y ax bx c =++关于x轴对称后,得到的解析式是2 y ax bx c =---; ()2 y a x h k =-+关于x轴对称后,得到的解析式是()2 y a x h k =---; 2. 关于y轴对称 2 y ax bx c =++关于y轴对称后,得到的解析式是2 y ax bx c =-+; ()2 y a x h k =-+关于y轴对称后,得到的解析式是()2 y a x h k =++; 3. 关于原点对称 2 y ax bx c =++关于原点对称后,得到的解析式是2 y ax bx c =-+-; ()2 y a x h k =-+关于原点对称后,得到的解析式是()2 y a x h k =-+-;
函数图象的对称变换
课题:函数图像的对称变换(2课时) 学情分析:相对于函数图象的平移变换,对称变换是学生的难点,对于具体函数,学生还有一定的思路,但结论性的结果,学生掌握的不是很好。 教学目标: (1) 通过具体实例的探讨与分析,得到一些对称变换的结论。 (2) 通过一定的应用,加强学生对对称变换结论的理解。 (3) 能数形结合解决想过题目。 教学过程: 欣赏图片,感受对称 一、师生共同分析讨论完成下列结论的形成。 1、(1)函数()y f x =-与()y f x =的图像关于 对称; (2)函数()y f x =-与()y f x =的图像关于 对称; (3)函数()y f x =--与()y f x =的图像关于 对称. 2、奇函数的图像关于 对称,偶函数图像关于 对称. 3、(1)若对于函数()y f x =定义域内的任意x 都有()()f a x f b x +=-,则 ()y f x =的图像关于直线 对称.
(2)若对于函数()y f x =定义域内的任意x 都有()2()f a x b f a x +=--,则()y f x =的图像关于点 对称. 4、对0a >且1a ≠,函数x y a =和函数log a y x =的图象关于直线 对 称. 5、要得到()y f x =的图像,可将()y f x =的图像在x 轴下方的部分以 为轴翻折到x 轴上方,其余部分不变. 6、要得到()y f x =的图像,可将()y f x =,[)0,x ∈+∞的部分作出,再利用偶函数的图像关于 的对称性,作出(),0x ∈-∞时的图像. 二、学生先独立完成,再分析点评 2 3、函数x y e =-的图象与函数 的图象关于坐标原点对称. 4、将函数1()2x f x +=的图象向右平移一个单位得曲线C ,曲线C '与曲线C 关于直线y x =对称,则C '的解析式为 . 5、设函数()y f x =的定义域为R ,则函数(1)y f x =-与(1)y f x =-的图像的关系为关 于 对称. 6、若函数()f x 对一切实数x 都有(2)(2)f x f x +=-,且方程()0f x =恰好有四个不同实根,求这些实根之和为 . 二、典例教学 【例1】填空题: (1 (2)对于定义在R 上的函数()f x ,有下列命题,其中正确的序号为 . ①若函数()f x 是奇函数,则(1)f x -的图象关于点(1,0)A 对称;②若对x R ∈,有
一次函数图象的变换对称.doc
一次函数图象的变换——对称求一次函数图像关于某条直线对称后的解析式是一类重要题型,同学们在做时经常做错,下面我介绍一种简便的方法:抓住对称点的坐标解决问题。 知识点: 1、与直线y=kx+b关于x轴对称的直线l,每个点与它的对应点都关于x轴对称,横坐标不变纵坐标互为相反数。设l上任一点的坐标为(x,y),则(x, -y)应当在直线y=kx+b上,于是有-y=kx+b,即l:y=-kx-b。 2、与直线y=kx+b关于y轴对称的直线l,每个点与它的对应点都关于y轴对称,纵坐标不变横坐标互为相反数。设l上任一点的坐标为(x,y),则(-x, y)应当在直线y=kx+b上,于是有y=-kx+b,即l:y=-kx+b。下面我们通过例题的讲解来反馈知识的应用: 例:已知直线y=2x+6.分别求与直线y=2x+6关于x轴,y轴和直线x=5对称的直线l的解析式。 分析:关于x轴对称时,横坐标不变纵坐标互为相反数; 关于y轴对称时,纵坐标不变横坐标互为相反数; 关于某条直线(垂直坐标轴)对称时,则相关点 解:1、关于x轴对称 设点(x , y )在直线l上,则点(x , -y )在直线y=2x+6上。 即:-y=2x+6 y=-2x-6 所以关于x轴对称的直线l的解析式为:y=-2x-6. 关于直线对称。 2、关于y轴对称 设点(x,y)在直线l上,则点(-x,y)在直线y=2x+6上。 即:y=2(-x) +6 y=-2x+6 所以关于y轴对称的直线l的解析式为:y=-2x+6.
3、关于直线x=5对称(作图) 由图可知:AB=BC则C点横坐标:-x+5+5=-x+10 所以点C (-x+10, y) 设点(x,y)在直线l上, 则点(-x+10, y)在直线y=2x+6上。 即:y=2(-x+10)+6 y=-2x+26 所以关于直线x=5对称的直线l的解析式为:y=-2x+26. 总结:根据对称求直线的解析式关键在找对称的坐标点。 关于x轴对称,横坐标不变纵坐标互为相反数; 关于y轴对称,纵坐标不变横坐标互为相反数; 关于某条直线(垂直对称轴)对称,可见例题 中分析的方法去求对称点。 练习:1、和直线y=5x-3关于y轴对称的直线解析式为,和直线y=-x-2关于x轴对称的直线解析式为。 2、已知直线y=kx+b与直线y= -2x+8关于y轴对称, 求k、b的值。 答案:1、y=-5x-3;y=x+2 分析:设点(x,y)在直线上,则点(-x,y)在关于y轴对称的直线y=5x-3上,所以直线为y=-5x-3;设点(x,y)在直线上,则点(x,-y)在
平移、旋转和轴对称的秘密
平移、旋转与轴对称的秘密 平移、旋转和轴对称都是平面图形的基本变换.他们之间存在着许多有意思的秘密,这秘密究竟是什么呢? 在一次关于图形变换的考试中,记得有这样一题: 如右图,请说出甲树是怎样由乙树变换得到的____________________. 许多同学都写出了错误的答案:乙向右平移AB 的距离,带绕点A 顺时针旋转30°等到甲。为什么会造成这种错误呢?首先,同学们没有仔细观察这个两棵树的特征或不明白平移、旋转和轴对称的意义。 一、平移变换转化为轴对称变换 如下图,已知△ABC ,直线l ∥k 且距离为a ,画△ABC 关于直线m 对称的△A ′B ′C ′,再画△A ′B ′C ′关于直线n 对称的△A ″B ″C ″。 60° 90°
那么△A″B″C″能否看成△ABC平移得到的呢? 事实证明这是可以的,即△ABC沿对称轴l(k)垂直方向平移2a个单位即可得到 △A″B″C″。 由此我们就可以得出一般结论:当对称轴平行时,两次轴对称相当于一次平移,且平移的方向垂直于对称轴,平移的距离是两条对称轴之间的距离的2倍。 二、旋转转化为轴对称变换 如下图,已知△ABC,直线l,k相交于点O,且夹角为a(0°<a≤90°),画△ABC 关于直线l对称的△A′B′C′。再画△A′B′C′,关于直线k对称的△A″B″C″。 观察图形,我们就可以发现△A″B″C″就是由△ABC绕点O顺时针旋转2a°得到的。 由此可猜想归纳一般结论:当两条对称轴相交于一点时,两次轴对称相当于一次旋转,且旋转中心为对称轴的交点,旋转角为对称轴夹角2a°,旋转方向与第一条对称轴旋转a的角度得到第二条对称轴的位置的方向一致。 数学中像这样的秘密还有很多,只是你还没有打开你智慧的窗口去感受它们,多去留意它们,你就会探索的路上收获丰硕的果实。
7函数图象的对称与变换高三复习专题
函数图象的变换及对称性 1.函数的对称性: 例1.函数()412 x x f x +=的图象( ) A. 关于原点对称 B. 关于直线y x =对称 C. 关于x 轴对称 D. 关于y 轴对称 演变1.函数1 2+-=x x y 的图像关于__________对称 例2.对任意实数x ,函数()f x 满足()(2)20f x f x -+++=,则函数()f x 的图象关于( ) A .直线1x =对称 B .直线2x =对称 C .点(1,1)-对称 D .点(1,1)-对称 演变1.函数()y f x =满足)2()2(x f x f +=-,且)(x f =0有且只有17个根,则这些实数根的和为 演变2.函数11y x =-的图象与函数2sin y x π=(24x -≤≤)的图象所有交点的横坐标之和等于__________ 2.函数图象的对称与不等式: 例1.已知定义域为R 的函数)(x f 满足)4()(+-=-x f x f ,且当2>x 时,)(x f 单调递增。如果421<+x x ,且0)2)(2(21<--x x ,则)()(21x f x f +的值的符号是____ 例2.已知()f x 是定义在(3,3)-上的奇函数,当03x <<时,()f x 的图像如下图所示,那么不等式()cos 0f x x ?<的解集是_____________(答:(,1)(0,1)(,3)22ππ --) 演变1.已知函数()y f x =,x ∈[-1, 1]的图象是由以原点为圆心的两段圆弧及原点构成(如 图所示), 则不等式的()()->+f x f x 的解集为 (答:)2 1,0()21,1[ --) 3.函数图象的变换: 例1.若函数x x y +=2与)(x g y =的图象关于点(-2,3)对称,则)(x g =______ 演变1.已知直线l 与直线220x y +-=关于点(1,2)对称,则直线l 方程为 演变 2.与函数|3|y x =+的图象关于直线1x =-对称的函数图象所对应的函数解析式是______________________
轴对称变换教案和教案说明
《轴对称变换》教案和教案说明 教学目标: (一)知识与技能 1. 通过实际操作,了解轴对称变换的概念和性质。 2.能作出一个图形经过一次或两次轴对称变换后的图形。 3.能利用轴对称变换设计一些简单的图案。 (二)过程与方法 1.经历实际操作,认真体验知识的产生过程,在感受数学知识的探索乐趣。 2.逐步学会用“动态”的眼观去看待几何图形,发展学生理性的抽象思维。 3.通过实践,真正领会轴对称变换在实际生活中的应用。 (三)情感态度与价值观 1.鼓励学生积极参与数学活动,在观察美、发现美的同时,从内心萌发创造美的热情。 2.初步认识数学和人类生活的密切联系,体验活动充满着探索与创造,感受数学的应用意识。 3.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心。 教学重点: 运用变换设计图案 教学难点: 探索归纳得出轴对称变换的特征 教学方法: 直观演示法、实验发现法,设疑诱导法等。 教具准备: 1.教师准备:教学课件 2.学生自备:作图的学习用具 教学过程设计: (一)创设情境,引入新课 师:同学们,我们前面已经研究了什么是轴对称图形,并且会寻找简单图形的对称轴。在课前,先请大家欣赏几组精美的图片,并认真思考:这些漂亮的图
案是如何制作的呢? 学生自由发言。 我们相信通过学习本课――轴对称变换,同学们能创作出更加精美的图案。(二)动手操作,感受变换。 师:问题1:在老师手中的纸上我画了一个简单的图案,你们知道用什么方法能快速地得出对称的另一支图案吗? 学生可能会列举出多种不同的方法,如:戳点、描图等,可让其比较后,得出最佳方法。(让学生动手作图) 活动1:两人合作,先在一张半透明的纸上画一个简单的图案,并用戳点的方法快速地得出对称的另一个图案,共同实现对特征的探究。 问题2:如果我想得到多个这样的图案,又该怎么做?怎样做最快?问题3:你能从中总结一下什么是轴对称变换吗? 我安排充足的时间让学生先独立思考,再与同桌自由交流,并适时的演示课件,引导学生观察生活中的轴对称变换现象,抽象出图形轴对称变换的特点。学生尝试回答时,若遇到困难可引导学生类比“平移变换”的概念进行归纳、总结,在学生回答的基础上,修改、完善,达成共识后我进行板书:由一个平面图形得到它的轴对称图形的过程,叫做轴对称变换。 问题3:轴对称变换它有哪些性质? ①折痕两侧的图形有什么关系? ②对应点A与点A’的连线与对称轴有什么关系? 学生自由发言,充分交流,师生共同总结出: ①轴对称变换不改变原图形的大小和形状 ----即所得图形和原图形全等。是保距变换、保型变换。 ②对应点连线被对称轴垂直平分。 (三)提升思维,运用变换。 师:利用这两点性质,我们就可以尝试制作一些图形轴对称变换后的图形。活动1:探究图形的轴对称变换的作法。 例1:若已知点A和直线l,你能作出点A关于直线l的对应点A’吗? 作法:过点A作AB⊥l,并延长AB至A’,使B A’ =BA,则点A’即为所求。
一次函数的对称变换
函数的平移与对称变换“三系列”之一: 一次函数的对称变换 一、直线型函数的关于“坐标轴”呈轴对称的变换 1、求直线3x 2y -=关于y 轴对称的新直线的表达式? ①、〈小明同学的解法〉:设旧直线3x 2y -=与x 、y 轴分别相交于A 、B 两点, 则点A 为(23,0),点B 为(0,3-), 又设新直线与x 轴交于点A ',则点A '与点A 关于y 轴对称,∴ 点A '为(23- ,0), 设新直线的表达式为:b kx y +=,把B (0,3-)、A '(23- ,0)代入之得: ,解之得:2k -=,3b -= ∴ 所求新直线的表达式为:3x 2y --= 2、求直线3x 2y -=关于x 轴对称的新直线的表达式? 请你模仿“小明同学”,写出解答过程: ?????=+=+?0b k 233b 0k --
②、〈小通同学的解法〉:设点E (0,m ),点F (1,n )是旧直线3x 2y -=上的两点,则易求点E 为(0,3-),点F 为(1,1-), 由题意知:点E 、F 关于y 轴的对称点1E (0-,3-)、1F (1-,1-)必在新直线上, 设新直线的表达式为:b kx y +=,把1E (0,3-) 、1F (1-,1-)代入之得: ,解之得:2k -=,3b -= ∴ 所求新直线的表达式为:3x 2y --= 〈老师〉问:为什么要把点E 、F 的横坐标分别预设为“0,1”? 〈小通〉答:因为原表达式中,自变量的取值范围是“一切实数”,并且由这些“简单横坐标”很容易算出对应的“纵坐标”! 〈小通〉自叹:我懂方法,也懂变通! 4、求直线3x 2y -=关于x 轴对称的新直线的表达式? 请你模仿“小通同学”,写出解答过程: 5、求直线3x 2y -=关于y 轴对称的新直线的表达式? ②、〈小王同学的解法〉:设点P (x ,y )是所求新直线上的任意一个点, 则点P 关于y 轴的对称点Q (x -,y ) ,必定在旧直线3x 2y -=的图像上 ∴ 把Q (x -,y )代入3x 2y -=得:()3x 2y --?= 整理得:3x 2y --=,即为所求新直线的表达式。 ???=+=+?1b k 3b 0k ---
一次函数的对称变换(2020年6月9日,有改动)
函数的平移与对称变换“三系列”之一: 一次函数的对称变换(初二上册学完一次函数就可用) 一、直线型函数的关于“坐标轴”呈轴对称的变换 1、求直线3x 2y -=关于y 轴对称的新直线的表达式? 〈小明同学的解法〉:设旧直线3x 2y -=与x 、y 轴分别相交于A 、B 两点, 则点A 为( ,0),点B 为(0, ), 又设新直线与x 轴交于点 A ',则点A '与点A 关于y 轴对称,∴ 点A '为( , ), 设新直线的表达式为:b kx y +=,把 B (0,3-)、A '(2 3-,0)代入之得: ?????=+=+?0b k 2 33b 0k --,解之得:2k -=,3b -= ∴ 所求新直线的表达式为: 。 2、求直线3x 2y -=关于x 轴对称的新直线的表达式(请你模仿“小明”,写出解答过程)。 3、求直线3x 2y -=关于y 轴对称的新直线的表达式? 〈小通同学的解法〉:设点E (0,m ),点F (1,n )是旧直线3x 2y -=上的两点, 则易求点E 为(0, ),点F 为(1, ),从而由题意知: 点E 、F 关于y 轴的对称点1E ( , )和1F ( , )必在新直线上。设新直线的表达式为:b kx y +=,把1E (0,3-)、1F (1-,1-)代入
之得:???=+=+?1b k 3b 0k ---,解之得:?????= = b k , ∴ 所求新直线的表达式为:3x 2y --= 〈老师〉问:为什么要把点E 、F 的横坐标分别预设为“0,1”? 〈小通〉答:因为原表达式中,自变量的取值范围是“一切实数”,并且由这些“简单横坐标”很容易算出对应的“纵坐标”,我懂方法,懂变通!俺的招牌是:深究本质,开创新招。 4、求直线3x 2y -=关于x 轴对称的新直线的表达式(请你模仿“小通”,写出解答过程)。 5、求直线3x 2y -=关于y 轴对称的新直线的表达式? 〈小王同学的解法〉:设点P (x ,y )是所求新直线上的任意一个点, 则点P 关于y 轴的对称点Q (x -,y ),必定在旧直线3x 2y -=的图像上 ∴ 把Q (x -,y )代入3x 2y -=得:()3x 2y --?= 整理得:3x 2y --=,即为所求新直线的表达式。 6、求直线3x 2y -=关于x 轴对称的新直线的表达式(请你模仿“小王”,写出解答过程)。
函数的对称性完美
函数的对称性 一、教学目标 函数图象的对称性是一类函数的特性,是函数性质的重要方面,它包括自身对称和两个函数图象之间的对称,理解掌握函数对称性,对数学问题的解决有很大的帮助,对也是数形结合思想的重要体现。 1.自身对称函数,函数图象本身具有对称轴或是对称中心,该函数的图象是轴对称图形或是中心对称图形,奇函数与偶函数是最典型的两类函数,其它自身对称的函数都可以由奇偶函数平移得到; 2.两个函数图象的对称,是指两个图形之间的关系,它们之间存在某种关联,即它们关于某一点对称或是关于某一条直线对称,研究其中一个函数的性质就可知另一个函数的特点(互为反函数的两个函数图象)。 二、举例分析 例1. 设()f x 是定义在R 上的函数, (1)若对任意x R ∈,都有()()f a x f b x -=+成立,则函数()f x 的图象关于直线2 a b x +=对称; (2)若对任意x R ∈,都有()()22f x f a x b +-=,则函数()f x 的图象关于点(),a b 成中心对称。 选题目的:通过此题的学习,让学生明白一个道理,函数()f x 的图象是轴对称或是中心对称,函数解析式()f x 应满足一关系式是什么,并能通过奇偶函数的平移获得理解这种关系式的钥匙。 思路分析: (1)要证明()f x 图象上任意一点()00,P x y 关于直线2 a b x +=对称的点()00,Q a b x y +-也在()f x 的图象上。 事实上,()()()()00000y f x f a a x f b a x f a b x ==--=+-=+-????????,即得点()00,Q a b x y +-也在()f x 的图象上。 特别地,当,a b 都为0时,就是偶函数的特征了。
对称变换
6对称变换 知识目标: 目标1:学会运用对称的思想解决将军饮马等最值问题 目标2:掌握倍角问题的常见处理方式 模块一“将军饮马”问题 例1 (1)如图,在上找一点P,使P A+PB最小. (2)如图,在上找一点P,使P A + PB最小. (3)如图,在上找一点P,使|P A—PB|最大. (4)如图,在上找一点P,使|P A—PB|最大. (5)如图,点P在锐角∠AOB的内部,在OB边上求作一点D,在OA边上求作一点C,使?PCD的周长最小.
(6)如图,点P是锐角∠AOB的内部一定点,在OB边上求作一点D,在OA边上求作一点C,使PD+CD 最小. (7)如图,点C、D在锐角∠AOB的内部,在OB边上求作一点F,在OA边上求作一点E,使四边形CEFD 的周长最小. (8)如图,直线外有两点A、B,有一定长线段,在直线上找到点M、N,使得MN间的距离等于定长a,使得四边形AMNB的周长最小. (9)如图,l1∥l2,点M、N分别是1、2上两动点,且满足MN⊥2,点A为1上方一定点,点B为2下方一定点,请确定M、N的位置,使AM+MN+BN最小.
例 2 (1)如图,等腰△底边的长为4,面积是122,腰的垂直平分线交于点,若为边上的中点,为线段上一动点,则△的周长最小值为 . F D E A B C M (2)(2013年武昌区八上期中) 如图,在△ABC 中,AC =BC =2,∠ACB =90°,D 是BC 边的中点,E 是AB 边上一动点,则EC +ED 的最小值. 例3 (1)如图,∠AOB =30°,点M 、N 分别是射线OA 、OB 上的动点,点P 位于∠AOB 内,且OP =3,求△PMN 的周长最小值. (2)(2015年武汉二中八上期中) 如图,为∠内一定点,、分别是射线、上一点,当△周长最小时,∠=110°,则∠= . (3)(2015年青山区八上期中)
函数变换对称变换与翻折变换
例说函数变换·对称变换与翻折变换 一、对称变换 还是从一个常见的例子开始: 引例1:(1997全国,文)设函数()y f x =定义在实数上,则函数(1)y f x =-与 (1)y f x =-的图像关于 ( ) A ,直线0y =对称 B ,直线0x =对称 C ,直线1y =对称 D ,直线1x =对称 引例2:(1997全国,文改)设函数()y f x =定义在实数上,且(1)(1)f x f x -=-,则()f x 的图像关于 ( ) A ,直线0y =对称 B ,直线0x =对称 C ,直线1y =对称 D ,直线1x =对称 答案:引例1 D ,引例2 B 。为何?还是要来一点深入的分析。 引例1的分析: 1()(1)y f x y f x =??????→=-向右平移个单位 1()()[(1)](1)y f x y f x f x f x =?????→=-??????→--=-关于y 轴对称向右平移个单位 故它是研究两个不同函数(1)y f x =-,(1)y f x =-图像的对称问题(异对称),这两个函数均由()y f x =经平移或对称产生。设点000(,)A x y 在()y f x =上,有 1000100(,)(1,)A x y A x y ??????→+向右平移个单位 1000200300(,)(,)(1,)A x y A x y A x y ?????→-??????→-+关于y 轴对称向右平移个单位 1A 与3A 的中点为0(1,)y ,故(1)y f x =-与(1)y f x =-的图像关于直线1x =对称。 引例2的分析: 该问题只在一个函数()y f x =的图像上研究对称性的问题(自对称)。设点000(,)A x y 在 ()y f x =上,则点100(1,)A x y -,200(1,)A x y -均在()y f x =上。1A 与3A 的中点为0(0,)y , ()f x 的图像关于直线0x =对称。 评注:是异对称问题还是自对称问题,其解题思路完全不同,前者通过函数变换,后者找自对称点。将上两例推广可得以结论:(1)函数()y f x a =-与函数()y f a x =-的图像关于
轴对称变换培优专题
3.如图2- 2, A ABC 中,AB = AC , AB 的垂直平分线交 AC 于P 点. (1)若/ A = 35° 求/ BPC ; ( 2)若 AB = 5 cm , BC = 3 cm ,求 A PBC 的周长. 4.如图,AD 为/ BAC 的平分线,DE 丄AB 于E , DF 丄AC 于F ,那么点E 、F 是否 关于AD 对 称?若对称,请说明理由. 【主要知识要点】 1有关概念:轴对称,轴对称图形、对称轴、对称点、线段的垂直平分线、等腰三角形、等边三角形; 2、有关结论和定理:轴对称性质;线段垂直平分线的性质与判定;关于坐标轴对称的点的特征,等腰三 角形的性质和判定;等边三角形的性质和判定。 3、作图要求:会作轴对称图形,会找对称轴;会作线段的垂直平分线,会作等腰三角形、等边三角形。 4、会解决距离最短冋题。 【主要思想方法】1、轴对称变换;2、转化的数学思想;3、分类讨论的思想;4、数形结合的思想; 【典例解析】 1 ?将一个正方形纸片依次按左图 a , b 的方式对折,然后沿图 c 中的虚线裁剪,成图 d 样式,将纸展 开铺 平,所得到的图形是右图中的 ( ) 2 ?如图,将矩形纸片 ABCD (图①)按如下步骤操作:(1)以过点A 的直线为折痕折叠纸片,使 点B 恰好落在AD 边上,折痕与BC 边交于点E (如图②);(2)以过点E 的直线为折痕折叠纸片,使 点A 落在BC 边上,折痕EF 交AD 边于点F (如图③);(3)将纸片收展平,那么/ AFE 的度数为 ___________
5.如图,从BC中,点A的坐标为(0, 1),点C的坐标为(4, 3), 点B的坐标为 (3, 1),如果要使A ABD与从BC全等,画出从BD , 并求点D的坐标. 6、如图8,在正方形网格上有一个△ ABC. (1)作厶ABC关于直线MN的对称图形(不写作法); (2)若网格上的最小正方形的边长为1,求厶 ABC的面积. 7、已知:如图3 —13,点M在锐角/ AOB的内部,在0A边上求作一点 P,在 0B边上求作一点Q,使得A PMQ的周长最小; &已知△ ABC中,/ C=90 °沿过B的一条直线BE折叠这个三角形,使点C与AB边上的一点D重合,如图9所示. (1)要使D恰为AB的中点,还应添加一个什么条件?(请写出一个你认为正确的添加条件) (2)将(1)中的添加条件作为题目的补充条件,试说明其能使D为AB中点的理由. 解:(1)添加条件: ________ (2)说明:
【高中数学】05函数图像的对称变换
函数图像的对称变换 函数y =f (x )与y =-f (x )、y =f (-x )及y =-f (-x )的图象分别关于x 轴、y 轴、原点对称 例1、设x x f 1)(= (x >0)作出y =-f (x )、y =f (-x )及y =-f (-x )的图象。 横坐标不变,纵坐标取相反数 纵坐标不变,横坐标取相反数 横坐标与纵坐标都取原来相反数 图象关于x 轴对称 图象关于y 轴对称 图象关于原点对称 定理:y =f (m -x )由函数y =f (-x )向右平移m 个单位得到。 证明:由于y =f (m -x )=f [-(x-m )],故可得知。 定理:y =f (m -x )与y =f (x-m )的图象关于直线x=m 对称。 证明:y =f (m -x )由函数y =f (-x )向右平移m 个单位得到;y =f (x-m )由函数y =f (x )向右平移m 个单位得到,而y =f (x )与y =f (-x )关于y 轴对称,故y =f (m -x )与y =f (x-m )的图象关于直线x=m 对称。 1.设函数y=f (x )定义在实数集R 上,则函数y=f (1﹣x )与y=f (x ﹣1)的图象关于( D ) A .直线y=0对称 B .直线x=0对称 C .直线y=1对称 D .直线x=1对称 2.若函数y=f (x )的图象如图所示,则函数y=f (1﹣x )的图象大致为( A ) y
A.B.C.D. 3.已知函数f(x)的值域是[﹣2,3],则函数f(x+2)的值域是(D)A.[﹣4,1] B.[0,5] C.[﹣4,1]∪[0,5]D.[﹣2,3] 4.关于函数y=f(x)与函数y=f(x+1)的叙述一定正确的是(C) A.定义域相同B.对应关系相同C.値域相同D.定义域、値域、对应关系都可以不相同 5.函数y=1+的图象是(A) A. B.C. D. 6.已知函数y=f(x)的图象与函数y=的图象关于原点对称,则f(x)=(B)A.B.C.﹣D.﹣ 7.若函数y=f(x)的图象过点(1,1),则函数f(4﹣x)的图象一定经过定点(C)A.(1,3)B.(﹣5,1)C.(3,1)D.(1,﹣5) 8.为了得到函数y=f(﹣2x)的图象,可以把函数y=f(1﹣2x)的图象适当平移,这个平移是(B) A.沿x轴向右平移1个单位B.沿x轴向右平移个单位 C.沿x轴向左平移1个单位D.沿x轴向左平移个单位 9.已知函数f(x)=ax2+x(a为常数),则函数f(x﹣1)的图象恒过点(D)A.(﹣1,0)B.(0,1)C.(1,1)D.(1,0) 10.函数f(x)的图象向右平移1个单位长度,所得图象与y=e x关于y轴对称,则f(x)=(D)
几何变换------对称2.doc
为折痕,当D' F_LCD时,空的值为【 FD 一、选择题 1.如图,在左ABC中,ZC=90° ,将ZXABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN//AB, MC=6, NC=2V3 ,则四边形MABN的面积是【 2.如图,菱形纸片ABCD +, ZA=60°,将纸片折叠,点A、D分别落在A'、D'处,且A' D'经过B, EF r 2V3-1 6 3.如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别和AE、AF折叠,点 B、D恰好都将在点G处,已知BE=1,则EF的长为[ 4.如图,矩形ABCD中,E是AD的中点,将ZSABE沿BE折叠后得到ZSGBE,延长BG交CD于F点,若CFF, FD=2,则BC的长为【 A. 3^2 B. 2y[6 C. 275 D. 2心 5.如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH, EH=12厘米,EF=16 厘米,则边AD的长是【】 几何变换对称2
A. 2 B. 4D. 2A /6 A. 12 厘米 B. 16厘米 C. 20厘米 D. 28厘米 6.如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合, 折痕为MN,连结CN.若ZiCDN的而积与Z\CMN的而积比为1 : 4,则世的值为【 BM 二、填空题 1.如图,在 RtAABC'K /C=90° , ZA=30° , BC=1,点 D 在AC±,将Z\ADB 沿直线 BD 翻折后,将点 A 落在点E处,如果AD1ED,那么线段DE的长为▲. B 2.如图,平面直角坐标系中有四个点,它们的横纵坐标均为整数.若在此平面直角坐标系内移动点A,使得这四个点构成的四边形是轴对称图形,并且点A的横坐标仍是整数,则移动后点A的坐标为▲ 3.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x 轴上使得|PA-PB|的值最大的点,Q是y轴上使得QA十QB的值最小的点,则OP OQ = ▲. 4.已知A (1, 5), B (3, —1)两点,在x轴上取一点M,使AM-BN取得最大值时,则M的坐标为▲ 5.把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=3cm, BC= 5cm, 则重叠部分ADEF的面积为 A cm七 6.如图,将AABC纸片的一角沿DE向下翻折,使点A落在BC边上的A '点处,且DE〃BC ,下列结论: ① ZAED=ZC; C .
对称变换.
对称变换 【将军饮马】据说古代希腊有一位将军向当时的大学者海伦请教一个问题:从A地出发到河边饮马,再到B地(如图4.32所示),走什么样的路最近?如何确定饮马的地点? 海伦的方法是这样的:如图4.33,设L为河,作AO⊥L交L于O点,延长AO至A',使A'O=AO。连结A'B,交L于C,则C点就是所要求的饮马地点。再连结AC,则路程(AC+CB)为最短的路程。 为什么呢?因为A'是A点关于L的对称点,AC与A'C是相等的。而A'B 是一条线段,所以A'B是连结A'、B这两点间的所有线中,最短的一条,所以AC+CB=A'C+CB=A'B也是最短的一条路了。这就是海伦运用对称变换,找到的一种最巧妙的解题方法。运用这种办法,可以巧妙地解决许多几何问题。 【划线均分】通过中心对称图形的对称中心,任意画一条直线,都可以把原图形均分成两个大小、形状完全相同的图形。利用这一性质,可以使某些较复杂的问题迅速地解答出来。例如 (1)把图形(图4.34)的面积,用一条直线分成相等的两个部分。
解题时,只要把这个图形看成是由两个矩形(长方形)组成的组合图形,而矩形既是轴对称图形,也是中心对称图形,所以只要找出两个对称中心(对角线交点),利用中心对称图形的上述性质,通过两个对称中心作一条直线,就能把它的面积分成相等的两个部分了。如前页的三种分法都行(如图4.35所示)。 (2)如图4.36,长方形ABCD内有一个以O点为圆心的圆,请画一条直线,同时将长方形和圆分为面积相等的两个部分。 大家知道,长方形和圆都既是轴对称图形,又是中心对称图形。长方形的对称中心是对角线的交点,圆的对称中心是它的圆心。 根据中心对称图形的上述性质,先找出这两个对称中心O点和P点(如图4.37),再过O、P作直线L,此直线L即是所画的那根直线。
图形变换中的轴对称变换
专题复习图形变换中的轴对称变换 左权二中徐旭芳 学生起点分析 学生的知识技能基础:学生在生活中已经对轴对称现象不陌生了,在本章前面两节课中,认识了轴对称的现象,加强了对图形的理解和认识,初步探索并了解了概念,为接下来的学习奠定了基础。 学生活动经验基础:在相关知识的学习过程中,学生通过想象,再动手操作验证自己的想象,解决了一些简单的现实问题,感受到了充分观察、操作的必要性和作用,获得了一些数学活动经验的基础;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。 一、教学任务分析 教科书基于学生对轴对称图形的认识,提出了本课的具体学习任务,认识等腰三角形和等边三角形的轴对称性及其有关性质。本节课的教学目标是: 1. 经历探索简单图形轴对称的过程,进一步体验轴对称的特征,发展空间观念。 2. 探索并掌握等腰三角形的轴对称性及其相关性质。 3. 通过学生的操作与思考,使学生掌握等腰三角形和等边三角形的轴对称性及其有关性质,从而发展空间观念。 二、教学设计分析 按照学生的认识规律,遵循教师为主导,学生为主体,训练为主线的指导思想,采用以实验发现法为主,直观演示法为辅。教学中,精心设计了一个又一个带有启发性和思考性的问题,创设问题情境,诱导学生思考、操作,教师适时地演示,并用电教媒体化静为动,激发学生探求知识的欲望,逐步推导归纳得出结论,使学生始终处于自主探索、合作交流的积极状态,从而培养学生的思维能力。 本节课设计了如下教学环节: 第一环节知识回顾 内容:观察下列各种图形,判断是不是轴对称图形, 能找出对称轴吗?
轴对称变换(含答案)-
§14.2 轴对称变换 1.轴对称变换 知识要点 1.由一个平面图形得到它的轴对称图形叫做轴对称变换.?成轴对称的两个图形中的任何一个可以看着由另一个图形经过轴对称变换后得到. 2.轴对称变换的性质: (1)经过轴对称变换得到的图形与原图形的形状、大小完全一样 (2)?经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点. (3)连接任意一对对应点的线段被对称轴垂直平分. 3.作一个图形关于某条直线的轴对称图形的步骤: (1)作出一些关键点或特殊点的对称点. (2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形. 典型例题 例:在锐角∠AOB内有一定点P,试在OA、OB上确定两点C、D,使△PCD的周长最短.分析:△PCD的周长等于PC+CD+PD,要使△PCD的周长最短,?根据两点之间线段最短,只需使得PC+CD+PD的大小等于某两点之间的距离,于是考虑作点P关于直线OA?和OB的对称点E、F,则△PCD的周长等于线段EF的长. 作法:如图.①作点P关于直线OA Array的对称点E; ②作点P关于直线OB的对称点F; ③连接EF分别交OA、OB于点C、D.则 C、D就是所要求作的点. 证明:连接PC、PD,则PC=EC,PD=FD. 在OA上任取异于点C的一点H,连 接HE、HP、HD,则HE=HP. ∵△PHD的周长 =HP+HD+PD=HE+HD+DF>ED+DF=EF 而△PCD的周长 =PC+CD+PD=EC+CD+DF=EF ∴△PCD的周长最短.
练习题 一、选择题 1.下列说法正确的是( ) A .任何一个图形都有对称轴; B .两个全等三角形一定关于某直线对称; C .若△ABC 与△A ′B ′C ′成轴对称,则△ABC ≌△A ′B ′C ′; D .点A ,点B 在直线1两旁,且AB 与直线1交于点O ,若AO=BO ,则点A 与点B?关于直线l 对称. 2.已知两条互不平行的线段AB 和A ′B ′关于直线1对称,AB 和A ′B ′所在的直线交于点P ,下面四个结论:①AB=A ′B ′;②点P 在直线1上;③若A 、A ′是对应点,?则直线1垂直平分线段AA ′;④若B 、B ′是对应点,则PB=PB ′,其中正确的是( ) A .①③④ B .③④ C .①② D .①②③④ 二、填空题 3.由一个平面图形可以得到它关于某条直 线对称的图形,?这个图形与原图形的 _________、___________完全一样. 4.数的运算中会有一些有趣的对称形式,仿照等式①的形式填空,并检验等式是否成 立. ①12×231=132×21; ②12×462=___________; ③18×891=__________; ④24×231=___________. 5.如图,点P 在∠AOB 的内部,点M 、N 分别是点P 关于直线OA 、OB?的对称点,线 段MN 交OA 、OB 于点E 、F ,若△PEF 的周长是20cm ,则线段MN 的长是___________. 三、解答题 6.如图,C 、D 、E 、F 是一个长方形台球桌的4个顶点,A 、B?是桌面上的两个球,怎样击打A 球,才能使A 球撞击桌面边缘CF 后反弹能够撞击B 球?请画出A?球经过的路线,并写出作法. 7.如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,?要在河边建一个
几何变换之一轴对称变换(生).
C B A 《几何解题方法》之一:轴对称变换 引例: 如图,半圆O 的直径AB =10cm ,把弓形AD 沿直线AD 折,交直径AB 于点C ’, 若AC ’=6cm ,则AD 的长为( ....8A B C D cm (导出课题)几何变换之一:轴对称变换 1、有关翻折的问题 如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠+∠12 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ) A. ∠=∠+∠A 12 B. 212∠=∠+∠A C. 3212∠=∠+∠A D. )21(23∠+∠=∠A 2、含有角平分线的问题 在△ABC 中,AB>AC ,∠BAC =54°,∠BAC 的角平分线 交BC 于D ,若AB-AC=CD ,求∠ABC 的度数。 思考:如图,在△ABC 中,∠BAC=54°,∠BAC 的外角平分线交直线BC 于D ,若AB+AC=BD ,求∠ABC 的度数。 3、有关轴对称图形的问题 如图,AB 是半圆O 的直径,C 、D 、E 三点在半圆上,H 、K 是直径AB 上的点,若∠AHC=∠DHB ,∠DKA=∠EKB ,已知2565____.AC BE HDK ==∠=,,则 4、含有特殊角的问题 如图,A 、B 、C 三个村庄在一条东西方向的公路沿线上,其中AB =3km ,BC=2km ,在B 村的正北方向有一个D 村,测得∠ADC =45o,现将△ADC 区域规划为开发区,试求这个开发区的面积。 E D C A B C D B
应用: 1、如图,AD是△ABC的角平分线,BE⊥AD,交AD的延长线于E,? EF?∥AC交AB于F.求证:AF=FB. 2、如图AB是半圆O的直径,点C在BA的延长线上 运动(不与A重合),以OC为直径的半圆M与半圆 O交于点D,∠DCB的平分线与半圆M交于点E。 (1)求证:CD是半圆O的切线; (2)过点E作EF⊥AB于F,则有OA=2EF,请说明理 由。 (拓展练习)1、在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若?ABC固定不动,?AFG绕点A旋转,AF、AG 与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重 合)。在旋转过程中,BD2+CE2=DE2是否成立,若成立,请证明;若不成立,请说明理由。 2、如图,正方形AMBD的边长为6,C,E分别在AD,BD上,且AC=2,BE=3,H、K是对角线AB上的点。若∠AHC=∠DHB,∠BKE=∠DKA,试求∠HDK的度数。 3、在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,AB=1,AD=2,在BC、CD上分别找一点M、N,使得△AMN的周长最小,则△AMN 的最小周长为 . C E D G F C B A
八年级学而思 第3讲 轴对称及轴对称变换
第3讲轴对称及轴对称变换 考点·方法·破译 1.轴对称及其性质 把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫对称轴. 轴对称的两个图形有如下性质:①关于某直线对称的两个图形是全等形;②对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上. 2.线段垂直平分线 线段垂直平分线也叫线段中垂线,它反映了与线段的两种关系:①位置关系——垂直;②数量关系——平分. 性质定理:线段垂直平分线上的点与这条线段两个端点的距离相等. 判定定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 3.当已知条件中出现了等腰三角形、角平分线、高(或垂线)、或求几条折线段的最小值等情况时,通常考虑作轴对称变换,以“补齐”图形,集中条件. 经典·考题·赏析 【例1】(兰州)如图所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是() 【解法指导】对折问题即是轴对称问题,折痕就是对称轴.故选D. 【变式题组】 01.将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是() 02.(荆州)如图,将矩形纸片ABCD沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH 折叠,使B落在点E上,点C落在点F上,叠完后,剪一个直径在BC上的半圆,再展开,则展开后的图形为() 【例2】(襄樊)如图,在边长为1的正方形网格中,将△ABC向右平移两个单位长度得到△A’B’C’,则与点B’关于x轴对称的点的坐标是()A.(0,-1)B.(1,1)C.(2,-1)D.(1,-1)
