ARMA模型及SAS求解

第6讲 时间序列分析

教材：应用时间序列分析课件（中国人民大学 王燕），SAS 如何解及下载例程。

时间序列分析(Time series analysis)是一种动态数据处理的统计方法。该方法基于随机过程理论和数理统计学方法，研究随机数据序列所遵从的统计规律，以用于解决实际问题。

时间序列是把反映现象发展水平的统计指标数值，按照时间先后顺序排列起来所形成的一组统计数字序列。时间序列又称动态数列或时间数列。时间序列分析就是利用这组数列，应用数理统计方法加以处理，以预测未来事物的发展。时间序列分析是定量预测方法之一，它的基本原理：一是承认事物发展的延续性。应用过去数据，就能推测事物的发展趋势。二是考虑到事物发展的随机性。任何事物发展都可能受偶然因素影响，为此要利用统计分析中加权平均法对历史数据进行处理。该方法简单易行，便于掌握，但准确性差，一般只适用于短期预测。时间序列预测一般反映三种实际变化规律:趋势变化、周期性变化、随机性变化。

时间序列分析是根据系统观测得到的时间序列数据，通过曲线拟合和参数估计来建立数学模型的理论和方法。时间序列分析常用在国民经济宏观控制、区域综合发展规划、企业经营管理、市场潜量预测、气象预报、水文预报、地震前兆预报、农作物病虫灾害预报、环境污染控制、生态平衡、天文学和海洋学等方面。

时间序列分析主要用途:①系统描述。根据对系统进行观测得到的时间序列数据，用曲线拟合方法对系统进行客观的描述。②系统分析。当观测值取自两个以上变量时，可用一个时间序列中的变化去说明另一个时间序列中的变化，从而深入了解给定时间序列产生的机理。③预测未来。一般用ARMA 模型拟合时间序列，预测该时间序列未来值。④决策和控制。根据时间序列模型可调整输入变量使系统发展过程保持在目标值上，即预测到过程要偏离目标时便可进行必要的控制。

基本步骤:①用观测、调查、统计、抽样等方法取得被观测系统时间序列动态数据。②根据动态数据作相关图，进行相关分析，求自相关函数。相关图能显示出变化的趋势和周期，并能发现跳点和拐点。跳点是指与其他数据不一致的观测值。如果跳点是正确的观测值,在建模时应考虑进去,如果是反常现象，则应把跳点调整到期望值。拐点则是指时间序列从上升趋势突然变为下降趋势的点。如果存在拐点，则在建模时必须用不同的模型去分段拟合该时间序列，例如采用门限回归模型。③辨识合适的随机模型,进行曲线拟合,即用通用随机模型去拟合时间序列的观测数据。对于短的或简单的时间序列，可用趋势模型和季节模型加上误差来进行拟合。对于平稳时间序列，可用通用ARMA 模型（自回归滑动平均模型）及其特殊情况的自回归模型、滑动平均模型或组合ARMA 模型等来进行拟合。当观测值多于50个时一般都采用ARMA 模型。对于非平稳时间序列则要先将观测到的时间序列进行差分运算，化为平稳时间序列，再用适当模型去拟合这个差分序列。

本章重点：1）建立p 阶自回归)(p AR 模型：t p t p t t t x x x x εφφφφ+++++=--- 22110 2）建立q 阶移动平均)(q MA 模型： q t q t t t t x -------+=εθεθεθεμ 2211

3）),(q p ARMA

模型：q t q t t t p t p t t t t x x x x -----------+++++=εθεθεθεφφφφ 221122110 三个模型的拖尾、截尾性

模型

自相关系数k ρ

偏自相关系数kk φ

)(p AR 拖尾

p 阶截尾

)(q MA

q 阶截尾

拖尾

),(q p ARMA

拖尾

拖尾

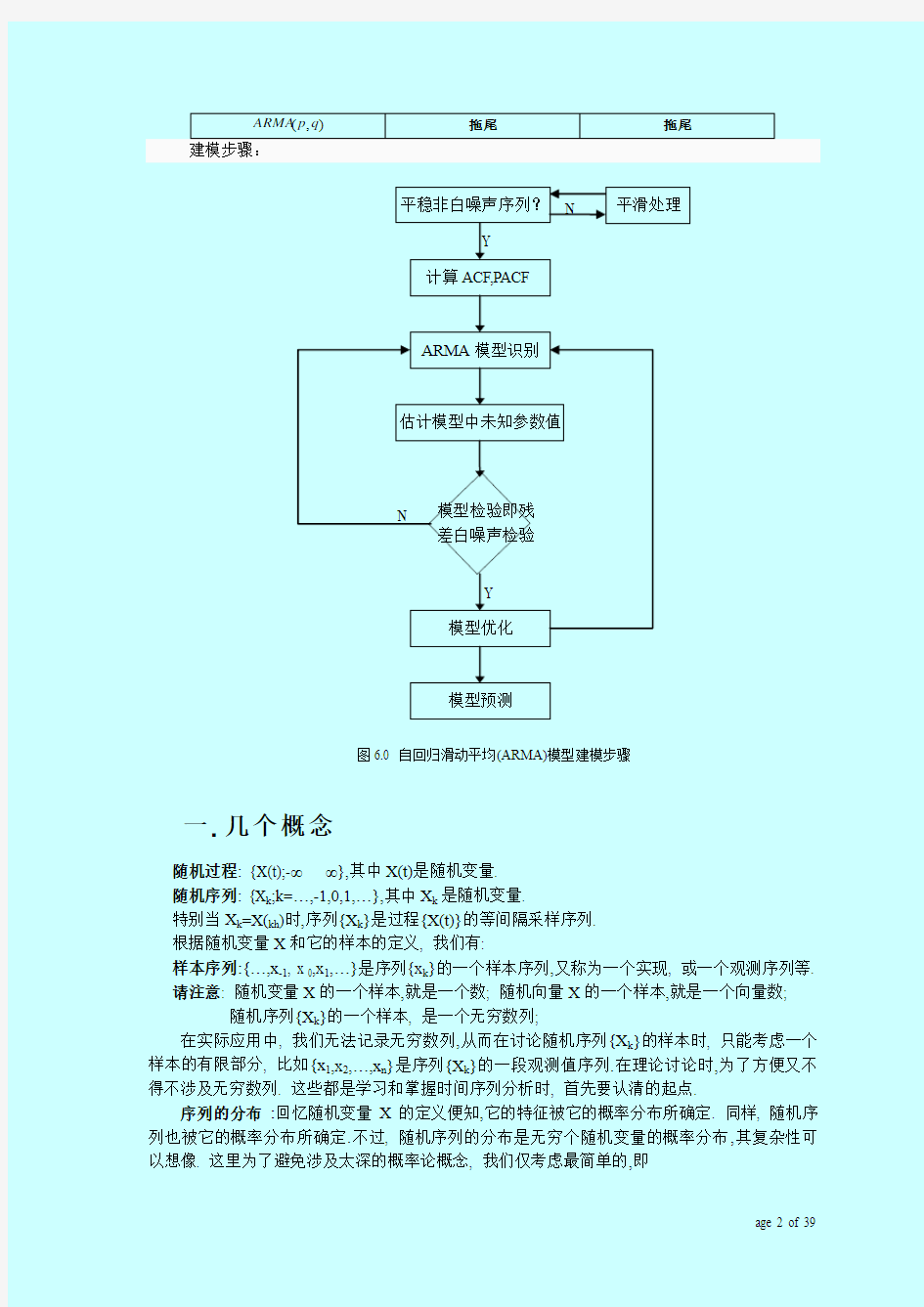
建模步骤：

一. 几个概念

随机过程: {X(t);-∞

特别当X k =X(kh )时,序列{X k }是过程{X(t)}的等间隔采样序列. 根据随机变量X 和它的样本的定义, 我们有:

样本序列:{…,x -1, x 0,x 1,…}是序列{x k }的一个样本序列,又称为一个实现, 或一个观测序列等. 请注意: 随机变量X 的一个样本,就是一个数; 随机向量X 的一个样本,就是一个向量数; 随机序列{X k }的一个样本, 是一个无穷数列;

在实际应用中, 我们无法记录无穷数列,从而在讨论随机序列{X k }的样本时, 只能考虑一个样本的有限部分, 比如{x 1,x 2,…,x n }是序列{X k }的一段观测值序列.在理论讨论时,为了方便又不得不涉及无穷数列. 这些都是学习和掌握时间序列分析时, 首先要认清的起点.

序列的分布 :回忆随机变量X 的定义便知,它的特征被它的概率分布所确定. 同样, 随机序列也被它的概率分布所确定.不过, 随机序列的分布是无穷个随机变量的概率分布,其复杂性可以想像. 这里为了避免涉及太深的概率论概念, 我们仅考虑最简单的,即

平稳非白噪声序列？ 计算ACF,PACF

ARMA 模型识别

估计模型中未知参数值

模型优化

模型预测

模型检验即残

差白噪声检验

N

Y 图6.0 自回归滑动平均(ARMA)模型建模步骤

Y

平滑处理

N

X k ~N(μk ,σ2k ), 它有密度f k (x)=(2πσ2k )-1/2exp{(x-μk )2/2σ2k }

而且(X k+1,X k+2,…,X k+m )有联合正态分布. 于是有: 期望(均值):

EX k =?xf k (x)dx=μk ,

方差:

Var(X k )=E(X k -μk )2=?(x-μk )2f k (x)dx=σ2k .

自协方差:

γkj =E[(X k -μk )(X j -μj )]=??(x-μk )(y-μj )f kj (x,y)dxdy

= E[(X j -μj )(X k -μk )]= γjk .

（注E[(X-EX)(Y-EY)]展开=E(XY)-E(X)E(Y)=cov(X,Y)，协方差，不同事件之间的相关性度量）

二. 平稳性检验

1. 严平稳和宽平稳

平稳时间序列有两种定义，根据限制条件的严格程度，分为:

● 严平稳时间序列（strictly stationary ）—指序列所有的统计性质都不会随着时间的推移而

发生变化，即(X k+1,X k+2,…,X k+m )的联合分布（实际很难求）与k 无关。

● 宽平稳时间序列（week stationary ）—指序列的统计性质只要保证序列的二阶矩平稳就

能保证序列的主要性质近似稳定。

如果在任取时间t 、s 和k 时，时间序列t X 满足如下三个条件：

∞<2t EX

(6.1) μ=t EX

(6.2) ))(())((t s k t s k k k s s t t X X E X X E -+-+--=--μμμμ

(6.3)

则称为宽平稳时间序列。也称为弱平稳或二阶平稳。对于正态随机序列而言，由于联合概率分布仅由均值向量和协方差阵决定，即只要二阶矩平稳，就等于分布平稳了。

2. 平稳时间序列的统计性质

根据平稳时间序列的定义，可以推断出两个重要的统计性质： ● 均值为常数。即式(6.2)的条件。

● 自协方差只依赖于时间的平均长度（只与起点有关与跨度无关）。即式(6.3)的条件。 如果定义自协方方差函数（autocovariance function ）为：

),())((),(t s X X E s t s s t t γμμγ=--=

(6.4)

那么它可由二维函数简化为一维函数)(t s -γ，由此引出延迟k 自协方差函数：

)(),()(k k t t k -=+=γγγ

(6.5)

容易推断出平稳时间序列一定具有常数方差：

)

0(),()(2

γγμ==-=t t X E Dx t t t

(6.6)

如果定义时间序列自相关函数（autocorrelation function ），简记为ACF ：

s

t s s t t DX DX X X E s t ?--=

)

)((),(μμρ

(6.7)

由延迟k 自协方差函数的概念可以等价得到延迟k 自相关函数的概念：

)()

0()

()()

0()

()0()0()())(()(k r k r k r k r k DX DX X X E k k t t k t k t t t -==

=

=?--=

+++ρργγγμμρ或直接定义： (6.8)

容易验证自相关函数具有几个基本性质： ● 1)0(=ρ； ●

)()(k k ρρ=-；

● 自相关阵为对称非负定阵； ● 非惟一性。 注意区分：

协方差函数和相关函数——度量两个不同事件彼此之间的相互影响的程度。

自协方差函数和自相关函数——度量同一事件在两个不同时期之间的相互影响的程度。 3. 样本的估计值

在平稳序列场合，序列的均值等于常数意味着原本含有可列多个随机变量的均值序列变成了只含有一个变量的常数序列，所以常数均值μ的估计值为

n

x x n

t t

∑===1

?μ

(6.9)

同样可以根据平稳序列二阶矩平稳的性质，得到基于样本计算出来的各种估计值。延迟k 自

协方差函数的估计值：

k

n x x x x

k k

n t k t t

---=

∑-=+1

))(()(?γ

(6.10)

总体方差的估计值：

k

n x x

n

t t

--=

∑=1

2

)()0(?γ

(6.11)

延迟k 自相关函数的估计值：

∑∑=-=+---=

=n

t t

k

n t k t t

x x

x x x x

k k 1

2

1

)()

)(()

0(?)(?)(?γγρ

(6.12)

4. 平稳性检验的方法

对序列的平稳性检验有两种方法：一种是根据时序图和自相关图显示的特征做出判断的图检验方法；一是构造检验统计量进行假设检验的单位根检验（unit root test ）方法。是建模的前提,可借助SAS(见例程)、SPSS 、Eviews 等软件实现。

● 时序图和自相关图检验 ●

单位根检验（unit root test ）

所谓单位根检验就是通过检验时间序列自回归特征方程的特征根是在单位圆内还是在单位圆外（包括在单元圆上），来检验时间序列的平稳性。

单位根检验统计量中最常用的是ADF 检验统计量，又称增广DF 检验（augmented Dickey-Fuller ）。对任一p 阶自回归AR (p )过程

t p t p t t x x x εφφ+++=-- 11

(6.13)

它的特征方程为

011=----p p p φλφλ

(6.14)

如果该方程所有的特征根都在单位圆内，即

p i i ,,2,1,1 =<λ则序列t X 平稳。如果至少存在

一个特征根不在单位圆内，不妨设11=λ，则序列t X 非平稳，且自回归系数之和恰好等于1。即

121=+++p φφφ

(6.15)

因而，对于AR (p )过程可以通过检验自回归系数之和是否大于等于1来考察该序列的平稳性。设

121-+++=p φφφρ ，那么原假设0H ：0≥ρ（序列t X 非平稳），ADF 检验统计量：

)?(?ρ

ρ

τS =

(6.16)

式中，)?(ρ

S 为参数ρ的样本标准差。1979年，Dickey 和Fuller 使用蒙特卡洛模拟方法算出了τ检验统计量的临界值表。

三. 纯随机性检验

如果序列值彼此之间没有任何相关性，那就意味着该序列是一个没有记忆的数据序列，即过去的行为对未来的发展没有丝毫影响，这种序列我们称之为纯随机序列。从统计分析的角度而言，纯随机序列是没有任何分析价值的序列。因此，为了确保平稳序列还值不值得分析下去，需要对平稳序列进行纯随机性检验。 5. 纯随机序列（白噪声序列）

如果在任取时间t 和s 时，时间序列t X 满足如下三个条件：

μ=t EX

(6.17) 时当s t s t r ==2),(σ (6.18) 时当s t s t r ≠=0

),(

(6.19)

称此序列为纯随机序列，也称为白噪声（white noise ）序列，简记为),(~2

σμWN X t 。之所以

称之为白噪声序列是因为人们最初发现白光具有这种特性。比较平稳时间序列的定义，可看出白噪声序列一定是平稳序列，且是一种最简单的平稳序列。见图6.1所示是随机生成的1000个服从标准正态分布的白噪声序列观察值。

标准正态分布白噪声序列Xt

-4

-3-2-1012

340

100

200

300

400

500

600

700

800

900

1000

时间

白噪声

图6.1 标准正态白噪声序列时序图

根据白噪声序列的定义，白噪声序列具有三个重要的性质： ● 常数均值（μ=t EX ）; ● 纯随机性（0),(=s t r ）;

● 方差齐性（2

),(σ=s t r ，即序列中每个度量的方差相等）。

6. 纯随机性检验

即白噪声检验(通常对残差序列做)。Barlett 证明，如果一个时间序列是纯随机的，得到一个观察期数为n 的观察序列t X ，那么该序列的延迟非零期的样本自相关系数将近似服从均值为零、方差为序列观察数倒数的正态分布，即

)1

,0(~)(n

N k ρ

(6.20)

式中k 为延迟期数，n 为样本观察期数。

根据Barlett 定理，可以构造BP Q 检验统计量和LB Q 检验统计量来检验序列的纯随机性。原假设：延迟期数小于或等于m 期的序列值之间相互独立，即)()2()1(:0m H ρρρ=== ；备选假设：延迟期数小于或等于m 期的序列值之间有相关性，即:1H 至少存在某个0)(≠k ρ。 1)

BP Q 检验统计量

由Box 和Pierce 推导出的BP Q 检验统计量为：

)(~)(?21

2m k n Q m

k BP χρ

∑== (6.21)

式中，n 为序列观察期数，m 为指定延迟期数。 2)

LB Q 检验统计量

因为BP Q 检验统计量在小样本场合时不太精确，所以Ljung 和Box 又推导出LB Q 检验统计量

为：

)(~)(?)2(2

12m k n k n n Q m

k LB

χρ∑=?

??

? ??-+= (6.22)

式中，n 为序列观察期数，m 为指定延迟期数。m 一般取值为6、12。为什么只需要检验前6期和前12期延迟的LB Q 检验统计量就可以直接判断序列是否为白噪声序列呢？这是因为平稳序列通常具有短期相关性，只要序列时期足够长，自相关系数都会收敛于零。所以，如果序列值之

间存在显著的相关关系，通常只存在在延迟时期比较短的序列值之间，而如果短期延迟的序列之间都不存在显著的相关关系，那么长期延迟之间就更不会存在显著的相关关系。

纯随机性检验小结：当Q 统计量的P 值大于给定的显著水平α（譬如=0.05）时，不拒绝原假设，即相关系数为0，认为序列是白噪声无任何信息可取，停止统计分析（建模）。

四. 方法性工具

7. 差分运算

差分运算分为两种：k 步差分和p 阶差分。

1)

k 步差分

相距k 期的两个序列值之间的减法运算称为k 步差分运算，记为k ?，表示t x 与k t x -之间的

减法运算，即：

k t t k x x --=?

(6.23)

2)

p 阶差分

相距一期的两个序列值之间的减法运算称为1阶差分运算，记为t x ?，表示t x 与1-t x 之间的

减法运算，即：

1--=?t t t x x x

(6.24)

对1阶差分运算后序列t x ?再进行一次1阶差分运算称为2阶差分，记为t x 2

?，表示t x ?与

1-?t x 之间的减法运算，即：

12-?-?=?t t t x x x

(6.25)

依此类推，对1-p 阶差分后序列t p x 1

-?

再进行一次1阶差分运算称为p 阶差分，记为

t p x ?，表示t p x 1-?与11--?t p x 之间的减法运算，即：

111---?-?=?t p t p t p x x x

(6.26)

8. 延迟算子

延迟算子类似于一个时间指针，一个延迟算子乘以当前序列值，就相当于把当前序列值的时间向过去拨了一个时间刻度，记B 为延迟算子，有

)!

(!!,)1()1(,

)(1

i

n 0

10221i n i n C B C B c x c x c B B x x B x x B x Bx i n i i n i n

t t p t t p t t t t -=

-=-?=?====∑=----其中为常数

(6.27)

用延迟算子表示的k 步差分为：

t k k t t k x B x x )1(-=-=?-

(6.28)

用延迟算子表示的p 阶差分为：

∑=--=-=?p

i i t i p i t p

t p

x C x B x 0

)1()1(

(6.29)

五. ARMA 模型

ARMA 模型的全称是自回归移动平均（auto regression moving average ）模型，它是目前最常用的拟合平稳时间序列的模型。ARMA 模型又可细分为AR 模型、MA 模型和ARMA 模型三大类。

9. )(p AR 模型

具有如下结构的模型称为p 阶自回归模型，简记为)(p AR ：

t p t p t t t x x x x εφφφφ+++++=--- 22110

(6.30)

其中包含三个限制条件：模型的最高阶数为p ，即0≠p φ；随机干扰序列t ε为零均值的白噪声

序列，即),0(~2

εσεWN t ；当期的随机干扰与过去的序列值无关，即t s Ex t s <=,0ε。

1) 中心化的)(p AR 模型

当00=φ时，式(6.30)又称为中心化的)(p AR 模型。非中心化的)(p AR 序列都可以通过假设满足平稳性条件，在式(6.30)两边取期望E ，根据平稳时间序列均值为常数的性质，有

μμμ===--p t t t Ex Ex Ex ,,,1 ，且因为t ε为零均值的白噪声，有0=t E ε，所以：

P

p t p t p t t t x x x E Ex φφφφμμφμφμφφμεφφφφ----=

++++=+++++=--- 210

210221101)

(

(6.31)

如果把非中心化的)(p AR 序列减去上式(6.31)中的μ，则转化为中心化)(p AR 序列。特别地，对于中心化)(p AR 序列，有0=t Ex 。

引进延迟算子，设P

p B B B B φφφ----=Φ 2

211)(，又称为p 阶自回归系数多项式，则中心化)(p AR 模型可以简记为：

t t x B ε=Φ)(

(6.32)

2)

)(p AR 模型的方差

要得到平稳)(p AR 模型的方差，需要借助于Green 函数的帮助。下面以求)1(AR 模型的方

差为例来说明：

1

21111----+=+=t t t t t t x x x x εφεφ

将第二式代入第一式，有

22111--++=t t t t x x φεφε

当我们继续将2312---+=t t t x x εφ代入上式，一直到1011εφ+=x x ，可得到

∑-=----+=+++++=1

00

110

111122111t i t i

t i

t t t t t t x

x x φε

φφεφεφεφε

如果∞→t ，设Green 函数为 ,1,0,1==j G j

j φ，上式可改为

∑∑∞

=-∞=-==0

1j j t j j j t j t G x εεφ

(6.33)

对t x 求方差为

2

12

121412120

21)1()

()(φσφφφφσεεε-=

++++++==∞∞

=-∑ j j j t j t Var G x Var

(6.34)

3)

)(p AR 模型的协方差

对中心化的平稳模型在等号两边同乘k t x -，再求期望得到

)()()()()(2211k t t k t p t p k t t k t t k t t x E x x E x x E x x E x x E --------++++=εφφφ

(6.35)

由)(p AR 模型的限制条件，有0)(=-k t t x E ε，再根据平稳时间序列的统计性质，有自协方差函数只依赖于时间的平均长度而与时间的起止点无关，于是可由(6.35)式得到自协方差函数的递推公式：

)()2()1()(21p k k k k p -++-+-=γφγφγφγ

(6.36)

例如，对于)1(AR 模型的自协方差函数的递推公式为：

2

12

1

11111)

0()2()

1()(φσφ

γφγφφγφγε-==-=-=k k k k k

(6.37)

4)

)(p AR 模型的自相关函数

由于平稳时间序列有自相关函数)0(/)()(γγρk k =，在自协方差函数的递推公式(6.36)等号

两边同除以方差函数)0(γ，就得到自相关函数的递推公式：

)()2()1()(21p k k k k p -++-+-=ρφρφρφρ

(6.38)

例如，对于)1(AR 模型的自相关函数的递推公式为：

k

k k k k 11111)0()2()

1()(φρφρφφρφρ==-=-= (6.39)

根据式(6.38)可以推出，平稳)(p AR 模型的自相关函数有两个显著的性质：

● 拖尾性——指自相关函数)(k ρ始终有非零取值，不会在k 大于某个常数之后就恒等

于零。

● 负指数衰减——随着时间的推移，自相关函数)(k ρ会迅速衰减，且以负指数k

i λ（其中

i λ为自相关函数的差分方程的特征根）的速度在减小。

见图6.2和图6.3所示是两个平稳)1(AR 模型的理论自相关图。

图6.2 ACF 按负指数单调收敛到零

图6.3 ACF 按正负相间地衰减到零

5)

)(p AR 模型的偏自相关系数

对于一个平稳)(p AR 模型，求出滞后k 自相关系数)(k ρ时，实际上得到的并不是t x 与k

t x -之间单纯的相关关系。因为这个)(k ρ还会受到中间1-k 个随机变量121,,,+---k t t t x x x 的影响，即这1-k 个随机变量既与t x 又与k t x -具有相关关系。为了能单纯测度t x 与k t x -之间的相关关系，引进了时间序列偏自相关函数（ partial autocorrelation function ），简记为PACF 。它是在剔除了中间1-k 个随机变量的干扰之后的滞后k 自相关系数，计算公式为：

AR(1)模型的自相关函数ACF(k)

-1.00

-0.90-0.80-0.70-0.60-0.50-0.40-0.30-0.20-0.100.000.100.200.300.400.500.600.700.800.901.000123456789101112

延迟k

自相关系数

t

t t x x ε+-=-18.0AR(1)模型的自相关函数ACF(k)

-1.00

-0.90-0.80-0.70-0.60-0.50-0.40-0.30-0.20-0.100.000.100.200.300.400.500.600.700.800.901.000123456789101112

延迟k

自相关系数

t

t t x x ε+=-18.0

]

)?[()]?)(?[(),,|,(211k t k t k

t k t t t k t t k

t t x E x E x E x x E x E x x x x ----+------= ρ (6.40)

式中],|[?11+--=k t t t t x x x E x E ，],|[?11+----=k t t k t k t x x x E x E 。如果我们用过去的k 期序列

值k t k t t t x x x x -+---,,,,121 对t x 作k 阶自回归拟合，即

t k t kk t k t k t x x x x εφφφ++++=--- 2211

(6.41)

那么有),,|,(11+---=k t t k t t kk x x x x ρφ。这说明滞后k 偏自相关系数实际上等于k 阶自回归模型第k 个回归系数的值。根据这个性质很容易计算PACF 的值。在公式(6.41)中等号两边同乘k t x -，求期望并除以)0(γ，得到

n k t k t kk t k t k t ,,,2,1,2211=+++=---ρφρφρφρ

(6.42)

取前k 个方程构成的方程组：

??

????

?+++=+++=+++=----0

22112

021121

12011ρφρφρφρρφρφρφρρφρφρφρkk k k k k k k kk k k k kk k k (6.43)

该方程组被称为Yule-Walker 方程。根据线性方程组求解的Gramer 法则，有

D

D k

kk =

φ (6.44)

式中：

k

k k k k k k k D D ρρρρρ

ρρρρρρρρ

212

1

11

2121

1

1

111

,1

111------==

可以证明对于平稳)(p AR 模型，当p k >时，有0=k D ，这样0=kk φ。也就是说平稳)(p AR 模型的偏自相关系数具有p 步截尾性。见图6.4和图6.5所示是两个平稳)1(AR 模型的样本偏自相关图。

图6.4 一个AR(1)模型n=101样本偏自相关函数PACF(k)图

图6.5 一个AR(1)模型n=101样本偏自相关函数PACF(k)图

由于样本的随机性，样本偏自相关系数不会和理论偏自相关系数一样严格截尾，但可以从图6.4和图6.5 中看出，两个平稳)1(AR 模型的样本偏自相关系数1阶显著不为零，1阶之后都近似为零。样本偏自相关图可以直观地验证平稳)(p AR 模型偏自相关系数具有p 步截尾性。

10. )(q MA 模型

具有如下结构的模型称为q 阶移动平均，简记为)(q MA ：

AR(1)模型的偏自相关函数PACF(k)

-1

-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.910123456789101112

延迟k

偏自相关系数

t

t t x x ε+=-18.0AR(1)模型的偏自相关函数PACF(k)

-1

-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.910123456789101112

延迟k

偏自相关系数

t

t t x x ε+-=-18.0

q t q t t t t x -------+=εθεθεθεμ 2211

(6.45)

其中包含两个限制条件：模型的最高阶数为q ，即0≠q θ；随机干扰序列t ε为零均值的白噪声

序列，即),0(~2

εσεWN t 。

1) 中心化的)(q MA 模型

当0=μ时，式(6.45)又称为中心化的)(q MA 模型。非中心化的)(q MA 序列都可以通过假设满足平稳性条件，在式(6.45)两边取期望E ，根据平稳时间序列均值为常数的性质，有μ=t Ex ，且因为t ε为零均值的白噪声，有0,,0,0,021====---q t t t t E E E E εεεε ，所以：

μεθεθεθεμ=----+=---)(2211q t q t t t t E Ex

(6.46)

如果把非中心化的)(q MA 序列减去上式(6.46)中的μ，则转化为中心化)(q MA 序列。特别地，对于中心化)(q MA 序列，有0=t Ex 。

引进延迟算子，设q

q B B B B θθθ----=Θ 2

211)(，又称为q 阶自移动平均系数多项式，则中心化)(q MA 模型可以简记为：

t t B x ε)(Θ=

(6.47)

2)

)(q MA 模型的方差

平稳)(q MA 模型的方差为：

2

222

2

1

2211)1()

()(ε

σθθθεθεθεθεμq

q t q t t t t Var x Var ++++=----+=--- (6.48)

3)

)(q MA 模型的自协方差

平稳)(q MA 模型的自协方差只与滞后阶数k 相关，且q 阶截尾。当0=k 时，

222221)1()()0(εσθθθγq t x V a r ++++== ；当q k >时，0)(=k γ；当q k ≤≤1时，有 2

111111)()])([()

()(εσθθθεθεθεμεθεθεμγ+-=--------∑+-=---+---+==k k

q i i k q k t q k t k t q t q t t k t t E x x E k (6.49)

4)

)(q MA 模型的自相关系数

平稳)(q MA 模型的自相关系数为

????

???

??

>≤≤++++-===∑-=+q

k k q k k q k q i k i k k ,

01,10

,1)0()(2

2

11

1

θθθθθγγρ (6.50)

5)

)(q MA 模型的偏自相关系数

在中心化的平稳)(q MA 模型场合，滞后k 阶偏自相关系数为：

)

,,|()

,,|(1111+---+---=

k t t k t k t t k t t kk x x x Var x x x x E φ

(6.51)

容易证明平稳)(q MA 模型的偏自相关系数拖尾性。见图6.6和图6.7所示是一个平稳)1(MA 模型的样本自相关图和样本偏自相关图。

图6.6 一个MA(1)模型n=101样本自相关函数截尾图

MA(1)模型的自相关函数ACF(k)

-1.000

-0.900-0.800-0.700-0.600-0.500-0.400-0.300-0.200-0.1000.0000.1000.2000.3000.4000.5000.6000.7000.8000.9001.000

0123456789101112

延迟k

自相关系数

1

8.0-+=t t t x εε

图6.7 一个MA(1)模型n=101样本偏自相关函数拖尾图

6)

)(q MA 模型的可逆性

容易验证当两个)1(MA 模型具有如下结构时：

1

1

111

:2:1---

=-=t t t t t t x x εθεεθε模型模型 (6.52)

根据公式(6.50)计算，)1/(2

111θθρ+-=，它们的自相关系数正好相等。即不同的模型却拥有完全相同的自相关系数。这种自相关系数的不惟一性将会导致拟合模型和随机时间序列之间不会是一一对应关系。为了保证一个给定的自相关函数能够对应惟一的)(q MA 模型，我们需要给模型增加约束条件。这个约束条件称为)(q MA 的可逆性条件。把上式(6.52)中两个)1(MA 模型表示成两个自相关AR 模型形式：

t t t

t

B

x B x εθεθ=-=-1

11

1:

21:

1模型模型 (6.53)

注意表示成自相关AR 模型时运用公式 ++++=--321

1)

1(a a a a ，其中

11/θθB a B a ==或。显然，当11<θ时，模型1收敛，而模型2不收敛；当11>θ时，则模

MA(1)模型的偏自相关函数PACF(k)

-1.000

-0.900-0.800-0.700-0.600-0.500-0.400-0.300-0.200-0.1000.0000.1000.2000.3000.4000.5000.6000.7000.8000.9001.0000123456789101112

延迟k

偏自相关系数

1

8.0-+=t t t x εε

型2收敛，而模型1不收敛。若一个)(q MA 模型能够表示成收敛的AR 模型形式，那么该)(q MA 模型称为可逆模型。一个自相关系数惟一对应一个可逆)(q MA 模型。

11. ),(q p ARMA 模型

具有如下结构的模型称为自回归移动平均模型，简记为),(q p ARMA ：

q t q t t t p t p t t t t x x x x -----------+++++=εθεθεθεφφφφ 221122110

(6.54)

若00=φ，该模型称为中心化),(q p ARMA 模型。模型的限制条件与)(p AR 模型、)(q MA 模型相同。引进延迟算子，中心化),(q p ARMA 模型简记为：

t t x B εΘ=Φ)(

(6.55)

式中：P

p B

B B B φφφ----=Φ 2

211)(，称为p 阶自回归系数多项式，

q q B B B B θθθ----=Θ 2211)(，称为q 阶自移动平均系数多项式。

显然，当0=q 时，),(q p ARMA 模型就退化成)(p AR 模型；当0=p 时，),(q p ARMA 模型就退化成)(q MA 模型。所以，)(p AR 模型和)(q MA 模型实际上是),(q p ARMA 的特例，它

们统称为ARMA 模型。而),(q p ARMA

模型的统计性质也正是)(p AR 模型和)(q MA 模型统计性质的有机组合。

由于),(q p ARMA 模型可以转化为无穷阶移动平均模型，所以),(q p ARMA 模型的自相关系数不截尾。同理，由于),(q p ARMA

模型也可以转化为无穷阶自回归模型，所以),(q p ARMA 模型的偏自相关系数也不截尾。总结)(p AR 模型、)(q MA 模型和),(q p ARMA

模型的自相关系数和偏自相关系数的规律，见表6.1所示。

表6.1 拖尾性和截尾性

模型

自相关系数k ρ

偏自相关系数kk φ

)(p AR 拖尾

p 阶截尾

)(q MA

q 阶截尾

拖尾 ),(q p ARMA

拖尾

拖尾

假如某个时间序列观察值可以判定为平稳非白噪声序列，计算出样本自相关系数（ACF ）和

样本偏自相关系数（PACF ）之后，就要根据它们表现出来的性质，选择阶数适当的ARMA 模型

拟合观察值序列。即根据样本的自相关系数和样本偏自相关系数性质估计自相关阶数p ?和移动平均阶数q

?。因此，这个过程也称为模型定阶过程或模型识别过程。 由于样本的随机性，样本的自相关系数和偏自相关系数不会呈现出理论截尾的完美情况，本

应截尾处仍会呈现出小值震荡的情况。同时，由于平稳时间序列通常都具有短期相关性，随着延迟阶数变大，自相关系数和偏自相关系数都会衰减至零值附近作小值波动。那么，如何判断自相关系数和偏自相关系数是截尾还是拖尾呢？以及如果为截尾那么相应的阶数为多少？

通常分析人员是依据样本的自相关系数和偏自相关系数近似分布来作出尽可能合理的判断。Jankins 和Watts 已经证明样本自相关系数是总体自相关系数的有偏估计：

k k n k E ρρ??

?

??-=1)?(

(6.56)

式中k 为延迟阶数，n 为样本容量。根据Bartlett 公式计算样本自相关系数的方差近似等于：

j k n n Var j

m m j j m m k >+=?∑∑=-=),

?1(1?1)?(1

2

2ρρρ

(6.57)

当延迟阶数k 足够大时，0)?(→k E ρ

；当样本容量n 充分大时，n Var k /1)?(→ρ。所以样本自相关系数近似服从正态分布：

)1

,0(~?n

N k ρ

(6.58)

Quenouille 证明，样本偏自相关系数也同样近似服从这个正态分布：

)1

,0(~?n

N kk

φ (6.59)

设显著水平取%5=α。如果样本自相关系数和样本偏自相关系数在最初的k 阶明显大于2倍标准差，而后几乎95%的系数都落在2倍标准差的范围内，且非零系数衰减为小值波动的过程非常突然，通常视为k 阶截尾；如果有超过5%的样本相关系数大于2倍标准差，或者非零系数衰减为小值波动的过程比较缓慢或连续，通常视为拖尾。

六. 参数估计和检验

对于一个非中心化),(q p ARMA

，有 t p q t B B x εμ)

()(ΦΘ+

=

(6.60)

通过样本的自相关系数和偏自相关系数的性质，估计出自相关阶数p

?和移动平均阶数q ?。为模型定阶后，该模型共含有2++q p 个未知参数：2

11,,,,,εσμθθφφq p 。参数μ用样本均值来估计总体均值（矩估计法）。对原序列中心化后，待估参数减少一个。对1++q p 个未知参数的估计方法有三种：矩估计、极大似然估计和最小二乘估计。

12. 参数的矩估计

用时间序列样本数据计算出延迟1阶到q p +阶的样本自相关系数k ρ?，延迟k 阶的总体自相

关系数为),,,(11q k k θ?φφρ ，公式中包含q p +个未知参数变量q p θθφφ ,,,11。如果用计算出的样本自相关系数来估计总体自相系数，那么有q p +个联立方程组：

??

???????===++q p q p q p k q p k q p ρ

θθφφρρθθφφρρ

θθφφρ?),,,(?),,,(?),,,(11111111 (6.61)

从中解出q p +个未知参数变量的值作为模型的参数估计值q

p θθφφ?,?,?,?11 。这种方法称为参数的矩估计。

白噪声序列的方差2εσ的矩估计，是用时间序列样本数据计算出样本方差2

?x σ

来估计总体方差2x σ求得。),(q p ARMA 模型的两边同时求方差，并把相应参数变量的估计值代入，可得白噪声

序列的方差估计为：

22212212

???1??1x q

p σθθφφσε++++++= (6.62)

13. 参数的极大似然估计

当总体分布类型已知时，极大似然估计ML （maximum-likelihood ）是常用的估计方法。极大似然估计的基本思想，是认为样本来自使该样本出现概率最大的总体。因此，未知参数的极大似然估计，就是使得似然函数（即联合密度函数）达到最大值的参数值。即：

{}),,,;,(max ),;?,?,?,?(111111q

P n n q P x x p x x L θθφφθθφφ = (6.63)

在时间序列分析中，序列的总体分布通常是未知的。为了便于分析和计算，通常假设序列服从多元正态分布，它的联合密度函数是可导的。当似然函数关于参数可导时，常常可以通过求导方法来获得似然函数极大值对应的参数值。在求极大似然估计时，为了求导方便，常对似然函数取对数，然后对对数似然函数中的未知参数求偏导数，得到似然方程组。理论上，只要求解似然方程组即可得到未知参数的极大似然估计。但是在实际上是使用计算机经过复杂的迭代算法求出未知参数的极大似然估计。

极大似然估计与矩估计的比较：矩估计的优点是不要求知道总体的分布，计算量小，估计思想简单直观。但缺点是只用到了样本自相关系数的信息，序列中的其他信息被忽略了，这导致矩估计方法是一种比较粗糙的估计方法，它的估计精度一般较差。因此，它常被作为极大似然估计和最小二乘估计的迭代计算的初始值。极大似然估计的优点是充分应用了每一个观察值所提供的信息，因而它的估计精度高，同时，还具有估计的一致性、渐近正态性和渐近有效性等优良统计性质，是一种非常优良的参数估计方法。 14. 参数的最小二乘估计

参数的最小二乘估计ULS （unconditional least squares ）是使),(q p ARMA

模型的残差平方和