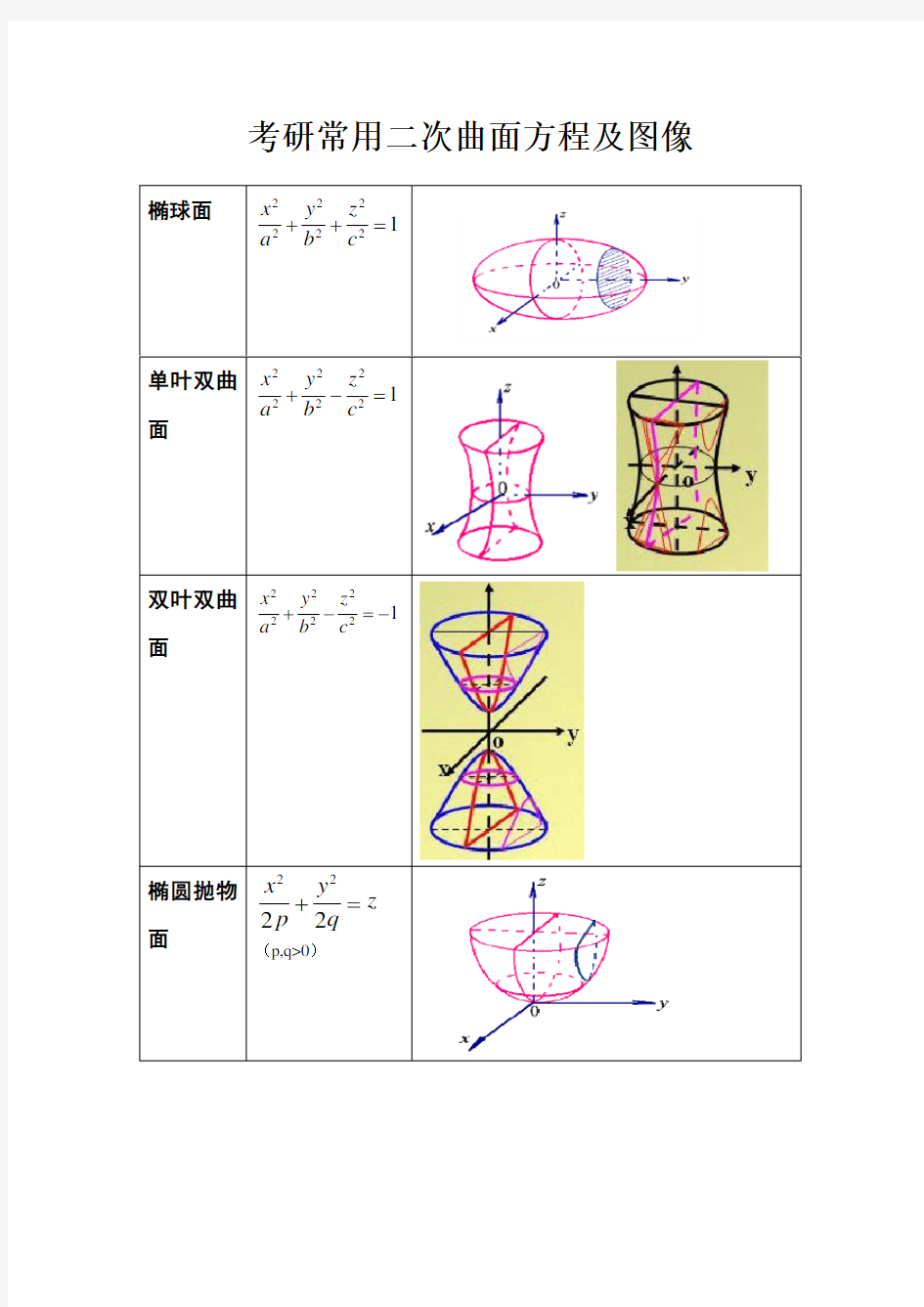
考研常用二次曲面方程及图像
考研常用二次曲面方程及图像
椭球面222
2221
x y z
a b c
++=
单叶双曲面
222
222
1 x y z
a b c
+-=
双叶双曲面
222
222
1 x y z
a b c
+-=-
椭圆抛物面
22
22
x y
z p q
+=(p,q>0)
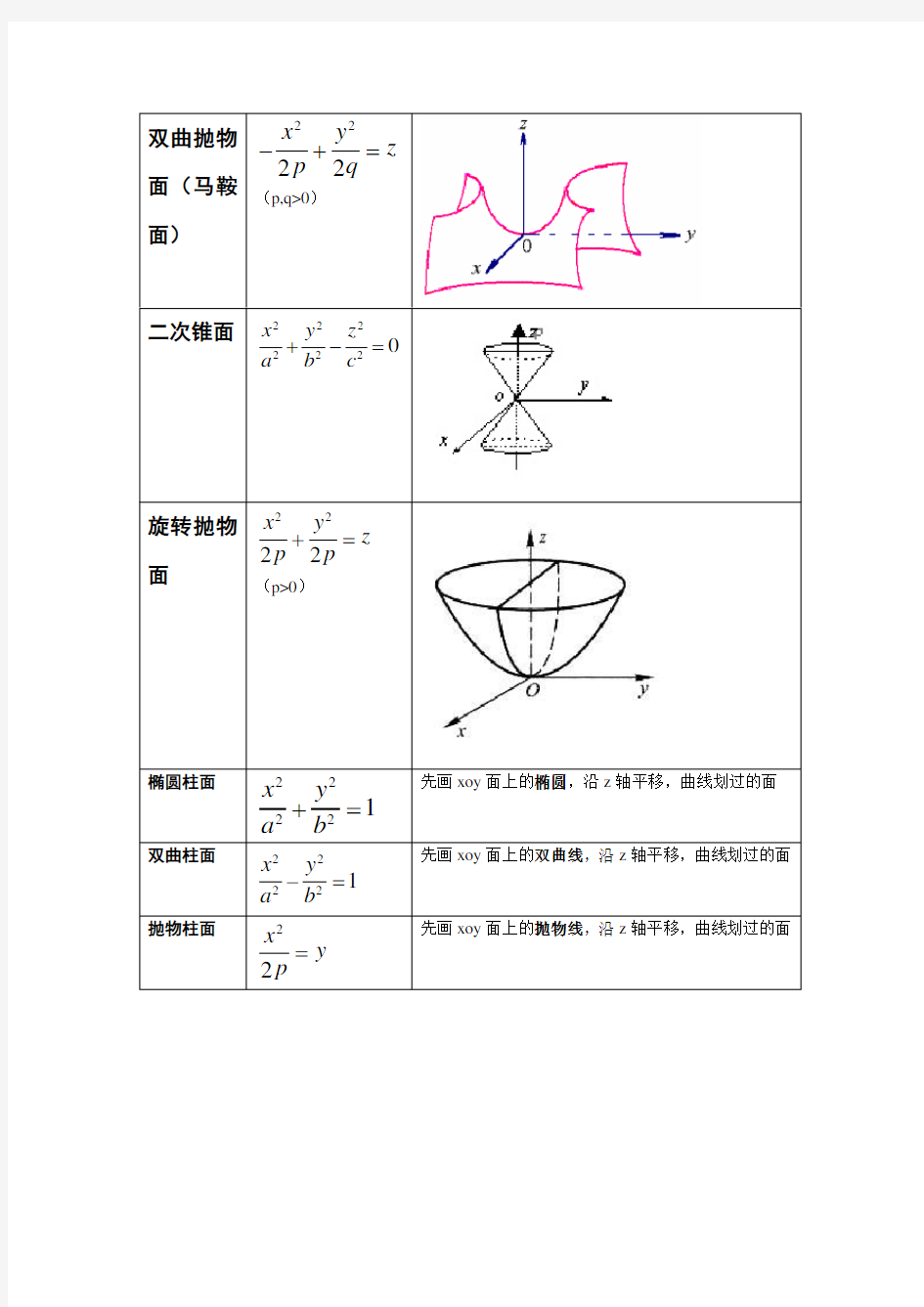
双曲抛物面(马鞍面) 2222x y z p q -+=(p,q>0)
二次锥面 222
2220x y z a b c
+-=
旋转抛物面 2222x y z p p
+= (p>0)
椭圆柱面 22
221x y a b += 先画xoy 面上的椭圆,沿z 轴平移,曲线划过的面 双曲柱面 22221x y a b -= 先画xoy 面上的双曲线,沿z 轴平移,曲线划过的面
抛物柱面 2
2x y p = 先画xoy 面上的抛物线,沿z 轴平移,曲线划过的面
4.5常见曲面的参数方程
§4.5 常见曲面的参数方程 本节重点:掌握空间中的三种坐标系:直角坐标系、球坐标系、柱坐标系。 掌握旋转曲面的参数方程的建立。 掌握直纹面的参数方程。 本节难点:旋转曲面的参数方程。直纹面的参数方程。 在第二章中,我们已经引进一般曲面与曲线的参数方程的概念、并给出简单曲面与曲线的参数表示,例如球面与圆柱螺旋线,直线的参数方程。现在再介绍旋转曲面、直纹面的参数方程,同时给出空间中另外两种坐标系:球坐标系与柱坐标系。 (一)旋转曲面的参数方程,球坐标与柱坐标 设旋转曲面的轴为Z 轴,母线Γ的参数方程是 )()()()(b t a t h Z t g Y t f X ≤≤=== 则此旋转曲面可由Γ上每一点生成的纬圆所构成的。由于这纬圆上动点),,(Z Y X P 与它在坐标面XOY 上的投影' P 具有相同的Y X ,坐标,所以Γ上任一点),,(1111Z Y X P 生成的纬圆的参数方程是 ??? ????=+=+=121212121sin cos Z Z Y X Y Y X X θθ )20(πθ<≤ 其中2121Y X +是纬圆半径,即1P 到Z 轴的距离,而参数θ是X 轴到1OP 的转角。设1P 对应的参数是1t ,则 )())(())((112 1212121t h Z t g t f Y X =+=+ 再让1t 在其取值范围内变动,即得这旋转曲面的参数方程 ??? ????=+=+=)(sin ))(())((cos ))(())((2222t h Z t g t f Y t g t f X θθ ???? ??<≤≤≤πθ20b t a (4.5.1) 特别地,当母线P 为坐标面XOZ 上的径线 )(0) (t h Z Y t f X === 时,(4.5.1)成为
不变量法化简二次曲面
不变量法化简二次曲面 徐晓利摘要:二次曲面的化简是一项复杂又高难度的工作.本文主要总结了计算简便易掌握的不变量法,即运用变量和不变量化简二次曲面的方法,并举例讲解方法.关键词:二次曲面;化简;不变量二次曲面是解析几何的重点内容,也是高等代数这一模块中重要的二次型理论的经典应用.我们往往通过化简其方程,判别二次曲面的类型,并确定其几何形状.化简二次曲面,是二次曲面一般理论中最重要的内容,也是难点所在.坐标变换法(正交变换)是化简二次曲面方程普遍常用的方法,但是由于相关高等代数理论抽象难懂,计算过程复杂,课堂教学显得很是困难.在欧式坐标系中,二次曲面存在着许多不变量,总结归纳不变量关系与二次曲面标准方程之间联系,由此来进行化简.1二次曲面定义1在三维空间中,用三元二次方程来表示的曲面称为二次曲面.设二次曲面的一般方程为:(1.1).二次曲面方程中的常用记号:将的二次项部分记为,将的系数排成矩阵,叫做二次曲面的矩阵..2不变量法化简二次曲面定义2二次曲面的标准方程:无法再使用平移、旋转变换进行化简的方程.即满足以下三者的方程:1)方程中不包含交叉项xy,xz,yz;2)若方程中存在某一坐标的二次项,就不存在这一坐标的一次项;3)若方程中只存在某一坐标的一次项,且此时其中不存在.在高等代数课程中,有一个重要理论,称为二次型理论.二次型理论告诉我们,通过求解矩阵的特征方程,求相应特征根,最后得到唯一的标准形.这也就是我们常常所说的正交变换.二次曲面方程中也有
相应的二次型矩阵,从而二次曲面便能用此变换化简,在这里不加以展开.在变换中我们发现,二次曲面方程在直角坐标变换后,方程虽然发生了一定变化,但是决定二次曲面的几何特征的性质却没有任何变化,那些不变的性质我们可以采用不变量来刻画.这种不变量可以用二次曲面方程的系数来表达.我们称,不因直角坐标变化而发生改变的量为正交不变量.正交不变量在解析几何研究中十分重要的一项,为二次曲面和二次曲线的化简有着尤为重要的作用,下面我将证明二次曲面中的不变量.引理 1.是二次曲面的不变量.即是正交不变量.推论 1.二次曲面的特征方程和特征根在任意直角坐标变换下都不变.引理2.和在转轴变换下不变,称为半不变量.引理3.给定二次曲面方程(1)当时,是不变量;(2)当时,是不变量.任意一个二次曲面方程在选取适当的直角坐标变化后可以被分为5大类别,表示为化简的五个方程之一,下面我们利用二次曲面在转轴变化下的不变量与半不变量对二次曲面进行化简.定理1.不变量得简化方程:(1)当时,简化方程为;(2)当时,简化方程为;(3)当时,简化方程为;(4)当时,简化方程为;(5)当时,简化方程为.其中表示非零特征根.证明:从略.例1:化簡下面二次曲面方程,并判断出它为何种二次曲面.解:二次曲面的矩阵,分别计算不变量,得,,,.特征方程为,特征根为:,,.又由,所以二次曲面的简化方程为:,该曲面为椭圆柱面.例2:化简二次曲面方程.解:二次曲面的矩阵,分别计算不变量,得,,,由故二次曲面为中心二次曲面,特征方程为,特征根为:,,又所以二次曲面的简化方程为:,这是一个
10三维空间中二次方程与二次曲面概要.
三维空间中二次方程与二次曲面 张晓青(2010073060029) 指导教师:李厚彪 【摘要】 利用正交变换可以将二次型化为标准型,在三维空间中一个二次方程对应着一种 二次曲面.在研究二次方程的几何意义时,先将二次方程进行正交变换进而研究所得到的标准型对应的几何图形,可以证明所得的几何图形是一个与原几何图形相同但位于特殊位置的图形,具有一定的对称性,为研究带来方便.这种正交变换法适用于一般情况具有探究价值,本文基于教材,进一步讨论正交变换后不同的标准型与几何图形的关系,并附有图解. 【关键词】正交表换 二次方程 二次曲面 1 引 言 教材第六章二次型与二次曲面的几何应用中告诉我们不同的标准型的参数对应17种不同的几何图形,那么它们究竟是什么样的曲面图形呢?接下来我们一一讨论. 2.正 文 如果线性变换=X CY 中的系数举矩阵C 是正交矩阵,则称这个线性变换为正交变换 对n 维实向量T 12(,,,)n a a a =α,T 12(,,,)n b b b =β,设A 为n 阶正交矩阵,作正交变 换 =X A α,=Y A β, 则 T T T T (,)(,)()()( ,).= ====X Y A αA βA αA βαΑA βαβ αβ 即,正交变换保持向量内积不变,因为也就保持向量的长度与夹角不变.于是在正交变换下, 几何图形的形状不会发生改变. 设 222 12311122233312121313 2323112233(,,)222? f x x x a x a x a x a x x a x x a x x b x b x b x c =+++++++++ (1.1) 则方程123(,,)0f x x x =在几何空间中表示一个二次曲面. 令11 121321 222331 32 33a a a a a a a a a ?? ? = ? ???A ,123x x x ?? ?= ? ???X ,123b b b ?? ?= ? ??? b 则(1.1)式可记为 T T ()f c =++X X AX b X (1.2) 下面,令T ()g =X X AX 1. 作正交变换=X CY ,其中T 123(,,)y y y =Y ,则 223''' 112233112233()f y y y b y b y b y c λλλ=++++++X (1.3)
常见的空间曲面与方程
常见的空间曲面与方程 常见的空间曲面有平面、柱面、锥面、旋转曲面和二次曲面。 1. 平面 空间中平面的一般方程为 0a x b y c z d +++= 其中,,a b c 均为常数,且,,a b c 不全为零。 例如,1x y z ++=(图8-6(a )),0x =(图8-6(b ))均表示空间中的平面, z yoz 平面(x =0) y y x 图8-6(a ) 图8-6 (b) 图8-6 2. 柱面 与给定直线L 平行的动直线l 沿着某给定的曲线C 移动所得到空间曲面,称为柱面, l 为母线,C 为准线。 如图8-7所示 图8-7 图8-8
例如,222x y R +=表示空间中母线平行于z 轴,准线是xoy 平面上的圆222x y R +=的 圆柱面的方程,简称圆柱面图(8-8)。 3. 二次曲面 三元二次方程 222 1231 2 31230a x a y a z b x y b y z b z x c x c y c z d +++ ++++++= 所表示的曲面称为二次曲面,其中,,(1,2,3),i i i a b c i d =均为常数,且,,i i i a b c 不全为0. 二次曲面有以下几种标准形式,它们分别为: 球面: 图8-9 椭球面:222 2221(,,0)x y z a b c a b c ++=>图8-10 图8-9 图8-10 单叶双曲面:222 2221(,,0)x y z a b c a b c -+=>图8-11 双叶双曲面:222 2221(,,0)x y z a b c a b c +-=->图8-12 2222(0)x y z R R + += >x z
第三章 常见曲面球面和旋转面
第三章 常 见 曲 面 §3.1 球面和旋转面 1.1球面的普通方程 球面方程的建立 首先建立球心在点()0000,,z y x M ,半径为0R ≥的球面方程。根据以下充分必要条件 (,,)M x y z 在球面上0M M R ?=, 得 ()()()2 2 2 2 000x x y y z z R -+-+-=, (3.1) 展开得 2221232220,x y z b x b y b z c ++++++= (3.2) 其中, 2222102030,000,,b x b y b z c x y z R =-=-=-=++-。 (3.1)或(3.2)就是所求球面方程,它是一个三元二次方程,没有交叉项(yz xz xy ,,项),平方项的系数相同。反之,任一形如(3.2)的方程经过配方后可写成: ()()(),0232221232221=---++++++b b b c b z b y b x 当c b b b >++2 32 22 1时,它表示一个球心在()321,,b b b ---,半径为c b b b -++2 32 22 1的 球面;当c b b b =++2 32221时,它表示一个点() 32,1,b b b ---;当c b b b <++2 32221时,它没有轨迹(或者说它表示一个虚球面)。 1.2球面的参数方程,点的球面坐标 如果球心在原点,半径为R ,在球面上任取一点()z y x M ,,,从M 作xOy 面的垂线,垂
足为N N ,连,O M O N 。设x 轴到ON 的角度为?,ON 到OM 的角度为θ(M 在xOy 面上方时,θ为正,反之为负),则有 cos cos ,cos sin ,02,.2 2 sin ,x R y R z R θ?π π θ??πθθ=?? =≤<- ≤≤ ??=? (3.3) (3.3)称为球心在原点,半径为R 的球面的参数方程,有两个参数θ?,,其中?称为经度,θ称为纬度。 球面上的每一个点(除去它与z 轴的交点)对应唯一的对实数()?θ,,因此()?θ,称为球面上点的曲纹坐标。 因为空间中任一点()z y x M ,,必在以原点为球心,以R OM =为半径的球面上,而球面上点(除去它与z 轴的交点外)又由它的曲纹坐标()?θ,唯一确定,因此,除去z 轴外,空间中的点M 由有序三元实数组()?θ,,R 唯一确定。我们把()?θ,,R 称为空间中点M 的球面坐标(或空间极坐标),其中0R ≥,,022 2 π π θ?π-≤≤ ≤≤。 点M 的球面坐标()?θ,,R 与M 的直角坐标()z y x ,,的关系为 cos cos , 0,cos sin , - ,22 sin , 02x R R y R z R θ?π π θ?θθ?π =≥??? =≤≤ ??=≤≤?? (3.4) 1.3曲面和曲线的普通方程、参数方程 从球面的方程(3.2)和球面的参数方程(3.3)看到,一般来说,曲面的普通方程是一个三元方程()z y x F ,,=0,曲面的参数方程是含有两个参数的方程: (,),(,), ,,(,),x x u v y y u v a u b c v d z z u v =?? =≤≤≤≤??=? (3.5) 其中,对于()v u ,的每一对值,由(3.5)确定的点()z y x ,,在此曲面上;而此曲面上任一点的坐标都可由()v u ,的某一对值(3.5)表示。于是通过曲面的参数方程(3.5),曲面上的
5常见曲面的参数方程
§ 常见曲面的参数方程 本节重点:掌握空间中的三种坐标系:直角坐标系、球坐标系、柱坐标系。 掌握旋转曲面的参数方程的建立。 掌握直纹面的参数方程。 本节难点:旋转曲面的参数方程。直纹面的参数方程。 在第二章中,我们已经引进一般曲面与曲线的参数方程的概念、并给出简单曲面与曲线的参数表示,例如球面与圆柱螺旋线,直线的参数方程。现在再介绍旋转曲面、直纹面的参数方程,同时给出空间中另外两种坐标系:球坐标系与柱坐标系。 (一)旋转曲面的参数方程,球坐标与柱坐标 设旋转曲面的轴为Z 轴,母线Γ的参数方程是 )()()()(b t a t h Z t g Y t f X ≤≤=== 则此旋转曲面可由Γ上每一点生成的纬圆所构成的。由于这纬圆上动点),,(Z Y X P 与它在坐标面XOY 上的投影' P 具有相同的Y X ,坐标,所以Γ上任一点),,(1111Z Y X P 生成的纬圆的参数方程是 ??? ????=+=+=121212121sin cos Z Z Y X Y Y X X θθ )20(πθ<≤ 其中2121Y X +是纬圆半径,即1P 到Z 轴的距离,而参数θ是X 轴到1OP 的转角。设1P 对应的参数是1t ,则 )())(())((112 1212121t h Z t g t f Y X =+=+ 再让1t 在其取值范围内变动,即得这旋转曲面的参数方程 ??? ????=+=+=)(sin ))(())((cos ))(())((2222t h Z t g t f Y t g t f X θθ ???? ??<≤≤≤πθ20b t a (4.5.1) 特别地,当母线P 为坐标面XOZ 上的径线
4.5常见曲面的参数方程
§4.5 常见曲面的参数方程 本节重点:掌握空间中的三种坐标系:直角坐标系、球坐标系、柱坐标系。 掌握旋转曲面的参数方程的建立。 掌握直纹面的参数方程。 本节难点:旋转曲面的参数方程。直纹面的参数方程。 在第二章中,我们已经引进一般曲面与曲线的参数方程的概念、并给出简单曲面与曲线的参数表示,例如球面与圆柱螺旋线,直线的参数方程。现在再介绍旋转曲面、直纹面的参数方程,同时给出空间中另外两种坐标系:球坐标系与柱坐标系。 (一)旋转曲面的参数方程,球坐标与柱坐标 设旋转曲面的轴为Z 轴,母线Γ的参数方程是 )()()()(b t a t h Z t g Y t f X ≤≤=== 则此旋转曲面可由Γ上每一点生成的纬圆所构成的。由于这纬圆上动点),,(Z Y X P 与它在坐标面XOY 上的投影' P 具有相同的Y X ,坐标,所以Γ上任一点),,(1111Z Y X P 生成的纬圆的参数方程是 ??? ????=+=+=121212121sin cos Z Z Y X Y Y X X θθ )20(πθ<≤ 其中2121Y X +是纬圆半径,即1P 到Z 轴的距离,而参数θ是X 轴到1OP 的转角。设1P 对应的参数是1t ,则 )())(())((1121212121t h Z t g t f Y X =+=+ 再让1t 在其取值范围内变动,即得这旋转曲面的参数方程 ???????=+=+=)(sin ))(())((cos ))(())((2222t h Z t g t f Y t g t f X θθ ??? ? ??<≤≤≤πθ20b t a (4.5.1) 特别地,当母线P 为坐标面XOZ 上的径线 )(0) (t h Z Y t f X === 时,(4.5.1)成为
高数下册常用常见知识点
高等数学下册常用常见知识点 第八章 空间解析几何与向量代数 (一) 向量及其线性运算 1、 向量,向量相等,单位向量,零向量,向量平行、共线、共面; 2、 线性运算:加减法、数乘; 3、 空间直角坐标系:坐标轴、坐标面、卦限,向量的坐标分解式; 4、 利用坐标做向量的运算:设),,(z y x a a a a = ,),,(z y x b b b b = , 则 ),,(z z y y x x b a b a b a b a ±±±=± , ),,(z y x a a a a λλλλ= ; 5、 ; 6、 7、 向量的模、方向角、投影: 1) 向量的模: 2 22z y x r ++= ; 2) 两点间的距离公式: 2 12212212)()()(z z y y x x B A -+-+-= 3) 方向角:非零向量与三个坐标轴的正向的夹角γβα,, 4) 方向余弦:r z r y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα 5) 投影:?cos Pr a a j u =,其中?为向量a 与u 的夹角。 | (二) (三) 数量积,向量积 1、 数量积:θcos b a b a =? 1)2 a a a =? 2)?⊥b a 0=?b a z z y y x x b a b a b a b a ++=? 2、 向量积:b a c ?=
大小:θsin b a ,方向:c b a ,,符合右手规则 1)0 =?a a 2)b a //? =?b a z y x z y x b b b a a a k j i b a =? 运算律:反交换律 b a a b ?-=? (四) 曲面及其方程 1、 ] 2、 曲面方程的概念: ),,(:=z y x f S 3、 旋转曲面:(旋转后方程如何写) yoz 面上曲线0),(:=z y f C , 绕y 轴旋转一周: 0),(22=+±z x y f 绕 z 轴旋转一周: 0),(22=+±z y x f 4、 柱面:(特点) 0),(=y x F 表示母线平行于z 轴,准线为?????==0 0),(z y x F 的柱面 5、 @ 6、 二次曲面(会画简图) 1) 椭圆锥面:2 2222z b y a x =+ 2) 椭球面:122 2222=++c z b y a x
6.5二次曲面方程的化简与位置确定
§6.5 二次曲面方程的化简与位置确定 本节重点:掌握利用不变量化简二次曲面的方法并能确定新坐标系的位置 一 有心二次曲面 对于有心二次曲面,取其一个中心为新坐标原点' O ,这时在新坐标系下,' O 的坐标为 )0,0,0(,它满足关于中心的方程 ?????=+++=+++=+++0 00'34''33''32''31 ' 24''23''22''21'14''13''12''11a z a y a x a a z a y a x a a z a y a x a (6.5.1) 把)0,0,0(代入(6.5.1)便得到' 34 '24'14a a a ==,因此有 6.5.1定理 若取有心二次曲面的一个中心为原点,则这个二次曲面在这个坐标系下的一次项系数为0。 结合上节结果得到,若二次曲面是有心二次曲面,则取其一个中心为新原点,对应于两个相异特征根21,λλ的两个单位特征向量为新坐标向量→→' ',j i ,取另一个坐标向量为 →→→ ?=' ''j i k ,那么在这个新坐标系下,二次曲面的方程为 0' 442'32'22'1=+++a z y x λλλ 其中3λ是这个二次曲面的另一个特征根,至于' 44a 可用下面方法得到 (1) 用中心的坐标表示' 44a , 因为转轴不改变常数项,因此常数项由移轴决定,由(6.3.20)可得 ),,(000'44z y x F a = 其中),,(000z y x 是新原点上的坐标。但因为 ),,(),,(),,(),,(),,(0004000300002000010000z y x F z y x F z z y x F y z y x F x z y x F +++= 而),,(000z y x 是二次曲面中心,因此)3,2,1(),,,(000=i z y x F i 因此 ),,(0004'44z y x F a = (2) 用不变量求' 44a 若二次曲面是中心二次曲面,则3I 是其中心方程组的系数行列式,因此03≠I ,即
常见曲面的参数方程
§4、5 常见曲面得参数方程 本节重点:掌握空间中得三种坐标系:直角坐标系、球坐标系、柱坐标系。 掌握旋转曲面得参数方程得建立。 掌握直纹面得参数方程、 本节难点:旋转曲面得参数方程。直纹面得参数方程。 在第二章中,我们已经引进一般曲面与曲线得参数方程得概念、并给出简单曲面与曲线得参数表示,例如球面与圆柱螺旋线,直线得参数方程。现在再介绍旋转曲面、直纹面得参数方程,同时给出空间中另外两种坐标系:球坐标系与柱坐标系。 (一)旋转曲面得参数方程,球坐标与柱坐标 设旋转曲面得轴为轴,母线得参数方程就是 则此旋转曲面可由上每一点生成得纬圆所构成得、由于这纬圆上动点与它在坐标面上得投影具有相同得坐标,所以上任一点生成得纬圆得参数方程就是 其中就是纬圆半径,即到轴得距离,而参数就是轴到得转角、设对应得参数就是,则 再让在其取值范围内变动,即得这旋转曲面得参数方程 (4、5.1) 特别地,当母线为坐标面上得径线 时,(4。5、1)成为 (4.5.2) 例1、如图,以原点为中心,为半径得球面可瞧作就是由坐标面上得半圆, ()绕轴旋转所生成得,由(4.5。2)得其参数方程为 (4、5。3) 它与§2。1中得球面参数方程得形式就是相同得。 (4、5、3)中得参数分别叫做经度与纬度,序对叫做地理坐标、显然,除两极外,球面上得点与序对一一对应。这种利用曲面参数方程中得两个参数来表示曲面上得点得坐标叫做曲纹坐标,它对于曲面理论得进一步研究有着重要得作用。 利用球面得这种曲纹坐标还可以引入空间得另一种坐标系。设为空间任意一点,它到原点得距离为,过作以原点为中心,以为半径得球面,则在这球面上具有地理坐标,可令点P对应有序数组;反之,由非负实数可确定所在得球面,再由在这球面上确定点。空间中点得这种坐标叫做球坐标。显然,轴上点得球坐标可取任意值、 把(4.5。3)中得常数换为变数,就成为球坐标与直角坐标得变换式,即 (4、5。4) 反之,有 (4。5.5) 当时,=0,于就是,对坐标面上得点,只需序对即可确定、这里不就是别得,正就是大家熟知得极坐标。这时原点就是极点,轴就是极轴,因此,球坐标可以瞧作就是平面极坐标在空间中得一种推广。 例2、如图4-17,以轴为对称轴,半径为得圆柱面可瞧作就是由坐标面上得直线: ,
二次曲面上课教案
第六章 二次曲面的一般理论 教学目的: 本章讨论了一般二次曲面的渐近方向、中心、切线、切平面、径面奇向、主径面与主方向等重要概念,从不同角度对二次曲面进行了分类. 研究了二次曲面的几何性质,并通过坐标变换和不变量、半不变量两种形式,化二次曲面的一般方程为规范方程,对二次曲面进行了分类和判定,是二次曲面理论的推广和扩充. 教学重难点: 通过坐标变换和运用不变量、半不变量化二次曲面的一般方程为规范方程,既是重点又是难点. 基本概念 二次曲面: 在空间,由三元二次方程 022222244342414231312233222211=+++++++++a z a y a x a yz a xz a xy a z a y a x a (1) 所表示的曲面. 虚元素:空间中,有序三复数组),,(z y x 叫做空间复点的坐标,如果三坐标全是实数,那么它对应的点是实点,否则叫做虚点 二次曲面的一些记号 ≡ ),,(z y x F 44 342414231312233222211222222a z a y a x a yz a xz a xy a z a y a x a +++++++++ 141312111),,(a z a y a x a z y x F +++≡ 242323122),,(a z a y a x a z y x F +++≡ 343323133),,(a z a y a x a z y x F +++≡ 443424144),,(a z a y a x a z y x F +++≡ yz a xz a xy a z a y a x a z y x 231312233222211222),,(+++++≡Φ z a y a x a z y x 1312111),,(++≡Φ z a y a x a z y x 2322122),,(++≡Φ
第二章第二节曲面的参数方程
第二章 曲面论 第二节 曲面的参数方程 一、 曲面的参数方程 设曲面∑是由显式 D y x y x f z ∈=),(),,( 所表示。 设),,(z y x 是曲面∑上的点,记向量),,(z y x r = ,则它们可构成一一对应。 于是曲面∑上的点可以用向量值函数 D y x y x f y x r ∈=),()),,(,,( 来表示, 也可以写为参数形式 ?????===),(, ,y x f z y y x x D y x ∈),(。
一般地,设3),(R v u r r ∈= ,其中参 数?∈),(v u ,这里?是2R 中的一 个区域。 我们称由3),(R v u r r ∈= , ?∈),(v u ,所构成的3R 中点集∑为一张参数曲面,(即曲面∑,可以表示为参数方程表示的点集。) 记为?∈=∑),(),,(:v u v u r r ,(1) 把(1)用分量表示出来,就是 ?? ???===),(),(),,(v u z z v u y y v u x x ,?∈),(v u (2) 通常,我们称(1)是曲面∑的向量方程,而(2)是曲面∑的参数方程。 显然方程(1)和(2)之间的转换是直截了当的,所以我们可以认为(1)与(2)是一回事。
二、 几个用参数方程表示的常见 曲面 例1 平面的参数方程, 设30000),,(R z y x p ∈= 是一个固定的点, ),,(321a a a a = 与),,(321b b b b = 是自0p 出发的两个不平行的向量。这时,由a 与b 张成的平面可以用向量方程, 20),(,R v u b v a u p r ∈++= 来表示; 写成分量表示为 v b u a x x 110++=, v b u a y y 220++=, v b u a z z 330++=,
常见曲面的参数方程
.常见曲面的参数方程
————————————————————————————————作者:————————————————————————————————日期:
§4.5 常见曲面的参数方程 本节重点:掌握空间中的三种坐标系:直角坐标系、球坐标系、柱坐标系。 掌握旋转曲面的参数方程的建立。 掌握直纹面的参数方程。 本节难点:旋转曲面的参数方程。直纹面的参数方程。 在第二章中,我们已经引进一般曲面与曲线的参数方程的概念、并给出简单曲面与曲线的参数表示,例如球面与圆柱螺旋线,直线的参数方程。现在再介绍旋转曲面、直纹面的参数方程,同时给出空间中另外两种坐标系:球坐标系与柱坐标系。 (一)旋转曲面的参数方程,球坐标与柱坐标 设旋转曲面的轴为Z 轴,母线Γ的参数方程是 )()()()(b t a t h Z t g Y t f X ≤≤=== 则此旋转曲面可由Γ上每一点生成的纬圆所构成的。由于这纬圆上动点),,(Z Y X P 与它在坐标面XOY 上的投影' P 具有相同的Y X ,坐标,所以Γ上任一点),,(1111Z Y X P 生成的纬圆的参数方程是 ??? ????=+=+=12 12121 21sin cos Z Z Y X Y Y X X θθ )20(πθ<≤ 其中 2121Y X +是纬圆半径,即1P 到Z 轴的距离,而参数θ是X 轴到1OP 的转角。设1P 对 应的参数是1t ,则 )())(())((112 1212121t h Z t g t f Y X =+=+ 再让1t 在其取值范围内变动,即得这旋转曲面的参数方程 ??? ????=+=+=)(sin ))(())((cos ))(())((2 222t h Z t g t f Y t g t f X θθ ??? ? ??<≤≤≤πθ20b t a (4.5.1) 特别地,当母线P 为坐标面XOZ 上的径线 )(0) (t h Z Y t f X === 时,(4.5.1)成为
4.5常见曲面的参数方程
4.5常见曲面的参数方程
§4.5 常见曲面的参数方程 本节重点:掌握空间中的三种坐标系:直角坐标系、球坐标系、柱坐标系。 掌握旋转曲面的参数方程的建立。 掌握直纹面的参数方程。 本节难点:旋转曲面的参数方程。直纹面的参数方程。 在第二章中,我们已经引进一般曲面与曲线的参数方程的概念、并给出简单曲面与曲线的参数表示,例如球面与圆柱螺旋线,直线的参数方程。现在再介绍旋转曲面、直纹面的参数方程,同时给出空间中另外两种坐标系:球坐标系与柱坐标系。 (一)旋转曲面的参数方程,球坐标与柱坐标 设旋转曲面的轴为Z 轴,母线Γ的参数方程是 )()()()(b t a t h Z t g Y t f X ≤≤=== 则此旋转曲面可由Γ上每一点生成的纬圆所构成的。由于这纬圆上动点),,(Z Y X P 与它在坐标面XOY 上的投影' P 具有相同的Y X ,坐标,所以Γ上任一点),,(1111Z Y X P 生成的纬圆的参数方程是 ???????=+=+=121212121sin cos Z Z Y X Y Y X X θ θ )20(πθ<≤
),(?θ叫做地理坐标。显然,除两极外,球面上的点),,(Z Y X P 与序对),(?θ一一对应。这种利用曲面参数方程中的两个参数来表示曲面上的点的坐标叫做曲纹坐标,它对于曲面理论的进一步研究有着重要的作用。 利用球面的这种曲纹坐标还可以引入空间的另一种坐标系。设P 为空间任意一点,它到原点的距离为r ,过P 作以原点为中心,以r 为半径的球面,则P 在这球面上具有地理坐标?θ,,可令点P 对应有序数组),,(?θr ;反之,由非负实数r 可确定P 所在的球面,再由),(?θ在这球面上确定P 点。空间中点的这种坐标叫做球坐标。显然,Z 轴上点的球坐标θ可取任意值。 把(4.5.3)中的常数a 换为变数r ,就成为球坐标与直角坐标的变换式,即 ?????===?θ ?θ?sin sin cos cos cos r Z r Y r X ?????? ??<<-<≤≥22200πππθt r (4.5.4) 反之,有 ?????????++=+=+=++=2222222222arcsin sin cos Z Y X Z Y X X Y X X Z Y X r ?θθ (4.5.5)
第二章第一节曲面的概念显式方程和隐式方程表示
第二章曲面的表示与曲面论 第一节曲面的显式方程和 隐式方程 一、由显式方程表示的曲面 设2R D?是有界闭区域,函数 :连续。我们称函数f的图 f→ D R 像 z y R z f x f ∈ = G∈= x : ,( } y ),, ),(), y x (3D {( ) 为一张曲面,它展布在D上,称这 个曲面是由显式方程 , =) z∈ (), , ( y f D y x x 所确定的。 ∑表示一个曲面。 通常用 二、几种常见的曲面 例1 在空间直角坐标系中,中心 a、在xy平面 在坐标原点、半径为 上方的那个半球面(称为上半球面),它的显式方程为
222y x a z --=,D y x ∈),(, 其中 }:),{(222a y x y x D ≤+=,即D 是xy 平面上以原点为中心、半径为a 的圆盘。 显然,下半球面的方程为 222y x a z ---=,D y x ∈),(; 同样可给出左半球面、右半球面的方程式。 例2 点集 }1,0,,:),,{(=++≥z y x z y x z y x 是3R 中的一块等边三角形。这块曲面有显式表达 y x z --=1,D y x ∈),(, 其中}1,0,:),{(≤+≥=y x y x y x D 。 例 3 由方程axy z =,2),(R y x ∈, (常数0>a ),所确定的曲面称为双曲抛物面。 由于这曲面在在xy 平面的上的,第一、第三象限中,在xy 平面的上
方,而在第二、第四象限中是在xy 平面的下方,因此在原点)0,0,0(的近旁,曲面呈鞍的形状,俗称马鞍面。 例4 旋转曲面的方程 1设想在xz 平面上有一条显式曲线)0(),(b x a x f z ≤≤≤=。 如果固定z 轴不动,让xz 平面绕着z 轴旋转 360,那么这一条曲线就扫出一张曲面,称之为旋转曲面∑。 设∑∈),,(z y x ,它在过点),0,0(z 平行于xy 平面的平面上,以),0,0(z 为中心,半径为r 的圆周上()(r f z =), 222r y x =+, 于是得这个旋转曲面∑的方程为):(),(222222b y x a D y x f z ≤+≤+=。
45常见曲面的参数方程
§4.5 常见曲面的参数方程 本节重点:掌握空间中的三种坐标系:直角坐标系、球坐标系、柱坐标系。 掌握旋转曲面的参数方程的建立。 掌握直纹面的参数方程。 本节难点:旋转曲面的参数方程。直纹面的参数方程。 在第二章中,我们已经引进一般曲面与曲线的参数方程的概念、并给出简单曲面与曲线的参数表示,例如球面与圆柱螺旋线,直线的参数方程。现在再介绍旋转曲面、直纹面的参数方程,同时给出空间中另外两种坐标系:球坐标系与柱坐标系。 (一)旋转曲面的参数方程,球坐标与柱坐标 设旋转曲面的轴为Z 轴,母线Γ的参数方程是 )()()()(b t a t h Z t g Y t f X ≤≤=== 则此旋转曲面可由Γ上每一点生成的纬圆所构成的。由于这纬圆上动点),,(Z Y X P 与它在坐标面XOY 上的投影' P 具有相同的Y X ,坐标,所以Γ上任一点),,(1111Z Y X P 生成的纬圆的参数方程是 ??? ????=+=+=121212121sin cos Z Z Y X Y Y X X θθ )20(πθ<≤ 其中2121Y X +是纬圆半径,即1P 到Z 轴的距离,而参数θ是X 轴到1OP 的转角。设1P 对应的参数是1t ,则 )())(())((112 1212121t h Z t g t f Y X =+=+ 再让1t 在其取值范围内变动,即得这旋转曲面的参数方程 ??? ????=+=+=)(sin ))(())((cos ))(())((2222t h Z t g t f Y t g t f X θθ ??? ? ??<≤≤≤πθ20b t a (4.5.1) 特别地,当母线P 为坐标面XOZ 上的径线 )(0) (t h Z Y t f X === 时,(4.5.1)成为
