R语言学习系列32-回归分析

27. 回归分析

回归分析是研究一个或多个变量（因变量）与另一些变量（自变量）之间关系的统计方法。主要思想是用最小二乘法原理拟合因变量与自变量间的最佳回归模型（得到确定的表达式关系）。其作用是对因变量做解释、控制、或预测。

回归与拟合的区别：

拟合侧重于调整曲线的参数，使得与数据相符；而回归重在研究两个变量或多个变量之间的关系。它可以用拟合的手法来研究两个变量的关系，以及出现的误差。

回归分析的步骤：

（1）获取自变量和因变量的观测值；

（2）绘制散点图，并对异常数据做修正；

（3）写出带未知参数的回归方程；

（4）确定回归方程中参数值；

（5）假设检验，判断回归方程的拟合优度；

（6）进行解释、控制、或预测。

（一）一元线性回归

一、原理概述

1. 一元线性回归模型：

Y=β0+β1X+ε

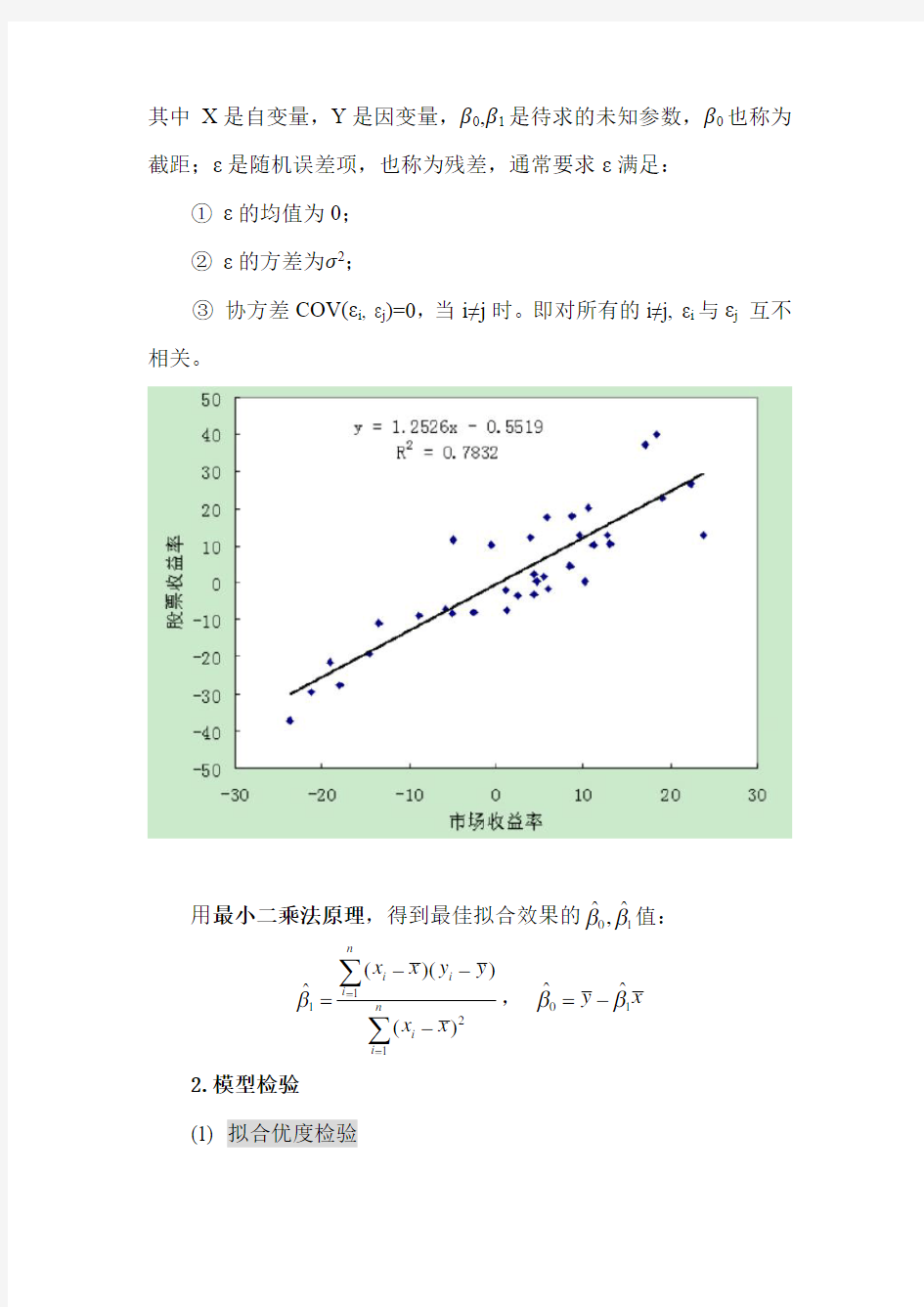
其中 X 是自变量，Y 是因变量，β0,β1是待求的未知参数，β0也称为截距；ε是随机误差项，也称为残差，通常要求ε满足：

① ε的均值为0；

② ε的方差为σ2；

③协方差COV(εi , εj )=0，当i≠j 时。即对所有的i≠j,εi 与εj 互不相关。

用最小二乘法原理，得到最佳拟合效果的01

??,ββ值： 1121()()?()n i i i n

i

i x x y y x x β==--=-∑∑，01

??y x ββ=- 2.模型检验

(1)拟合优度检验

计算R 2，反映了自变量所能解释的方差占总方差的百分比，值越大说明模型拟合效果越好。通常可以认为当R 2大于0.9时，所得到的回归直线拟合得较好，而当R 2小于0.5时，所得到的回归直线很难说明变量之间的依赖关系。

(2)回归方程参数的检验

回归方程反应了因变量Y 随自变量X 变化而变化的规律，若β1=0，则Y 不随X 变化，此时回归方程无意义。所以，要做如下假设检验：

H 0: β1=0, H 1: β1≠0；

① F 检验

若β1=0为真，则回归平方和RSS 与残差平方和ESS/(N-2)都是σ2的无偏估计，因而采用F 统计量：

来检验原假设β1=0是否为真。

②T 检验

对H 0: β1=0的T 检验与F 检验是等价的（t 2=F ）。

3. 用回归方程做预测

得到回归方程01???Y X ββ=+后，预测X=x 0处的Y 值0010

???y x ββ=+. 0?y

的预测区间为：

其中t

的自由度为N-2.

α/2

二、R语言实现

使用lm()函数实现，基本格式为：

lm(formula, data, subset, weights, na.action,

method="qr", ...)

其中，formula为要拟合的回归模型的形式，一元线性回归的格式为：y~x，y表示因变量，x表示自变量，若不想包含截距项，使用y~x-1；

data为数据框或列表；

subset选取部分子集；

weights取NULL时表示最小二乘法拟合，若取值为权重向量，则用加权最小二乘法；

na.action设定是否忽略缺失值；

method指定拟合的方法，目前只支持“qr”（QR分解），method=“model.frame”返回模型框架。

三、实例

例1现有埃及卡拉马村庄每月记录儿童身高的数据，做一元线性回归。

datas<-data.frame(age=18:29,height=c(76.1,77,78.1,78.2, 78.8,79.7,79.9,81.1,81.2,81.8,82.8,83.5))

datas

age height

1 18 76.1

2 19 77.0

3 20 78.1

4 21 78.2

5 22 78.8

6 23 79.7

7 24 79.9

8 25 81.1

9 26 81.2

10 27 81.8

11 28 82.8

12 29 83.5

plot(datas)#绘制散点图

res.reg<-lm(height~age,datas)#做一元线性回归

summary(res.reg) #输出模型的汇总结果

Residuals:

Min 1Q Median 3Q Max

-0.27238 -0.24248 -0.02762 0.16014 0.47238

Coefficients:

Estimate Std.Errort value Pr(>|t|) (Intercept) 64.9283 0.5084 127.71 < 2e-16 ***

age0.6350 0.0214 29.66 4.43e-11 ***

---

Signif.codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.256 on 10 degrees of freedom Multiple R-squared: 0.9888, Adjusted R-squared: 0.9876

F-statistic: 880 on 1 and 10 DF, p-value: 4.428e-11

说明：输出了残差信息Residuals；

回归系数估计值、标准误、t统计量值、p值，可得到回归方程：

height=64.9283+0.6350*age

回归系数p值（< 2e-16，4.43e-11）很小，非常显著的≠0；***也表示显著程度非常显著。

拟合优度R2=0.9888>0.5, 表示拟合程度很好。

F统计量=880，p值=4.428e-11远小于0.05，表示整个回归模型显著，适合估计height这一因变量。

coefficients(res.reg)#返回模型的回归系数估计值

(Intercept) age

64.928322 0.634965

confint(res.reg,parm="age",level=0.95) #输出参数age的置信区间，若不指定parm将返回所有参数的置信区间

2.5 % 97.5 %

age 0.5872722 0.6826578

fitted(res.reg)#输出回归模型的预测值

1 2 3 4 5 6 7 8 9 10 11 12

76.35769 76.99266 77.62762 78.26259 78.89755 79.53252 80.16748 80.80245 81.43741 82.07238 82.70734 83.34231

anova(res.reg)#输出模型的方差分析表

Response: height

Df Sum Sq Mean Sq F value Pr(>F)

age 1 57.655 57.655 879.99 4.428e-11 ***

Residuals 10 0.655 0.066

---

Signif.codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 vcov(res.reg)#输出模型的协方差矩阵

(Intercept) age

(Intercept) 0.25848098 -0.010*******

age -0.01076686 0.0004581642

residuals(res.reg)#输出模型的残差

1 2 3 4 5 6 7 8 9 10 11 12

-0.257692308 0.007342657 0.472377622 -0.062587413 -0.097552448 0.167482517 -0.267482517 0.297552448 -0.237412587 -0.272377622 0.09 2657343 0.157692308

AIC(res.reg)#输出模型的AIC值

[1] 5.161407

BIC(res.reg)#输出模型的BIC值

[1] 6.616127

logLik(res.reg)#输出模型的对数似然值

'logLik.' 0.4192965 (df=3)

abline(res.reg)#给散点图加上一条回归线

par(mfrow=c(2,2))

plot(res.reg)#绘制回归诊断图

说明：分别是残差与拟合值图，二者越无关联越好，若有明显的曲线关系，则说明需要对线性回归模型加上高次项；

残差的Q-Q图，看是否服从正态分布；

标准化残差与拟合值图，也叫位置-尺度图，纵坐标是标准化残差的平方根，残差越大，点的位置越高，用来判断模型残差是否等方差，若满足则水平线周围的点应随机分布；

残差与杠杆图，虚线表示Cooks距离（每个数据点对回归线的影响力）等高线，从中可以鉴别出离群点（第3个点较大，表示删除该数据点，回归系数将有实质上的改变，为异常值点）、高杠杆点、强影响点。

datas<-datas[-3,]#删除第3个样本点，重新做一元线性回归

res.reg2<-lm(height~age,datas)

summary(res.reg2)

新的回归方程为：height=64.5540+0.6489*age，拟合优度R2=0.993，拟合效果变得更好。

#用回归模型预测

ages<-data.frame(age=30:34)

pre.res<-predict(res.reg2,ages,interval="prediction",l evel=0.95)#注意predict函数的第1个参数必须是回归模型的自变量数据构成的数据框或列表

pre.res

fitlwrupr

1 84.02034 83.46839 84.57228

2 84.66921 84.09711 85.24132

3 85.31809 84.72365 85.91254

4 85.96697 85.3482

5 86.58569

5 86.61585 85.97114 87.26056

（二）多元线性回归

一、基本原理

1. 多元线性回归模型：

Y=β0+β1X1+…+ βN X N+ε

其中X1,…,X N是自变量，Y是因变量，β0,β1…, βN是待求的未知参数，ε是随机误差项（残差），若记

多元线性回归模型可写为矩阵形式：

Y=Xβ+ε

通常要求：矩阵X的秩为k+1（保证不出现共线性）, 且k

用最小二乘法原理，令残差平方和

最小，得到

为β的最佳线性无偏估计量（高斯－马尔可夫定理）。

2. σ2的估计和T检验

选取σ2的估计量：

则

假如t 值的绝对值相当大，就可以在适当选定的置信水平上否定原假设，参数的1-α置信区间可由下式得出：

其中t α/2为与α%显著水平有关的t 分布临界值。

3. R 2和F 检验

若因变量不具有0平均值，则必须对R 2做如下改进：

随着模型中增添新的变量，R 2的值必定会增大，为了去掉这种增大的干扰，还需要对R 2进行修正（校正拟合优度对自由度的依赖关系）：

2

2/(1)111(1)/(1)1ESS N k N R R TSS N N k ---=-=----- 做假设检验：

H0: β1=…=βN=0; H1: β1…, βN至少有一个≠0；

使用F统计量做检验，

若F值较大，则否定原假设。

4. 回归诊断

（1）残差图分析

ε=-为纵坐标，某一个合适的自变量为横残差图就是以残差??

y y

坐标的散点图。

回归模型中总是假定误差项是独立的正态分布随机变量，且均值为零和方差相等为σ2. 如果模型适合于观察到的数据，那么残差作为误差的无偏估计，应基本反映误差的假设特征。即残差图应该在零点附近对称地密布，越远离零点的地方就疏散（在形象上似有正态趋势），则认为模型与数据拟合得很好。

若残差图呈现如图（a）所示的形式，则认为建立的回归模型正

确，更进一步再诊断“学生化残差”是否具有正态性：

图（b ）表明数据有异常点，应处理掉它重新做回归分析（在SAS 的REG 回归过程步中用来度量异常点影响大小的统计量是COOKD 统计量）；

图（c ）残差随x 的增大而增大，图（d ）残差随x 的增大而先增后减，都属于异方差。此时应该考虑在回归之前对数据y 或x 进行变换，实现方差稳定后再拟合回归模型。原则上，当误差方差变化不太快时取变换y ；当误差方差变化较快时取变换log y 或ln y ；当误差方差变化很快时取变换1/y ；还有其他变换，如著名的Box-Cox 幂变换λλ1

-y .

图（e ）（f ）表示选用回归模型是错误的。

（2）共线性

回归分析中很容易发生模型中两个或两个以上的自变量高度相关，从而引起最小二乘估计可能很不精确（称为共线性问题）。

在实际中最常见的问题是一些重要的自变量很可能由于在假设检验中t 值不显著而被不恰当地剔除了。共线性诊断问题就是要找出哪些变量间存在共线性关系。

（3）误差的独立性

回归分析之前，要检验误差的独立性。若误差项不独立，那么回归模型的许多处理，包括误差项估计、假设检验等都将没有推导依据。

由于残差是误差的合理估计，因此检验统计量通常是建立在残差的基础上。检验误差独立性的最常用方法，是对残差的一阶自相关性进行Durbin-Watson检验。

H0: 误差项是相互独立的; H1: 误差项是相关的

检验统计量：

DW接近于0，表示残差中存在正自相关；如果DW接近于4，表示残差中存在负自相关；如果DW接近于2，表示残差独立性。

二、R语言实现

还是用lm()函数实现，不同是需要设置更复杂的formula格式：y~x1+x2——只考虑自变量的主效应（y=k1x1+k2x2），y~.表示全部自变量的主效应；

y~x1+x2+x1:x2——考虑主效应和交互效应（y=k1x1+k2x2+k3x1x2）；

y~x1*x2——考虑全部主效应和交互效应的简写（效果同上）；

y~(x1+x2+x3)^2——考虑主效应以及至2阶以下的交互效应，相当于x1+x2+x3+x1:x2+x2:x3+x1:x3

y~x1%in%x2——x1含于x2，相当于x2+x2:x1

y~(x1+x2)^2-x1:x2——表示从(x1+x2)^2中去掉x1:x2

y~x1+I((x2+x3)^2)——使用I()函数，相当于用(x2+x3)^2计算出新变量h，然后y~x1+h

function——在表达式中使用数学函数，例如log(y)~x1+x2

三、实例

例2现有1990~2009年财政收入的数据revenue.txt：

各变量分别表示：

y：财政收入（亿元）

x1：第一产业国内生产总值（亿元）

x2：第二产业国内生产总值（亿元）

x3：第三产业国内生产总值（亿元）

x4：人口数（万人）

x5：社会消费品零售总额（亿元）

x6：受灾面积（万公顷）

做多元线性回归分析。

setwd("E:/办公资料/R语言/R语言学习系列/codes")

revenue=read.table("revenue.txt",header=TRUE)

lm.reg=lm(y~x1+x2+x3+x4+x5+x6,revenue)

summary(lm.reg)

Residuals:

Min 1Q Median 3Q Max

-295.71 -173.52 26.59 90.16 370.01

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 6.046e+04 3.211e+03 18.829 8.12e-11 *** x1 -1.171e-01 8.638e-02 -1.356 0.19828

x2 3.427e-02 3.322e-02 1.032 0.32107

x3 6.182e-01 4.103e-02 15.067 1.31e-09 ***

x4 -5.152e-01 2.930e-02 -17.585 1.91e-10 ***

x5 -1.104e-01 2.878e-02 -3.837 0.00206 **

x6 -1.864e-02 1.023e-02 -1.823 0.09143.

---

Signif.codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 234.8 on 13 degrees of freedom

Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999 F-statistic: 2.294e+04 on 6 and 13 DF, p-value: < 2.2e-16

说明：拟合优度R2=0.9999, 效果非常好。但是多元回归时，自变量个数越多，拟合优度必然越好，所以还要看检验效果和回归系数是否显著。结果解释、回归方程、回归预测与前文类似（略）。

结合显著性代码可看出：x1和x2不显著，x6只在0.1显著水平下显著，故应考虑剔除x1和x2.

R语言中提供了update()函数，用来在原模型的基础上进行修正，还可以对变量进行运算，其基本格式为：

update(object, formula., ..., evaluate=TRUE)

其中，object为前面拟合好的原模型对象；

formula指定模型的格式，原模型不变的部分用“.”表示，只写出需要修正的地方即可，例如

update(lm.reg, .~.+x7)表示添加一个新的变量

update(lm.reg, sqrt(.)~.)表示对因变量y开方，再重新拟合回归模型lm.reg2<-update(lm.reg, .~.-x1-x2)#剔除自变量x1,x2

summary(lm.reg2)

Residuals:

Min 1Q Median 3Q Max

-325.62 -147.54 14.07 108.28 427.42

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 6.339e+04 2.346e+03 27.020 3.89e-14 ***

x3 6.584e-01 1.548e-02 42.523 < 2e-16 ***

x4 -5.438e-01 1.981e-02 -27.445 3.09e-14 ***

x5 -1.392e-01 1.918e-02 -7.256 2.80e-06 ***

x6 -1.803e-02 9.788e-03 -1.842 0.0854 .

---

Signif.codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 233.6 on 15 degrees of freedom

Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999 F-statistic: 3.476e+04 on 4 and 15 DF, p-value: < 2.2e-16

（三）逐步回归

多元线性回归模型中，并不是所有的自变量都与因变量有显著关系，有时有些自变量的作用可以忽略。这就需要考虑怎样从所有可能有关的自变量中挑选出对因变量有显著影响的部分自变量。

逐步回归的基本思想是，将变量一个一个地引入或剔出，引入或剔出变量的条件是“偏相关系数”经检验是显著的，同时每引入或剔出一个变量后，对已选入模型的变量要进行逐个检验，将不显著变量剔除或将显著的变量引入，这样保证最后选入的所有自变量都是显著的。

逐步回归每一步只有一个变量引入或从当前的回归模型中剔除，当没有回归因子能够引入或剔出模型时，该过程停止。

R语言中，用step()函数进行逐步回归，以AIC信息准则作为选入和剔除变量的判别条件。AIC是日本统计学家赤池弘次，在熵概念的基础上建立的：

AIC=2(p+1)-2ln(L)

其中，p为回归模型的自变量个数，L是似然函数。

注：AIC值越小越被优先选入。

基本格式：

step(object, direction=,steps=, k=2, ...)

其中，object是线性模型或广义线性模型的返回结果；

direction确定逐步回归的方法，默认“both”综合向前向后法，“backward”向后法（先把全部自变量加入模型，若无统计学意义则剔出模型），“forward”向前法（先将部分自变量加入模型，再逐个添加其它自变量，若有统计学意义则选入模型）；

steps表示回归的最大步数，默认1000；

k默认=2, 输出为AIC值，= log(n)有时输出BIC或SBC值。

另外，有时还需要借助使用drop1(object)和add1(object)函数，其中object为逐步回归的返回结果，判断剔除或选入一个自变量，

AIC值的变化情况，以筛选选入模型的自变量。

lm.step<-step(lm.reg)

summary(lm.step)

Call:

lm(formula = y ~ x3 + x4 + x5 + x6, data = revenue)

Residuals:

Min 1Q Median 3Q Max

-325.62 -147.54 14.07 108.28 427.42

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 6.339e+04 2.346e+03 27.020 3.89e-14 *** x3 6.584e-01 1.548e-02 42.523 < 2e-16 ***

x4-5.438e-01 1.981e-02 -27.445 3.09e-14 ***

x5-1.392e-01 1.918e-02 -7.256 2.80e-06 ***

x6-1.803e-02 9.788e-03 -1.842 0.0854 .

---

Signif.codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 233.6 on 15 degrees of freedom

Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999 F-statistic: 3.476e+04 on 4 and 15 DF, p-value: < 2.2e-16

说明：默认输出每步的结果（略），进行了3步回归，逐步剔除了自变量x1和x2，AIC值逐步减小，最终得到最优的模型。

drop1(lm.step)

Single term deletions

Model:

y ~ x3 + x4 + x5 + x6

Df Sum of Sq RSS AIC

818775 222.40

x3 1 98701814 99520589 316.40

x4 1 41113643 41932417 299.12

x5 1 2873929 3692704 250.52

x6 1 185123 1003898 224.47

lm.reg3<-lm(y~x3+x4+x5,revenue)

summary(lm.reg3)

Call:

lm(formula = y ~ x3 + x4 + x5, data = revenue)

Residuals:

Min 1Q Median 3Q Max

-336.34 -186.82 1.52 89.46 437.84

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 6.284e+04 2.494e+03 25.191 2.66e-14 *** x3 6.614e-01 1.651e-02 40.066 < 2e-16 ***

x4 -5.467e-01 2.118e-02 -25.813 1.81e-14 *** x5 -1.412e-01 2.053e-02 -6.877 3.72e-06 *** ---

Signif.codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 250.5 on 16 degrees of freedom

Multiple R-squared: 0.9999, Adjusted R-squared: 0.9998 F-statistic: 4.032e+04 on 3 and 16 DF, p-value: < 2.2e-16

说明：使用drop1()函数考察分别剔除每个自变量，AIC值变化的情况，可以看出不剔除x6与剔除x6，AIC值只从222.40变大到224.47，相对其它自变量变化很小。所以，可以考虑剔除掉x6，重新做多元线性回归。

（四）回归诊断

回归分析之后，还需要从残差的随机性、强影响分析、共线性方面进行诊断。

一、残差诊断

(1) 残差

y.res<-lm.reg3$residuals#回归模型的残差

y.fit<-predict(lm.reg3)#回归模型的预测值

plot(y.res~y.fit,main="残差图")#绘制残差图，以预测值作为横坐标

说明：从图形看，残差分布比较均匀，大致满足随机性。

shapiro.test(y.res)#残差的正态性检验

Shapiro-Wilk normality test

data: y.res

W = 0.94206, p-value = 0.2622

说明：p值=0.2622>0.05, 接受原假设，即残差服从正态分布。

(2) 标准化残差

残差与数据的数量级有关，除以标准误差后得到标准化残差。理想的标准化残差服从N(0,1).

rs<-rstandard(lm.reg3)#得到标准化残差

plot(rs~y.fit,main="标准残差图")

shapiro.test(rs)#标准化残差的正态性检验

Shapiro-Wilk normality test

data: rs

W = 0.97766, p-value = 0.9004

(3) 学生化残差

为了回避标准化残差的方差齐性假设，使用学生化残差。

rst<-rstudent(lm.reg3)

plot(rs~y.fit,main="学生化残差图")

shapiro.test(rst)

Shapiro-Wilk normality test

data: rst

W = 0.97463, p-value = 0.848

(4) 残差自相关性的Durbin-Watson检验

使用car包中的函数：

durbinWatsonTest(model,alternative=c("two.side","positive

","negative"))

H0：序列不存在自相关性