杭电电路分析第五章解题过程
合集下载
电路 第四版 答案(第五章)
第五章 含有运算放大器的电阻电路运算放大器是电路理论中一个重要的多端器件。
在电路分析中常把实际运算放大器理想化，认为其（1）输入电阻∞→in R ；（2）输出电阻00=R ；（3）电压放大倍数∞→A 。
在分析时用理想运算放大器代替实际运算放大器所引起的误差并不严重，但使分析过程大大简化。
由理想化的条件，可以得出理想运放的两条规则：（1）侧向端和非倒向端的输入电流均为零，即，0==+-i i （称为“虚断路”）； （2）对于公共端（地），倒向输入端电压u -与非倒向输入端的电压+u 相等，即+-=u u （成为“虚短路”）。
以上两条规则是分析含有理想运放电路依据，合理的应用这两条规则，并与结点电压法结合起来加以运用，是分析含有理想运放电路的有效方法。
5－1 设要求图示电路的输出o u 为212.03u u u o +=-已知Ω=k R 103，求1R 和2R 。
解：题5－1图所示电路中的运放为理想运放，应用其两条规则，有解法一：由规则1，0=-i ，得21i i i +=，故22113R u u R u u R u u o ----+-=-- 根据规则2，得0==+-u u ，代入上式中，可得）（2211322113R u R u R u R u R u R u o o +=-+=-代入已知条件，得213113212.03u R Ru R R u u +=+ 故，Ω==Ω==k RR k R R 502.0 ; 33.333231解法二：对结点○1列出结点电压方程，并注意到规则1，0=-i ，可得 221133211)111(R u R u u R u R R R o +=-++- 应用规则2，得0=-u ，所以)(2211332113R uR u R u R u R u R u o o +=-+=-后面求解过程和结果同解法一。
注：对含有理想运放电路的分析，需要紧紧抓住理想运放的两条规则：○1“虚断”——倒向端和非倒向端的输入电流均为零；○2“虚短”——对于公共端（地），倒向端的电压与非倒向输入端的电压相等。
南京邮电大学 电路分析基础 课后习题解答 第5--11章 (课堂PPT)
uC (T ) 10(1 et )V
(2)T t 2T时：
uC (T ) uC (T ) 10(1 et )V
uC () US
14
uC (t)
U S
[10(1
e1
)
U
s
]e
t T RC
V
uC (2T ) US [10(1 e1) Us ]e1 0
US 10e1 3.68V
13
5-38 题图5-38中所示脉冲宽度T=RC，施加于RC串联
电路，电路为零状态。试求使uS (t) 在t=2T时仍能回到
零状态所需负脉冲的幅度U
。
S
uS /V
10
U S
T 2T
t/s
+
us
-
+
-uC
解：(1) 0 t T 时：
uC () us 10V
t
uC (t) 10(1 e RC )V
3)求时间常数：
R0C
[(100 //100) 50] C1C2 C1 C2
104 S
5
4) 写出响应表达式： uC1(t) 5(1 e104t )V ,t 0 i1(t) 0.2 0.05e104t A,t 0
6
5-34 电路如图5-34所示，已知 is (t) 10 15 (t) A ，试
50
+
+
40V
-
100
10-V
i1(0 )
用迭加法求 i1(0 )：
i1
(0
)
100
40 100
//
50
50 100
50
10
100
50 100 //100 100 100
高等教育出版社第六版《电路》第5章_含有运放的电阻电路
1 Ro
)u
1 R2
uo – 1 §5-2 比例电路的分析( u
R2
+
uo
u in R1
1 R2Βιβλιοθήκη )u o Au Ro
i1
R1
R1
①
i2
RR2 2
整理:
R0 ② R
+
+
u-
id
+
(
1 R1
1 R2 1 R2
1 R in
)u 1 Ro
1 R2 1 R2
- uin
②
u1
u n1 u n 2 u L
u 由②有： o 2 u n 2
R RL
i1
代入①得：u L
RL R
u1
RL R
R in
R
2
R RL
12
习题： 5-3、 5-4、 5-6、5-7。
13
第五章
结 束
14
9
uo R f (
u1 R1
u2 R2
u3 R3
)
+
i3 i2
R3
i
Rf
+ i1 R2 u3 u + R1
2
①
+ i– u– –
– – –
u1
∞ – + +
uo
+ –
又解：对结点①列结点方程：
u1 R1
u2 R2
u3 R3
uo Rf
0
则 uo (u1 u2 u3 )
)u
1 R2
uo – 1 §5-2 比例电路的分析( u
R2
+
uo
u in R1
1 R2Βιβλιοθήκη )u o Au Ro
i1
R1
R1
①
i2
RR2 2
整理:
R0 ② R
+
+
u-
id
+
(
1 R1
1 R2 1 R2
1 R in
)u 1 Ro
1 R2 1 R2
- uin
②
u1
u n1 u n 2 u L
u 由②有： o 2 u n 2
R RL
i1
代入①得：u L
RL R
u1
RL R
R in
R
2
R RL
12
习题： 5-3、 5-4、 5-6、5-7。
13
第五章
结 束
14
9
uo R f (
u1 R1
u2 R2
u3 R3
)
+
i3 i2
R3
i
Rf
+ i1 R2 u3 u + R1
2
①
+ i– u– –
– – –
u1
∞ – + +
uo
+ –
又解：对结点①列结点方程：
u1 R1
u2 R2
u3 R3
uo Rf
0
则 uo (u1 u2 u3 )
电路分析第五章答案
24 iL (0 ) iL (0 ) 3A 26
24 6 iL ( ) i ( ) 2.4A 6 6 // 2 6 2 t iL (t ) iL () [iL (0 ) iL ()]e
L 2.5 103 103 s R 2.5
R2 uC (0 ) U S 6V R1 R2
+ uR1 + R1
−
R2 K
uC (0 ) uC (0 ) 6V
US
iC + uC(0-)
−
用6V电压源替代电容，求解iC(0+)、 uR1(0+)
uR1 (0 ) U S 6 4V
u R1 (0 ) 4 iC (0 ) 2mA US+ R1 2
51电路如图所示已知u3kc4f电路处于稳态试求开关打开瞬间ur1开关打开前电路处于稳态电容相当于开路电容两端的电压为r52电路如图所示已知u6l5mh电路处于稳态试求开关打开瞬间ir1开关打开前电路处于稳态电感相当于短路电感电流等于电阻r53电路如图所示开关未动之前电路处于稳定状态
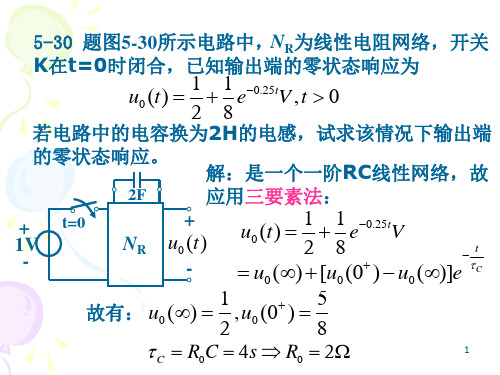
5-1 电路如图所示，已知US=10V，R1=2kΩ， R2=3kΩ，C=4μF，电路处于稳态，试求开关打 开瞬间uC(0+)、 iC(0+)、 uR1(0+)各为多少？ uR1 − + 解：设uC、 iC、 uR1。 iC 开关打开前，电路处于稳态， + R1 R2 + C u C 电容相当于开路，电容两端 US − K 的电压为R2两端电压。
t
400 t
)V
i(t ) i() [i(0 ) i()]e
40e 400 t mA
电路与电子技术基础第五章习题答案
V1 R + uS (a) 题图 5-5 习题 5-12 电路图 L + V2 (b) V1 R V2 L C V3
uS
解：电压表的读数为正弦电压的有效值。 用相量图求解，设电流为 I = I∠0 ，电阻电压与电流同相，电感电压超前电流 90°，电容电
o
(b)
解：原电路的相量模型如题图 5-4(b)所示，输入阻抗为
Z = 2+
(1 + j 2ω )(− j 1 + j 2ω − j
1 1
ω = 2+
)
ω
1 + j (−4ω 3 + ω ) ω − j (2ω 2 − 1) 2 = + ω + j (2ω 2 − 1) ω − j (2ω 2 − 1) ω 2 + (2ω 2 − 1) 2 × Ω
2ω − j
=
8ω 4 − 6ω 2 + 3 + j (−4ω 3 + ω ) 4ω 4 − 3ω 2 + 1
当ω=0 时，Z=3Ω
《电路与电子技术基础》第五章参考答案
第6页
5-12
电路如题图 5-5 所示， 电压源均为正弦电压， 已知图(a)中电压表读数为 V1： 30V，
V2：60V；图(b)中的 V1：15V，V2：80V，V3：100V。求电源电压 US。
• • R R 应改为 U R = U R + ωL R + jωL • • •
改为 U m = U Lm + U rm ， 即用最大值相量表示也是正确的。 式 U m = U Lm + U rm 是不正确的， 5-4 电路如题图 5-2(a)所示，问频率ω为多大时，稳态电流 i(t)为零？
uS
解：电压表的读数为正弦电压的有效值。 用相量图求解，设电流为 I = I∠0 ，电阻电压与电流同相，电感电压超前电流 90°，电容电
o
(b)
解：原电路的相量模型如题图 5-4(b)所示，输入阻抗为
Z = 2+
(1 + j 2ω )(− j 1 + j 2ω − j
1 1
ω = 2+
)
ω
1 + j (−4ω 3 + ω ) ω − j (2ω 2 − 1) 2 = + ω + j (2ω 2 − 1) ω − j (2ω 2 − 1) ω 2 + (2ω 2 − 1) 2 × Ω
2ω − j
=
8ω 4 − 6ω 2 + 3 + j (−4ω 3 + ω ) 4ω 4 − 3ω 2 + 1
当ω=0 时，Z=3Ω
《电路与电子技术基础》第五章参考答案
第6页
5-12
电路如题图 5-5 所示， 电压源均为正弦电压， 已知图(a)中电压表读数为 V1： 30V，
V2：60V；图(b)中的 V1：15V，V2：80V，V3：100V。求电源电压 US。
• • R R 应改为 U R = U R + ωL R + jωL • • •
改为 U m = U Lm + U rm ， 即用最大值相量表示也是正确的。 式 U m = U Lm + U rm 是不正确的， 5-4 电路如题图 5-2(a)所示，问频率ω为多大时，稳态电流 i(t)为零？
电路分析 胡俊翔 第二版 第五章 课后答案【khdaw_lxywyl】
w.
解：
ww
题图 5－12
u oc
isc
也可以用外加电流源iS 计算电压 u ab 500 iS Ro uS 500 iS
w.
Ri u R1 R2 i Rf
2V 6V 4mA 1000 Ro u oc 500 isc
4
co
R2 u1 R1
根据传输参数方程，可以求得四个传输参数
w.
T11 u1 u2 T21 i1 u2
u1 T11u 2 T12 i2 i1 T11u 2 T22 i2
i2 0
da
1 H 12 u1 u2
i1 0
后 答
2
H 22
0.1 1 2 2.1 0.1S
解：
da
题图 5－11
课
后 答
案 网
5－11 题图 5－11 电路中的运放工作于线性区，求输入电阻 Ri u / i 。
kh
u R1i1 R1
500 6V 2V 1000 500
R2 i R1 R2 i Rf Rf
5－12 题图 5－12 电路中的运放工作于线性区，试求 ab 两点间的戴维宁等效电路。
ww
i2 0
也可以利用求得的电阻参数和电导参数方程，求得四个传输参数
i2 G21u1 G22 u 2 2u1 4.2u 2 u1 2.1u 2 0.5i2 T11 2.1 T12 0.5 u 2 R21i1 R22 i2 10i1 5i2 i1 0.1u 2 0.5i2 T21 0.1S T22 0.5
7
w.
2 i2 u2 0.2S
杭电第五章-3
满招损，谦受益。
——《尚书 · 大禹谟 》
言必行，行必果。
——《论语 ห้องสมุดไป่ตู้子路》 ——《礼记 ·中庸》
2014-6-14
《自动控制原理》 第五章 频域分析
1
5.4 频域稳定性判据
引言
映射定理（幅角定理）
Nyquist稳定判据
虚轴上有开环极点的Nyquist稳定判据
对数频率稳定判据
线Γs 顺时针方向移动一周时，在F(s)平面上的映射
曲线ΓF 按逆时针方向包围坐标原点 P-Z 周。
可见， F(s) 平面上曲线绕原点的周数和方向与 s 平 面上封闭曲线包围F(s)的零、极点数目有关。
2014-6-14
《自动控制原理》 第五章 频域分析
17
二、Nyquist 稳定性判据 1. 辅助函数
2014-6-14
《自动控制原理》 第五章 频域分析
22
3. Nyquist 稳定判据
设复变函数 F(s) 在 s 平面的右半部有 Z 个零点
和 P 个极点。根据映射定理，当s沿着s平面上
的 Nyquist 回线移动一周时，在 F(s) 平面上的 映射曲线 CF 将按逆时针方向围绕坐标原点旋转 N = P－Z 周
s平面 q2
j
j1
jV
F(s) 0 U
s-p2
p2
s-p1
s-z1
z1
0
p1 z2
q1
s-z2
j2
s
封闭曲线包围 z1 时的映射情况
向量 s-z1的相角变化了-2π 弧度，其余三个向量的相角变化均为0。
2014-6-14 《自动控制原理》 第五章 频域分析 15
——《尚书 · 大禹谟 》
言必行，行必果。
——《论语 ห้องสมุดไป่ตู้子路》 ——《礼记 ·中庸》
2014-6-14
《自动控制原理》 第五章 频域分析
1
5.4 频域稳定性判据
引言
映射定理（幅角定理）
Nyquist稳定判据
虚轴上有开环极点的Nyquist稳定判据
对数频率稳定判据
线Γs 顺时针方向移动一周时，在F(s)平面上的映射
曲线ΓF 按逆时针方向包围坐标原点 P-Z 周。
可见， F(s) 平面上曲线绕原点的周数和方向与 s 平 面上封闭曲线包围F(s)的零、极点数目有关。
2014-6-14
《自动控制原理》 第五章 频域分析
17
二、Nyquist 稳定性判据 1. 辅助函数
2014-6-14
《自动控制原理》 第五章 频域分析
22
3. Nyquist 稳定判据
设复变函数 F(s) 在 s 平面的右半部有 Z 个零点
和 P 个极点。根据映射定理，当s沿着s平面上
的 Nyquist 回线移动一周时，在 F(s) 平面上的 映射曲线 CF 将按逆时针方向围绕坐标原点旋转 N = P－Z 周
s平面 q2
j
j1
jV
F(s) 0 U
s-p2
p2
s-p1
s-z1
z1
0
p1 z2
q1
s-z2
j2
s
封闭曲线包围 z1 时的映射情况
向量 s-z1的相角变化了-2π 弧度，其余三个向量的相角变化均为0。
2014-6-14 《自动控制原理》 第五章 频域分析 15
电子科大《电路分析》第05章 多端元件
Z=ZA+ZB
2. 二端口网络的并联
Y = YA + YB
3. 二端口网络的级联
T = T T T n T 1 2 3
第五章结束
n R
2
例：求5欧姆电阻所吸收的功率P。
例：已知1欧姆电阻吸收的功率为16W，求2 欧姆电阻吸收的功率P2。
例：P书169，5－5，求单口网络的等效电阻Rab。 169， 求单口网络的等效电阻Rab。 Rab
第五章结束
第五章( 第五章(第2部分) 部分) 双口网络
§5.2 运算放大器的电路模型
Z---G(Y) ---G(Y)
11 12 Y Y Z11 Z12 Y21 Y22 = Z 21 Z 22 1
Z22 Z12 z z = Z11 Z21 z z z
其 中 z =
Z11 Z12 Z 21 Z 22
= Z11Z22
Z12 Z2
二端口网络的连接与等效
1. 二端口网络的串联
课堂例2 课堂例2
i2 例2．P214 ,5-9 运放工作在线性区，求转移电流比。 a = i1
其它例见教材P214 其它例见教材P214
§5.4 双口网络的电压电流关
一. 电阻矩阵
系
对于如下所示的双口网络。
I1
U1
U2
I2
u1 = R11i1 + R12i2
u2 = R21i1 + R22i2
课堂特殊例
例
理想变压器的性质
理想变压器的两个基本性质： 理想变压器的两个基本性质： 1．理想变压器不能消耗 ． 能量，也不储存能量， 能量，也不储存能量，在 任何一时刻进入理想变压 器的功率等于零。 器的功率等于零。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
L1
1+ -
R RC
1 = - arctan - arctan
RC
L1 -
R RC
5-3
5.3 算下列增益 HdB 对应的
。
（a）0.02dB （b）-8.5dB
由于 HdB = 20 log10 H j
（a）1.0023 （b）0.3758 （c）0.0708 （d）5.6234 5-4
（c）-23dB
1
cL = - + 2L
2L
+ =LC 2
10-3 +
2 10-3 + 10-3 0.4 10-6 = 48k rad / s
2
2
R R1
4
4
1
cH
=
+ 2L
2L
+= LC 2
10-3 +
2 10-3 + 10-3 0.4 10-6 = 52k rad / s
（2） 回 的带宽和品 因数分别为
BW = cH - cL = 52k - 48k = 4k rad / s
0L = 200 = 10 ，且
0 = 1000rad / s ，所以
20
R 20
QR 10 1 L = = = 10mH
0 1000
1
由公式 0 =
，可得
LC
1
1
C=
2 0
L
=
10002
= 100 F 10m
5-12
5.12 RLC 并联 振电 如 图 5-12 所示，其中 R = 4kW ， L = 0.4mH ， C = 16 F ，求
HdB / dB
20
① ②
-20dB/dec
0.5 1
5 10
-20
③
-40dB/dec
图 5-6
传 函数 H j 对应于直线波特图时， 点使幅 特性直线波特图在 折 率处
向上 折，而极点使幅 特性直线波特图在 折 率处向下 折。 由直线段①可知， 分为由常数 K=10 产生的。
直线段①到②的 折在 = 0.5rad / s 处发生，且斜率从 0 变为 -20dB / dec ，即 折
，所以 H j
（d）15dB
H dB
= 10 20 ，可得各小 的值分别为
5.4 算下列 H j 在 = 2 时的增益 HdB 及相位。
（a）0.02
（b）120
20 j
（c）
3+ j
2
3
（d）
+
2+ j 1+ j
（a） HdB =2 = 20 log10 0.02 = -33.98dB ， 2 = 0 。
BW =
0
12.5k =
= 15.625
rad / s
Q 800
（2）半功率点 率 cL 和 cH 分别为
2
1
1
1
cL = -
+
+
2RC 2RC LC
2
1
1
1
=2
4
103
16
10-6 +
2 4 103 16 10-6
+ 0.4
10-3
16
10-6
= 12.492k rad / s
2
1
1
1
cH = 2RC +
5
5.1
算
图 5-1 所示电
传
Vo
函数
j
的幅 特性和相 特性。
Vi j
（a） 图 5-1
（a）对于电 图（a），可得传 函数为
（b）
H j = Vo = R = 1 =
1
L - arctan
Vi R + j L 1+ j L R
2
L 1+
R
R
所以幅 特性和相 特性分别为
Hj
1 =
2
L 1+
R
L = - arctan
H dB 20
20 log10 1 + j 10
图形相加可以得
1 2 5 10
-20
-20 log10 1+ j 2
100 -20 log10 1+ j 5
（a）
90 arctan 10
0.2 0.5 1 2 5 10
- arctan
100
2
- arctan 5
-90
（b） 5-6
5.6 已知传 函数的幅 直线波特图如 图 5-6 所示，求传 函数 H j 。
IS
I R IS
jL 1
jC
根据电 可得传 函数为
I Hj =
IS 1
R+ jC
= 1
R+ j L+ jC
1
1- j
=
RC
L1
1+ j -
R RC
2
1
1+
RC
=
2
L1
1+ -
R RC
图 5-2
1 - arctan - arctan
RC
L1 -
R RC
所以幅 特性和相 特性分别为
2
1
1+
RC
Hj =
2
向下，所以 折 率对应的是单极点。
直线段②到③的 折在 = 5rad / s 处发生，且斜率从 -20dB / dec 变为 -40dB / dec ， 即 折 率处产生 -20dB / dec 的 折，所以 折 率对应的是单极点。
综合上 ，可以得到传 函数为
10
25
Hj =
=
j
j
1+ 1+
j + 0.5 j + 5
= 2mH 5 10-6
由于 Q = 0CR ，所以
Q
50
R=
= 0C 10
103
5 10-6 = 1000W
（2）
振回 的带宽为
BW =
0
10k =
=
200
rad / s
Q 50
5-14
5.14 一个 RLC 并联电 ，使其 振 率为 0 = 50 rad/s ，品 因数为 Q=100，且
振时 抗为10W 。
（1） 0 、 及 Q ；
（2）半功率点 率 cL 和 cH ；
（3）在电压源 率分别为 0 、 cL 和 cH 时 振回 消耗的有功功率。
+
10 2 cos t V
-
C
L
R
图 5-12
（1） RLC 并联 振回 的 0 、 Q 及 BW 分别为
1
1
0=
= LC
= 12.5k rad s 0.4 10-3 16 10-6
R
（b）对于电 图（b），可得传 函数为
L
L
H j = Vo = j L = j R =
R
L 90 - arctan
Vi R + j L 1+ j L R
2
L 1+
R
R
所以幅 特性和相 特性分别为
L
Hj
R
2
L
1+
R
L = 90 - arctan
R
5-2
I
5.2 算 图 5-2 所示电 传 函数 的幅 特性和相 特性。
功率为
1 P CL = P CH = P 0 = 12.5 mW
2
5-13
5.13 RLC 并联 振电 中，已知 C = 5 F ， 求 振 率
，且品 因数
Q = 50 ，求
（1） 回 中的 R 和 L 的值；
（2） 振回 的带宽。
1
（1）由于 0 =
rad s ，所以
LC
1
1
L=
02C = 10k 2
即R和C 满
无源低 滤波器的半功率点 率为
1 c = = 10k 2 rad / s
RC
1
RC =
16 W F
10k 2
可 ，只 R 和 C 的乘积为16 W F 就可以满
求，例如可以 择， R = 1kW
且 C = 16nF 。
5-16 5.16 利用 5.5 的一 无源
滤波器电 ，
一个截止 率为 50kHz 的一 无源
Q=
0
126.92k =
101
BW 1256.64
5-18 5.18 利用 5.5 的有源低 滤波器电 ，
c = 50k rad/s 。
一个有源低 滤波器， 求增益为 10 且
依据 本 5.5 的有源低 滤波器电 ，为满 增益为 10 且 c = 50k rad / s
A = 1+ R2 = 10 R1
0.5
5
5-7
5.7 RLC 串联 振电 中， R = 4W ， L =1mH ， C = 0.4 F ，求：
（1） 振 率及半功率点 率； （2）带宽和品 因数。
（1） RLC 串联 振回 的 振 率为
1
1
0=
= LC
10-3
= 50k rad s 0.4 10-6
半功率点 率分别为
2
2
R
R
1
4
4
（b） HdB =2 = 20 log10 120 = 41.58dB ， 2 = 0 。
20 j2
（c） H
j2 =
= 11.09 56.31
3+ j2
，所以