Chapter9 受限因变量模型

第1章 受限因变量模型

这一章讨论响应变量仅仅被部分观测到的情况。引入被部分观测到的潜在随机变量y *，y *的实际观测变量为y i 。引入二元指示变量D i ，如果a i < y *

****,,,i i i

i i i i i i i i a y a y y a y b b y b ?

= ≤≤?? >?

如果如果如果。 （1）

如果只有当D i = 1时实际观测变量y i 才有观测数据，即：当D i = 1时，潜在变量与实际观测变量相等，而当D i = 0时，y i 没有观测值，这时称数据被截断（truncated ），即小于a i 的数据和大于a i 的数据被截断了。因此截断数据与归并数据的区别在于，对于观测区间外的数据，归并数据将将其都归并为一点，而截断数据没有观测值。

将潜在随机变量y *的基本模型设定为：

*i i i y v μσ=+。 （2）

其中μi 为位置参数，σ为刻度参数；v i 为独立于x i 的连续随机扰动项，均值为0，方差为1，其分布函数、密度函数分别为F 、f 。在这些假定条件下，y i *

的均值为μi ，方差为σ2

，分布函数为*()i i

y F μσ

-，

概率密度函数为*(

)/i i

y f μσσ

-（证明请参见附录1）。a i < y i * < b i 等价于i i

i i

i i i a b c v d μμσ

σ

--=

<<

=，

那么y i *被观测到的概率为：

*Pr()Pr(1)()()i i i i i i a y b D F d F c <<===- （3）

下面对截断数据模型和归并数据模型分别进行介绍

1.1 截断数据模型

如果样本数据是从总体的一部分抽取得到，我们把这类数据称为截断数据。比如，研究高收入阶层（月收入x ≥ 10000）的消费与收入的关系，所采集的数据只是位于收入总体分布的一个区间里。假设所有居民的收入服从正态分布，那么高收入阶层的收入只是在x ≥ 10000的区间里观测得到的。下面介绍截断数据的分布特征和模型估计。

1.1.1 截断数据的分布特征

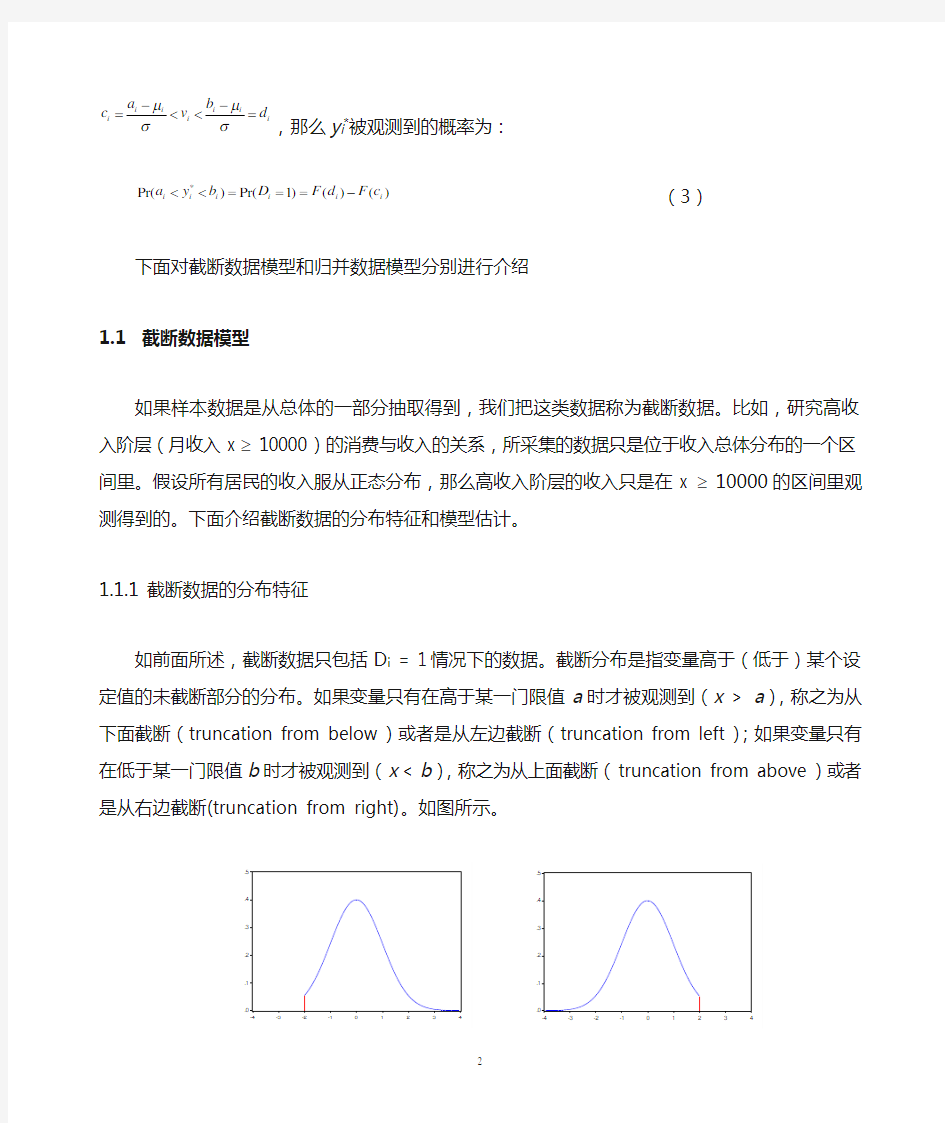
如前面所述，截断数据只包括D i = 1情况下的数据。截断分布是指变量高于（低于）某个设定值的未截断部分的分布。如果变量只有在高于某一门限值a 时才被观测到（x > a ），称之为从下面截断（truncation from below ）或者是从左边截断（truncation from left ）；如果变量只有在低于某一门限值b 时才被观测到（x < b ），称之为从上面截断（truncation from above ）或者是从右边截断(truncation from right)。如图所示。

图一 截断分布图（上面截断（左图）、下面截断（右图））

下面分析截断数据的分布函数、密度函数、均值和方差。

1． 截断变量的分布函数和密度函数

给定模型（1）及相应的观测概率（2），那么第i 个观测变量y i 的条件分布函数为（证明请参见附录2）：

()()()()***0,()/(),1,i i

i i i y i i i i i i i i y a F y F c F y a y b F d F c y b

μσ?

--?= ≤≤?-?

? >?

如果如果如果 （4）

（注：此处及后面的,,,i i i i a b c d 的定义均与前面相同）

密度函数为：

()

()()

*()/1,()0,i i i i i i i y i f y a y b F d F c f y μσσ?- ≤≤?

-=?? ?

如果其他 （5） 从截断数据的密度函数（4）式我们可以推出从下面截断或从上面截断的各种不同分布的变量的密度函数。读者可以参阅下面介绍的几个例子。 例1 截断均匀分布的密度函数和分布函数

如果x *在区间[a ，b ]上服从均匀分布（uniform distribution ），那么

1

(),()()x a

f x F x a x b b a

b a

-=

=

<<--， （6） 如果在x *= c 处截断，即实际观测值x = x *，如果x *≥ c ；x = c ，如果x *< c 。

这是左截断的例子，即右截断点=b 。根据（5）式，在x = c 处截断的随机变量x 的截断分布的密

度函数为：

**()()1/()1

()(1)()()1()/()i f x f x b a f x P D F b F c c a b a b c

-====

=----- （7） 分布函数为：

()()()/()()/()()Pr(1)1()/()i F x F c x a b a c a b a x c

F x D c a b a b c

-------=

===---- （8）

例2 截断正态分布的密度函数

模型设定为：

*i i i y v μσ=+，

y i = y i *，如果*i i i a y b << （9） y i = a i ，如果*i i y a ≤ y i = b i ，如果*i i y b ≥

其中v i ~N (0, 1)。即 y i * ~N (μi , σ2)，其中μi 、σ分布表示y i 的均值和标准差。以φ、Φ分别表示标准正态分布密度函数和分布函数。那么：

Pr()Pr(

)

()()

()()

i i

i i

i i

i i i i i i i

i i a y b a y b b a d c μμμσσσ

μμσσ

---<<=<

<

-- =Φ-Φ = Φ-Φ （10）

其中，,i i

i i

i i b a d c μμσ

σ

--=

=

。

根据截断正态分布的密度函数公式：

()

()()

*()/1,()0,i i i i i i i y i f y a y b F d F c f y μσσ?- ≤≤?

-=?? ?

如果其他 可直接得到*i i i a y b ≤≤时y i 的密度函数：

1

(

)

()()()

()1()

()11()

i i

y i i i i i i i i i i i y f y d c y if a d y if b c μφσ

σ

μφσσμφσσ-=Φ-Φ-?? →-∝?Φ? =

?-?? →+∝

?-Φ?

（11） 根据截断正态分布的分布函数公式：

()()()()***0,()/(),1,i i i i i y i i i i i i i i y a F y F c F y a y b F d F c y b

μσ?

--?= ≤≤?-?

? >?

如果如果如果

可直接得到*i i i a y b ≤≤时y i 的分布函数：

(

)()

()()

()()()()()

()()

()()1()i i

i i

i i y i i i i i i i

i

i i i i i i y y a c F y d c d c y if a d y c if b c μμσ

σ

μσμσ--Φ-ΦΦ-Φ=

=

Φ-ΦΦ-Φ-?Φ? →-∝?Φ? =

?-?Φ-Φ? →+∝?-Φ?

（12）

图二 截断正态分布变量的累积分布函数图

（设潜变量y *~N (0, 1)，图中虚线表示标准正态分布函数，实线表示截断正态分布函数，截断点为-1、1）

2． 截断变量的均值和方差

截断随机变量的均值和方差称之为截断均值（truncated mean ）和截断方差（truncated variance ），由下面的（5）、（6）式可以推出各种不同截断分布的均值和方差。给定模型（9），

y i 的均值为：

[]i i i E y μσ?=+ （13）

其中，()

[]()()

i

i d i i i i i c i i f v E v |c v d v

dv F d F c ?=<<=-?

y i 的方差为：

2[|1][|]i i i i i i Var y D Var v c v d σ==<< （14）

其中，2

2()

[]()()

i

i d i i i i i c i i f v Var v |c v d v dv F d F c ?<<=--?。

（证明请参见附录3）。

例3：均匀分布的截断均值和截断方差

给定模型（6），截断变量x 的均值和方差分别为：

2222211

()(|)()2

()[(|)](|)11

[()]21

[()()]

2

b b

c

c

b c

b

c E x xf x x c dx x

dx b c b c Var x x E x x c f x x c dx x b c dx

b c b c c a b c =>==+-=->> =-+- =---+???? （15）

例4：正态分布的截断均值和截断方差

给定模型（9），那么y i 的均值和方差分别为：

[]i i i E y μσ?=+ （16）

其中，()()

[|]()()

i i i i i i i i i d c E v c v d d c φφ?-=<<=-

Φ-Φ

y i 的方差为：

2[|1][|]i i i i i i Var y D Var v c v d σ==<< （17）

其中，2

()()()()[]1[]()()()()

i i i i i i i i i i i i i i d d c c d c Var v |c v d d c d c φφφφ--<<=-

-Φ-ΦΦ-Φ。

其中，φ、Φ分别表示正态分布的密度函数和分布函数。

（1） 如果c i -∝，即数据只是在右边截断，这时φ( c i ) = 0、Φ( c i ) = 0，因此：

()

[]()()

i i i i i i i d E v |v d d d φ?λ=<=-

=Φ<0 （17a ）

2[]1()-()i i i i i i Var v |v d d d d λλ<=+ （17b ）

（2） 如果d i +∝，即数据只是在左边截断，这时φ( d i ) = 0、Φ( d i ) = 1，因此：

()

[]()1()

i i i i i i i c E v |v c c c φ?λ=>=

=-Φ>0 （18a ）

2[]1()-()i i i i i i Var v |v c c c c λλ>=+ （18b ）

（17a ）式中()

()=-

()

i i i d d d φλΦ称之为Inverse Mills Ratio ，将（18a ）式中()

()=

1()

i i i c c c φλ-Φ称之为风险

函数（Hazard Function ）。 结论1

(|)()(|)E y y b E y E y y a <<<>。即，如果变量为从上面截断，则截断变量的均值小于初始

变量的均值；如果变量为从下面截断，则截断变量的均值大于初始变量的均值。 结论2 截断变量的方差低于初始变量的方差。

图三 截断分布的均值（左图）、方差（右图）(假定潜在变量y *

~N (2, 2))

1.1.2 截断回归模型估计

下面以左截断模型为例说明截断回归模型的估计。

设回归模型为：i i i y v σ=+x β (19)

其中，v i ~N (0, 1)。那么，2~(,)i i y N σx β。根据例4，我们可以得到截断随机变量y i 的均值和方差。

()

[|][|]()1()

i i i i i i i i i i E y y a E y v φαασ

σλαα>=>=+=+-Φx βx β (20)

其中，-i i a ασ

=

x β

，()()/[1()]i i i λαφαα=-Φ

2[|]1()()1()i i i i i i Var y y a αλαλαδα>=+-=- （21）

其中，()()[()]i i i i δαλαλαα=-

由（20）式可以看出，截断均值为β和x i 的非线性函数。同一般的非线性模型一样，变量x k 对y 的边际影响不等于其系数：

()2[|]()()()[1()]

E y y a d d λαα

σ

ασλααλασδα?>?=+??-??

= +- ???

=-βx x

βββ （22）

因为0()1i δα<<，所以变量x k 对y 的边际影响要小于其系数。y i 的方差也存在类似的缩减（attenuation ）：

22(|)[1()]i i i Var y y a σδασ>=-< （23）

注：

对于y i < b 的情况，可以得到相同的结论。

下面分析截断模型中参数的最小二乘估计和极大似然估计。 1． OLS 估计

根据[|]()i i i i E y y a σλα>=+x β，截断模型可以写为：

[|]i i i i i i i

y E y y a v u σσλ=>+ =++x β （24）

其中，u i = σv i 为y i 减去其条件期望，E(u i )=0。

如果以最小二乘法估计（19）式，就忽略了非线性项λi ，因此OLS 估计量是有偏的。

另外，y i |y i >a 的方差与u i 的方差相同，由2(|)[1()]i i i Var y y a σδα>=-可知，y i 存在异方差，为：

2222[][][|](1)(1())

i i i i i i i i i Var y Var u Var v v σασλλασδα==> =-+ = - （25）

它是x i 的函数。

2． ML 估计

对于模型（19），由截断随机变量的概率密度函数可得y i 的密度函数为，

(

)

1

()1()

i i y i i y f y φσ

σα-=

-Φx β

， （26）

可以得到y i 的对数似然函数：

222-11

[log(2)log ]()log[1()]22i i i i a LogL y πσσσ

=-+----Φx βx β （27）

对于N 个观测值(y 1, …, y N )，其联合对数似然函数为：

22

2

1

1

-1

[log(2)log ]()log[1(

)]22N N

i i i i i i a N LogL y πσσσ

===-+-

---Φ∑∑x β

x β （28）

通过最优化方法可以解得上式的参数β和σ的值。

1.2 归并数据模型

计量经济学当中经常能碰到数据的归并问题，简单地说，归并数据即是被解释变量在某个区间的观测值都转化为同一个值。比如，研究电影院的座位需求情况，电影院总的座位是20000个。如果实际的需求量少于20000，那么观测到的需求量就等于实际需求量；但如果实际需求量大于（等于）20000，那么实际可观测到的需求数量只能为20000。这时我们说需求量数据被归并，即所有大于20000的数据都被归并为20000。

格林（Greene ，2000）列举了经验文献中归并数据的应用。其中包括：

1， 家庭耐用品消费支出[Tobin(1958)] 2， 婚外情次数[Fair(1977,1978)]

3， 劳动力市场中妇女工作的小时数[Quester and Greene(1982)] 4， 罪犯重新入狱的次数[White(1980)]等。

下面分别介绍归并数据的分布特征和模型估计。

1.2.1 归并数据的分布特征

如前所述，归并数据与截断数据的区别在于，归并变量包含D i = 1和D i = 0两种情况下的数据。

****

,,,i i i i i i i i i i i

a y a y y a y

b b y b ? ≤?

= <

或者写作：*max[,min(,)]i i i i y a y b =。即当*i i y a ≤时，所有值被归并为a i ；当*i i y b ≥时，所有值被归并为b i 。

归并数据按照归并点a i , b i 是随机的还是确定的分为固定归并（fixed censoring ）和随机归并（random censoring ）两种。如果a i , b i 是确定性的，我们称之为固定归并；如果a i , b i 是随机的，我们称之为随机归并。本章只介绍固定归并的情况。

归并数据按照归并点与观测区间的关系还可以分为左边归并和右边归并。如果：

*

**

,,i i i

i i

i i a y a y y y a ? ≤?=? >??如果如果 称潜在变量y *被从下面归并（censored below ）或者从左边归并（censored from left ）；

如果：

**

*

,,i i i

i i

i i b y b y y y b ? ≥?=?

图 归并变量示意图

1．归并变量的分布函数和密度函数

给定基本模型（1）的假定，y i 的分布函数为：

10()((-)/) i y i i i i i i

i i i y a F y F y a y b y b μσ<≤≤ ? ?

= ??

>

?如果如果如果 （30）

归并变量的分布函数为一种混合分布（连续型和离散型综合在一起）。在y i = a i 和y i = b i 两点的概率分别为*()()((-)/) i i i i i i P y a P y a F a μσ==≤=和*()()1((-)/)i i i i i i P y b P y b F b μσ==≥=-，因此对于同一个潜在变量，其归并变量和截断变量的分布函数不相同，在观测区间内，归并分布同潜在变量的分布重叠在一起。

图四 归并正态分布变量的分布函数图

密度函数（概率分布）为：

()*

*

()Pr()()(-)/(),()Pr()1()i i y i

i i i i i y i

i i y i

i i i y i i i a P y a y a F f y f y a b b P y b y b F μσ

μσσμσ<<-?==≤= ??

?

= ??

-?==≥=-??

如果 （31） 例5：正态分布归并变量的密度函数。

假定潜在变量（latent variable ）y i *服从均值为μi 、方差为σ2的正态分布，*i i i y v μσ=+，v i ~N (0, 1)。y i 为实际观测变量：y i =a ，如果y i *≤ a ；y i =b ，如果y i * ≥ b ；y i = y i *，如果a i < y i * < b i 。的概率密度函数为：

当y i * ≤ a i 时，y i =a i 。其概率为，

*Pr()Pr()(

)i i

i i i i a y a y a μσ

-==≤=Φ

当a i < y i * < b i 时，y i 与y i *的概率密度函数相同，

*()()(

)/i i

i i y f y f y f μσσ

-==

当y i * ≥b i 时，y i =b i 。其概率为，

*Pr()Pr()1(

)i i

i i i i b y b y b μσ

-==≥=-Φ

（1）当仅从左边归并时，即：y i =a i ，如果y i * ≤ a i ；y i = y i *，如果y i * > a i 。 当y i * ≤ a i 时，y i =a i 。其概率为，

*Pr()Pr()(

)i i

i i i i a y a y a μσ

-==<=Φ

当y i * > a i 时，y i 与y i *的概率密度函数相同，

*()()(

)/i i

i i y f y f y f μσσ

-==

因此，可以将y i 的密度函数综合写成：

2

-1()12-()[(

)]

]i i i

i y D D i i

i a f y μ

μσ

--=Φ，当y i * > a i 时，D i = 1；否则，D i = 0。

（2）当仅从右边归并时，即：y i =b i ，如果y i * ≥ b i ；y i = y i *，如果y i * < b i 。 当y i * ≥b i 时，y i =b i 。其概率为，

*Pr()Pr()1(

)i i

i i i i b y b y b μσ

-==>=-Φ

当y i * < b i 时，y i 与y i *的概率密度函数相同，

*()()(

)/i i

i i y f y f y f μσσ

-==

因此，可以将y i 的密度函数综合写成：

2

-1()12-()[1(

)]

]i i i

i y D D i i

i b f y μσ

μσ

--=-Φ，当y i * > a i 时，D i = 1；否则，D i = 0。

2．归并变量的均值和方差

归并随机变量的均值和方差，我们称之为归并均值（censored mean ）和归并方差（censored variance ） 归并均值为：

**[][|1]Pr(1)Pr()Pr()i i i i i i i i i i E y E y D D a y a b y b ===+≤+≥ （32）

其中，

**[|1]Pr(1)[()()]()Pr()()Pr()1()

i

i

d i i i i i i c i i i i i i E y D D F d F c vf v dv

y a F c y b F d μσ===-+≤=≥=-? （33）

归并方差为：

2[][|1]()[|1][]i i i i i i i Var y Var y D E D E y D Var D ==+= （34）

其中，D i 服从0-1分布，()()()i i i E D F d F c =-，[][](1[])i i i Var D E D E D =-。 （证明请参见附录4）。

设潜在变量y *~N (0, 1)，下图显示了标准正态分布和归并正态分布的分布函数间的差异，虚线表示正态分布函数，实线表示归并正态变量分布函数，归并点为-1、1，在区间[-1，1]上实线和虚线重合。

例6：正态分布归并变量的均值和方差

如果*2~[,]i i y N μσ。y i =a ，如果y i *≥ a ；y i =b ，如果y i * ≥ b ；y i = y i *，如果a i < y i * < b i 。那么 y i 的均值为：

[][()()][()()]()[1()]i i i i i i i i i i E y d c d c a c b d μσφφ=Φ-Φ+-+Φ+-Φ （35）

（证明请参见附录5）。

（1）如果a i -∝（仅从上面归并），那么

[]()()[1()]i i i i i i E y d d b d μσφ=Φ-+-Φ

= ()()[1()]()i i i i i i d d b d d φμσ??

Φ-+-Φ ?Φ?

?

= ()()()[1()]i i i i i d d b d μσλΦ++-Φ （37）

()()2

2[](1()()1()i i i i i Var y d d d d σδλ??=Φ-+--Φ??

， （38）

其中，()()/()i i i d d d λφ=-Φ，2()=()()i i i i d d d d δλλ-

（2）如果b i +∝（仅从下面归并），那么

[][1()]()()i i i i i i E y c c a c μσφ=-Φ++Φ

=()[1()]()1()i i i i i i c c a c c φμσ??

-Φ++Φ ?-Φ?

?

=()[1()]()()i i i i i c c a c μσλ-Φ++Φ （39）

()22[]1()[(1)()()]i i i i i i Var y c c c σδλ=-Φ-+-Φ （40）

其中，()()/[1()]i i i c c c λφ=-Φ，2i i i i c δλλ=- （证明请参见格林（Greene(2000)P907）。

由（37）式和（39）式可以推出：

结论3 对于从上面归并的变量来讲，当归并点为b i = 0时，

()[][1(

)()i

i i i E y d μμσλσ

=-Φ+， （41） 其中(/)(/)

()(/)1(/)

i i i i i d φμσφμσλμσμσ-=-

=-

Φ--Φ 对于从下面归并的变量来讲，当归并点为a i = 0时，

()[](

)()i

i i i E y c μμσλσ

=Φ+ ， （42） 其中()()

//()1(/)(/)

i i i i i c φμσφμσλμσμσ-==

-Φ-Φ

例7：以电影院的座位需求为例，我们来看一下如何利用归并数据模型通过实际观测到的变量来推断潜在变量的均值、方差。设电影院总共有20000个座位，平均售出的座位数为18000，有25%的时间全部售出。那么潜在的座位需求量和方差各是多少呢？

图二 座位需求图

解：设潜在座位需求量为μ，座位需求模型可以设定为：

****

,2000020000,20000

i i

i i i i y v y y y y μσ=+?

20000()(

)Pr(*18000)=0.75d y μ

σ

-Φ=Φ=Φ=<=

200000.675d μ

σ

-== （43）

因此，()()/()(0.675)/0.750.424d d d λφφ=-Φ=-=-； 又由平均观测到的需求量为18000，根据归并变量的均值公式可得：

()()()()[1()]=0.75(0.424)200000.2518000

E y d d b d μσλμσ=Φ++-Φ -+?= （44）

综合（43）（44）可以解出潜在变量y *的均值和方差分别为μ=2426、σ2=18362。即，对电影院座位的平均需求量是2426个。

1.2.2 归并模型的极大似然估计

设归并回归模型中，潜在变量y *和实际观测变量y 有：

*'i i i y u =+βx i i y a =，如果*i i y a ≤ i i y b =，如果*i i y b ≥

*i i y y =，其它

设f (u )、F (u )为u 的密度函数和分布函数。假定u 是均值为0，方差为σ2的连续随机变量，u 与x 不相关。

由归并模型的概率密度函数可知其对数似然函数为：

222

()1[log(2)log ]2--log[(

)]log[1(

)]

i i i i i

i i

i i a y b i i i i y a y b y LogL a b πσσσ

σ

≤≤==-=-+- + Φ+ -Φ∑∑∑x βx β

x β

虽然它是离散分布和连续分布的总和，但Amemiya （1973b ）证明，按照普通的最优化方式使得对数似然函数极大化，得到的估计量仍然具有极大似然估计量的合意的性质。

归并回归模型的边际影响为：

()*[|]

Pr[]()()k i i i k i i k

E y a y b

F d F c ββ?=?<<=-?x x （证明请参见Greene(2000)P909）。

例：考察囚犯在释放后被再次被捕入狱的时间，共1445名调查者，其中只有552名被再次被捕入狱。（file ：recid.raw ）。

例：妇女就业时间的案例（在0点截断）。（file ：mroz.raw ）

1.3 Tobit 模型

1.3.1 Tobit 模型的设定与估计

Tobin 在1958年第一次提出归并模型，因此归并模型又称为Tobit 模型。设潜在变量y *的回归模型为：

****0,0,0

i i i

i i i i i y v y y y y y σ=+= ≤= >x β如果如果， 潜在变量y *的期望值为：

*[]i i E y =x β

其中，(/)

(/)

i i i φσλσ=

Φx βx β

因此，解释变量对被解释变量y *的边际影响为常数：

*[|]

k k

E y x x β?=? 实际观测变量y 的期望值为：

()(|1)(1)i i i i E y E y D P D ===

而(1)(/)i i P D σ==Φx β，(|1)(/)i i i i E y D σλσ==+x βx β，将其代入上式可得：

[](

)()(

)(

)i i i i i i i E y σλσφσ

σ

σ

=Φ+=Φ+x β

x β

x β

x βx β

解释变量对实际观测变量的边际影响是非线性的。

由()(|1)(1)i i i i E y E y D P D ===可得：

(1)

(|1)()(|1)(1)i i i i i i k k k

P D E y D E y E y D P D x x x ?=?=?==+=??? 其中，

(1)(1)(/)(/)i k

i k P D P D x βσφσσ

?===Φ?

=?x βx β

(|1)(/)(|1)(/)(/)(/)()

i i i i i i i i k k i k E y D E y D x x σλσλσσβσ

σ==+?=???

=+???x βx βx βx βx β

= (/)

(/)

i k k

i λσββσ?+?x βx β

= []()1(/)/(/)k i i i βλσσλσ-+x βx βx β

因此，

()

(/)k k

E y x βσ?=Φ?x β Tobit 模型的似然函数为：

22

2

00

()1[log(2)log ]log[1()]2i i i i i y y y LogL πσσσ>=-=-+- + -Φ∑∑x βx β 利用最优化方法可以求出参数估计量。

例：考察不同变量对妇女工作时间的影响。（file ：mroz.raw ）。共753个观测值，其中325个为0。用Tobit 模型进行估计。

Tobit 模型的一个重要局限是，*(|0,)i i E y y >x 与*(0)i P y >直接相关。x k 对*(0)i P y >的边际影响

(0|)k P y x ?>?x 与βk 呈正比，x k 对*

(|0,)i i E y y >x 的边际影响*(|0,)i i k

E y y x ?>?x 与βk 也呈正比，即x k 对

*(0)i P y >的影响和对*(|0,)i i E y y >x 的影响在方向上是相同的。在一些情况下，这一暗含的假定可

能不合适。

1.3.2 模型的设定分析

衡量Tobit 模型是否合适的一种方法是将Tobit 模型的估计结果与Probit 模型的估计结果相比较。由Tobit 模型的设定，*(0)(0)(/)1(/)i i i i P y P y P v σσ==≤=≤-=-Φx βx β，(0)(/)i i P y σ>=Φx β。因此，如果将y 降级为二元选择变量w （如果y =0，w =0；如果y ≠0，w =1），那么上述Tobit 模型就转化为Probit 模型。如果Probit 模型估计的结果与Tobit 模型的估计结果近似相同，说明Tobit 模型设定合适；否则，Tobit 模型的设定不合适。需要注意的是，在Probit 模型中，(1|)(|)()P y E y ===Φx x x γ；

而在Tobit 模型中，(1)(/)P w σ==Φx β。因此，应该将Probit 模型中的参数估计量?γ

与Tobit 模型中的参数估计量??/σβ

进行比较。如果?γ与??/σβ符号不同，或者二者差异很大，都表明Tobit 模型设定不合适。

事实上，Tobit 模型是截断模型和Probit 模型的结合。 对于Tobit 模型：

~(0,1)

0i i i i i i i i v v N y y y y y σ***

*

=+, ? , >0?=?, ≤0

??x β (A)

设共有N 个观测值，其中y i =0有N 0个观测值，y i =1有N 1个观测值，N = N 0+ N 1。 其似然函数为

()11

01(|)(0)1(/)i i i i i N N Tobit

i i i N N y f y y y LnL P y y φσσσ*

**?-??>0= , >0 ????=??==-Φ, ≤0

?∑∑∑∑x βx β

对于截断模型（截断点为0）：

,~(0,1),i i i i i i i v v N y y y y σ**

*

=+ = >0

x β

其似然函数为：

1

111(|)1(/)()1(/),i i i i Trucn i N

N i i i i i N

N f y y y LnL P y y y φσσσφσσσ***>0-??

==Φ, ?>0??

-??

=- Φ >0 ???

∑∑∑∑x βx βx βx β

对于Probit 模型

(1)()(0)1()i i i i P D P D ==Φ

??

==-Φ?

x γx γ 其似然函数为：

()10

Pr ()1()i i N obit

i

i N y LnL y **

?Φ

, >0?= ?-Φ ≤ , 0??∑∑x γx γ 因此，截断模型与Probit 模型的似然函数之和为：

()()1

11010

Pr 1(/)()1()11()i i Trunc obit i i i N

N N N i i i N N y LnL y φσσσφσσ+-??=- Φ +Φ+-Φ ???

-??

= +-Φ ???∑∑∑∑∑∑x βx βx γx γx βx γ

与Tobit 模型的似然函数()1

011(/)i i Tobit i N

N y LnL φσσσ-??

=+-Φ ???

∑∑x βx β相比较，可以发现，Tobit 模型是Truncated 模型和Probit 模型之和的约束形式，约束条件为：/σ=γβ。因此，检验Tobit 设定是否合适可以利用似然比检验方法。具体步骤为： Step1：分别估计截断模型、Probit 模型和Tobit 模型；

Step2：计算似然比统计量：LR =2(LL Trunc + LL Probit – LL Tobit )，自由度为Tobit 模型中未知参数的个数。

例：考察不同变量对妇女工作时间的影响。（file ：mroz.raw ）。分析Tobit 模型的估计是否恰当。

如果检验结果表明Tobit 模型设定不恰当，那么可以利用Hurdle （或称之为Two-Part ）方法。（略）

注：

1． 在EViews 中，截断回归模型和归并回归模型中，对于随机扰动项可以设定为三种不同的形式：标准正态、Logistic 分布和极值分布。对于模型

'i i i y v σ=+βx

v i 服从标准正态分布：E(v i )=0, Var(v i )=σ2。 v i 服从Logistic 分布：E(v i )=0, Var(v i )=π2/3。 v i 服从标准正态分布：E(v i )≈0.5772，Var(v i )=σ2/6。

2． 对于归并模型，归并点可以已知，也可以未知；但对于截断模型，截断点必须是已知的。

附录：截断分布的矩

1．随机变量的截断分布特征

2．标准正态分布变量的截断分布特征