知识要点整合圆锥曲线的定义、标准方程与几何性质

知识要点整合
1、圆锥曲线的定义、标准方程与几何性质
名称椭圆双曲线抛物线定义
标准方程
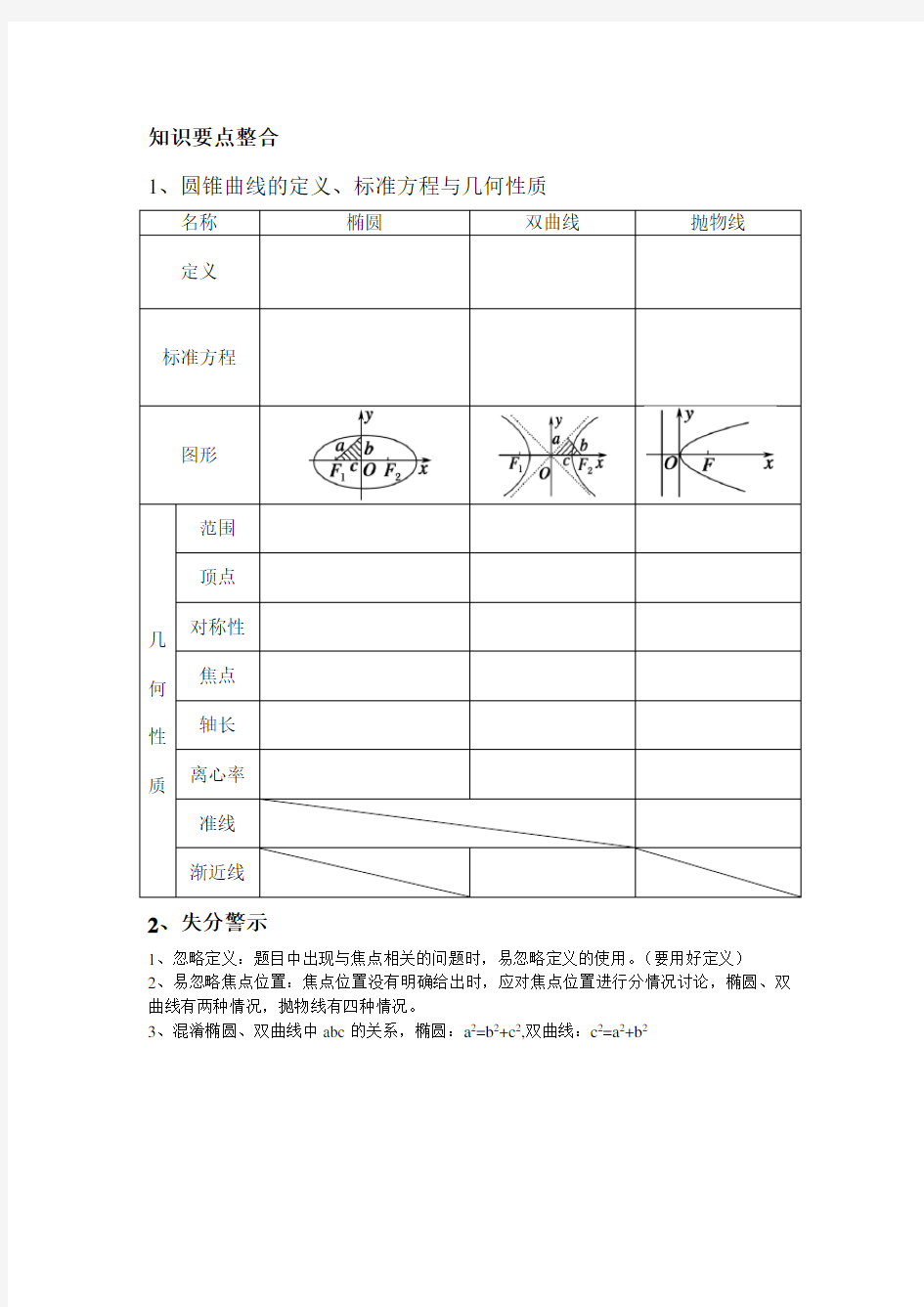
图形
几何性质
范围顶点对称性焦点轴长离心率准线渐近线
2、失分警示
1、忽略定义:题目中出现与焦点相关的问题时,易忽略定义的使用。(要用好定义)
2、易忽略焦点位置:焦点位置没有明确给出时,应对焦点位置进行分情况讨论,椭圆、双曲线有两种情况,抛物线有四种情况。
3、混淆椭圆、双曲线中abc的关系,椭圆:a2=b2+c2,双曲线:c2=a2+b2
预习自测
1、(大纲卷)双曲线C :22
221(0,0)x y a b a b
-=>>的离心率为2,,
则C 的焦距等于( )
A .2
B .
C .4
D .
2、(辽宁)已知点(2,3)A -在抛物线C :2
2y px =的准线上,记C 的焦点为F ,则直线AF 的斜率为( ) A .43- B .-1 C .34- D .12
-
3、[全国新课标卷Ⅰ] 已知双曲线x 2a 2-y 2
3
=1(a >0)的离心率为2,则a =( )
A .2 B.
62 C.5
2
D .1 4、(重庆)设21F F ,分别为双曲线)0,0(122
22>>=-b a b y a x 的左、右焦点,双曲线上存在
一点P 使得,3|)||(|2
2
21ab b PF PF -=-则该双曲线的离心率为( ) A.2 B.15 C.4 D.17
5、[广东卷] 若实数k 满足0 5 =1的( ) A .实半轴长相等 B .虚半轴长相等 C .离心率相等 D .焦距相等 真题演练 1、(安徽)抛物线2 4 1x y = 的准线方程是( ) A. 1-=y B. 2-=y C. 1-=x D. 2-=x , 2、(全国卷)双曲线C :x 2a 2-y 2 b 2=1(a >0,b >0)的离心率为2,焦点到渐近线的距离为3, 则C 的焦距等于( ) A .2 B .2 2 C .4 D .4 2 3、[天津卷] 已知双曲线x 2a 2-y 2 b 2=1(a >0,b >0)的一条渐近线平行于直线l :y =2x +10,双 曲线的一个焦点在直线l 上,则双曲线的方程为( ) A.x 25-y 220=1 B.x 220-y 2 5=1 C.3x 225-3y 2100=1 D.3x 2100-3y 2 25 =1 4、(全国卷)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点为F 1,F 2,离心率为3 3,过F 2 的直线l 交C 于A ,B 两点.若△AF 1B 的周长为4 3,则C 的方程为( ) A.x 23+y 22=1 B.x 23+y 2=1 C.x 212+y 28=1 D.x 212+y 2 4=1 5、[2014·四川卷] 双曲线 x 24 -y 2 =1的离心率等于________. 8. [2014·辽宁卷] 已知点A (-2,3)在抛物线C :y 2=2px 的准线上,记C 的焦点为F ,则直线AF 的斜率为( ) A .-43 B .-1 C .-34 D .-1 2 高二数学圆锥曲线知识整理 解析几何的基本问题之一:如何求曲线(点的轨迹)方程。它一般分为两类基本题型:一是已知轨迹类型求其方程,常用待定系数法,如求直线及圆的方程就是典型例题;二是未知轨迹类型,此时除了用代入法、交轨法、参数法等求轨迹的方法外,通常设法利用已知轨迹的定义解题,化归为求已知轨迹类型的轨迹方程。因此在求动点轨迹方程的过程中,一是寻找与动点坐标有关的方程(等量关系),侧重于数的运算,一是寻找与动点有关的几何条件,侧重于形,重视图形几何性质的运用。 在基本轨迹中,除了直线、圆外,还有三种圆锥曲线:椭圆、双曲线、抛物线。 1、三种圆锥曲线的研究 (1)统一定义,三种圆锥曲线均可看成是这样的点集:? ?????>=0e ,e d |PF ||P ,其中 F 为定点,d 为P 到定直线的距离,如图。 因为三者有统一定义,所以,它们的一些性质,研究它们的一些方法都具有规律性。 当0 椭圆的定义、性质及标准方程 1. 椭圆的定义: ⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。 ⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(< 高中数学复习:圆锥曲线的方程与性质 1.已知A 为抛物线C :y 2 =2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =( ) A.2 B.3 C.6 D.9 解析 设A (x ,y ),由抛物线的定义知,点A 到准线的距离为12,即x +p 2=12. 又因为点A 到y 轴的距离为9,即x =9, 所以9+p 2=12,解得p =6.故选C. 答案 C 2.设O 为坐标原点,直线x =2与抛物线C :y 2 =2px (p >0)交于D ,E 两点,若OD ⊥OE ,则C 的焦点坐标为( ) A.? ????14,0 B.? ?? ??12,0 C.(1,0) D.(2,0) 解析 将x =2与抛物线方程y 2 =2px 联立, 可得y =±2p , 不妨设D (2,2p ),E (2,-2p ), 由OD ⊥OE ,可得OD →·OE → =4-4p =0,解得p =1, 所以抛物线C 的方程为y 2 =2x .其焦点坐标为? ?? ??12,0.故选B. 答案 B 3.设F 1,F 2是双曲线C :x 2 -y 2 3 =1的两个焦点,O 为坐标原点,点P 在C 上且|OP |=2,则△ PF 1F 2的面积为( ) A.72 B.3 C.52 D.2 解析 法一 由题知a =1,b =3,c =2,F 1(-2,0),F 2(2,0), 如图,因为|OF 1|=|OF 2|=|OP |=2,所以点P 在以F 1F 2为直径的圆上,故PF 1⊥PF 2,则|PF 1|2 +|PF 2|2 =(2c )2 =16. 由双曲线的定义知||PF 1|-|PF 2||=2a =2,所以|PF 1|2 +|PF 2|2 -2|PF 1||PF 2|=4,所以|PF 1||PF 2|=6, 所以△PF 1F 2的面积为1 2 |PF 1||PF 2|=3.故选B. 法二 由双曲线的方程可知,双曲线的焦点F 1,F 2在x 轴上,且|F 1F 2|=21+3=4.设点P 的坐标为(x 0,y 0),则?????x 20-y 2 03=1,x 20+y 20 =2,解得|y 0|=32. 所以△PF 1F 2的面积为12|F 1F 2|·|y 0|=12×4×3 2=3.故选B. 答案 B 4.已知椭圆C 1:x 2a 2+y 2 b 2=1(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点 重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=4 3|AB |. (1)求C 1的离心率; (2)设M 是C 1与C 2的公共点.若|MF |=5,求C 1与C 2的标准方程. 解 (1)由已知可设C 2的方程为y 2 =4cx ,其中c =a 2 -b 2 . 不妨设A ,C 在第一象限,由题设得A ,B 的纵坐标分别为b 2a ,-b 2 a ;C ,D 的纵坐标分别为2c , -2c ,故|AB |=2b 2 a ,|CD |=4c . 由|CD |=43|AB |得4c =8b 2 3a ,即3×c a =2-2? ?? ??c a 2 . 解得c a =-2(舍去)或c a =1 2 . 所以C 1的离心率为12 . (2)由(1)知a =2c ,b =3c ,故C 1:x 24c 2+y 2 3c 2=1. 设M (x 0,y 0),则x 204c 2+y 203c 2=1,y 2 0=4cx 0, 故x 20 4c 2+4x 03c =1.① 回顾复习五:圆锥曲线及其几何性质 ☆考点梳理 1.圆锥曲线的轨迹定义与统一定义. 2.圆锥曲线的标准方程及其推导. 3.圆锥曲线的几何性质:范围、对称性、焦点、离心率、准线、渐近线.☆基础演练 1.如图,椭圆中心为O,A、B为左右顶点,F为左焦点, 左准线l交x轴于C,点P、Q在椭圆上,PD⊥l于D, QF⊥OA于F.给出下列比值: 其中为离心率的有_________________. 2.若 12 ,F F为椭圆 22 1 25 x y m +=的焦点,且 12 8 F F=,则m的 值为. 3.过抛物线的焦点F作直线交其于A、B两点,A、B在抛物线准线上的射影分别为A1、 B1,则 11 A FB ∠=____________. 4.经过两点() 143 ,, ?? - ? ? ?? 的圆锥曲线的标准方程是________________. 5.过双曲线 22 22 1 x y a b -=的右焦点F作一条渐近线的垂线分别交于A、B两点,O为坐标 原点,若OA、AB、OB成等差数列,且BF,FA u u u r u u u r 同向,则离心率e=_________. 6.椭圆 22 1 2516 x y +=的两个焦点为F1、F2,弦AB过F1,若 2 ABF ?的内切圆周长为π, ()() 1122 A x,y, B x,y,则 12 y y -=____________. ☆典型例题 1.椭圆的定义 例1.如图,已知E,F为平面上的两个定点,G为动点, 610 EF,FG, ==点P为线段EG的中垂线与GF的交点. ⑴建立适当的平面直角坐标系求出点P的轨迹方程; ⑵若点P的轨迹上存在两个不同的点A、B,且线段AB 的中垂线与EF(或EF的延长线)相交于一点C,线段EF 的中点为O,证明: 9 5 OC<. 2.中点弦问题 例3.直线l交椭圆 22 1 2016 x y +=于M,N两点,点() 04 B,,若⊿BMN的重心恰为椭圆 右焦点,则直线l的方程是_________________. 3.椭圆的几何性质 例2.已知 1 F、 2 F分别是椭圆() 22 22 10 x y a b a b +=>>的左右焦点,右准线l,离心率e. ⑴若P为椭圆上的一点,且 12 F PF ∠=θ,则 12 PF F S ? =_____________. ⑵若椭圆上存在一点P,使得 12 PF PF ⊥,则e的范围是_____________. ⑶若椭圆上存在一点P,使得 12 PF ePF =,则e的范围是_____________. ⑷若在l上存在一点P,使得线段 1 PF的中垂线经过 2 F,则e的范围是___________. ⑸若P为椭圆上的一点,线段 2 PF与圆222 x y b +=相切于中点Q,则e=________. ⑹过F且斜率为k的直线交椭圆于A、B两点,且3 AF FB = u u u r u u u r ,若 2 e=,则k=___. 4.最值问题 例4.已知动点P在椭圆 22 1 1612 x y +=上,(,(2,0) A B. ⑴若2 PA PB +取最小值,则点P的坐标为____________; ⑵若动点M满足||1 BM= u u u u r ,且0 PM BM= u u u u r u u u u r g,则| |的最小值是; ⑶PA PB +的取值范围是________________________. 例5.椭圆W的中心在原点,焦点在x轴上,离心率为 3 两条准线间的距离为6.椭 圆W的左焦点为F,过左准线与x轴的交点M任作一条斜率不为零的直线l与椭圆W 交于不同的两点A、B,点A关于x轴的对称点为C. ⑴求椭圆W的方程;⑵求证:CF FB λ = u u u r u u u r ;⑶求MBC ?面积S的最大值. ☆方法提炼 1.椭圆的标准方程有两种形式,有时需要就焦点位置进行讨论. 2.椭圆有两种定义方式,解题时要学会“回到定义去”. 3.椭圆有两个焦点、两条准线,解题时建议联系起来考虑. 4.解解析几何问题,“画个图”是个好建议;中点弦问题利用“点差法”可简化运算. 5.在处理直线与椭圆相结合的问题时,要学会利用韦达定理整体处理. P H E F G 第 1 页 圆锥曲线知识点总结 TPMK standardization office【 TPMK5AB- TPMK08- TPMK2C- TPMK18】 圆锥曲线的方程与性质 1.椭圆 (1)椭圆概念 平面内与两个定点1F 、2F 的距离的和等于常数2a (大于21||F F )的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离2c 叫椭圆的焦距。若M 为椭圆上任意一点,则有21||||2MF MF a +=。 椭圆的标准方程为:22221x y a b +=(0a b >>)(焦点在x 轴上)或1 22 22=+b x a y (0a b >>)(焦点在y 轴上)。 注:①以上方程中,a b 的大小0a b >>,其中222b a c =-; ②在22221x y a b +=和22 221y x a b +=两个方程中都有0a b >>的条件,要分清焦点的位置, 只要看2 x 和2 y 的分母的大小。例如椭圆22 1x y m n + =(0m >,0n >,m n ≠)当m n >时表示焦点在x 轴上的椭圆;当m n <时表示焦点在y 轴上的椭圆。 (2)椭圆的性质 ①范围:由标准方程22 221x y a b +=知||x a ≤,||y b ≤,说明椭圆位于直线x a =±, y b =±所围成的矩形里; ②对称性:在曲线方程里,若以y -代替y 方程不变,所以若点(,)x y 在曲线上时,点 (,)x y -也在曲线上,所以曲线关于x 轴对称,同理,以x -代替x 方程不变,则曲线关于y 轴对称。若同时以x -代替x ,y -代替y 方程也不变,则曲线关于原点对称。 所以,椭圆关于x 轴、y 轴和原点对称。这时,坐标轴是椭圆的对称轴,原点是对称中心,椭圆的对称中心叫椭圆的中心; ③顶点:确定曲线在坐标系中的位置,常需要求出曲线与x 轴、y 轴的交点坐标。在椭圆的标准方程中,令0x =,得y b =±,则1(0,)B b -,2(0,)B b 是椭圆与y 轴的两个交点。同理令0y =得x a =±,即1(,0)A a -,2(,0)A a 是椭圆与x 轴的两个交点。 所以,椭圆与坐标轴的交点有四个,这四个交点叫做椭圆的顶点。 同时,线段21A A 、21B B 分别叫做椭圆的长轴和短轴,它们的长分别为2a 和2b ,a 和 b 分别叫做椭圆的长半轴长和短半轴长。 由椭圆的对称性知:椭圆的短轴端点到焦点的距离为a ;在22Rt OB F ?中,2||OB b =, 2||OF c =,22||B F a =,且2222222||||||OF B F OB =-,即222c a b =-; ④离心率:椭圆的焦距与长轴的比c e a = 叫椭圆的离心率。∵0a c >>,∴01e <<,且e 越接近1,c 就越接近a ,从而b 就越小,对应的椭圆越扁;反之,e 越接近于0,c 就越接近于0,从而b 越接近于a ,这时椭圆越接近于圆。当且仅当a b =时,0c =,两焦点重合,图形变为圆,方程为222x y a +=。 2.双曲线 (1)双曲线的概念 圆锥曲线的几何性质 一、选择题(' ' 6636?=) 1. .设22221(0)x y a b a b +=>>为 黄金椭圆,F 、A 分别是它的左焦点和右端点,B 是它的短轴的一个端点,则ABF ∠=( ) A ,60 B ,75 C ,90 D ,120 2.已知双曲线22 221(0,0)x y a b a b -=>>右焦点为F ,右准线为l ,一直线交双曲线于P ,Q 两点,交l 于R 点,则( ) A ,PFR QFR ∠>∠ B ,PFR QFR ∠=∠ C ,PFR QFR ∠<∠ D ,PFR ∠与QFR ∠的大小不确定 3.已知点A(0,2)和抛物线24y x =+上两点B 、C ,使得AB BC ⊥,当点B 在抛物线上移动时,点C 的纵坐标的取值范围是 ( ) A ,(,0][4,)-∞+∞ B ,(,0]-∞ C ,[4,)+∞ D ,[0,4,] 4.设椭圆方程2 213 x y +=,(0,1)A -为短轴的一个端点,M ,N 为椭圆上相异两点。若总存在以MN 为底边的等腰AMN ?,则直线MN 的斜率k 的取值范围是 ( ) A ,(1,1)- B ,[1,1]- C ,(1,0]- D ,[0,1] 5.已知12,F F 分别为双曲线22 221(0,0)x y a b a b -=>>的左、右焦点,P 为双曲线右支上的任 意一点,若 2 12 PF PF 的最小值为8a ,则双曲线的离心率e 的取值范围是 ( ) A ,(1,)+∞ B ,(1,2] C , D ,(1,3] 6.已知P 为抛物线2 4y x =上一点,记P 到此抛物线的准线的距离为1d ,P 到直线 2120x y +-=的距离为2d ,则12d d +的最小值为 ( ) 八、圆锥曲线 1.圆锥曲线的两个定义: (1)第一定义中要重视“括号”内的限制条件: (1)已知定点)0,3(),0,3(21F F -,在满足下列条件的平面上动点P 的轨迹中是椭圆的是 A .421=+PF PF B .621=+PF PF C .1021=+PF PF D .122 2 2 1=+PF PF (答:C ) ; (2)方程8表示的曲线是_____(答:双曲线的左支) (2)第二定义 已知点)0,22(Q 及抛物线4 2x y =上一动点P (x ,y ),则y+|PQ|的最小值是_____ (答:2) 2.圆锥曲线的标准方程 (1)椭圆: (1)已知方程1232 2=-++k y k x 表示椭圆,则k 的取值范围为____ (答:11 (3,)(,2)22 --- U ); (2)若R y x ∈,,且62322=+y x ,则y x +的最大值是____,2 2 y x +的最小值是___ 2) (2)双曲线: (1)双曲线的离心率等于25 ,且与椭圆14 922=+y x 有公共焦点, 则该双曲线的方程_______(答:2 214 x y -=) ; (2)设中心在坐标原点O ,焦点1F 、2F 在坐标轴上,离心率2= e 的双曲线C 过点 )10,4(-P ,则C 的方程为_______(答:226x y -=) (3)抛物线: 3.圆锥曲线焦点位置的判断: 椭圆:已知方程1212 2=-+-m y m x 表示焦点在y 轴上的椭圆,则m 的取值范围是__(答: )2 3 ,1()1,(Y --∞) 4.圆锥曲线的几何性质: (1)椭圆 (1)若椭圆1522=+m y x 的离心率510 = e ,则m 的值是__(答:3或3 25); (2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__(答:22) (2)双曲线 (1)双曲线的渐近线方程是023=±y x ,则该双曲线的离心率等于______ (答: 2或3 ); 高中数学知识点大全—圆锥曲线 一、考点(限考)概要: 1、椭圆: (1)轨迹定义: ①定义一:在平面内到两定点的距离之和等于定长的点的轨迹是椭圆,两定点是焦点,两定点间距离是焦距,且定长2a大于焦距2c。用集合表示为: ; ②定义二:在平面内到定点的距离和它到一条定直线的距离之比是个常数e,那么这个点的轨迹叫做椭圆。其中定点叫焦点,定直线叫准线,常数是离心 率用集合表示为: ; (2)标准方程和性质: 注意:当没有明确焦点在个坐标轴上时,所求的标准方程应有两个。 (3)参数方程:(θ为参数); 3、双曲线: (1)轨迹定义: ①定义一:在平面内到两定点的距离之差的绝对值等于定长的点的轨迹是双曲线,两定点是焦点,两定点间距离是焦距。用集合表示为: ②定义二:到定点的距离和它到一条定直线的距离之比是个常数e,那么这个点的轨迹叫做双曲线。其中定点叫焦点,定直线叫准线,常数e是离心率。 用集合表示为: (2)标准方程和性质: 注意:当没有明确焦点在个坐标轴上时,所求的标准方程应有两个。 4、抛物线: (1)轨迹定义:在平面内到定点和定直线的距离相等的点的轨迹是抛物线,定点是焦点,定直线是准线,定点与定直线间的距离叫焦参数p。用集合表示为 : (2)标准方程和性质: ①焦点坐标的符号与方程符号一致,与准线方程的符号相反;②标准方程中一次项的字母与对称轴和准线方程的字母一致;③标准方程的顶点在原点,对称轴是坐标轴,有别于一元二次函数的图像; 二、复习点睛: 1、平面解析几何的知识结构: 2、椭圆各参数间的关系请记熟“六点六线,一个三角形”,即六点:四个顶点,两个焦点;六线:两条准线,长轴短轴,焦点线和垂线PQ;三角形:焦点三角形。则椭圆的各性质(除切线外)均可在这个图中找到。 椭圆的标准方程与性质 教学目标: 1了解椭圆的实际背景,了解椭圆在刻画现实世界和解决实际问题中的作用; 2 掌握椭圆的定义、几何图形、标准方程及简单几何性质. 高考相关点: 在高考中所占分数:13分 考查出题方式:解答题的形式,而且考查方式很固定,涉及到的知识点有:求曲线方程,弦长,面积,对称关系,范围问题,存在性问题。 涉及到的基础知识 1.引入椭圆的定义 在平面内与两定点F1,F2的距离的和等于常数(大于|F1F2|=2c)的点的轨迹叫做椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数: 有以下3种情况 (1)若a>c,则集合P为椭圆; (2)若a=c,则集合P为线段; (3)若a 标准方程x2 a2 +\f(y2,b2)=1 (a>b>0) \f(y2,a2)+错误!=1 (a>b>0) 图形 性质范围 -a≤x≤a -b≤y≤b -b≤x≤b -a≤y≤a 对称性对称轴:坐标轴;对称中心:原点 顶点 A1(-a,0),A2(a,0) B1(0,-b),B2(0,b) A1(0,-a),A2(0,a) B1(-b,0),B2(b,0)轴长轴A1A2的长为2a;短轴B1B2的长为2b 焦距|F1F2|=2c 离心率e=错误!∈(0,1) a,b,c的关系c2=a2-b2题型总结 类型一椭圆的定义及其应用 例1:如图所示,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( ) A.椭圆? B.双曲线 C.抛物线 D.圆 【解析】根据CD是线段MF的垂直平分线.可推断出,进而可以知道 结果为定值,进而根据椭圆的定义推断出点P的轨迹【答案】根据题意知,CD是线段MF的垂直平分线.,(定值),又显然,根 据椭圆的定义可推断出点P轨迹是以F、O两点为焦点的椭圆.所以A选项是正确的 练习1:已知F1,F2是椭圆C: 22 22 1 x y a b +=(a>b>0)的两个焦点,P为椭圆C 上的一点,且 错误! 1⊥2 PF,若△PF1F2的面积为9,则b=________. 【解析】由题意的面积∴故答案为: 【答案】3 练习2:已知F1,F2是椭圆错误!+错误!=1的两焦点,过点F2的直线交椭圆于A,B两点,在△AF1B中,若有两边之和是10,则第三边的长度为() A.6?B.5 C.4 D.3 圆锥曲线方程知识点总结-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII §8.圆锥曲线方程 知识要点 一、椭圆方程. 1. 椭圆方程的第一定义:为端点的线段 以无轨迹方程为椭圆21212121212121,2, 2, 2F F F F a PF PF F F a PF PF F F a PF PF ==+=+ =+ ⑴①椭圆的标准方程:i. 中心在原点,焦点在x 轴上:)0(12 2 22 b a b y a x =+. ii. 中心在原点,焦点在y 轴上:)0(12 22 2 b a b x a y =+ . ②一般方程:)0,0(122 B A By Ax =+. ③椭圆的标准方程: 122 2 2=+ b y a x 的参数方程为???==θ θ sin cos b y a x (一象限θ应是属于2 0π θ ). ⑵①顶点:),0)(0,(b a ±±或)0,)(,0(b a ±±. ②轴:对称轴:x 轴,y 轴;长轴长a 2,短轴长b 2. ③焦点:)0,)(0,(c c -或),0)(,0(c c -. ④焦距:2221,2b a c c F F -==. ⑤准线:c a x 2±=或c a y 2 ±=. ⑥离心率:)10( e a c e =. ⑦焦点半径: i. 设),(00y x P 为椭圆 )0(12222 b a b y a x =+ 上的一点,21,F F 为左、右焦点,则 ii.设),(00y x P 为椭圆 )0(12 22 2 b a a y b x =+ 上的一点,21,F F 为上、下焦点,则 由椭圆第二定义可知:)0()(),0()(0002 200201 x a ex x c a e pF x ex a c a x e pF -=-=+=+=归结起来为“左加 右减”. 注意:椭圆参数方程的推导:得→)sin ,cos (θθb a N 方程的轨迹为椭圆. ⑧通径:垂直于x 轴且过焦点的弦叫做通经.坐标:),(222 2a b c a b d -= 和),(2 a b c ?-=+=0201,ex a PF ex a PF ? -=+=0201,ey a PF ey a PF 64. 熟记下列公式了吗? [)()直线的倾斜角,,,102 212112l απααπ∈==--≠≠?? ???k y y x x x x tan ()()()P x y P x y a k 1112221,,,是上两点,直线的方向向量,l l → = (2)直线方程: ()点斜式:(存在)y y k x x k -=-00 斜截式:y kx b =+ 截距式:x a y b +=1 一般式:(、不同时为零)Ax By C A B ++=0 ()()点,到直线:的距离30000022P x y Ax By C d Ax By C A B l ++==+++ ()到的到角公式:41122112 l l t a n θ=--k k k k l l 122112 1与的夹角公式:tan θ=--k k k k 65. 如何判断两直线平行、垂直? A B A B A C A C 1221122112=≠??? ?l l ∥ k k l 1212=?l ∥(反之不一定成立) A A B B 1212120+=?l l ⊥ k k 12121·⊥=-?l l 66. 怎样判断直线l 与圆C 的位置关系? 圆心到直线的距离与圆的半径比较。 直线与圆相交时,注意利用圆的“垂径定理”。 67. 怎样判断直线与圆锥曲线的位置? 联立方程组关于(或)的一元二次方程“” 相交;相切;相离??>?=? 第一定义椭圆,双曲线,抛物线?+=>=?-=<=?=???????PF PF a a c F F PF PF a a c F F PF PK 12121212222222 第二定义:e PF PK c a == 0111<?=?e e e 椭圆;双曲线;抛物线 y b O F 1 F 2 a x x a c =2 ()x a y b a b 222 210+=>> () a b c 222=+ ()x a y b a b 222 2100-=>>, ()c a b 222=+ 圆锥曲线 一、椭圆 1、定义:平面内与两个定点1F ,2F 的距离之和等于常数(大于12F F )的点的轨迹称为椭圆. 即:|)|2(,2||||2121F F a a MF MF >=+。 这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距. 2、椭圆的几何性质: 焦点的位置 焦点在x 轴上 焦点在y 轴上 图形 标准方程 ()22 2210x y a b a b +=>> ()22 2210y x a b a b +=>> 范围 a x a -≤≤且 b y b -≤≤ b x b -≤≤且a y a -≤≤ 顶点 ()1,0a A -、()2,0a A ()10,b B -、()20,b B ()10,a A -、()20,a A ()1,0b B -、()2,0b B 轴长 短轴的长2b = 长轴的长2a = 焦点 ()1,0F c -、()2,0F c ()10,F c -、()20,F c 焦距 ()222122F F c c a b ==- 对称性 关于x 轴、y 轴、原点对称 离心率 ()2 2101c b e e a a ==-< 二、双曲线 1、定义:平面内与两个定点1F ,2F 的距离之差的绝对值等于常数(小于 12F F )的点的轨迹称为双曲线.即:|)|2(,2||||||2121F F a a MF MF <=-。 这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距. 2、双曲线的几何性质: 焦点的位置 焦点在x 轴上 焦点在y 轴上 图形 标准方程 ()22 2210,0x y a b a b -=>> ()22 2 210,0y x a b a b -=>> 范围 x a ≤-或x a ≥,y R ∈ y a ≤-或y a ≥,x R ∈ 顶点 ()1,0a A -、()2,0a A ()10,a A -、()20,a A 轴长 虚轴的长2b = 实轴的长2a = 焦点 ()1,0F c -、()2,0F c ()10,F c -、()20,F c 焦距 ()222122F F c c a b ==+ 对称性 关于x 轴、y 轴对称,关于原点中心对称 离心率 ()2 211c b e e a a ==+>,e 越大,双曲线的开口越阔 渐近线方程 b y x a =± a y x b =± 5、实轴和虚轴等长的双曲线称为等轴双曲线. 三、抛物线 圆锥曲线的定义及几何性质 1. 椭圆 222 2 1x y a b + =和 222 2 x y k a b + =(0)k >一定具有( ) A .相同的离心率 B .相同的焦点 C .相同的顶点 D .相同的长轴长 2. 已知1F 、2F 是椭圆的两个焦点,过1F 且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若2 ABF ?是正三角形,则这个椭圆的离心率是( ) A . 2 B . 3 C 2 D 3 3. 已知1F 、2F 是椭圆的两个焦点,满足120M F M F ?= 的点M 总在椭圆内部,则椭圆离心率的 取值范围是( )A .(01), B .1(0]2 , C .(02 D .1)2 4. 过椭圆 222 2 1(0) x y a b a b + =>>的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若 1260F PF ∠=°,则椭圆的离心率为( ) A . 2 B . 3 C .12 D .1 3 5. 已知椭圆 2222 1x y a b +=的左、 右焦点分别为1F 、2F ,且12||2F F c =,点A 在椭圆上,1120AF F F ?= ,2 12AF AF c ?= ,则椭圆的离心率e = ( ) A . 3 B . 2 C 2 D 2 6. 已知P 是以12F F ,为焦点的椭圆 222 2 1(0)x y a b a b + =>>上的一点,若 120 PF PF ?= , 121tan 2 PF F ∠= ,则此椭圆的的离心率为( ) A . 12 B . 23 C .1 3 D 3 7. 已知椭圆 2 2 15 x y m + = 的离心率e 5 =m 的值为( ) A .3 B . 253 或3 C . D 8. 椭圆的长轴为12A A ,B 为短轴的一个端点,若∠012120A BA =,则椭圆的离心率为( ) A . 12 B 3 C 3 D 2 9. 椭圆 222 2 1(0)x y a b a b + =>>的四个顶点为A 、B 、C 、D ,若四边形ABC D 的内切圆恰好过椭 圆的焦点,则椭圆的离心率是( ) A . 2 B . 4 C 2 D 4 10. 设12F F ,分别是椭圆 222 2 1x y a b + =(0a b >>)的左、右焦点,若在直线2 :a l x c = 上存在P (其 中c =),使线段1PF 的中垂线过点2F ,则椭圆离心率的取值范围是( ) A .0, 2? ?? B .0, 3? ? ? C .,12????? D .,13? ???? 11. 椭圆上一点A 看两焦点的视角为直角,设1AF 的延长线交椭圆于B ,又2||||AB AF =,则椭圆的 离心率e =( ) A .2-+ B . C 1- D 12. 椭圆() 222 2 10x y a b a b + =>>的右焦点F ,其右准线与x 轴的交点为A ,在椭圆上存在点满足线 段AP 的垂直平分线过点F ,则椭圆离心率的取值范围是( ) 13. A .02? ? ? B .102? ? ?? ?, C .)11 , D .112 ???? ??, 14. 已知椭圆() 222 2 10x y a b a b + =>>,A 是椭圆长轴的一个端点,B 是椭圆短轴的一个端点,F 为 椭圆的一个焦点. 若AB BF ⊥,则该椭圆的离心率为 ( ) 224416. 在ABC △中,A B B C =,7cos 18 B =- .若以A B ,为焦点的椭圆经过点C ,则该椭圆的离 心率e = . 17. 在平面直角坐标系xOy 中,设椭圆 222 2 1(0) x y a b a b +=>>的焦距为2c ,以点O 为圆心,a 为 半径作圆M .若过点20a P c ?? ? ?? ,作圆M 的两条切线互相垂直,则椭圆的离心率为 . 18. 直线:220l x y -+=过椭圆的左焦点1F 和一个顶点B ,该椭圆的离心率为_________. 19. 设12(0)(0)F c F c -,,,是椭圆 222 2 1(0) x y a b a b + =>>的两个焦点,P 是以12F F 为直径的圆与椭 圆的一个交点,若12 21 2PF F PF F ∠=∠,则椭圆的离心率等于________. 20. 椭圆 222 2 1(0)x y a b a b + =>>的半焦距为c ,若直线2y x =与椭圆一个交点的横坐标恰为c ,椭圆 的离心率为_________ 21. 已知1F ,2F 是椭圆的两个焦点,过1F 且与椭圆长轴垂直的直线交椭圆于A B ,两点,若 2ABF △是正三角形,则这个椭圆的离心率是_________. §8.圆锥曲线方程 知识要点 一、椭圆方程. 1. 椭圆方程的第一定义:为端点的线段 以无轨迹方程为椭圆21212121212121,2, 2, 2F F F F a PF PF F F a PF PF F F a PF PF ==+=+=+ ⑴①椭圆的标准方程:i. 中心在原点,焦点在x 轴上:)0(12 222 b a b y a x =+ . ii. 中心在原点,焦点在y 轴上:)0(12 22 2 b a b x a y =+ . ②一般方程:)0,0(122 B A By Ax =+. ③椭圆的标准方程:12 22 2=+ b y a x 的参数方程为?? ?==θ θsin cos b y a x (一象限θ应是属于20π θ ). ⑵①顶点:),0)(0,(b a ±±或)0,)(,0(b a ±±. ②轴:对称轴:x 轴,y 轴;长轴长a 2,短轴长b 2. ③焦点:)0,)(0,(c c -或),0)(,0(c c -. ④焦距:2221,2b a c c F F -==. ⑤准线:c a x 2±=或c a y 2 ±=. ⑥离心率:)10( e a c e =. ⑦焦点半径: i. 设),(00y x P 为椭圆)0(12 22 2 b a b y a x =+上的一点,21,F F 为左、右焦点,则 ii.设),(00y x P 为椭圆 )0(12 22 2 b a a y b x =+ 上的一点,21,F F 为上、下焦点,则 由椭圆第二定义可知:)0()(),0()(0002 2002 01 x a ex x c a e pF x ex a c a x e pF -=-=+=+=归结起来为“左加右减”. 注意:椭圆参数方程的推导:得→)sin ,cos (θθb a N 方程的轨迹为椭圆. ⑧通径:垂直于x 轴且过焦点的弦叫做通经.坐标:),(222 2a b c a b d -=和),(2a b c ⑶共离心率的椭圆系的方程:椭圆 )0(12 22 2 b a b y a x =+的离心率是)(22b a c a c e -== ,方程t t b y a x (2 22 2=+是大于0的参数,)0 b a 的离心率也是a c e = 我们称此方程为共离心率的椭圆系方程. ⑸若P 是椭圆:12 22 2=+ b y a x 上的点.21,F F 为焦点,若θ=∠21PF F ,则21F PF ?的面积为2 tan 2θ b (用 余弦定理与a PF PF 221=+可得). 若是双曲线,则面积为2 cot 2θ ?b . ?-=+=0201,ex a PF ex a PF ? -=+=0201,ey a PF ey a PF 高中数学椭圆的知识总结 1.椭圆的定义: 平面内一个动点P 到两个定点12,F F 的距离之和等于常数 (12122PF PF a F F +=>),这个动点P 的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距. 注意:若1212PF PF F F +=,则动点P 的轨迹为线段12F F ;若1212PF PF F F +<,则动点P 的轨迹无图形. (1)椭圆:焦点在x 轴上时12 2 22 =+b y a x (222 a b c =+)?{ cos sin x a y b ??==(参数方程,其中?为参数),焦点在y 轴上时22 22b x a y +=1(0a b >>)。 2. 椭圆的几何性质: (1)椭圆(以122 22=+b y a x (0a b >>)为例):①范围: ,a x a b y b -≤≤-≤≤;②焦点:两个焦点(,0)c ±;③对称性:两条对称轴0,0x y ==,一个对称中心(0,0),四个顶点(,0),(0,)a b ±±,其中长 轴长为2a ,短轴长为2b ; ④离心率:c e a =,椭圆?01e <<,e 越 小,椭圆越圆;e 越大,椭圆越扁。⑥ (2).点与椭圆的位置关系:①点00(,)P x y 在椭圆外?2200 221x y a b +>; ②点00(,)P x y 在椭圆上?220 220b y a x +=1;③点00(,)P x y 在椭圆内?2200 221x y a b +< 3.直线与圆锥曲线的位置关系: (1)相交:0?>?直线与椭圆相交;(2)相切:0?=?直线与椭圆相切; (3)相离:0?>相交于A 、B 两点, 且线段AB 的中点在直线L :x -2y=0上,则此椭圆的离心率为_______; (3)试确定m 的取值范围,使得椭圆13 42 2=+y x 上有不同的两点关于直 线m x y +=4对称; 特别提醒:因为0?>是直线与圆锥曲线相交于两点的必要条件,故在求解有关弦长、对称问题时,务必别忘了检验0?>! 椭圆知识点的应用 1.如何确定椭圆的标准方程? 任何椭圆都有一个对称中心,两条对称轴。当且仅当椭圆的对称中心在坐标原点,对称轴是坐标轴,椭圆的方程才是标准方程形式。此时,椭圆焦点在坐标轴上。 确定一个椭圆的标准方程需要三个条件:两个定形条件b a ,;一个定位 4.2解析几何--圆锥曲线的概念及性质 一、选择题 1.(2010·安徽双曲线方程为x2-2y2=1,则它的右焦点坐标为 ( A. B. C. D.(,0 解析:∵原方程可化为-=1,a2=1, b2=,c2=a2+b2=, ∴右焦点为. 答案:C 2.(2010·天津已知双曲线-=1(a>0,b>0的一条渐近线方程是y=x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为 ( A.-=1 B.-=1 C.-=1 D.-=1 解析:∵渐近线方程是y=x,∴=.① ∵双曲线的一个焦点在y2=24x的准线上, ∴c=6.② 又c2=a2+b2,③ 由①②③知,a2=9,b2=27, 此双曲线方程为-=1. 答案:B 4.(2010·辽宁设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的斜率为-,那么|PF|= ( A.4 B.8 C.8 D.16 解析:解法一:AF直线方程为: y=-(x-2, 当x=-2时,y=4,4A(-2,4. 当y=4时代入y2=8x中,x=6, 4P(6,4, 4|PF|=|PA|=6-(-2=8.故选B. 解法二:5PA∞l,4PA%x轴. 又5 AFO=60°,4 FAP=60°, 又由抛物线定义知PA=PF, 4≥PAF为等边三角形. 又在Rt≥AFF′中,FF′=4, 4FA=8,4PA=8.故选B. 答案:B 5.高8 m和4 m的两根旗杆笔直竖在水平地面上,且相距10 m,则地面上观察两旗杆顶端仰角相等的点的轨迹为 ( A.圆 B.椭圆 C.双曲线 D.抛物线 解析:如图1,假设AB、CD分别为高4 m、8 m的旗杆,P点为地面上观察两旗杆顶端仰角相等的点,由于∠BPA=∠DPC,则Rt△ABP∽Rt△CDP,=,从而 PC=2PA.在平面APC上,以AC为x轴,AC的中垂线为y轴建立平面直角坐标系(图2,则A(-5,0,C(5,0,设P(x,y,得=2 化简得x2+y2+x+25=0,显然,P点的轨迹为圆. 答案:A 二、填空题 解析:由题知,垂足的轨迹为以焦距为直径的圆,则c圆锥曲线知识点整理
圆锥曲线的定义方程和性质知识点总结
高中数学复习:圆锥曲线的方程与性质
第五讲 圆锥曲线及其几何性质
圆锥曲线知识点总结
高二数学 圆锥曲线的几何性质练习
圆锥曲线必考知识点总结及答案
(完整版)高中数学圆锥曲线知识点总结
椭圆的标准方程与性质
圆锥曲线方程知识点总结
高中数学知识点总结之圆锥曲线篇
圆锥曲线知识点总结
圆锥曲线的定义及几何性质
圆锥曲线方程知识点总结
高中圆锥曲线知识点总结全面经典
解析几何-- 圆锥曲线的概念及性质
