微积分及经济学应用

第3章 微积分及其经济学应用

3.1 一元函数和多元函数

在数学上，函数的定义为：如果在一个变化过程中有两个变量x 和y ，对任意给定的x 值，仅存在一个y 值与其对应，则称y 是x 的函数，表示为)(x f y =。

其中x 为自变量，y 为因变量。由于函数关系中仅有一个自变量，因此该函数称为一元函数。x 能够取得的所有值的集合称为函数定义域，y 能够取得的所有值的集合称为函数值域。

在对经济问题的分析过程中，我们通常用函数来描述经济变量之间的变化关系。例如，在商品的供求关系中，定义某种商品价格为P ，需求量为D Q ，供给量为S Q 。那么，需求与价格的函数关系可以表示为：)(P f Q D =，)(P g Q S =。

然而我们所处的经济环境是非常复杂的，每一个经济变量都要受到多种因素的影响。因此，采用一元函数来分析经济问题就会有很大的局限性。所以我们常常采用多元函数来研究经济问题。多元函数是在一个函数关系中函数值是由多个变量确定的，用

),,,(21n x x x f y =的形式来表示，它表示因变量y 的值取决于n 个自变量n

x x x ,,,21 的大小。

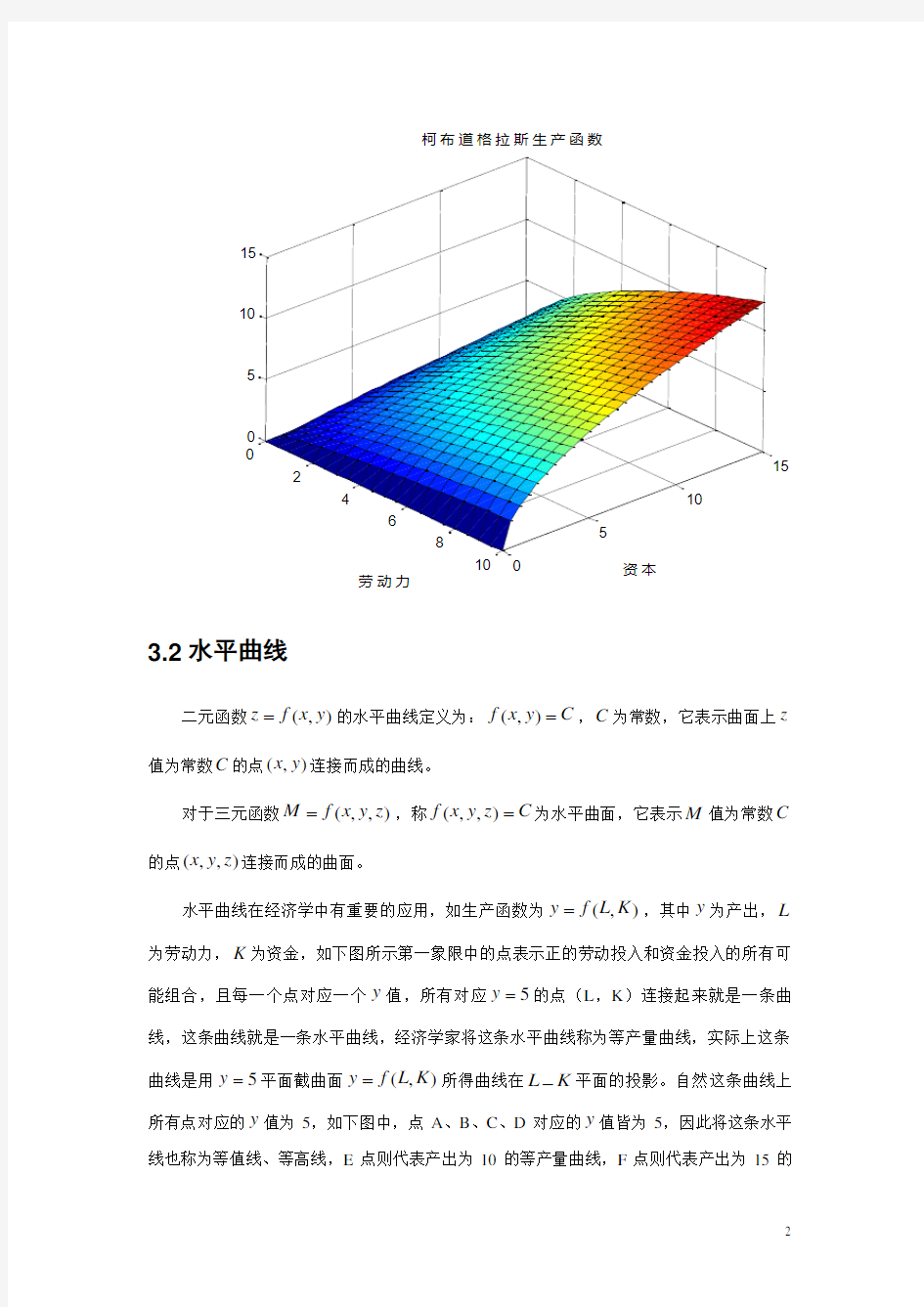
例如在消费理论的基本假设中，每个消费者都同时对多种商品有需求，“效用”取决于所消费的各种商品的数量，效用函数就可以表示为),,,(21n x x x f U =，其中U 表示消费者的效用，n x x x ,,,21 是对n 种商品的消费量。这个函数称为效用函数。同样，生产函数常表示为),(K L f y =，y 为产出水平，K 表示资本，L 表示劳动力。它说明产出水平既取决于劳动力又取决于资本。

Q=A*L^ alpha *K^ belta A=1;alpha=0.5;belta=0.5;

15

资本

柯布道格拉斯生产函数

劳动力

产值

3.2水平曲线

二元函数),(y x f z =的水平曲线定义为：C y x f =),(，C 为常数，它表示曲面上z 值为常数C 的点),(y x 连接而成的曲线。

对于三元函数),,(z y x f M =，称C z y x f =),,(为水平曲面，它表示M 值为常数C 的点),,(z y x 连接而成的曲面。

水平曲线在经济学中有重要的应用，如生产函数为),(K L f y =，其中y 为产出，L 为劳动力，K 为资金，如下图所示第一象限中的点表示正的劳动投入和资金投入的所有可能组合，且每一个点对应一个y 值，所有对应5=y 的点（L ，K ）连接起来就是一条曲线，这条曲线就是一条水平曲线，经济学家将这条水平曲线称为等产量曲线，实际上这条曲线是用5=y 平面截曲面),(K L f y =所得曲线在K L -平面的投影。自然这条曲线上所有点对应的y 值为5，如下图中，点A 、B 、C 、D 对应的y 值皆为5，因此将这条水平线也称为等值线、等高线，E 点则代表产出为10的等产量曲线，F 点则代表产出为15的

等产量曲线，可见越向右上方向的等产量曲线的产出值越大。

生产函数的水平曲线

在消费理论中，假设消费者只消费两种商品，那么它的效用取决于这两种商品消费量的组合。如果用U 表示效用，21,x x 分别表示这两种商品的消费量，那么它的效用函数就是二元函数，可以表示为),(21x x U U =。平面直角坐标系第一象限中的点表示出两种商品消费量的所有可能组合，平面上的每一点对应),(21x x U 曲面上的一个值。如果将对应

0U 的点连起来就表示在效用水平为0U 的情况下的一条水平曲线。经济学上将这条水平曲

线称为无差异曲线或等效用曲线。

3.3 极限

1.极限的定义

数列极限的定义：在数列{}n a 中，任取0>ε，如果存在N ，使得当N n >时，ε<-A a n ，则称当n 趋于无穷大时，A 为n a 的极限。表示为：

A a n n =∞

→lim 或者A a n →)(∞→n 。 在数列{}n a 中，n a 与n 一一对应，因此可以将n a 视为定义域为正整数n 的函数

)(n f a n =。因此对数列极限的定义进行推广，就可以得到函数)(x f 当∞→x 和0

x x →

极限的定义。

函数极限的定义

当∞→x 时函数极限的定义：任取0>ε，存在X ，使得当X x >时，

ε<-A x f )(，那么常数A 为当∞→x 时)(x f 的极限，记为A x f x =∞

→)(lim 或者 A x f →)()(∞→x 。

当0x x →时函数极限的定义：任取0>ε，存在0>δ，使得当δ<-<00x x 时，ε<-A x f )(，那么常数A 为当0x x →时)(x f 的极限，记为A x f x x

=→)(lim 0

或者A x f →)()(0x x →。

2. 左极限与右极限

当x 从0x 的左侧（即小于0x 的方向）趋向于0x （记为-

→0x x ），若此时)(x f 有极

限A ，则称A 为当-→0x x 时的左极限。记为A x f x

x =-

→)(lim 0

或者A x f →)()(0-→x x 。 当x 从0x 的右侧（即大于0x 的方向）趋向于0x （记为+

→0x x ），若此时)(x f 有极

限A ，则称A 为当+→0x x 时的右极限。记为A x f x

x =+

→)(lim 0

或者A x f →)()(0+→x x 。 3. 极限的运算法则

定理：如果A x f x x =→)(lim 0

，B x g x

x =→)(lim 0

，且A ，B 有限则 (1) B A x g x f x g x f x

x x x x x

±=±=±→→→)(lim )(lim )]()([lim 0

(2) AB x g x f x g x f x

x x x x x =-=→→→)(lim )(lim )]()([lim 0

(3) )(lim )(lim 0

x f c x cf x

x x x →→= (4) n

x

x n x x x f x f )](lim [)]([lim 0

→→= 4. 两个重要的极限

(1) 1sin lim

=→x

x x ，(2) e x

x

x =+

∞

→)

11(lim

3.4连续复利

连续复利的计算，是函数极限在经济学的经典应用。假设一个人将a 元存入银行，银

行年利率为r ，若利息按复利计息，每年计算一次，则年底时他的存款总额为)1(r a +。

如果银行改为半年计算一次利息，年利率不变，则半年的利率为2

r ，则年底时，他的

存款总额应为2

)21(r a +

元。

当银行每年计息n 次，可以推得，年底时存款总额应为n

n

r a )1(+

元。

当银行在年内连续计息时，即∞→n 时，年底存款总额为n

n n

r a )1(lim +

∞

→元。对其求

极限可以得到：

r r r n

n r

r n

n n

n ae n

r a n

r a n

r a =+

=+

=+

∞

→∞

→∞

→])1(lim [])1[(lim )1(lim

因此，在连续计息的情况下，年底时这个人的存款的余额为r ae 元。

我们可以将其推广到存款多年的情况，在连续计息时，第二年年底的存款余额为

r

r

r

ae

e ae 2=?元，则可以得出t 年末的存款余额为tr ae 元。

因此，连续复利时，本金为a 元，年利率为r ，则t 年末的资金余额为：tr

ae FV =元。

同样可以得到，t 年末的资金a 元，在连续复利的情况下，贴现值为：tr ae PV -=。

3.5一元函数的导数

1. 一元函数导数的定义：设)(x f y =为定义在集合D 上的一元函数，D x ∈0，

则函数在0x 点处的导数定义为：

0)

()(lim

x x x f x f dx

dy x x x x --=→=或x

x f x x f x f x ?-?+=→?)

()(lim

)(000

0'

2. 导数的四则运算法则：

设函数)(x f 和)(x g 都在x 点可导，则这两个函数的和、差、积、商均在x 点可导。 (1) )()](['

'

x cf x cf =(c 为常数)；

(2) )()()]()(['

''x g x f x g x f ±=±；

(3) )()()()()]()(['''x g x f x g x f x g x f +=；

(4) )

()

()()()(])

()([2

'

''

x g x g x f x g x f x g x f -=

，]0)([≠x g

3．复合函数的导数——链式法则

设函数))(()(x g f x h =是和)(x g u =的复合函数，且函数)(x g u =在x 点处可导，

)(u f y =在u 点处可导，则有)())(())](([)('

'''x g x g f x g f x h ==

或

dx

du du dy dx

dy =

（链式法则）

3.6二元函数求偏导

3.6.1二元函数的一阶偏导数

二元函数的偏导数的定义为：设函数),(y x f z =在点),(00y x 的一个邻域有定义，当

y 固定在0y 而x 在0

x 处有增量x ?时，如果极限x

y x f y x x f x ?-?+=→?)

,(),(lim 00000

存

在，则称此极限为函数),(y x f z =在点),(00y x 的对x 的偏导数，记作

)

,(00y x x

z ??，

)

,(00y x x

f ??，),(00y x z x 或),(00y x f x

类似地，函数),(y x f z =在点),(00y x 处对y 的偏导数定义为

y y x f y y x f y ?-?+=

→?)

,(),(lim 00000

记作

)

,(00y x y

z ??，

)

,(00y x y

f ??，),(00y x z y 或),(00y x f y

如果函数),(y x f z =在定义域D 内每一点),(y x 对x 的偏导数都存在，那么这个偏导数是x 、y 的函数，它就称为对x 的偏导数函数。记作

x

z ??，x z ，),(y x f x

类似地，可以定义对自变量y 的偏导数函数，

y

z ??，y z ，),(y x f y

在),(y x f z =求偏导数时，实际上和一元函数求导方法相同，求

x

f ??时，只要把y 看

作常量而对x 求导数；求y

f ??时，只要把x 看作常量而对y 求导数。

3.6.2二元函数高阶偏导数

设函数),(y x f z =在定义域D 内具有偏导数),(y x f x ，),(y x f y ，那么在D 内

),(y x f x ，),(y x f y 都是x 、y 的函数，如果这两个函数的偏导数也存在，则称它们是函

数),(y x f z =的二阶偏导数，按照对变量求导次序的不同有下列四个二阶偏导数：

),(22

y x f x z x z x xx =??=??? ??????， ),(2

y x f y

x z

x z y xy =???=?

?? ?????? ),(2

y x f x y z y z x yx =???=???

? ??????，),(22

y x f y

z y z

y yy =??=???? ??????

类似地，可以定义三阶、四阶以及n 阶偏导数，二阶以上的偏导数称为高阶偏导数，在二阶偏导数计算中引出一个重要定理：

杨格定理 如果函数),(y x f z =的两个二阶混合偏导数

x

y z ???2

，

y

x z ???2

在区域D

内连续，那么自该区域内这两个二阶混合偏导数必相等。

杨格定理说明在求导时不必关心求导的顺序。

3.7多元函数的求导

二元函数偏导数的概念可以推广到多元的情况，定义为： x

x x x x f x x x x x f x x x f f n i n i x n ?-?+==→?)

,,,,,(),,,,,(lim

),,,()(21210

21 x 多元偏导数的计算并不需要引入新的方法。因为在函数中仅有一个自变量在变化，其他各个自变量都是固定的，所以，在计算时只需要将其他自变量看作常量，对变动的自变量运用一元函数求导法则计算即可。

二元函数的杨格定理也可以直接推广到多元函数

如果n 元函数),,,(21n x x x f 对于i x 的一阶偏导数函数是连续的，则有

i

j j

i x x f x x f ???=

???)()(2

2

x x

对于多元函数的求导有一个重要的向量和矩阵，称为梯度向量和海赛（Hessian ）矩阵 定义

n 元函数),,,()(21n x x x f f =x 对于i x 的一阶偏导数构成的n 维列向量称为梯度向

量，记为)(x f ?，即

????

? ??=?)()()(1x x x n f f f ，其中i

i x f f ??=)

()(x x

n 元函数),,,()(21n x x x f f =x 的所有二阶偏导数组成的矩阵称为)(x f 的海赛

（Hessian ）矩阵，记为)(x H ：即

????

?

?

?

??=)()()()

()()

()(1

221111x x x x x x x nn n n n f f f f f f H

其中j

i ij x x f f ???=

)()(x x 2

，

根据杨格定理，ji ij f f =，故)(x H 为对称矩阵。

3.8隐函数

3.8.1 定义

我们将方程0),,,,(21=n x x x y F 确定的函数关系，称为隐函数，既对于任意一组变量),,,(21n x x x =X ，相应地总有满足方程0),,,,(21=n x x x y F 的唯一的y 值存在，那么就称方程0),,,,(21=n x x x y F 确定了一个隐函数1。

1

隐函数不一定能写为y=f(x)的形式，因此按照函数“设x 和y 是两个变量，D 是实数集的某个子集，

把隐函数化成显函数，叫做隐函数的显化。例如将方程

),,,,(21=n x x x y F 解出

)

,,,(21n x x x F y =，就把隐函数化成显函数。要注意的是方程0),(=y x F 能确定隐函

数，一般并不都能从方程中解出y ，并用自变量x 的算式来表示。对于方程

.0s i n 2

1=-

-y x y 可以证明确实存在一个定义在),(+∞-∞上的函数)(x f ，使得,0)(sin 2

1)(≡+

-x f x x f 但这函数)(x f 却无法用x 的算式来表达。

3.8.2隐函数经济问题的应用

在经济问题分析中，需要计算隐函数的导数和偏导数。例如，经济学中的一个内生变量y 和一组外生变量n x x x ,,,21 常满足一个方程

0),,,,(21=n x x x y F

在一定条件（或一定经济背景）下，对某给定区域给定上述变量，由方程

0),,,,(21=n x x x y F 可确定唯一的内生变量y 的值。我们需要研究外生变量

i

x 的变化

如何影响内生变量y 的变化，即需要求内生变量关于外生变量的偏导数x y ??/，用作经济理论的分析。

3.8.3 隐函数定理 3.8.3.1一个方程的情形

隐函数存在惟一性定理 若函数),(y x F 满足下列条件：

（1）函数),(y x F 在以0P ),(00y x 为内点的某一区域2R D ?上连续；

（2）0),(00=y x F （通常称为初始条件）；（iii ）在D 内存在连续的偏导数

()y x F y ,；

（3）()00,y x F y ≠0，则在0P 的某邻域D P U ?)(0内，方程()y x F ,=0惟一地确

定一个定义

则在某区间),(00αα+-x x 内的函数（隐函数）)(x f y =，使得

若对于D 中的每个值x ，变量y 按照一定的法则有一个确定的值y 与之对应，称变量y 为变量x 的函数，记作 y=f(x).”的定义，隐函数不一定是“函数”，而是“方程”。 总的说来，函数都是方程，但方程却不一定是函数。

① ()00y x f =,当),(00αα+-∈x x x 时，)())(,(0P U x f x ∈且()0)(,≡x f x F ； ② ()x f 在),(00αα+-x x 内连续.

例如方程为.0)(),(22222=+-+=y x y x y x F 由于0)0,0(=F ，F

与

y y x y F y 2)(42

2

++=均连续，故满足定理条件(1) (2) (3)．但因0)0,0(=y F ，致使

在原点的无论怎样小的邻域内都不可能存在唯一的隐函数．

隐函数可微性定理

（1）设),(y x F 满足隐函数存在唯一性定理中的条件)3()1(-，又设在D 内还存在连续的偏导数),(y x F y ，则由方程0),(=y x F 所确定的隐函数在)(x f y =在其定义域

),(00αα+-x x 内有连续导函数，且

.)

,(),()('y x F y x F x f dx

dy y x -

==

（2）设三元函数),,(z y x F 满足隐函数存在唯一性定理中的条件)3()1(-，又设在

3

R D ?内还存在连续的偏导数),,(z y x F z ，则由方程0),,(=z y x F 所确定的隐函数在

),(y x f z =在其定义域内有连续偏导函数，且

,

)

,,(),,(z y x F z y x F x

z z x -

=??)

,,(),,(z y x F z y x F y

z z y -

=??

3.8.3.2方程组的情况

我们将隐函数存在定理作另一方面的推广。我们不仅增加方程中变量的个数，而且增加方程的个数。例如，考虑方程组

这时，在四个变量中，一般只能有两个变量独立变化，因此该方程组就有可能确定两个二元函数。在这种情况下，我们可以由函数F 、G 的性质来断定由该方程组所确定的两个二元函数的存在，以及它们的性质，我们有下面的定理。

方程组的隐函数定理 设函数),,,(v u y x F ，),,,(v u y x G 满足下列条件 （1）在点00000(,,,)P x y u v 的某邻域内具有对各个变量的连续偏导数； （2）0),,,(0000=v u y x F ，0),,,(0000=v u y x G ；

（3）函数v u G F ,,对的偏导数所组成的函数行列式(或雅可比行列式)

??

?==0

),,,(0),,,(v u y x G v u y x F

0)

,(),(≠=

??=

v

u

v u G G F F v u G F J ，在点00000(,,,)P x y u v

则方程组0),,,(=v u y x F ，0),,,(=v u y x G 在点0P 的某一邻域内恒能唯一确定一组单值连续且具有连续偏导数的函数),(),,(y x v v y x u u ==，满足条件),(000y x u u =，

),(000y x v v = 并有偏导数公式

),(),(1v x G F J x u ??-

=?? ，

),(),(1x u G F J x v ??-

=??

)

,(),(1v y G F J y

u ??-

=?? ，

)

,(),(1y u G F J x

v ??-

=??

3.8.4 隐函数求导例子

根据以上三个定理，可对隐函数进行求导。 例1 设2sin y e xy x =+，求

dx

dy .

解 设 2s i n ),(y e xy y x F x -+=，因为y xy x F e xy y F y x

x 2cos ,cos -=+= 所以

y

xy x e

xy y F F dx

dy x

y

x 2cos cos -+-

=-

=

例 2设方程0=-yv xu ，1=+xv yu ，求偏导数y

v

x v y u x u ????????,

,,． 解 将所给方程的两边对x 求偏导数并移项，得 ???????-=??+??-=??-??v x u x x

u y u x

u y x u

x

在02

2≠+=-=

y

x x

y

y x F 条件下，

2

2

2

2

y

x yv xu y

x x

v

y u x

u ++-

=+---=??；

2

2

2

2

y

x xv yu y

x v

y

u x

x

v +--

=+--=

??．

同理，方程的两边对y 求偏导数，解方程组得

2

2

y

x yu xv y

u +-=

??，

2

2

y

x yv xu y

v ++-

=??．

例3 假设方程0),,(=L K Q F 隐含地定义了一个生产函数),(L K f Q =，让我们求出表示与函数F 相关的边际物质产品K MPP 和L MPP 的方法。

因为边际产品仅为偏导数

K

Q ??和

L

Q ??,我们可应用隐函数法则并写出：

Q

K K F F K

Q MPP -

=??=

和 Q

L L F F L

Q MPP -=??=

.

此外，我们还可由方程0),,(=L K Q F 得到另一个偏导数 K

L F F L

K -=??.

它的经济含义是：当劳动力L 发生变化时，为了保持产量不变，资本K 的变化。因此，此偏导数所描述的K 和L 的变化实质上是一种“补偿”变化，从而使产出Q 维持在某一特定水平不变，因而这种变化属于沿着等产量曲线上的移动，该等产量曲线以K 为纵轴，L 为横轴绘制。实际上，导数

L

K ??表示等产量线斜率，它在正常情况下为负。而

L

K ??则是两种投入的边际技术替代率。

例4 设?????=+=+x

yu v y

xv u 3

3，求x u ??和x v ??，y u ??和y v ??.

解 令

?????-+=-+=x

yu v v u y x G y

xv u v u y x F 3

3

),,,(),,,( 则xy v u v

y

x u G G F F v u G F J v

u

v u -==

=

??=2

22

2

933)

,(),(

而

x

v v

x v G G F F v x G F v x v x +=-=

=

??3

2

331),(),(vy u y

v u G G F F x u G F x

u

x u --=-=

=??2

2

31

3)

,(),(

xu v v

u x G G F F v y G F v y v y --=-=

=

??2

2

331),(),(

y u u

y

u G G F F y u G F y

u

y u +=-=

=??3

2

313)

,(),(

从而

2

2

3

93),(),(1v

u xy x v v x G F J x u -+=

??-

=??，

2

2

2

93)

,(),(1v u xy vy u x u G F J x

v -+-

=??-

=??

2

2

3

93)

,(),(1v

u xy xu v v y G F J y

u -+-

=??-=??，

2

2

2

93)

,(),(1v

u xy y u y u G F J y

u -+=??-

=??

事实上，对具体题目可以不用该公式计算，而直接用隐函数方程两边同时求偏导解方程组的方法来做。

3.9边际、弹性和增长率

3.6.1 边际（Marginality ）

在经济学研究中许多重要的概念是用导数来描述的，数学上的导数概念对应经济学上的边际概念，利用导数进行经济分析，简称边际分析。经常用到的边际量有边际收入、边际成本、边际产量、边际利润等。

在经济学上对于函数)(x f y =在0x 点的边际定义为：)()1(00x f x f -+，记为

)(0x Mf 边际的数值可以用)(0'x f 近似的代替，虽然一阶导数的概念和边际的概念不

同，但是为了边际计算的简单性，经济学家在计算边际数值时仍然采用一阶导数的数值代替。

例 设某商品的总成本函数为1262)(2

++=Q Q Q C ，求200=Q 时的边际成本

解按照边际的概念求200=Q 时的边际成本为：88)20()21(=-C C

200=Q 时的一阶导数值为：86)20('=C

可见用导数计算出的数值和边际定义计算出的数值不同，但比较接近边际数值。 对于多元函数),,,(21n x x x f y =关于i x 的边际的定义为：

),,,(),1,,,(),,,(212121n n i n x x x f x x x x f x x x Mf -+=，

边际表示在其他变量均不发生改变的情况下，第i 个变量增加一个单位因起函数值的变化。对于多元函边际数值的计算可以用偏导近似代替。如当消费者消费n 种商品时，其效用函数为),,,(21n x x x U U =，如果其中第i 种商品的消费量发生改变，其边际效用为：

i

n n i x x x x U x x x MU ??=

)

,,,(),,,(2121

例3.1 给定生产函数7

.03

.096L

K

Q =，求边际产出K MPP 和L MPP 。

解：对生产函数两边取对数可得：L K Q ln 7.0ln 3.096ln ln ++= 由此可以得到：

7

.0)

(

8.283.0ln ln K L K Q K

d Q d K Q dK dQ MPP K =?

==

=

3

.0)(2.677.0ln ln L

K L Q

L d Q

d L Q dL dQ

MPP L

=?=== 定理 两个函数乘积的弹性等于两个函数弹性的和； 两个函数商的弹性等于两个函数弹性的差；

两个符合函数的弹性等于两个函数弹性的乘积，即

设)(),(x g u u f y ==，则ux yu yx εεε=。

3.6.2弹性(Elasticity)

函数)(x f y =关于0x 的弹性定义为

ln ln x x yx dx

dy y x x

d y d =

=ε，表示当x 由0x 增加一个百分比时，y 的增加或减少的百

分比。

当1

当1>yx ε时，称y 关于x 弹性充足或富有弹性，此时y 变动的百分率大于x 变动的百分率。

当1=yx ε时，称y 关于x 为单位弹性，此时y 变动的百分率等于x 变动的百分率。 n 元函数),,,(21n x x x f y =对i x 的弹性定义为：y

x x y E i i yx i ??=

，由于采用偏导数

来定义故对于多元函数称为偏弹性。

由弹性的定义可以看到，弹性表示自变量x 的变化的百分率引起因变量y 变化的百分率的比值，是无量纲的。

例 3.2 某种商品的需求函数为)(P Q Q =，Q 为该商品的需求量，P 为商品价格，则收益PQ R =。讨论其需求价格弹性。

求其边际收益可以得到：)1(dP

dQ Q P Q dP

dQ P Q dP

dR +=+=

因为它的需求价格弹性为dP

dQ Q P Qp =

ε，且通常情况下，

0

dQ ，因此，代入可

得：

)1(ε-=Q dP

dR 。

当1>ε时，0

0>dP

dR ，此时收益是价格的减函数，如果提高商品价格，能够提高收益。

进一步，根据需求函数)(P Q Q =，取其反函数可以求得价格函数为)(Q P P =，则

)(Q QP R =，其边际收益为：

)11()1(ε-=+

=+==

P dQ

dP P Q P dQ

dP Q

P dQ

dR MR

在经济学中，厂商生产的均衡条件为：MC MR =，从而)11(ε-=P MC ，将其变

形可得：ε

11-=

MC P

这个公式可以作为厂商定价的依据。根据这个公式我们可以发现，在边际成本一定的情况下，需求价格弹性越大价格就越低，需求价格弹性越小价格就越高，因此，垄断企业在具有不同价格弹性的市场，产品的定价不同。

例 3.3 设某个消费者关于n 种商品的需求函数为),,,,(21Y P P P f x n i i =

),,2,1(n i =，其中n P P P ,,,21 分别为n 种商品的价格，Y 为该消费者的收入。求：

(1)第i 种商品的需求价格弹性；(2) 第i 种商品需求关于第j 种商品的价格的交叉价格弹性；(3) 第i 种商品的需求收入弹性。

解：(1) 第i 种商品的需求价格弹性可表示为i

i i i p x x P P x i

i

??=

,ε。

(2) 需求的交叉价格弹性，用来描述一种商品的需求量对另外一种商品价格变化的灵敏度，可表示为i

j j i j

i j

i P x x P P x P x P x j i ??=??=

,ε,(j i ≠)。

则第i 种商品需求关于第j 种商品的价格的交叉价格弹性为i

j j i P x x P P x j

i

??=

,ε, (j i ≠)。

(3) 商品的需求收入弹性表示一种商品的需求量对收入变化的敏感程度。 第i 种商品的需求收入弹性为：i

i Y

x

x Y Y x i

??=,ε

3.6.3 增长率(Growth rate)

设y 是t 的函数且)(t f y =，则在0t 时刻y 的增长率定义为：

'

ln t t t t y y

y dt

y d r ===

=

定理 给定两个可导函数)(t f u =，)(t g v =，用v u r +，v u r -，uv r ，v u r /分别表示两个函数和、差、积、商的增长率，则

（1）v u uv r r r += （2）v u v u r r r -=/ （3）v u v u r v u v r v u u r +++=+ （4）v u v u r v

u v r v

u u r +-

+=

-

例 3.4 若货币需求d M 是国民收入)(t Y Y =及利息率)(t i i =的函数，求证：d M 增长率可以表成Y r 与i r 的加权之和，其中权数分别为d M 对Y 与i 的弹性。

证明：由于))(),((t i t Y f M

d

=，由增长率的定义，应用全导数公式可以得到：

i

i M Y Y M d

d

d

d d

d

d

d

d

M r r dt

di i i

M M

i dt

dY Y Y

M M

Y dt

di i M dt dY Y M M

dt dM M r d d d εε+=?

??+

?

??=

??+

??==

11)

(

11

即d M 的增长率可以表示成Y r 与i r 的加权之和，其权重分别为d M 对Y 与i 的弹性。

3.10水平曲线的分析

（1）边际递减规律

经济学家认为生产函数是增函数，因此0>L f 、0>K f ，又认为投入要素的边际生产率是递减的，就是随着要素投入量的增加，总产量增加，但是边际产量是不断减少的，即0,0<

（2）边际替代率分析

对于生产函数),(K L f y =来讲，水平曲线上点的位置虽不同但是却有相同的产量，如何来解释这一现象呢？如下图所示，从A 点到B 点的移动分为两步，由A 点减少资金量

K ?，保持劳动力L 不变垂直移动到C 点，再由C 点增加劳动力L ?，保持资金量K 不变

移动到B 点，从A 点到C 点产出量y 的改变量为A 点的资金边际产量乘以资金减少量，记作K f K ?，从C 点到B 点产出量y 的改变量为B 点的劳动力边际产量乘以劳动力增加量，记作L f L ?，由于A 点和B 点y 的量并没有改变，因此有

K f y K ?=?+L f L ?0=

当0,0→?→?K L 时，上式就成为全微分形式，0=+dK f dL f K L

即 K

L f f dL

dK -

= 2—1

从几何上来看dL

dK 是水平曲线的斜率，因此可以看出水平曲线的斜率为生产函数的一

阶偏导数之比的负值，因此方程)(L K K =与C L K L f y ==))(,(是等价的，当0

=K f

时，水平曲线变成一条垂线，它的导数不存在。

从经观济学看水平曲线表示如果产量一定，在减少资金K ?的同时要增加劳动力

L ?。劳动与资本之间存在着替代关系，经济学上把

K

L f f 称为劳动力对资本的边际替代

率，因此边际替代率就是等产量曲线斜率的负值，即

dL

dK f f K

L -

=。

等产量曲线的分析

实际上对于任意二元函数),(K L f y =的水平曲线0),(y K L f = (0y 为常数)，由于方程中仅含有两个未知变量。这样，如果可以将其中一个未知变量能表示为另一个未知变量的函数。例如，)(L K K = ，将其带入水平曲线，得0))(,(y L K L f =，式中K 随L 变化而变化。

任何一个水平曲线的斜率都可以表示为导数

dL

dK ，在等式0))(,(y L K L f =两边同时

对L 求导，得到00=??=

??+??L

y dL

dK K f L

f 或0=+dL

dK f f K

L 。注意这里我们把K 看作L

的函数。

我们假设0≠K f ，则有

K

L f f dL

dK -

=。得到和式2—1相同的结果。

在消费者理论中用同样的方法可以分析效用函数),(21x x U U =的水平曲线，在效用

不变的条件下，减少对产品2x 的消费量就要同时增加对产品1x 的消费量，称

2

1U U 为商品

1x 与2x 之间的边际替代率，因此有同样的结论为

1

22

1dx dx U U -

=

（3）水平曲线的凸性分析

曲线的的凸性是说明曲线的形状，从原点观察水平曲线的形状是凸的，如果换个视角观察水平曲线的形状可能是凹的，从数学上来看水平曲线是凸的就是曲线的二阶导数非负，即

当用要素L 代替要素K 时，K 不断减少，L 不断增加，从而K f 不断增加，L f 不断减少。因此，

K

L f f 不断减少，既

0

?

??K L

f f dL d ，这就是边际替代率递减规律。 由于

02

2

≥???

?

??-

=K

L

f f dL d dL

K d 因此，水平曲线的斜率为负且水平曲线的形状是凸的； 下面用偏导数来表示

22

dL

K d

))

(,())(,(L K L f L K L f dL

dK K L -

=

222

1

))](,([))](,([K

K L L K f L K L f dL d f L K L f dL d f dL

K d ??????--=

21K K K L L L K f KdL dK f LdL dL

f f KdL dK f LdL dL f f ????????? ????+??-??? ????+??-=

21K KK KL L LK LL

K f dL dK f f f dL dK f f f ?????

???? ??

+-??? ??+-= 而

fK

f dL

dK L -

=，且KL LK f f =带入上式得：

2222

12K

K KK L LK L LL K f f f f f f f f dL

K d ??

?? ?

?-+-=

(

)

3

2

22

2

12K

KK

L LK K L LL K f f f f f f f f dL

K d -+-=

根据上面的计算我们得到边际替代率递减法则成立的条件

定理 设),(K L f y =

，边际产出0>K f ，则

边际替代率

()

3

2

212K

KK L LK K L LL K K L

f f f f f f f f f f dL d +-=???

? ??

如果(

)

01

232

2≤+-K

KK

L LK K L LL K f f f f f f f f ，则边际替代率是递减的。

3.11齐次函数和欧拉定理

为了有效的研究许多重要经济模型的结构，我们学习一类重要的函数，这类函数称为齐次函数，研究这类函数的兴趣主要来自于对分配理论问题的探讨。边际生产理论的发展得出了这样的结论：生产要素的投入应该依据生产要素的边际产出，即1单位生产要素的边际成本应该等于1单位生产要素对边际产出的贡献。如果用),(21x x f y =表示生产函数，i ω表示第i 种要素的价格，p 表示产品价格，i

i x f f ??=

表示第i 种要素的边际产出，

那么要素的投入应满足如下法则：i i pf ω=。但是，这种分析方法仅仅针对每一种要素的投入。那么对于多种要素的总投入和总产出应当如何分析呢？

数学家欧拉（Euler ）的一个定理，可以用来分析这个问题。这个定理告诉我们：如果生产函数是规模报酬不变的，那么所有要素的支出之和应该等于总产出。即投入1单位的第i 种要素的成本为i i pf =ω，则投入i x 单位的第i 种要素的成本为i i i i x pf x =ω。所以，所有要素的总支出额为：∑∑=i i i i x f p x pf 。

考虑两种生产要素时，规模报酬不变的情况下有：),(212211x x f y x f x f =≡+，因此，有：py x f x f p x pf x pf x x =+=+=+)(221122112211ωω

而规模报酬不变的生产函数意味着，投入的各种要素变化相同的比例，那么产出也会变化相同的比例，即：),,(),,(11n n x x tf tx tx f ≡，这是齐次函数的一个特例。