指数及指数函数知识点

指数函数
(一)整数指数幂
1.整数指数幂概念:
a
n n
a a a a 个???= )(*
∈N n ()010a a =≠ ()1
0,n
n a
a n N a
-*=
≠∈ 2.整数指数幂的运算性质:(1)(),m n m n a a a m n Z +?=∈ (2)()
(),n
m mn a
a m n Z =∈
(3)()()n
n n
ab a b
n Z =?∈
其中m n m n
m n
a a a a
a
--÷=?=, ()1n
n n n n
n a a a b a b b b --??=?=?= ???
.
3.a 的n 次方根的概念 一般地,如果一个数的n 次方等于a (
)*
∈>N
n n ,1,那么这个数叫做a 的n 次方根,
即: 若a x
n
=,则x 叫做a 的n 次方根, ()*
∈>N n n ,1
例如:27的3次方根3273=, 27-的3次方根3273-=-,
32的5次方根2325=, 32-的5次方根2325-=-.
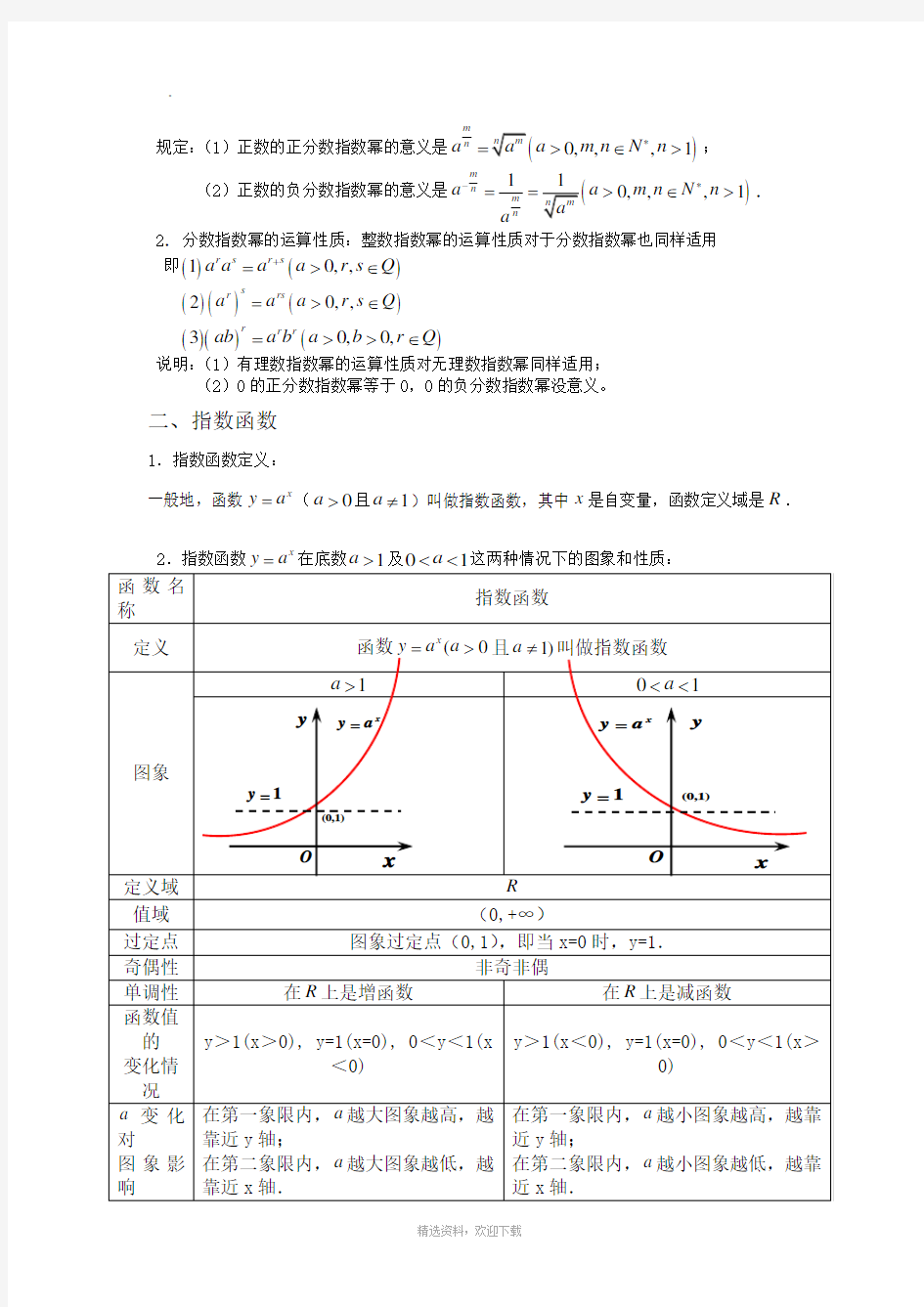
说明:①若n 是奇数,则a 的n 次方根记作n a ; 若0>a 则0>n a ,若o a <则0 ②若n 是偶数,且0>a 则a 的正的n 次方根记作n a ,a 的负的n 次方根,记作: n a -;(例如:8的平方根228±=± 16的4次方根2164±=±) ③若n 是偶数,且0a <则n a 没意义,即负数没有偶次方根; ④( )* ∈>=N n n n ,100 0=; ⑤式子n a 叫根式,n 叫根指数,a 叫被开方数。 ∴ n a =. . 4.a 的n 次方根的性质 一般地,若n 是奇数,则a a n n =; 若n 是偶数,则?? ?<-≥==0 0a a a a a a n n . (二)分数指数幂 1.分数指数幂:()102 5 0a a a ==>()124 3 0a a a ==> 即当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式; 如果幂的运算性质(2)() n k kn a a =对分数指数幂也适用, 例如:若0a >,则3 223233a a a ???== ??? ,4 554544a a a ???== ???, 23a =45a =. 即当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式。 规定:(1 )正数的正分数指数幂的意义是)0,,,1m n a a m n N n *=>∈>; (2 )正数的负分数指数幂的意义是)10,,,1m n m n a a m n N n a -* == >∈>. 2.分数指数幂的运算性质:整数指数幂的运算性质对于分数指数幂也同样适用 即()()10,,r s r s a a a a r s Q +=>∈ ()() ()20,,s r rs a a a r s Q =>∈ ()()()30,0,r r r ab a b a b r Q =>>∈ 说明:(1)有理数指数幂的运算性质对无理数指数幂同样适用; (2)0的正分数指数幂等于0,0的负分数指数幂没意义。 二、指数函数 1.指数函数定义: 一般地,函数x y a =(0a >且1a ≠)叫做指数函数,其中x 是自变量,函数定义域是R . 2.指数函数x y a =在底数 及这两种情况下的图象和性质: 1.1 实数指数幂及其运算(一) (一)选择题 1.下列正确的是( ) A .a 0 =1 B .221a a = - C .10-1 =0.1 D .a a =2 2.4 16的值为( ) A .±2 B .2 C .-2 D .4 3.3 2 )27 125(-的值为( ) A . 9 25 B . 25 9 C .9 25- D .25 9- 4.化简6 5253 5 2 a a a a ??? - 的结果是( ) A .a B .3 2a C .a 2 D .a 3 (二)填空题 5.把下列根式化成分数指数幂的形式(其中a ,b >0) (1)=3 2 1a ______;(2) 3 2a b =______; 6.=-?-÷-3 273223)()4()2(a b a b a b ______. 7.化简=- 3 2 32 9 m m ______. 8.25.031 5 .0625)27 1() 25.0(-+- -=______ (三)解答题 9.计算)4 1(23 2 413 14 1----÷b a b a 10.计算6 3 125.132?? 1.2 实数指数幂及其运算(二) (一)选择题(每道题的四个选择答案中有且只有一个答案是正确的) 1.下列说法正确的是(n ∈N * )( ) A .正数的n 次方根是正数 B .负数的n 次方根是负数 C .0的n 次方根是0 D .n a 是无理数 2.函数3 3 21x x y + =的定义域为( ) A .R B .[0,+∞) C .(0,+∞) D .(-∞,1] 3.5 83 23 1)(- -x x 可以简化为( ) A .3 1 -x B .5 2x C .15 4x D .15 4- x 4.化简 3 8 2313 23 2- --x x x x x x 的结果是( ) A .3 4 x B .x 2 C .x 3 D .x 4 (二)填空题 5.=3 28________,=- 2 1100 ________=-3)4 1 (________=23 25________. 6.=-+- -31 23 2)27 1()21(125________. 7.计算=÷-4325)12525(________. 8.若a +a -1 =3,则a 2 +a -2 =______. (三)解答题 10.若,122-=x a 求x x x x a a a a --++33的值. 1.3 指数函数(一) (一)选择题(每道题的四个选择答案中有且只有一个答案是正确的) 1.一种细胞在分裂时由一个分裂成两个,两个分裂成四个,四个分裂成八个……每天分裂一次.现在将一个该细胞放入一个容器,发现经过10天就可充满整个容器,则当细胞分裂到充满容器一半时需要的天数是( ) A .5 B .9 C .6 D .8 2.下列函数中为指数函数的是( ) A .y =2·3x B .y =-3x C .y =3-x D .y =1x 3.若0.2m =3,则( ) A .m >0 B .m <0 C .m =0 D .以上答案都不对 4.函数f (x )=a x +1(其中a >0且a ≠1)的图象一定经过点( ) A .(0,1) B .(0,2) C .(0,3) D .(1,3) (二)填空题 5.若函数f (x )是指数函数且f (3)=8,则f (x )=______. 6.函数x y 21-=的定义域为______,值域为______. 7.函数y =2x -1的图象一定不经过第______象限;若函数b y x +=)2 1(的图象不经过 第一象限,则实数b 的取值范围是______. 8.若2m >4,则m 的取值范围是______;若(0.1)t >1,则t 的取值范围是______. 9.指数函数y =(a 2-1)x 在R 上是减函数,则实数a 的取值范围是______. (三)解答题 10.根据函数f (x )=2x 的图象,画出下列函数的草图. (1)y =-2x (2)y =-2x +1 (3)y =2|x | 11.求函数1 1 2 2+=x y 的定义域和值域. 12.已知a >0且a ≠1,函数f 1(x )=1 32+x -x a ,f 2(x )=5 22-+x x a ,若f 1(x )<f 2(x ),求x 的取值范围. 1.4 指数函数(二) (一)选择题(每道题的四个选择答案中有且只有一个答案是正确的) 1.若1()273 x >,则x 的取值范围是( ) A .(-∞,-3] B .(-∞,-3) C .[-3,+∞) D .R 2.已知三个数M =0.32-0.32,P =0.32-3.2,Q =3.2-0.32 ,则它们的大小顺序是( ) A .M <P <Q B .Q <M <P C .P <Q <M D .P <M <Q 3.如图是指数函数①y =a x ,②y =b x ,③y =c x ,④y =d x 的图象,则a ,b ,c ,d 与0和1的大小关系是( ) A .0<a <b <1<c <d B .0<b <a <1<d <c C .1<a <b <c <d D .0<a <b <1<d <c 4.函数y =2x -2-x ( ) A .在R 上减函数 B .在R 上是增函数 C .在(-∞,0)上是减函数,在(0,+∞)上是增函数 D .无法判断其单调性 (二)填空题 5.函数y =3x +1-2的图象是由函数y =3x 的图象沿x 轴向______平移______个单位,再沿y 轴向______平移______个单位得到的. 6.函数f (x )=3x +5的值域是______. 7.函数y =a x -1 +1(其中a >0且a ≠1)的图象必经过点______. 8.若指数函数y =a x 在区间[0,1]上的最大值和最小值的差为2 1 ,则底数a =______. 9.函数g (x )=x 2 -x 的单调增区间是______,函数y =x x -22 的单调增区间是______. (三)解答题 10.函数f (x )是R 上的奇函数,且当x ≥0时,f (x )=2x -1,求x <0时函数的解析式. 11.若关于x 的方程|2x -1|=a 有两个解,借助图象求a 的取值范围. 12.已知函数f (x )=22x -2x +1 -3,其中x ∈[0,1],求f (x )的值域. Welcome !!! 欢迎您的下载,资料仅供参考! 指数函数 (一)整数指数幂 1.整数指数幂概念: a n n a a a a 个???=)(* ∈N n ()010a a =≠ ()1 0,n n a a n N a -*= ≠∈ 2.整数指数幂的运算性质:(1)(),m n m n a a a m n Z +?=∈ (2)() (),n m mn a a m n Z =∈ (3)()()n n n ab a b n Z =?∈ 其中m n m n m n a a a a a --÷=?=, ()1n n n n n n a a a b a b b b --??=?=?= ??? . 3.a 的n 次方根的概念 一般地,如果一个数的n 次方等于a ( )* ∈>N n n ,1,那么这个数叫做a 的n 次方根, 即: 若a x n =,则x 叫做a 的n 次方根,()* ∈>N n n ,1 例如:27的3次方根3273=, 27-的3次方根3273-=-, 32的5次方根2325=, 32-的5次方根2325-=-. 说明:①若n 是奇数,则a 的n 次方根记作n a ; 若0>a 则0>n a ,若o a <则0 课时4指数函数 一. 指数与指数幂的运算 (1)根式的概念 ①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n n 是偶数时,正数a 的正的n n 次方 根用符号表示;0的n 次方根是0;负数a 没有n 次方根. n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥. ③根式的性质:n a =;当n 为奇数时, a =;当n 为偶数时, (0) || (0) a a a a a ≥?==? -∈且1)n >.0的正分数指数幂等 于0.②正数的负分数指数幂的意义是: 1()0,,,m m n n a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质 ① (0,,) r s r s a a a a r s R +?=>∈ ② ()(0,,) r s rs a a a r s R =>∈ ③ ()(0,0,)r r r ab a b a b r R =>>∈ 二.指数函数及其性质(4)指数函数 三.例题分析 1.设a 、b 满足0 一、指数的性质 (一)整数指数幂 1.整数指数幂概念: a n n a a a a 个???= )(* ∈N n ()010a a =≠ ()1 0,n n a a n N a -*= ≠∈ 2.整数指数幂的运算性质:(1)(),m n m n a a a m n Z +?=∈ (2)()(),n m mn a a m n Z =∈ (3)()()n n n ab a b n Z =?∈ 其中m n m n m n a a a a a --÷=?=, ()1n n n n n n a a a b a b b b --??=?=?= ??? . 3.a 的n 次方根的概念 一般地,如果一个数的n 次方等于a ( )* ∈>N n n ,1,那么这个数叫做a 的n 次方根, 即: 若a x n =,则x 叫做a 的n 次方根, ()* ∈>N n n ,1 例如:27的3次方根3273=, 27-的3次方根3273-=-, 32的5次方根2325=, 32-的5次方根2325-=-. 说明:①若n 是奇数,则a 的n 次方根记作n a ; 若0>a 则0>n a ,若o a <则0 ⑤式子n a 叫根式,n 叫根指数,a 叫被开方数。 ∴ n a =. . 4.a 的n 次方根的性质 一般地,若n 是奇数,则a a n n =; 若n 是偶数,则?? ?<-≥==0 0a a a a a a n n . 5.例题分析: 例1.求下列各式的值: (1)() 338- (2) ()210- (3)()44 3π- (4) ()()b a b a >-2解:略。 例2.已知,0<N n n ,1, 化简:()()n n n n b a b a ++-. 解:当n 是奇数时,原式a b a b a 2)()(=++-= 当n 是偶数时,原式a b a a b b a b a 2)()(||||-=--+-=++-= 所以,()()n n n n b a b a ++-22a n a n ?=? -?为奇数 为偶数 . 例3.计算:407407-++ 解:407407-++52)25()25(22=-++= 例4.求值: 54 925-+. 解:549 25-+4 25254 5 49252 )(-+=-+= 452622525+=-+= 2 1 54152 += +=)( (二)分数指数幂 1.分数指数幂: ()10 2 5 0a a a ==> ()124 3 0a a a ==> 即当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式; 如果幂的运算性质(2)() n k kn a a =对分数指数幂也适用, 例如:若0a >,则3 223233a a a ???== ??? ,4 554544a a a ???== ???, 23a = 4 5 a =. 即当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式。 规定:(1)正数的正分数指数幂的意义是)0,,,1m n a a m n N n *=>∈>; (2)正数的负分数指数幂的意义是)10,,,1m n m n a a m n N n a -* == >∈>. 2.分数指数幂的运算性质:整数指数幂的运算性质对于分数指数幂也同样适用 指数函数与对数函数知识点总结 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次 方根,其中n >1,且n ∈N * . 当n 是奇数时, a a n n =,当n 是偶数时, ?? ?<≥-==) 0() 0(||a a a a a a n n 2.分数指数幂 正数的分数指数幂的意义,规定: ) 1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(1 1*>∈>= = - n N n m a a a a n m n m n m 3.实数指数幂的运算性质 (1)r a ·s r r a a += ),,0(R s r a ∈>; (2)rs s r a a =)( ),,0(R s r a ∈>; (3)s r r a a ab =)( ),,0(R s r a ∈>. (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自变量,函数的定义域为R . 二、对数函数 (一)对数 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 叫做以.a 为底..N 的对数, 记作:N x a log =(a — 底数,N — 真数,N a log — 对数式) 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数 71828.2=e 为底的对数的对数N ln . 指数式与对数式的互化 幂值 真数 (二)对数的运算性质 如果0>a ,且1≠a ,0>M ,0>N ,那么: ○ 1 M a (log ·=)N M a log +N a log ; ○ 2 =N M a log M a log -N a log ; ○ 3 n a M log n =M a log )(R n ∈. 注意:换底公式 a b b c c a log log log = (0>a ,且1≠a ;0>c ,且1≠c ; 0>b ). 利用换底公式推导下面的结论 (1)b m n b a n a m log log =; (2)a b b a log 1log =. (二)对数函数 指数函数知识总结 (一)指数与指数幂的运算 1.根式的概念: 一般地,如果a x n =,那么x 叫做a 的n 次方根,其中n >1,且n ∈N * . ①负数没有偶次方根;②0的任何次方根都是0,记作00=n 。 ③当n 是奇数时,a a n n =, 当n 是偶数时,???<≥-==) 0() 0(||a a a a a a n n 2.分数指数幂 正数的分数指数幂的意义,规定: ) 1,,,0()1(*>∈>=n N n m a a a n m n m )1,,,0(1 1)2(*>∈>= = - n N n m a a a a n m n m n m (3)0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)r a ·s r r a a += ),,0(R s r a ∈>; (2)rs s r a a =)( ),,0(R s r a ∈>; (3) s r r a a ab =)( ),,0(R s r a ∈>. 题型一、计算 1.44 等于( ) A 、16a B 、8a C 、4a D 、2 a 2.⑴ 33 )2(-= ⑵ 44 )2(-= ⑶ 66)3(π-= ⑷ 2 22y xy x ++= 3.① 625625++- ② 335252-++ 4.计算(1 + 2048 21)(1 + 1024 21)…(1 + 421)(1 + 2 21)(1 + 21 ). 5. 计算(0.0081)4 1-- [3×(87)0]1-·[8125 .0-+(38 3)31-]21 -. 题型二、化简 1. 3 2 13 2b a b a ?- ÷3 2 11- --??? ? ? ?a b b a 2. 322a a a ?(a >0). 3.化简: 3 32 b a a b b a (a >0,b >0). 题型三、带附加条件的求值问题 1. 已知a 2 1+ a 2 1-= 3,求下列各式的值: ⑴ a + a 1 - ⑵ a 2+ a 2 - ⑶ 2 12 1232 3- - --a a a a 2. 已知2a x x =+-2(常数),求8x x -+8的值。 3. 已知x + y = 12, xy = 9,且x <y ,求 2 12 1 212 1y x y x +-的值。 4.已知a 、b 是方程x 2 - 6x + 4 = 0的两根,且a >b >0,求b a b a +-的值。 指数函数 【知识点梳理】 要点一、指数函数的概念: 函数y=ax(a>0且a ≠1)叫做指数函数,其中x 是自变量,a 为常数,函数定义域为R. 要点诠释: (1)形式上的严格性:只有形如y=a x (a>0且a ≠1)的函数才是指数函数.像23x y =?, 1 2x y =,31x y =+等函数都不是指数函数. (2)为什么规定底数a 大于零且不等于1: ①如果0a =,则000x x ?>??≤??x x 时,a 恒等于, 时,a 无意义. ②如果0a <,则对于一些函数,比如(4)x y =-,当11 ,,24 x x ==???时,在实数范围 内函数值不存在. ③如果1a =,则11x y ==是个常量,就没研究的必要了. 要点二、指数函数的图象及性质: 要点诠释: (1)当底数大小不定时,必须分“1a >”和“01a <<”两种情形讨论。 (2)当01a <<时,,0x y →+∞→;当1a >时,0x y →-∞→。 当1a >时,a 的值越大,图象越靠近y 轴,递增速度越快。 当01a <<时,a 的值越小,图象越靠近y 轴,递减的速度越快。 (3)指数函数x y a =与1x y a ?? = ??? 的图象关于y 轴对称。 要点三、指数函数底数变化与图像分布规律 (1)①x y a = ②x y b = ③x y c = ④x y d = 则:0<b <a <1<d <c 又即:x ∈(0,+∞)时,x x x x b a d c <<< (底大幂大) x ∈(-∞,0)时,x x x x b a d c >>> (2)特殊函数 11 2, 3, (), ()2 3 x x x x y y y y ====的图像: 要点四、指数式大小比较方法 (1)单调性法:化为同底数指数式,利用指数函数的单调性进行比较. (2)中间量法 (3)分类讨论法 (4)比较法 比较法有作差比较与作商比较两种,其原理分别为: ①若0A B A B ->?>;0A B A B -,或1A B <即可 指数函数与对数函数总结与练习 一、指数的性质 (一)整数指数幂 1.整数指数幂概念: a n n a a a a 个???= )(* ∈N n ()010a a =≠ ()1 0,n n a a n N a -*= ≠∈ 2.整数指数幂的运算性质:(1)(),m n m n a a a m n Z +?=∈ (2)() (),n m mn a a m n Z =∈ (3)()()n n n ab a b n Z =?∈ 其中m n m n m n a a a a a --÷=?=, ()1n n n n n n a a a b a b b b --??=?=?= ??? . 3.a 的n 次方根的概念 一般地,如果一个数的n 次方等于a ( )* ∈>N n n ,1,那么这个数叫做a 的n 次方根, 即: 若a x n =,则x 叫做a 的n 次方根, ()* ∈>N n n ,1 说明:①若n 是奇数,则a 的n 次方根记作n a ; 若0>a 则0>n a ,若o a <则0 (一)整数指数幂 1.整数指数幂概念: 43 421Λa n n a a a a 个???= )(* ∈N n ()0 10a a =≠ ()10,n n a a n N a -* = ≠∈ 2.整数指数幂的运算性质:(1)(),m n m n a a a m n Z +?=∈ (2)() (),n m mn a a m n Z =∈ (3)()()n n n ab a b n Z =?∈ 其中m n m n m n a a a a a --÷=?=, ()1n n n n n n a a a b a b b b --??=?=?= ??? . 3.a 的n 次方根的概念 一般地,如果一个数的n 次方等于a ( )* ∈>N n n ,1,那么这个数叫做a 的n 次方根, 即: 若a x n =,则x 叫做a 的n 次方根, ()* ∈>N n n ,1 例如:27的3次方根3273=, 27-的3次方根3273-=-, 32的5次方根2325=, 32-的5次方根2325-=-. 说明:①若n 是奇数,则a 的n 次方根记作n a ; 若0>a 则0>n a ,若o a <则0 指数函数 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次方根,其中n >1,且n ∈N * . 负数没有偶次方根;0的任何次方根都是0,记作00=n 。 当n 是奇数时,a a n n =,当n 是偶数时,???<≥-==) 0() 0(||a a a a a a n n 2.分数指数幂 正数的分数指数幂的意义,规定: ) 1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(1 1*>∈>= = - n N n m a a a a n m n m n m 0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)r a ·s r r a a += ),,0(R s r a ∈>; (2)rs s r a a =)( ),,0(R s r a ∈>; (3) s r r a a ab =)( ),,0(R s r a ∈>. (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函 数,其中x 是自变量,函数的定义域为R . 注意:指数函数的底数的取值范围,底数不能是负数、零和1. 2 注意:利用函数的单调性,结合图象还可以看出: (1)在[a ,b]上,)1a 0a (a )x (f x ≠>=且值域是)]b (f ),a (f [或)]a (f ),b (f [ (2)若0x ≠,则1)x (f ≠;)x (f 取遍所有正数当且仅当R x ∈; (3)对于指数函数)1a 0a (a )x (f x ≠>=且,总有a )1(f =; 指数函数·例题解析 一、幂函数 1、幂的有关概念 正整数指数幂: ...() n n a a a a n N =∈ g123 零指数幂: 01(0) a a =≠ 负整数指数幂: 1 (0,) p p a a p N a -=≠∈ 分数指数幂:正分数指数幂的意义是: (0,,,1) m n m n a a a m n N n =>∈> 且 负分数指数幂的意义是: 1 (0,,,1) m n m n m n a a m n N n a a - ==>∈> 且 2、幂函数的定义 一般地,函数 a y x =叫做幂函数,其中x是自变量,a是常数(我们只讨论a是有理数的情况). 3、幂函数的图象 幂函数a y x = 当 11 ,,1,2,3 32 a= 时的图象见左图;当 1 2,1, 2 a=--- 时的图象见上图: 由图象可知,对于幂函数而言,它们都具有下列性质: a y x =有下列性质: (1)0a >时: ①图象都通过点(0,0),(1,1); ②在第一象限内,函数值随x 的增大而增大,即在(0,)+∞上是增函数. (2)0a <时: ①图象都通过点(1,1); ②在第一象限内,函数值随x 的增大而减小,即在(0,)+∞上是减函数; ③在第一象限内,图象向上与y 轴无限地接近,向右与x 轴无限地接近. (3)任何幂函数的图象与坐标轴至多只有一个交点; (4)任何幂函数图象都不经过第四象限; (5)任何两个幂函数的图象最多有三个交点. 二、指数函数 ①定义:函数)1,0(≠>=a a a y x 且称指数函数, 1)函数的定义域为R ; 2)函数的值域为),0(+∞; 3)当10<a 时函数为增函数. 4)有两个特殊点:零点(0,1),不变点(1,)a . 5)抽象性质: ()()(),()()/()f x y f x f y f x y f x f y +=?-= 三、对数函数 如果b a N =(0a >,1a ≠),那么b 叫做以a 为底N 的对数,记作log a N b = log b a a N N b =?=(0a >,1a ≠,0N >). 1.对数的性质 ()log log log a a a MN M N =+. log log log a a a M M N N =-. 指 数函数 2.1.1指数与指数幂的运算 (1)根式的概念 ①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 次 当n 是偶数时,正数a 的正的n 负的n 次方根用符号表示;0的n 次方根是0;负数a 没有n 次方根. n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数 时,0a ≥. n a =;当n a =;当n (0) || (0) a a a a a ≥?==? -∈且1)n >.0的正分数指数幂等于0.② 正数的负分数指数幂的意义是: 1()0,,,m m n n a a m n N a -+==>∈且1)n >.0 的负分数指 数幂没有意义. 注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质 ① (0,,) r s r s a a a a r s R +?=>∈ ② ()(0,,) r s rs a a a r s R =>∈ ③ ()(0,0,)r r r ab a b a b r R =>>∈ 2.1.2指数函数及其性质 2.1指数函数练习 1.下列各式中成立的一项 ( ) A .71 7 7)(m n m n = B .31243)3(-=- C .4 3433)(y x y x +=+ D . 33 39= 2.化简)3 1 ()3)((65 61 3 12 12 13 2b a b a b a ÷-的结果 ( ) A .a 6 B .a - C .a 9- D .2 9a 3.设指数函数)1,0()(≠>=a a a x f x ,则下列等式中不正确的是 ( ) A .f (x +y )=f(x )·f (y ) B .) () (y f x f y x f =-) ( C .)()] ([)(Q n x f nx f n ∈= D .)()]([· )]([)(+∈=N n y f x f xy f n n n 4.函数2 10 ) 2()5(--+-=x x y ( ) A .}2,5|{≠≠x x x B .}2|{>x x C .}5|{>x x D .}552|{>< 指数函数知识点汇总 ————————————————————————————————作者:————————————————————————————————日期:指数与指数函数知识点
高一数学上册指数函数知识点及练习题含答案
《指数函数和对数函数》知识点汇总及习题详解)
指数函数与对数函数知识点总结
指数函数知识点总结
必修一指数函数各种题型大全最新版
指数函数及对数函数复习(有详细知识点及习题详细讲解)
指数及指数函数知识点
指数函数知识点总结
指数函数、对数函数和幂函数知识点归纳
高一数学指数函数知识点及练习题含答案)
指数函数知识点汇总
