高中数学专题——立体几何专题.docx

专题三立体几何专题

【命题趋向】高考对空间想象能力的考查集中体现在立体几何试题上，着重考查空间

点、线、面的位置关系的判断及空间角等几何量的计算．既有以选择题、填空题形式出现的试

题，也有以解答题形式出现的试题．选择题、填空题大多考查概念辨析、位置关系探究、空间

几何量的简单计算求解，考查画图、识图、用图的能力；解答题一般以简单几何体为载体，考

查直线与直线、直线与平面、平面与平面的位置关系，以及空间几何量的求解问题，综合考查

空间想象能力、推理论证能力和运算求解能力．试题在突出对空间想象能力考查的

同时，关注对平行、垂直关系的探究，关注对条件或结论不完备情形下的开放性问题的探究．【考点透析】立体几何主要考点是柱、锥、台、球及其简单组合体的结构特征、三视

图、直观图，表面积体积的计算，空间点、直线、平面的位置关系判断与证明，（理科）空间向量在平行、垂直关系证明中的应用，空间向量在计算空间角中的应用等．

【例题解析】

题型 1 空间几何体的三视图以及面积和体积计算

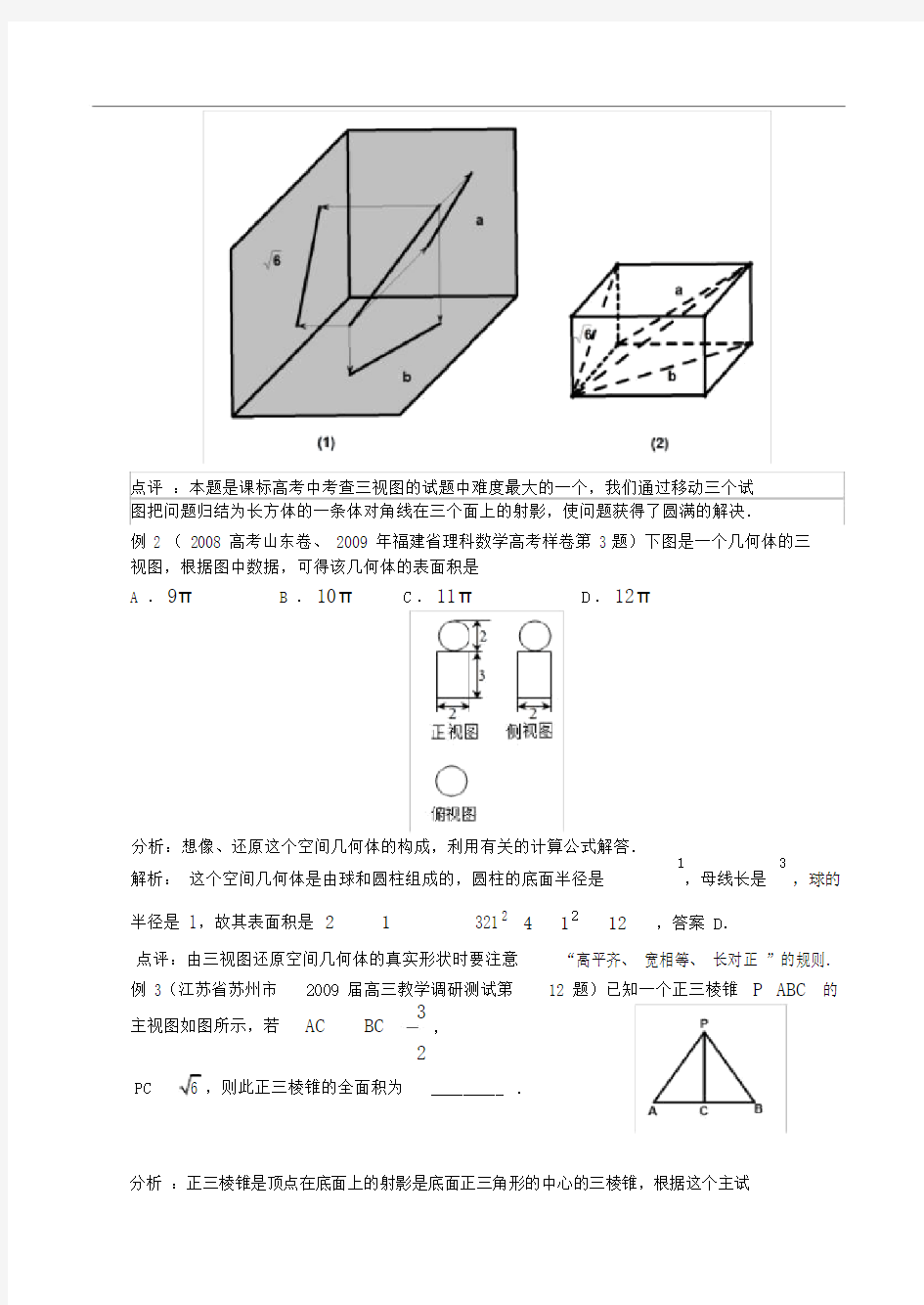
例 1（ 2008 高考海南宁夏卷）某几何体的一条棱长为7 ，在该几何体的正视图中，这条棱的投影是长为 6 的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是

长为 a 和b的线段，则a b 的最大值为

A．22B．23C． 4D．25

分析：想像投影方式，将问题归结到一个具体的空间几何体中解决．

解析：结合长方体的对角线在三个面的投影来理解计算，如图设长方体的高宽高分别为

m, n, k ，由题意得m2n2k27 ，m2k26n 1 ，

1 k

2 a ， 1m2 b ，所以( a21)(b21)6

a2b28，∴ (a b)2a22ab b282ab8 a2b216 a b 4当且仅当 a b 2时取等号．

点评 ：本题是课标高考中考查三视图的试题中难度最大的一个，我们通过移动三个试图把问题归结为长方体的一条体对角线在三个面上的射影，使问题获得了圆满的解决．

例 2 （ 2008 高考山东卷、 2009 年福建省理科数学高考样卷第 3 题）下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是 A ． 9π

B ． 10π

C ． 11π

D ． 12π

分析：想像、还原这个空间几何体的构成，利用有关的计算公式解答． 解析： 这个空间几何体是由球和圆柱组成的，圆柱的底面半径是 1 3

，球的

，母线长是 半径是 1，故其表面积是 2

1

3212 4 12

12

，答案 D ．

点评：由三视图还原空间几何体的真实形状时要注意 “高平齐、 宽相等、 长对正 ”的规则．

例 3（江苏省苏州市 2009 届高三教学调研测试第

12 题）已知一个正三棱锥 P

ABC 的

主视图如图所示，若

AC

BC

3

，

2

PC 6 ，则此正三棱锥的全面积为 _________ ．

分析 ：正三棱锥是顶点在底面上的射影是底面正三角形的中心的三棱锥，根据这个主试

图知道，主试图的投影方向是面对着这个正三棱锥的一条侧棱，并且和底面三角形的一

条边垂直，这样就知道了这个三棱锥的各个棱长．

解析：这个正三棱锥的底面边长是3、高是 6 ，故底面正三角形的中心到一个顶点的

距离是2

33 3 ，故这个正三棱锥的侧棱长是22 3 ，由此知道这个

36

32

正三棱锥的侧面也是边长为 3 的正三角形，故其全面积是43329 3，答案9 3 ．

4

点评：由空间几何体的一个视图再加上其他条件下给出的问题，对给出的这“一个视图”要仔细辨别投影方向，这是三视图问题的核心．

题型 2 空间点、线、面位置关系的判断

42009

届高三教学调研测试7m,n

是两条不同的直线，,为

例（江苏苏州市）已知

两个不同的平面，有下列四个命题：

①若 m, n， m n ，则；

②若 m //, n //, m n ，则//；

③若 m,n //, m n ，则//；

④若 m,n //, //，则m n ．

其中正确的命题是（填上所有正确命题的序号）_______________ ．

分析：根据空间线面位置关系的判定定理和性质定理逐个作出判断．

解析：我们借助于长方体模型解决．①中过直线m,n 作平面，可以得到平面,所成的二面角为直二面角，如图（1），故①正确；②的反例如图（2）；③的反例如图（ 3）；④中由m,P可得m，过n 作平面可得n 与交线g 平行，由于m g ，故m n．答案①④．

点评：新课标的教材对立体几何处理的基本出发点之一就是使用长方体模型，本题就

是通过这个模型中提供的空间线面位置关系解决的，在解答立体几何的选择题、填空题

时合理地使用这个模型是很有帮助的．

例 5（浙江省2009 年高考省教研室第一次抽样测试理科第 5 题）设m, n是两条不同的直线，,是两个不同的平面，下列命题正确的是

A ．若m n, m, n //，则C．若m, n // , //，则

//B．若

m n D．若

m // , n // , // , 则m // n m //

n,m // , n // , 则 //

分析：借助模型、根据线面位置关系的有关定理逐个进行分析判断．

解析：对于//，结合 m, n // , 则可推得m n．答案C．

点评：从上面几个例子可以看出，这类空间线面位置关系的判断类试题虽然形式上各异，

但本质上都是以空间想象、空间线面位置关系的判定和性质定理为目标设计的，主要是

考查考生的空间想象能力和对线面位置关系的判定和性质定理掌握的程度．

题型 3 空间平行与垂直关系的证明、空间几何体的有关计算（文科解答题的主要题型）

例 6．(2009江苏泰州期末 16)如图所示，在棱长为2的正方体ABCD A1B1C1D1中，E、F 分别为DD1、 DB 的

中点．

（ 1）求证：EF //平面ABC1D1；

（ 2）求证：EF B1C ；

（ 3）求三棱锥V B1EFC 的体积．

分析：第一问就是找平行线，最明显的就是EF PBD1；第二问转化为线面垂直进行证明；第三问采用三棱锥的等积变换解决．

解析：（ 1）连结BD1，如图，在DD1B 中，

E 、

F 分别为 D1D ， DB 的中点，则

EF / /D1B

D1 B平面ABC1D1EF / / 平面ABC1D1．

EF 平面 ABC1D1

（2）

B 1

C AB

B 1

C BC 1

B 1

C 平面 ABC 1

D 1 B 1C BD 1

EF

B 1C

AB,B 1C

平面 ABC 1D 1

BD 1

平面 ABC 1D 1

EF / /BD 1

AB I BC 1

B

（ 3）Q CF

平面

BDD 1B 1 ，

CF 平面 EFB 1 且 CF BF

2 ，

Q EF

1

BD 1

3，B 1F

BF 2

BB 12

( 2)2 22

6 ，

2

B 1E

B 1 D 12 D 1E 2 12 (2 2)2

3 ∴ EF 2

B 1F 2 B 1E 2

即 EFB 1

90o ，

V B

EFC

V C B EF

1 S B EF CF = 1

1

EF B 1F CF = 1 1

36

2 1

1

1

3 1

3 2

3 2

．

点评 ：这个题目也属于文科解答题的传统题型．空间线面位置关系证明的基本思想是转化，根据线面平行、垂直关系的判定和性质，进行相互之间的转化，如本题第二问是证明线线垂直，但问题不能只局限在线上，要把相关的线归结到某个平面上（或是把与这些线平行的直线归结到某个平面上，通过证明线面的垂直达到证明线线垂直的目的，但证明线面垂直又得借助于线线垂直，在不断的相互转化中达到最终目的．立体几何中的

三棱柱类似于平面几何中的三角形，可以通过 “换顶点 ”实行等体积变换，这也是求点面距离的基本方法之一．

例 7．（江苏省苏州市 2009 届高三教学调研测试第 17 题） 在四棱锥 P ABCD 中，

ABC

ACD

90o ， BAC

CAD

60o ， PA 平面 ABCD ， E 为 PD 的中

点， PA

2AB 2．

（ 1）求四棱锥 P ABCD 的体积 V ；

（ 2）若 F 为 PC 的中点，求证 PC 平面 AEF ； （ 3）求证 CE ∥平面 PAB ．

分析 ：第一问只要求出底面积和高即可；第二问的线面垂直通过线线垂直进行证明；第三问的线面平行即可以通过证明线线平行、利用线面平行的判定定理解决，也可以通过

证明面面平行解决，即通过证明直线CE 所在的一个平面和平面PAB 的平行解决．解析：（ 1）在Rt ABC中， AB1, BAC60o，∴BC3，AC 2．

在 Rt ACD 中，AC2, ACD60o，∴ CD 2 3,AD4．

∴ S

11

AC CD

115

3 ．

AB BC 1 3 2 2 3

ABCD22222

则 V15 3 25

3 ．

323

（ 2）∵PA CA ， F 为 PC 的中点，∴ AF PC ．

∵ PA平面 ABCD ，∴ PA CD ，∵ AC CD ， PAI AC A，∴ CD平面PAC ，∴ CD PC ．

∵ E为PD中点， F 为PC中点，∴ EF ∥CD ，则 EF CD，∵ AFI EF F ，∴PC 平面 AEF ．

（ 3）证法一：

取 AD中点 M ，连EM,CM．则 EM ∥ PA，∵ EM平面PAB，PA平面

PAB ，

∴EM ∥平面 PAB ．

在 Rt ACD 中，CAD 60o，AC AM 2 ，∴ACM 60o．而BAC60o，∴MC ∥ AB．

∵ MC平面PAB，AB平面PAB，

∴MC ∥平面 PAB ．

∵EMI MC M ，∴平面 EMC ∥平面 PAB ．

∵ EC平面 EMC ，∴ EC ∥平面 PAB ．

证法二：延长DC , AB ，设它们交于点N，

连PN．∵NAC DAC60o，AC CD ，

∴ C为 ND的中点．∵E为PD中点，∴ EC∥PN．

∵ EC平面 PAB ， PN平面 PAB ，

∴EC ∥平面 PAB ．

点评：新课标高考对文科的立体几何与大纲的高考有了

诸多的变化．一个方面增加了空间几何体的三视图、表

面积和体积计算，拓展了命题空间；另一方面删除了三

垂线定理、删除了凸多面体的概念、正多面体的概念

与性质、球的性质与球面距离，删除了空间向量，这就给立体几何的试题加了诸多的枷锁，

由于这个原因课标高考文科的立体几何解答题一般就是空间几何体的体积和表面积

的计算、空间线面位置关系的证明（主要是平行与垂直）．

题型 4 空间向量在立体几何中的应用（理科立体几何解答题的主要题型）

例8 ．（ 2009 年福建省理科数学高考样卷第18 题）如图，在棱长为 2 的正方体ABCD A1B1C1D1中，E、F分别为 A1D1和 CC1的中点．

（1）求证：EF∥平面ACD1；

（2）求异面直线EF与AB所成的角的余弦值；

（3）在棱BB1上是否存在一点P，使得二面角P AC P的大小为30o ?若存在，求出BP 的长；若不存在，请说明理由．

【解析】解法一：如图分别以DA, DC , DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D xyz ，

由已知得D 0,0,0、A 2,0,0 、 B 2,2,0、 C 0,2,0、 B1 2,2,2、D10,0,2E 1,0,2、、 F0,2,1．

（ 1）取AD1中点G，则G 1,0,1，

uuur uuur

1,2, 1 ，

CG1, 2,1 ，又 EF

uuur uuur

由 EF CG ，

uuur uuur

∴ EF 与CG共线．从而EF∥CG，

∵ CG平面 ACD1，EF平面 ACD1，∴EF∥平面 ACD1．

uuur

0,2,0 （ 2）∵ AB

，

uuur uuur

uuur uuur 4 6

cos

EF AB

，

EF, AB

uuur

uuur

2 6

3

|EF | |AB|

∴异面直线 EF 与 AB 所成角的余弦值为

6 ．

3

（ 3）假设满足条件的点

P 存在，可设点 P 2,2, t （ 0 t

2 ），平面 ACP 的一个法向

r

x, y, z 量为 n

，

r uuur uuur

uuur

2x 2y 0, n

AC 0, 0,2, t

2,2,0 则 r

uuur

0. ∵ AP AC ，∴ 2 y tz

0,

n AP

r

(1,1, 2

取 n

) ．

t

uuur

易知平面 ABC 的一个法向量

BB 1 (0,0,2) ，

uuur r 30o 或 150o ， 依题意知，

BB 1, n

uuur uur

| 4 |

3

4 3 4

6

∴ cos BB 1 , N

t

4

2

，即

t 2 (2

2 ) ，解得 t

.

2

4

t

3

2

t 2

∵

6 (0, 2] ，∴在棱 BB 1 上存在一点 P ，当 BP 的长为 6 时，二面角 P AC B 的

3 3

大小为 30o ．

解法二：

uuur

uuuur uuur

（1）同解法一知 EF

1,2, 1 ， AD 1 2,0,2 ，

AC

2,2,0 ，

uuur uuur 1 uuuur uuur uuur uuuur 共面．又∵ EF

平面 ACD 1 ，∴ EF ∥

∴ EF AC AD 1 ，∴ EF 、 AC 、 AD 1 2

平面 ACD 1 ．

（ 2）、（ 3）同解法一．

uuuur uuur

解法三：易知平面 ACD1的一个法向量是 DB12,2,2 ．又∵ EF1,2, 1 ，由

uuur uuuur

EF DB10 ·，

uuur uuuur

平面 ACD 1，∴EF∥平面 ACD1．

∴ EF DB ，而 EF

1

（ 2）、（ 3）同解法一．

点评：本题主要考查直线与直线、直线与平面的位置关系、二面角的概念等基础知识；

考查空间想像能力、推理论证能力和探索问题、解决问题的能力．利用空间向量证明线

面平行的方法基本上就是本题给出的三种，一是证明直线的方向向量和平面内的一条直

线的方向向量共线，二是证明直线的方向向量和平面内的两个不共线的向量共面、根据

共面向量定理作出结论；三是证明直线的方向向量与平面的一个法向量垂直．

例 9（浙江宁波市2008 学年度第一学期期末理科第20 题）已知几何体A BCED 的三视图如图所示，其中俯视图和侧视图都是腰长为 4 的等腰直角三角形，正视图为直角梯形．

（1）求异面直线DE与AB所成角的余弦值；

（2）求二面角A ED B的正弦值；

（3）求此几何体的体积V的大小．

【解析】（ 1）取EC的中点是 F ，连结 BF ，则BF PDE，∴FBA 或其补角即为异面直线DE与AB所成的角．在BAF中，AB 4 2，

BF AF

2 5 ．∴ cos ABF

10 ．

5

∴异面直线 DE 与 AB 所成的角的余弦值为

10 ．

5

（2） AC 平面 BCE ，过C 作CG DE 交 DE 于G ，连结 AG ．

可得 DE 平面 ACG ，从而 AG DE ,

∴ AGC 为二面角 A ED B 的平面角．

在 Rt

ACG 中， ACG 90o ， AC

4 ，

CG

8 5

AGC

5

,∴ tan

．

5

2

∴ sin 5 ．

AGC

3

∴二面角 A ED

B 的的正弦值为

5 ．

3

（3）V

1

S BCED AC 16 ，∴几何体的体积 V 为16．

3

方法二：（坐标法）（1）以 C 为原点，

以 CA,CB, CE 所在直线为 x, y, z 轴建立空间直角坐标系．

则 A 4,0,0 ， B(0,4,0) ， D (0,4,2) ， E 0,0,4

，

uuur

(0, uuur

4, 4,0) ， DE

4,2), AB (

∴ cos

uuur uuur 10 DE,AB

5

∴异面直线 DE 与 AB 所成的角的余弦值为

10 ．

5

uuur (4,0,0)

（ 2）平面 BDE 的一个法向量为 CA ，

r

设平面 ADE 的一个法向量为 n (x, y, z) ，

r uuur r uuur uuur uuur

4,2) n AD , n DE , AD( 4,4, 2), DE (0,

r uuur r uuur

∴ ngAD0, ngDE

从而 4 x 4 y 2z 0, 4 y 2z 0 ,

r uuur r

2

令 y 1 ，则 n (2,1,2), cos CA, n

3

∴二面角 A ED B 的的正弦值为 5 ．

3

（3）V 1

S BCED AC16 ，∴几何体的体积V 为16．3

点评：本题考查异面直线所成角的求法、考查二面角的求法和多面体体积的求法．空

间向量对解决三类角（异面直线角、线面角、面面角）的计算有一定的优势．对理科考

生来说除了要在空间向量解决立体几何问题上达到非常熟练的程度外，不要忽视了传统

的方法，有些试题开始部分的证明就没有办法使用空间向量．

【专题训练与高考预测】

说明：文科以选择题、填空题和解答题前三题为主．理科以选择题、填空题和解答题后

三题为主．

一、选择题

1．如图为一个几何体的三视图，尺寸如图所示，则该几何体的表面积为（不考虑接触点）

（）A．63B．18 3 4C．1823D．32

2．某几何体的三视图如图所示，根据图中数据，可得该几何体的体积是

（

）

A ．3

2

3

B ．

2

3 3

C ．2 2

3 3

D ． 3 2

2 3

3．已知一个几何体的主视图及左视图均是边长为

2 的正三角形， 俯视图是直径为 2的圆，则

此几何体的外接球的表面积为

（ ）

4

B ．

8

A ．

3

3

C ．

16

D ． 32

3

3

4．一个水平放置的平面图形的斜二测直观图是一个底角为

45o ，腰和上底长均为 1的等腰梯

形，则这个平面图形的面积是

（

）

A ．

1

2 B ． 1

2 C ． 1

2

D ． 2

2

2

2

2

5． 一个盛满水的三棱锥容器 S

ABC ，不久发现三条侧棱上各有一个小洞

D, E,F ，且知

SD: DA SE: EB

CF :FS

2:1 ，若仍用这个容器盛水，则最多可盛原来水的（

）

23

19

30

23

A ．

B ．

C ．

D ．

29

27

31

27

6． 点 P 在直径为 2 的球面上，过 P 作两两垂直的三条弦，若其中一条弦长是另一条弦长的

2 倍，则这三条弦长之和为最大值是

（

）

2

70

3 70

4

15

6 15

A ．

B ．

C ．

D ．

5

5

5

5

7．正方体 ABCD A' B 'C 'D ' 中， AB 的中点为 M ，DD ' 的中点为 N ，异面直线 B 'M 与 CN

所成的角是

（ ） A ． 30o

B ． 90o

C ． 45o

D ． 60o

．已知异面直线 a 和

b 所成的角为

o ，P 为空间一定点， 则过点 P 且与 a,b 所成角都是 30o

8

50

的直线有且仅有

（

）

A ． 1条

B ． 2条

C ． 3条

D ． 4条

9．如图所示，四边形

ABCD 中， AD / / BC, AD

AB, BCD

45o , BAD 90 o ，将

△ ABD 沿 BD 折起，使平面 ABD

平面 BCD ，构成三棱锥

A BCD ，则在三棱锥

A BCD 中，下列命题正确的是

（

）

A ．平面 ABD 平面 ABC

B ．平面 AD

C 平面 BDC C ．平面 ABC 平面 BDC

D ．平面 ADC

平面 ABC

10．设 x 、 y 、 z 是空间不同的直线或平面，对下列四种情形：①

x 、 y 、 z 均为直线；

② x 、 y 是直线， z 是平面；③ z 是直线， x 、 y 是平面；④ x 、 y 、 z 均为平面．

其中使 “x ⊥ z 且 y ⊥ z x ∥ y ”为真命题的是

（

）

A ． ③④

B ． ①③

C ． ②③

D ． ①②

11

m 、 n 、 l 两个不重合的平面

、 ，有下列命题

．已知三条不重合的直线

①若 m / / n, n

，则 m / / ；

②若③若l， m且l Pm，则P；

m, m，m P, n P，则P；

④若，I m ， n， n m ，则 n．

中正确的命题个数是（）

A ．1

B ．2C．3D．4

12．直线AB与直二面角l的两个面分别交于A, B 两点，且 A, B 都不在棱上，设直线 AB 与平面,所成的角分别为 ,，则的取值范围是（）

A．(0,)B． 0,C．(, )D．{}

2222

二、填空题

13．在三棱锥P ABC 中， PA PB PC 2，APB BPC CPA30o，一只

蚂蚁从 A 点出发沿三棱锥的侧面绕一周，再回到 A 点，则蚂蚁经过的最短路程

是．

14．四面体的一条棱长为x ，其它各棱长为1V

表示成 x 的函数 f x ，，若把四面体的体积

则 f x 的增区间为，减区间为．

15．如图，是正方体平面展开图，在这个正方体中：①BM 与 ED 平行；②CN 与BE 是异面直线；

③ CN与 BM 成60o角；④ DM与 BN 垂直．以上四个说法中，正确说法的序号

依次是．

16．已知棱长为1的正方体ABCD A1B1C1D1中，E是 A1B1的中点，则直线AE 与平面

ABC1D1所成的角的正弦值是．

三、解答题

17．已知，如图是一个空间几何体的三视图．

（1）该空间几何体是如何构成的；

（2）画出该几何体的直观图；

（3）求该几何体的表面积和体积．

18．如图，已知等腰直角三角形RBC ，其中RBC90o，RB BC2．点A, D分别是RB ,RC的中点，现将RAD 沿着边 AD 折起到PAD 位置，使 PA AB ，连结 PB 、

PC ．

（ 1）求证：BC PB ；

（ 2）求二面角A CD P 的平面角的余弦值．

19．如下图，在正四棱柱ABCD A1B1C1 D1中，AA11 AB，点E,M分别为

2

A1B,CC1的

中点，过点A1, B, M 三点的平面A1 BMN交 C1D1于点N．

（ 1）求证：EM P平面A1B1C1D1；

（ 2）求二面角B A1N B1的正切值；

（ 3）设截面A1BMN把该正四棱柱截成的两个几何体的体积分别为V1,V2（ V1V2），求V1 : V2的值．

20．如图，在四棱锥P 直于底面 ABCD ，

ABCD 中，底面为直角梯形，AD // BC , BAD 90 ，

PA AD AB 2BC 2,M ,N 分别为 PC , PB的中点．

PA 垂

（ 1）求证：PB DM；（ 2）求BD 与平面ADMN所成的角；（ 3）求截面ADMN的面积．

21．如图，正方形ACDE所在的平面与平面ABC 垂直，M 是 CE 和 AD 的交点， AC BC ，且 AC BC．

（ 1）求证：AM平面EBC；

（2）求直线AB与平面EBC所成的角的大小；

（3）求二面角A EB C的大小．

22．已知斜三棱柱ABC A1B1C1，BCA 90o，AC BC 2 ，A1在底面 ABC 上的射影恰为 AC 的中点 D ，又知BA1AC1．

（ 1）求证：AC1平面A1BC；（2）求CC1到平面A1AB的距离；

（ 3）求二面角 A A1B C 的一个三角函数值．

【参考答案】

1．解析： C 该几何体是正三棱柱上叠放一个球．故其表面积为

312

32322241823．

42

2．解析： B这个空间几何体的是一个底面边长为 3 的正方形、高为 3 的四棱柱，上半

部分是一个底面边长为

3的正方形、高为 2的四棱锥，故其体积为

3

3

3 1 3

3

2

3 3

2 ．

3

3．解析：C

由三视图知该几何体是底面半径为

1，高为

3 的圆锥，其外接球的直径为

4 3 ．

3 4．解析： D 如图设直观图为

O ' A ' B ' C '，建立如图所示的坐标系，按照斜二测画法的规则，

在原来的平面图形中

OC

OA ，且 OC 2， BC

1，OA 1 2

2 2 ，故

1

2

其面积为

1

1 2 2

2 2

2

2

5．解析： D

当平面 EFD 处于水平位置时，容器盛水最多

1

V

F SDE

S 3 V

C SAB

1

S

3

SDE

h 1

1

SD SE sin DSE h 1

3 SD SE h 1 2 2 1

4

SAB

h 2

1

SA SB sin ASB h 2

SA SB h 2

3 3 3 27

3

最多可盛原来水得 1

4 23 ．

27 27

6．解析： A 设三边长为

x,2 x, y ，则 5x 2 y 2

4 ，

4 4 2 70 ．

令 x cos , y 2sin , 3x y 3 cos 2sin

5

5

5

7．解析： B 如图，取 AA '的中点 P ，连结 BP ，在正方形 ABB' A'中易证 BP B'M ．

8

B 过点 P 作 a Pa ， b Pb ，若 P a ，则取 a 为 a ，若 P b ，则取 b 为 b ．这时

．解析： a

， 相交于

P 点，它们的两组对顶角分别为

50

o 和 130o

． 记 a ，b 所确定的平面为 ，

b

那么在平面 内，不存在与 a ， b 都成 30o 的直线． 过点 P 与 a ， b 都成 30o

角的直

线必在平面

外，这直线在平面

的射影是 a ，b 所成对顶角的平分线． 其中射影是 50o

对顶角平分线的直线有两条

l 和 l ，射影是 130o 对顶角平分线的直线不存在．故答案选

B ．

9．解析：D 如图，在平面图形中 CD

BD ，折起后仍然这样， 由于平面 ABD 平面 BCD ，

故 CD

平面 ABD

CD AB

，又 AB AD

，故 AB

平面 ADC

，所以平面 ADC

，

平面 ABC ．

10．解析： C x 、 y 、 z 均为直线，显然不行；由于垂直于同一个平面的两条直线平行，故

②， 可以使 “x ⊥ z 且 y ⊥ z x ∥ y ”为真命题； 又由于垂直于同一条直线的两个平面 平行，故③可以使 “ ⊥ z 且 y

⊥ z x ∥ y

”为真命题；当 x 、 y

、 z 均为平面时，也

x

不能使 “x ⊥ z 且 y ⊥ z x ∥ y ”为真命题．

11．解析： B ①中有 m

的可能； l Pm 且 l

，可得 m

，又 m ，故 P

，

②正确；③中当

m Pn 时，结论不成立；④就是面面垂直的性质定理，④正确．故两个

正确的．

12．解析： B如图，在Rt ADC 中，AD AB cos , AC AB sin，而AD AC ，即cos sin cos，故，即，而当AB l时，．

2222

13．解析：22将如图⑴三棱锥P ABC ，沿棱PA 展开得图⑵，蚂蚁经过的最短路程应是AA ，又∵APB BPC CPA30o，APA '90o，∴AA=2 2．

66， f ( x)x 3 x2，利用不等式或导数即可判断．

14．解析： 0,，3

4

22

15．解析：③④如图，逐个判断即可．

16．解析：10

取 CD 的中点 F ，连接 EF 交平面ABC1D1于 O ，连 AO ．由已知正方体，5

易知 EO平面 ABC1 D1，所以EAO为所求．在 Rt EOA 中，EO1EF1A1 D 2 ，

222