第2讲 参数方程

第2讲参数方程一、知识梳理
1.参数方程和普通方程的互化
(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地,可以通过消去参数,从参数方程得到普通方程.
(2)如果知道变数x ,y 中的一个与参数t 的关系,例如x =f (t ),把它代入普通方程,求
出另一个变数与参数的关系y =g (t ),那么?
????x =f (t ),
y =g (t )就是曲线的参数方程,在参数方程与
普通方程的互化中,必须使x ,y 的取值范围保持一致.
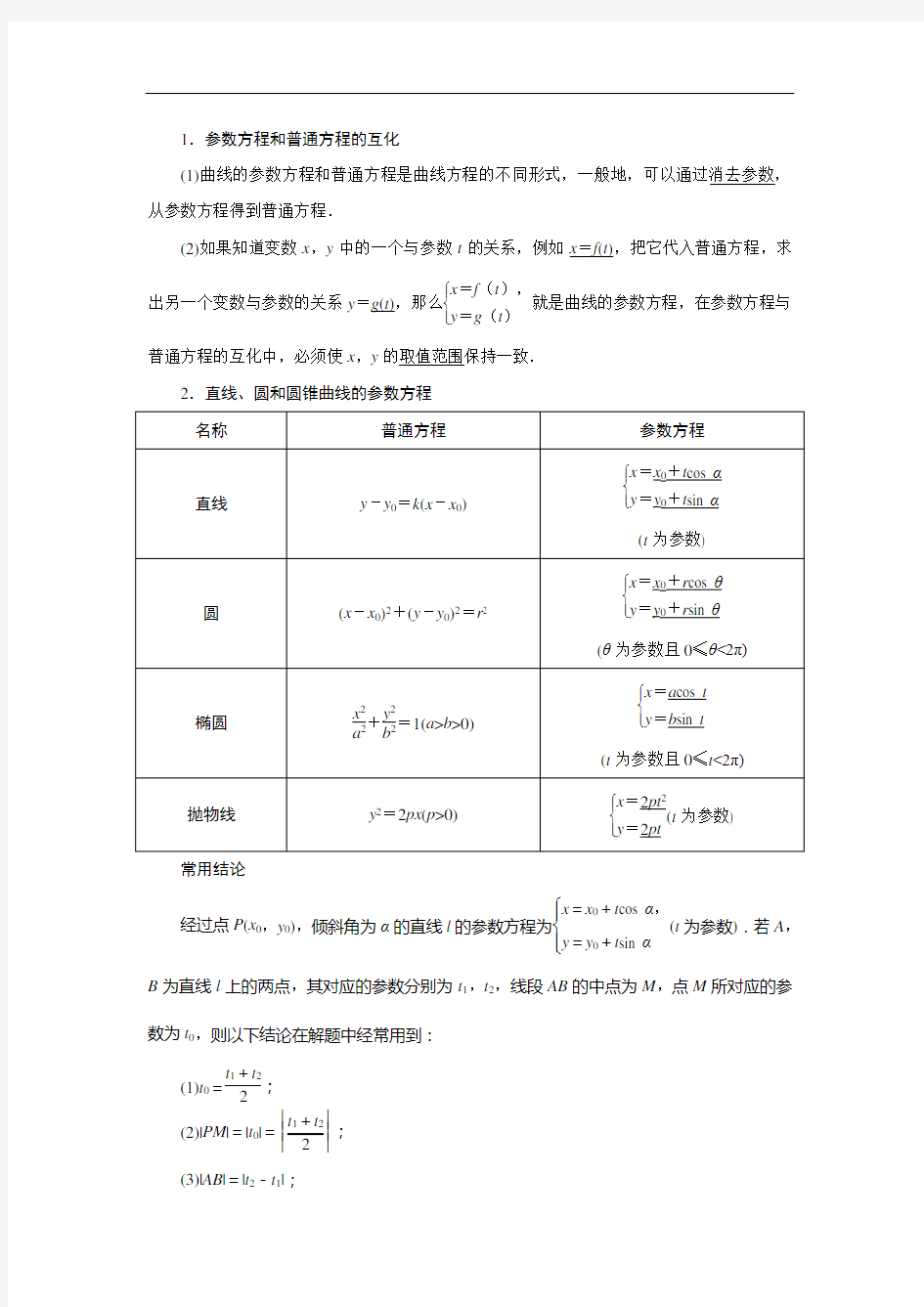
2.直线、圆和圆锥曲线的参数方程
常用结论
经过点P (x 0,y 0),倾斜角为α的直线l 的参数方程为?
????x =x 0+t cos α,
y =y 0+t sin α(t 为参数).若A ,
B 为直线l 上的两点,其对应的参数分别为t 1,t 2,线段AB 的中点为M ,点M 所对应的参数为t 0,则以下结论在解题中经常用到:
(1)t 0=
t 1+t 2
2
; (2)|PM |=|t 0|=??
??
??
t 1+t 22; (3)|AB |=|t 2-t 1|;
(4)|P A |·|PB |=|t 1·t 2|. 二、教材衍化
1.已知曲线C 的参数方程为?
????x =3t ,y =2t 2+1(t 为参数),点M (-6,a )在曲线C 上,则a = .
解析:由题意得?????-6=3t ,a =2t 2
+1,所以?
????t =-2,a =9.
答案:9
2.在直角坐标系xOy 中,直线l 的参数方程为???x =2+22t ,
y =2
2t
(t 为参数),与圆C :(x -
3)2+(y -3)2=4交于A ,B 两点,求|AB |.
解:将直线l 的参数方式代入圆C 的直角坐标方程,得????22t -12+???
?22t -32
=4, 即t 2-42t +6=0,设两交点A ,B 所对应的参数分别为t 1,t 2,从而t 1+t 2=42,t 1t 2
=6,
则|AB |=|t 1-t 2|=
(t 1+t 2)2-4t 1t 2=2 2.
一、思考辨析
判断正误(正确的打“√”,错误的打“×”)
(1)参数方程?
????x =f (t ),
y =g (t )中的x ,y 都是参数t 的函数.( )
(2)过M 0(x 0,y 0),倾斜角为α的直线l 的参数方程为?
????x =x 0+t cos α,
y =y 0+t sin α(t 为参数).参数t
的几何意义表示:直线l 上以定点M 0为起点,任一点M (x ,y )为终点的有向线段M 0M →
的数量.( )
(3)已知椭圆的参数方程?
????x =2cos t ,y =4sin t (t 为参数),点M 在椭圆上,对应参数t =π
3,点O
为原点,则直线OM 的斜率为 3.( )
答案:(1)√ (2)√ (3)× 二、易错纠偏
常见误区(1)不注意互化的等价性致误; (2)直线参数方程中参数t 的几何意义不清致误.
1.在平面直角坐标系中,曲线C 的参数方程为?
????x =2+sin 2θ,
y =-1+cos 2θ
(θ为参数),求曲线C 的普通方程. 解:由x =2+sin 2θ,0≤sin 2θ≤1 ?2≤2+sin 2θ≤3?2≤x ≤3,
???
??x =2+sin 2θ,y =-1+cos 2θ??????x -2=sin 2θ,y =-1+1-2sin 2θ??????x -2=sin 2θ
y =-2sin 2
θ
?2x +y -4=0(2≤x ≤3). 2.在平面直角坐标系xOy 中,直线l 的参数方程为???x =2+t ,y =1+3t
(t 为参数),曲线C 的普
通方程为(x -4)2+(y -3)2=4,设点M (2,1),直线l 与曲线C 相交于A ,B 两点,求|MA |·|MB |的值.
解:设点A ,B 对应的参数分别为t 1,t 2,
将?????x =2+t ,
y =1+3t
(t 为参数)代入(x -4)2+(y -3)2=4, 得t 2-(3+1)t +1=0,
所以t 1t 2=1,
直线l :?????x =2+t
y =1+3t
(t 为参数),
可化为???x =2+1
2
(2t )
y =1+3
2(2t )
,
所以|MA |·|MB |=|2t 1||2t 2|=4|t 1t 2|=4.
参数方程与普通方程的互化(师生共研)
已知曲线C 1:?
????x =-4+cos t ,
y =3+sin t (t 为参
数),曲线C 2:?
????x =8cos θ,
y =3sin θ(θ为参数).化C 1,C 2的方程为普通方程,并说明它们分别表示
什么曲线.
【解】 曲线C 1:(x +4)2+(y -3)2=1, 曲线C 2:x 264+y 2
9
=1,
曲线C 1是以(-4,3)为圆心,1为半径的圆;
曲线C 2是中心为坐标原点,焦点在x 轴上,长半轴长是8,短半轴长是3的椭圆.
将参数方程化为普通方程的方法
(1)将参数方程化为普通方程,需要根据参数方程的结构特征,选取适当的消参方法.常
见的消参方法有:代入消参法、加减消参法、平方消参法等.对于含三角函数的参数方程,常利用同角三角函数关系式消参,如sin 2θ+cos 2θ=1等.
(2)将参数方程化为普通方程时,要注意两种方程的等价性,不要增解.
1.求直线?????x =2+t ,y =-1-t (t 为参数)与曲线?
????x =3cos α,
y =3sin α(α为参数)的交点个数.
解:将?????x =2+t ,
y =-1-t 消去参数t 得直线x +y -1=0;
将?????x =3cos α,
y =3sin α
消去参数α得圆x 2+y 2=9. 又圆心(0,0)到直线x +y -1=0的距离d =
2
2
<3. 因此直线与圆相交,故直线与曲线有2个交点.
2.如图,以过原点的直线的倾斜角θ为参数,求圆x 2+y 2-x =0的参数方程.
解:圆的半径为12,记圆心为C ????12,0,连接CP ,则∠PCx =2θ,故x P =12+1
2cos 2θ=cos 2θ,
y P =1
2
sin 2θ=sin θcos θ(θ为参数).
所以圆的参数方程为?????x =cos 2θ,
y =sin θcos θ
(θ为参数).
参数方程的应用(师生共研)
(2019·高考全国卷Ⅰ)在直角坐标系
xOy 中,曲线C 的参数方程为????
?x =1-t 21+t 2
,y =4t
1+t
2
(t 为参数).以坐标原点O 为极点,x 轴的正半轴
为极轴建立极坐标系,直线l 的极坐标方程为2ρcos θ+3ρsin θ+11=0.
(1)求C 和l 的直角坐标方程;
(2)求C 上的点到l 距离的最小值.
【解】 (1)因为-1<1-t 21+t 2≤1,且x 2
+????y 22=? ????1-t 21+t 22+4t 2(1+t 2)
2=1,所以C 的直角坐标方程为x 2+
y 2
4
=1(x ≠-1).l 的直角坐标方程为2x +3y +11=0. (2)由(1)可设C 的参数方程为?????x =cos α,
y =2sin α(α为参数,-π<α<π).C 上的点到l 的距离为
|2cos α+23sin α+11|7=4cos ????α-π3+117
.当α=-2π3时,4cos(α-π
3)+11取得最小值7,故C
上的点到l 距离的最小值为7.
(1)解决与圆、圆锥曲线的参数方程有关的综合问题时,要注意普通方程与参数方程的互化公式,主要是通过互化解决与圆、圆锥曲线上和动点有关的问题,如最值、范围等.
(2)根据直线的参数方程的标准式中t 的几何意义,有如下常用结论:过定点M 0的直线与圆锥曲线相交,交点为M 1,M 2,所对应的参数分别为t 1,t 2,①弦长l =|t 1-t 2|;②M 0为弦M 1M 2的中点?t 1+t 2=0;③|M 0M 1|·|M 0M 2|=|t 1t 2|.
1.已知曲线C 的普通方程为x 212+y 2
4=1,求曲线C 的内接矩形周长的最大值.
解:由曲线C 的直角坐标方程为x 212+y 2
4=1,可设曲线C 上的动点A (23cos α,2sin α),
0<α<π2
,
则以A 为顶点的内接矩形的周长为4(23cos α+2sin α)=16sin(α+π3),0<α<π
2.
因此该内接矩形周长的最大值为16,当且仅当α=π
6
时取得最大值.
2.(2020·成都第一次诊断性检测)在平面直角坐标系xOy 中,已知直线l 的参数方程为
???
x =1
2
t ,y =32t -1
(t 为参数).在以坐标原点O 为极点,x 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线C 的极坐标方程是ρ=22sin ????
π4+θ.
(1)求直线l 的普通方程与曲线C 的直角坐标方程;
(2)设点P (0,-1),若直线l 与曲线C 相交于A ,B 两点,求|P A |+|PB |的值. 解:(1)将直线l 的参数方程消去参数t 并化简, 得直线l 的普通方程为3x -y -1=0. 曲线C 的极坐标方程可化为ρ2=22ρ??
?
?22sin θ+22cos θ,
即ρ2=2ρsin θ+2ρcos θ,所以x 2+y 2=2y +2x , 故曲线C 的直角坐标方程为(x -1)2+(y -1)2=2. (2)将直线l 的参数方程代入(x -1)2+(y -1)2=2中,
得????12t -12+???
?32t -22
=2,
化简,得t 2-(1+23)t +3=0.
可得Δ>0,所以此方程的两根为直线l 与曲线C 的交点A ,B 对应的参数t 1,t 2. 由根与系数的关系,得t 1+t 2=23+1,t 1t 2=3,故t 1,t 2同正.
由直线的参数方程中参数的几何意义,知|P A |+|PB |=|t 1|+|t 2|=t 1+t 2=23+1.
极坐标与参数方程的综合问题(师生共研)
(一题多解)(2020·贵州省适应性考试)
曲线C 1的参数方程为????
?x =2+2cos α,y =2sin α
(α为参数),在以原点O 为极点,x 轴的非负半轴为极
轴的极坐标系中,曲线C 2的极坐标方程为ρcos 2θ=sin θ.
(1)求曲线C 1的极坐标方程和曲线C 2的直角坐标方程;
(2)过原点且倾斜角为α(π6<α≤π
4)的射线l 与曲线C 1,C 2分别相交于A ,B 两点(A ,B 异
于原点),求|OA |·|OB |的取值范围.
【解】 (1)曲线C 1的普通方程为(x -2)2+y 2=4, 即x 2+y 2-4x =0,
故曲线C 1的极坐标方程为ρ2=4ρcos θ,即ρ=4cos θ.
由曲线C 2的极坐标方程为ρcos 2θ=sin θ,两边同乘以ρ,得ρ2cos 2θ=ρsin θ, 故曲线C 2的直角坐标方程为x 2=y .
(2)法一:射线l 的极坐标方程为θ=α,π6<α≤π
4
,
把射线l 的极坐标方程代入曲线C 1的极坐标方程得|OA |=ρ=4cos α, 把射线l 的极坐标方程代入曲线C 2的极坐标方程得|OB |=ρ=sin α
cos 2α,
所以|OA |·|OB |=4cos α·sin α
cos 2α=4tan α,
因为π6<α≤π4
,
所以|OA |·|OB |的取值范围是??
?
?
433,4.
法二:射线l 的参数方程为?
????x =t cos α,y =t sin α(t 为参数,π6<α≤π
4
).
把射线l 的参数方程代入曲线C 1的普通方程得t 2-4t cos α=0. 解得t 1=0,t 2=4cos α.故|OA |=|t 2|=4cos α. 同理可得|OB |=
sin αcos 2α
, 所以|OA |·|OB |=4cos α·sin α
cos 2α=4tan α,
因为π6<α≤π4
,
所以|OA |·|OB |的取值范围是??
?
?
433,4.
处理极坐标、参数方程综合问题的方法
(1)涉及参数方程和极坐标的综合问题时,求解的一般方法是分别化为普通方程和直角坐标方程后求解.当然,还要结合题目本身特点,确定选择何种方程.
(2)数形结合的应用,即充分利用参数方程中参数的几何意义,或者利用ρ和θ的几何意义,直接求解,能达到化繁为简的解题目的.
(一题多解)(2020·河南新乡模拟考试)
在平面直角坐标系xOy 中,曲线C 的参数方程为???x =3cos α,
y =1+3sin α
(α为参数),以坐标原点O
为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为ρsin ???
?θ+π
6=2 3. (1)求曲线C 的普通方程和直线l 的直角坐标方程;
(2)射线OP 的极坐标方程为θ=π
6(ρ≥0),若射线OP 与曲线C 的交点为A ,与直线l 的
交点为B ,求线段AB 的长.
解:(1)由?????x =3cos α,y =1+3sin α,可得?
????x =3cos α,
y -1=3sin α,
所以x 2+(y -1)2=3cos 2α+3sin 2α=3, 所以曲线C 的普通方程为x 2+(y -1)2=3.
由ρsin ????θ+π6=23,可得ρ????32sin θ+1
2cos θ=23, 所以
32ρsin θ+1
2
ρcos θ-23=0, 所以直线l 的直角坐标方程为x +3y -43=0. (2)法一:曲线C 的方程可化为x 2+y 2-2y -2=0, 所以曲线C 的极坐标方程为ρ2-2ρsin θ-2=0. 由题意设A ????ρ1,π6,B ?
???ρ2,π
6, 将θ=π
6代入ρ2-2ρsin θ-2=0,可得ρ2-ρ-2=0,
所以ρ=2或ρ=-1(舍去),即ρ1=2, 将θ=π
6代入ρsin ????θ+π6=23, 可得ρ=4,即ρ2=4, 所以|AB |=|ρ1-ρ2|=2.
法二:因为射线OP 的极坐标方程为θ=π
6(ρ≥0),
所以射线OP 的直角坐标方程为y =
3
3
x (x ≥0), 由?????x 2+(y -1)2=3,y =33x (x ≥0),
解得A (3,1), 由?????x +3y -43=0y =33x (x ≥0)
,解得B (23,2),
所以|AB |=(23-3)2+(2-1)2=2.
[基础题组练]
1.在平面直角坐标系中,以原点为极点,x 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C 的极坐标方程为ρ=2cos θ,直线l 的参数方程为
?
????x =-1+t cos α,y =t sin α(t 为参数,α为直线的倾斜角). (1)写出直线l 的普通方程和曲线C 的直角坐标方程; (2)若直线l 与曲线C 有唯一的公共点,求角α的大小. 解:(1)当α=π
2时,直线l 的普通方程为x =-1;
当α≠π
2时,直线l 的普通方程为y =(x +1)tan α.
由ρ=2cos θ,得ρ2=2ρcos θ, 所以x 2+y 2=2x ,
即为曲线C 的直角坐标方程.
(2)把x =-1+t cos α,y =t sin α代入x 2+y 2=2x ,整理得t 2-4t cos α+3=0. 由Δ=16cos 2α-12=0,得cos 2α=3
4,
所以cos α=
32或cos α=-32
, 故直线l 的倾斜角α为π6或5π
6
.
2.以极点为原点,以极轴为x 轴正半轴建立平面直角坐标系,已知曲线C 的极坐标方
程为ρ=10,曲线C ′的参数方程为?
????x =3+5cos α,
y =-4+5sin α,(α为参数).
(1)判断两曲线C 和C ′的位置关系;
(2)若直线l 与曲线C 和C ′均相切,求直线l 的极坐标方程. 解:(1)由ρ=10得曲线C 的直角坐标方程为x 2+y 2=100,
由?
????x =3+5cos α,
y =-4+5sin α得曲线C ′的普通方程为(x -3)2+(y +4)2=25. 曲线C 表示以(0,0)为圆心,10为半径的圆; 曲线C ′表示以(3,-4)为圆心,5为半径的圆.
因为两圆心间的距离5等于两圆半径的差,所以圆C 和圆C ′的位置关系是内切.
(2)由(1)建立方程组?
????x 2+y 2=100,(x -3)2+(y +4)2
=25,
解得?????x =6,y =-8,
可知两圆的切点坐标为(6,-8),且公切线的斜率为3
4
,
所以直线l 的直角坐标方程为y +8=3
4(x -6),
即3x -4y -50=0,
所以极坐标方程为3ρcos θ-4ρsin θ-50=0.
3.(2020·成都市第二次诊断性检测)在平面直角坐标系xOy 中,直线l 的参数方程为
?????x =t cos α,y =t sin α(t 为参数,α为倾斜角),曲线C 的参数方程为?
????x =4+2cos β,y =2sin β(β为参数,β∈[0,π]).以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系.
(1)写出曲线C 的普通方程和直线l 的极坐标方程; (2)若直线l 与曲线C 恰有一个公共点P ,求点P 的极坐标.
解:(1)由曲线C 的参数方程?????x =4+2cos β
y =2sin β
,得(x -4)2+y 2=4.
因为β∈[0,π],所以曲线C 的普通方程为(x -4)2+y 2=4(y ≥0).
因为直线l 的参数方程为?????x =t cos α,
y =t sin α
(t 为参数,α为倾斜角),
所以直线l 的倾斜角为α,且过原点O (极点). 所以直线l 的极坐标方程为θ=α,ρ∈R . (2)由(1)可知,曲线C 为半圆弧.
若直线l 与曲线C 恰有一个公共点P ,则直线l 与半圆弧相切. 设P (ρ,θ)(ρ>0).由题意,得sin θ=24=12,故θ=π
6.
而ρ2+22=42,所以ρ=2 3. 所以点P 的极坐标为?
???23,π
6. 4.(2020·陕西铜川模拟)在平面直角坐标系xOy 中,直线l 的参数方程为???
x =1+35
t ,
y =1+4
5
t (t
为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ2
=
21+sin 2θ
,点P 的极坐标为??
??2,π4. (1)求曲线C 的直角坐标方程和点P 的直角坐标;
(2)设l 与C 交于A ,B 两点,线段AB 的中点为M ,求|PM |. 解:(1)由ρ2=21+sin 2θ得ρ
2+ρ2sin 2θ=2,① 将
ρ2=x 2+y 2,y =ρsin θ
代入①并整理得,曲线C 的直角坐标方程为x 22
+y 2
=1.
设点P 的直角坐标为(x ,y ),因为点P 的极坐标为????2,π
4, 所以x =ρcos θ=2cos π4=1,y =ρsin θ=2sin π
4=1.
所以点P 的直角坐标为(1,1).
(2)将???
x =1+35
t ,
y =1+4
5
t 代入x 22
+y 2
=1,并整理得41t 2+110t +25=0,
Δ=1102-4×41×25=8 000>0,故可设方程的两根分别为t 1,t 2,
则t 1,t 2为A ,B 对应的参数,且t 1+t 2=-110
41.
依题意,点M 对应的参数为t 1+t 2
2,
所以|PM |=??
????t 1+t 22=55
41
. 5.(2020·河南省六校联考)在平面直角坐标系xOy 中,直线l 的参数方程为?
????x =7-t ,
y =-2+t (t
为参数).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C :ρ=42sin ???
?θ+π
4. (1)求直线l 的普通方程和曲线C 的直角坐标方程;
(2)设曲线C 与直线l 的交点为A ,B ,Q 是曲线C 上的动点,求△ABQ 面积的最大值.
解:(1)由?????x =7-t ,
y =-2+t
消去t 得x +y -5=0,所以直线l 的普通方程为x +y -5=0.
由ρ=42sin ????θ+π
4=4sin θ+4cos θ,得ρ2=4ρsin θ+4ρcos θ, 化为直角坐标方程为x 2+y 2=4x +4y ,
所以曲线C 的直角坐标方程为(x -2)2+(y -2)2=8.
(2)由(1)知,曲线C 是以(2,2)为圆心,22为半径的圆,直线l 过点P (3,2),可知点P 在圆内.
将直线l 的参数方程化为???x =7-22t
y =-2+2
2t ,
代入圆的直角坐标方程,得t 2
-9
2t +33=0.
设A ,B 对应的参数分别为t 1,t 2,则t 1+t 2=92,t 1t 2=33, 所以|AB |=|t 2-t 1|=
(t 1+t 2)2-4t 1t 2=30.
又圆心(2,2)到直线l 的距离d =|2+2-5|2=2
2,
所以△ABQ 面积的最大值为12×30×????2
2+22
=515
2
. 6.(2020·吉林第三次调研测试)在直角坐标系xOy 中,曲线C 1的参数方程为
?
??x =1-
22
t ,y =1+2
2
t
(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρsin 2θ=4cos θ.
(1)求曲线C 1的普通方程与曲线C 2的直角坐标方程;
(2)若C 1与C 2交于A ,B 两点,点P 的极坐标为????2,π4,求1|P A |+1|PB |
的值. 解:(1)曲线C 1
的参数方程为???x =1-22t ,
y =1+2
2t ,
(t 为参数),两式相加消去t 可得普通方程为
x +y -2=0.由ρcos θ=x ,ρsin θ=y ,曲线C 2的极坐标方程为ρsin 2θ=4cos θ,可得曲线C 2的直角坐标方程为y 2=4x .
(2)把曲线C 1
的参数方程???x =1-22t ,
y =1+2
2
t (t 为参数)代入y 2
=4x ,得t 2
+6
2t -6=0,
设t 1,t 2是A ,B 对应的参数,则t 1+t 1=-62,t 1·t 2=-6, 所以1|P A |+1
|PB |=|P A |+|PB ||P A |·|PB |=|t 1-t 2||t 1·t 2|
=
(t 1+t 2)2-4t 1·t 2
|t 1·t 2|
=
966=26
3
. [综合题组练]
1.(2020·辽宁大连第一次(3月)双基测试)在平面直角坐标系xOy 中,曲线C 1的参数方
程为?????x =t cos α,y =t sin α????t 为参数且t >0,α∈????0,π2,曲线C 2的参数方程为???
??x =cos β,y =1+sin β
????β为参数,且β∈????-π2,π2,以O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 3的
极坐标方程为ρ=1+cos θ???
?θ∈????0,π2,曲线C 4的极坐标方程为ρcos θ=1. (1)求C 3与C 4的交点到极点的距离;
(2)设C 1与C 2交于P 点,C 1与C 3交于Q 点,当α在????0,π
2上变化时,求|OP |+|OQ |的最大值.
解:(1)联立?????ρ=1+cos θ????θ∈????0,π2,ρcos θ=1
得ρ2
-ρ-1=0,解得ρ=1+52
,即交点到极点
坐标系与参数方程知识点
坐标系与参数方程 知识点 1.平面直角坐标系中的坐标伸缩变换 设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0) x x y y λλ?μμ'=>?? '=>?g g 的作用 下,点P(x,y)对应到点(,)P x y ''',称?为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念 (1)极坐标系 如图所示 ,在平面内取一个定点O ,叫做极点,自极点O 引一条射 线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系. 注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系. (2)极坐标 设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ. 一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个 点的极坐标有无数种表示. 如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的. 3.极坐标和直角坐标的互化
(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示 : (2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是 (,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表: 点M 直角坐标(,)x y 极坐标(,)ρθ 互化公式 cos sin x y ρθ ρθ=?? =? 222 tan (0)x y y x x ρθ=+= ≠ 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程 曲线 图形 极坐标方程 圆心在极点,半径为r 的圆 (02)r ρθπ=≤< 圆心为(,0)r ,半径为r 的圆 2cos ()2 2 r π π ρθθ=- ≤< 圆心为(, )2 r π ,半 径为r 的圆 2sin (0)r ρθθπ≤<
第十二章第二节参数方程
第十二章第二节参数方程 课下练兵场 1.(2018·天津高考)设直线l 1的参数方程为? ??? ?x =1+t ,y =1+3t ,(t 为参数),直线l 2的方程为y =3x +4, 那么l 1与l 2间的距离为 ( ) A.10 B.3105 C.210 5 D .310 解析:直线l 1的参数方程????? x =1+t , y =1+3t (t 为参数). 化为一般方程为:x -11=y -1 3,即 3x -y -2=0. 又l 2:3x -y +4=0.由两平行线间距离公式知 d = |c 1-c 2| a 2+ b 2 =|4-(-2)|10=310 5. 答案:B 2.(2018·广东高考)假设直线? ???? x =1-2t , y =2+3t (t 为参数)与直线4x +ky =1垂直,那么常数k =( ) A .25 B .-6 C .6 D .7 解析:直线l 1:3x +2y -7=0,直线l 2:4x +ky -1=0. 由l 1⊥l 2,∴2k +3·4=0,∴k =-6. 答案:B
3.点P (x ,y )在曲线? ???? x =-2+cos θy =sin θ(θ为参数)上,那么y x 的取值范畴为 ( ) A .(- 22,22] B .[-33,33] C .[-1,1] D .[-55,5 5 ] 解析: 曲线? ???? x =-2+cos θy =sin θ(θ为参数)是以(-2,0)为圆心,以1为半径的圆,设y x =k , 求y x 的取值范畴,即求当直线y =kx 与圆有公共点时k 的取值范畴,如图结合圆的几何性质可得- 33≤k ≤33 . 答案:B 4.设直线参数方程为??? x =2+t 2 , y =3+3 2 t (t 为参数),那么它的斜截式方程为 ( ) A .y =3x +(23-3) B .y =3x +(3-23) C .y =3x +(22-3) D .y =3x +(3-22) 解析:设直线的斜率为3,当t =-4时,x =0,y =3-23,故直线的斜截式方程为y = 3x +( 3-23). 答案:B 5.点P (x ,y )是椭圆2x 2+3y 2=12上的一个动点,那么x +2y 的最大值为 ( ) A.21 B.22 C.23 D .26 解析:椭圆x 26+y 2 4=1,设点P (6cos θ,2sin θ), 那么x +2y =6cos θ+4sin θ=22sin(θ+φ)≤22. 答案:B
北师大版数学高二选修4-4讲义第二讲参数方程3参数方程化成普通方程习题解答
习题2-3 第42页 A 组 1.解 (1)2x -y -7=0,直线. (2)x 216+y 29=1,椭圆. (3)x 2a 2-y 2 b 2=1,双曲线. (4)原参数方程变形为?????x =1-1t +2,y =2-4t +2, 所以y -2x -1=4. 所以4x -y -2=0,直线. (5)? ?? ??y -122=x +54,抛物线. 2.圆的普通方程为x 2+y 2=25,半径为5. 3.椭圆的普通方程为(x -4)24+(y -1)225 =1,焦距为221. 4.椭圆的普通方程为(x -1)216 +y 29=1,c =7,左焦点(1-7,0). 5.双曲线的普通方程为(x -2)24-(y -1)24 =1,中心坐标(2,1). 6.双曲线的普通方程为(y +2)29-(x -1)23 =1,所以a =3,b =3,渐近线的斜率为±3,两条渐近线的夹角为60°. 7.抛物线的普通方程为x 2=2(y -1),准线方程为y =12. 8.解 根据一元二次方程根与系数的关系得sin α+cos α=-a 2,sin α·cos α=b 2, 点(a ,b )的轨迹的普通方程是a 2=4(b +1). B 组 1.设动点A (x ,y ),则???x =sin θ+cos θ,y =sin θ-cos θ, 即x 2+y 2=2. 2.解 设动点M (x ,y ),则? ????x =3cos φ-4sin φ-1,y =125cos φ+95sin φ+2.
所以?????x +1=3cos φ-4sin φ,53 (y -2)=4cos φ+3sin φ.两式平方相加,得(x +1)2+25(y -2)29=25. 即(x +1)225+(y -2)29 =1. 3.解 曲线的方程可以变形为(x -3cos θ)2=4(y -2sin θ), 顶点为(3cos θ,2sin θ),焦点(3cos θ,2sin θ-1). 所以焦点的轨迹方程为x 29-(y -1)24 =1. 4.(1)普通方程为y =3x -2g v 20 x 2,射程为3v 202g , (2)证明略.
选修4-4坐标系与参数方程_知识点总结知识讲解
选修4-4坐标系与参数方程_知识点总结
坐标系与参数方程 知识点 (一)坐标系 1.平面直角坐标系中的坐标伸缩变换 设点(,)P x y 是平面直角坐标系中的任意一点,在变换(0):(0) x x y y λλ?μμ'=>?? '=>?g g 的作用下,点 (,)P x y 对应到点(,)P x y ''',称?为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念 (1)极坐标系 如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系. 注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系. (2)极坐标 设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ. 一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示. 如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.
3.极坐标和直角坐标的互化 (1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示: (2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是 (,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式 如表: 点M 直角坐标(,)x y 极坐标(,)ρθ 互化公式 cos sin x y ρθ ρθ=?? =? 222 tan (0) x y y x x ρθ?=+? ?=≠?? 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程 曲线 图形 极坐标方程 圆心在极点,半径为r 的圆 (02)r ρθπ=≤< 圆心为(,0)r ,半径为r 的圆 2cos ()2 2 r π π ρθθ=- ≤< 圆心为(,)2r π ,半径为r 的 圆 2sin (0)r ρθθπ=≤< 圆心为(,)2r π ,半径为r 的 圆 2sin (0)r ρθθπ=≤<
步步高理科数学第二讲参数方程
第二讲 参数方程 1.参数方程的概念 一般地,在平面直角坐标系中,如果曲线上__________的坐标x ,y 都是某个变数t 的函数 ? ?? ?? x =f t ,y =g t , 并且对于t 的每一个允许值,由方程组所确定的点M (x ,y )都在 ____________,那么方程就叫做这条曲线的参数方程,联系变数x ,y 的变数t 叫做参变数,简称______.相对于参数方程而言,直接给出点的坐标间关系的方程叫做__________. 2.几种常见曲线的参数方程 (1)直线:经过点P 0(x 0,y 0),倾斜角为α的直线的参数方程是____________(t 为参数). (2)圆:以O ′(a ,b )为圆心,r 为半径的圆的参数方程是____________,其中α是参数. 当圆心在(0,0)时,方程??? ?? x =r cos α,y =r sin α. (3)椭圆:中心在原点,坐标轴为对称轴的椭圆的参数方程有以下两种情况: 椭圆x 2a 2+y 2 b 2=1(a >b >0)的参数方程是____________,其中φ是参数. 椭圆x 2b 2+y 2 a 2=1(a >b >0)的参数方程是____________,其中φ是参数. (4)抛物线:抛物线y 2 =2px (p >0)的参数方程是??? ?? x =2pt 2 , y =2pt . (t 为参数). 1.(课本习题改编)若直线的参数方程为??? ?? x =1+2t , y =2-3t (t 为参数),则直线的斜率为 ________. 2.椭圆? ?? ?? x =2cos θ, y =5sin θ(θ为参数)的离心率为________. 3.已知点P (3,m )在以点F 为焦点的抛物线? ?? ?? x =4t 2 , y =4t (t 为参数)上,则|PF |=________.
2013届高考数学一轮复习课时检测 第二节 参数方程 理
选修4-4 第二节 参数方程 1.(2011·江苏高考)在平面直角坐标系xOy 中,求过椭圆? ?? ?? x =5cos φ, y =3sin φ(φ为参 数)的右焦点,且与直线? ?? ?? x =4-2t , y =3-t (t 为参数)平行的直线的普通方程. 解:由题设知,椭圆的长半轴长a =5,短半轴长b =3,从而c =a 2 -b 2 =4,所以右焦点为(4,0).将已知直线的参数方程化为普通方程:x -2y +2=0. 故所求直线的斜率为12,因此其方程为y =1 2(x -4), 即x -2y -4=0. 2.在椭圆x 29+y 2 4=1上求一点M ,使点M 到直线x +2y -10=0的距离最小,并求出最小 距离. 解:因为椭圆的参数方程为??? ?? x =3cos φ, y =2sin φ (φ为参数), 所以可设点M 的坐标为(3cos φ,2sin φ). 由点到直线的距离公式,得到点M 到直线的距离为 d = |3cos φ+4sin φ-10|5 =|5cos φ·35+sin φ·4 5 -10| 5 = 1 5 |5cos(φ-φ0)-10|, 其中φ0满足cos φ0=35,sin φ0=4 5. 由三角函数的性质知, 当φ-φ0=0时,d 取最小值 5. 此时,3cos φ=3cos φ0=9 5, 2sin φ=2sin φ0=8 5. 因此,当点M 位于(95,8 5 )时, 点M 到直线x +2y -10=0的距离取最小值 5.
3.已知曲线C 的极坐标方程是ρ=2sin θ,直线l 的参数方程是 ????? x =-3 5t +2,y =45t (t 为参数). (1)将曲线C 的极坐标方程化为直角坐标方程; (2)设直线 l 与x 轴的交点是M ,N 是曲线C 上一动点,求|MN |的最大值. 解:(1)曲线C 的极坐标方程可化为ρ2 =2ρsin θ, 又x 2 +y 2 =ρ2 ,x =ρcos θ,y =ρsin θ, 所以曲线C 的直角坐标方程为x 2 +y 2 -2y =0. (2)将直线l 的参数方程化为普通方程, 得y =-4 3(x -2), 令y =0得x =2, 即M 点的坐标为(2,0). 又曲线C 为圆,且圆心坐标为(0,1),半径r =1, 则|MC |= 5. 所以|MN |≤|MC |+r =5+1. 即|MN |的最大值为5+1. 4.已知圆M :??? ? ? x =1+cos θ,y =sin θ (θ为参数)的圆心F 是抛物线E :??? ? ? x =2pt 2 ,y =2pt 的 焦点,过焦点F 的直线交抛物线于A 、B 两点,求AF ·FB 的取值范围. 解:圆M :? ?? ?? x =1+cos θ, y =sin θ的普通方程是(x -1)2+y 2 =1, 所以F (1,0). 抛物线E :??? ?? x =2pt 2 , y =2pt 的普通方程是y 2 =2px , 所以p 2 =1,p =2,抛物线的方程为y 2 =4x . 设过焦点F 的直线的参数方程为??? ?? x =1+t cos θ y =t sin θ ,(t 为参数), 代入y 2 =4x ,得 t 2sin 2θ-4t cos θ-4=0. 所以AF ·FB =|t 1t 2|=4 sin 2θ .
最新选修4-4坐标系与参数方程-知识点总结
坐标系与参数方程 知识点 (一)坐标系 1.平面直角坐标系中的坐标伸缩变换 设点(,)P x y 是平面直角坐标系中的任意一点,在变换(0):(0) x x y y λλ?μμ'=>?? '=>?g g 的作用下,点(,) P x y 对应到点(,)P x y ''',称?为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念 (1)极坐标系 如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系. 注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标 系都是平面坐标系. (2)极坐标 设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ. 一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有 无数种表示. 如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标 (,)ρθ表示的点也是唯一确定的. 3.极坐标和直角坐标的互化 (1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示: (2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐
选修4-4《第二讲参数方程》高考真题
第二讲 参数方程 本章归纳整合 高考真题 1.若曲线的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x 轴正半轴建立直角坐标系,则该曲线的直角坐标方程为________. [命题意图]本小题主要考查了极坐标系、极坐标方程与直角坐标方程的互化. 解析 由???x =ρcos θy =ρsin θ 得,cos θ=x ρ,sin θ=y ρ,ρ2=x 2+y 2,代入ρ=2sin θ+4cos θ得,ρ=2y ρ+4x ρ?ρ2=2y +4x ?x 2+y 2-4x -2y =0. 答案 x 2+y 2-4x -2y =0 2.已知两曲线参数方程分别为?????x =5cos θ,y =sin θ(0≤θ<π)和???x =54 t 2,y =t (t ∈R ),它们的交点坐标为________. [命题意图]本题考查参数方程问题,主要考查转化与化归思想.将参数方程转化为直角坐标方程的关键在于消去参数,但也要注意所给参数的取值范围. 解析 由???x =5cos θ,y =sin θ(0≤θ<π),得x 25+y 2=1(y ≥0,x ≠-5),
由?????x =54t 2,y =t (t ∈R ),得x =54y 2,联立方程可得?????x 25+y 2=1,x =54y 2, 则5y 4+16y 2-16=0,解得y 2 =45或y 2=-4(舍去),则x =54y 2=1,又y ≥0,所以其交点坐标为? ????1,255. 答案 ? ????1,255 3.在平面直角坐标系xOy 中,求过椭圆? ????x =5cos φ,y =3sin φ(φ为参数)的右焦点,且与直线? ????x =4-2t ,y =3-t (t 为参数)平行的直线的普通方程为________. [命题意图]本小题主要考查椭圆及直线的参数方程等基础知识,考查转化问题的能力. 解析 由题设知,椭圆的长半轴长a =5,短半轴长b =3,从而c =a 2-b 2=4,所以右焦点为(4,0).将已知直线的参数方程化为普 通方程:x -2y +2=0.故所求直线的斜率为12,因此其方程为y =12(x -4),即x -2y -4=0. 答案 x -2y -4=0 4.在直角坐标系xOy 中,曲线C 1的参数方程为? ????x =cos α,y =1+sin α(α为参数).在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线C 2的方程为ρ(cos θ
第二节参数方程-高考状元之路
第二节 参数方程 预习设计 基础备考 知识梳理 1.参数方程的概念 一般地,在平面直角坐标系中,如果曲线上 的坐标x ,y 都是某个变数t 的函数:???==). (),(t g y t f x 并且对于t 的每一个允许值,由方程组所确定的点M(x ,y)都在 ,那么方程叫做这条曲线的参数方程,t 叫做参变数,简称 相对于参数方程而言,直接给出点的坐标间关系的方程叫做 2.直线的参数方程 过定点),(000y x p 且倾斜角为α的直线的参数方程为 (t 为参数),则参数t 的几何意义是 3.圆的参数方程 圆心为(a ,b),半径为r ,以圆心为顶点且与x 轴同向的射线,按逆时针方向旋转到圆上一点所在半径成的角α为参数的圆的参数方程为 ).2,0[πα∈ 4.椭圆的参数方程 以椭圆的离心角θ为参数,椭圆)0(122 22>>=+b a b y a x 的参数方程为 ).2,0[πθ∈ 典题热身 1.已知直线l 的参数方程为??? ????+=--=t y t x 222,221(t 为参数),则直线l 的斜率为( ) 1.A 1.-B 2 2. c 22.-D 答案:B 2.过点M(2,1)作曲线θθ θ,sin 4cos 4:?? ?==y x c 为参数)的弦,使M 为弦的中点,则此弦所在直线的方程为 ( ) )2(2 11--=-?x y A )2(21--=-?x y B )1(2 12--=-?x y C )1(22--=-?x y D 答案:B
3.圆),0()(222>=+-r r y r x 点M 在圆上,O 为原点,以?=∠MOx 为参数,那么圆的参数方程为 ( ) ???==??sin ,cos .r y r x A ???=+=??sin ),cos 1(.r y r x B ???+==)sin 1(,cos .??r y r x c ? ??=+=??2sin ),2cos 1(.r y r x D 答案:D 4.直线t t y t x (531,541??? ????-=+=为参数)被曲线)4(2πθρ+∞=s 所截的弦长为 答案:5 7 课堂设计 方法备考 题型一 直线的参数方程及应用 【例1】已知直线l 经过点A(l ,2),倾斜角为 ?3 π (1)求直线l 的参数方程; (2)求直线l 和圆922=+y x 的两个交点到点A 的距离之积. 题型二 圆的参数方程及应用 【例2】已知P(x ,y)是圆022 2=-+y y x 上的动点. (1)求y x +2的取值范围. (2)若0≥++c y x 恒成立,求实数C 的取值范围. 题型三 椭圆的参数方程及应用 【例3】如图所示,已知点M 是椭圆)0(122 22>>=+b a b y a x 上在第一象限的点,A(a ,O)和B(O ,b)是椭圆的两个顶点,O 为原点,求四边形MAOB 的面积的最大值. 题型四 参数方程与极坐标的综合问题 【例4】(2011.课标全国卷)在直角坐标系xOy 中,曲线1c 的参数方程为?? ???+==.sin 22(,cos 2αααy x 为参数)M 是C ,上的动点,P 点满足P OM OP ,2=点的轨迹为曲线?2c
【2021模块复习】第十二章 第1节 第2课时 参数方程+参考答案
1 第2课时 参数方程 最新考纲 1.了解参数方程,了解参数的意义;2.能选择适当的参数写出直线、圆和椭圆的参数方程. 知 识 梳 理 1.曲线的参数方程 一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数t 的函数?????x =f (t ),y =g (t ), 并且对于t 的每一个允许值,由这个方程组所确定的点M (x ,y )都在这条曲线上,那么这个方程组就叫做这条曲线的参数方程,联系变数x ,y 的变数t 叫做参变数,简称参数. 2.参数方程与普通方程的互化 通过消去参数从参数方程得到普通方程,如果知道变数x ,y 中的一个与参数t 的关系,例如x =f (t ),把它代入普通方程,求出另一个变数与参数的关系y =g (t ), 那么?????x =f (t ),y =g (t ) 就是曲线的参数方程.在参数方程与普通方程的互化中,必须使x ,y 的取值范围保持一致. 3.常见曲线的参数方程和普通方程 点的轨迹 普通方程 参数方程 直线 y -y 0=tan α(x -x 0) ?????x =x 0+t cos α,y =y 0+t sin α (t 为参数)
2 圆 x 2+y 2=r 2 ?????x =r cos θ,y =r sin θ(θ为参数) 椭圆 x 2a 2+y 2b 2=1(a >b >0) ?????x =a cos φ,y =b sin φ(φ为参数) 温馨提醒 直线的参数方程中,参数的系数的平方和为1时,才有几何意义且几何意义为:|t |是直线上任一点M (x ,y )到M 0(x 0,y 0)的距离. [微点提醒] 1.将参数方程化为普通方程时,要注意防止变量x 和y 取值范围的扩大或缩小,必须根据参数的取值范围,确定函数f (t )和g (t )的值域,即x 和y 的取值范围. 2.参数方程化普通方程常用的消参技巧:代入消元、加减消元、平方后加减消元等,经常用到公式cos 2 θ+sin 2 θ=1,1+tan 2 θ= 1cos 2 θ. 基 础 自 测 1.判断下列结论正误(在括号内打“√”或“×”) (1)参数方程?????x =f (t ),y =g (t ) 中的x ,y 都是参数t 的函数.( ) (2)过M 0(x 0,y 0),倾斜角为α的直线l 的参数方程为?????x =x 0+t cos α,y =y 0+t sin α (t 为参数).参数t 的几何意义表示:直线l 上以定点M 0为起点,任一点M (x ,y )为终点的有 向线段M 0M →的数量.( ) (3)方程?????x =2cos θ,y =1+2sin θ (θ为参数)表示以点(0,1)为圆心,以2为半径的圆.( )
高中数学选修4-4坐标系与参数方程完整教案(精选.)
选修4-4 教案 教案1 平面直角坐标系(1 课时) 教案2 平面直角坐标系中的伸缩变换(1 课时)教案3 极坐标系的的概念(1 课时) 教案4 极坐标与直角坐标的互化(1 课时) 教案5 圆的极坐标方程(2 课时) 教案6 直线的极坐标方程(2 课时) 教案7 球坐标系与柱坐标系(2 课时) 教案8 参数方程的概念(1 课时) 教案9 圆的参数方程及应(2 课时) 教案10 圆锥曲线的参数方程(1 课时) 教案11圆锥曲线参数方程的应用(1 课时)教案12 直线的参数方程(2 课时) 教案13 参数方程与普通方程互化(2 课时)教案14 圆的渐开线与摆线(1 课时)
课题:1、平面直角坐标系教学目的: 知识与技能:回顾在平面直角坐标系中刻画点的位置的方法能力与与方法:体会坐标系的作用 情感、态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识教学重点:体会直角坐标系的作用教学难点:能够建立适当的直角坐标系,解决数学问题授课类型:新授课 1 2 坐标系的作用————教学过程————复习回顾和预习检查 1 平面直角坐标系中刻画点的位置的方法 情境1:为了确保宇宙飞船在预定的轨道上运行,并在按计划完成科学考察任务后,安全、准确的返回地球,从火箭升空的时刻开始,需要随时测定飞船在空 中的位置机器运动的轨迹。 情境2:运动会的开幕式上常常有大型团体操的表演,其中不断变化的背景图案是由看台上座位排列整齐的人群不断翻动手中的一本画布构成的。要出现正确 的背景图案,需要缺点不同的画布所在的位置。 刻画一个几何图形的位置,需要设定一个参照系 1、数轴它使直线上任一点P都可以由惟一的实数x 确定 2、平面直角坐标系 在平面上,当取定两条互相垂直的直线的交点为原点,并确定了度量单位和这两条直线的方向,就建立了平面直角坐标系。它使平面上任一点P 都可以由惟一的实数对(x,y)确定 3、空间直角坐标系 在空间中,选择两两垂直且交于一点的三条直线,当取定这三条直线的交点为原点,并确定了度量单位和这三条直线方向,就建立了空间直角坐标系。它使空间上任一点P 都可以由惟一的实数对(x,y,z)确定1、建立坐标系是为了确定点的位置,因此,在所建的坐标系中应满足:任意一点都有确定的坐标与其对应;反之,依据一个点的坐标就能确定这个点的位置 2、确定点的位置就是求出这个点在设定的坐标系中的坐标 word.
2012-2013高中数学《第二讲 参数方程》真题考点 新人教A版选修4-4
第二讲 参数方程 本章归纳整合 高考真题 1.(2011·江西高考)若曲线的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x 轴正半轴建立直角坐标系,则该曲线的直角坐标方程为________. [命题意图]本小题主要考查了极坐标系、极坐标方程与直角坐标方程的互化. 解析 由??? ? ?x =ρcos θy =ρsin θ 得,cos θ=x ρ,sin θ=y ρ ,ρ2=x 2+y 2 ,代入ρ=2sin θ+4cos θ得,ρ=2y ρ+4x ρ?ρ2=2y +4x ?x 2+y 2-4x -2y =0. 答案 x 2 +y 2 -4x -2y =0 2.(2011·广东高考)已知两曲线参数方程分别为???x =5cos θ, y =sin θ(0≤θ<π)和?????x =54t 2,y =t (t ∈R ),它们的 交点坐标为________. [命题意图]本题考查参数方程问题,主要考查转化与化归思想.将参数方程 转化为直角坐标方程的关键在于消去参数,但也要注意所给参数的取值范围. 解析 由???x =5cos θ,y =sin θ (0≤θ<π),得x 25+y 2 =1(y ≥0, x ≠-5),由?????x =54t 2,y =t (t ∈R ),得x =54y 2,联立方程可得?????x 2 5+y 2 =1,x =54 y 2 , 则5y 4 +16y 2-16=0,解得y 2=45或y 2 =-4(舍去),则x =54 y 2=1,又y ≥0,所以 其交点坐标为? ???? 1,255. 答案 ? ???? 1,255 3.(2011·江苏高考)在平面直角坐标系xOy 中,求过椭圆??? ? ?x =5cos φ,y =3sin φ (φ为参数)的右焦点,且与直线 ? ????x =4-2t , y =3-t (t 为参数)平行的直线的普通方程为________. [命题意图]本小题主要考查椭圆及直线的参数方程等基础知识,考查转化问
2参数方程知识讲解及典型例题
参数方程 一、定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个参数 t 的函数,即 ?? ?==)()(t f y t f x ,其中,t 为参数,并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数t 叫做参变数,简称参数. 1 y x Eg1(1 Eg2(1总结:参数方程化为普通方程步骤:(1)消参(2)求定义域 2、椭圆的参数方程: 中心在原点,焦点在x 轴上的椭圆: θ θsin cos b y a x == (θ为参数,θ的几何意义是离心角,如图角AON 是离心角)
注意:离心率和离心角没关系,如图,分别以椭圆的长轴和短轴为半径画两个同心圆,M 点的轨迹是椭圆,中心在(x 0,y 0 θ θ sin cos 00b y y a x x +=+= Eg 3, 4 pt y pt x 222 == (t 为参数,p >0,t 的几何意义为过圆点的直线的斜率的倒数) 直线方程与抛物线方程联立即可得到。 三、一次曲线(直线)的参数方程 过定点P 0(x 0,y 0),倾角为α的直线, P 是直线上任意一点,设P 0P=t ,P 0P 叫点P 到定点P 0的有向距离,在P 0两侧t 的符号相反,直线的参数方程
αα sin cos 00t y y t x x +=+= (t 为参数,t 的几何意义为有向距离) 说明:①t 的符号相对于点P 0,正负在P 0点两侧 ②|P 0P |=|t | 直线参数方程的变式: bt y y at x x +=+=00,但此时t 的几何意义不是有向距离,只有当 t 得 y x Eg
人教新课标版数学高二-练习2014人教数学选修4-4【综合检测】第二讲 参数方程
(时间:120分钟,满分:150分) 一、选择题(本大题共12小题.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.参数方程? ??? ? x =3t 2+2y =3t 2-1(0≤t ≤5)表示的曲线是( ) A .线段 B .双曲线的一支 C .圆弧 D .射线 答案:A 2.圆的参数方程为? ???? x =4cos θy =4sin θ(θ为参数,0≤θ<2π),若Q (-2,23)是圆上一点,则 参数θ的值是( ) A.π3 B.2π 3 C.4π3 D.5π3 答案:B 3.直线y =2x +1的参数方程是( ) A.? ???? x =t 2y =2t 2+1(t 为参数) B.????? x =2t -1y =4t +1(t 为参数) C.????? x =t -1y =2t -1(t 为参数) D.? ???? x =sin θy =2sin θ+1(θ为参数) 答案:C 4.参数方程??? x =2+t y =3-4-t 2 (t 为参数)表示的曲线为( ) A .半圆 B .圆 C .双曲线 D .椭圆 答案:A
5.参数方程? ???? x =2+sin 2θ y =-1+cos 2θ(θ为参数)化为普通方程是( ) A .2x -y +4=0 B .2x +y -4=0 C .2x -y +4=0 x ∈[2,3] D .2x +y -4=0 x ∈[2,3] 答案:D 6.已知集合A ={(x ,y )|(x -1)2+y 2=1},B ={(x ,y )|y x ·y x -2 =-1},C ={(ρ,θ)|ρ=2cos θ,θ≠k π 4,k ∈Z },D ={(x ,y )|? ???? x =1+cos θy =sin θ,θ≠k π,k ∈Z },下列等式成立的是( ) A .A = B B .B =D C .A =C D .B =C 答案:B 7.设圆? ???? x =3+r cos θy =-5+r sin θ(θ为参数)上有且仅有两点到直线-4x +3y +2=0的距离等于 1,则r 的取值范围是( ) A .4 一 曲线的参数方程 庖丁巧解牛 知识·巧学 一、参数方程的概念 一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即? ??==)(),(t g y t f x (*).并且对于t 的每一个允许值,由方程组(*)所确定的点M(x,y)都在这条曲线上,那么方程组(*)就叫做这条曲线的参数方程,联系x 、y 之间关系的变数t 叫做参变数,简称参数.相对于参数方程来说,以前所学习过的关于x 、y 的直角坐标方程,叫做曲线的普通方程. 在求曲线的方程时,一般需要建立曲线上动点P (x ,y )的坐标x,y 之间满足的等量关系F (x ,y )=0,这样得到的方程F (x ,y )=0就是曲线的普通方程;而有时要想得到联系x,y 的方程F (x ,y )=0是比较困难的,于是可以通过引入某个中间变量t ,使之与曲线上动点P 的坐标x,y 间接地联系起来,此时可得到方程组???==) (),(t g y t f x 即点P 的运动通过变量t 的变化进行描述.若对t 的每一个值,由方程组确定的点(x ,y )都在曲线C 上;反之,对 于曲线C 上的每一个点(x ,y ),其中x,y 都是t 的函数,则把方程组? ??==)(),(t g y t f x 叫做曲线C 的参数方程,其中的t 称为参数.在具体问题中的参数可能有相应的几何意义,也可能没有什么明显的几何意义. 疑点突破 参数的选取应根据具体条件来考虑.但有时出于题目需要,也可以选两个或两个以上的参数,然后再设法消去其中的参数得到普通方程,或剩下一个参数得到参数方程.但这样做往往增加了变形与计算的麻烦,因此参数的选取一般应尽量少.一般说来,选择参数时应注意考虑以下两点:一是曲线上每一点的坐标(x,y)都不可能由参数取某一值唯一地确定出来;二是参数与x 、y 的相互关系比较明显,容易列出方程. 深化升华 参数法在求曲线的轨迹方程时是一种常用的甚至是简捷的解题方法.参数的思想方法就是在运动变化的哲学思想指导下的函数的思想方法,因此也可认为引入参数就是引入函数的自变量. 二、圆的参数方程 1.圆心在原点、半径为r 的圆的参数方程:???==θ θsin ,cos r y r x (θ为参数). 2.圆心为O 1(a,b),半径为r 的圆的参数方程:?? ?+=+=θθsin ,cos r b y r a x (θ为参数). 参数θ的几何意义是:以x 轴正半轴为始边,以OP 为终边的角(其中O 为坐标原点,P 为圆上一动点). 圆的参数方程还可以表示为x=???+=+=θ θcos ,sin r b y r a x (θ为参数). 坐标系与参数方程 1.平面直角坐标系中的坐标伸缩变换 设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0) x x y y λλ?μμ'=>?? '=>?的 作用下,点P(x,y)对应到点(,)P x y ''',称?为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念 (1)极坐标系 如图所示, 在平面取一个定点O ,叫做极点, 自极点O 引一条射线Ox ,叫做极轴; 再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系. 注:(i)极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景; (ii)平面直角坐标系的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系. (2)极坐标 设M 是平面一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ; 以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ. 有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ. 一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面一个点的极坐标有无数种表示. 如果规定0,02ρθπ>≤<,那么除极点外,平面的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的. 3.极坐标和直角坐标的互化 (1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴 作为极轴,并在两种坐标系中取相同的长度单位,如图所示: (2)互化公式:设M 是坐标平面任意一点,它的直角 坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与 直角坐标的互化公式如下: 极坐标(,)ρθ 直角坐标(,)x y : cos sin x y ρθ ρθ=??=? 直角坐标(,)x y 极坐标(,)ρθ: 222 tan (0) x y y x x ρθ=+=≠ 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程 第二节参数方程 目录 第二节参数方程 (1) 考点一求曲线的参数方程 (3) 考点二参数方程与普通方程的互化 (3) 考点三圆和圆锥曲线的参数方程问题应用及其最值问题 (5) 考点五直线的参数方程及其应用 (10) 考点六利用参数法求轨迹方程 (13) 考点七极坐标参数方程的综合应用 (13) 一、基础知识 1.曲线的参数方程 在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数t 的函数????? x =f (t ),y =g (t ),并且对于t 的每一个允许值,由这个方程组所确定的点M (x ,y )都在这条曲线上,那么这个方程组就叫做这条曲线的参数方程,联系变数x ,y 的变数t 叫做参变数,简称参数. 相对于参数方程而言,直接给出点的坐标间关系的方程F (x ,y )=0叫做普通方程. 2.参数方程和普通方程的互化 (1)参数方程化普通方程:利用两个方程相加、减、乘、除或者代入法消去参数. (2)普通方程化参数方程:如果x =f (t ),把它代入普通方程,求出另一个变数与参数的关系y =g (t ),则 得曲线的参数方程????? x =f (t ),y =g (t ). 3.直线、圆、椭圆的参数方程 (1)过点M (x 0,y 0),倾斜角为α的直线l 的参数方程为()00cos sin x x t t y y t αα =+??=+?为参数. 注意:直线的参数方程可以写成这样的形式:()00x x at t y y bt =+??=+?为参数,当221a b +=且b >0时,0t M M = 此时,我们可以认为cos sin a b αα==,若[)0απ∈,,则α为倾斜角。 直线参数方程的标准形式的应用 过点M 0(x 0,y 0),倾斜角为α的直线l 的参数方程是()00cos sin x x t t y y t αα =+?? =+?为参数,若M 1,M 2是l 上的两点,其对应参数分别为t 1,t 2,则. ①|M 1M 2|=|t 1-t 2|. ②若线段M 1M 2的中点M 所对应的参数为t ,则t =t 1+t 22,中点M 到定点M 0的距离|MM 0|=|t |=???? ??t 1+t 22. ③若M 0为线段M 1M 2的中点,则t 1+t 2=0. ④|M 0M 1||M 0M 2|=|t 1t 2|. 选修4-4教案 教案1平面直角坐标系(1课时) 教案2平面直角坐标系中的伸缩变换(1课时) 教案3极坐标系的的概念(1课时) 教案4极坐标与直角坐标的互化(1课时) 教案5圆的极坐标方程(2课时) 教案6直线的极坐标方程(2课时) 教案7球坐标系与柱坐标系(2课时) 教案8参数方程的概念(1课时) 教案9圆的参数方程及应(2课时) 教案10圆锥曲线的参数方程(1课时) 教案11圆锥曲线参数方程的应用(1课时) 教案12直线的参数方程(2课时) 教案13参数方程与普通方程互化(2课时) 教案14圆的渐开线与摆线(1课时) 课题:1、平面直角坐标系 教学目的: 知识与技能:回顾在平面直角坐标系中刻画点的位置的方法 能力与与方法:体会坐标系的作用 情感、态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识。 教学重点:体会直角坐标系的作用 教学难点:能够建立适当的直角坐标系,解决数学问题 授课类型:新授课 教学模式:互动五步教学法 教具:多媒体、实物投影仪 复习及预习提纲: 1平面直角坐标系中刻画点的位置的方法 2坐标系的作用 ————教学过程———— 复习回顾和预习检查 1平面直角坐标系中刻画点的位置的方法 2坐标系的作用 创设情境,设置疑问 情境1:为了确保宇宙飞船在预定的轨道上运行,并在按计划完成科学考察任务后,安全、准确的返回地球,从火箭升空的时刻开始,需要随时测定飞船在空中的位置机器运动的 轨迹。 情境2:运动会的开幕式上常常有大型团体操的表演,其中不断变化的背景图案是由看台上座位排列整齐的人群不断翻动手中的一本画布构成的。要出现正确的背景图案,需要缺 点不同的画布所在的位置。 问题1:如何刻画一个几何图形的位置? 问题2:如何创建坐标系? 分组讨论 刻画一个几何图形的位置,需要设定一个参照系 1、数轴它使直线上任一点P都可以由惟一的实数x确定 2、平面直角坐标系 在平面上,当取定两条互相垂直的直线的交点为原点,并确定了度量单位和这两条直线的方向,就建立了平面直角坐标系。它使平面上任一点P都可以由惟一的实数对(x,y)确定 3、空间直角坐标系 在空间中,选择两两垂直且交于一点的三条直线,当取定这三条直线的交点为原点,并确定了度量单位和这三条直线方向,就建立了空间直角坐标系。它使空间上任一点P都可以由惟一的实数对(x,y,z)确定 1、建立坐标系是为了确定点的位置,因此,在所建的坐标系中应满足: 任意一点都有确定的坐标与其对应;反之,依据一个点的坐标就能确定这个点的位置 2、确定点的位置就是求出这个点在设定的坐标系中的坐标 例1 选择适当的平面直角坐标系,表示边长为1的正六边形的顶点。 *变式训练 如何通过它们到点O的距离以及它们相对于点O的方位来刻画,即用”距离和方向”确定点的位置? 例2 已知B村位于A村的正西方1公里处,原计划经过B村沿着北偏东60的方向设一条地下管线m.但在A村的西北方向400米出,发现一古代文物遗址W.根据初步勘探的结果,文物管理部门将遗址W 周围100米范围划为禁区.试问:埋设地下管线m的计划需要修改吗? 落实目标 *变式训练 1.一炮弹在某处爆炸,在A处听到爆炸的时间比在B处晚2s,已知A、B两地相距800米,并且(新)高中数学第二讲参数方程一曲线的参数方程导学案新人教A版选修4-41
坐标系与参数方程-知识点总结
破解高考数学压轴题之 参数方程
高中数学选修4-4坐标系与参数方程完整教案
