中考数学圆与相似综合经典题及答案解析.docx

中考数学圆与相似综合经典题及答案解析一、相似

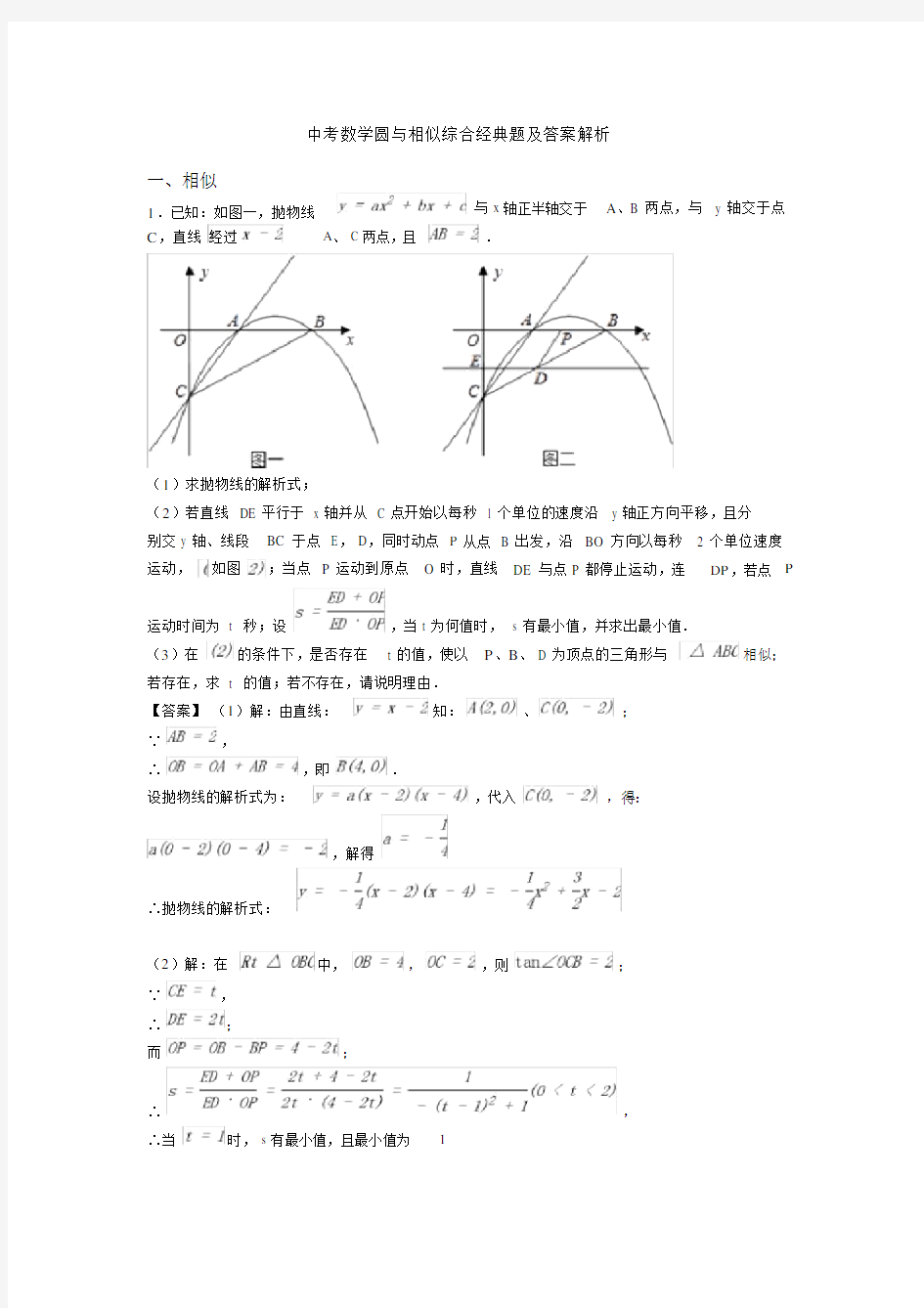
1．已知：如图一，抛物线

C，直线经过A、 C 两点，且与 x

．

轴正半轴交于A、B 两点，与y 轴交于点

（1）求抛物线的解析式；

（2）若直线 DE 平行于 x 轴并从 C 点开始以每秒 1 个单位的速度沿 y 轴正方向平移，且分

别交 y 轴、线段BC 于点 E， D，同时动点P 从点运动，如图；当点P 运动到原点O 时，直线B 出发，沿BO 方向以每秒 2 个单位速度DE 与点 P 都停止运动，连DP，若点P

运动时间为 t秒；设，当 t 为何值时， s 有最小值，并求出最小值．

（3）在的条件下，是否存在t 的值，使以P、B、 D 为顶点的三角形与相似；若存在，求 t的值；若不存在，请说明理由．

【答案】（1）解：由直线：知：、；

∵，

∴，即．

设抛物线的解析式为：，代入，得：

，解得

∴抛物线的解析式：

（2）解：在中，，，则；

∵，

∴；

而；

∴，

∴当时， s 有最小值，且最小值为1

（3）解：在中，在中，，

∴

以 P、 B、 D 为顶点的三角形与

；

，，则

，则

相似，已知

；

；

，则有两种情况：，解得；

，解得；

综上，当或时，以P、B、D为顶点的三角形与相似

【解析】【分析】（ 1）由直线与坐标轴相交易求得点A、 C 的坐标，用待定系数法即可求

得抛物线的解析式；

（2）由题意可将ED、 OP 用含 t 的代数式表示出来，并代入题目中的s 与 OP、 DE 的关系

式整理可得s=（0

值越小，则当分母最大时，分式的值越小，即t=1 时， s 有最小值，且最小值为1；

（ 3）解直角三角形可得BC 和 CD、 BD 的值，根据题意以P、 B、 D 为顶点的三角形与

△ABC相似所得的比例式有两种情况：，，将这些线段代入比例式即可求

解。

2．

（1）问题发现：

如图 1，在等边三角形ABC中，点 M 为 BC 边上异于B、 C 的一点，以AM 为边作等边三角

形 AMN ，连接 CN， NC 与 AB 的位置关系为 ________；

（2）深入探究：

如图 2，在等腰三角形 ABC中， BA=BC，点 M 为 BC边上异于 B、C 的一点，以 AM 为边作等腰三角形 AMN ，使∠ ABC=∠ AMN， AM=MN ，连接 CN，试探究∠ ABC 与∠ACN 的数量关系，并说明理由；

（3）拓展延伸：

如图 3，在正方形ADBC 中， AD=AC，点 M 为 BC 边上异于B、C 的一点，以AM 为边作正方形 AMEF，点 N 为正方形AMEF 的中点，连接CN，若

【答案】（1） NC∥ AB

BC=10， CN=，试求EF的长．

（2）解：∠ ABC=∠ ACN，理由如下：

∵=1 且∠ ABC=∠ AMN ，∴△ ABC～△ AMN

∴，

∵A B=BC，

∴∠ BAC=（180°﹣∠ABC），

∵AM=MN

∴∠ MAN=（180﹣°∠ AMN），

∵∠ ABC=∠ AMN ，

∴∠ BAC=∠ MAN ，

∴∠ BAM=∠ CAN，

∴△ ABM～△ ACN，

∴∠ ABC=∠ ACN

（3）解：如图3，连接 AB， AN，

∵四边形 ADBC， AMEF 为正方形，

∴∠ ABC=∠ BAC=45 ，°∠ MAN=45 °，∴∠ BAC﹣∠MAC=∠ MAN ﹣∠ MAC 即∠ BAM=∠ CAN，

∵，

∴，

∴△ ABM～△ ACN

∴，

∴=cos45 = °，

∴，

∴B M=2，

∴CM=BC﹣ BM=8，

在 Rt△ AMC，

AM=，

∴EF=AM=2．

【解析】【解答】解：（1） NC∥ AB，理由如下：

∵△ ABC与△ MN 是等边三角形，

∴A B=AC， AM=AN，∠BAC=∠

MAN=60 °，∴∠ BAM=∠ CAN，

在△ ABM 与△ ACN 中，

，

∴△ ABM≌ △ ACN（ SAS），

∴∠ B=∠ACN=60 ，°

∵∠ ANC+∠ ACN+∠ CAN=∠ ANC+60 +°∠CAN=180 ，°

∴∠ ANC+∠ MAN+∠ BAM=∠ANC+60 +°∠ CAN=∠ BAN+∠

ANC=180 ，°∴CN∥ AB；

【分析】（1）由题意用边角边易得△ABM≌△ACN，则可得∠B=∠ACN=60°，所以∠BCN+∠

B=∠BCA+∠ ACN+∠ B=180 ，°根据平行线的判定即可求解；

（2）由题意易得△ABC～△AMN，可得比例式，由三角形内角和定理易得

∠BAM=∠ CAN，根据相似三角形的判定可得△ ABM～△ACN，由相似三角形的性质即可求

解；

（3）要求EF 的值，只须求得CM 的值，然后解直角三角形AMC 即可求解。连接AB，AN，由正方形的性质和相似三角形的判定易得△ABM～△ACN，可得比例式

，可求得 BM 的值，而 CM=BC﹣ BM，解直角三角形 AMC 即可求得

AM 的值，即为 EF的值。

3．如图 1，在矩形ABCD 中， AB=6cm， BC=8cm， E、 F 分别是AB、 BD 的中点，连接EF，

点 P 从点 E 出发，沿EF方向匀速运动，速度为1cm/s ，同时，点Q 从点 D 出发，沿DB 方

向匀速运动，速度为 2cm/s ，当点 P 停止运动时，点 Q 也停止运动．连接 PQ，设运动时间为 t

（0＜ t＜ 4） s，解答下列问题：

（1）求证：△ BEF∽△ DCB；

（2）当点 Q 在线段 DF 上运动时，若△ PQF的面积为 0.6cm2，求 t 的值；（3）当 t 为何值时，△ PQF为等腰三角形？试说明理由．

【答案】（1）解：∵四边形 ABCD是矩形，

∴AD∥ BC，

在中，

∵别是的中点，

∴EF∥ AD，

∴EF∥ BC，

∴

∴

（2）解：如图1，过点Q 作于，

∴QM∥ BE，

∴

∴

∴（舍）或秒

（3）解：当点 Q 在 DF 上时，如图2，

∴

∴.

当点 Q 在 BF 上时，，如图3，

∴

∴

时，如图 4，

∴

∴

时，如图 5，

∴

∴

综上所述， t=1 或 3 或或秒时，△ PQF是等腰三角形

【解析】【分析】（ 1）根据题中的已知条件可得△BEF和△ DCB中的两角对应相等，从而

可证△ BEF∽ △ DCB；（ 2）过点 Q 作 QM ⊥ EF 于 M ，先根据相似三角形的预备定理可证△QMF ∽ △BEF；再由△ QM F ∽ △ BEF可用含 t 的代数式表示出QM 的长；最后代入三角

形的面积公式即可求出 t 的值。（ 3）由题意应分两种情况：（ 1）当点 Q 在 DF 上时，因为∠PFQ为钝角，所以只有 PF = QF 。（ 2）当点 Q 在 BF 上时，因为没有指明腰和底，所以有

PF=QF； PQ = FQ； PQ = PF三种情况，因此所求的 t 值有四种结果。

4．如图 1，在△ ABC 中，∠ BAC=90°， AB=AC=4， D 是 BC 上一个动点，连接 AD，以 AD 为边向右侧作等腰直角△ ADE，其中∠ ADE=90°．

（1）如图2，G，H 分别是边AB，BC 的中点，连接DG，AH，EH．求证：△AGD∽ △AHE；

（2）如图 3，连接 BE，直接写出当 BD 为何值时，△ABE 是等腰三角形；

（3）在点 D 从点 B 向点 C 运动过程中，求△ABE 周长的最小值．

【答案】（1）证明：如图2，由题意知△ABC和△ ADE都是等腰直角三角形，

∴∠ B=∠DAE=45 ．°

∵H 为 BC中点，

∴AH⊥ BC．

∴∠ BAH=45 =°∠ DAE．

∴∠ GAD=∠HAE．

在等腰直角△ BAH 和等腰直角△ DAE 中，

AH＝AB＝AG， AE＝AD．

∴，

∴△ AGD∽△ AHE；

（2）解：分三种情况：① 当B与D重合时，即BD=0，如图 3，此时 AB=BE；

②当 AB=AE 时，如图4，此时 E 与 C 重合，

∴D 是 BC的中点，

∴B D= BC=2 ；

③当 AB=BE时，如图 5，过 E 作 EH⊥ AB 于 H，交 BC 于 M，连接 AM，过 E 作 EG⊥BC 于G，连接 DH，

∵A E=BE，EH⊥AB，

∴AH=BH，

∴AM=BM ，∵∠

ABC=45 ，°

∴AM ⊥ BC，△ BMH 是等腰直角三角形，

∵AD=DE，∠ ADE=90 ，°

易得△ ADM≌ △ DEG，

∴DM=EG，

∵∠ EMG=∠ BMH=45 °，

∴△ EMG 是等腰直角三角形，

∴ME=MG，

由（ 1）得：△ AHD∽△ AME，且，

∴∠ AHD=∠AME=135 ，°ME=DH，

∴∠ BHD=45 ，°MG=DH，

∴△ BDH 是等腰直角三角形，

∴BD=DH=EG=DM=；

综上所述，当BD=0 或或2时，△ ABE是等腰三角形；

（3）解：当点 D 与点 B 重合时，点 E 的位置记为点M，连接 CM，如图 6，

此时，∠ ABM=∠BAC=90°，∠ AMB=∠ BAM=45°，BM=AB=AC．

∴四边形 ABMC 是正方形．

∴∠ BMC=90 °，

∴∠ AMC=∠ BMC-∠ AMB=45 °，

∵∠ BAM=∠ DAE=45 ，°

∴∠ BAD=∠ MAE，

在等腰直角△ BAM 和等腰直角△ DAE中，

AM＝AB，AE＝AD．

∴．

∴△ ABD∽△ AME．

∴∠ AME=∠ ABD=45 °

∴点 E 在射线 MC 上，

作点 B 关于直线MC 的对称点 N，连接 AN 交 MC 于点 E′，

∵B E+AE=NE+AE ≥ AN=NE ′ +AE ′， =BE ′ +AE ′

∴△ ABE就′是所求周长最小的△ ABE．

在 Rt△ ABN 中，

∵A B=4， BN=2BM=2AB=8，

∴AN＝．

∴△ ABE 周长最小值为AB+AN＝ 4+4．

【解析】【分析】（ 1 ）由等腰直角三角形的性质可得∠B=∠DAE=∠ BAH=45°，所以

∠GAD=∠ HAE，计算可得比例式：，根据有两对边对应相等，且它们的夹角也相等

的两个三角形相似可得△ AGD∽△ AHE；

（2）根据等腰三角形的定义可知分 3 种情况讨论：①当 B 与 D 重合时，即BD=0，此时AB=BE；

C 重合，用勾股定理可求得B

D 的值；

②当 AB=AE 时，此时E

与

③ 当AB=BE时，

过E 作EH⊥ AB 于H，交BC

于

M，连接AM，过 E 作EG⊥ BC 于G，连接

DH，由已知条件和（1）的结论可求解；

（3）当点 D 与点 B 重合时，点 E 的位置记为点M，连接 CM，作点 B 关于直线MC 的对称

点 N，连接 AN 交 MC 于点 E′，由已知条件易证四边形ABMC 是正方形，由已知条件通过计

算易得比例式：,根据有两对边对应相等，且它们的夹角也相等的两个三角形相似

可得△ ABD∽ △ AME,则∠AME=∠ABD=45°，于是可得点 E 在射线MC 上，根据轴对称的性质可得△ ABE′就是所求周长最小的△ABE，在Rt△ ABN中，用勾股定理即可求得AN 的值，

则△ ABE 周长最小值 =AB+AN 即可求解。

5．已知抛物线 y＝ ax2＋ bx＋ 5 与 x 轴交于点 A(1， 0)和点 B(5， 0)，顶点为 M．点 C 在 x 轴的负

半轴上，且 AC＝ AB，点 D 的坐标为 (0， 3)，直线 l 经过点 C、D．

（1）求抛物线的表达式；

（2）点 P 是直线 l 在第三象限上的点，联结 AP，且线段 CP是线段 CA、 CB的比例中项，求

tan∠ CPA的值；

（3）在（ 2）的条件下，联结 AM、 BM，在直线 PM 上是否存在点 E，使得∠ AEM=∠AMB.

若存在，求出点 E 的坐标；若不存在，请说明理由．

【答案】（1）解：∵抛物线与x轴交于点A（ 1， 0）， B（5， 0），

∴,

解得

∴ 抛物线的解析式为

（2）解：∵ A（1， 0）， B（ 5， 0），

∴OA=1， AB=4.

∵AC=AB且点 C 在点 A 的左侧，

∴ AC=4 .

∴CB=CA+AB=8.

∵线段 CP 是线段 CA、 CB 的比例中项，

∴.

∴CP=.

又∵ ∠ PCB是公共角，

∴ △CPA∽△CBP .

∴ ∠ CPA=∠ CBP.

过 P 作 PH⊥ x 轴于 H.

∵OC=OD=3，∠DOC=90 ，°∴

∠ DCO=45 .°∴ ∠ PCH=45 °

∴ PH=CH=CP=4，

∴H（ -7， 0）， BH=12，

∴P（ -7，-4），

∴，

tan∠ CPA=.

（3）解：∵抛物线的顶点是 M （3， -4），又∵ P（ -7，-4），

∴PM∥x 轴 .

当点 E 在 M 左侧，则∠BAM=∠ AME.

∵ ∠ AEM=∠ AMB，

∴ △ AEM∽ △ BMA.

∴,

∴.

∴ME=5，∴ E（ -2， -4） .

过点 A 作 AN⊥ PM 于点 N，则 N（ 1， -4） .

当点 E 在 M 右侧时，记为点，

∵ ∠ A N=∠AEN，

∴ 点与 E 关于直线 AN 对称，则（4，-4） .

综上所述， E 的坐标为（ -2， -4）或（ 4，-4） .

【解析】【分析】（ 1）用待定系数法即可求解。即;由题意把A（ 1，0）， B（5，0），代

入解析式可得关于a、 b 的方程组， a + b + 5 = 0 ， 25 a + 5 b + 5 = 0,解得 a=1、 b=-6，所以

抛物线的解析式为y =- 6 x + 5；

(2)过 P 作 PH⊥ x 轴于H.由题意可得OA=1， AB=4.而 AC=AB 且点 C 在点 A 的左侧，所以

AC=4 ，则CB=CA+AB=8，已知线段CP 是线段 CA、 CB 的比例中项，所以,解得 CP=

4 ，因为∠PCB 是公共角，所以根据相似三角形的判定可得△ CPA∽△ CBP，所以∠ CPA=

∠CBP；因为OC=OD=3，∠ DOC=90 ，°∠ DCO=45 .°所以∠ PCH=45 ，°在直角三角形PCH 中，PH=CH=CP sin 45 ° =4，所以 H（ -7， 0）， BH=12，则 P（ -7，-4），在直角三角形PBH

中， tan∠CBP ==tan∠ CPA;

（3）将（1）中的解析式配成顶点式得y=-4,所以抛物线的顶点是M（ 3， -4），而

P 点的纵坐标也为-4 ，所以PM∥ x 轴.分两种情况讨论：当点∠BAM=∠ AME，而∠AEM=∠ AMB，根据相似三角形的判定可得

E在M左侧，则△ AEM∽ △ BMA，所以可

得比例式,即,解得 ME=5，所以E（ -2，-4）；当点 E 在 M 右侧时，记为点 E ′，过点 A 作 AN⊥ PM 于点 N，则 N（ 1， -4），因为∠ A E′ ∠N=AEN，所以根据轴对

称的意义可得点 E ′与 E 关于直线AN 对称，则（4，-4）.

6．问题提出；

（1）如图1，矩形 ABCD， AB＝4， BC＝ 8，点 E 为 CD 的中点，点P 为 BC 上的动点， CP＝________时，△ APE的周长最小 .

（2）如图2，矩形 ABCD， AB＝ 4，BC＝ 8，点 E 为 CD 的中点，点P、点 Q 为 BC 上的动点，且 PQ＝ 2，当四边形 APQE的周长最小时，请确定点P 的位置（即 BP 的长）

问题解决；

（3）如图3，某公园计划在一片足够大的等边三角形水域内部（不包括边界）点P 处修一个凉亭，设计要求PA 长为 100 米，同时点M ，N 分别是水域AB， AC 边上的动点，连接

AMPN的面积最大，请你帮忙算算此时四边形

P、 M 、N 的水上浮桥周长最小时，四边形

AMPN 面积的最大值是多少？

【答案】（ 1）

（2）解：点 A 向右平移 2 个单位到 M，点 E 关于 BC的对称点 F，连接 MF，交 BC 于 Q，此时MQ+EQ 最小，

∵PQ＝ 3， DE＝ CE＝2，AE＝ 2，

∴要使四边形APQE的周长最小，只要AP+EQ最小就行，

即 AP+EQ＝MQ+EQ，过 M 作 MN ⊥BC于 N，

∴MN ∥ CD

∴△ MNQ∽ △ FCQ，

∴

∴

∴NQ＝ 4

∴BP＝ BQ﹣ PQ＝ 4+2﹣ 2＝4

（3）解 :如图，作点 P 关于 AB 的对称点 G，作点 P 关于 AC 的对称点 H，连接 GH，交AB， AC 于点 M， N，此时△PMN 的周长最小 .

∴AP＝AG＝ AH＝ 100 米，∠ GAM＝∠ PAM，∠ HAN＝∠ PAN，

∵∠ PAM+∠ PAN＝ 60 °，

∴∠ GAH＝ 120 ，°且 AG＝ AH，

∴∠ AGH＝∠AHG＝ 30 °，

过点 A 作 AO⊥ GH，

∴AO＝50 米， HO＝ GO＝50米，

∴GH＝ 100米，

∴S△AGH＝GH× AO＝ 2500平方米，

∵S 四边形AMPN＝ S△AGM+S△ANH＝ S△AGH﹣S△AMN，

∴S△AMN的值最小时，S 四边形AMPN的值最大，

∴MN ＝ GM＝ NH＝时

∴S 四边形AMPN＝ S△AGH﹣ S△AMN＝2500﹣＝平方米 .

【解析】【解答】（ 1）∵四边形 ABCD是矩形，

∴∠ D＝ 90 °＝∠ABC ， AB＝ CD＝ 4， BC＝ AD＝ 8，

∵E 为 CD中点，

∴DE＝CE＝2，

在 Rt△ ADE中，由勾股定理得： AE＝＝＝ 2，

即△ APE的边 AE 的长一定，

要△ APE的周长最小，只要 AP+PE最小即可，

延长 AB 到 M ，使 BM＝AB＝4，则 A 和 M 关于 BC对称，

连接 EM 交 BC 于 P ，此时 AP+EP 的值最小，

∵四边形 ABCD是矩形，

∴AB∥ CD ，

∴△ ECP∽ △ MBP ，

∴

∴

∴CP＝

故答案为：

【分析】（ 1）延长 AB 到 M ，使 BM=AB，则 A 和 M 关于 BC 对称，连接EM 交 BC 于 P，此时AP+EP 的值最小，根据勾股定理求出AE 长，根据矩形性质得出AB∥ CD，推出△ECP∽ △ MBP，得出比例式，代入即可求出CP 长；（ 2）点 A 向右平移 2 个单位到M，点 E 关于BC 的对称点F，连接MF，交BC 于 Q，要使四边形APQE 的周长最小，只要

AP+EQ 最小就行，证 △ MNQ ∽ △ FCQ 即可求 BP 的长；（ 3）作点 P 关于 AB 的对称点 G ，作点 P 关于 AC 的对称点 H ，连接 GH ，交 AB ，AC 于点 M ，N ，此时 △ PMN 的周长最小 .S 四

边形 AMPN =S △ AGM +S ANH =S AGH -S AMN ， 即 S AMN 的值最小时， S AMPN 的值最大 .

△△△ △ 四边形

7．如图所示，在 △ ABC 中， AB ＝ AC ＝5 ，O 为 BC 边中点，动点（不与端点重合），点 H 、 F 是线段 AC 上的动点，且

BC ＝ 8，点 E 、 G 是线段 AB 上的 EF ∥ GH ∥ BC ． 设点 O 到 EF 、

GH 的距离分别为 x 、 y ．

（1）若 △ EOF 的面积为 S ：

① 用关于 x 的代数式表示线段

EF 的长；

② 求 S 的最大值；

（2）以点 O 为圆心，当以

OE 为半径的圆与以 OG 为半径的圆重合时，求 x 与 y 应满足的

关系式，并求 x 的取值范围．

【答案】 （1）解： ① 如图 1，连接 OA ，交 EF 于 M ，

∵AB ＝ AC ， O 为 BC 边中点，

∴OA ⊥BC ，

∵ E F ∥ BC ，

∴AM ⊥EF ，

∵ B C ＝ 8，

∴OB ＝ BC ＝ 4，

在 Rt △ AOB 中，根据勾股定理得， OA ＝ ＝ 3，

∵点 O 到 EF 的距离为为 x ，

∴OM ＝ x ，

∴AM ＝ OA ﹣ OM ＝ 3﹣ x ，

∵EF ∥ BC ，

∴△ AEF ∽ △ ABC ，

∴ ，

∴，

∴；

②由①知，，

∴S＝S△OEF＝＝＝，∵﹣＜ 0，

∴当 x＝时，S最大＝3

（2）解：如图2，

∵以 OE为半径的圆与以OG 为半径的圆重合，

∴OE＝OG ，过点 O 作 OD⊥AB 于 D ，

∴DE＝DG ，

连接OA，

由（ 1）知， OA⊥BC ， OA＝ 3，

在 Rt△ AOB 中， sinB=，cosA＝，

过点 E 作 EP⊥ BC 于 P ， PE＝ x ，

在 Rt△ BPE中， sinB＝，

∴BE＝，

过点 G 作 DQ⊥ BC 于 Q ， GQ＝y ，

在 Rt△ BQG 中， BG＝，

∴DE＝＝，

在 Rt△ BDO 中， BD＝ OB?cosB＝，

∴DE＝BD﹣ BE＝，

∴＝，

∴（Ⅰ ）

∵点 E、 G 是线段 AB 上的动点（不与端点重合），

∴0＜ y＜ 3（Ⅱ），

由（Ⅰ）（Ⅱ）得，，

∵x＞ 0，

∴，

即：．

【解析】【分析】（ 1）①连接 OA，判断出AO 是△ABC 的高， AM 是△ AEF的高，再利用相似三角形的对应边上的高的比等于相似比，即可得出结论；② 利用三角形面积公式得出

S 与 x 的函数关系式，即可得出结论；（2）先判断出DE=DG，再用三角函数表示出BE，BD， BG，即可得出结论．

8．如图（ 1）， P为△ABC所在平面上一点，且∠ APB=∠ BPC=∠ CPA=120°，则点P 叫做△ABC 的费马点．

（1）如果点P 为锐角△ ABC 的费马点，且∠ ABC=60°．

①求证：△ ABP∽ △ BCP；

（2）已知锐角△ ABC，分别以 AB、 AC 为边向外作正△ ABE和正△ ACD， CE和 BD 相交于 P 点．如图（ 2）

①求∠ CPD的度数；

②求证： P 点为△ ABC的费马点．

【答案】（1）证明：① ∵ ∠ PAB+∠ PBA=180°﹣∠APB=60°，∠ PBC+∠ PBA=∠ ABC=60°，∴∠ PAB=∠PBC，

又∵∠ APB=∠BPC=120°，

∴△ ABP∽ △BCP

2

②若 PA=3， PC=4，则 PB=．

2

（2）解：如图，

① ∵△ ABE与△ ACD都为等边三角形，

∴∠ BAE=∠ CAD=60 ，°AE=AB， AC=AD，

∴∠ BAE+∠ BAC=∠CAD+∠BAC，即∠ EAC=∠ BAD，

在△ ACE和△ ABD 中，

，

∴△ ACE≌ △ ABD（ SAS），

∴∠ 1=∠ 2，

∵∠ 3=∠ 4，

∴∠ CPD=∠ 6=∠ 5=60 ；°

②证明：∵ △ ADF∽ △ CFP，

∴A F?PF=DF?CF，

∵∠ AFP=∠ CFD，

∴△ AFP∽△ CDF．

∴∠ APF=∠ ACD=60 ，°

∴∠ APC=∠CPD+∠ APF=120 ，°

∴∠ BPC=120，°

∴∠ APB=360 ﹣°∠ BPC﹣∠ APC=120 ，°

∴P 点为△ ABC的费马点．

【解析】【解答】（ 1）②解：∵△ ABP∽ △BCP，

∴，

∴PB2=PA?PC=12，

∴PB=2；

【分析】 (1) 由已知可知∠APB=∠BPC=，利用三角形内角和可知，∠BAP+∠ ABP=，又因为∠ ABP+∠CBP=，所以可知∠BAP=∠CBP，所以△ABP∽ △ BCP；

（2）①由等边三角形可知AD=AC ， AB=AE，∠EAC=∠ BAD=∠ BAC+，所以

△EAC≌ △ BAD，由全等可知∠ CPD=；

②利用△ADF∽△CFP，可得对应边成比例，由对应边成比例夹角相等，得到△AFP∽ △CDF，所以∠ APC=，即点P为△ ABC的费马点.

二、圆的综合

9．如图， AB 是⊙ O 的直径，弦CD⊥ AB，垂足为H，连结 AC，过?

BD上一点 E 作 EG∥ AC

交 CD的延长线于点 G，连结 AE 交 CD 于点 F，且 EG=FG，连结CE．（1）求证：∠ G=∠ CEF；

（2）求证： EG是⊙O 的切线；

（3）延长 AB 交 GE的延长线于点M ，若 tanG = 3

， AH=3 3 ，求EM的值．4

【答案】（ 1）证明见解析；（2）证明见解析；（3）253

.

8

【解析】

试题分析：（ 1）由 AC∥EG，推出∠ G=∠ACG，由 AB⊥ CD 推出?

AD ∠CEF=∠ ACD，推出∠ G=∠ CEF，由此即可证明；

（2）欲证明 EG是⊙O 的切线只要证明 EG⊥ OE即可；

（3）连接 OC．设⊙ O 的半径为 r．在 Rt△ OCH中，利用勾股定理求出

AH HC

△AHC∽ △ MEO，可得，由此即可解决问题；

EM OE ?，推出AC

r，证明

试题解析：（ 1）证明：如图 1．∵ AC∥ EG，∴ ∠G=∠ ACG，∵ AB⊥ CD，∴∴∠ CEF=∠ ACD，∴ ∠ G=∠ CEF，∵ ∠ ECF=∠ ECG，∴ △ ECF∽ △ GCE．?? ，AD AC

（2）证明：如图 2 中，连接OE．∵ GF=GE，∴∠ GFE=∠ GEF=∠ AFH，∵ OA=OE，

∴∠ OAE=∠ OEA，∵∠ AFH+∠ FAH=90 ，°∴∠GEF+∠ AEO=90 ，°∴∠

GEO=90 ，°∴GE⊥ OE，∴EG 是⊙O 的切线．

（3）解：如图 3 中，连接 OC ．设 ⊙ O 的半径为 r ．

在 Rt △ AHC 中， tan ∠ACH=tan ∠ G= AH

=

3

，∵AH=

3 3，∴HC=4

3 ，在 Rt △ HOC 中，

HC

4

∵OC=r ， OH=r ﹣

3 3 ，HC=

4 3 ， ∴ ( r

3 3)

2

(4 3) 2

r 2

， ∴r =

25 3

，

6

AH HC ∵GM ∥ AC ，∴ ∠ CAH=∠ M ， ∵ ∠OEM=∠AHC ，∴ △ AHC ∽ △ MEO ，∴

，

EM

OE

3 3

4 3

∴

EM

25 3 ，∴EM=

25

3 ．

8

6

点睛：本题考查圆综合题、垂径定理、相似三角形的判定和性质、锐角三角函数、勾股定

理等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，正确寻找相

似三角形，构建方程解决问题吗，属于中考压轴题．

10． 已知 e O 的半径为 5，弦 AB 的长度为 m ，点 C 是弦 AB 所对优弧上的一动点．

1 如图 ① ，若 m

5 ，则 C 的度数为 ______ o ；

2 如图 ② ，若 m

6 ．

① 求

C 的正切值；

② 若 VABC 为等腰三角形，求 VABC 面积．