中考二次函数与几何图形动点问题--答案

二次函数与几何图形

模式1：平行四边形

分类标准：讨论对角线

例如：请在抛物线上找一点p 使得P C B A 、、、四点构成平行四边形，则可分成以下几种情况

（1）当边AB 是对角线时，那么有BC AP //

（2）当边AC 是对角线时，那么有CP AB //

（3）当边BC 是对角线时，那么有BP AC //

1、本题满分14分）在平面直角坐标系中，已知抛物线经过A(-4，0)，B(0，-4)，C(2，0)三点.

(1)求抛物线的解析式；

(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S.求S 关于m 的函数关系式，并求出S 的最大值；

(3)若点P 是抛物线上的动点，点Q 是直线y=－x 上的动点，判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标.

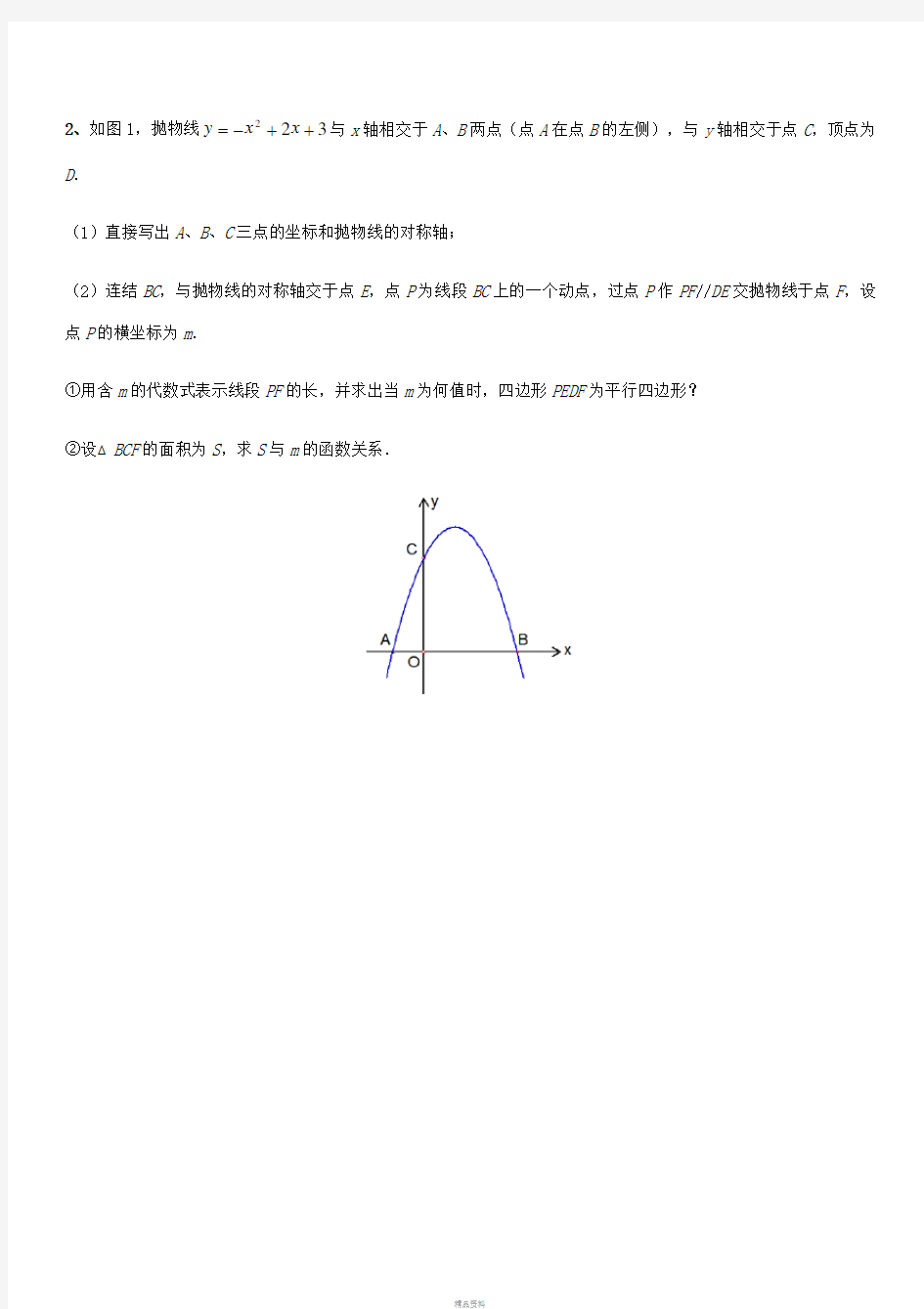
2、如图1，抛物线322

++-=x x y 与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D ．

（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴；

（2）连结BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF //DE 交抛物线于点F ，设点P 的横坐标为m ．

①用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？

②设△BCF 的面积为S ，求S 与m 的函数关系．

模式2：梯形

分类标准：讨论上下底

例如：请在抛物线上找一点p 使得P C B A 、、、四点构成梯形，则可分成以下几种情况

（1）当边AB 是底时，那么有PC AB //

（2）当边AC 是底时，那么有BP AC //

（3）当边BC 是底时，那么有AP BC //

3、已知，矩形OABC 在平面直角坐标系中位置如图1所示，点A 的坐标为(4,0)，点C 的坐标为)20(-，，直线x y 3

2-=与边BC 相交于点D ． (1)求点D 的坐标；

(2)抛物线c bx ax y ++=2

经过点A 、D 、O ，求此抛物线的表达式； (3)在这个抛物线上是否存在点M ，使O 、D 、A 、M 为顶点的四边形是梯形？若存在，请求出所有符合条件的点M 的坐标；若不存在，请说明理由．

4、已知二次函数的图象经过A（2，0）、C(0，12) 两点，且对称轴为直线x＝4，设顶点为点P，与x轴的另一交点为点B．

（1）求二次函数的解析式及顶点P的坐标；

（2）如图1，在直线 y＝2x上是否存在点D，使四边形OPBD为等腰梯形？若存在，求出点D的坐标；若不存在，请说明理由；

（3）如图2，点M是线段OP上的一个动点（O、P两点除外），以每秒2个单位长度的速度由点P向点O 运动，过点M作直线MN//x轴，交PB于点N．将△PMN沿直线MN对折，得到△P1MN．在动点M的运动过程中，设△P1MN与梯形OMNB的重叠部分的面积为S，运动时间为t秒，求S关于t的函数关系式．

模式3：直角三角形

分类标准：讨论直角的位置或者斜边的位置

例如：请在抛物线上找一点p 使得P B A 、、三点构成直角三角形，则可分成以下几种情况

（1）当A ∠为直角时，AB AC ⊥

（2）当B ∠为直角时，BA BC ⊥

（3）当C ∠为直角时，CB CA ⊥

5、如图1，已知抛物线y ＝x 2

＋bx ＋c 与x 轴交于A 、B 两点（点A 在点B 左侧），与y 轴交于点C (0，－3)，对称轴是直线x ＝1，直线BC 与抛物线的对称轴交于点D ．（1）求抛物线的函数表达式；

（2）求直线BC 的函数表达式；

（3）点E 为y 轴上一动点，CE 的垂直平分线交CE 于点F ，交抛物线于P 、Q 两点，且点P 在第三象限． ①当线段34

PQ AB =时，求tan ∠CED 的值； ②当以C 、D 、E 为顶点的三角形是直角三角形时，请直接写出点P 的坐标．

6：如图1，直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ，点A 的坐标是（-2，0）．（1）试说明△ABC 是等腰三角形；

（2）动点M 从A 出发沿x 轴向点B 运动，同时动点N 从点B 出发沿线段BC 向点C 运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，△MON 的面积为S ．

① 求S 与t 的函数关系式；

② 设点M 在线段OB 上运动时，是否存在S ＝4的情形？若存在，求出对应的t 值；若不存在请说明理由； ③在运动过程中，当△MON 为直角三角形时，求t 的值．

二次函数与几何图形结合练习

3.2 与几何图形结合3.2.1 与等腰三角形结合1、如图，直线y=3x+3交x 轴于A 点，交y 轴于B 点，过A 、B 两点的抛物线交 x 轴于另一点C （3,0）. ⑴求抛物线的解析式 ; ⑵在抛物线的对称轴上是否存在点Q ，使△ABQ 是等腰三角形？若存在，求出符合条件的 Q 点坐标；若不存在，请说明理由 2、如图，已知直线y=x 与交于A 、B 两点．（1）求交点A 、B 的坐标；（2）记一次函数y=x 的函数值为y 1，二次函数的函数值为y 2．若y 1＞y 2，求x 的取值范围；（3）在该抛物线上存在几个点，使得每个点与AB 构成的三角形为等腰三角形？并求出不少于3个满足条件的点 P 的坐标． y =x 2 y =x 2

3、如图，已知二次函数的图象经过点A （3，3）、B （4，0）和原点O 。P 为二次函数图象上的一个动点，过点 P 作x 轴的垂线，垂足为 D （m ，0），并与直线OA 交于点C ．（1）求出二次函数的解析式；（2）当点P 在直线OA 的上方时，求线段PC 的最大值；（3）当m ＞0时，探索是否存在点P ，使得△PCO 为等腰三角形，如果存在，求出 P 的坐标；如果不存在，请说明理由． 3.2.2 与直角三角形结合1、二次函数的图象的一部分如图所示．已知它的顶点 M 在第二象限，且经过点A(1，0)和点B(0，l)．(1)试求，所满足的关系式；(2)设此二次函数的图象与x 轴的另一个交点为 C ，当△AMC 的面积为△ABC 面积的倍时，求a 的值；(3)是否存在实数a ，使得△ABC 为直角三角形．若存在，请求出 a 的值；若不存在，请说明理由． 2 y ax bx c a b 5 4

平面图形与立体图形的认识

【几何图形】从实物中抽象出来的各种图形，包括立体图形和平面图形。立体图形分为柱体，锥体，球体多面体：围城棱柱和棱锥的面都是平的面，像这样的立体图形叫做多面体欧拉公式：定点数+面数-棱数=2 练习： 1．下面几何体中，不是多面体的是（） A球体 B 三棱锥 C 三棱柱D四棱柱 2．下列判断正确的是 A长方形是多面体B柱体是多面体 C圆锥是多面体D棱柱、棱锥都是多面体 3、将半圆绕它的直径旋转一周形成的几何体是（） A、圆柱 B、圆锥 C、球 D、正方体【点、线、面、体】（1）几何图形的组成点：线和线相交的地方是点，它是几何图形中最基本的图形。线：面和面相交的地方是线，分为直线和曲线。面：包围着体的是面，分为平面和曲面。体：几何体也简称体。（2）点动成线，线动成面，面动成体。例、右侧这个几何体的名称是_______；它由_______个面组成；它有_______个顶点；经过每个顶点有_______条边。解答：五棱柱，7，10，3 【直线】 1、概念：一根拉得很紧的线，就给我们以直线的形象，直线是直的，并且是向两方无限延伸的。 2、直线的性质（1）直线公理：经过两个点有一条直线，并且只有一条直线。它可以简单地说成：过两点有且只有一条直线。（2）过一点的直线有无数条。（3）直线是是向两方面无限延伸的，无端点，不可度量，不能比较大小。（4）直线上有无穷多个点。（5）两条不同的直线至多有一个公共点。 3、表示：一条直线可以用一个小写字母表示；或者用两个大写字母表示练习： 1.经过一点,有______条直线;经过两点有_____条直线,并且______条直线. 2、我们在用玩具枪瞄准时，总是用一只眼对准准星和目标，用数学知识解释为__________________．【射线】直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。

初三数学二次函数知识点总结及经典习题含答案

初三数学二次函数知识点总结一、二次函数概念： 1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征： ⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数的基本形式 1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。 2. 2y ax c =+的性质：上加下减。 3. ()2 y a x h =-的性质：左加右减。 4. ()2 y a x h k =-+的性质： a 的符号开口方向顶点坐标对称轴性质 0a > 向上 ()00， y 轴 0x >时，y 随x 的增大而增大；0x <时，y 随 x 的增大而减小；0x =时，y 有最小值0． 0a < 向下 ()00， y 轴 0x >时，y 随x 的增大而减小；0x <时，y 随x 的增大而增大；0x =时，y 有最大值0． a 的符号开口方向顶点坐标对称轴性质 0a > 向上 ()0c ， y 轴 0x >时，y 随x 的增大而增大；0x <时，y 随x 的增大而减小；0x =时，y 有最小值c ． 0a < 向下 ()0c ， y 轴 0x >时，y 随x 的增大而减小；0x <时，y 随x 的增大而增大；0x =时，y 有最大值c ． a 的符号开口方向顶点坐标对称轴性质 0a > 向上 ()0h ， X=h x h >时，y 随x 的增大而增大；x h <时，y 随x 的增大而减小；x h =时，y 有最小值0． 0a < 向下 ()0h ， X=h x h >时，y 随x 的增大而减小；x h <时，y 随x 的增大而增大；x h =时，y 有最大值0．

平面图形与立体图形教案

4．1几何图形 4.1.1立体图形与平面图形【教学目标】 1、能从实物图形中抽取出几何图形；能在生活中寻找出相应的几何图形；会认识多见的平面几何图形和立体几何图形。 2、通过实物抽取几何图形的体验，培养自己的几何图形感，能用几何图形描述生活中的物体。 3、通过对多彩多姿的图形世界体验，激发自己对几何学习的兴趣，也体会学习的喜悦。【教学重难点】 1．重点：（1）掌握立体图形与平面图形的关系，学会它们之间的相互转化；?初步建立空间观念．（2）理解几何图形是从实物图形中抽象出来的。（3）从实际出发，用直观的形式，让学生感受图形的丰富多彩，激发学生学习的兴趣． 2．难点：（1）立体图形与平面图形之间的互相转化．（2）从现实情境中，抽象概括出几何图形【教具准备】长方体、正方体、球、圆柱、圆锥等几何体模型，墨水瓶包装盒（每个学生都准备一个），及多媒体教学设备和课本图4．1-5的教学幻灯片．【教学过程】

一、引入新课由多媒体展示美丽的图形世界在同学们所观看中，有哪些是我们熟悉的几何图形？二、新授 1．学生在回顾刚才所看到的图片，充分发表自己的意见，?并通过小组交流，补充自己的意见，积累小组活动经验． 2．指定一名学生回答问题，并能正确说出这些几何图形的名称．学生回答：有圆柱、长方体、正方体等等．教师活动：纠正学生所说几何图形名称中的错误，并出示相应的几何体模型让学生观察它们的特征． 3．立体图形的概念．（1）长方体、正方体、球、圆柱、圆锥等都是立体图形．（2）学生活动：看课本图4．1-3后学生思考：这些物体给我们什么样的立体图形的形象？（棱柱和棱锥）（3）用多媒体放映课本4．1-4的幻灯片（4）提出问题：在这个幻灯片中，包含哪些简单的平面图形？（5）探索解决问题的方法． ①学生进行小组交流，教师对各小组进行指导，通过交流，得出问题的答案． ②学生回答：包含的平面图形有长方形、圆、正方形、多边形和三角形等．4．平面图形的概念．长方形、正方形、三角形、圆等都是我们十分熟悉的平面图形．

2020年中考二次函数与几何图形经典题型汇编【含中考相似三角形中考线段中的动点问题】

2020 年中考二次函数与几何图形

1.中考相似三角形 2.中考线段中的动点问题目录中考复习战略汇集 (1) 二次函数与几何图形 (2) 模式1：平行四边形 (2) 模式2：梯形 (4) 模式3：直角三角形 (6) 模式4：等腰三角形 (8) 模式5：相似三角形 (10) 模拟题汇编之动点折叠问题 (11)

二次函数与几何图形模式 1：平行四边形分类标准：讨论对角线例如：请在抛物线上找一点 p 使得 A 、B 、C 、P 四点构成平行四边形，则可分成以下几种情况（（（ 1）当边 AB 是对角线时，那么有 AP // BC 2）当边 AC 是对角线时，那么有 AB //CP 3）当边 BC 是对角线时，那么有 AC // BP 1 、在平面直角坐标系中，已知抛物线经过 A(-4，0)，B(0，-4)，C(2，0)三点. (1)求抛物线的解析式； (2)若点 M 为第三象限内抛物线上一动点，点 M 的横坐标为 m ，△AMB 的面积为 S. 求 S 关于 m 的函数关系式，并求出 S 的最大值； (3)若点 P 是抛物线上的动点，点 Q 是直线 y=－x 上的动点，判断有几个位置能使以点 P 、Q 、B 、0 为顶点的四边形为平行四边形，直接写出相应的点 Q 的坐标.

2 、如图，抛物线 y x 2 2x 3与 x 轴相交于 A 、B 两点（点 A 在点 B 的左侧），与 y 轴相交于点 C ，顶点为 D ．（（ 1）直接写出 A 、B 、C 三点的坐标和抛物线的对称轴； 2）连结 BC ，与抛物线的对称轴交于点 E ，点 P 为线段 BC 上的一个动点，过点 P 作 PF//DE 交抛物线于点 F ，设点 P 的横坐标为 m ． ① 用含 m 的代数式表示线段 PF 的长，并求出当 m 为何值时，四边形 PEDF 为平行四边形？ ② 设△BCF 的面积为 S ，求 S 与 m 的函数关系．

中考二次函数压轴题经典题型

中考二次函数压轴题经典题型 1、如图，已知；边长为4的正方形截去一角成为五边形ABCDE，其中AF=2，BF=l，在AB上的一点P，使矩形PNDM 有最大面积，求矩形PNDM的面积最大值？ 2、如图，二次函数的图象经过点D(0， 3 9 7 )，且顶点C的横坐标为4，该图象在x 轴上截得的线段AB的长为6. ⑴求二次函数的解析式； ⑵在该抛物线的对称轴上找一点P，使PA+PD最小，求出点P的坐标； ⑶在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由． 3．如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（1 2 ， 5 2 ）和B（4，m），点P是线段AB 上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．（1）求抛物线的解析式；（2）是否存在这样的P点，使线段PC的长有最大值，若存在，求出这个最大值；若不存在，请说明理由；（3）求△PAC为直角三角形时点P的坐标．

4、如图，二次函数y=a+bx的图象经过点A（2，4）与B（6，0）．（1）求a，b的值；（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB 的面积S关于点C的横坐标x的函数表达式，并求S的最大值。 5、如图1，对称轴x=为直线的抛物线经过B（2，0）、C（0，4）两点，抛物线与轴的另一交点为A．（1）求抛物线的解析式；（2）若点P为第一象限内抛物线上一点，设四边形COBP的面积为S，求S的最大值；（3）如图2，若M是线段BC上一动点，在轴上是否存在这样有点Q，使△MQC为等腰三角形且△MQB 为直角三角形？若存在，求出Q点坐标；若不存在，请说明理由．

二次函数与几何图形结合题及答案

1.如图，已知抛物线2 1y x =-与x 轴交于A 、B 两点，与y 轴交于点C ．（1）求A 、B 、C 三点的坐标; （2）过点A 作AP ∥CB 交抛物线于点P ，求四边形ACBP 的面积; （3）在x 轴上方的抛物线上是否存在一点M ，过M 作MG ⊥x 轴于点G ，使以A 、M 、G 三点为顶点的三角形与?PCA 相似．若存在，请求出M 点的坐标；否则，请说明理由．解：（1）令0y =，得2 10x -= 解得1x =± 令0x =，得1y =- ∴ A (1,0)- B (1,0) C (0,1)- ……………………3分（2）∵O A =O B =O C =1 ∴∠BAC =∠AC O=∠BC O= 45 ∵A P ∥CB ， ∴∠P AB = 45 过点P 作P E ⊥x 轴于E ，则?A P E 为等腰直角三角形令O E =a ，则P E =1a + ∴P (,1)a a + ∵点P 在抛物线21y x =-上 ∴2 11a a +=- 解得12a =，21a =-（不合题意，舍去） ∴P E =3……………………………………………………………………………5分 ∴四边形ACB P 的面积S =12AB ?O C +12AB ?P E =11 2123422 ??+??=………………………………6分 (3)．假设存在 ∵∠P AB =∠BAC =45 ∴P A ⊥AC ∵MG ⊥x 轴于点G ， ∴∠MG A =∠P AC =90 在Rt △A O C 中，O A =O C =1 ∴AC =2 在Rt △P AE 中，AE =P E =3 ∴A P= 32 ………8分设M 点的横坐标为m ，则M 2 (,1)m m - ①点M 在y 轴左侧时，则1m <- (ⅰ) 当?A MG ∽?P CA 时，有 AG PA =MG CA ∵A G=1m --，MG=2 1m -即2322 = 解得11m =-（舍去） 23m =（舍去）………9分 G M C B y P A o x

二次函数动点问题解答方法技巧(含例解答案)33935

函数解题思路方法总结： ⑴ 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程； ⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式； ⑶ 根据图象的位置判断二次函数ax 2+bx+c=0中a,b,c 的符号，或由二次函数中a,b,c 的符号判断图象的位置，要数形结合； ⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴的一个交点坐标，可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式，二次三项式ax 2+bx+c ﹙a ≠0﹚本身就是所含字母x 的二次函数；下面以a ＞0时为例，揭示二次函数、二次三项式和一元二次方程之间的内在联系：动点问题题型方法归纳总结动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。下面就此问题的常见题型作简单介绍，解题方法、关键给以点拨。二、抛物线上动点 5、（湖北十堰市）如图①，已知抛物线32++=bx ax y （a ≠0）与x 轴交于点A (1，0)和点B (－3，0)，与y 轴交于点C ． (1) 求抛物线的解析式；

(2) 设抛物线的对称轴与x轴交于点M ，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由． (3) 如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．注意：第（2）问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为顶点时，以C为圆心CM为半径画弧，与对称轴交点即为所求点P，②M为顶点时，以M 为圆心MC为半径画弧，与对称轴交点即为所求点P，③P为顶点时，线段MC的垂直平分线与对称轴交点即为所求点P。第（3）问方法一，先写出面积函数关系式，再求最大值（涉及二次函数最值）；方法二，先求与BC平行且与抛物线相切点的坐标（涉及简单二元二次方程组），再求面积。

中考数学二次函数-经典压轴题及答案

一、二次函数真题与模拟题分类汇编（难题易错题） 1．如图，抛物线y＝x2﹣mx﹣（m+1）与x轴负半轴交于点A（x1，0），与x轴正半轴交于点B（x2，0）（OA＜OB），与y轴交于点C，且满足x12+x22﹣x1x2＝13．（1）求抛物线的解析式；（2）以点B为直角顶点，BC为直角边作Rt△BCD，CD交抛物线于第四象限的点E，若EC ＝ED，求点E的坐标；（3）在抛物线上是否存在点Q，使得S△ACQ＝2S△AOC？若存在，求出点Q的坐标；若不存在，说明理由．【答案】（1）y＝x2﹣2x﹣3；（2）E 113 +113 + 3）点Q的坐标为（﹣3，12）或（2，﹣3）．理由见解析. 【解析】【分析】（1）由根与系数的关系可得x1+x2＝m，x1?x2＝﹣（m+1），代入x12+x22﹣x1x2＝13，求出m1＝2，m2＝﹣5．根据OA＜OB，得出抛物线的对称轴在y轴右侧，那么m＝2，即可确定抛物线的解析式；（2）连接BE、OE．根据直角三角形斜边上的中线等于斜边的一半得出BE＝1 2 CD＝CE．利用SSS证明△OBE≌△OCE，得出∠BOE＝∠COE，即点E在第四象限的角平分线上，设E点坐标为（m，﹣m），代入y＝x2﹣2x﹣3，求出m的值，即可得到E点坐标；（3）过点Q作AC的平行线交x轴于点F，连接CF，根据三角形的面积公式可得S△ACQ＝S△ACF．由S△ACQ＝2S△AOC，得出S△ACF＝2S△AOC，那么AF＝2OA＝2，F（1，0）．利用待定系数法求出直线AC的解析式为y＝﹣3x﹣3．根据AC∥FQ，可设直线FQ的解析式为y＝﹣3x+b，将F（1，0）代入，利用待定系数法求出直线FQ的解析式为y＝﹣3x+3，把它与抛物线的解析式联立，得出方程组 223 33 y x x y x ?=-- ? =-+ ? ，求解即可得出点Q的坐标．【详解】（1）∵抛物线y＝x2﹣mx﹣（m+1）与x轴负半轴交于点A（x1，0），与x轴正半轴交于点B（x2，0）， ∴x1+x2＝m，x1?x2＝﹣（m+1），

二次函数与几何图形综合题(可编辑修改word版)

二次函数与几何图形综合题类型 1 二次函数与相似三角形的存在性问题 1．(2015·昆明西山区一模)如图，已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－1，0)，B(4，0)，C(0，2) 三点． (1)求这条抛物线的解析式； (2)P 为线段BC 上的一个动点，过P 作PE 垂直于x 轴与抛物线交于点E，设P 点横坐标为m，PE 长度为y，请写出y 与m 的函数关系式，并求出PE 的最大值； (3)D 为抛物线上一动点，是否存在点D 使以A、B、D 为顶点的三角形与△COB 相似？若存在，试求出点D 的坐标；若不存在，请说明理由．

2．(2013·曲靖)如图，在平面直角坐标系xOy 中，直线y＝x＋4 与坐标轴分别交于A，B 两点，过A，B 两点的抛物线为y＝－x2＋bx＋c.点D 为线段AB 上一动点，过点D 作CD⊥x 轴于点C，交抛物线于点E. (1)求抛物线的解析式； (2)当DE＝4 时，求四边形CAEB 的面积； (3)连接BE，是否存在点D，使得△DBE 和△DAC 相似？若存在，求出D 点坐标；若不存在，说明理由． 3．(2015·襄阳)边长为 2 的正方形OABC 在平面直角坐标系中的位置如图所示，点D 是边OA 的中点，连接CD，点E 在第一象限，且DE⊥DC，DE＝DC.以直线AB 为对称轴的抛物线过C，E 两点．

(1)求抛物线的解析式； (2)点P 从点C 出发，沿射线CB 以每秒 1 个单位长度的速度运动，运动时间为t 秒．过点P 作PF⊥CD 于点F.当t 为何值时，以点P，F，D 为顶点的三角形与△COD 相似？ (3)点M 为直线AB 上一动点，点N 为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E 为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．类型 2 二次函数与平行四边形的存在性问题 1．(2014·曲靖)如图，抛物线y＝ax2＋bx＋c 与坐标轴分别交于A(－3，0)，B(1，0)，C(0，3)三点，D

中考数学二次函数动点问题解答方法技巧(含例解答案)

动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。下面就此问题的常见题型作简单介绍，解题方法、关键给以点拨。二、抛物线上动点 5、（湖北十堰市）如图①，已知抛物线3 2+ y（a≠0）与x轴 ax + =bx 交于点A(1，0)和点B (－3，0)，与y轴交于点C． (1) 求抛物线的解析式； (2) 设抛物线的对称轴与x轴交于点M ，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由． (3) 如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．注意：第（2）问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为顶点时，以C为圆心CM为半径画弧，与对称轴交点即为所求点P，②M为顶点时，以M为圆心MC为半径画弧，与对称轴交点即为所求点P，③P为顶点时，线段MC的垂直平分线与对称轴交点即为所求点P。

北师大版中考复习二次函数经典总结及典型题

二次函数知识点一、二次函数概念： 1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征： ⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数的基本形式 1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。 2. 2y ax c =+的性质：上加下减。

)2 h k +方法一：⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．

概括成八个字“左加右减，上加下减”．方法二： ⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成 m c bx ax y +++=2（或m c bx ax y -++=2） ⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成 c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2 y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即2 2424b ac b y a x a a -? ?=++ ??? ，其中2424b ac b h k a a -=-= ，．五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点. 六、二次函数2y ax bx c =++的性质 1. 当0a >时，抛物线开口向上，对称轴为2b x a =-，顶点坐标为2424b ac b a a ??-- ??? ，．当2b x a <- 时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2b x a =-时，y 有最小值2 44ac b a -． 2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ??-- ??? ，．当2b x a <- 时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2b x a =-时，y 有最大值 244ac b a -．七、二次函数解析式的表示方法 1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）； 2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）； 3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点

(完整版)二次函数与几何图形综合题.doc

二次函数与几何图形综合题类型 1二次函数与相似三角形的存在性问题 1． (2015 ·明西山区一模昆)如图，已知抛物线y＝ ax2＋bx＋ c(a≠0)经过 A(－ 1， 0)， B(4， 0)， C(0 ，2) 三点． (1)求这条抛物线的解析式； (2)P 为线段 BC 上的一个动点，过P 作 PE 垂直于 x 轴与抛物线交于点 E，设 P 点横坐标为 m， PE 长度为 y，请写出 y 与 m 的函数关系式，并求出PE 的最大值； (3)D 为抛物线上一动点，是否存在点 D 使以 A、B、D 为顶点的三角形与△ COB 相似？若存在，试求出点 D 的坐标；若不存在，请说明理由．

2． (2013 ·靖曲 )如图，在平面直角坐标系xOy 中，直线y＝ x＋ 4 与坐标轴分别交于A， B 两点，过A，B 两点的抛物线为y＝－ x2＋ bx＋ c.点 D 为线段 AB 上一动点，过点 D 作 CD⊥ x 轴于点 C，交抛物线于点 E. (1)求抛物线的解析式； (2)当 DE＝ 4 时，求四边形CAEB 的面积； (3)连接 BE，是否存在点 D ，使得△ DBE 和△ DAC 相似？若存在，求出 D 点坐标；若不存在，说明理由．

3．(2015 襄·阳 )边长为 2 的正方形O ABC 在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接 CD ，点 E 在第一象限，且DE⊥ DC ， DE ＝DC.以直线 AB 为对称轴的抛物线过C， E 两点． (1)求抛物线的解析式； (2)点 P 从点 C 出发，沿射线 CB 以每秒 1 个单位长度的速度运动，运动时间为t 秒．过点 P 作 PF ⊥ CD 于点 F .当 t 为何值时，以点P， F ，D 为顶点的三角形与△COD 相似？ (3)点 M 为直线 AB 上一动点，点N 为抛物线上一动点，是否存在点M， N，使得以点M，N， D， E 为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．

几何图形与平面图形

课题 4.1.1几何图形与平面图形一、学习目标 1、通过观察生活中的大量图片或实物，经历把实物抽象成几何图形的过程； 2、能由实物形状想象出几何图形，由几何图形想象出实物形状； 3、能识别一些简单几何体，正确区分平面图形与立体图形。学习重点：识别简单的几何体学习难点：从具体事物中抽象出几何图形二、自主探究 1、几何图形（1）仔细观察图4.1-1,让同学们感受是丰富多彩的图形世界；（2）出示一个长方体的纸盒，让同学们观察图4.1-2回答问题：从整体上看，它的形状是从不同侧面看，你看到的图形是看棱得到的是看顶点的到的是。我们见过的长方体、圆柱、圆锥、球、圆、线段、点等，以及小学学习过的三角形、四边形等，都是从形形色色的物体外形中得出的。我们把这些图形称为几何图形。 2、立体图形说一说下面这些几何图形有什么共同特点？有些几何图形的各部分不都在同一平面内，它们是 .(如：）请再举出一些立体图形的例子. 想一想生活中还有哪些物体的形状类似于这些立体图形呢？ 3、平面图形（1）纸盒（1）长方体（2）长方形（3）正方形（4）线段点

说一说下面这些几何图形又有什么共同特点？平面图形的概念线段、角、三角形、长方形、圆等它们的各部分都在同一平面内，它们是。请再举出一些平面图形的例子。思考：立体图形与平面图形是两类不同的几何图形，它们的区别在哪里？它们有什么联系？三、课堂练习课本119页练习四、要点归纳 1、 2、平面图形与立体图形的关系：立体图形的各部分不都在同一平面内，而平面图形的各部分都在同一平面内；立体图形中某些部分是平面图形。五、拓展训练 1.下列几种图形：①长方形；②梯形；③正方体；④圆柱；⑤圆锥；⑥球. 其中属于立体图形的是（） A. ①②③； B. ③④⑤； C. ① ③⑤； D. ③④⑤⑥ 【总结反思】现实物体几何图形平面图形立体图形看外形

二次函数与几何图形动点问题--答案

二次函数与几何图形模式1：平行四边形分类标准：讨论对角线例如：请在抛物线上找一点p 使得P C B A 、、、四点构成平行四边形，则可分成以下几种情况（1）当边AB 是对角线时，那么有BC AP // （2）当边AC 是对角线时，那么有CP AB // （3）当边BC 是对角线时，那么有BP AC // 1、本题满分14分）在平面直角坐标系中，已知抛物线经过A(-4，0)，B(0，-4)，C(2，0)三点. (1)求抛物线的解析式； (2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S.求S 关于m 的函数关系式，并求出S 的最大值； (3)若点P 是抛物线上的动点，点Q 是直线y=－x 上的动点，判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标.

2、如图1，抛物线322 ++-=x x y 与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D ．（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴；（2）连结BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF //DE 交抛物线于点F ，设点P 的横坐标为m ． ①用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？ ②设△BCF 的面积为S ，求S 与m 的函数关系．

模式2：梯形分类标准：讨论上下底例如：请在抛物线上找一点p 使得P C B A 、、、四点构成梯形，则可分成以下几种情况（1）当边AB 是底时，那么有PC AB // （2）当边AC 是底时，那么有BP AC // （3）当边BC 是底时，那么有AP BC // 3、已知，矩形OABC 在平面直角坐标系中位置如图1所示，点A 的坐标为(4,0)，点C 的坐标为)20(-，，直线 x y 3 2 -=与边BC 相交于点D ． (1)求点D 的坐标； (2)抛物线c bx ax y ++=2 经过点A 、D 、O ，求此抛物线的表达式； (3)在这个抛物线上是否存在点M ，使O 、D 、A 、M 为顶点的四边形是梯形？若存在，请求出所有符合条件的点M 的坐标；若不存在，请说明理由．

《立体图形与平面图形》练习题

4.1 多姿多彩的图形(1) 几何图形长方形的是（）1．如图所示，水平放置的下列几何体，从正面看到的视图不是．． 2．下列几何体中，直棱柱的个数是（） A．5 B．4 C．3 D．2 3．直四棱柱、长方体和正方体之间的包含关系是（） A B C D 4．若一个棱柱有10个顶点，则下列说法正确的是（） A．这个棱柱有4个侧面 B．这个棱柱有5条侧棱 C．这个棱柱的底面是十边形 D．这个棱柱是一个十棱柱 5．小明用如下左图所示的胶漆滚从左到右滚涂墙壁，下列平面图形中符合胶漆滚涂出的图案是（） A B C D 6．举出两个俯视图为圆的实物例子: 、． 7．写出下列立体图形的名称（从左到右依次写出）：． 8．如果直六棱柱的其中一条侧棱长为4cm，那么它的所有侧棱长度之和为 cm． 9．分别画出图中的物体的三个视图： 10．如图①②③④四个图形都是平面图形，观察图②和表中对应数值，探究计数的方法并解答下面的问题．

（1）数一数每个图各有多少顶点、多少条边、这些边围成多少区域，将结果填入下表：（2）根据表中的数值，写出平面图的顶点数、边数、区域数之间的关系；（3）如果一个平面图形有20个顶点和11个区域，求这个平面图形的边数．参考答案 1．答案: B 解析：B答案中圆锥的主视图是三角形． 2．答案: C 解析：直棱柱的侧面应是矩形，符合这个条件的有第一个，第五个和第六个．故选C．

3．答案:A 解析：正方体是特殊的长方体，长方体又是特殊的直四棱柱，故选A．4．答案:B 解析：一个棱柱有10个顶点，则它是五棱柱，五棱柱有5个侧面，有5条侧棱，底面是五边形．故选B． 5．答案:A 解析：由胶漆滚得图形可得，最左边中间为一小黑正方形，胶漆滚从左到右，则最先留下印记的即为中间有一小黑正方形的图形．故选A． 6．圆柱，球，圆锥． 7．从左到右依次为：圆柱、长方体、四棱锥、圆锥． 8．直六棱柱的其中一条侧棱长为4cm，那么它的所有侧棱长度之和为6×4=24cm．故答案为24． 9．三个视图如下： 10．解：（1）结和图形我们可以得出：图①有4个顶点、6条边、这些边围成3个区域；图②有7个顶点、9条边、这些边围成3个区域；图③有8个顶点、12条边、这些边围成5个区域； 10个顶点、15条边、这些边围成6区域．

中考数学压轴题专题动点问题

2012年全国中考数学（续61套）压轴题分类解析汇编专题01：动点问题 25. （2012吉林长春10分）如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=4cm，D、E分别为边AB、BC的中点，连结DE，点P从点A出发，沿折线AD－DE－EB运动，到点B停止．点P在AD的速度运动，在折线DE－EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作 PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上．设点P的运动时间为t(s). （1）当点P在线段DE上运动时，线段DP的长为______cm,（用含t的代数式表示）．（2）当点N落在AB边上时，求t的值．（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S（cm2），求S与t的函数关系式．（4）连结CD．当点N于点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s 的速度沿M-N-M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P 在线段EB上运动时，点H始终在线段MN的中心处．直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．【答案】解：（1）t－2。（2）当点N落在AB边上时，有两种情况： ①如图（2）a，当点N与点D重合时，此时点P在DE上，DP=2=EC，即t－2=2，t=4。 ②如图（2）b，此时点P位于线段EB上． ∵DE=1 2 AC=4，∴点P在DE段的运动时间为4s， ∴PE=t-6，∴PB=BE-PE=8-t，PC=PE+CE=t-4。 ∵PN∥AC，∴△BNP∽△BAC。∴PN：AC = PB：BC=2，∴PN=2PB=16-2t。由PN=PC，得16-2t=t-4，解得t=20 3 。综上所述，当点N落在AB边上时，t=4或t=20 3 。（3）当正方形PQMN与△ABC重叠部分图形为五边形时，有两种情况：

立体图形与平面图形

4.1.1立体图形与平面图形一.教学内容解析 1.内容几何图形、立体图形、平面图形的概念及它们之间的关系． 2.内容解析我们生活在一个多姿多彩的图形世界里，生活中处处存在着具有各种各样形状的物体，我们可以从这些物体中抽象出几何图形，如长方体、圆柱、球、长方形、三角形、圆、线段、点等．几何图形可分为立体图形和平面图形两类，常见立体图形有圆柱、棱柱、圆锥、棱锥、球等，常见的平面图形有线段、角、三角形、四边形、圆等．立体图形的表面中包含着平面图形，平面图形可以围成立体图形．七年级第四章《几何图形初步》引入的是几何图形的一些最基本的概念，这些知识是“空间与图形”领域学习的基础．本课的内容属于初中几何图形知识学习的起始阶段，对于发展学生的空间观念，培养学生的空间想象力有着重要的作用，对后续几何知识的学习影响深远．基于以上分析，确定本节课的教学重点：认识基本的几何图形，能从具体事物中抽象出几何图形．二.教学目标解析 1.目标（1）认识一些简单几何体（长方体、正方体、棱柱、棱锥、圆柱、球等）的基本特征，能识别这些几何体．（2）丰富学生对几何图形的感性认识，理解立体图形与平面图形的联系，发展学生的空间观念，培养学生的空间想象力． 2.目标解析达成目标（1）的标志是：通过观察生活中的大量图片或实物，认识生活中以实物为原型的几何图形，能准确识别圆柱、棱柱、圆锥、棱锥等几何体，并准确说出它们的名称．达成目标（2）的标志是：经历从现实世界中抽象出几何图形的过程，感受图形世界的丰富多彩，能指出一个立体图形中所包含的平面图形，能由实物形状想象出相应的几何图形，能由几何图形想象出与之形状相对应的实物．三.学生学情分析学生在小学阶段初步认识了一些较简单的几何图形，但对于棱柱、棱锥这两类几何体还比较陌生，对于几何图形之间的区别和联系也模糊不清，小学阶段对几何图形的认识是形象化的、感性的，需要通过进一步学习提高到理性认识．七年级学生抽象逻辑思维能力还有待发展，对于从现实生活中的实物抽象出几何图形，如从一个纸盒抽象出长方体、长方形、线段、点，学生不容易理解，在教学过程中需要借助精心挑选的实物和特制的模型，来帮助学生理解．本节课的教学难点是：从实物中抽象出几何图形．四.教学策略分析

初中数学二次函数动点问题

函数性问题专题—动点问题函数及其图象是初中数学中的主要内容之一，也是初中数学与高中数学相联系的纽带．它与代数、几何、三角函数等知识有着密切联系，中考命题中既重点考查函数及其图象的有关基础知识，同时以函数为背景的综合性问题也是命题热点之一，多数省市作压轴题．因此，在中考复习中，关注这一热点显得十分重要．以函数为背景的综合性问题往往都可归结为动点性问题，我们把它归纳为以下七种题型（附例题）一、因动点而产生的面积问题例1：如图10，已知抛物线P ：y =ax 2 +bx +c (a ≠0 与x 轴交于A 、B 两点(点A 在x 轴的正半轴上，与y 轴交于点C ，矩形DEFG 的一条边DE 在线段AB 上，顶点F 、G 分别在线段BC 、AC 上，抛物线P 上部分点的横坐标对应的纵坐标如下： (1 求A 、B 、C 三点的坐标； (2 若点D 的坐标为(m ，0 ，矩形DEFG 的面积为S ，求S 与m 的函数关系，并指出m 的取值范围； (3 当矩形DEFG 的面积S 取最大值时，连接DF 并延长至点M ，使FM =k ·DF ，若点M 不在抛物线P 上，求k 的取值范围. 若因为时间不够等方面的原因，经过探索、思考仍无法圆满解答本题，请不要轻易放弃，试试将上述(2、(3小题换为下列问题解答(已知条件及第(1小题与上相同，完全正确解答只能得到5分： (2 若点D 的坐标为(1，0 ，求矩形DEFG 的面积 . 例2：如图1，已知直线

12 y x =-与抛物线2 164 y x =- +交于A B ，两点．（1）求A B ，两点的坐标；（2）求线段A B 的垂直平分线的解析式；（3）如图2，取与线段A B 端点分别固定在A B ，两处．用铅笔拉着这根橡皮筋使笔尖P 在直线A B 动点P 将与A B ，构成无数个三角形，这些三角求出最大面积，并指出此时P 点的坐标；如果不存在，请简要说明理由．图2 图1 图10 第-2-页共4页例3：如图1，矩形ODEF 的一边落在矩形ABCO 的一边上，并且矩形ODE F ∽矩形ABCO ，其相似比为1 : 4，矩形ABCO 的边 AB=4,BC=4