解析几何和立体几何交汇问题的解法

立体几何与解析几何交汇问题的解法
近几年的高考特别关注知识的综合性,注意在知识的网络交汇处设计试题,旨在考查学生综合利用所学知识分析和解决问题的能力。解几和立几交汇的问题因为其新颖性、应用性和综合性备受命题者的青睐,本文精选几例近几年来的高考题或高考模拟题作简要地分析,以期窥一斑而见全豹。
1以解析几何为背景的立体几何题
有些几何体通过投影、切割等方式得到解析几何中的曲线或解几中的一些曲线经过翻转和旋转得到立几中的几何体,通过研究解几中的曲线,从而计算几何体的面积、体积等度量。
例1如图1,一个球形广告气球被一束入射角为30°的平行光线照射,其投影是一个长半轴为5 米的椭圆,
2果中保留
π)。
分析:本题旨在考查球的面积公式,属简单题, 只需找到球的半径与椭圆长轴之间的关系即可。
解:设球的直径为r 2,椭圆的长轴为a 2, 则有:030cos 22?=a r
,即2
3
52
3==a r , 所以广告气球的面积:ππ7542==r S 。
例2由曲线y x 42=,y x 42-=,4=x ,4-=x 围成图形(如图2—1)绕y 轴旋转一周所得为旋转体的体积为V 1,满足1622≤+y x ,4)2(22≥-+y x ,4)2(22≥++y x 的点),(y x 组成的图形(如图2—2)绕y 轴旋转一周所得旋转体的体积为V 2,则( )
(A) V 1=21V 2 (B) V 1=3
2 (D) V 1=2V 2 分析:两个图形中的平面曲 线围成图形绕y 轴旋转后都不是 常见的旋转体,不能直接用公式 求出体积,所以要考虑用祖暅原 理比较两个几何体的体积。
解:用任意一个与y 轴垂直 的平面去截这两个旋转体,设 截面与原点距离为 ||y ,则
所得截面面积:|)|44(21y S -=π,|)|44()]||2(4[)4(222y y y S -=----=π,所以
21S S =。由祖暅原理,这两个旋转体的体积相等,故选C 。
图1
2以立体几何为背景的解析几何题
有些问题以几何体为背景,通过研究立体几何中点、线、面的位置关系或数量关系,从而转化为平面图形问题,在坐标系的基础上,从而判断动点的轨迹、求曲线的方程等。
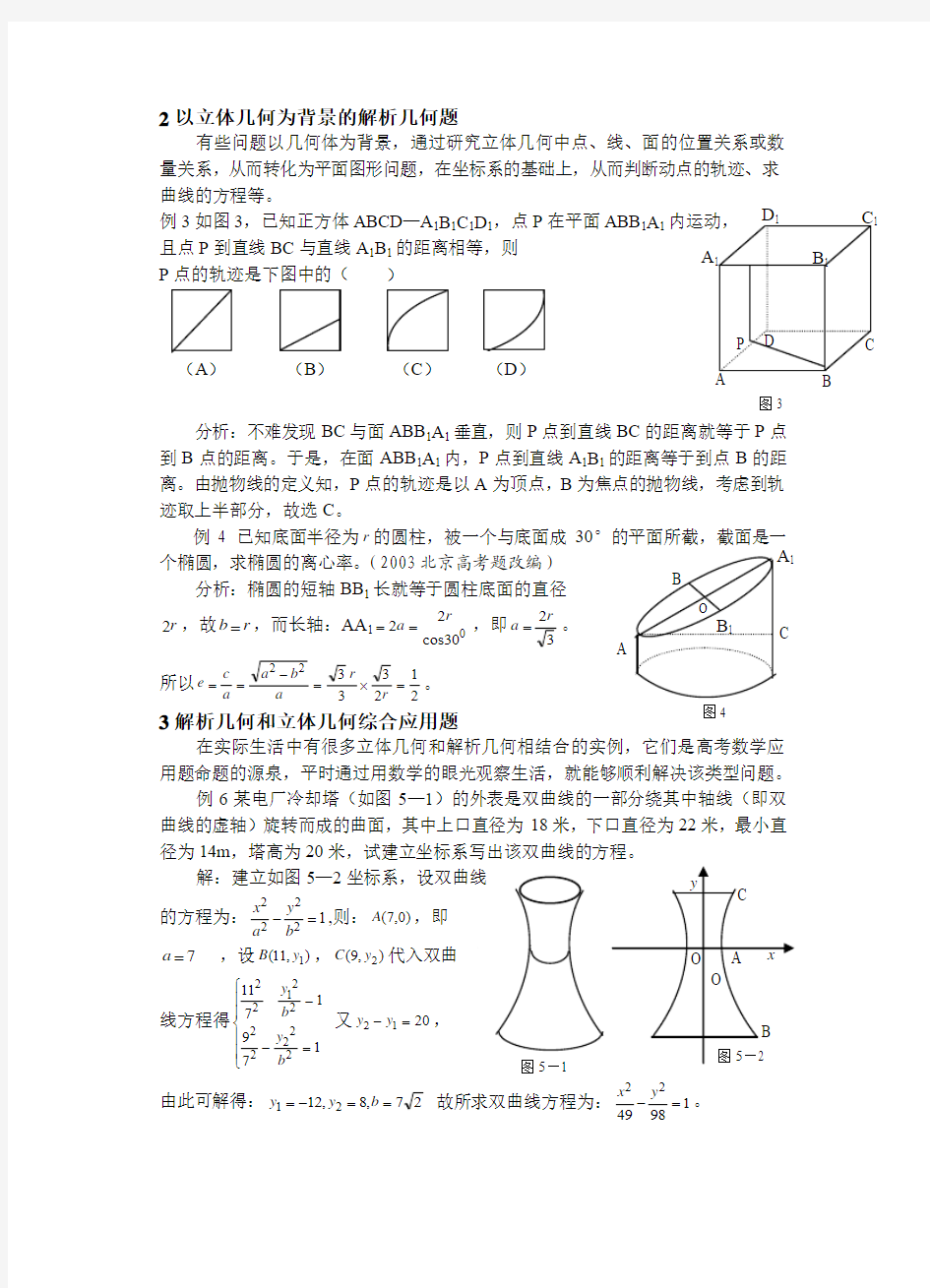
例3如图3,已知正方体ABCD —A 1B 1C 1D 1,点P 在平面ABB 1A 1
内运动, 且点P 到直线BC 与直线A 1B 1的距离相等,则 P 点的轨迹是下图中的( )
分析:不难发现BC 与面ABB 1A 1垂直,则P 点到直线BC 的距离就等于P 点到B 点的距离。于是,在面ABB 1A 1内,P 点到直线A 1B 1的距离等于到点B 的距离。由抛物线的定义知,P 点的轨迹是以A 为顶点,B 为焦点的抛物线,考虑到轨迹取上半部分,故选C 。
例4 已知底面半径为r 的圆柱,被一个与底面成30°的平面所截,截面是一
个椭圆,求椭圆的离心率。(2003北京高考题改编)
分析:椭圆的短轴BB 1长就等于圆柱底面的直径
r 2,故r b =,而长轴:AA 130cos 22r a =
=,即3
2r a =
。
所以2
1233 32
2=?=-=
=r r a
b a a
c
e 。 3解析几何和立体几何综合应用题
在实际生活中有很多立体几何和解析几何相结合的实例,它们是高考数学应
用题命题的源泉,平时通过用数学的眼光观察生活,就能够顺利解决该类型问题。
例6某电厂冷却塔(如图5—1)的外表是双曲线的一部分绕其中轴线(即双曲线的虚轴)旋转而成的曲面,其中上口直径为18米,下口直径为22米,最小直径为14m ,塔高为20米,试建立坐标系写出该双曲线的方程。
解:建立如图5—2的方程为:122
22=-b
y a
x ,则:)0,7(A ,即
7=a
,设),11(1y B ,),9(2y C 代入双曲
线方程得???????=-=-1
7
9
171122222
22
122b y b
y 又2012=-y y , 由此可解得:27,8,1221==-=b y y 故所求双曲线方程为:
198
492
2=-y x 。 (A ) (B ) (C ) (D )
1
B
A 1 C
A D
B 1 D 1
C 1
图3 P
例4 如图6—1,平地上有一条水沟,沟沿是两条长100米的平行线段,沟宽AB 为2米,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为O ,对称轴与地面垂直,沟深1.5米,沟中水深1米。
(1) 求水面宽; (2) 沟中水的体积有多少立方米;
(3) 若要把这条水沟改挖(不准填土)成为
截面为等腰梯形的沟,使沟的底面与地面平行,则改
挖后的沟宽为多少米时,所挖的土最少? 解:(1)如图6—2建立平面直角坐标系,设抛物
线的方程为2ax y =,则由抛物线过点)23,1(,得23
=a , 于是抛物线方程为22
3x y =,当1=y 时,3
6
±=x ,故 水面宽为
3
6
2。 (2)由于求体积要用到积分知识,故这里从略。
(3)为了使挖掉的土最少,等腰梯形的两腰必须同抛物线相切。设切点为)2
3
,(2t t P )10(≤ 形OCDE ,且t y k t x CD 3|/===,则切线CD 的方程是:222 3323)(3t tx t t x t y -=+-=,于是)0,2 1(t C ,)2 3),1(2 1(t t D +,记梯形OCDE 的面积为S ,则t t t t S 21243)21(43??≥+ = 4 23= ,)10(≤ 3时,S 取到最小值,此时挖土最少。 由于立体几何和解析几何综合问题能够为学生能力发展和提升创造更广阔的 空间,所以正在成为高考新的热点,在平时的学习和复习中应该引起足够的重视。 A C E 立体解析综合题练习1 1.如图,正方形ADEF 与梯形ABCD 所在平面互相垂直,已知//,AB CD AD CD ⊥,1 2 AB AD CD ==. (Ⅰ)求证:BF //平面CDE ; (Ⅱ)求平面BDF 与平面CDE 所成锐二面角的余弦值; (Ⅲ)线段EC 上是否存在点M ,使得平面BDM ⊥平面 BDF ?若存在, 求出EM EC 的值;若不存在,说明理由. 2.已知1(2,0)F -,2(2,0)F 两点,曲线C 上的动点P 满足12123 ||||||2 PF PF F F +=. (Ⅰ)求曲线C 的方程; (Ⅱ)若直线l 经过点(0,3)M ,交曲线C 于A ,B 两点,且12 MA MB = ,求直线l 的方程. 立体解析综合题练习2 1. 在如图所示的多面体中,EA ⊥平面ABC ,DB ⊥平面ABC ,BC AC ⊥, 且22====AE BD BC AC ,M 是AB 的中点. (Ⅰ)求证:CM ⊥EM ; (Ⅱ)求平面EMC 与平面BCD 所成的锐二面角的余弦值; (Ⅲ)在棱DC 上是否存在一点N ,使得直线MN 与平面EMC 所成的角为60?.若存在,指出点N 的位置;若不存在,请说明理由. 2.椭圆C:22 221(0)x y a b a b +=>>的两个焦点为F 1,F 2,点P 在椭圆C 上,且11212414,||,||.33PF F F PF PF ⊥== (Ⅰ)求椭圆C 的方程; (Ⅱ)若直线l 过圆M: x 2+y 2+4x-2y=0的圆心,交椭圆C 于,A B 两点,且A 、B 关于点M 对称, 求直线l 的方程. 立体解析综合题练习3 1.在如图所示的几何体中,四边形ABCD 为正方形,PA ⊥平面ABCD ,PA //BE ,AB =PA =4,BE =2. (Ⅰ)求证:CE //平面PAD ; (Ⅱ)求PD 与平面PCE 所成角的正弦值; (Ⅲ)在棱AB 上是否存在一点F ,使得 平面DEF ⊥平面PCE ?如果存在,求AF AB 的值; 如果不存在,说明理由. 2.已知抛物线C :2 2y px =(0p >)的焦点F (1,0),O 为坐标原点,A ,B 是抛物线C 上 异于O 的两点. (Ⅰ)求抛物线C 的方程; (Ⅱ)若直线OA ,OB 的斜率之积为1 2 - ,求证:直线AB 过x 轴上一定点. A B F E D C 立体几何中几类典型问题的向量解法 空间向量的引入为求立体几何的空间角和距离问题、证线面平行与垂直以及解决立体几 何的探索性试题提供了简便、快速的解法。它的实用性是其它方法无法比拟的, 因此应加强 运用向量方法解决几何问题的意识, 提高使用向量的熟练程度和自觉性, 注意培养向量的代 数运算推理能力,掌握向量的基本知识和技能,充分利用向量知识解决图形中的角和距离、 平行与垂 直问题。 「、利用向量知识求点到点,点到线,点到面,线到线,线到面,面到面的距离 (1) 求点到平面的距离除了根据定义和等积变换外还可运用平面的法向量求得,方法是: (3)求点P 到直线AB 的距离,可在 AB 上取一点Q ,令AQ 的最小值求得参数 ■,以确定Q 的位置,贝U PQ 为点P 到直线AB 的距离。还可以在AB 上 任取一点Q 先求cos ::: PQ, AB ?,再转化为sin ::: PQ, AB ?,则 点P 到直线AB 的距离。 (4)求两条异面直线li,l2之间距离,可设与公垂线段 例 1:设 A(2,3,1), B(4,1,2), C(6,3,7), D(-5,-4,8),求点 D 到平面 ABC 的距离 例2:如图,正方形 ABCD 、ABEF 的边长都是1,而且平面 ABCD 、ABEF 互相垂直。 点M 在AC 上移动,点 N 在BF 上移动,若CM 二BN 二a (0 ::: a 2)。 求出平面的一个法向量的坐标,再求出已知点 P 与平面内任一点 M 构成的向量 M P 的坐 标, 那么P 到平面的距离d = MP ?'cosen,MP > (2)求两点P,Q 之间距离,可转化求向量 PQ 的模。 sin :: PQ, AB 为 AB 平行的向量n , C,D 分别是ht 上 的任意两点,贝y h,l2之间距离 AB = 1.已知△ABC的顶点B、C在椭圆x2/4+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( ) A.2B.6 C.8D.12 2.抛物线上的点到直线距离的最小值是() A.B.C.D. 3.已知以椭圆的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两 点,则该椭圆的离心率的取值范围是() A.B.C.D. 4.已知椭圆的焦点是F1、F2,P是椭圆上的一个动点,过点F2向∠F1PF2的外角平分线作垂线,垂足为 M,则点M的轨迹是() A.圆B.椭圆C.直线D.双曲线的一支 5.如图,已知点B是椭圆的短轴位于x轴下方的端点,过B 作斜率为1的直线交 椭圆于点M,点P在y轴上,且PM//x轴,,若点P的坐标为(0,t),则t的取值范围 是() A.0 ①AD+AE=AB+BC+CA; ②AF·AG=AD·AE ③△AFB ~△ADG 其中正确结论的序号是 A.①②B.②③C.①③D.①②③ 7. 如图2,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD 相交与点F,则AF的长 为____________。 8.如图,已知圆中两条弦与相交于点,是延长线上一点,且 若与圆相切,则线段的长为__________. 9.已知点,动点满足条件.记动点的轨迹 为.则的方 程是____________. 10. 矩形的两条对角线相交于点,边所在直线的方程为 ,点在边所在直线上. (I)求边所在直线的方程; (II)求矩形外接圆的方程; (III)若动圆过点,且与矩形的外接圆外切,求动圆的圆心的轨迹方程. 11. 已知平面上两定点M(0,-2)、N(0,2),P为一动点,满足. (I)求动点P的轨迹C的方程; (II)若A、B是轨迹C上的两不同动点,且. 分别以A、B为切点作轨迹C 的切线,设其交点 Q,证明为定值. 【参考答案】 1.C 解析:由椭圆定义知,△ABC的周长=4a。 2.A 解析:由几何知识知道,平移直线与抛物线相切, 切点到直线的距离最小。 3.C 解析: 高中数学必修二复习 基本概念 公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。 公理3:过不在同一条直线上的三个点,有且只有一个平面。 推论1: 经过一条直线和这条直线外一点,有且只有一个平面。 推论2:经过两条相交直线,有且只有一个平面。 推论3:经过两条平行直线,有且只有一个平面。 公理4 :平行于同一条直线的两条直线互相平行。 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。 空间两直线的位置关系: 空间两条直线只有三种位置关系:平行、相交、异面 1、按是否共面可分为两类: (1)共面:平行、相交 (2)异面: 异面直线的定义:不同在任何一个平面内的两条直线或既不平行也不相交。 异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。 两异面直线所成的角:范围为( 0°,90° ) esp.空间向量法 两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法 2、若从有无公共点的角度看可分为两类: (1)有且仅有一个公共点——相交直线;(2)没有公共点——平行或异面 直线和平面的位置关系: 直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行 ①直线在平面内——有无数个公共点 ②直线和平面相交——有且只有一个公共点 直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。 esp.空间向量法(找平面的法向量) 规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角 由此得直线和平面所成角的取值范围为[0°,90°] 最小角定理: 斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角 三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直 esp.直线和平面垂直 直线和平面垂直的定义:如果一条直线a和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直.直线a叫做平面的垂线,平面叫做直线a的垂面。 用向量方法求空间角和距离 在高考的立体几何试题中,求角与距离是常考查的问题,其传统的“三步曲”解法:“作图、证明、解三角形”,作辅助线多、技巧性强,是教学和学习的难点.向量进入高中教材,为立体几何增添了活力,新思想、新方法与时俱进,本专题将运用向量方法简捷地解决这些问题. 1 求空间角问题 空间的角主要有:异面直线所成的角;直线和平面所成的角;二面角. (1)求异面直线所成的角 设a 、b 分别为异面直线a 、b 的方向向量, 则两异面直线所成的角α=arccos |||||| a b a b (2)求线面角 设l 是斜线 l 的方向向量,n 是平面α的法向量, 则斜线l 与平面α所成的角α=arcsin |||||| l n l n (3)求二面角 法一、在α内a l ⊥,在β内b l ⊥,其方向如图,则二面角l αβ--的平面角α=arccos |||| a b a b 法二、设12,,n n 是二面角l αβ --的两个半平面的法向量, 其方向一个指向内侧,另一个指向外侧,则二面角l α β --的平面角α=12 12arccos |||| n n n n 2 求空间距离问题 构成空间的点、线、面之间有七种距离,这里着重介绍点面距离的求法,象异面直线间的距离、线面距离;面面距离都可化为点面距离来求. (1)求点面距离 法一、设n 是平面α的法向量,在α内取一点B, 则 A 到α的距离|| |||cos ||| AB n d AB n θ== 法二、设A O α ⊥于O,利用A O α ⊥和点O 在α内 的向量表示,可确定点O 的位置,从而求出||A O . (2)求异面直线的距离 法一、找平面β使b β?且a β ,则异面直线a 、b 的距离就转化为直线a 到平面β的距离,又转化为点A 到平面β的距离. 法二、在a 上取一点A, 在b 上取一点B, 设a 、b 分别 为异面直线a 、b 的方向向量,求n (n a ⊥ ,n b ⊥ ),则 异面直线a 、b 的距离|| |||cos ||| AB n d AB n θ== (此方法移植 于点面距离的求法). 立体与平面解析解析几何 1. 常见多面体:棱柱,棱锥,棱台 常见的旋转体:圆柱,圆锥,圆台,球 平面的表示:通常用希腊字母α、β、γ表示,如平面α 直线一般用小写英语字母a, b, l或者大写字母直线上的两个点AB表示。 点与平面的关系:点A在平面内,记作;点不在平面内, 记作 点与直线的关系:点A的直线l上,记作:A∈l;点A在直线l外,记作A l; 直线与平面的关系:直线l在平面α内,记作lα;直线l不在平面α内,记作lα。 4. 四个公理 公理1:如果一条直线的两点在一个平面内,那么这条直线是所有的点都在这个平面内。 符号语言 公理2:经过不在同一条直线上的三点,有且只有一个平面。 公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 符号:平面α和β相交,交线是a,记作α∩β=a。 公理4:平行于同一条直线的两条直线互相平行 5. 直线和平面之间的位置关系 ★线面平行: ⑴判定:平面外一条直线与此平面内的一条直线平行,则该直线与此 平面平行 ⑵性质:一条直线与一个平面平行,则过这条直线的任一平面与此平 面的交线与该直线平行 ★面面平行: ⑴判定:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行 ⑵性质:如果两个平行平面同时和第三个平面相交,那么它们的交线平行 ★线面垂直: ⑴定义:如果一条直线垂直于一个平面内的任意一条直线,那么就说这条直线和这个平面垂直。 ⑵判定:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直 ⑶性质:垂直于同一个平面的两条直线平行。 ★面面垂直: ⑴定义:两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。 ⑵判定:一个平面经过另一个平面的一条垂线,则这两个平面垂直 ⑶性质:两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面。 6. 思考途径 证明直线与直线的平行的思考途径 (1)转化为二直线同与第三条直线平行; (2)转化为线面平行; 证明直线与平面的平行的思考途径 (1)转化为线线平行; (2)转化为面面平行. 证明平面与平面平行的思考途径 (1)转化为线面平行; (2)转化为线面垂直. 证明直线与直线的垂直的思考途径 (1)转化为线面垂直; (2)转化为线与另一线的射影垂直; 证明直线与平面垂直的思考途径 (1)转化为该直线与平面内相交二直线垂直; (2)转化为该直线与平面的一条垂线平行; (3)转化为该直线垂直于另一个平行平面; 证明平面与平面的垂直的思考途径 新课标立体几何解析几何常考题汇总 1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点 (1) 求证:EFGH 是平行四边形 (2) 若BD=AC=2,EG=2。求异面直线AC 、BD 所成的角和EG 、BD 所成的角。 证明:在ABD ?中,∵,E H 分别是,AB AD 的中点∴1 //,2 EH BD EH BD = 同理,1 //,2 FG BD FG BD =∴//,EH FG EH FG =∴四边形EFGH 是平行四边形。 (2) 90° 30 ° 考点:证平行(利用三角形中位线),异面直线所成的角 2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。 求证:(1)⊥AB 平面CDE; (2)平面CDE ⊥平面ABC 。 证明:(1)BC AC CE AB AE BE =??⊥?=? 同理, AD BD DE AB AE BE =? ?⊥?=? 又∵CE DE E ?= ∴AB ⊥平面CDE (2)由(1)有AB ⊥平面CDE 又∵AB ?平面ABC , ∴平面CDE ⊥平面ABC 考点:线面垂直,面面垂直的判定 A H G F E D C B A E D B C 3、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点, 求证: 1//A C 平面BDE 。 证明:连接AC 交BD 于O ,连接EO , ∵E 为1AA 的中点,O 为AC 的中点 ∴EO 为三角形1A AC 的中位线 ∴1//EO AC 又EO 在平面BDE 内,1A C 在平面BDE 外 ∴1//A C 平面BDE 。 考点:线面平行的判定 4、已知ABC ?中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC . 证明:90ACB ∠=∵° BC AC ∴⊥ 又SA ⊥面ABC SA BC ∴⊥ BC ∴⊥面SAC BC AD ∴⊥ 又,SC AD SC BC C ⊥?=AD ∴⊥面SBC 考点:线面垂直的判定 5、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点. 求证:(1) C 1O ∥面11AB D ;(2)1 AC ⊥面11AB D . 证明:(1)连结11A C ,设 11111 A C B D O ?=,连结1AO ∵ 1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形 ∴A 1C 1∥AC 且 11A C AC = 又1,O O 分别是11,A C AC 的中点,∴O 1C 1∥AO 且11O C AO = 11AOC O ∴是平行四边形 111,C O AO AO ∴? ∥面11AB D ,1C O ?面11AB D ∴C 1O ∥面11AB D (2)1CC ⊥面1111A B C D 11!CC B D ∴⊥ 又1111 A C B D ⊥∵, 1111B D A C C ∴⊥面 1 11AC B D ⊥即 同理可证11A C AD ⊥, 又 1111 D B AD D ?= A 1 E D 1 C 1 B 1 D C B A S D C B A D 1O D B A C 1 B 1 A 1 C 《空间解析几何2》教学大纲 课程编号:12307229 学时:22 学分:1.5 课程类别:限制性选修课 面向对象:小学教育专业本科学生 课程英语译名:In terspace An alytic Geometry (2) 一、课程的任务和目的 任务:本课程要求学生熟练掌握解析几何的基本知识和基本理论,正确地理解和使用向 量代数知识,并解决一些实际问题。深刻理解坐标观念和曲线(面)与方程相对应的观念,熟练掌握讨论空间直线、平面、曲线、曲面的基本方法,训练学生的空间想象能力和运算能力。 目的:通过本课程的学习,使学生掌握《空间解析几何》的基本知识、基本思想及基本方法,培养学生的抽象思维能力及空间想象力,培养学生用代数方法处理几何问题的能力,提高学生从几何直观分析问题和和解决问题的能力。为学习《高等代数》及《数学分析》及后继课程打下坚实基础,为日后胜任小学教学工作而作好准备。 二、课程教学内容与要求 (一)平面与空间直线(14学时) 1.教学内容与要求:本章要求学生熟练掌握平面与空间直线的各种形式的方程,能判别空间有关点、直线与平面的位置关系,能熟练计算它们之间的距离与交角。 2?教学重点:根据条件求解平面和空间直线的方程,及点、直线、平面之间的位置关系 3?教学难点:求解平面和空间直线的方程。 4.教学内容: (1)平面的方程(2课时):掌握空间平面的几种求法(点位式、三点式、点法式、一般式)。 (2)平面与点及两个平面的相关位置(2课时):掌握平面与点的位置关系及判定方法;掌握空间两个平面的位置关系及判定方法。 (3)空间直线的方程(2课时):掌握空间直线的几种求法(点向式、两点式、参数式、一般式、射影式)。 (5)直线与平面的相关位置(2课时):掌握空间直线与平面的位置关系及判定方法。 (6)空间两直线的相关位置(2课时):掌握空间两直线的位置关系及判定方法。 (7)空间直线与点的相关位置(2课时):掌握直线与点的位置关系及判定方法。 (8)平面束(2课时):掌握平面束的定义(有轴平面束和平行平面束),并能根据题意求平面束的方程。 (二)特殊曲面(8学时) 基本要求① .掌握两条直线平行、垂直的条件,能根据直线方程判断两条直线的位置关系; ②.掌握两条直线的夹角公式、到角公式和点到直线的距离公式。 ③ . 掌握圆的标准方程和一般方程 . ④ . 掌握圆的方程的两种形式,并能合理合理运用; ⑤. 灵活运用圆的几何性质解决问题 . 1 直线方程的五种形式 点斜式:y y0k ( x x0 ) ,(斜率存在 ) 斜截式:y kx b (斜率存在 ) 两点式: y y1 x x 1, (不垂直坐标轴 ) y2 y1 x2 x1 截距式:x y 1 (不垂直坐标轴 ,不过原点 ) a b 一般式: Ax By C 0 2.直线与直线的位置关系: ( 1)有斜率的两直线 l1:y=k 1x+b1; l2:y=k 2x+b2;有:① l1∥ l2 k1=k2且 b1≠ b2;② l 1⊥ l2 k1·k2 =-1 ; ③ l 1与 l 2相交k 1≠ k2 ④l 1与 l 2重合k1=k2 且 b1=b2。( 2)一般式的直线l : A x+B y+C =0, l : A x+B y+C =0 有:① l ∥ l 2 AB-A B=0;且 BC-B 2 C ≠ 0 1 1 1 1 2 2 2 2 1 1 2 2 1 1 2 1 ② l1⊥ l2A1A2+B1B2=0 ③ l1与 l2相交 A 1B2-A 2B1≠ 0 ④ l1与 l2重合 A 1B2-A 2B1=0 且 B1C2-B 2C1=0。 3.点与直线的位置关系: 点 P( x , y )到直线 Ax+By+C=0的距离: d Ax0 By0 C 。 00 A2 B 2 平行直线 Ax+By+C1=0 与 Ax+By+C2=0 之间的距离为 d C1 C2 A2 B 2 两点间距离公式:| PP | (x x )2 ( y y )2 1 2 1 2 1 2 .4 直线系方程 ①过直线 l 1:A1x+B1y+C1=0, l 2:A2x+B2y+C2=0交点的直线系方程为:A1x+B1y+C1+λ( A2x+B2y+C2)=0(λ∈R)( 除l2外 ) 。 ②过定点 M ( x0 , y0 ) 的直线系方程为 y y0 k( x x0 ) (其中不包括直线x x0) ③和直线 Ax By C 0 平行的直线方程为Ax By C ' 0 (C C ') ④和直线 Ax By C 0 垂直的直线方程为Bx Ay C ' 0 5.圆的定义 : 平面内与定点距离等于定长的点的集合( 轨迹 ) 叫圆 . 在平面直角坐标系内确定一个圆需要三个独立条件: 如三个点 , 半径和圆心 ( 两个坐标 ) 等 . 2 2 2 6. 圆的方程 (1)标准式: (x-a) +(y-b) =r (r>0),其中 r 为圆的半径, (a, b)为圆心。 2 2 2 2 D E 1 D 2 E 2 4F (2)一般式: x +y +Dx+Ey+F=0(D+E -4F>0),其中圆心为( , ) ,半径为 2 2 2 (3) 参数方程 : x r cos , x a r cos (是参数) . 消去θ可得普通方程y r sin y b r sin ( 4) A(x 1, y1)B(x 2,y2)为直径的圆: (x-x1)(x-x 2)+(y-y 1)(y-y 2)=0; (5) .过圆与直线(或圆)交点的圆系方程: i)x2+y2+Dx+Ey+F+λ (Ax+By+C)=0,表示过圆与直线交点圆的方程 高三数学《立体几何》、《解析几何》的复习建议 仙居中学赵娅芳 《立体几何》 一、2009年浙江(文科)考题分析 紧张又期待的2009年新高考已过去,为迎接不久到来的2010年高考,我们又得时刻准备着,整装待发……大家都十分关注新高考考什么?怎么考?非常疑惑高三复习教什么?怎么教?我想:2009年的浙江省高考试题为我们所有高三数学老师的复习起了一定的导向作用.2009年的浙江文科数学试题仍保持“1+1+1”的题型,即一道选择题,一道填空题和一道解答题组成,分值23分,占全卷的15.3%.从考查内容来看:线线、线面、面面的平行与垂直关系是立体几何的主干知识,还是今年新高考考查的重点.如浙江文(4)、文(19)第(Ⅰ)题;求角的问题主要考了直线与平面所成的角(应该是重点考查对象),如浙江文(19)第(Ⅱ)题;值得我们眼睛一亮和重视的是填空题第12题对新增内容——三视图的考查.从考查要求看:试题均可用常规常法和通性通法来解决,淡化特殊技巧,但是考生要完整准确地解答,则需要有扎实的双基和良好的数学素养.方法能力上:在考查空间想象能力的同时,又考查了推理论证能力、运算能力和分析问题、解决问题的能力. 二、几点复习建议 1. 重视对《考试说明》的研究,并结合对2009年高考题的认真分析,深化对新课程高考题的认识. 《考试说明》是高考命题的指挥棒,它规定了考试的性质、考试的要求、考试的内容、考试形式及试卷结构等各方面的要求,而且对考查不同的知识提出了明确的层次要求.因此认真研究《考试说明》,并以此为复习备考的依据,也为复习的指南,做到复习既不超纲,又能有针对性、有重点地进行复习,切实提高复习的效率. (1)细心推敲对考试内容三个不同层次的要求.准确掌握哪些内容是了解,哪些是理解,哪些是掌握.这样既明了知识系统的全貌,又知晓了知识体系的主干及重点内容.如2009年《考试说明》(文科)对求角的的问题指出:了解两条异面直线所成角及二面角的概念,理解并会求直线与平面所成角.因此复习时就没有必要在求两条异面直线所成角及二面角的问题上进行过于复杂的探讨,应重点放在求直线与平面所成角的问题上.今年文科第19题的第(Ⅱ)题就 高考解析几何与立体几何复习的几点思考 北师大昆明附中 宋祖发 第一部分 解析几何 解析几何是初等数学与高等数学的衔接点,是中学数学的重要内容.解析几何的核心思想是“ 坐标思想”,即通过坐标系,使点对应到数对,直线与曲线对应于方程,从而把几何问题转化为代数问题,通过代数方程来表示和研究曲线,从而使代数和几何之间建立实质性的联系,可以说,解析几何是各种数学思想方法的综合点,是主干知识的交汇点。 一、解析几何命题的特点 题型相对稳定,一般考查三个小题,一 个大题,文理科差异主要体现在小题上。 三个小题着重考查基本概念与性质,一般会出现一个较难的题目,但入口较容易。 二、解析几何的命题趋势(从内容上来看) 1.直线以倾斜角、斜率、夹角、距离、平行与垂直、线性规划等有关的问题为基本问题,其中要重视“对称问题”的解答方法; 2.与圆的位置有关的问题,一是研究方程组,二是充分利用平面几何知识,后者是常用方法; 3.求曲线的方程或轨迹问题,涉及圆锥曲线的概念和几何性质问题; 4.直线与圆椎曲线的位置关系问题,如参数的取值范围、最值问题等,这是高考的重点内容之一;(学科内的小综合) 5.以圆锥曲线为载体在知识网络的交汇点设计问题,其目的是加强联系、注重应用,以考查学生的应变能力以及分析问题和解决问题的能力。(大综合) 三、需要突破的几个难点: (一)直线与圆的位置关系问题 取值范围是 的倾斜角的则直线的交点位于第一象限,与直线若直线例l y x kx y l 06323:. 1=-+-=?? ??????? ????? ????????2,6D. 2,3C. 2,6B. 3,6A.ππππππππ 得到 由的两侧必在与点点线性规划的另用方法旋转得出结果绕点让的直线系看成过点把直线直线旋转法方法再求倾斜角的范围的范围由交点的坐标解出求交点方法0)32)(3(-3k .l (0,2)(3,0) .:3.G l ,)3(0,-l ,:2. ,k , :1<++∴G 第五章 向量代数与空间解析几何 5.1向量 既有大小又有方向的量 表示:→ -AB 或a (几何表示)向量的大小称为向量的模,记作||AB 、|a |、||a 1. 方向余弦:? ?? ? ??=||,||,||)cos ,cos ,(cos r r r z y x γβα r =(x ,y ,z ),| r |=2 22z y x ++ 2. 单位向量 )cos ,cos ,(cos γβα=→ ο a 模为1的向量。 3. 模 → →→ ?=++=a a z y x a 2 22|| 4. 向量加法(减法) ),,(212121z z y y x x b a ±±±=±→ → 5. a ·b =| a |·| b |cos θ212121z z y y x x ++= a ⊥ b ?a ·b =0(a ·b =b ·a ) 6. 叉积、外积 |a ?b | =| a || b |sin θ= z y x z y x b b b a a a k j i a // b ?a ?b =0.( a ?b= - b ?a ) ? 2 1 2121z z y y x x == 7. 数乘:),,(kz ky kx ka a k ==→ → 例1 1||,2||==→ → b a ,→a 与→ b 夹角为3 π ,求||→ →+b a 。 解 22 ||cos ||||2||2)()(||→ →→→ →→→→→→→→→→→ →++=?+?+?=+?+=+b b a a b b b a a a b a b a b a θ 713 cos 12222=+???+= π 例2 设2)(=??c b a ,求)()]()[(a c c b b a +?+?+。 解 根据向量的运算法则 )()]()[(a c c b b a +?+?+ 立体几何(向量法)—找点难(定比分点公式) 例1(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱 ABCD -A 1B 1C 1D 1中, 侧棱A 1A ⊥底面ABCD , AB (Ⅰ) 证明B 1C 1⊥CE ; (Ⅱ) 求二面角B 1-CE -C 1的正弦值. (Ⅲ) 设点M 在线段C 1E 上, 且直线AM 与平面ADD 1A 1所成角的正弦值为6 , 求线段AM 的长. 【答案】解:方法一:如图,以点A 为原点建立空间直角坐标系,依题意得A (0,0,0),B (0,0,2),C (1,0,1),B 1(0,2,2),C 1(1,2,1),E (0,1,0). (1)证明:易得B 1C 1→=(1,0,-1),CE →=(-1,1,-1),于是B 1C 1→·CE → =0,所以B 1C 1⊥CE . (2)B 1C → =(1,-2,-1), 设平面B 1CE 的法向量=(x ,y ,z ), 则?????·B 1C →=0,m · CE →=0,即?????x -2y -z =0,-x +y -z =0,消去x ,得y +2z =0,不妨令z =1,可得一个法向量 为=(-3,-2,1). 由(1),B 1C 1⊥CE ,又CC 1⊥B 1C 1,可得B 1C 1⊥平面CEC 1,故B 1C 1→ =(1,0,-1)为平面CEC 1 的一个法向量. 于是cos 〈,B 1C 1→〉=m ·B 1C 1→ |m |·|B 1C 1→|=-414×2=-2 77,从而sin 〈,B 1C 1→ 〉=217. 所以二面角B 1-CE -C 1的正弦值为217. (3)AE →=(0,1,0),EC 1→=(1,1,1).设EM →=λEC 1→=(λ,λ,λ),0≤λ≤1,有AM →=AE →+EM →=(λ,λ+1,λ).可取AB → =(0,0,2)为平面ADD 1A 1的一个法向量. 设θ为直线AM 与平面ADD 1A 1所成的角,则 sin θ=|cos 〈AM →,AB → 〉|=|AM →·AB →||AM →|·|AB →|= 2λ λ2+(λ+1)2+λ2×2=λ3λ2+2λ+1. 于是 λ3λ2+2λ+1=26 ,解得λ=1 3(负值舍去),所以AM = 2. 方法二:(1)证明:因为侧棱CC 1⊥平面A 1B 1C 1D 1, B 1 C 1?平面A 1B 1C 1 D 1,所以CC 1⊥B 1C 1.经计算可得B 1 E =5,B 1C 1=2,EC 1=3,从而 B 1E 2=B 1 C 21+EC 21,所以在△B 1EC 1中,B 1C 1⊥C 1E .又CC 1,C 1E ? 平面CC 1E ,CC 1∩C 1E =C 1,所以B 1C 1⊥平面CC 1E ,又CE ?平面CC 1E ,故B 1C 1⊥CE . (2)过B 1 作B 1G ⊥CE 于点G ,联结C 1G .由(1),B 1C 1⊥CE .故CE ⊥平面B 1C 1G ,得CE ⊥C 1G , 《立体几何、解析几何初步》训练题 满分:100分 考试时间:100分钟 、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的 1.已知直线l、m、n及平面 A. 若丨IIm, mil n,则丨// n C.若丨 m,m〃n,则丨 n ,下列命题中的假命题是: B. 若丨,n〃,则丨n D. 若丨〃,nll ,则l//n 2. 设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是 A.若AC与BD共面,则AD与BC共面; B. 若AC与BD是异面直线,则AD与BC是异面直线 C. 若AB AC, DB DC,则AD BC ; D.若AB AC, DB DC,则AD BC 3. “直线a平行于直线b ”是“直线a平行于过直线b的平面”成立的: A.充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 4. 如果正方体ABCD A'B'C'D'的棱长为a,那么四面体A' ABD的体积是: 5. 一个梯形采用斜二测画法作出其直观图,则其直观图的面积是原来梯形面积的: 、2 A. 2倍 4 1 B. —倍 C. 2 空倍D. 2 、2倍 6.已知过点A( 2,m)和B(m,4)的直线与直线2x y 1 0平行,则m的值为 A. 0 B. 8 C. 2 D. 10 7. 已知点A(1,2)和B(3,1),则线段AB的垂直平分线的方程为: A. 4x 2y 5 0 B. 4x 2y 5 0 C. x 2y 5 0 D. x 2y 5 0 8. 已知点A(1,2, 1),点C与点A关于平面xOy对称,点B与点A关于x轴对称,则BC的长为: A. 2.5 B. 4 C. 2,2 D. 2.J 9.若圆C与圆(x 2)2(y 1)21关于原点对称,则圆C的方程是: A. (x 2)2 (y 1)2 1 B. (x 2)2 (y 1)2 1 C. (x 1)2 (y 2)2 1 D. (x 1)2 (y 2)2 1 10.若直线(1 a)x y 1 0与圆 2 2 x y 2x 0相切,则a的值为: A. 1 B. 2 C. 1 D. 1 二、填空题:本大题共4小题,每小题5 分,共20分. 把答案填在题中的横线上 11. 已知点A( 1,0)和B(1,0).若直线y 2x b与线段AB相交,则b的取值范围是_________________________ . 12. 已知m、n是不同的直线,、是不重合的平面,给出下列命题:①若// ,m , n ,则m〃n :② 若m, n ,m〃,n〃,则// ;③若m ,n ,m〃n,贝U // :④ m、n是两条异面直线,若m〃、m〃, n// , n// ,则// .上面的命题中,真命 题的序号是___________ .(写出所有真命题的序号) 13. ____________________________________________________________________________ 设圆x2 y2 4x 5 0的弦AB的中点为P(3,1),则直线AB的方程为 ____________________________________ . A. B. C. D. 解析几何与平面几何选讲 1 ?已知△ ABQ的顶点B、C在椭圆x/4+ y = 1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ ABC的周长是() A. 2 B. 6 C. 8 D. 12 2.抛物线' -:;±的点到直线-- 11距离的最小值是() A. 3?已知以椭圆的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两点,则该椭圆的离心率的取值范围是() 4.已知椭圆的焦点是F1、F2, P是椭圆上的一个动点,过点F2向/ F1PF2的外角平分线作垂线,垂足为 M,则点M的轨迹是() D ?双曲线的一支 B. H 2 5.如图,已知点B是椭圆;;厂…”的短轴位于x 轴下方的端点,过B作斜率为1的直线交 椭圆于点M,点P在y轴上,且PM// x 轴,丽.踰=9,若点P的坐标为(0,t),则t的取值范围是() 0 ① AD+AE=AB+BC+CA ; ② AF ?AG=A D AE ③ 厶AFB ?△ ADG 其中正确结论的序号是 A ?①② B ?②③ D ?①②③ 7.如图2,A,E 是半圆周上的两个三等分点, 直径 BC=4,AD 丄BC,垂足为D,BE 与AD 相交 与点F ,则AF 的长 为 ______________ 。 8如图,已知圆中两条弦丄与上相交于点」, ,是 丄延长线上一点,且 C .①③ n D m 71 -「若二与圆相切,则 线段翅的长为_____________ . 9 .已知点门,动点/满足条件宀‘记动点」的轨迹为丁.则丁的方 程是_______________ . 10.矩形一匸?的两条对角线相交于点』-1, 旳边所在直线的方程为点丁(-1,1)在曲边 所在直线上. (I)求丄:边所在直线的方程; (II )求矩形」二外接圆的方程; (III )若动圆」过点--■■,且与矩形—二的外 接圆外切,求动圆「的圆心的轨迹方程. 11.已知平面上两定点M(0,—2)、N(0, E P D A 1.若3,1,2(x a =,)9,2,1(y b -=,如果a 、b 是共线向量,则( ) A .1,1x y == B .11,22x y ==- C .13 ,62 x y ==- D .13 ,62 x y =-= 2.直三棱柱ABC —A 1B 1C 1中,若CA = a ,CB = b ,1CC = c , 则1A B = ( ) A.+-a b c B. -+a b c C. -++a b c D. -+-a b c 3.已知点(1 21)A -,,关于面xOy 的对称点为B ,而B 关于x 轴的对称点为C ,则BC = ( ) A.(042), , B.(042)--,, C.(040),, D.(202)-, , 4.已知()()()2,5,1,2,2,4,1,4,1A B C ---,则向量AB AC 与的夹角为( ) A. 030 B.045 C.060 D.090 5.若向量λ∈μλμ+λ=且向量和垂直向量R b a n b a m ,(,、则)0≠μ( ) A .n m // B .n m ⊥ C .n m n m 也不垂直于不平行于, D .以上三种情况都可能 6.如图,非零向量C b a ,,,⊥==且为垂足,设向量a λ=,则λ的值为( ) A . 2|a|b a ? B .||||b a b a ?? C .2||b b a ? D . b a b a ??| ||| 7.已知△ABC 的三个顶点为A (3,3,2),B (4,-3,7),C (0,5,1),则BC 边上的 中线长为( ) A .2 B .3 C .4 D .5 8.如图四棱锥P-ABCD 的的底面是正方形,PD ⊥面ABCD ,PD AD =,E 为PC 的中点,则异面直线BE 与 PA 所成角的余弦值等于( ) A. 2 B. 22 C. 3 2 D. 3 3 9.如图,在平行六面体ABCD –A 1B 1C 1D 1中,M 为AC 与BD 的交点.若 a B A =11, b D A =11, c A =1,则下列 向量中与B 1相等的向量是( ) A .c b a ++- 2121 B .c b a ++2 1 21 C .c b a +-2121 D .c b a +--2 121 11.已知空间三点的坐标为)2,5,1(-A ,)1,4,2(B ,)2,3,(+q p C ,若A 、B 、C 三点共线,则=+q p . 12. 已知A 、B 、C 三点不共线,M 、A 、B 、C 四点共面,则对平面ABC 外的任一点O ,有1123 OM OA OB tOC =++ , 则t = . 13.已知(1,1,),(1,,1)t t t t =+=-a b ,则||-a b 的最小值为________. 14.已知△ABC 的顶点为)1,1,1(A ,(0,1,3)B -,(3,2,3)C ,则△ABC 的面积是 . 1、(1)3 1 ,cos ->= 第十三讲 圆锥曲线 一:学习目标 通过具体问题的综合解法与解析解法的比较,让学生体验解析几何处理几何问题,形成用代数方法解决几何问题的能力,提高学生的数学素养,培养学生良好的思维品质。 二:知识梳理 1. 椭圆的定义 第一定义:平面上到两个定点的距离之和等于定长(大于两个定点之间的距离)的点的轨迹,即 |PF 1|+|PF 2|=2a (2a>|F 1F 2|=2c). 第二定义:平面上到一个定点的距离与到一条定直线的距离之比为同一个常数e(0立体几何与解析几何综合题训练
立体几何典型问题的向量解法
解析几何与平面几何选讲
高中数学立体几何解析几何 判定&性质&公式整理(全)
用向量方法解立体几何题(老师用)
立体与平面解析解析几何(研究生整理)
高中数学立体几何解析几何常考题汇总
《空间解析几何2》教学大纲.
平面解析几何知识点总结.doc
高三数学立体几何,解析几何复习建议
高考解析几何与立体几何复习的几点思考
高等数学-向量代数与空间解析几何复习
立体几何(向量法)—找点难(定比分点公式)
《立体几何、解析几何初步》训练题.
解析几何与平面几何选讲
立体几何的向量解法
圆锥曲线与立体几何
