二次函数的存在性问题之菱形(含答案)

二次函数的存在性问题之菱形

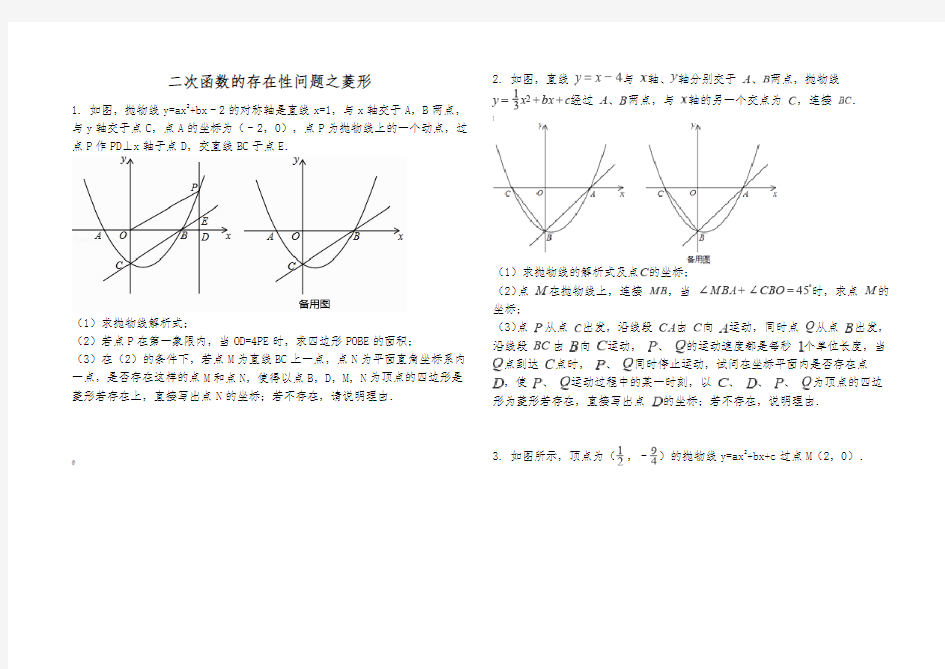
1. 如图，抛物线y=ax2+bx﹣2的对称轴是直线x=1，与x轴交于A，B两点，与y轴交于点C，点A的坐标为（﹣2，0），点P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E．

（1）求抛物线解析式；

（2）若点P在第一象限内，当OD=4PE时，求四边形POBE的面积；

（3）在（2）的条件下，若点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B，D，M，N为顶点的四边形是菱形若存在上，直接写出点N的坐标；若不存在，请说明理由．

@ 2. 如图，直线与

轴、轴分别交于、两点，抛物线

经过、

两点，与轴的另一个交点为，连接．

]

（1）求抛物线的解析式及点的坐标；

（2）点在抛物线上，连接，当时，求点的坐标；

（3）点从点出发，沿线段由向运动，同时点从点出发，沿线段由向运动，、的运动速度都是每秒个单位长度，当点到达点时，、同时停止运动，试问在坐标平面内是否存在点，使、运动过程中的某一时刻，以、、、为顶点的四边形为菱形若存在，直接写出点的坐标；若不存在，说明理由．

3. 如图所示，顶点为（，﹣）的抛物线y=ax2+bx+c过点M（2，0）．

（1）求抛物线的解析式；/

（2）点A是抛物线与x轴的交点（不与点M重合），点B是抛物线与y轴的交点，点C是直线y=x+1上一点（处于x轴下方），点D是反比例函数y= （k ＞0）图象上一点，若以点A，B，C，D为顶点的四边形是菱形，求k的值．

4. 综合与探究如图1所示，直线y=x+c与x轴交于点A（﹣4，0），与y轴交于点C，抛物线y=﹣x2+bx+c经过点A，C．

#

（1）求抛物线的解析式

（2）如图2所示，M是线段OA的上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N

若点P恰好是线段MN的中点，点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D，F，P，M为顶点的四边形是菱形若存在，请直接写出点D 的坐标；若不存在，请说明理由．

注：二次函数y=ax2+bx +c（a≠0）的顶点坐标为（﹣，）

}

5. 如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根，且OA＞OB．

（1）求OA、OB的长．

（2）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形若存在，直接写出F点的坐标，若不存在，请说明理由．

。

}

6. 如图，在平面直角坐标系xOy中，抛物线y=a（x+1）2﹣3与x轴交于A，B 两点（点A在点B的左侧），与y轴交于点C（0，﹣），顶点为D，对称轴与x轴交于点H，过点H的直线l交抛物线于P，Q两点，点Q在y轴的右侧．（1）求a的值及点A，B的坐标；

（2）当点P位于第二象限时，设PQ的中点为M，点N在抛物线上，则以DP

为对角线的四边形DMPN能否为菱形若能，求出点N的坐标；若不能，请说明理由．

·

7. 如图，在平面直角坐标系中，直线AB和抛物线交于点A（﹣4，0），B（0，4），且点B是抛物线的顶点．

（1）求直线AB和抛物线的解析式．

（2）M是直线AB上一动点，在平面直角坐标系内是否存在点N，使以O、B、M、N为顶点的四边形是菱形若存在，请求出点N的坐标；若不存在，请说明理由．

#

|

8. 如图，抛物线y=ax2﹣2x+c（a≠0）与x轴、y轴分别交于点A，B，C三点，已知点A（﹣2，0），点C（0，﹣8），点D是抛物线的顶点．（1）求抛物线的解析式及顶点D的坐标；

（2）如图2，设BC交抛物线的对称轴于点F，作直线CD，点M是直线CD上的动点，点N是平面内一点，当以点B，F，M，N为顶点的四边形是菱形时，请直接写出点M的坐标．

；

*

9. 如图，抛物线 y=x2﹣x﹣2与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，M是直线BC下方的抛物线上一动点．

（1）求A、B、C三点的坐标；

'

（2）连接MO、MC，并把△MOC沿CO翻折，得到四边形MO M′C，那么是否存在点M，使四边形MO M′C为菱形若存在，求出此时点M的坐标；若不存在，说明理由；

|

10. 抛物线y= x2+bx+c经过点A（﹣4，0）、B（2，0）两点，与y轴交于点C，顶点为D，对称轴与x轴交于点H，过点H的直线m交抛物线于P、Q两点，其中点P位于第二象限，点Q在y轴的右侧．

(（1）求D点坐标；

（2）若∠PBA= ∠OBC，求点P的坐标；

（3）设PQ的中点为M，点N在抛物线上，则以DP为对角线的四边形DMPN能否为菱形若能，求出点N的坐标；若不能，请说明理由．

]

…

11. 如图，抛物线y=ax2+bx+c（a≠0）与x轴、y轴分别交于A（﹣1，0）、B （3，0）、C（0，3）三点．

（1）试求抛物线的解析式；

（2）设点M是x轴上的动点，在平面直角坐标系中，是否存在点N，使得以点A、C、M、N为顶点的四边形是菱形若存在，求出所有符合条件的点N坐标；若不存在，说明理由．

}

…

12. 如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与X轴交于点A、B两点B处的坐标为（3，0），与y轴交于c（0，﹣3），点P是直线BC下方抛物线上的动点．（1）求出二次函数的解析式；

（2）连接PO、PC，并将△POC沿y轴对折，得到四边形POP′C，那么是否存在点P，使得四边形POP′C为菱形若存在，求出点P的坐标，若存在，请说明理由；

#

.

13. 如图，已知抛物线经过原点o和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x轴交于点D．直线y=﹣2x﹣1经过抛物线上一点B（﹣2，m）且与y轴交于点C，与抛物线的对称轴交于点F．

（1）求m的值及该抛物线对应的解析式；

（2）点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M 四点为顶点的四边形是菱形．若能，请直接写出点M的运动时间t的值；若不能，请说明理由．

…

；

14. 如图，在平面直角坐标系中，二次函数y=-x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．（1）求这个二次函数的表达式．

（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形若存在，请求出此时点P的坐标；若不存在，请说明理由．

;

，

15. 如图1，在平面直角坐标系中，抛物线y= 与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为点D，过点B 作BC的垂线，交对称轴于点E．

（1）求证：点E 与点D 关于x 轴对称；

（2）如图2，平移抛物线，使抛物线的顶点D 在射线AD 上移动，点D 平移后的对应点为D′，点A 的对应点A′，设抛物线的对称轴与x 轴交于点F ，将△FBC 沿BC 翻折，使点F 落在点F′处，在平面内找一点G ，若以F′、G 、D′、A′为顶点的四边形为菱形，求平移的距离．

—

@

16. 如图，在平面直角坐标系中，点 在抛物线 上,且横坐

标为1，点 与点 关于抛物线的对称轴对称，直线

与 轴交于点 ，

点 为抛物线的顶点，点 的坐标为

（1）求线段 的长；

（2）点

为线段 上方抛物线上的任意一点，过点 作

的垂线交

于点

，点 为 轴上一点，当

的面积最大时，求

的最小值； （3）在（2）中， 取得最小值时，将 绕点 顺时针旋转

后得到

,过点

作

的垂线与直线

交于点 ，

点 为抛物线对称轴上的一点，在平面直角坐标系中是否存在点 ，使得点

为顶点的四边形为菱形，若存在，请直接写出点 的坐标，若不存

在，请说明理由. ）

17. 如图，在平面直角坐标系中，已知矩形ABCD 的三个顶点B （1，0），C （3，0），D （3，4）．以A 为顶点的抛物线y=ax 2+bx+c 过点C ．动点P 从点A 出发，沿线段AB 向点B 运动．同时动点Q 从点C 出发，沿线段CD 向点D 运动．点P ，

Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．

（1）直接写出点A的坐标，并求出抛物线的解析式；

（2）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形请直接写出t的值．

[

18. 已知，抛物线y=ax2+bx+4与x轴交于点A（-3，0）和B（2，0），与y 轴交于点C．（1）求抛物线的解析式；

（2）如图2，若点D为直线BC或直线AC上的一点，E为x轴上一动点，抛物线对称轴上是否存在点F，使以B，D，F，E为顶点的四边形为菱形若存在，请求出点F的坐标；若不存在，请说明理由．

/

'

答案解析部分

一、综合题

1.【答案】（1）解：∵抛物线y=ax2+bx﹣2的对称轴是直线x=1，A（﹣2，0）在抛物线上，∴ ，解得：，抛物线解析式为y=

x2﹣x﹣2；

（2）解：令y= x2﹣x﹣2=0，解得：x1=﹣2，x2=4，当x=0时，y=﹣2，∴B（4，0），C（0，﹣2），设BC的解析式为y=kx+b，则，解得：，∴y= x﹣2，

设D（m，0），

∵DP∥y轴，

∴E（m，m﹣2），P（m，m2﹣m﹣2），

∵OD=4PE，

∴m=4（m2﹣m﹣2﹣m+2），

∴m=5，m=0（舍去），

∴D（5，0），P（5，），E（5，），

∴四边形POBE的面积=S△OPD﹣S△EBD= ×5× ﹣1× = ；

（3）解：存在，设M（n，n﹣2），

①以BD为对角线，如图1，∵四边形BNDM是菱形，∴MN垂直平分BD，

∴n=4+ ，

∴M（，），

∵M，N关于x轴对称，∴N（，﹣）；

②以BD为边，如图2，

∵四边形BNDM是菱形，∴MN∥BD，MN=BD=MD=1，过M作MH⊥x轴于H，

∴MH2+DH2=DM2，

即（n﹣2）2+（n﹣5）2=12，

∴n1=4（不合题意），n2=，

∴N（，），

同理（n﹣2）2+（4﹣n）2=1，

∴n1=4+ （不合题意，舍去），n2=4﹣，

∴N（5﹣，），

③以BD为边，如图3，

过M作MH⊥x轴于H，

∴MH2+BH2=BM2，

即（n﹣2）2+（n﹣4）2=12，

∴n1=4+ ，n2=4﹣（不合题意，舍去），

∴N（5+ ，），

综上所述，当N（，﹣）或（，）或（5﹣，）或（5+ ，），以点B，D，M，N为顶点的四边形是菱形．【解析】【分析】（1）由抛物线y=ax2+bx﹣2的对称轴是直线x=1，A（﹣2，

0）在抛物线上，于是列方程即可得到结论；（2）根据函数解析式得到B（4，0），C（0，﹣2），求得BC的解析式为y= x﹣2，设D（m，0），得到E（m，m﹣2），P（m，m2﹣m﹣2），根据已知条件列方程得到m=5，m=0（舍去），求得D（5，0），P（5，），E（5，），根据三角形的面积公式即可得到结论；（3）设M（n，n﹣2），①以BD为对角线，根据菱形的性质得到MN垂直平分BD，求得n=4+ ，于是得到N（，﹣）；②以BD 为边，根据菱形的性质得到MN∥BD，MN=BD=MD=1，过M作MH⊥x轴于H，根据

勾股定理列方程即可得到结论．

—

2.【答案】（1）解：直线解析式，令，得；令，得．∴ 、．∵点、在抛物线上，

∴ ，解得，∴抛物线解析式为：．令

，解得：或，∴ ．

（2）解：，设，①当时，如答图

所示．

∵ ，∴ ，故点满足条件．过点作轴于点，则，，∴ ．∵

，∴ ，∴直线的解析式为：．联立与，得：

，解得：，，∴ ，

，∴ ；

②当与关于轴对称时，如答图所

示．∵

，，∴

，故点满足条件．过点作轴于点，则，，∴ ．∵

，∴ ，∴直线的解析式为：．联立与得：

，解得：，，∴ ，，∴ ．综上所述，满足条件的点的坐标为：或（3）解：设，则，，．假设存在满足条件的点，设菱形的对角线交于点，设运动时间为．

①若以为菱形对角线，如答图．此时，菱形边长．

∴ ．

在中，，

解得．∴ ．过点作轴于点，则，，

∴ ．∴ ．∵点与点横坐标相差个单位，

∴ ；

②若以为菱形对角线，如答图．此时，菱形边长．

∵ ，∴ ，点为中点，

∴ ．∵点与点横坐标相差个单位，∴ ；

③若以为菱形对角线，如答图．此时，菱形边长．

在中，，

解得．∴ ，

．

∴ ．综上所述，存在满足条件的点，点坐标为：

或或．【解析】【分析】（1）根据直线与坐标轴交点的坐标特点求出A,B两点的坐标，将A,B两点的坐标分别代入抛物线 y=x2+bx+c得出关于b,c的方程组，求解得出b,c的值，从而得出抛物线的解析式，再根据抛物线与x轴交点的纵坐标是0，将y=0代入抛物线的解析式，楸树对应的自变量的值，从而求出C 点的坐标；

（2）设 M ( x , y )①当BM⊥BC 时，如答图 2 ? 1 所示．根据等腰直角三角形的性质及垂直的定义得出∠MBA+∠CBO=45°，故点 M 满足条件，过点 M1作M1E⊥y轴于点E ，则M1E=x ， OE=?y 进而表示出BE，根据同角的余角相等及等角的同名三角函数值相等得出tan∠M1BE=tan∠BCO=，根据正切函数的定义得出关于x,y的方程，变形即可得出直线BM1的解析式，解联立直线BM 1的解析式与抛物线的解析式组成的方程组，即可求出M1的坐标；

②当 BM与BC关于y轴对称时，如答图 2 ? 2 所示．根据根据角的和差及对称的性质得出∠ABO=∠MBA+∠MBO=45°，∠MBO=∠CBO ，故

∠MBA+∠CBO=45°，故点 M 满足条件过点 M2 作 M2E⊥y 轴于点 E ，则

M2E=x ， OE=?y 进而表示出BE，根据同角的余角相等及等角的同名三角函数值相等得出tan∠M2BE=tan∠CBO=，根据正切函数的定义得出关于x,y的方程，变形即可得出直线BM2的解析式，解联立直线BM2的解析式与抛物线的解析式组成的方程组，即可求出M2的坐标，综上所述即可得出M点的坐标；（3）设∠BCO=θ，则 tanθ= ， sinθ= ， cosθ=．假设存在满足条件的点 D ，设菱形的对角线交于点 E ，设运动时间为 t ．①若以 CQ 为菱形对角线，如答图 3 ? 1 ．此时 BQ=t ，菱形边长=t ，根据菱形的对角线互相平分得出 CE=CQ=(5?t) ，根据余弦函数的定义，由cosθ=,即可列出方程，求解得出t的值，进而得出CQ的值，过点Q作QF⊥x 轴于点F，则 QF=CQ ? sinθ， CF=CQ ? cosθ，分别计算出QF,CF的长，进而得出OF的长，从而得出Q点的坐标，根据点 D1与点Q横坐标相差 t 个单位即可得出D1的坐标；②若以PQ为菱形对角线，如答图 3 ? 2 ．此时 BQ=t ，菱形边长=t，根据线段中点坐标公式，由点 Q为BC中点得出Q

点的坐标，根

据点 D2与点Q横坐标相差 t 个单位即可得出D1的坐标；③若以CP为菱形对角线，如答图 3 ? 3 ．此时BQ=t ，菱形边长=5?t．根据cosθ =列出方程，求解得出t的值，进而求出OE, 由 D3E=QE=CQ ? sinθ，从而得出D3的坐标，综上所述即可得出答案。

3.【答案】（1）解：依题意可设抛物线方程为顶点式y=a（x﹣）2﹣（a≠0），将点M（2，0）代入可得：a（2﹣）2﹣=0，

解得a=1．

故抛物线的解析式为：y=（x﹣）2﹣

（2）解：由（1）知，抛物线的解析式为：y=（x﹣）2﹣．

则对称轴为x= ，

∴点A与点M（2，0）关于直线x= 对称，

∴A（-1，0）．

令x=0，则y=﹣2，

∴B（0，﹣2）．

在直角△OAB中，OA=1，OB=2，则AB= ．

设直线y=x+1与y轴交于点G，易求G（0，1）．

∴直角△AOG是等腰直角三角形，

∴∠AGO=45°．

∵点C是直线y=x+1上一点（处于x轴下方），而k＞0，所以反比例函数y= （k＞0）图象位于点一、三象限．

故点D只能在第一、三象限，因此符合条件的菱形只能有如下2种情况：

①此菱形以AB为边且AC也为边，如图1所示，过点D作DN⊥y轴于点N，

在直角△BDN中，∵∠DBN=∠AGO=45°，

∴DN=BN= = ，

∴D（﹣，﹣﹣2），

∵点D在反比例函数y= （k＞0）图象上，

∴k=﹣×（﹣﹣2）= + ；

②此菱形以AB为对角线，如图2，

作AB的垂直平分线CD交直线y=x+1于点C，交反比例函数y= （k＞0）的图象于点D．

再分别过点D、B作DE⊥x轴于点F，BE⊥y轴，DE与BE相较于点E．

在直角△BDE中，同①可证∠AGO=∠DBO=∠BDE=45°，

∴BE=DE．

可设点D的坐标为（x，x﹣2）．

∵BE2+DE2=BD2，

∴BD= BE= x．

∵四边形ABCD是菱形，

∴AD=BD= x．

∴在直角△ADF中，AD2=AF2+DF2，即（x）=（x+1）2+（x﹣2）2，

解得x= ，

∴点D的坐标是（，）．

∵点D在反比例函数y= （k＞0）图象上，

∴k= × = ，

综上所述，k的值是+ 或．

【解析】【分析】（1）设抛物线方程为顶点式y=a（x﹣）2﹣，将点M 的坐标代入求a的值即可；（2）设直线y=x+1与y轴交于点G，易求G（0，1）．则直角△AOG是等腰直角三角形∠AGO=45°．点C是直线y=x+1上一点（处于x 轴下方），而k＞0，所以反比例函数y= （k＞0）图象位于点一、三象限．故点D只能在第一、三象限，因此符合条件的菱形只能有如下2种情况：①此菱形以AB为边且AC也为边，②此菱形以AB为对角线，利用点的坐标与图形的性质，勾股定理，菱形的性质和反比例函数图象上点的坐标特征求得k的值即可．

4.【答案】（1）解：将A（﹣4，0）代入y=x+c

∴c=4

将A（﹣4，0）和c=4代入y=﹣x2+bx+c

∴b=﹣3

∴抛物线解析式为y=﹣x2﹣3x+4

（3）解：

存在

设M坐标为（a，0）

则N为（a，﹣a2﹣3a+4）

则P点坐标为（a，）

把点P坐标代入y=﹣x+4

解得a1=﹣4（舍去），a2=﹣1

当PF=FM时，点D在MN垂直平分线上，则D（）

当PM=PF时，由菱形性质点D坐标为（﹣1+ ，）（﹣1﹣，﹣）

当MP=MF时，M、D关于直线y=﹣x+4对称，点D坐标为（﹣4，3）

"

5.【答案】（1）解：方程x2﹣7x+12=0，

分解因式得：（x﹣3）（x﹣4）=0，

可得：x﹣3=0，x﹣4=0，

解得：x1=3，x2=4，

∵OA＞OB，

∴OA=4，OB=3

（2）解：AO⊥BC，

、

∴AO平分∠BAC，

分四种情况考虑：

①AC、AF是邻边，点F在射线AB上时，AF=AC=5，

∴点F与B重合，即F（﹣3，0）；

②AC、AF是邻边，点F在射线BA上时，M应在直线AD上，且FC垂直平分AM，此时点F坐标为（3，8）；

③AC是对角线时，做AC垂直平分线L，AC解析式为y=﹣x+4，直线L过（，2），且k值为（平面内互相垂直的两条直线k值乘积为﹣1），

,

∴L解析式为y= x+ ，

联立直线L与直线AB，得：，

解得：x=﹣，y=﹣，

∴F（﹣，﹣）；

④AF是对角线时，过C做AB垂线，垂足为N，

∵S△ABC= BC?OA= AB?CN=12，

∴CN= = ，

在△BCN中，BC=6，CN= ，

（

根据勾股定理得BN= = ，即AN=AB﹣BN=5﹣= ，

做A关于N的对称点，记为F，AF=2AN= ，

过F 做y 轴垂线，垂足为G，FG=AFsin∠BAO= × = ，

∴F（﹣，），综上所述，满足条件的点有四个：F 1（﹣3，0）；F 2（

3，8）；F 3（﹣，﹣）；F4（﹣，）．

【解析】【分析】（1）解一元二次方程求出OA，OB的长度即可；（2）先根据三角形的面积求出点E的坐标，并根据平行四边形的对边相等的性质求出点D的坐标，然后利用待定系数法求解直线的解析式；分别求出两三角形夹直角的两对应边的比，如果相等，则两三角形相似，否则不相似；（3）根据菱形的性质，分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况，以及AC与AF分别是对角线的情况分别进行求解计算．

,

6.【答案】（1）解：∵抛物线与y轴交于点C（0，﹣）．

∴a﹣3=﹣，解得：a= ，

∴y= （x+1）2﹣3

当y=0时，有（x+1）2﹣3=0，

∴x1=2，x2=﹣4，

∴A（﹣4，0），B（2，0）

（2）解：设P（x1， y1）、Q（x2， y2）且过点H（﹣1，0）的直线PQ的解析式为y=kx+b，

,

∴﹣k+b=0，

∴b=k，

∴y=kx+k．

由，

∴ +（﹣k）x﹣﹣k=0，

∴x1+x2=﹣2+3k，y1+y2=kx1+k+kx2+k=3k2，

∵点M是线段PQ的中点，∴由中点坐标公式的点M（k﹣1，k2）．

]

假设存在这样的N点如图，直线DN∥PQ，设直线DN的解析式为y=kx+k﹣3由，解得：x1=﹣1，x2=3k﹣1，∴N（3k﹣1，3k2﹣3）

∵四边形DMPN是菱形，

∴DN=DM，

∴（3k）2+（3k2）2=（）2+（）2，

整理得：3k4﹣k2﹣4=0，

∵k2+1＞0，

∴3k2﹣4=0，

解得k=± ，

∵k＜0，

∴k=﹣，

∴P（﹣3 ﹣1，6），M（﹣﹣1，2），N（﹣2 ﹣1，1）∴PM=DN=2 ，

∵PM∥DN，

∴四边形DMPN是平行四边形，

∵DM=DN，

∴四边形DMPN为菱形，

∴以DP为对角线的四边形DMPN能成为菱形，此时点N的坐标为（﹣2 ﹣1，1）．

7.【答案】（1）

答案

解：设直线的解析式为y=kx+b．

∵将A（﹣4，0），B（0，4）代入得：，解得k=1，b=4，

∴直线AB的解析式为y=x+4．

设物线的解析式为y=ax2+4．

∵将A（﹣4，0）代入得：16a+4=0，解得a=﹣，

∴抛物线的解析式为y=﹣x2+4．

（2）解：如图2所示：延长MN交x轴与点C．

∵MN∥OB，OB⊥OC，

∴MN⊥OC．

∵OA=OB，∠AOB=90°，

∴∠BA0=45°．

∵ON∥AB，

∴∠NOC=45°．

∴OC=ON× =4× =2 ，NC=ON× =4× =2 ．∴点N的坐标为（2 ，2 ）．

如图3所示：过点N作NC⊥y轴，垂足为C．∵OA=OB，∠AOB=90°，

∴∠OBA=45°．

∵ON∥AB，

∴∠NOC=45°．

∴OC=ON× =4× =2 ，NC=ON× =4× =2 ．∴点N的坐标为（﹣2 ，﹣2 ）．

如图4所示：连接MN交y轴与点C．

∵四边形BNOM为菱形，OB=4，

∴BC=OC=2，MC=CN，MN⊥OB．

∴点的纵坐标为2．

∵将y=2代入y=x+4得：x+4=2，解得：x=﹣2，

∴点M的坐标为（﹣2，2）．

∴点N的坐标为（2，2）．

如图5所示：

∵四边形OBNM为菱形，

∴∠NBM=∠ABO=45°．

∴四边形OBNM为正方形．

∴点N的坐标为（﹣4，4）．

综上所述点N的坐标为或或（﹣4，4）或（2，2）

【解析】【分析】（1）设直线的解析式为y=kx+b，将A（﹣4，0），B（0，4）代入得到关于k、b的方程组，然后解得k、b的值即可；设抛物线的解析式为y=ax2+4，然后将点A的坐标代入求得a的值即可；（2）先根据题意画出图形，需要注意本题共有4种情况，然后依据菱形的性质、等腰直角三角形的性质以及特殊锐角三角函数值求解即可．

8.【答案】（1）解：将点A、点C的坐标代入抛物线的解析式得：，解得：a=1，c=﹣8．

∴抛物线的解析式为y=x2﹣2x﹣8．

∵y=（x﹣1）2﹣9，

∴D（1，﹣9）．

（2）解：设CD的解析式为y=kx﹣8，将点D的坐标代入得：k﹣8=﹣9，解得k=﹣1，

∴直线CD的解析式为y=﹣x﹣8．设直线CB的解析式为y=k2x﹣8，将点B的坐标代入得：4k2﹣8=0，解得：k2=2．∴直线BC的解析式为y=2x﹣8．

将x=1代入直线BC的解析式得：y=﹣6，

∴F（1，﹣6）．

设点M的坐标为（a，﹣a﹣8）．

当MF=MB时，（a﹣4）2+（a+8）2=（a﹣1）2+（a+2）2，整理得：6a=﹣75，解得：a=﹣．

∴点M的坐标为（﹣，）．

当FM=FB时，（a﹣1）2+（a+2）2=（4﹣1）2+（﹣6﹣0）2，整理得：a2+a ﹣20=0，解得：a=4或a=﹣5．

∴点M的坐标为（4，﹣12）或（﹣5，﹣3）．

综上所述，点M的坐标为（﹣，）或（4，﹣12）或（﹣5，﹣3）．9.【答案】（1）解：令y=0，则x2﹣x﹣2=0，

解得：x1=4，x2=﹣1，

∵点A在点B的左侧，

∴A（﹣1，0），B（4，0），

令x=0，则y=﹣2，

∴C（0，﹣2）

（2）解：

存在点M，使四边形MO M′C是菱形，如图1所示：

设M点坐标为（x，x2﹣x﹣2）

若四边形MO M′C是菱形，

则M M′垂直平分OC，

∵OC=2，

∴M点的纵坐标为﹣1，

∴x2﹣x﹣2=﹣1，

解得：x1=，x2=（不合题意，舍去），

∴M点的坐标为（，﹣1）

10.【答案】（1）解：∵y= x2+bx+c经过点A（﹣4，0）、B（2，0）两点，∴y= （x+4）（x﹣2）= （x2+2x﹣8）= （x+1）2﹣3．

∴D（﹣1，﹣3）．

（2）解：在x轴上点E（﹣2，0），连接CE，并延长CE交PB于点F，过点F 作FG⊥x轴，垂足为G．∵点E与点B关于y轴对称，

∴∠OBC=∠OEC．

∴∠OBC=∠GEF．

∵∠PBA= ∠OBC，

∴∠PBA=∠EFB．

∴EF=EB=4．

∵OE=2，OC= ，

∴EC= ．

∵GF∥OC，

∴△FGE∽△COE．

∴ = = ，即= = ，

解得：FG= ，EG= ，

∴F（﹣，）．

设BP的解析式为y=kx+b，将点F和点B的坐标代入得：，解得：k=﹣，b=1，

∴直线BP的解析式为y=﹣x+1．