定积分在几何中的应用教案

定积分在几何中的简单应用授课班级:高二(5)班授课人:石林红
一.教学目标
【知识与技能目标】通过本节课的探究,学生能够应用定积分解决不太规则的平面图形的面积,能够初步掌握应用定积分解决实际问题的基本思想和方法。
【过程与方法目标】探究过程中通过数形结合的思想,加深对知识的理解,同时体会到数学研究的基本思路和方法。
【情感、态度与价值观目标】探究式的学习方法能够激发学生的求知欲,培养学生对学习的浓厚兴趣;探究式的学习过程能够培养学生严谨的科学思维习惯和方法,培养学生勇于探索和实践的精神;探究过程中对学生进行数学美育的渗透,用哲学的观点指导学生自主探究。
二.教学重点
难点
【教学重点】应用定积分解决平面图形的面积,使学生在解决问题的过程中体会定积分的价值。
【教学难点】如何恰当选择积分变量和确定被积函数。
三.教学方法
教学方法是“问题诱导——启发讨论——探索结果”、“直观观察——抽象归纳——总结规律”的一种研究性教与学的方法,过程中注重“诱、思、探、练”的结合,从而引导学生转变学习方式。
(一)复习引入:
1.复习定积分的概念、定积分的计算、定积分的几何意义.
2.热身训练:计算
dx
x
?--
2
2
2
42.计算?-2
2
sin
π
π
dx
x
(二).精讲点拨
1.几种典型的平面图形面积的计算:
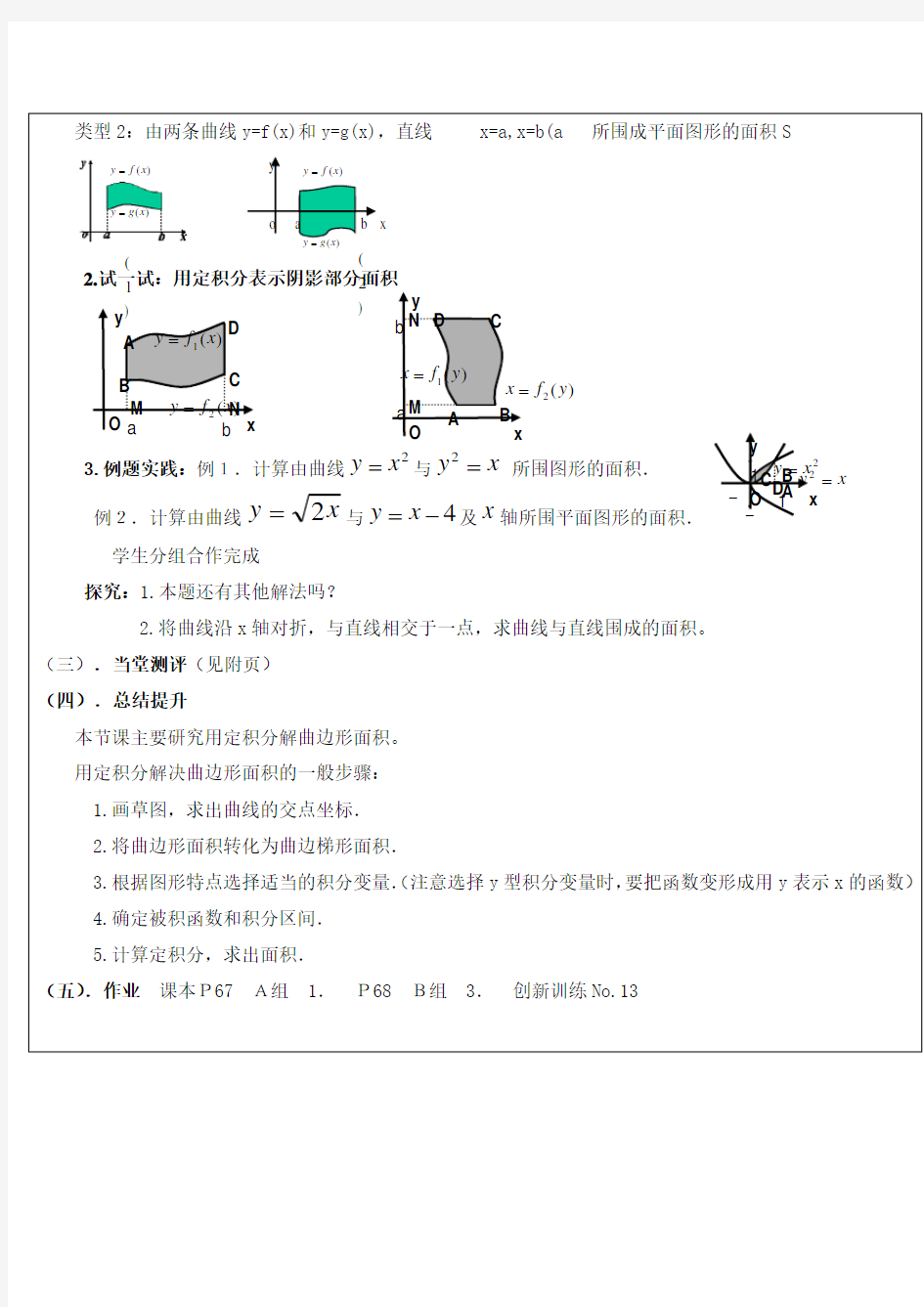
类型1:求由一条曲线y=f(x)和直线x=a,x=b(a ( 2 ) x y o a b c )(x f y= 3 ) 1 ) x y o ) (x f y= a b 类型2:由两条曲线y=f(x)和y=g(x),直线 x=a,x=b(a 2.试一试:用定积分表示阴影部分面积 3.例题实践:例1.计算由曲线 2x y =与x y =2 所围图形的面积. 例2.计算由曲线x y 2=与4-=x y 及x 轴所围平面图形的面积. 学生分组合作完成 探究:1.本题还有其他解法吗? 2.将曲线沿x 轴对折,与直线相交于一点,求曲线与直线围成的面积。 (三).当堂测评(见附页) (四).总结提升 本节课主要研究用定积分解曲边形面积。 用定积分解决曲边形面积的一般步骤: 1.画草图,求出曲线的交点坐标. 2.将曲边形面积转化为曲边梯形面积. 3.根据图形特点选择适当的积分变量.(注意选择y 型积分变量时,要把函数变形成用y 表示x 的函数) 4.确定被积函数和积分区间. 5.计算定积分,求出面积. (五).作业 课本P67 A组 1. P68 B组 3. 创新训练No.13 x y N M O a b A B C D )(1x f y =)(2x f y =x y O A B C D 2x y = x y =2 1 1 --x y N M O a b A B C D )(1y f x =)(2y f x =y x o b a )(x f y =)(x g y =(2) )(x f y =)(x g y =(1) 教学设计 定积分在几何中的简单应用 选送学校:南海九江中学 设计教师:林洁 《定积分》教学设计与反思 学习目标 1、通过实例,直观了解微积分基本定理的含义,会用牛顿-莱布尼兹公式求简单的定积分. 2、通过实例体会用微积分基本定理求定积分的方法. 教学重点:通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分. 教学难点:了解微积分基本定理的含义. 一、自主学习: 1.定积分的定义:, 2.定积分记号: 思想与步骤 几何意义. 3.用微积分基本定理求定积分 二、新知探究 新知1:微积分基本定理: 背景:我们讲过用定积分定义计算定积分,但如果要计算,其计算过程比较复杂,所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法,也是比较一般的方法。 探究问题1:变速直线运动中位置函数S(t)与速度函数v(t)之间的联系 设一物体沿直线作变速运动,在时刻t时物体所在位移为S(t),速度为v(t)(), 则物体在时间间隔内经过的位移记为,则 一方面:用速度函数v(t)在时间间隔求积分,可把位移= 另一方面:通过位移函数S(t)在的图像看这段位移还可以表示为 探究问题2: 位移函数S(t)与某一时刻速度函数v(t)之间的关系式为 上述两个方面中所得的位移可表达为 上面的过程给了我们启示 上式给我们的启示:我们找到了用的原函数(即满足)的数值差来计算在上的定积分的方法。 定理如果函数是上的连续函数的任意一个原函数,则 该式称之为微积分基本公式或牛顿—莱布尼兹公式。它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁。它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法。 例1.计算下列定积分: 新知2:用定积分几何意义求下列各式定积分: 若求 新知3:用定积分求平面图形的面积 1、计算函数在区间的积分 2、计算函数在区间的积分 3、求与在区间围成的图形的面积 通过此题的计算你发现了什么? 教学反思 本课的教学设计,是在新课程标准理念指导下,根据本班学生实际情况进行设计的。从实施情况来看,整堂课学生情绪高涨、兴趣盎然。在教学中,教师一改往日应用题教学的枯燥、抽象之面貌,而是借用学生已有的知识经验和生活实际,有效地理解了微积分的基本定理,具体反思如下: 1、改变定理的表述形式,丰富信息的呈现方式。 根据高中学生的认知特点,我在教学过程中,出示例题、习题时,呈现形式力求多样、新颖,让学生多种感官一起参与,以吸引学生的注意力,培养对数学的兴趣。本课的教学中,我大胆地改变了教材中实例分析顺序,重组和创设了这样一个情境,从而引入速度关于时间的定积分背景,即切合学生的生活实际,又让学生发现了定理的实际意义,理解了定理的本质,激发了学生学习的兴趣。并更好地为下一环节的自主探索、主动发展作好充分的准备。 2、突出数学应用价值,培养学生的应用意识和创新能力 《数学课程标准》中指出,要让学生能够“初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中和其他学科学习中的问题,增强应用数学的意识。”本课的设计充分体现了这一理念,例题中涉及路程和速度,让学生感受到数学与生活的密切联系,通过自己的探究,运用数学的思维方式解决问题,又能运用掌握的知识去研究解决生活的其它数学问题,,培养了学生的应用意识。 教学题目: 选修2-2 1.7.1定积分在几何中的应用 教学目标: 一、知识与技能: 1.让学生深刻理解定积分的几何意义以及微积分的基本定理; 2.通过本节课的探究,学生能够应用定积分解决不太规则的平面图形的面积,能够初步掌握应用定积分解决实际问题的基本思想和方法 3.初步掌握利用定积分求曲边梯形的几种常见题型及方法 二、过程与方法: 1. 探究过程中通过数形结合的思想,加深对知识的理解,同时体会到数学研究的基本思路和方法。 三、情感态度与价值观: 探究式的学习方法能够激发学生的求知欲,培养学生对学习的浓厚兴趣;探究式的学习过程能够培养学生严谨的科学思维习惯和方法,培养学生勇于探索和实践的精神; 教学重点: 应用定积分解决平面图形的面积,使学生在解决问题的过程中体会定积分的价值。 教学难点: 如何恰当选择积分变量和确定被积函数。 课型、课时: 新课,一课时 教学工具: 常用教具,多媒体,PPT课件 教学方法: 引导法,探究法,启示法 教学过程 积分?b a f (x )dx 在几何上表示 x =a 、x =b 与x 轴所围成的曲边梯形 的面积。 当f (x )≤0时由y =f (x )、x =a 、x =b 与 x 轴所围成的曲边梯形面积的负值 类型1.求由一条曲线y=f(x)和直线x=a,x=b(a 定积分的几何应用例题与习题 、曲线 的极坐标方程 1 cos ,(0 ), 求该曲线在 所对应的点处的切线 的 1 4 L 2 直角坐标方程,并求曲线 、切线 L 与x 轴所围图形的面积。 2、设直线 y ax 与抛物线 y x 2 所围成的面积为 S 1,它们与直线 x 1所围成的 面积为 S 2 ,并且 a 1 (1)试确定 a 的值,使 S 1 S 2达到最小,并求出最小值; (2)求该最小值所对应的平面图形绕 x 轴旋转一周所得旋转体的体积。 、设 平面上有正方形 D ( x, y) 0 x 1,0 y 1 及直线 L : x y t (t 0) 3 xoy x 若 S(t)表示正方形 D 位于直线 l 左下部分的面积 ,试求 S(t )dt (x 0) 4、 求由曲线 x sin ( 0) 与 轴所围图形绕 轴旋转所得旋转体的体积 y e x x x x V x 5、求由曲线 x a cos 3 t 与直线 y=x 及 y 轴所围成的图形 y asin 3 t ( a 0, 4 t 2 ) 绕 x 轴旋转所得立体的全表面积。 ( S=( 11 2 ) a 2 ) 5 40 6. 曲线 y e x e x 与直线 x 0, x t(t 0)及 y 0围成一曲边梯形,该曲边梯 2 形绕 x 轴旋转一周得一旋转体,其体积为 V (t), 侧面积为 S(t),在 x t 处的底面积为 F (t ) 求 S(t) 的值; 计算极限 S(t ) (1) (2) lim V (t) t F (t ) S(t ) 2, lim S(t ) 1 V (t ) F (t) t 7、求由摆线 x= a(t sin t) ,y= 的一拱 (0 t 2 ) 与横轴所围成的平面图形的面积, a(1 cost) 及该平面图形分别绕 x 轴、 y 轴旋转而成的旋转体的体积。 (1)A 3 a 2 , (2)V x 5 2 a 3 , (3)V y 6 3 a 3 8、设平面图形 由 x 2 y 2 2 x 及 y 所确定,求图形 绕直线 x 2 旋转一周所得 A x A 旋转体的体积。 2 V 2 2 3 第六章定积分的应用 教学目的 1、理解元素法的基本思想; 2、掌握用定积分表达和计算一些几何量(平面图形的面积、平面曲线的弧长、旋转体的体 积及侧面积、平行截面面积为已知的立体体积)。 3、掌握用定积分表达和计算一些物理量(变力做功、引力、压力和函数的平均值等)。教学重点: 1、计算平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知 的立体体积。 2、计算变力所做的功、引力、压力和函数的平均值等。 教学难点: 1、截面面积为已知的立体体积。 2、引力。 §6. 1 定积分的元素法 回忆曲边梯形的面积: 设y=f (x)≥0 (x∈[a,b]).如果说积分, ?=b a dx x f A) (是以[a,b]为底的曲边梯形的面积,则积分上限函数 ?=x a dt t f x A)( ) ( 就是以[a,x]为底的曲边梯形的面积.而微分dA(x)=f (x)dx表示点x处以dx为宽的小曲边梯形面积的近似值?A≈f (x)dx, f (x)dx称为曲边梯形的面积元素. 以[a,b]为底的曲边梯形的面积A就是以面积元素f(x)dx为被积表达式,以 [a,b]为积分区间的定积分: ?=b a dx x f A) (. 一般情况下,为求某一量U,先将此量分布在某一区间[a,b]上,分布在[a,x]上的量用函数U(x)表示,再求这一量的元素dU(x),设dU(x)=u(x)dx,然后以u(x)dx为被积表达式,以[a,b]为积分区间求定积分即得 ?=b a dx x f U) (.用这一方法求一量的值的方法称为微元法(或元素法). §6. 2 定积分在几何上的应用 一、平面图形的面积 1.直角坐标情形 设平面图形由上下两条曲线y =f 上(x )与y =f 下(x )及左右两条直线x =a 与x =b 所围成, 则面积元素为[f 上(x )- f 下(x )]dx , 于是平面图形的面积为 dx x f x f S b a ?-=)]()([下上. 类似地, 由左右两条曲线x =?左(y )与x =?右(y )及上下两条直线y =d 与y =c 所围成设平面图形的面积为 ?-=d c dy y y S )]()([左右??. 例1 计算抛物线y 2=x 、y =x 2所围成的图形的面积. 解 (1)画图. (2)确定在x 轴上的投影区间: [0, 1]. (3)确定上下曲线: 2)( ,)(x x f x x f ==下上. (4)计算积分 31]3132[)(10323102=-=-=?x x dx x x S . 例2 计算抛物线y 2=2x 与直线y =x -4所围成的图形的面积. 解 (1)画图. (2)确定在y 轴上的投影区间: [-2, 4]. (3)确定左右曲线: 4)( ,2 1)(2+==y y y y 右左??. (4)计算积分 ?--+=422)2 14(dy y y S 18]61421[4232=-+=-y y y . 例3 求椭圆12222=+b y a x 所围成的图形的面积. 解 设整个椭圆的面积是椭圆在第一象限部分的四倍, 椭圆在第一象限部分在x 轴上的投影区间为[0, a ]. 因为面积元素为ydx , 所以 ?=a ydx S 04. 椭圆的参数方程为: x =a cos t , y =b sin t , 于是 ?=a ydx S 04?=0 )cos (sin 4πt a td b 定积分的概念教案 人教A版必修一教材 教材内容分析微积分的出现和发展,极大的推动了数学的发展,同时也推动了天文学、力学、物理学、化学、生物学等自然科学、社会科学及应用科学各个分支中的发展。本节课是定积分概念的第一节课,教材借助求曲边梯形的面积和物理中变速直线运动的路程,通过直观具体的实例引入到定积分的学习中,为定积分概念构建认知基础,为理解定积分概念及几何意义起到了铺垫作用,同时也为今后进一步学习微积分打下基础。 学生情况分析 本节课的教学对象是本校实验班学生,学生思维比较活跃,理解能力、运算能力和学习交流能力较强。学生前面已经学习了导数,并利用导数研究函数的单调性、极值及生活中的优化问题等,渗透了微分思想。从学生的思维特点看,比较容易把刘徽的“割圆术”与本节课知识联系到一起,能够初步了解到“以直代曲”和“无限逼近”的重要数学思想,但是在具体的“以直代曲”过程中,如何选择适当的直边图形来代替曲边梯形会有一些困难。在对“极限”和“无限逼近”的理解,即理解为什么将直边图形面积和取极限正好是曲边梯形面积的精确值及在对定积分定义的归纳中符号的理解上也会有一些困难。 教学目标 1.从物理问题情境中了解定积分概念的实际背景,初步掌握求曲边梯形的面积的方法和步骤:分割、近似代替、求和、取极限; 2.经历求曲变梯形面积的过程,借助几何直观体会“以直代曲”和“逼近”的思想,学习归纳、类比的推理方式,体验从特殊到一般、从具体到抽象、化归与转化的数学思想; 3.认同“有限与无限的对立统一”的辩证观点,感受数学的简单、简洁之美. 教学重点直观体会定积分的基本思想方法:“以直代曲”、“无限逼近”的思想; 初步掌握求曲边梯形面积的方法步骤——“四步曲”(即:分割、近似代替、求和、取 极限) 教学难点对“以直代曲”、“逼近” 思想的形成过程的理解. 教学方式教师适时引导和学生自主探究发现相结合. 辅助工具投影展台,几何画板. 教学过程 引入新课问题:汽车以速度v做匀速直线运动时,经过时间t所行驶的路程为 S vt =.如果汽车作变速直线运动,在时刻t的速度为()2 v t t=(单 位:km/h),那么它在0≤t≤1(单位:h)这段时间内行驶的路程S (单位:km)是多少? 创设情境,引入 这节课所要研究的 问题. 类比探究,形成方法如图,阴影部分类似于一个梯形,但有一边是曲线() y f x =的一 段,我们把由直线,(),0 x a x b a b y ==≠=和曲线() y f x =所围 成的图形称为曲边梯形. 如何计算这个曲边梯形的面积? (1)温故知新,铺垫思想 问题1:我们在以前的学习经历中有没有用直边 图形的面积计算曲边图形面积这样的例子? 问题2:在割圆术中为什么用正多边形的面积计算圆的面积?为什么 要逐次加倍正多边形的边数? (2)类比迁移,分组探究 问题3:能不能类比割圆术的思想和操作方法把曲边梯形的面积问题 转化为直边图形的面积问题? 学生活动:学生进行分组讨论、探究。 (3)汇报比较,形成方法 学生需要用原有的 知识与经验去同化 或顺应当前要学习 的新知识,所以问 题1引导学生回忆 割圆术的作法,通 过问题2引导学生 思考割圆术中的思 想方法----“以直代 曲”,和“无限逼 近”。 通过问题3激 发学生探索的愿 望,明确解决问题 的方向。 高中数学 定积分的简单应用教案 选修2-2 一:教学目标 知识与技能目标 1、 进一步让学生深刻体会“分割、以直代曲、求和、逼近”求曲边梯形的思想方法; 2、 让学生深刻理解定积分的几何意义以及微积分的基本定理; 3、 初步掌握利用定积分求曲边梯形的几种常见题型及方法; 4、 体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。 过程与方法 情感态度与价值观 二:教学重难点 重点 曲边梯形面积的求法 难点 定积分求体积以及在物理中应用 三:教学过程: 1、复习 1、求曲边梯形的思想方法是什么? 2、定积分的几何意义是什么? 3、微积分基本定理是什么? 2、定积分的应用 (一)利用定积分求平面图形的面积 例1.计算由两条抛物线2 y x =和2 y x =所围成的图形的面积. 【分析】两条抛物线所围成的图形的面积,可以由以两条曲线所对应的曲边梯形的面积的差得到。 解:2 01y x x x y x ?=??==?=??及,所以两曲线的交点为(0,0)、(1,1),面积S=1 1 20 0xdx x dx = -? ?,所以 ?1 20S =(x -x )dx 32 1 3023 3x x ??=-????=13 【点评】在直角坐标系下平面图形的面积的四个步骤: 1.作图象;2.求交点;3.用定积分表示所求的面积;4.微积分基本定理求定积分。 巩固练习 计算由曲线3 6y x x =-和2 y x =所围成的图形的面积. 例2.计算由直线4y x =-,曲线2y x = 以及x 轴所围图形的面积S. 分析:首先画出草图(图1.7 一2 ) ,并设法把所求图形的面积问题转化为求曲边梯 2 x y =y x A B C D O 1.7.1定积分在几何中的应用 学习目标: 1.体会“分割、以直代曲、求和、逼近”求曲边梯形面积的思想方法; 2.初步掌握利用定积分求曲边梯形的几种常见题型及方法; 3.理解定积分的几何意义以及微积分的基本定理。 学习方法: 情境一:展示精美的赵州桥图片,讲述古代数学家的故事及伟大发现:拱形的面积 问题1:桥拱与水面之间的切面的面积如何求解呢? 问题2:需要用到哪些知识?(定积分) 问题3:求曲边梯形的思想方法是什么? 问题4:定积分的几何意义是什么? 问题5:微积分基本定理是什么? 情境二:利用定积分求平面图形的面积 例1. 计算由两条抛物线2 y x =和2 y x =所围成的图形的面积. 问题1:你能在平面直角坐标系内画出两条抛物线吗? 问题2:能在图中找出所要求的图形吗?(用阴影部分表示出来) (如右图) 问题3:这个图形以前见过吗?有没有直接的公式求它的面积吗? 问题4:既然没有直接的公式求其面积,那能不能转化成我们学过的曲边梯形的面积来间接求解呢?(可看做两个曲边梯形的面积之差,进而可以用定积分来解决) 解:解方程组?????==2 2x y x y 得到交点横坐标为0=x 或1=x x y O A B C D 2 x y =x y =2 1 1 -1 -1 4 x y O 8 4 2 2 ∴ OABD OABC S S S 曲边梯形曲边梯形-=dx x ? = 1 dx x ?-1 2 1031 0233132x x -=313132=-= 情境三 学生探究: 例2.计算由直线4y x =-,曲线y =x 轴所围图形的面积S. 分析:模仿例1,先画出草图(左图),并设法把所求图形的面积问题转化为求曲边梯形的面积问题. 问题1:阴影部分图形是曲边梯形吗? 问题2:不是曲边梯形怎么办?能否构造出曲边梯形来呢? 问题3:如果转化成两部分的面积和,应该怎样作辅助线?(过点(4,0)作x 轴的垂线将阴影部分分为两部分) 问题4:两部分面积用定积分分别应该怎样表示?(注意积分上下限的确定) 问题5:做辅助线时应该注意什么?(尽量将曲边图形转化成我们熟悉的平面图形,如三角形、矩形、梯形和曲边梯形组合成的图形.) 规范的解题过程此处略去 思考:1.本题还有没有其它的解决方案?(可以将此阴影部分看做一个曲边梯形和一个三角形的面积之差) 2.上面的解法是将x 看作积分变量,能不能将y 看作积分变量?尝试解决之。 情境四:结合以上两个例题,总结利用定积分求平面图形面积的基本步骤。 解由曲线所围的平面图形面积的解题步骤: 1.画草图,求出曲线的交点坐标 2.将曲边形面积转化为曲边梯形面积 3.根据图形特点选择适当的积分变量 4.确定被积函数和积分区间 5.计算定积分,求出面积. 定积分的几何应用例题与习题 11cos ,(0),2 4 L π π ρθθθΓ=+≤≤ = Γ、曲线的极坐标方程求该曲线在所对应的点处的切线的 直角坐标方程,并求曲线、切线L 与x 轴所围图形的面积。212122,1,1 (1)2y ax y x S x S a a S S x ===<+、设直线与抛物线所围成的面积为它们与直线所围成的 面积为并且试确定的值,使达到最小,并求出最小值; ()求该最小值所对应的平面图形绕轴旋转一周所得旋转体的体积。 {}0 3(,)01,01:(0) (),()(0) x xoy D x y x y L x y t t S t D l S t dt x =≤≤≤≤+=≥≥?、设平面上有正方形及直线若表示正方形位于直线左下部分的面积试求 4 、0)x y e x x -=≥求由曲线与轴所围图形绕x 轴旋转所得旋转体的体积V 3 3 2cos (0,)42sin 11)5x a t a t y a t a πππ?=?>≤≤?=??5、求由曲线与直线y=x 及y 轴所围成的图形绕x 轴旋转所得立体的全表面积。(S=( 6.0,(0)02 (),()() ()()(1)(2)lim () ()()() 2,lim 1 () ()x x t t e e y x x t t y x V t S t x t F t S t S t V t F t S t S t V t F t -→+∞→+∞+===>=====曲线与直线及围成一曲边梯形,该曲边梯 形绕轴旋转一周得一旋转体,其体积为侧面积为,在处的底面积为求的值;计算极限22333 (sin )(1cos )3, (2)5, (3)6x y a t t a t a V a V a ππππ--≤≤===7、求由摆线x=,y=的一拱(0t 2)与横轴所围成的平面图形的面积,及该平面图形分别绕x 轴、y 轴旋转而成的旋转体的体积。(1)A 222 222 23 A x y x y x A x V ππ+≤≥== -8、设平面图形由及所确定,求图形绕直线旋转一周所得旋转体的体积。 《数学分析》 之九 第九章定积分(14+4学时) 教学大纲 教学要求: 1.理解Riemann定积分的定义及其几何意义 2.了解上和与下和及其有关性质 3.理解函数可积的充要条件,了解Riemann可积函数类 4.熟练掌握定积分的主要运算性质以及相关的不等式 5.了解积分第一中值定理 6.掌握变上限积分及其性质 7.熟练掌握Newton-Leibniz公式,定积分换元法,分部积分法 教学内容: 问题的引入(曲边梯形的面积及变速直线运动的路程),定积分定义,几何意义,可积的必要条件,上和、下和及其性质,可积的充分条件,可积函数类,定积分的性质,积分中值定理,微积分学基本定理,牛顿一莱布尼兹公式,定积分的换元法及分部法。 第页 此表2学时填写一份,“教学过程”不足时可续页 第页 =i 1 。 则称函数)(x f 在[b a .]上可积或黎曼可积。数J 称为函数)(x f 在[b a .]上 的定积分或黎曼积分,记作: ?=b a dx x f J )( 其中)(x f 称为被积函数,x 称为积分变量,[b a .]称为积分区间,dx x f )(称为被积式,b a ,分别称为积分的下限和上限。 定积分的几何意义; 连续函数定积分存在(见定理9.3) 三、举例: 例1 已知函数 在区间 上可积 .用定义求积分 . 解 取 等分区间 作为分法 n b x T i = ?, 取 .= . 由函数)(x f 在区间],0[b 上可积 ,每个特殊积分和之极限均为该积分值 . 例2 已知函数2 11 )(x x f += 在区间]1,0[上可积 ,用定义求积分 . 解 分法与介点集选法如例1 , 有 . 上式最后的极限求不出来 , 但却表明该极限值就是积分 3.1定积分的应用:平面图形的面积 教材分析: 《定积分的简单应用》是人教版选修2-2第1章第7节的内容,从题目中可以看出这节教学的要求,就是让学生在充分认识导数与积分的概念、计算、几何意义的基础上,掌握用积分手段解决实际问题的基本思想和方法,从而进一步认识到数学知识的实用价值以及数学在实际应用中的强大生命力。在整个高中数学体系中,这部分内容也是学生在高等学校进一步学习数学的基础。 教学构思:应用型的课题是培养学生观察分析、发现、概括、推理和探索能力的极好素材,本节课通过创设情景、问题探究、抽象归纳、巩固练习、应用提升等探究性活动,培养学生的数学创新精神和实践能力,使学生们掌握定积分解题的规律,体会数学学科研究的基本过程与方法。 学情分析:知识层面,学生已经学习了定积分的定义,由来及微积分基本定理。在定积分与曲边梯形面积关系中,许多学生默认相等,这就与定积分本质相违背。能力层面,学生有一定的推理和探索能力,面对知识点,学生还需有归纳概括的能力。还需体会数学学科研究的基本过程与方法。情感层面,学生对数学新内容的学习有相当的兴趣和积极性,但探究问题的能力以及合作交流等方面发展不够均衡,有待加强。 教学理念:以学生发展为主线。新型的教学方式,新型的呈现方式。 教学目标: 知识与技能: 1.理解定积分的几何意义,会通过定积分求由两条或多条曲线围成的图形的面积. 2.掌握利用定积分求曲边梯形面积的几种常见题型及方法. 过程与方法:通过体验解决问题的过程,体现定积分的使用价值,加强观察能力和归纳能力,强化数形结合和化归思想的思维意识,达到将数学和其他学科进行转化融合的目的。 情感态度与价值观:通过教学过程中的观察思考总结,养成自主学习的良好学习习惯,培养数学知识应用于生活的意识。 定积分在几何学上的应用 ( 比赛课教案 ) 教学题目: 选修 2-2 1.7.1定积分在几何中的应用 教学目标: 一、知识与技能: 1.让学生深刻理解定积分的几何意义以及微 积分的基本定理; 2.通过本节课的探究,学生能够应用定积分解决不太规则的平面图形的面积,能够初步掌握应用定积分解决实际问题的基本思想和方法 3.初步掌握利用定积分求曲边梯形的几种常见题型及方法 二、过程与方法: 1.探究过程中通过数形结合的思想,加深对知识的理解,同时体会到数学研究的基本思路和方法。 三、情感态度与价值观: 探究式的学习方法能够激发学生的求知欲,培养学生对学习的浓厚兴趣;探究式的学习过程能够培养学生严谨的科学思维习惯和方法,培养学生勇于探索和实践的精神; 教学重点: 应用定积分解决平面图形的面积,使学生在解决问题的过程中体会定积分的 价值。 教学难点: 如何恰当选择积分变量和确定被积函数。 课型、课时: 新课,一课时 教学工具: 常用教具,多媒体, PPT课件 教学方法: 引导法,探究法,启示法 教学过程 当 f(x) 0 时,积分 b y=f (x)、 f (x)dx 在几何上表示由x a a、x b 与 x 轴所围成的曲边梯形的面积。 y f (x) O a b x O a b x y f (x) 当 f ( x) b f (x)dx 在几何上表示y f ( x)、x a、x b 与 x 轴 0时由积分 a b f ( x ) dx c f ( x ) dx b f ( x ) dx 。 所围成的曲边梯形面积的负值 a S a c 类型 1. 求由一条曲线 y=f(x) 和直线 x=a,x=b(a 课 题: 定积分的几何应用 目的要求: 掌握定积分的微分元素法 掌握利用定积分求平面图形面积的方法 掌握利用定积分求体积的方法 掌握利用定积分求弧长的方法 教学重点: 利用定积分求面积和体积的方法 教学难点: 利用定积分求面积和体积的方法 教学课时:4 教学方法:讲练结合 教学内容与步骤: 定积分解题的条件: (1) 所求量(设为 F )与一个给定区间 [a,b]有关,且在该区间上具有可加性. 就是说,F 是确定于 [a,b]上的整体量,当把 [a,b]分成许多小区间时,整体量等于各部分量之和,即1 n i i F F == ∑ . (2) 所求量 F 在区间 [a,b]上的分布是不均匀的,也就是说, F 的值与区间 [a,b]的长不成正比.(否则的话, F 使用初等方法即可求得,而勿需用积分方法了) 用定积分概念解决实际问题的四个步骤: 第一步:将所求量 F 分为部分量之和,即: 1 Δn i i F F ==∑; 第二步:求出每个部分量的近似值, Δi F ≈()Δ(1,2,,);i i f x i n ξ=L 第三步:写出整体量 F 的近似值,1 Δn i i F F == ∑≈1 ()Δn i i i f x ξ=∑; 第四步:取max{Δ}0i x λ=→时的 1 ()Δn i i i f x ξ=∑极限,则得 1 lim ()Δ()d n b i i a i F f x f x x λξ→===∑?. 观察上述四步我们发现,第二步最关键,因为最后的被积表达式的形式就是在这一步被确定的,这只要把近似式()Δi i f x ξ中的变量记号改变一下即可( i ξ换为x ;i x ?换为 dx ). 而第三、第四两步可以合并成一步:在区间 [a,b]上无限累加,即在 [a,b]上积分. 至于第一步,它只是指明所求量具有可加性,这是 F 能用定积分计算的前提,于是,上述四步简化后形成实用的微元法. 定积分应用的微元法: (一) 在区间 [a,b]上任取一个微小区间 [],d x x x +,然后写出在这个小区间上的部分量ΔF 的近似值,记为d ()d F f x x =(称为 F 的微元); (二) 将微元dF 在[a,b]上积分(无限累加),即得: ()d .b a F f x x =? 微元法中微元的两点说明: (1) ()d f x x 作为ΔF 的近似值表达式,应该足够准确,确切的说,就是要求其差是关于Δx 的高阶无穷小. 即 Δ()d (Δ)F f x x o x -=.这样我们就知道了,称作微元的量 ()d f x x ,实际上是所求量的微分 dF; (2) 具体怎样求微元呢? 这是问题的关键,这要分析问题的实际意义及数量关系,一般按着在局部 [],d x x x + 上,以“常代变”、“匀代不匀”、“直代曲”的思路(局部线性化),写出局部上所求量的近似值,即为微元 d ()d F f x x = . 用定积分求平面图形的面积 1. 直角坐标系下的面积计算 用微元法不难将下列图形面积表示为定积分. (1) 曲线()(()0),y f x f x =≥,x a x b ==及 OX 轴所围图形,如下页左图,面积微元d ()d A f x x =,面积()d b a A f x x = ? . (2) 由上、下两条曲线(),()(()())y f x y g x f x g x ==≥及,x a x b ==所围成的图形,如下页右图,面积微元d [()()]d ,A f x g x x =-,面积[()()]d b a A f x g x x = -? . (3)由左右两条曲线(),()x y x y ψ?==及,y c y d ==所围成图形(图见下左)面积微元(注意,这时就应取横条矩形 dA ,即取 y 为积分变量) 定积分的简单应用 一:教学目标 知识与技能目标 1、 进一步让学生深刻体会“分割、以直代曲、求和、逼近”求曲边梯形的思想方法; 2、 让学生深刻理解定积分的几何意义以及微积分的基本定理; 3、 初步掌握利用定积分求曲边梯形的几种常见题型及方法; 4、 体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。 过程与方法 情感态度与价值观 二:教学重难点 重点 曲边梯形面积的求法 难点 定积分求体积以及在物理中应用 三:教学过程: 1、复习 1、求曲边梯形的思想方法是什么? 2、定积分的几何意义是什么? 3、微积分基本定理是什么? 2、定积分的应用 (一)利用定积分求平面图形的面积 例1.计算由两条抛物线2 y x =和2 y x =所围成的图形的面积. 【分析】两条抛物线所围成的图形的面积,可以由以两条曲线所对应的曲边梯形的面积的差得到。 解:2 01y x x x y x ?=??==?=??及,所以两曲线的交点为(0,0)、(1,1),面积S=1 1 20 xdx x dx = -? ?,所以 ?1 20S =(x -x )dx 32 1 3023 3x x ??=-????=13 【点评】在直角坐标系下平面图形的面积的四个步骤: 1.作图象;2.求交点;3.用定积分表示所求的面积;4.微积分基本定理求定积分。 巩固练习 计算由曲线3 6y x x =-和2 y x =所围成的图形的面积. 例2.计算由直线4y x =-,曲线2y x =以及x 轴所围图形的面积S. 分析:首先画出草图(图1.7 一2 ) ,并设法把所求图形的面积问题转化为求曲边梯 2 x y =y x A B C D O 1.7.1 定积分在几何中的应用 主讲:XXXX 卞志业 教学目标: 1、 进一步让学生深刻体会“分割、以直代曲、求和、逼近”求曲边梯形的思想方法; 2、 让学生深刻理解定积分的几何意义以及微积分的基本定理; 3、 初步掌握利用定积分求曲边梯形的几种常见题型及方法; 教学重难点: 重点 曲边梯形面积的求法 难点 定积分求体积以及在物理中应用 教学过程: 一、复习回顾 1.微积分基本定理是什么? 学生回答:若函数f(x)在区间[a,b]上连续, ,这就是微积分基本定理,又叫牛顿—莱布尼茨公式。 2.定积分的几何意义是什么? 学生回答: x=a 、x=b 与 x 轴所围成的曲边梯形的面积。 需要注意的是:当f(x)≤0时,由y=f (x)、x=a 、x=b 与 x 轴所围成的曲边梯形位于 x 轴的下方。 ,那么并且)()(x f x F ='? -=b a a F b F dx x f )()()( 当f (x )≥0时,积分dx x f b a )(?在几何上表示由y =f (x )、 a b y f (x) ()b a S f x dx =?即:O x y x y O a b y f (x) ()b a S f x dx =-?即: 二、例题讲解 例1.计算由两条抛物线2y x =和2y x =所围成的图形的面积. 【分析】从图像中可以看出:两条抛物线所围成的图形的面积,可以由以两条曲线所对应的曲边梯形的面积的差得到。 解:2 01y x x x y x ?=??==?=??及,所以两曲线的交点为 (0,0)、(1,1), 面积S=S曲边梯形OABC-S曲边梯形OABD 1 1 2 xdx x dx =-? ? 【点评】 求两曲线围成的平面图形面积的一般步骤: (1)画草图,求出曲线的交点坐标; (2)将曲边形面积转化为曲边梯形面积; (3)确定被积函数及积分区间; (4)计算定积分,求出面积。 例2计算由直线y 2x = 曲线y x 4,=-以及x 轴所围图形的面积S. 【分析】 1 2 332x = 1 0331x -= = 323 1-31 4 x y O 8 4 2 2 B x y 2=4 -=x y S 2 S 1 S 2 S 1 4 y O 8 4 2 2 A ? ? ? ?????-+= +=??442122844 21dx x dx x s s s A: 4 42 1 28 21??-= -=? dx x s s s B: 教学题目: 选修 2-2 1.7.1定积分在几何中的应用 教学目标: 一、知识与技能: 1.让学生深刻理解定积分的几何意义以及微积分的基本定理; 2.通过本节课的探究,学生能够应用定积分解决不太规则的平面图形的面积,能够初步掌握应用定积分解决实际问题的基本思想和方法 3.初步掌握利用定积分求曲边梯形的几种常见题型及方法 二、过程与方法: 1.探究过程中通过数形结合的思想,加深对知识的理解,同时体会到数学研究的基本思 路和方法。 三、情感态度与价值观: 探究式的学习方法能够激发学生的求知欲,培养学生对学习的浓厚兴趣;探究式的学习过程能够培养学生严谨的科学思维习惯和方法,培养学生勇于探索和实践的精神; 教学重点: 应用定积分解决平面图形的面积,使学生在解决问题的过程中体会定积分的价值。 教学难点: 如何恰当选择积分变量和确定被积函数。 课型、课时: 新课,一课时 教学工具: 常用教具,多媒体, PPT课件 教学方法: 引导法,探究法,启示法 教学过程 — b y=f (x) 、 x a 、 x b 与 x 轴所围成的曲边梯形 当 f(x) 0 时,积分 a f (x)dx 在几何上表示由 的面积。 y f (x) O a b x O a b x y f (x) 当 f ( x ) 0 时由 积分 b y f ( x ) 、x a 、x b 与 x 轴 f (x)dx 在几何上表示 a b c b f ( x ) dx 。 所围成的曲边梯形面积的负值 f ( x ) dx f ( x ) dx c a S a 类型 1. 求由一条曲线 y=f(x) 和直线 x=a,x=b(a 定积分的简单应用 教学目标 知识与技能: 初步掌握利用定积分求曲边梯形的几种常见题型及方法;体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。 过程与方法: 通过实例体会用微积分基本定理求定积分的方法 情感、态度与价值观: 通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力。 教学重点与难点 重点: 应用定积分的思想方法,解决一些简单的诸如求曲边梯形面积、变速直线运动的路程、变力作功等实际问题.在解决问题的过程中体验定积分的价值。 难点: 将实际问题化归为定积分的问题。 教学过程 给出教学目标: 应用定积分的思想方法,解决一些简单的诸如求曲边梯形面积、变速直线运动的路程、变力作功等实际问题.在解决问题的过程中体验定积分的价值。 一、复习回顾 1、定积分的几何意义 2、微积分基本定理内容 二、新课引入 如图. 问题1:图中阴影部分是由哪些曲线围成? 提示:由直线x=a,x=b和曲线y=f(x)和y=g(x)围成. 问题2:你能求得其面积吗?如何求? 三、新课讲解 (一)平面图形的面积 一般地,设由曲线y =f (x ),y =g (x )以及直线x =a ,x =b 所围成的平面图形的面积为S ,则 S =∫b a f (x )d x -∫ b a g (x )d x ,f (x )≥g (x ). 解题关键是根据图形确定被积函数以及积分上、下限. 考点一:求平面图形的面积 [例1] 求由抛物线y =x 2-4与直线y =-x +2所围成图形的面积. [一点通] 求由曲线围成图形面积的一般步骤: ①画图; ②求交点,确定积分上、下限; ③确定被积函数; ④将面积用定积分表示; ⑤用牛顿-莱布尼兹公式计算定积分,求出结果. 题组集训 1.(2011·湖南高考)由直线x =-π3,x =π3 ,y =0与曲线y =cos x 所围成的封闭图形的面积为 ( ) A.12 B .1 C. 32 D. 3 2.求y =-x 2与y =x -2围成图形的面积S . 3、求由曲线xy =1及直线x =y ,y =3所围成平面图形的面积. [一点通] 分割型图形面积的求解: (1)通过解方程组求出曲线的交点坐标 (2)将积分区间进行分段 (3)对各个区间分别求面积进而求和(被积函数均是由图像在上面的函数减去下面的函数) 第5节 定积分的几何应用举例(考点) 定积分的应用就是要用定积分计算某个量A : ()b a A f x dx =? 可见,量A 分布在区间[,]a b 上。在实际应用时,要求我们把[,]a b 和 ()f x 找出来。 [,]x a b ?∈,考虑 ()()x a A x f t dt =? ()A x 是A 在[,]a x 上的分布。 让x 有增量x ?使[,]x x a b +?∈。 ()()()A dA dx f x dx dx ?=+=+ A ?是A 在[][](),,x x x x x x +?+?或上的分布。 因此,用积分计算量A 的步骤如下: (1) 找到A 的分布区间[,]a b ; (2) ,[,]x x dx a b ?+∈,把A 在[][](),,x x dx x dx x ++或上的分布 量A ?计算成如下式子 ()()A f x dx dx ?=+即()dA f x dx = (3)算出定积分 ()b a A f x dx =? 以上步骤称为定积分应用的微元法。 5.1 平面图形的面积 5.1.1.直角坐标系中 连续曲线(),(),,y f x y g x x a x b ====所围图形的面积A 。 A 分布在[,]a b 区间上;,[,]x x dx a b ?+∈,在区间[,]x x dx +部分的面积()()()A f x g x dx dx ?=-+;所以 ()()b a A f x g x dx =-? 当()0,()0f x g x ≥≡时 ()b a A f x dx =? 【例5.1】 求由曲线e x y ,e x y 以及直线1x 围成的图形面积. 解、面积A 分布在[0,1]区间上;,[0,1]x x dx ?+∈, 在区间[,]x x dx +部分的面积()()x x A e e dx dx -?=-+;所以 ()1 1 1 2x x x x A e e dx e e e e ---??=-=+=+-?? ? 【例5.2】 求由曲线2 y x , 20x y 所围成图形的面积A . 解1 积; ,x x ?图5.1 y = 2 定积分的几何应用 定积分的几何应用 内容摘要 自十七世纪下半叶牛顿和莱布尼茨确定了微积分的基础以来,微积分已经经历了近四百年的发展,微积分不仅在数学领域,在现代科学各个领域都发挥了巨大的作用,微积分的思想更是达到了哲学的高度。可以预见,微积分在将来的应用会越来越广泛,越来越深入,但微积分由于其思想的复杂性、系统性,给使用者带来了不便,本文就微积分在数学几何领域的应用做了一些总结和创新,得出了在直角坐标系和极坐标系情况下,平面图形的面积、旋转体体积、光滑曲线的弧长和旋转曲面的面积的求解方法,以方便相关领域的人士在工作和学习中参考使用。。 【关键词】定积分几何坐标系面积体积弧长 The application of definite integral geometry Abstract Since the second half of the seventeenth Century the Newtonian and Leibniz to determine the basis of calculus, calculus has experienced nearly four hundred years of development, not only in the field of mathematics calculus, in modern scientific fields have played an important role, the calculus idea is to achieve a high degree of philosophy. Can foreknow, calculus in the future will be more widely used, more and more deeply, but due to the complexity of ideas of calculus, system, users have inconvenience, the calculus in mathematics geometry application some summary and innovation, derived in Cartesian coordinate and polar coordinate conditions, planar graph area, the volume of body of rotation, smooth arc length of a curve and a rotating surface area method, so as to facilitate the related people in the working and learning reference. 【Key words】Integral geometry coordinates area volume arc length《定积分》教学设计与反思
定积分在几何学上的应用(比赛课教案)
定积分的几何应用例题与习题.doc
定积分的应用教案
定积分的概念教案知识讲解
北师大版数学高二定积分的简单应用教案 选修2-2
《定积分在几何中的应用》教学教案
定积分的几何应用例题与习题
(完整版)定积分教案
定积分的应用教学设计比赛一等奖
定积分在几何学上的应用(比赛课教案).doc
高数教案_定积分应用
定积分在物理中的应用 说课稿 教案 教学设计
定积分在几何中的应用
定积分在几何学上的应用比赛课教学教案.docx
《定积分的简单应用》教案
定积分的几何应用举例
定积分的几何应用
